一 : 能力培养与测试五年级下册数学的答案有木有?
最佳答案可以吗?网友:惊叹号jay,评论时间:2013-06-11 14:34
4
二 : Miller-Rabin素数测试学习笔记
好几天前看了算导上的Miller-Rabin素数测试算法,今天正好总结一下,写写笔记。[www.61k.com)
说Miller-Rabin测试以前先说两个比较高效的求a*b% n 和 ab%n 的函数,这里都是用到二进制思想,将b拆分成二进制,然后与a相加(相乘)
// a * b % n
//例如: b = 1011101那么a * b mod n = (a * 1000000 mod n + a * 10000 mod n + a * 1000 mod n + a * 100 mod n + a * 1 mod n) mod n
ll mod_mul(ll a, ll b, ll n) {
ll res = 0;
while(b) {
if(b&1) res = (res + a) % n;
a = (a + a) % n;
b >>= 1;
}
return res;
}
//a^b % n
//同理
ll mod_exp(ll a, ll b, ll n) {
ll res = 1;
while(b) {
if(b&1) res = mod_mul(res, a, n);
a = mod_mul(a, a, n);
b >>= 1;
}
return res;
}
下面开始说Miller-Rabin测试:
费马小定理:对于素数p和任意整数a,有ap≡ a(mod p)(同余)。反过来,满足ap≡ a(mod p),p也几乎一定是素数。
伪素数:如果n是一个正整数,如果存在和n互素的正整数a满足 an-1≡ 1(mod n),我们说n是基于a的伪素数。如果一个数是伪素数,那么它几乎肯定是素数。
Miller-Rabin测试:不断选取不超过n-1的基b(s次),计算是否每次都有bn-1≡ 1(mod n),若每次都成立则n是素数,否则为合数。
伪代码:
Function Miller-Rabin (n : longint) :boolean;
begin
for i := 1 to s do
begin
a := random(n - 2) + 2;
if mod_exp(a, n-1, n) <> 1 then return false;
end;
return true;
end;
注意,MIller-Rabin测试是概率型的,不是确定型的,不过由于多次运行后出错的概率非常小,所以实际应用还是可行的。(一次Miller-Rabin测试其成功的概率为3/4)
前边说的伪代码实现很简短,下面还有一个定理,能提高Miller测试的效率:
二次探测定理:
如果p是奇素数,则 x2≡ 1(mod p)的解为 x = 1 || x = p - 1(mod p);
可以利用二次探测定理在实现Miller-Rabin上添加一些细节,具体实现如下:
bool miller_rabin(ll n) {
if(n == 2 || n == 3 || n == 5 || n == 7 || n == 11) return true;
if(n == 1 || !(n%2) || !(n%3) || !(n%5) || !(n%7) || !(n%11)) return false;
ll x, pre, u;
int i, j, k = 0;
u = n - 1; //要求x^u % n
while(!(u&1)) { //如果u为偶数则u右移,用k记录移位数
k++; u >>= 1;
}
srand((ll)time(0));
for(i = 0; i < S; ++i) { //进行S次测试
x = rand()%(n-2) + 2; //在[2, n)中取随机数
if((x%n) == 0) continue;
x = mod_exp(x, u, n); //先计算(x^u) % n,
pre = x;
for(j = 0; j < k; ++j) { //把移位减掉的量补上,并在这地方加上二次探测
x = mod_mul(x, x, n);
if(x == 1 && pre != 1 && pre != n-1) return false; //二次探测定理,这里如果x = 1则pre 必须等于 1,或则 n-1否则可以判断不是素数
pre = x;
}
if(x != 1) return false; //费马小定理
}
return true;
}前边这个算法经过测试还是比较靠谱的,可以用作模板。本菜也找过其他模板,可是有的居然把9测成素数,汗 -_-!
AC_Von 原创,转载请注明出处:
扩展:miller rabin素数测试 / millerrabin质数测试 / miller rabin素性测试
三 : 2013年南宁三中外地学生入学测试数学与答案
2013年南宁三中外地学生入学测试
(考试时间:2013年6月30日下午)
数 学
一、选择题(本大题共6小题,每小题4分,共24分)每小题都给出代号为(A)、(B)、(C)、(D)四个结论,其中只有一个是正确的.请考生用2B铅笔在答题卡上将选定的答案标号涂黑.
1.在半径等于4的圆中,垂直平分半径的弦长为( )
A
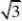
.
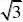
.
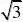
.
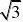
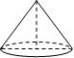
2.如图,小红同学要用纸板制作一个高4cm,底面周长是6πcm的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是( )
A.12πcm B.15πcm C.18πcm D.24πcm
3
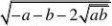
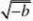
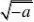
?2222 )
(A)a?b (B)a?b (C)a?b?0 (D)b?a?0
24.已知一个直角三角形的两条直角边长恰好是方程2x-8x+7=0的两根,则这个直角三角形的斜边长
等于( ) (A
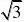
(B)3 (C)6 (D)9
5.对于实数c、d,我们可用min{ c,d }表示c、d两数中较小的数,如min{3,?1} = ?1.若关于x的函数y = min{2x2,a(x?t)2}的图象关于直线x?3对称,则a、t的值可能是( )
A.3,6 B.2,?6 C.2,6 D.?2,6
6.如图,已知M为□ABCD的边AB的中点,CM交BD于点E,则图中阴影部分的面积与□ABCD面积的比是( ) A.1115 B. C. D. 34612
二、填空题(本大题共6小题,每小题4分,共24分) 第6题图
7.等腰三角形ABC中,BC?8,AB、AC的长是关于x的方程x2?10x?m?0的两根,则m的值是___________.
8.若?ABC的面积为S,且三边长分别为a、b、c,则?ABC的内切圆的半径是 。[www.61k.com]
1x2119如果f(x)=,那么f (4) + f (3) + f (2) + f (1)+f ()+ f () + f () = . 1?x2234
10.不等式:x??x?3>4的解集是
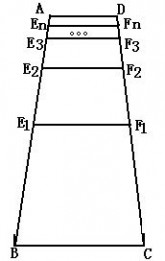
11.如图,梯形ABCD中上底AD=a,下底BC=b,若E1、F1分别为AB、CD的中点,则
E1F1=a?b) ;
若E2、F2分别为AE1、DF1的中点,则E2F2=121?1?1??a?a?b??3a?b?;
??2?2?4
南宁三中 2013年南宁三中外地学生入学测试数学与答案
若E3 、F3分别为AE2、DF2的中点,则E3F3=1?1?1??a?3a?b??7a?b? ……; ??2?4?8
若En、Fn分别为AEn-1、DFn-1的中点,则EnFn=
12.函数y?x2?2x?5?x2?4x?5的最小值为
三、解答题(本大题共5小题,第13---16题每小题10分,第17题12分,共52分)
13.如图,已知⊙O的半径长为2,以⊙O的弦AB为直径作⊙M,点C是⊙O优弧AB上的一个动点(不与点A、点B重合).连结AC、BC,分别与⊙M相交于点D、点E,连结DE

.若AB?
(1)求?C的度数;
(2)求DE的长;
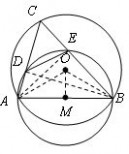
14.如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物...
线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.

南宁三中 2013年南宁三中外地学生入学测试数学与答案
15.关于x的方程x?mx?2m?2?0在区间?0,?内有解,求实数m的范围。[www.61k.com] 2
16.设二次函数y?ax2?bx?c(a、b、c?Z,且a?0)对一切实数x恒有x?y?2x?
二次函数的解析式。
22??x?y?p,17.已知关于x ,y的方程组?有整数解?x,y?,求满足条件的质数p。 2??3xy?p(x?y)?p22?3???1成立,求 4
参考答案
一、选择题(本大题共6小题,每小题4分,共24分)
A B D B C A
二、填空题(本大题共6小题,每小题4分,共24分)
7. 25或16 8.2S7 9. 10.x<0,或x>4 a?b?c2
(2n?1)a?b
2n11. 12.32
三、解答题(本大题共5小题,第13---16题每小题10分,第17题12分,共52分)
13.解:(1)连结OB,OM.
南宁三中 2013年南宁三中外地学生入学测试数学与答案
则在Rt△OMB中,
OB?
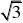
2,MB?,
?OM?1.……………………1分 OM?1OB,??OBM?30.……………3分 2
??MOB?60.……………4分
连结OA.则?AOB?120.
??C?1?AOB?60.………………5分 2
[或:延长BO与O相交于点F,连结AF.
则有?ACB??AFB,且?FAB?90.
在Rt△ABF中,
又sin?AFB?BO?2,?BF?2BO?2?2?4.
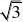
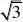
AB,??AFB?60.?AFB??ACB,??C?60. ??BF42
(2)在△CDE和△CBA中, ?CDE??CBA,?ECD??ACB,
?△CDE∽△CBA.
?DEDC?.………………7分 ABBC
连结BD.则?BDC??ADB?90.
在Rt△BCD中, ?BCD?60,??CBD?30.…………8分
?BC?2DC.
DC1DE1??.即?.


BC2AB211?DE?AB???.………………10分 22
[或:点C在AB上移动,??C恒为60,DE长始终不变.当点C移动到BO延长线与O交点处
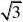

时,可求得DE?ABsin30? 1?] 2
,;F(1,2).………………2分 14.解:(1)E(31)
(2)在Rt△EBF中,?B?90
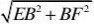
,
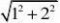

?EF
南宁三中 2013年南宁三中外地学生入学测试数学与答案
设点P的坐标为(0,n),其中n?0,
顶点F(1,2),………………3分
?设抛物线解析式为y?a(x?1)2?2(a?0).
22当EF?PF时,EF?PF,
;n2?4. ?12?(n?2)2?5.解得n1?0(舍去)
?P(0,4).?4?a(0?1)2?2.
解得a?2.?抛物线的解析式为y?2(x?1)2?2
22当EP?FP时,EP?FP,?(2?n)2?1?(1?n)2?9. 解得n??5(舍去). 2
当EF?
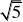
EP时,EP??3,这种情况不存在.
综上所述,符合条件的抛物线解析式是y?2(x?1)2?2.………………6分
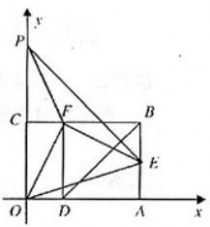
南宁三中 2013年南宁三中外地学生入学测试数学与答案

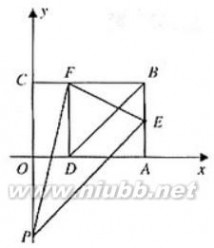
(3)存在点M,N,使得四边形MNFE的周长最小.
如图,作点E关于x轴的对称点E?,作点F关于y轴的对称点F?,连接E?F?,分别与x轴、y轴交于点M,N,则点M,N就是所求点.………………7分
?E?(3,?1),F?(?1,,2)NF?NF?,ME?ME?.
?BF??4,BE??3.
?FN?NM?ME?F?N?NM?
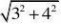
ME??F?E???5.…9分 又EF?
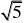
?FN?NM?ME?EF?5,此时四边形MNFE
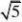
的周长最小值是510分
15.解:设f(x)?x2?mx?2m?2,依题意有以下情况:
(1)有解为0,则f(0)?2m?2?0,所以m?1;…………2分 33931,则f()??m?2m?2?0,所以m??;…………4分 22422
33311(3)在(0,)内有且仅有一个解,且0、不是解,则f(0)?f()?(2m?2)(m?)?0,所以22224
1??m?1;…………6分 2
???m2?4(2m?2)?0??0?m?3
3?22(0)(4)在内有两个解(包括重根),则?, 2f(0)?0??3?f()?0?2
?m?4?22或m?4-22?0?m?3??得?m?1,即1?m?4?22…………9分 ??m??1
?2?
?1?综上可知,实数m的取值范围是??,4?22?.…………10分 ?2?
112216.解:由题设知对一切实数x有x?ax?bx?c?2x?,当x=0时,上式为0?c??c?0,44
?ax2?(b?1)x?0,............?1??故?对一切实数x均成立。[www.61k.com)…………2分 12?2??(2?a)x?bx??0......4?
2由式(1)得a>0,且⊿1?(b?1)?0?b?1;…………4分
1当a?2时,式(2)化为?x??0,与题设矛盾;…………6分 4(2)有解为
南宁三中 2013年南宁三中外地学生入学测试数学与答案
?2?a?0,?当a?2时,由式(2)得?…………8分 12??(?1)?4(2?a)??0?a?1.2?4?
由式(1)a>0?a?1
所以,二次函数的解析式为y?x2?x…………10分
17.解:?p??x?y??x?y?
由p为质数知??x?y?p,?x?y??p,?x?y?1,?x?y??1,或? 或? 或?.…………4分 x?y?1x?y??1x?y?px?y??p????
p?1?x?,??x?y?p,32?22(1)当?时,?将其代入3xy?p(x?y)?p2中,得p?1)?p?p,即4?x?y?1?y?p?1
?2?
。(www.61k.com)…………8分 p2?4p?3?0,解得p?3 或p?1(舍)
(2)当??x?y??p,?x?y?1,?x?y??1,或?或?时,经计算可知没有符合条件的质数p,所以,符合
?x?y??1?x?y?p?x?y??p
条件的质数p?3。…………12分
四 : 3年22课《金子》《练习7》测试
一、看拼音写词语:
jí jiāng sǎo xìng wéi yī móu shēng qīng fén dà yǔ fēng yōng ér zhì
( )( ) ( )( ) ( ) ( )
yī wú suǒ huò mái tóu kǔ gàn ruò yǒu suǒ wù
( ) ( ) ( )
二画线的字注音:挖掘( )河畔( ) 甘心( )落空( )附近( )几乎( )
三、多音字注音组词: 埋( )( )( )( )
要( )( )( )( ) 发( )( )( )( )
四、形近字组词: 买( )卖( )实( ) 唯( )维( )
钱( )线( ) 府( )附( )符( )
五、填空:1、彼得的梦想是( ),他是靠自己的( )让梦想实现的。
2、彼得是一个( )的人。
3、《金子》一文告诉我们的道理是( )。
4、你的梦想是什么?你将怎样让它实现呢?
————————————————————————————————————————————
5、语段分析:
a听说有人在萨文河畔无意中发现了金子,淘金者便蜂拥而至。
1、写反义词。 无意——
2、写人多的一个成语是( ),我还知道( )( )也是形容人多的成语。
3、“在萨文河畔无意中发现了金子”,这里的金子指的是( )
b五年以后,彼得终于实现了他的梦想。他不无骄傲地对人说:“我是唯一找到真金的人!我的金子就在这块土地里。”
1、写近义词。 终于—— 骄傲—— 梦想——
2、“我是唯一找到真金的人!我的金子就在这块土地里。”这里的“真金”指的是什么?
———————————————————————————————————————————
《练习7》测试
一、成语填空:
食( )不( ) 气喘( )( ) ( )马一生 身经( )( ) 刮骨( )( )
传为( )( )( )( )三章 ( )( )无犯 运筹( )( )好( )善( )
二、脸谱连线: 三、填空:1、身怕不动,( )。
关羽 奸诈 白脸 2、、师傅领进门,( )
包公 正直 黑脸 3、( ),脑越用越灵。
秦桧 忠勇 红脸 4、三天打鱼,( )。
5、( )能生巧,( )。
三、展销会中,要想让自己的闹钟卖个好价,该怎样说?要想从别人手买到闹钟,该怎样说?
卖家说:——————————————————————————————————————
买家说:——————————————————————————————————————
五 : 小学五年级科学下册测试题及答案
小学五年级科学下册测试题及答案
一、填空
1、物体在水中排开水的体积叫做( )。
2、水受热体积膨胀,受冷体积缩小,水的这种变化叫做( )。
3、阳光下,把一根木棒竖直插在地上,随着时间变化,影子的()和( )都会发生变化。
4、波兰天文学家( )提出“日心说”的观点。
5、( )可以证明地球在自传。
6、地球转动时,地轴始终倾斜着指向( )。
7、太阳的东升西落,地球昼夜交替变化时因为地球在( )。
8、热总会从温度较( )的一端传递到温度较( )的一端,这种传热方式叫做( )。
9、潜水艇是用改变自身的( )来改变沉浮的。
10、古人用的水钟有( )和( )两种类型。
二、判断题
1、同一块橡皮不管切成大小如何,它的沉浮状况不会发生改变( )
2、摆绳越长,摆动越快;摆绳越短,摆动越慢。( )
3、铜砝码不管放在哪种液体中,它都是沉的。( )
4、物体只要在水中,它都排开了一定的水量。( )
5、沉在水底的物体没有受到浮力的作用。( )
6、冷水在加热的过程中体积、重量都会增大。( )
7、坐在向前行驶的车上,看窗外的物体都是移动的。( )
8、常见的物体都是由微粒组成的。( )新 课标 第一 网
9、摆锤越重,摆动的速度越慢。( )
10、体积相同的热水和冷水,重量也相同。( )
三、选择题
1、地球自转的方向是( )
A、由南向北 B、由西向东 C、由东向西
2、用钢铁制成的轮船能浮在水面上,这是改变了( )
A、它的重量 B、它的体积 C、液体的浓度
3、要使橡皮泥在水中浮起来,做法错误的是( )
A、做成空心的 B、消掉一半 C、绑在木块上
4、相邻两段铁轨之间的缝隙( )
A、冬天大 B、夏天大 C、冬天夏天一样大
5、古代人们制作的利用太阳计量时间的仪器叫( )
A、日晷 B、浑天仪 C、滴漏
6、压瘪的乒乓球,浸入开水里烫一下,还能重新鼓起来,这是利用了( )
A、液体的热胀冷缩 B、固体的热胀冷缩 C、气体的热胀冷缩
7、下列金属中,会热缩冷胀的是( )
A、 铁 B、铝 C、锑
8、首先用实验证明地球在自传的科学家是( )
A、傅科 B、哥白尼 C、托勒密
9、沉在水底的水泥船,受到的浮力和重力的关系是( )
A、浮力<重力 B、浮力=重力 C、浮力>重力
10、下列三个勺子,热传递本领最好的是( )
A、铝勺 B、木勺 C、塑料勺
四、连一连
(1)
纸盒 气球
木块 沉入水底 石子
小刀 铅笔
橡皮 浮在水面 排球
泡沫 羽毛球
玻璃球 铅球
(2)
塑料
铝勺 传热快
铁锅 传热慢
木棒
课本
钥匙
五、简答题
1、把鸡蛋放入水中是沉入水底的,你有什么办法能让它浮起来?
2、铁路的铁轨在连接处总是留出一条缝隙,这条缝隙的大小会变化吗?怎样的规律呢?
六、实验操作
为了证明液体具有热胀冷缩的性质,你有什么办法?写出你的实验方案:
我需要的材料:
我的实验方法及步骤:
我的实验结论:
试卷答案:
一、1、排开水量 2、热胀冷缩 3、方向 长短 4、哥白尼
5、傅科摆 6、北极星 7、自传 8、高 低 热传递 9、重量
10、受水型 泄水型
二、1、∨ 2、× 3、× 4、∨ 5、 × 6、 × 7、 ×
8、 ∨ 9、× 10、×
三、1、B 2、B 3、B 4、A 5、A 6、C 7、C
8、A 9、A 10、A
五、1、答:在水里放入盐。
2、答:有变化,冬天缝隙最大,夏天缝隙最小。
六、
我需要的材料:烧杯、热水、冷水、红水、胶塞、烧瓶、玻璃管、皮筋等。
我的实验方法及步骤:
1、用红水注满烧瓶,瓶口塞入带有玻璃管的胶塞,用皮筋
标注玻璃管上红水的最高水位;
2、将烧瓶放入冷水中,观察红水液面下降,用皮筋标注玻
璃管红水最高水位;
3、将烧瓶放入热水中,观察红水液面上升,用皮筋标注玻璃管红水最高水位。对三个皮筋的高度进行比较。
我的实验结论:在热水中水位上升,在冷水中水位下降,证明液体具有热胀冷缩的性质。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1