一 : 为了探索代数式x2+1+(8
为了探索代数式
(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得
(2)请你根据上述的方法和结论,试构图求出代数式
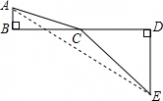 |
| (1)过点E作EF∥BD,交AB的延长线于F点, 根据题意,四边形BDEF为矩形. AF=AB+BF=5+1=6,EF=BD=8. ∴AE=
即AC+CE的最小值是10.
∵EF∥BD, ∴
∴
解得:x=
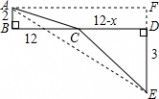 (2)过点A作AF∥BD,交DE的延长线于F点, (2)过点A作AF∥BD,交DE的延长线于F点,根据题意,四边形ABDF为矩形. EF=AB+DE=2+3=5,AF=DB=12. ∴AE=
即AC+CE的最小值是13. 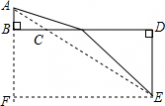 |
考点:
考点名称:轴对称轴对称的定义:轴对称的性质:
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等;
(3)关于某直线对称的两个图形是全等图形。
轴对称的判定:
如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
这样就得到了以下性质:
1.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
2.类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
3.线段的垂直平分线上的点与这条线段的两个端点的距离相等。
4.对称轴是到线段两端距离相等的点的集合。
轴对称作用:
可以通过对称轴的一边从而画出另一边。
可以通过画对称轴得出的两个图形全等。
扩展到轴对称的应用以及函数图像的意义。
轴对称的应用:
关于平面直角坐标系的X,Y对称意义
如果在坐标系中,点A与点B关于直线X对称,那么点A的横坐标不变,纵坐标为相反数。
相反的,如果有两点关于直线Y对称,那么点A的横坐标为相反数,纵坐标不变。
关于二次函数图像的对称轴公式(也叫做轴对称公式 )
设二次函数的解析式是 y=ax2+bx+c
则二次函数的对称轴为直线 x=-b/2a,顶点横坐标为 -b/2a,顶点纵坐标为 (4ac-b2)/4a
在几何证题、解题时,如果是轴对称图形,则经常要添设对称轴以便充分利用轴对称图形的性质。
譬如,等腰三角形经常添设顶角平分线;
矩形和等腰梯形问题经常添设对边中点连线和两底中点连线;
正方形,菱形问题经常添设对角线等等。
另外,如果遇到的图形不是轴对称图形,则常选择某直线为对称轴,补添为轴对称图形,
或将轴一侧的图形通过翻折反射到另一侧,以实现条件的相对集中。
二 : 除了贡献代码 Amaze UI首次探索国内开源商业模式
8月27日,由中国最大的HTML5社区——HTML5梦工场主办的2016HTML5峰会“iWeb峰会”在北京国际会议中心召开。Amaze UI 作为国内最受欢迎前端框架,受邀参与了本次盛会本届峰会,并分享了Amaze UI在前端开发效率上的实践经验及在开源发展模式探索!
与时俱进, 多版本产品组合满足开发者多业务需求
Amaze UI是全球领先的HTML5企业移动化解决方案供应商——云适配旗下三大产品之一。自2014年上线后,目前已经拥有了近50多万开发者用户,形成了一个国内较大的技术交流社区,在Github上取得了7500多个Star的关注度,已经成为国内最流行的前端开发工具。
Amaze UI Web是Amaze UI最先诞生的版本。它是一款完全针对HTML5开发的轻量级、模块化、强调移动优先的开源跨屏前端框架,通过拆分、封装了一些常用的网页组件,让开发者只需复制代码便可将这些跨屏组件写入到自己的网站中。
但随着移动互联时代,移动开发需求的不断延伸和变化,特别是在Amaze U开发者用户群里出现了跨屏(响应式)和移动端两个主流开发需求。为此,Amaze UI产品团队根据这些需求,也对产品进行了版本升级和细分,形成了以“跨屏”和“移动端”两大产品组合策略。具体来说,包括: 用于快速构建HTML5跨屏网站的Amaze UI for Web;帮助开发者构建混合HTML5应用的Amaze UI Touch及 Amaze UI for 钉钉。
大家可能对“Amaze UI for 钉钉”比较陌生,它是Amaze UI产品组和阿里钉钉产品组联合推出的,专门针对阿里钉钉开发者的移动应用开发框架,它基于HTML5的技术属性,不仅能提供一套完美符合阿里钉钉设计风格的开源Web组件,同时借助Amaze UI 组件式产品理念,能够帮助阿里钉钉入驻企业的开发者高效完成移动应用开发。
随着移动化建设的全面推进,HTML5的逐步成熟,个人开发者和企业端需求不断提升,两年的时间Amaze UI积累了非常丰富的组件,形成了一个较强大的社区,拥有了近50万的粘性用户。今天,Amaze UI除了是开源代码的贡献者,更形成了一个以“开发者”为中心的良性生态,在这个生态圈,开发者之间、开发者和企业之间可以互动、交流、协作,凝聚起来,避免单兵作战。
构建可持续开发者生态 尝试开源产品商业模式
生态的构建离不开对行业上下游资源的整合。为此,Amaze UI 决定从开发者工具、人才培养、社区运营等角度入手,打通应用开发的需求方和供给方,并通过结合一条有商业模式的运营方式,来为开源做出贡献及对开发者提供更好的服务。最终,Amaze UI推出了以开源开放为宗旨、包括“工具”、“人才”、“商业”、“社区”四大部分的全新生态环境组合。

Amaze UI开发者生态
具体来说,Amaze UI “工具”性是其作为开源产品的核心属性之一,它将根据开发者、企业等需求方要求,不断进行产品功能升级。但如果只靠Amaze UI 团队的开发人员是无法完成这么大批量的需求开发的,因此需要将更多的需求通过平台的方式分发给能提供相应技术支持的开发者,这个平台便是Amaze UI“商业”领域中的“模板中心(众包平台)”。一方面它通过运营人员完成开发者与企业的需求对接、模板管理等工作,从而在帮助开发者获得利益的同时为企业提高开发效率。另一方面通过提供多类型的免费模版的方式帮助开发者极大提高开发效率。基于开源社区的众包模式本质是对需求方和技术提供方的一种新商业尝试。
其次,开源本身的含义是开放共享,因此开源产品的运营必然离不开社区,即不同的技术群体围绕同一领域,不断提供和交换在技术上的心得体会,这样才能让开源产品获得强大的技术支持,并推动开源项目逐步壮大。为此,Amaze UI 生态构建中将形成以技术分享、答疑和学习为三大目标的社区运营方式。
最后,就是人才!虽然目前HTML5开发如火如荼,但出于教育体系的落后及市面上开发者培训机构的鱼龙混杂,具备实战能力,能为企业提供有效HTML5开发人才缺口非常大。在这种背景下,Amaze UI结合自身工具实力以及实战经验,参与到了HTML5产业研究院推出“HTML5人才培养计划”中,主要通过真实项目为HTML5学习者提供实战课程,同时Amaze UI的社区也为人才培养计划提供强大的技术支持“后盾”。
开源是一种精神,更是一种力量。国内开源项目很多,但大多是开发者自己的兴趣爱好,成功者甚少,究其原因,主要是因为还没有找到一个好的商业模式,Amaze UI 此次打破常规,第一次提出对开源产品商业模式的探索,不仅是对国内开源环境破冰的一次勇敢尝试,对国内开源项目发展也具有重要的实践和指导意义。
三 : 为了探索代数式x2+1+(8
为了探索代数式
(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得
(2)请你根据上述的方法和结论,试构图求出代数式
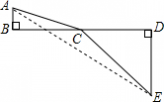 |
| (1)过点E作EF∥BD,交AB的延长线于F点, 根据题意,四边形BDEF为矩形. AF=AB+BF=5+1=6,EF=BD=8. ∴AE=
即AC+CE的最小值是10.
∵EF∥BD, ∴
∴
解得:x=
 (2)过点A作AF∥BD,交DE的延长线于F点, (2)过点A作AF∥BD,交DE的延长线于F点,根据题意,四边形ABDF为矩形. EF=AB+DE=2+3=5,AF=DB=12. ∴AE=
即AC+CE的最小值是13. 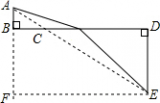 |
考点:
考点名称:轴对称轴对称的定义:轴对称的性质:
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等;
(3)关于某直线对称的两个图形是全等图形。
轴对称的判定:
如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
这样就得到了以下性质:
1.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
2.类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
3.线段的垂直平分线上的点与这条线段的两个端点的距离相等。
4.对称轴是到线段两端距离相等的点的集合。
轴对称作用:
可以通过对称轴的一边从而画出另一边。
可以通过画对称轴得出的两个图形全等。
扩展到轴对称的应用以及函数图像的意义。
轴对称的应用:
关于平面直角坐标系的X,Y对称意义
如果在坐标系中,点A与点B关于直线X对称,那么点A的横坐标不变,纵坐标为相反数。
相反的,如果有两点关于直线Y对称,那么点A的横坐标为相反数,纵坐标不变。
关于二次函数图像的对称轴公式(也叫做轴对称公式 )
设二次函数的解析式是 y=ax2+bx+c
则二次函数的对称轴为直线 x=-b/2a,顶点横坐标为 -b/2a,顶点纵坐标为 (4ac-b2)/4a
在几何证题、解题时,如果是轴对称图形,则经常要添设对称轴以便充分利用轴对称图形的性质。
譬如,等腰三角形经常添设顶角平分线;
矩形和等腰梯形问题经常添设对边中点连线和两底中点连线;
正方形,菱形问题经常添设对角线等等。
另外,如果遇到的图形不是轴对称图形,则常选择某直线为对称轴,补添为轴对称图形,
或将轴一侧的图形通过翻折反射到另一侧,以实现条件的相对集中。
四 : 为了探索代数式的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动
为了探索代数式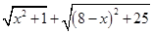 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作 的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作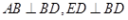 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则 ,连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则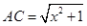 , ,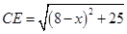 则问题即转化成求AC+CE的最小值. 则问题即转化成求AC+CE的最小值.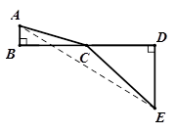 (1)我们知道当A、C、E在同一直线上时, AC+CE的值最小,于是可求得 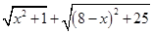 的最小值等于,此时 的最小值等于,此时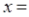 ; ;(2)请你根据上述的方法和结论,试构图求出代数式 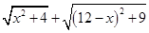 的最小值. 的最小值. |
(1)10,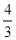 (2) 13. (2) 13. |
(1)根据两点之间线段最短可知AC+CE的最小值就是线段AE的长度.过点E作EF∥BD,交AB的延长线于F点.在Rt△AEF中运用勾股定理计算求解.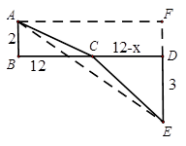 (2)由(1)的结果可作BD=12,过点A作AF∥BD,交DE的延长线于F点,使AB=2,ED=3,连接AE交BD于点C,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值就是代数式 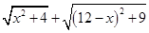 的最小值. 的最小值. |
考点:
考点名称:相似多边形的性质相似多边形:
如果两个边数相同的多边形的对应角相等,对应边成比例,这两个或多个多边形叫做相似多边形,相似多边形对应边的比叫做相似比。(或相似系数)
判定:
如果对应角相等,对应边成比例的多边形是相似多边形.
如果所有对应边成比例,那么这两个多边形相似
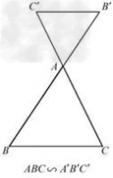
相似三角形的判定:
1.基本判定定理
(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。
(2)如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。(简叙为:两边对应成比例且夹角相等,两个三角形相似。)
(3)如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。(简叙为:三边对应成比例,两个三角形相似。)
(4)如果两个三角形的两个角分别对应相等(或三个角分别对应相等),那么这两个三角形相似。
2.直角三角形判定定理
(1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
(2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
3.一定相似:
(1).两个全等的三角形
(全等三角形是特殊的相似三角形,相似比为1:1)
(2).两个等腰三角形
(两个等腰三角形,如果其中的任意一个顶角或底角相等,那么这两个等腰三角形相似。)
(3).两个等边三角形
(两个等边三角形,三个内角都是60度,且边边相等,所以相似)
(4).直角三角形中由斜边的高形成的三个三角形。
相似三角形性质定理:
(1)相似三角形的对应角相等。
(2)相似三角形的对应边成比例。
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
(4)相似三角形的周长比等于相似比。
(5)相似三角形的面积比等于相似比的平方。
(6)相似三角形内切圆、外接圆直径比和周长比都和相似比相同,内切圆、外接圆面积比是相似比的平方
(7)若a/b =b/c,即b2=ac,b叫做a,c的比例中项
(8)c/d=a/b 等同于ad=bc.
(9)不必是在同一平面内的三角形里
①相似三角形对应角相等,对应边成比例.
②相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.
③相似三角形周长的比等于相似比
定理推论:
推论一:顶角或底角相等的两个等腰三角形相似。
推论二:腰和底对应成比例的两个等腰三角形相似。
推论三:有一个锐角相等的两个直角三角形相似。
推论四:直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
推论五:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
推论六:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1