一 : 2010年高考浙江卷文言文阅读解析及翻译
阅读下面的文言文,完成17—21题。(18分)未完待续,更多精彩请关注比比读小说网微信公众号
二 : 名校必备2010年高考浙江卷语文复习系列教案(4)
天兵下北荒,
胡马欲南饮。(www.61k.com]
横戈从百战,
直为衔恩甚。
握雪海上餐,
拂沙陇头寝。
何当破月氏,
然后方高枕
2010年高考浙江卷语文复习系列教案(4)
辨析和修改病句
【教学目标】
知识与技能:
1、了解考纲考查的病句的基本类型和主要修改手法;
2、能够准确的找出病句;
3、能够适当的修改病句;
4、能够在日常生活中避免制造病句,能够纠正病句。
过程与方法:
1、能够在修改病句的过程中掌握适当的语法知识;
2、能够从不同的角度和层面识别病句;
3、能够探究在病句修改过程中的疑点和难点,提出自己的见解。
情感态度与价值观:
通过对病句修改的系统复习,培养学生养成良好的语言习惯和表达能力。
【教学重点】
1、分析病句的基本类型和主要修改手法;
2、从不同的角度和层面分辨和识别病句;
3、探讨病句在现实生活中所产生的影响。
【教学难点】
1、从不同的角度和层面分辨和识别病句;
2、能够适当的修改病句。
【教学课时】
总课时安排10课时左右。
第一课时
【考点解读】
所谓“病句”,是指不符合现代汉语语法规则、不合逻辑事理的句子。它是历年来高考考查的一个重点。《考试大纲》对病句的测试要求是“辨析并修改病句”,能力层级为D级。
一般来讲,本考点的考查范围是病句的辨析和修改两大项。高考试卷中通常以两种形式进行考查:一是辨析病句,以选择题形式出现在第I卷中,这种形式占多数;二是修改病句,以主观题形式出现在第II卷中(湖南近年无此题型)。
主要考查以下六种病句类型:表意不明、语序不当、不合逻辑、搭配不当、成分残缺或赘余、结构混乱。
2010年浙江高考语文试卷 名校必备2010年高考浙江卷语文复习系列教案(4)
【高考分析】
一、2004—2009湖南高考语病题分析
【2004】5.下列各句中没有语病的一句是
A.由于加强了生产过程中的生态环境监控,该基地每年的无公害蔬菜的生产量,除供应本省主要市场外,还销往河南、河北等省。(www.61k.com)
B.滥用外来语所造成的支离破碎的语境,既破坏了汉语言文字的严谨与和谐,影响了汉语表意功能的发挥,也消解了中国文化精深而丰富的内涵。
C.山鸡椒的花、叶和果实均含芳香油,从油中提取的柠檬醛,为配制食用香精和化妆品香精的主要原料,都离不开它。
D.与作家不同的是,摄影家们把自己对山川、草木、城市、乡野的感受没有倾注于笔下,而是直接聚焦于镜头。
5.B A句是搭配不当,生产量不能供应,供应的应是无公害蔬菜,另外,首句说了前提,后面没有与之相应的结果句,是个残句;C句,结构混乱,可将“都离不开它”删去;D句语序不当,应将没有一词调至把字前。
【2005】下列各句中有语病的一句是 ( )
A.一项新的研究成果显示,动物不但具有独特的性格,而且性格相当复杂,它们性格的复杂性甚至能够与人类的相媲美。
B.进入21世纪,随着经济全球化进程的加快和知识经济的深入发展,国与国之间的竞争越来越集中到知识和人才方面。
c.电视的普及,在给现代人带来丰富多彩的视听艺术的同时,也悄然改变着人们在印刷媒介时代所形成的审美趣味和欣赏习惯。
D.生物入侵就是指那些本来不属于某一生态系统,但通过某种方式被引入到这一生态系统,然后定居、扩散、暴发危害的物种。
[解析] D 犯(主宾)搭配不当的语病。
改正:生物入侵就是指那些本来不属于某一生态系统的物种,通过某种方式被引入到这一生态系统,然后定居、扩散、暴发危害。
【2006】4.下列各句中有语病的一句是
A.经过艰难跋涉,我们发现,如果没有科学发展观作指导,任何理顺国家、市场、社会关系的举措,都将事倍功半。
B.人们认为,团队有效性的关键因素不只是个体贡献的简单相加,而是能使队员行动一致、互相配合的团队协作技能。
C.自然界中存在着一种共生现象,如燕千鸟从鳄鱼牙中啄取水蛭,为鳄鱼提供口腔卫生服务,同时它自己也得到了所需的食物。
D.世界各地的人们都把当地的主要河流称为母亲河,是因为这些河流不仅是他们赖以生存的基础,而且是区域文化的摇篮。
4.[答案] B
[解析] 本题考查学生对常见语病的辨析能力,能力层级为D级。B项属关联词语搭配不当,“不只是”不能与“而是”搭配,应将“不只是”改为“不是”。
【2007】4、下列各句中有语病的一句是
A.当我在一个白夜从易卜生的故乡斯凯恩返回奥斯陆的时候,沿途那幽深的有野鹿出没的森林里,那起伏着绿色的松涛的山谷里,到处都响着娜拉出走时的关门声。
B.文学经典是历史的回声,是审美体验的延伸,也是后代作家超越自我的精神刻度,作家只有在与经典大师的竞争中,才能拓展文学的想象空间,为未来提供崭新的审美体验。
C.三峡围堰爆破使用的是世界上最先进的数码雷管,每个雷管都有唯一的编号,就像我们的身份证有自己的号码一样,而且人们还能像给手机设定闹铃那样,给每个雷管单独设定起爆时间。
D.中国史学家在世纪之交进一步提升了自己的辨析能力,越来越显示出相当高的学术含量,从对外国史学的一般性介绍走向研究和判断的层面,从而为中外史学家的真正对话提供了可能和前提
答案:D
2010年浙江高考语文试卷 名校必备2010年高考浙江卷语文复习系列教案(4)
【2008年】4下列各句中有语病的一句是
A.超越种族、信仰、社会制度的差异,增进各国人民之间的相互了解,促进和平、友谊与团结,在尊重世界多样性的基础上实现人类和谐发展,已成为奥林匹克精神的深刻内涵。(www.61k.com]
B文艺复兴揭开了欧洲腾飞的序幕,工业革命拉大了欧洲与中国的距离,当火车在欧洲大地高歌猛进的时候,中国的辽阔土地上,木制独轮车还在吱吱呀呀地唱着千年的凄凉。
C风云变幻的20世纪已经过去,那些为中国的命运呐喊的诗界前辈也已经走远,在新的世纪,面对商品经济大潮的冲击,我们应该如何拨开喧嚣的迷雾,高扬起前辈诗人使命意识的旗帜?
2、动宾搭配不当
例6. 以“和谐之旅”命名的北京奥运火炬全球传递活动,激发了我国各族人民的爱国热情,也吸引了世界各国人民的高度关注。【2008年高考安徽卷】
【解析】B项是搭配不当,“吸引”不能与“关注”搭配。
例7、我国的文化遗产是我们民族悠久历史的证明,是我们与祖先沟通的重要渠道,也是我们走向未来的坚实根基,我们应当永远保持对古代文明成果的尊重和珍惜,以及祖先的缅
2010年浙江高考语文试卷 名校必备2010年高考浙江卷语文复习系列教案(4)
怀和感恩【2008年高考湖南卷】
【解析】 D项“我们应当永远保持对古代文明成果的尊重和珍惜,以及祖先的缅怀和感恩”,保持??缅怀和感恩。(www.61k.com)搭配不当
例8、在新形势下,我们应该树立新的文化发展观,推进和挖掘文化体制创新和特色文化内涵,着力开发富有时代精神和四川特色的文化产品。(07四川卷)
例9、厚道有如参天的大树,替你遮挡暑热炎凉;厚道有如母亲的怀抱,替你抚慰喜怒哀乐。(07重庆卷)
解析:例8、例9为动宾搭配不当,例8中“推进和挖掘文化体制创新和特色文化内涵”应为“推进文化体制创新和挖掘特色文化内涵”。例9中“炎凉”一般只用它的比喻义,即人事中的亲疏冷暖,用在这里不恰当,也不能与“遮挡”搭配;“喜”“乐”是不需要“抚慰”的,因此也有搭配不当的问题。
3、主宾搭配不当
例:(1)(2004高考 天津卷)孩子的教育问题,是一个复杂的过程,它远不是一两句话就能奏效的。(删掉孩子后的“的”)
(2)我们坚信,有这么一天,中国的工业和农业会成为发达的国家。(此句宾语是由一个主谓短语充当的,但这个主谓短语的主干是"工业和农业成为国家"。主宾意义明显不当、可将"国家"改为"行业"等)
(3)这最后一天的劳动是同学们最紧张、最愉快、最有意义的一天。(“劳动”不可能是“一天”,删去“的劳动”)
4、修饰成分与中心词搭配不当
例1:在翻阅中国话剧100周年纪念活动资料时,他萌生了创作一台寻找中国话剧源头的剧本的意念。(2007北京卷)
例2、早晨五六点钟,在通往机场的大街两旁便站满了数万名欢送的人群。("人群"是在整体性名词,前面不能再用"数万名"予以限制。可将"人群 "改为"人")
5、关联词搭配不当
1、应用这种罗盘,无论在阴云密布以及早晚看不到太阳的时候,也不会迷失方向。 “无论??(还是)??(都)”
2、球员们深深理解这一点:一个球的输赢,不仅仅关系到个人的面子,而是关系到祖国的荣誉。
改为:而且是
6、一面与两面搭配不当
例1:说实话,当时对自己的稿子能否被刊用,没抱太大的希望,因为那时经常在该报发表文章的都是一些大家。(07山东卷)
例2.教育在综合国力的形成中处于基础地位,国力的强弱越来越多地取决于劳动者素质的提高,取决于各类人才培养的质量与数量。(2008年高考四川卷)
【解析】B.“国力的强弱”与“取决于劳动者素质的提高”不一致,搭配不当;
7、并列短语做句子成分搭配不当
例 老人那清晰的思路、开朗的性格、乐观的情绪以及坚定的信心,深深地感染了我们。 解析:主语是“清晰的思路、开朗的性格、乐观的情绪以及坚定的信心”,谓语是“感染”。“思路”是不好“感染的,主谓搭配不当。并列短语充当句子的主语时,常常会和谓 语、宾语不搭配。
三、方法总结
1.望见句中有关联词语,检查是否患关联词搭配不当症。
不管气候条件和地理环境都极端不利,运动员们仍然克服了困难,胜利攀登到峰顶。
2010年浙江高考语文试卷 名校必备2010年高考浙江卷语文复习系列教案(4)
2.望见句中有数量词,检查是否患与中心词搭配不当症。(www.61k.com]
蜜蜂每酿一斤蜜,大约要采集50万朵的花粉。
3.望见句中有并列短语,检查是否患彼此失应症。
春节期间,这个市的210辆消防车、300多名消防官兵,放弃休假,始终坚持在各自执勤的岗位上。
4.望见句中有双面词语,检查是否患前后失应症。
我们能不能培养出“四有”新人,是关系我们党和国家前途命运的大事,也是教育战线的根本任务。
5.望见“是”字句,检查是否患动宾搭配不当症。
三枪集团的内衣产品,是1994年全国同行业率先突破十亿大关的著名品牌。
四、课堂训练
1.我们一定能在奥运之际展现出古老文明大国的风范,那时我们的城市不仅会变得更加美丽,每一个人也会更讲文明。【2008年高考天津卷】
【解析】此题考查辨析病句的能力。B项关联词语使用不当,“不仅”应放在“那时”之后
2.天安门广场等七个红色旅游景点是否收门票的问题,国家旅游局新闻发言人已在记者招待会上予以否认。(2006全国卷1)
一面对两面。是否收门票不能被“否认”。
3.来这里聚会的无论老少,都被他清晰思路、开朗的性格、乐观的情绪及坚定的信心深深地感染了。(2006全国卷2)
“清晰思路、开朗的性格、乐观的情绪及坚定的信心”与“感染了”不搭配。
4、漫步桃园,那一排排、一行行、一树树的桃林让人流连忘返;中国后还可去自费采摘,那柔软多汁的大桃更让你大快朵颐。(2006北京卷)
搭配不当,“一排排,一行行”修饰“桃林这个表集合概念的词不妥。”;
5、某些商家违背商业道德,利用中小学生具有的好奇心理和在考试作弊并不鲜见的情况下,为“隐形笔”大做广告。
“利用”与“在考试作弊并不鲜见的情况下”不能搭配。(2006北京卷)
6.六年间,我国航天技术完成了从单舱到三舱,从无人到有人,从“一人一天”到“两人五天”的进步。(2006安徽卷)
“完成”与“进步”不搭配,“完成”宜改为“实现”。
7.看完那部电视剧后,除了荧屏上活跃着的那些人物给我留下的印象之外,我仿佛还感到有一个没有出场的人物,那就是作者自己。(2006广东卷)
搭配不当,应改为“我仿佛还感到有一个没有过场的人物”。
8.工厂实行了生产责任制以后,效率有了显著的提高,每月废品由原先一千只下降到一百只,废品率下降了九倍。(2006广东卷)
三 : 2010年浙江省高考数学试卷(文科)
2010年浙江省高考数学试卷(文科)
一、选择题(共10小题,每小题5分,满分50分)
1、(2010?浙江)设P={x|x<1},Q={x|x2<4},则P∩Q( )
A、{x|﹣1<x<2} B、{x|﹣3<x<﹣1}
C、{x|1<x<﹣4} D、{x|﹣2<x<1}
2、(2010?浙江)已知函数f(x)=log2(x+1),若f(α)=1,α=( )
A、0 B、1
C、2 D、3
3、(2010?浙江)设i为虚数单位,则=( )
A、﹣2﹣3i B、﹣2+3i
C、2﹣3i D、2+3i
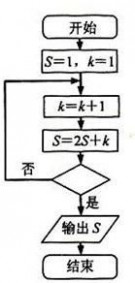
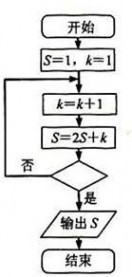
4、(2010?浙江)某程序框图如图所示,若输出的S=57,则判断框内位(
A、k>4 B、k>5
C、k>6 D、k>7
5、(2010?浙江)设sn为等比数列{an}的前n项和,8a2+a5=0则=( )
A、﹣11 B、﹣8
C、5 D、11
6、(2010?浙江)设0<x<,则“x sin2x<1”是“x sinx<1”的( )
A、充分而不必要条件 B、必要而不充分条件
C、充分必要条件 D、既不充分也不必要条件
)
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
?x?3y?3?0?7、(2010浙江)若实数x,y满足不等式组合?2x?y?3?0则x+y的最大值为
?x?y?1?0?
A、9 B、15 C、1 7 D、7 15
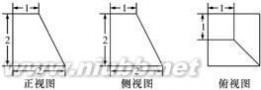
8、(2010?浙江)一个空间几何体的三视图及其尺寸如下图所示,则该空间几何体的体积是( )
A、 B、 D、14 C、7
9、(2010?浙江)已知x0是函数f(x)=2x+的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
A、f(x1)<0,f(x2)<0 C、f(x1)>0,f(x2)<0 B、f(x1)<0,f(x2)>0 D、f(x1)>0,f(x2)>0
10、(2010?浙江)设O为坐标原点,F1,F2是双曲线﹣=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|=a,则该双曲线的渐近线方程为( )
A、x±y=0 C、x±y=0 B、x±y=0 D、x±y=0
二、填空题(共7小题,每小4分,满分28分)
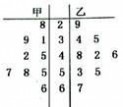
11、(2010?浙江)在如图所示的茎叶图中,甲、乙两组数据的中位数分别是.
12、(2010?浙江)函数的最小正周期是
13、(2010?浙江)已知平面向量α,β,|α|=1,|β|=2,α⊥(α﹣2β),则|2a+β|的值是 .
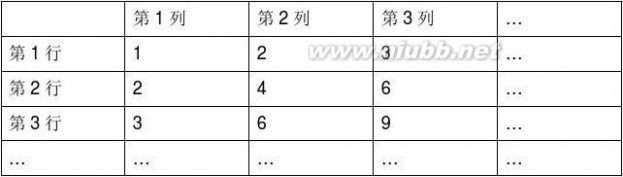
14、(2010?浙江)在如下数表中,已知每行、每列中的树都成等差数列,那么,位于下表中的第n行第n+1列的数是 _________ .
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
15、(2010?浙江)若正实数X,Y满足2X+Y+6=XY,则XY的最小值是.
16、(2010?浙江)某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x的最小值 _________ .
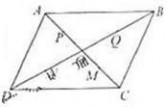
17、(2010?浙江)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 _________ .
三、解答题(共5小题,满分72分)
18、(2010?浙江)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足.
(Ⅰ)求角C的大小;
(Ⅱ)求sinA+sinB的最大值.
19、(2010?浙江)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0.
(Ⅰ)若S5=5,求S6及a1;
(Ⅱ)求d的取值范围.
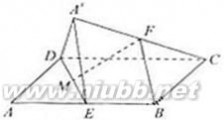
20、(2010?浙江)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点. (Ⅰ)求证:BF∥平面A′DE;
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
(Ⅱ)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
21、(2010?浙江)已知函数f(x)=(x﹣a)2(x﹣b)(a,b∈R,a<b).
(I)当a=1,b=2时,求曲线y=f(x)在点(2,f(x))处的切线方程;
(II)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2. 证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后的等差数列,并求x4.
22、(2010?浙江)已知m是非零实数,抛物线C:y2=2px(p>0)的焦点F在直线上. (I)若m=2,求抛物线C的方程
(II)设直线l与抛物线C交于A、B,△AA2F,△BB1F的重心分别为G,H,求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外.

2010浙江数学高考 2010年浙江省高考数学试卷(文科)
答案与评分标准
一、选择题(共10小题,每小题5分,满分50分)
1、(2010?浙江)设P={x|x<1},Q={x|x2<4},则P∩Q( )
A、{x|﹣1<x<2} C、{x|1<x<﹣4} B、{x|﹣3<x<﹣1} D、{x|﹣2<x<1}
考点:交集及其运算。[www.61k.com]
专题:计算题。
分析:欲求两个集合的交集,先得化简集合Q,为了求集合Q,必须考虑二次不等式的解法,最后再根据交集的定义求解即可.
解答:解:∵x2<4得﹣2<x<2,
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
∴Q={x|﹣2<x<2},
∴P∩Q={x|﹣2<x<1}.
故答案选D.
点评:本题主要考查了集合的基本运算,属容易题.
2、(2010?浙江)已知函数f(x)=log2(x+1),若f(α)=1,α=( )
A、0 B、1
C、2 D、3
考点:对数函数的单调性与特殊点。[www.61k.com)
分析:根据f(α)=log2(α+1)=1,可得α+1=2,故可得答案. 解答:解:∵f(α)=log2(α+1)=1
∴α+1=2,故α=1,
故选B.
点评:本题主要考查了对数函数概念及其运算性质,属容易题.
3、(2010?浙江)设i为虚数单位,则=( )
A、﹣2﹣3i B、﹣2+3i
C、2﹣3i D、2+3i
考点:复数代数形式的混合运算。
分析:复数的分子、分母、同乘分母的共轭复数化简即可.
解答:解:∵
故选C.
点评:本题主要考查了复数代数形式的四则运算,属容易题.
4、(2010?浙江)某程序框图如图所示,若输出的S=57,则判断框内位(
A、k>4 B、k>5
C、k>6 D、k>7
考点:程序框图。 )
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输入S的值,条件框内的语句是决定是否结束循环,模拟执行程序即可得到答案. 解答:解:程序在运行过程中各变量值变化如下表:
K S 是否继续循环
循环前 1 1/
第一圈 2 4 是
第二圈 3 11 是
第三圈 4 26 是
第四圈 5 57 否
故退出循环的条件应为k>4
故答案选A.
点评:算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.
5、(2010?浙江)设sn为等比数列{an}的前n项和,8a2+a5=0则=( )
A、﹣11 C、5 B、﹣8 D、11
考点:等比数列的前n项和。[www.61k.com]
分析:先由等比数列的通项公式求得公比q,再利用等比数列的前n项和公式求之即可. 解答:解:设公比为q,
由8a2+a5=0,得8a2+a2q3=0,
解得q=﹣2,
所以==﹣11.
故选A.
点评:本题主要考查等比数列的通项公式与前n项和公式.
6、(2010?浙江)设0<x<,则“x sin2x<1”是“x sinx<1”的( )
A、充分而不必要条件 C、充分必要条件 B、必要而不充分条件 D、既不充分也不必要条件
考点:不等关系与不等式;必要条件、充分条件与充要条件的判断;正弦函数的单调性。 分析:xsin2x<1,xsinx<1是不一定成立的.不等关系0<sinx<1的运用,是解决本题的
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
重点.
解答:解:因为0<x<,所以0<sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知“x sin2x<1”是“x sinx<1”的必要而不充分条件
故选B.
点评:本题主要考查了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题.
7、(2010?浙江)若实数x,y满足不等式组合则x+y的最大值为( )
A、9 B、 D、 C、1
考点:简单线性规划。[www.61k.com]
分析:先根据条件画出可行域,设z=x+y,再利用几何意义求最值,将最大值转化为y轴上的截距,只需求出直线z=x+y,过可行域内的点A(4,5)时的最大值,从而得到z最大值即可.
解答:解:先根据约束条件画出可行域,
设z=x+y,
∵直线z=x+y过可行域内点A(4,5)时
z最大,最大值为9,
故选A.
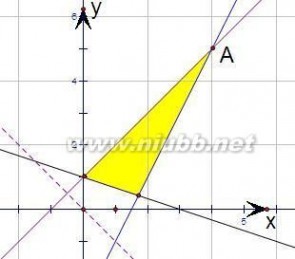
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.
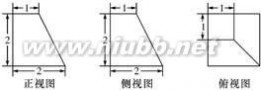
8、(2010?浙江)一个空间几何体的三视图及其尺寸如下图所示,则该空间几何体的体积是( )
A、 B、
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
C、7 D、14
考点:由三视图求面积、体积。(www.61k.com]
专题:计算题;综合题。
分析:三视图复原几何体是四棱台,一条侧棱垂直底面,底面是正方形,根据三视图数据,求出几何体的体积.
解答:解:三视图复原几何体是四棱台,底面边长为2的正方形,一条侧棱长为2,并且垂直底面,上底面是正方形边长为1,
它的体积是:
故选B.
点评:本题考查三视图求体积,考查空间想象能力,计算能力,是基础题.
9、(2010?浙江)已知x0是函数f(x)=2x+的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
A、f(x1)<0,f(x2)<0 C、f(x1)>0,f(x2)<0 B、f(x1)<0,f(x2)>0 D、f(x1)>0,f(x2)>0
考点:函数零点的判定定理。
分析:因为x0是函数f(x)=2x+的一个零点 可得到f(x0)=0,再由函数f(x)的单调性可得到答案.
解答:解:∵x0是函数f(x)=2x+的一个零点∴f(x0)=0
∵f(x)=2x+是单调递增函数,且x1∈(1,x0),x2∈(x0,+∞),
∴f(x1)<f(x0)=0<f(x2)
故选B.
点评:本题考查了函数零点的概念和函数单调性的问题,属中档题.
10、(2010?浙江)设O为坐标原点,F1,F2是双曲线﹣=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|=a,则该双曲线的渐近线方程为( )
A、x±y=0 C、x±y=0 B、x±y=0 D、x±y=0
考点:双曲线的简单性质。
专题:计算题。
分析:假设|F1P|=x,进而分别根据中线定理和余弦定理建立等式求得c2+5a2=14a2﹣2c2,求得a和c的关系,进而根据b=求得a和的关系进而求得渐进线的方程.
解答:解:假设|F1P|=x
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
OP为三角形F1F2P的中线,
根据三角形中线定理可知
x2+(2a+x)2=2(c2+7a2)
整理得x(x+2a)=c2+5a2由余弦定理可知
x2+(2a+x)2﹣x(2a+x)=4c2整理得x(x+2a)=14a2﹣2c2进而可知c2+5a2=14a2﹣2c2求得3a2=c2∴c=a
b=a
那么渐近线为y=±x,即x±y=0
故选D
点评:本题将解析几何与三角知识相结合,主要考查了双曲线的定义、标准方程,几何图形、几何性质、渐近线方程,以及斜三角形的解法,属中档题
二、填空题(共7小题,每小4分,满分28分)
11、(2010?浙江)在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 45,46 .
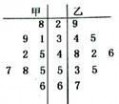
考点:茎叶图;众数、中位数、平均数。(www.61k.com)
分析:本题主要考察了茎叶图所表达的含义,以及从样本数据中提取数字特征的能力,属容易题.
解答:解:由茎叶图可得甲组共有9个数据中位数为45
乙组共9个数据中位数为46
故答案为45、46
点评:茎叶图的茎是高位,叶是低位,所以本题中“茎是十位”,叶是个位,从图中分析出参与运算的数据,根据中位数的定义即可解答.从茎叶图中提取数据是利用茎叶图解决问题的关键.
12、(2010?浙江)函数的最小正周期是 π .
考点:三角函数中的恒等变换应用;三角函数的周期性及其求法。
分析:本题考察的知识点是正(余)弦型函数的最小正周期的求法,由函数化简函数的解析式后可得到:
f(x)=,然后可利用T=求出函数的最小正周期.
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
解答:解:
=
=
=
∵ω=2
故最小正周期为T=π,
故答案为:π.
点评:函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,由周期由ω决定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|,最小值为﹣|A|,周期T=进行求解.、
13、(2010?浙江)已知平面向量α,β,|α|=1,|β|=2,α⊥(α﹣2β),则|2a+β|的值是. 考点:平面向量的坐标运算。[www.61k.com]
分析:先由α⊥(α﹣2β)可知α?(α﹣2β)=0求出,再根据|2a+β|2=4α2+4α?β+β2可得答案. 解答:解:由题意可知α?(α﹣2β)=0,
结合|α|2=1,|β|2=4,解得,
所以|2a+β|2=4α2+4α?β+β2=8+2=10,
开方可知|2a+β|=
故答案为.
点评:本题主要考查了平面向量的四则运算及其几何意义,属中档题.
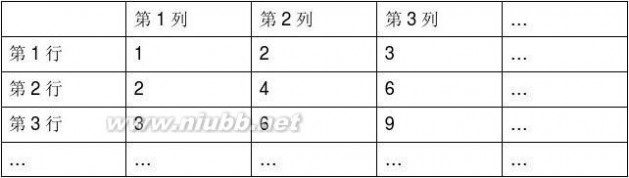
14、(2010?浙江)在如下数表中,已知每行、每列中的树都成等差数列,那么,位于下表中的第n行第n+1列的数是 n2
考点:等差数列;等差数列的通项公式。
专题:规律型。
分析:由表格可以看出第n行第一列的数为n,观察得第n行的公差为n,这样可以写出各行的通项公式,本题要的是第n行第n+1列的数字,写出通项求出即可.
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
解答:解:由表格可以看出第n行第一列的数为n,
观察得第n行的公差为n,
∴第n0行的通项公式为an=n0+(n﹣1)n0,
∵为第n+1列,
∴可得答案为n2+n.
故答案为:n2+n
点评:本题主要考查了等差数列的概念和通项公式,以及运用等差关系解决问题的能力,属中档题.这是一个考查学生观察力的问题,主要考查学生的能力.
15、(2010?浙江)若正实数X,Y满足2X+Y+6=XY,则XY的最小值是 考点:平均值不等式;一元二次不等式的应用。[www.61k.com)
专题:计算题。
分析:本题主要考察了用基本不等式解决最值问题的能力,以及换元思想和简单一元二次不等式的解法,属中档题.运用基本不等式,,令xy=t2,可得,注意到t>0,解得t≥,故xy的最小值为18
解答:解:根据均值不等式有:,
令xy=t2,可得,
注意到t>0,
解得t≥,
xy=t2≥18
故xy的最小值为18.
点评:本题运用了均值不等式和换元思想,从而转化为一元二次不等式的问题,这是一种常见的求最值或值域的方法.
16、(2010?浙江)某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等,若一月至十月份销售总额至少至少达7000万元,则,x的最小值 20 .
考点:一元二次不等式的解法;一元二次不等式的应用。
分析:先求一月至十月份销售总额,列出不等关系式,解不等式即可.
解答:解:依题意 3860+500+2[500(1+x%)+500(1+x%)2]≥7000,
化简得(x%)2+3x%≥0.64,所x≥20.
故答案为:20
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
点评:本题主要考查了用一元二次不等式解决实际问题的能力,属中档题.
17、(2010?浙江)在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .

考点:几何概型。[www.61k.com)
专题:计算题。
分析:本题主要考察了古典概型的综合运用,属中档题.关键是列举出所有G点的个数,及落在平行四边形ABCD不含边界)的G点的个数,再将其代入古典概型计算公式进行求解. 解答:解:由题意知,G点的位置受到E、F点取法不同的限制,令(E,F)表示E、F的一种取法,则
(A,B),(A,Q),(A,N),(A,D)
(P,B),(P,Q),(P,N),(P,D)
(M,B),(M,Q),(M,N),(M,D)
(C,B),(C,Q),(C,N),(C,D)共有16种取法,
而只有(P,Q),(P,N),(M,Q),(M,N)落在平行四边形内,故符合要求的G的只有4个,
落在平行四边形ABCD外(不含边界)的概率P==.
故答案为:
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.
三、解答题(共5小题,满分72分)
18、(2010?浙江)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足.
(Ⅰ)求角C的大小;
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
(Ⅱ)求sinA+sinB的最大值.
考点:余弦定理的应用。(www.61k.com)
专题:计算题。
分析:(1)根据三角形的面积公式题中所给条件可得=absinC,可求出tanC的值,再由三角形内角的范围可求出角C的值.
(2)根据三角形内角和为180°将角AB转化为同一个角表示,然后根据两角和的正弦定理可得答案.
解答:(Ⅰ)解:由题意可知absinC=×2abcosC.
所以tanC=.
因为0<C<π,
所以C=;
(Ⅱ)解:由已知sinA+sinB
=sinA+sin(π﹣C﹣A)
=sinA+sin(﹣A)
=sinA+cosA+sinA=sinA+cosA=sin(A+)≤.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是.
点评:本题主要考查余弦定理、三角形面积公式、三角变换等基础知识,同时考查三角运算求解能力.
19、(2010?浙江)设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0.
(Ⅰ)若S5=5,求S6及a1;
(Ⅱ)求d的取值范围.
考点:等差数列的前n项和。
分析:(I)根据附加条件,先求得s6再求得a6分别用a1和d表示,再解关于a1和d的方程组.
(II)所求问题是d的范围,所以用“a1,d”法.
解答:解:(Ⅰ)由题意知S6==﹣3,
a6=S6﹣S5=﹣8
所以
解得a1=7
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
所以S6=﹣3,a1=7;
解:(Ⅱ)因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
即2a12+9da1+10d2+1=0.
故(4a1+9d)2=d2﹣8.
所以d2≥8.
故d的取值范围为d≤﹣2或d≥2.
点评:本题主要考查等差数列概念、求和公式通项公式等基础知识,同时考查运算求解能力及分析问题解决问题的能力.
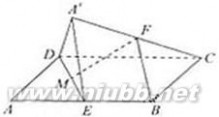
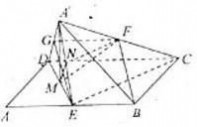
20、(2010?浙江)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点. (Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
考点:直线与平面所成的角;直线与平面平行的判定。(www.61k.com]
专题:计算题;证明题。
分析:(Ⅰ)欲证BF∥平面A'DE,只需在平面A'DE中找到一条线平行于BF即可;而取A′D的中点G,并连接GF、GE,易证四边形BEGF为平行四边形,则BF∥EG,即问题得证. (Ⅱ)欲求直线FM与平面A′DE所成角的余弦值,需先找到直线FM与平面A′DE所成的角;而连接A′M,CE,由平面A′DE⊥平面BCD易证CE⊥A′M,且由勾股定理的逆定理可证CE⊥DE;再取A′E的中点N,连线NM、NF,则NF⊥平面A′DE,即∠FMN为直线FM与平面A′DE所成的角;最后在Rt△FMN中,易得cos∠FMN的值.
解答:(Ⅰ)证明:取A′D的中点G,
连接GF,GE,由条件易知
FG∥CD,FG=CD.
BE∥CD,BE=CD.
所以FG∥BE,FG=BE.
故所以BF∥EG.
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
又EG?平面A'DE,BF?平面A'DE
所以BF∥平面A'DE.
(Ⅱ)解:在平行四边形ABCD中,设BC=a,
则AB=CD=2a,AD=AE=EB=a,
连接A′M,CE
因为∠ABC=120°
在△BCE中,可得CE=a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE所成的角.
在Rt△FMN中,NF=a,MN=a,FM=a,
则cos∠FMN=.
所以直线FM与平面A′DE所成角的余弦值为.
点评:本题主要考查空间线线、线面、面面位置关系及线面角等基础知识,同时考查空间想象能力和推理论证能力.
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
21、(2010浙江)已知函数f(x)=(x﹣a)2(x﹣b)(a,b∈R,a<b).
(I)当a=1,b=2时,求曲线y=f(x)在点(2,f(x))处的切线方程;
(II)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2. 证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后的等差数列,并求x4.
考点:利用导数研究函数的极值;简单复合函数的导数;等差数列的性质。[www.61k.com]
专题:证明题;综合题。
分析:(1)将a,b的值代入后对函数f(x)进行求导,根据导数的几何意义即函数在某点的导数值等于该点的切线的斜率,可得答案.
(2)对函数f(x)求导,令导函数等于0解出x的值,然后根据x3是f(x)的一个零点可得到x3=b,然后根据等差数列的性质可得到答案.
解答:(Ⅰ)解:当a=1,b=2时,
因为f′(x)=(x﹣1)(3x﹣5)
故f′(2)=1
f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x﹣2;
(Ⅱ)证明:因为f′(x)=3(x﹣a)(x﹣),
由于a<b.
故a<.
所以f(x)的两个极值点为x=a,x=.不妨设x1=a,x2=,
因为x3≠x1,x3≠x2,
且x3是f(x)的零点,故x3=b.
又因为﹣a=2(b﹣),
x4=(a+)=,
所以a,,,b依次成等差数列,
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
所以存在实数x4满足题意,且x4=.
点评:本题主要考查函数的极值概念、导数运算法则、切线方程、导线应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识.
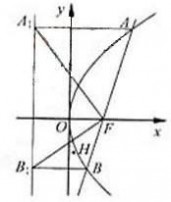
22、(2010?浙江)已知m是非零实数,抛物线C:y2=2px(p>0)的焦点F在直线上. (I)若m=2,求抛物线C的方程
(II)设直线l与抛物线C交于A、B,△AA2F,△BB1F的重心分别为G,H,求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外.
考点:抛物线的简单性质;抛物线的标准方程;直线与圆锥曲线的综合问题。(www.61k.com)
专题:综合题。
分析:(1)根据焦点F(,0)在直线l上,将F代入可得到ρ=m2,再由m=2可确定p的值,进而得到答案.
(2)设A(x1,y1),B(x2,y2),然后联立消去x表示出两根之和、两根之积,然后设M1,M2分别为线段AA1,BB1的中点,根据重心的定义可得到关系2,进而得到G(),H(),和GH的中点坐标M,再由可得到关于m的关系式,然后表示出|MN|整理即可得证. 解答:解:(1)因为焦点F(,0)在直线l上,
得ρ=m2
又m=2,故ρ=4
所以抛物线C的方程为y2=2m2x
(2)证明设A(x1,y1),B(x2,y2)
由消去x得
y2﹣2m3y﹣m4=0,
由于m≠0,故△=4m6+4m4>0,
且有y1+y2=2m3,y1y2=﹣m4,
设M1,M2分别为线段AA1,BB1的中点,
由于2,
可知G(),H(),
2010浙江数学高考 2010年浙江省高考数学试卷(文科)
所以,,
所以GH的中点M.
设R是以线段GH为直径的圆的半径,
则
设抛物线的标准线与x轴交点N,
则
=m4(m4+8m2+4)
=m4[(m2+1)(m2+4)+3m2]
>m2(m2+1)(m2+4)=R2.
故N在以线段GH为直径的圆外.
点评:本题主要考查抛物线几何性质,直线与抛物线、点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力.
本文标题:2010年浙江高考语文试卷-2010年高考浙江卷文言文阅读解析及翻译61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1