等比数列前n项和-等比数列求和一、(a-1)+(a^2-2)+...+(a^n-n

发布时间：2018-01-02 所属栏目：数学

一 : 等比数列求和一、(a-1)+(a^2-2)+...+(a^n-n

等比数列求和

一、(a-1)+(a^2-2)+...+(a^n-n)二、(2-3*5^(-1))+(4-3*5^(-2)+...*(2n-3*5^(-n)三、1+2x+3x^2+...+nx^(n-1)

1.解：原式=(a+a^2+a^3+...+a^n)-(1+2+3+...+n)

=a(1-a^n)/(1-a)-n(1+n)/2

2,解：原式=（2+4+...+2n)-3[5^(-1)+5^(-2)+...+5^(-n)]

= n(n+1)-3/4[1-(1/5)^n]

3,解: 令Sn=1+2x+3x^2+...+nx^(n-1)------A

那么xSn= x+2x^2+...+(n-1)x^(n-1)+nx^n-------B

由A-B得（1-x)Sn=1+x+X^2+...+x^(n-1)-nx^n

所以 Sn=(1-x^n)/(1-x)^2-nx^n/(1-x)

二 : 等比数列前n项和

2.5 等比数列的前n项和 (一）

学习目标
1.会推导等比数列的前n项和公式，并体会其中的方法。 2.能够用等比数列的前n项和公式解决等比数列中的一些问题。

复习回顾
1. 等比数列的定义：

定义：如果一个数列从第 2 项起，每一项与它的前一项的比都等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母 q 来表示. 即 an?1 ? q (an ? q ? 0, n ? N *) ?
an

2.

等比数列的通项公式：
an ? a1 ? qn?1 (n ? N*)

an ? am ? q

n ?m

(n、m ? N*, q ? 0);

思考探究
? 相传国王要奖励国际象棋发明者，问他有什

么要求，发明者说：“请在棋盘上的64格中的第1格放入1粒麦粒，第2格放入2粒麦粒，第3格放入4粒麦粒，第4格放入8粒麦粒，依此类推，每一个格子放的麦粒数都是前一个格子里放的麦粒数的2倍，直到放完64个格子为止．”国王立即答应了． ? 问国王将会给发明者多少粒麦粒？国王能否实现他的诺言？

新课学习
解决关于国际象棋的传说问题：也就是求数列： 1，2，4，8，· · 63 的和. · ，2 S 64 = 1 + 2 + 4 + 8 + · ·+ 263 · ①. 两边同时乘以等比数列的公比 2 ， 2 S 64 = 2 + 4 + 8 + 16 + · ·+ 263 +264 ②. · 比较这两个式子： ② - ① 得， S 64 = 264 –1 . 264 –1 ? 1.84×1019（粒），假定千粒重为40g，那么麦粒的总重量约为7378.7亿吨，若铺在地球表面上，可以得出一个麦粒层，厚度约为9毫米．国王是拿不出这么多麦子的.

等比数列的前 n 项和公式的推导：

设有等比数列

a 1 ，a 2 ，a 3 ，· · n ，· · · ，a ·.

它的公比是 q ，它的前 n 项和为 Sn=a1 +a2 +a3 +·· an . ·+ 由等比数列的通项公式，上式可以写成： S n = a 1+ a 1q+ a 1q 2+ · · a 1q n –2+ a 1q n –1 ·+ ① ②

两边同时乘以公比 q，
q S n = a 1q+ a 1q 2+ · · a 1q n –2+ a 1q n –1 +a 1q n ·+ ① - ② 得， ( 1 - q ) S n = a 1– a 1q n.

( 1 - q ) Sn = a1 – a1 qn .

当 q ? 1 时，等比数列an} 的前n 项和公式为 {

a1 (1 ? q n ) Sn ? 1?q
因为 a 1 q n = ( a 1 q n-1 ) q = a n q , 所以等比数列的前 n 项和公式还可以写成

a1 ? an q Sn ? . 1?q
当 q = 1 时，S n = n a 1 .

等比数列的前n项和公式：

na
Sn=

1

(q=1)

a1 (1 - q ) a1 - an q ? (q≠1) 1- q 1- q

n

注：
（1）当已知 a 1，q，n 时用第一个公式，当已知 a 1，q，a n 时用第二个公式 . （2）如果公比 q 是一个字母，在求和时要对公比是否为 1 进行讨论. （3）要把公式记准，通项公式 a n 中，q 的指数是 n -1，前 n 项和公式 S n 中， q 的指数是n.

例题解析
1 1 1 例1：已知等比数列 , , ??. 2 4 8 (1)求前8项之和． (2)求第5项到第10项的和． (3)求此数列前2n项中所

有偶数项的和．解：

1 1 (1 ? 8 ) 2 2 ? 255 , (1) S8 ? 1 256 1? 2

1 1 1 例1、已知等比数列 , , ??. 2 4 8 (2)求第5项到第10项的和．解： 2)S ? a ? a ? a ? a ? a ? a , ( 5 6 7 8 9 10

1 1 5 ?1 1 5 1 但首项是确定 ? 6, q ? , a5 ? ? ( ) ? ( ) , n 2 2 2 2 1 1 10 1 1 4 1 1 6 此题也可用5 (1 ? ( ) ) (1 ? ( ) )
( ) [1 ? ( ) ] S ? S10 ? S 4 ? 2 1 2 10 2 2 ? ( 1 ) 4 ? ( )1 . ?S ? 1? 1 2 2 解得． 1? 2 2
?2 2 1 1? 2

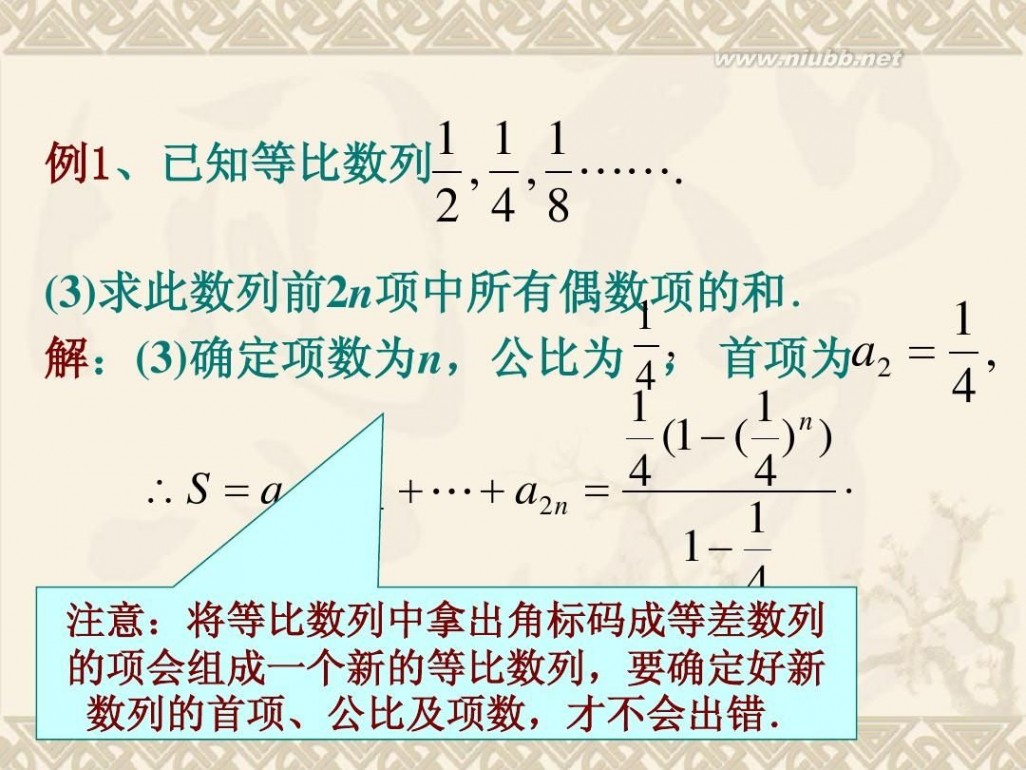
1 1 1 例1、已知等比数列 , , ??. 2 4 8
(3)求此数列前2n项中所有偶数项的和． 1 1 , 解：(3)确定项数为n，公比为 4 ，首项为a2 ? , 4 1 1 n (1 ? ( ) ) 4 ? ? S ? a2 ? a4 ? ? ? a2 n ? 4 1 1? 4
注意：将等比数列中拿出角标码成等差数列的项会组成一个新的等比数列，要确定好新数列的首项、公比及项数，才不会出错．

例 2 、某商场第 1 年销售计算机 5000 台，如果平均每年的销售量比上一年增加 10%，那么从第 1 年起，约几年内可使总销售量达到 30 000台（保留到个位）？分析：根据题意，每年销售量比上一年增加的百分数相同，所以从第一年起，每年的销售量组成一个等比数列 { a n }，其中， a 1 = 5000 ，q = 1+10% = 1.1，S n = 30000，代入等比数列求和公式，即可得关于 n 的一个方程，解方程即可求得 n .（解答见教材）

例3 、等比数列{an}中，S2=7,S6=91,求S4．解：由题设有：当q=1时，不满足上面条件， 2 当q≠1时，

(1 ? q 6 ) ? 13,? q 4 ? q 2 ? 1 ? 13, (2)÷(1)得： 1 ? q2 解得 q 2 ? 3, q 2 ? ?4 (舍去)．

? a1 (1 ? q ) ? S 2 ? 1 ? q ? 7 (1) ? ? a1 (1 ? q 6 ) ?S 6 ? ? 91 (2) ? 1? q ?

4 a1 7 a1 (1 ? q ) 2=3代人(1)得 ? ? ?? S 4 ? 将q ? 28. 1?q 2 1? q

? 说明：

(1)前面在等比数列一节中，已经分析了在等比数列解题中的运算特点，在本节牵涉到和的运算中，仍要注意消元方法；

(2)另外在和的运算中，还要注意整体意 a1 识，即将 1?q 作为一整体求解； (3)另外还要注意：套用求和公式时是在 q≠1的时候成立的，要注意讨论 q是否能为 1．

例4.（2009 辽宁理）设等比数列{an}的前n 项和为Sn，若 S9 S6 =3 ，则 = B S6 S3 7 8 （A） 2 （B）（C) （D）3 3 3
S6 (1 ? q3 ) S3 ? 解析: 设公比为q ,则 =1＋q3=3 ? q3=2 S3 S3
w.w.w.k.s.5.u.c.o.m

于是

S9 1 ? q 3 ? q 6 1 ? 2 ? 4 7 ? ? ? 3 S6 1? q 1? 2 3

例5、已知{an}为等比数列, 且Sn=a, S2n=b,（ab≠0），求S3n．解法一：设等比数列{an}的公比为q．若q=1（此时数列为常数列），则 Sn=na1=a, S2n=2na1=b, 从而有2a=b ∴S3n=3na1=3a (或 S3n= 3 b ).
2

若q≠1（即2a≠b），由已知
a1 (1 ? q 2 n ) a1 (1 ? q ) ?b (2) Sn ? ? a (1) S2 n ? 1? q 1? q b n b n 又 ab ≠0 (2)÷(

1)得 1 ? q ? q ? ? 1 (3) a a 2
n

将(3)代入(1)，得

a1 a ? 1 ? q 2a ? b

a1 (1 ? q ) a1 3n ? S3 n ? ? ? (1 ? q ) 1? q 1? q
3n

a2 b 3 ? ? [1 ? ( ? 1) ] 2a ? b a 2 2 a ? ab ? b ? a
（解法二：见练习）

练习
? 1.

教科书练习 1、2． 2.辨析下面证法：
已知数列{an}是等比数列，Sn是前n项和，证明： S7, S14-S7, S21-S14成等比数列．

a1 (1 ? q 21 ) a1 (1 ? q ) a1 (1 ? q ) , 证明:S 7 ? , S 21 ? , S14 ? 1? q 1? q 1? q a1q 7 (1 ? q 7 ) S ? S ? a1q14 (1 ? q 7 ) , ? S14 ? S7 ? , 21 14 1? q 1? q
7
14

a12 q14 (1 ? q 7 ) 2 ( S14 ? S 7 ) 2 ? , 2 (1?q)

a1 (1 ? q 7 ) a1q14 (1 ? q 7 ) a12 q14 (1 ? q 7 ) 2 S7 (S 21 ? S14 ) ? ? ? , 2 (1?q) 1? q 1? q

? S7 (S21 ? S14 ) ? (S14 ? S7 ) ,
2

? S7 , S14 ? S7 , S21 ? S14 成等比数列．
评析: 套用求和公式时是在q≠1的时候成立的，要注意讨论q是否能为l．所以,上面的证明是在q≠1的时候成立,当q=1时,S7=7a1,S14=14a1,S21=21a1,…可证之.

所以对公比q为字母时一定要有讨论意识．

3、{an}是等比数列，Sn是其前n项和，数列Sk, S2k-Sk, S3k-S2k,(k∈N*）是否仍成等比数列？
解析：①当q=－1且k为偶数时， Sk, S2k-Sk,S3k-S2k，不是等比数列.∵此时， Sk= S2k-Sk=S3k-S2k=0

＝

（＝

王新敞
奎屯

新疆

评述：应注意等比数列 ②当q≠－1或k为奇数时，中的公比q的 Sk＝a1+a2+a3+· · k≠0 ·+a 各种取值情况的讨论， S2k-Sk＝pk(a1+a2+a3+· · k)≠0 ·+a 还易忽视等 S3k-S2k＝p2k(a1+a2+a3+· · k)≠0 ·+a 比数列的各项应全不为0 ? Sk, S2k-Sk,S3k-S2k,(k∈N*）成等比数列的前提条件. （

例5 解法二：由Sn, S2n-Sn,S3n-S2n,(n∈N*）成等比数列
即 a, b-a, S3n－b成等比数列，所以a(S3n －b)=( b-a)2

从而有 S3n=

a 2 ? ab ? b 2 （包含了q=1的情况） a

小结
1.等比数列前n项和公式
a1 (1 ? q ) Sn ? (q ? 1) ? 1? q
n

a1 ? an q Sn ? 1? q

(q ? 1). ?
(q ? 1)

Sn ? na1

2.熟悉并应用公式，要掌握好错位相减法．