一 : IBM报告:七成“程序猿”年龄小于30岁
原标题:七成“程序猿”年龄小于30岁
IBM发布《2015中国开发者调查报告》显示
北京晨报讯(记者韩元佳)“程序猿”越来越年轻了,80后和90后已成为中国开发者群体的中坚力量。在昨日召开的IBM Bluemix云计算大会上,IBM携手服务平台CSDN共同发布《2015中国开发者调查报告》显示,21岁至35岁的开发者人数已88%,其中年龄在30岁以下的开发者占比达七成。
该报告针对来自北上广深等20多座城市、30个行业、500多家企业的超过1200名开发者进行的调查结果显示,80后与90后已是中国开发者群的中坚力量,70%的开发者年龄小于30岁。在研究方向上,65%的开发者在关注云计算、大数据相关技术,超过半数的开发者在关注移动开发、物联网等相关技术。
企业对优秀的开发者相当饥渴,1个优秀的开发人员平均有5个公司在争抢,APP和大数据技术的开发人才更是成为最抢手的香饽饽。但68%的开发者表示,由于新技术更新太快,没有时间进行系统性的学习。
随着移动互联网和智能终端的发展,开发者年龄更年轻,小而美的团队也更多,吸引更多大公司的关注。去年年中,IBM首次全面针对开发者推出名为Bluemix的云计算平台。IBM大中华区云计算及软件业务总经理胡世忠表示:“我们正在迎来一个属于开发者的时代,各种移动应用和云计算应用逐渐成为人们消费主流,IBM要以合作伙伴的心态拥抱开发者与创业者。”
二 : NPM小结 - 程序猿小卡
nodejs的出现,可以算是前端里程碑式的一个事件,它让前端攻城狮们摆脱了浏览器的束缚,踏上了一个更加宽广的舞台。[www.61k.com)前端的可能性,从此更加具有想象空间。
随着一系列基于nodes的应用/工具的出现,工作中与nodejs打交道的机会越来越多。无论在node应用的开发,还是使用中,包管理都扮演着一个很重要的作用。NPM(node package manager),作为node的包管理工具,极大地便利了我们的开发工作,很有必要了解一下。
NPM是什么
NPM(node package manager),通常称为node包管理器。顾名思义,它的主要功能就是管理node包,包括:安装、卸载、更新、查看、搜索、发布等。
npm的背后,是基于couchdb的一个数据库,详细记录了每个包的信息,包括作者、版本、依赖、授权信息等。它的一个很重要的作用就是:将开发者从繁琐的包管理工作(版本、依赖等)中解放出来,更加专注于功能的开发。
npm官网:
我们需要了解什么
npm包安装模式
在具体介绍npm包的管理之前,我们首先得来了解一下npm包的两种安装模式。
本地安装 vs 全局安装(重要)
node包的安装分两种:本地安装、全局安装。两者的区别如下,后面会通过简单例子说明
npm install pkg - 本地安装
运行如下命令,就会在当前目录下安装grunt-cli(grunt命令行工具)
npm install grunt-cli安装结束后,当前目录下回多出一个node_modules目录,grunt-cli就安装在里面。同时注意控制台输出的信息:
grunt-cli@0.1.9node_modules/grunt-cli
├──resolve@0.3.1
├──nopt@1.0.10(abbrev@1.0.4)
└──findup-sync@0.1.2(lodash@1.0.1,glob@3.1.21)
简单说明一下:
npm install -g pkg- 全局安装
上面已经安装了grunt-cli,然后你跑到其他目录下面运行如下命令
grunt果断提示你grunt命令不存在,为什么呢?因为上面只是进行了本地安装,grunt命令只能在对应安装目录下使用。
-bash: grunt: command not found如果为了使用grunt命令,每到一个目录下都得重新安装一次,那不抓狂才怪。肿么办呢?
很简单,采用全局安装就行了,很简单,加上参数-g就可以了
npm install -g grunt-cli于是,在所有目录下都可以无压力使用grunt命令了。这个时候,你会注意到控制台输入的信息有点不同。主要的区别在于安装目录,现在变成了/usr/local/lib/node_modules/grunt-cli,/usr/local/lib/node_modules/也就是之前所说的全局安装目录啦。
grunt-cli@0.1.9/usr/local/lib/node_modules/grunt-cli
├──resolve@0.3.1
├──nopt@1.0.10(abbrev@1.0.4)
└──findup-sync@0.1.2(lodash@1.0.1,glob@3.1.21)
npm包管理
npm的包管理命令是使用频率最高的,所以也是我们需要牢牢记住并熟练使用的。其实无非也就是几个动作:安装、卸载、更新、查看、搜索、发布等。
安装最新版本的grunt-cli
npm install grunt-cli安装0.1.9版本的grunt-cli
npm installgrunt-cli@"0.1.9"通过package.json进行安装
如果我们的项目依赖了很多package,一个一个地安装那将是个体力活。我们可以将项目依赖的包都在package.json这个文件里声明,然后一行命令搞定
npm install其他package安装命令
运行如下命令,列出所有npm install可能的参数形式
npm install --help输出如下,有兴趣的童鞋可以了解下
npm install <tarball file>npm install <tarball url>npm install <folder>npm install <pkg>npm install <pkg>@<tag>npm install <pkg>@<version>npm install <pkg>@<version range>卸载grunt-cli
比如卸载grunt-cli
npm uninstall grunt-cli卸载0.1.9版本的grunt-cli
npm uninstallgrunt-cli@"0.1.9"npm ls:查看安装了哪些包
运行如下命令,就可以查看当前目录安装了哪些package
npm ls输出如下
/private/tmp/npm└─┬grunt-cli@0.1.9 ├─┬findup-sync@0.1.2 │ ├─┬glob@3.1.21 │ │ ├──graceful-fs@1.2.3 │ │ ├──inherits@1.0.0 │ │ └─┬minimatch@0.2.12 │ │ ├──lru-cache@2.3.0 │ │ └──sigmund@1.0.0 │ └──lodash@1.0.1 ├─┬nopt@1.0.10 │ └──abbrev@1.0.4 └──resolve@0.3.1输出如下,同样,如果是要查看package的全局安装信息,加上-g就可以
npm ls pkg:查看特定package的信息
运行如下命令,输出grunt-cli的信息
npm ls grunt-cli输出的信息比较有限,只有安装目录、版本,如下:
/private/tmp/npm└──grunt-cli@0.1.9如果要查看更详细信息,可以通过npm info pkg,输出的信息非常详尽,包括作者、版本、依赖等。
npm info grunt-clinpm update pkg:package更新
npm update grunt-clinpm search pgk:搜索
输入如下命令
npm search grunt-cli返回结果如下
npm http GEThttp://registry.npmjs.org/-/all/since?stale=update_after&startkey=1375519407838npm http 200http://registry.npmjs.org/-/all/since?stale=update_after&startkey=1375519407838NAME DESCRIPTION AUTHOR DATE KEYWORDSgrunt-cli The grunt command line interface. =cowboy =tkellen 2013-07-27 02:24grunt-cli-dev-exitprocess The grunt command line interface. =dnevnik 2013-03-11 16:19grunt-client-compiler Grunt wrapper for client-compiler. =rubenv 2013-03-26 09:15 gruntplugingrunt-clientside Generate clientside js code from CommonJS modules =jga 2012-11-07 01:20 gruntpluginnpm发布
这个命令我自己也还没实际用过,不误导大家,语法如下,也可参考官方对于package发布的说明:
npm publish <tarball>npm publish <folder>NPM配置
npm的配置工作主要是通过npm config命令,主要包含增、删、改、查几个步骤,下面就以最为常用的proxy配置为例。
设置proxy
内网使用npm很头痛的一个问题就是代理,假设我们的代理是 http://proxy.example.com:8080,那么命令如下:
npm config set proxyhttp://proxy.example.com:8080由于npm config set命令比较常用,于是可以如下简写
npm set proxyhttp://proxy.example.com:8080 查看proxy
设置完,我们查看下当前代理设置
npm config get proxy输出如下:
http://proxy.example.com:8080/同样可如下简写:
npm get proxy删除proxy
代理不需要用到了,那删了吧
npm delete proxy查看所有配置
npm config list直接修改配置文件
有时候觉得一条配置一条配置地修改有些麻烦,就直接进配置文件修改了
npm config edit关于package.json
这货在官网似乎没有详细的描述,其实就是包的描述信息啦。假设当我们下载了node应用,这个node应用依赖于A、B、C三个包,如果没有package.json,我们需要人肉安装这个三个包(如果对版本有特定要求就更悲剧了):
npm install Anpm install Bnpm install C有了package.json,一行命令安装所有依赖。
npm installpackage.json字段简介
字段相当多,但最重要的的是下面几个
package版本
在package.json里,你经常会在包名后看到类似"~0.1.0"这样的字符串,这就是包的版本啦。下面会列举最常见的版本声明形式,以及版本书写的要求:
常见版本声明形式
a、"~1.2.3" 是神马意思呢,看下面领悟
"~1.2.3" = ">=1.2.3 <1.3.0""~1.2" = ">=1.2.0 <1.3.0""~1" = ">=1.0.0 <1.1.0"b、"1.x.x"是什么意思呢,继续自行领悟
"1.2.x" = ">=1.2.0 <1.3.0""1.x.x" = ">=1.0.0 <2.0.0""1.2" = "1.2.x""1.x" = "1.x.x""1" = "1.x.x"版本书写要求
写在后面
内容只是简单地把最常见的命令,以及一些需要了解的内容列了出来。如要进一步了解,可参考官网说明。此外,npm help是我们最好的朋友,如果忘了有哪些命令,命令下有哪些参数,可通过help进行查看。
最关键的:如果文章内容有误,请指出!!!
三 : 逗比之——程序猿装逼手冊(进阶版)

1. 着装
一根牛X的程序猿是根本没有时间打理自己外貌的,发型就要像爱因斯坦一样,顶着一脑袋鸡窝,凌乱蓬松美,给人随时能从头发里掏出一个鸡蛋的感觉。[ www.61k.com )胡子一大把,彰显自信又从容,不近视则以,近视就要戴酒瓶底子那么厚的大眼镜,一种科研工作者的风格。牛X程序猿对自己着装是有高要求的,不管是春夏秋冬,白天晚上,刮风下雨,一个牛X的程序猿都要十分在意自己着装,T恤+大花裤衩子+拖鞋是标配,一年365天风雨无阻。换衣服保持一年3-5件T恤的更新频率就能够,T恤大多是參见开源大会免费获得的,上面印着ruby on rails、eclipse、apache……天冷的实在熬不住了,就弄一个大棉脑,大耳包,款式任意,把自己裹上,以冻不死为标准。
2.装备
程序猿电脑配置都极高,可是外表非常糟烂,磕碰的外表+沾满了炉灰渣滓的破包,随背随走。开会的时候,把笔记本往桌子上一砸,咣当一声,掉一堆烟灰和方便面渣。从不用壁纸,无不论什么美化,给人一种WIN98的感觉。仅仅装文本编辑器+开发工具软件。越简朴越纯粹,代表你越牛X。能不用IDE就不要用,实在装不了,不管IDE是什么,一定要调成DOS或linux那种黑色背景的,给人一种你随时敲几行代码,朝鲜的大浦洞导弹就要射向白宫的感觉。牛X程序猿的桌面必须乱糟糟一大片,开发文档,代码,图片混杂当中,除了自己没有人能知道核心文件放哪了,进来商业间谍想偷都偷不走,可是须要指定文件的时候,自己分分钟就能找到。
3.环境
程序猿不用和客户直接打交道,办公室一般选在阴暗的角落里即可了。硕大的办公桌上,至少要摆两台电脑,一个笔记本,一个台式连接双显示器,一个横屏,一个竖屏。竖屏编写代码,横屏调试效果。显示出你信息量非常大,效率非常高。桌子上能够任意放几本书,一定要是英文原版,最次也是影印版,越厚越好,不要整齐的罗列在书架上,一定要堆在桌上,半打开状,上面全是手印子,菜汤,大鼻涕。其它锅碗瓢盆,方便面,快餐盒子任意摆放,显示出你废寝忘食的工作状态,让人刮目相看。
4.工作
提溜一个糖水黄桃罐头瓶,放在桌边,坐下以后,脖子稍微后仰,翘着二郎腿,低头盯着屏幕看需求。最好点一根烟,牌子无所谓,能冒烟即可,要得就是云山雾绕的感觉,从烟雾中眯着眼睛看出去,一副胸有成竹的样。一根烟抽完,流程图也在脑子里走完了,啪一下把烟头掐灭到茶缸子里。再点燃一根,開始闷声写程序。心无旁骛的专心敲,烟灰都不要弹,敲好之后,编译,调试,再编译,再调试,功能跑通,SVN提交代码。(地震火灾,也一定要先提交代码再行离开),“啪”,笔记本合上,下班走人,喝啤酒撸串子去了。
5.经历
程序猿在一起最喜欢的就是吹牛X,谈一些什么时尚炫酷的技术,整个啥云计算,web3.0,移动互联网开发……你要是也谈论这些,你就too young了,太低端。那玩意各大IT站点哪都有,一抓一大把,都被人说烂了。至少你也得谈点什么小榕,流光,冰河木马显示出你一个有资历的老黑客,再高一点的,默默的点燃一根红梅,拿出一张泛黄的照片:“这是我们1999年美国炸中国大使馆后,中国黑客联盟集体黑掉美国各大站点之后的合影留念。当年的这些人被招安的招安,卖烧饼的卖烧饼去了,中国黑客联盟也随着历史烟消云散了。” 望着窗外淅淅沥沥的小雨,若有所思的惆怅。
“老大,那您当年的肉鸡一定非常多吧?能有多少啊?DDOS吗?”
“呵呵,呵呵。”
深藏功与名。
6.情感
谈到情感,不得不说这是程序猿的硬伤。程序猿通常都是智商非常高,情商却非常低。我每次谈恋爱,都是在loop循环里面用select语句,循环一次,就须要遍历,select一次,而不是所有select出来,然后再剔除。这都是深受谭浩强的垃圾0基础读物《C语言程序设计》的毒害。造成了大量时间的损耗和我体能的透支。我把我敲代码的思维用在了恋爱上,恋爱的时候脑子里是一张大大的流程图。都是IF,Y的时候走一条路,N的时候走还有一条路,没有第三条路的选择。就是爱约约,不约滚的节奏,这也导致了我多次被人利用却无法辩解。所以,这一章节,我自己眼下还仍在研究之中。
四 : 教你透彻了解红黑树 - Jessica程序猿
概要
目录
1 红黑树的介绍
2 红黑树的应用
3 红黑树的时间复杂度和相关证明
4 红黑树的基本操作(一) 左旋和右旋
5 红黑树的基本操作(二) 添加
6 红黑树的基本操作(三) 删除
作者:Sky Wang 于 2013-08-08
概述:R-B Tree,又称为“红黑树”。(www.61k.com]本文参考了《算法导论》中红黑树相关知识,加之自己的理解,然后以图文的形式对红黑树进行说明。本文的主要内容包括:红黑树的特性,红黑树的时间复杂度和它的证明,红黑树的左旋、右旋、插入、删除等操作。
请尊重版权,转载注明出处:
更多内容: 数据结构与算法系列 目录
(01)红黑树(一)之 原理和算法详细介绍
(02) 红黑树(二)之 C语言的实现
(03)
红黑树(三)之 Linux内核中红黑树的经典实现
(04)红黑树(四)之 C++的实现
(05) 红黑树(五)之 Java的实现R-B Tree简介
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意:
(01) 特性(3)中的叶子节点,是只为空(NIL或null)的节点。
(02) 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
红黑树示意图如下:

红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
红黑树的时间复杂度和相关证明
红黑树的时间复杂度为: O(lgn)
下面通过“数学归纳法”对红黑树的时间复杂度进行证明。
定理:一棵含有n个节点的红黑树的高度至多为2log(n+1).
证明:
"一棵含有n个节点的红黑树的高度至多为2log(n+1)" 的逆否命题是 "高度为h的红黑树,它的包含的内节点个数至少为 2h/2-1个"。
我们只需要证明逆否命题,即可证明原命题为真;即只需证明 "高度为h的红黑树,它的包含的内节点个数至少为 2h/2-1个"。
从某个节点x出发(不包括该节点)到达一个叶节点的任意一条路径上,黑色节点的个数称为该节点的黑高度(x's black height),记为bh(x)。关于bh(x)有两点需要说明:
第1点:根据红黑树的"特性(5) ,即从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点"可知,从节点x出发到达的所有的叶节点具有相同数目的黑节点。这也就意味着,bh(x)的值是唯一的!
第2点:根据红黑色的"特性(4),即如果一个节点是红色的,则它的子节点必须是黑色的"可知,从节点x出发达到叶节点"所经历的黑节点数目">= "所经历的红节点的数目"。假设x是根节点,则可以得出结论"bh(x) >= h/2"。进而,我们只需证明 "高度为h的红黑树,它的包含的黑节点个数至少为 2bh(x)-1个"即可。
到这里,我们将需要证明的定理已经由
"一棵含有n个节点的红黑树的高度至多为2log(n+1)"
转变成只需要证明
"高度为h的红黑树,它的包含的内节点个数至少为 2bh(x)-1个"。
下面通过"数学归纳法"开始论证高度为h的红黑树,它的包含的内节点个数至少为 2bh(x)-1个"。
(01) 当树的高度h=0时,
内节点个数是0,bh(x) 为0,2bh(x)-1 也为 0。显然,原命题成立。
(02) 当h>0,且树的高度为 h-1 时,它包含的节点个数至少为 2bh(x)-1-1。这个是根据(01)推断出来的!
下面,由树的高度为 h-1 的已知条件推出“树的高度为 h 时,它所包含的节点树为 2bh(x)-1”。
当树的高度为 h 时,
对于节点x(x为根节点),其黑高度为bh(x)。
对于节点x的左右子树,它们黑高度为 bh(x) 或者 bh(x)-1。
根据(02)的已知条件,我们已知 "x的左右子树,即高度为 h-1 的节点,它包含的节点至少为 2bh(x)-1-1 个";
所以,节点x所包含的节点至少为 ( 2bh(x)-1-1 ) + ( 2bh(x)-1-1 ) + 1 = 2^bh(x)-1。即节点x所包含的节点至少为 2bh(x)-1。
因此,原命题成立。
由(01)、(02)得出,"高度为h的红黑树,它的包含的内节点个数至少为 2^bh(x)-1个"。
因此,“一棵含有n个节点的红黑树的高度至多为2log(n+1)”。
红黑树的基本操作(一) 左旋和右旋 61阅读请您转载分享:
红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后,都会用到旋转方法。为什么呢?道理很简单,添加或删除红黑树中的节点之后,红黑树就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。
旋转包括两种:左旋 和 右旋。下面分别对它们进行介绍。
1. 左旋
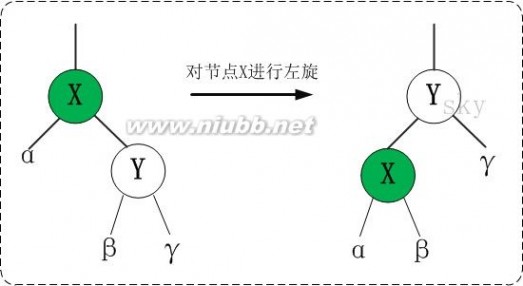
对x进行左旋,意味着"将x变成一个左节点"。
左旋的伪代码《算法导论》:参考上面的示意图和下面的伪代码,理解“红黑树T的节点x进行左旋”是如何进行的。
LEFT-ROTATE(T, x) 01 y ← right[x] // 前提:这里假设x的右孩子为y。下面开始正式操作02 right[x] ← left[y] // 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子03 p[left[y]] ← x // 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x04 p[y] ← p[x] // 将 “x的父亲” 设为 “y的父亲”05 if p[x] = nil[T] 06 then root[T] ← y // 情况1:如果 “x的父亲” 是空节点,则将y设为根节点07 else if x = left[p[x]] 08 then left[p[x]] ← y // 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”09 else right[p[x]] ← y // 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”10 left[y] ← x // 将 “x” 设为 “y的左孩子”11 p[x] ← y // 将 “x的父节点” 设为 “y”
理解左旋之后,看看下面一个更鲜明的例子。你可以先不看右边的结果,自己尝试一下。

2. 右旋
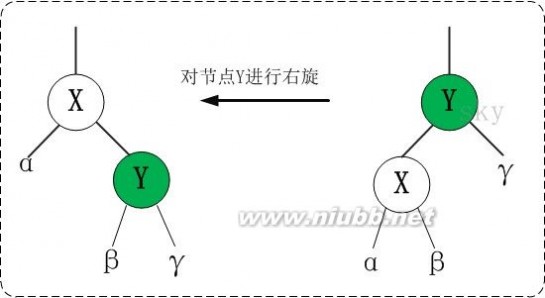
对x进行左旋,意味着"将x变成一个左节点"。
右旋的伪代码《算法导论》:参考上面的示意图和下面的伪代码,理解“红黑树T的节点y进行右旋”是如何进行的。
RIGHT-ROTATE(T, y) 01 x ← left[y] // 前提:这里假设y的左孩子为x。下面开始正式操作02 left[y] ← right[x] // 将 “x的右孩子” 设为 “y的左孩子”,即 将β设为y的左孩子03 p[right[x]] ← y // 将 “y” 设为 “x的右孩子的父亲”,即 将β的父亲设为y04 p[x] ← p[y] // 将 “y的父亲” 设为 “x的父亲”05 if p[y] = nil[T] 06 then root[T] ← x // 情况1:如果 “y的父亲” 是空节点,则将x设为根节点07 else if y = right[p[y]] 08 then right[p[y]] ← x // 情况2:如果 y是它父节点的右孩子,则将x设为“y的父节点的左孩子”09 else left[p[y]] ← x // 情况3:(y是它父节点的左孩子) 将x设为“y的父节点的左孩子”10 right[x] ← y // 将 “y” 设为 “x的右孩子”11 p[y] ← x // 将 “y的父节点” 设为 “x”
理解右旋之后,看看下面一个更鲜明的例子。你可以先不看右边的结果,自己尝试一下。
旋转总结:
(01) 左旋 和 右旋 是相对的两个概念,原理类似。理解一个也就理解了另一个。
(02) 下面谈谈如何区分 左旋 和 右旋。 在实际应用中,若没有彻底理解 左旋 和 右旋,可能会将它们混淆。下面谈谈我对如何区分 左旋 和 右旋 的理解。
3. 区分 左旋 和 右旋
仔细观察上面"左旋"和"右旋"的示意图。我们能清晰的发现,它们是对称的。无论是左旋还是右旋,被旋转的树,在旋转前是二叉查找树,并且旋转之后仍然是一颗二叉查找树。

左旋示例图(以x为节点进行左旋):
z x / / \ --(左旋)--> x y z / y
对x进行左旋,意味着,将“x的右孩子”设为“x的父亲节点”;即,将 x变成了一个左节点(x成了为z的左孩子)!。 因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
右旋示例图(以x为节点进行右旋):
y x \ / \ --(右旋)--> x y z \ z
对x进行右旋,意味着,将“x的左孩子”设为“x的父亲节点”;即,将 x变成了一个右节点(x成了为y的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
红黑树的基本操作(二) 添加
将一个节点插入到红黑树中,需要执行哪些步骤呢?首先,将红黑树当作一颗二叉查找树,将节点插入;然后,将节点着色为红色;最后,通过旋转和重新着色等方法来修正该树,使之重新成为一颗红黑树。详细描述如下:
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
红黑树本身就是一颗二叉查找树,将节点插入后,该树仍然是一颗二叉查找树。也就意味着,树的键值仍然是有序的。此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。这也就意味着,任何的旋转和重新着色操作,都不会改变它仍然是一颗二叉查找树的事实。
61阅读请您转载分享:
好吧?那接下来,我们就来想方设法的旋转以及重新着色,使这颗树重新成为红黑树!
第二步:将插入的节点着色为"红色"。
为什么着色成红色,而不是黑色呢?为什么呢?在回答之前,我们需要重新温习一下红黑树的特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
将插入的节点着色为红色,不会违背"特性(5)"!少违背一条特性,就意味着我们需要处理的情况越少。接下来,就要努力的让这棵树满足其它性质即可;满足了的话,它就又是一颗红黑树了。o(∩∩)o...哈哈
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
第二步中,将插入节点着色为"红色"之后,不会违背"特性(5)"。那它到底会违背哪些特性呢?
对于"特性(1)",显然不会违背了。因为我们已经将它涂成红色了。
对于"特性(2)",显然也不会违背。在第一步中,我们是将红黑树当作二叉查找树,然后执行的插入操作。而根据二叉查找数的特点,插入操作不会改变根节点。所以,根节点仍然是黑色。
对于"特性(3)",显然不会违背了。这里的叶子节点是指的空叶子节点,插入非空节点并不会对它们造成影响。
对于"特性(4)",是有可能违背的!
那接下来,想办法使之"满足特性(4)",就可以将树重新构造成红黑树了。
下面看看代码到底是怎样实现这三步的。
添加操作的伪代码《算法导论》
RB-INSERT(T, z) 01 y ← nil[T] // 新建节点“y”,将y设为空节点。02 x ← root[T] // 设“红黑树T”的根节点为“x”03 while x ≠ nil[T] // 找出要插入的节点“z”在二叉树T中的位置“y”04 do y ← x 05 if key[z] < key[x] 06 then x ← left[x] 07 else x ← right[x] 08 p[z] ← y // 设置 “z的父亲” 为 “y”09 if y = nil[T] 10 then root[T] ← z // 情况1:若y是空节点,则将z设为根11 else if key[z] < key[y] 12 then left[y] ← z // 情况2:若“z所包含的值” < “y所包含的值”,则将z设为“y的左孩子”13 else right[y] ← z // 情况3:(“z所包含的值” >= “y所包含的值”)将z设为“y的右孩子” 14 left[z] ← nil[T] // z的左孩子设为空15 right[z] ← nil[T] // z的右孩子设为空。至此,已经完成将“节点z插入到二叉树”中了。16 color[z] ← RED // 将z着色为“红色”17 RB-INSERT-FIXUP(T, z) // 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转,让树T仍然是一颗红黑树
结合伪代码以及为代码上面的说明,先理解RB-INSERT。理解了RB-INSERT之后,我们接着对 RB-INSERT-FIXUP的伪代码进行说明。
添加修正操作的伪代码《算法导论》
RB-INSERT-FIXUP(T, z)01 while color[p[z]] = RED // 若“当前节点(z)的父节点是红色”,则进行以下处理。02 do if p[z] = left[p[p[z]]] // 若“z的父节点”是“z的祖父节点的左孩子”,则进行以下处理。03 then y ← right[p[p[z]]] // 将y设置为“z的叔叔节点(z的祖父节点的右孩子)”04 if color[y] = RED // Case 1条件:叔叔是红色05 then color[p[z]] ← BLACK ? Case 1 // (01) 将“父节点”设为黑色。06 color[y] ← BLACK ? Case 1 // (02) 将“叔叔节点”设为黑色。07 color[p[p[z]]] ← RED ? Case 1 // (03) 将“祖父节点”设为“红色”。08 z ← p[p[z]] ? Case 1 // (04) 将“祖父节点”设为“当前节点”(红色节点)09 else if z = right[p[z]] // Case 2条件:叔叔是黑色,且当前节点是右孩子10 then z ← p[z] ? Case 2 // (01) 将“父节点”作为“新的当前节点”。11 LEFT-ROTATE(T, z) ? Case 2 // (02) 以“新的当前节点”为支点进行左旋。12 color[p[z]] ← BLACK ? Case 3 // Case 3条件:叔叔是黑色,且当前节点是左孩子。(01) 将“父节点”设为“黑色”。13 color[p[p[z]]] ← RED ? Case 3 // (02) 将“祖父节点”设为“红色”。14 RIGHT-ROTATE(T, p[p[z]]) ? Case 3 // (03) 以“祖父节点”为支点进行右旋。15 else (same as then clause with "right" and "left" exchanged) // 若“z的父节点”是“z的祖父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。16 color[root[T]] ← BLACK
根据被插入节点的父节点的情况,可以将"当节点z被着色为红色节点,并插入二叉树"划分为三种情况来处理。
① 情况说明:被插入的节点是根节点。
处理方法:直接把此节点涂为黑色。
② 情况说明:被插入的节点的父节点是黑色。
处理方法:什么也不需要做。节点被插入后,仍然是红黑树。
③ 情况说明:被插入的节点的父节点是红色。
处理方法:那么,该情况与红黑树的“特性(5)”相冲突。这种情况下,被插入节点是一定存在非空祖父节点的;进一步的讲,被插入节点也一定存在叔叔节点(即使叔叔节点为空,我们也视之为存在,空节点本身就是黑色节点)。理解这点之后,我们依据"叔叔节点的情况",将这种情况进一步划分为3种情况(Case)。
| 现象说明 | 处理策略 | |
| Case 1 | 当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色。 | (01) 将“父节点”设为黑色。 (02) 将“叔叔节点”设为黑色。 (03) 将“祖父节点”设为“红色”。 (04) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。 |
| Case 2 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子 | (01) 将“父节点”作为“新的当前节点”。 (02) 以“新的当前节点”为支点进行左旋。 |
| Case 3 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子 | (01) 将“父节点”设为“黑色”。 (02) 将“祖父节点”设为“红色”。 (03) 以“祖父节点”为支点进行右旋。 |
上面三种情况(Case)处理问题的核心思路都是:将红色的节点移到根节点;然后,将根节点设为黑色。下面对它们详细进行介绍。
1. (Case 1)叔叔是红色
1.1 现象说明
当前节点(即,被插入节点)的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色。
1.2 处理策略
(01) 将“父节点”设为黑色。
(02) 将“叔叔节点”设为黑色。
(03) 将“祖父节点”设为“红色”。
(04) 将“祖父节点”设为“当前节点”(红色节点);即,之后继续对“当前节点”进行操作。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
“当前节点”和“父节点”都是红色,违背“特性(4)”。所以,将“父节点”设置“黑色”以解决这个问题。
但是,将“父节点”由“红色”变成“黑色”之后,违背了“特性(5)”:因为,包含“父节点”的分支的黑色节点的总数增加了1。 解决这个问题的办法是:将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”。关于这里,说明几点:第一,为什么“祖父节点”之前是黑色?这个应该很容易想明白,因为在变换操作之前,该树是红黑树,“父节点”是红色,那么“祖父节点”一定是黑色。 第二,为什么将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”;能解决“包含‘父节点’的分支的黑色节点的总数增加了1”的问题。这个道理也很简单。“包含‘父节点’的分支的黑色节点的总数增加了1” 同时也意味着 “包含‘祖父节点’的分支的黑色节点的总数增加了1”,既然这样,我们通过将“祖父节点”由“黑色”变成“红色”以解决“包含‘祖父节点’的分支的黑色节点的总数增加了1”的问题; 但是,这样处理之后又会引起另一个问题“包含‘叔叔’节点的分支的黑色节点的总数减少了1”,现在我们已知“叔叔节点”是“红色”,将“叔叔节点”设为“黑色”就能解决这个问题。 所以,将“祖父节点”由“黑色”变成红色,同时,将“叔叔节点”由“红色”变成“黑色”;就解决了该问题。
按照上面的步骤处理之后:当前节点、父节点、叔叔节点之间都不会违背红黑树特性,但祖父节点却不一定。若此时,祖父节点是根节点,直接将祖父节点设为“黑色”,那就完全解决这个问题了;若祖父节点不是根节点,那我们需要将“祖父节点”设为“新的当前节点”,接着对“新的当前节点”进行分析。
1.3 示意图

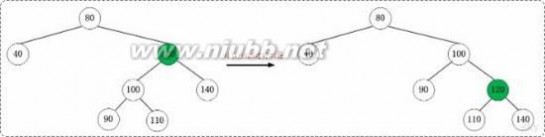
2. (Case 2)叔叔是黑色,且当前节点是右孩子
2.1 现象说明
当前节点(即,被插入节点)的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子
2.2 处理策略
(01) 将“父节点”作为“新的当前节点”。
(02) 以“新的当前节点”为支点进行左旋。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
首先,将“父节点”作为“新的当前节点”;接着,以“新的当前节点”为支点进行左旋。 为了便于理解,我们先说明第(02)步,再说明第(01)步;为了便于说明,我们设置“父节点”的代号为F(Father),“当前节点”的代号为S(Son)。
为什么要“以F为支点进行左旋”呢?根据已知条件可知:S是F的右孩子。而之前我们说过,我们处理红黑树的核心思想:将红色的节点移到根节点;然后,将根节点设为黑色。既然是“将红色的节点移到根节点”,那就是说要不断的将破坏红黑树特性的红色节点上移(即向根方向移动)。 而S又是一个右孩子,因此,我们可以通过“左旋”来将S上移!
按照上面的步骤(以F为支点进行左旋)处理之后:若S变成了根节点,那么直接将其设为“黑色”,就完全解决问题了;若S不是根节点,那我们需要执行步骤(01),即“将F设为‘新的当前节点’”。那为什么不继续以S为新的当前节点继续处理,而需要以F为新的当前节点来进行处理呢?这是因为“左旋”之后,F变成了S的“子节点”,即S变成了F的父节点;而我们处理问题的时候,需要从下至上(由叶到根)方向进行处理;也就是说,必须先解决“孩子”的问题,再解决“父亲”的问题;所以,我们执行步骤(01):将“父节点”作为“新的当前节点”。
61阅读请您转载分享:
2.2 示意图
3. (Case 3)叔叔是黑色,且当前节点是左孩子
3.1 现象说明
当前节点(即,被插入节点)的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子
3.2 处理策略
(01) 将“父节点”设为“黑色”。
(02) 将“祖父节点”设为“红色”。
(03) 以“祖父节点”为支点进行右旋。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“叔叔节点”为U(Uncle),“父节点”为F(Father),祖父节点为G(Grand-Father)。
S和F都是红色,违背了红黑树的“特性(4)”,我们可以将F由“红色”变为“黑色”,就解决了“违背‘特性(4)’”的问题;但却引起了其它问题:违背特性(5),因为将F由红色改为黑色之后,所有经过F的分支的黑色节点的个数增加了1。那我们如何解决“所有经过F的分支的黑色节点的个数增加了1”的问题呢? 我们可以通过“将G由黑色变成红色”,同时“以G为支点进行右旋”来解决。
2.3 示意图
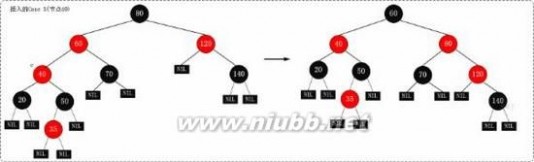
提示:上面的进行Case 3处理之后,再将节点"120"当作当前节点,就变成了Case 2的情况。
红黑树的基本操作(三) 删除
将红黑树内的某一个节点删除。需要执行的操作依次是:首先,将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除;然后,通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。详细描述如下:
第一步:将红黑树当作一颗二叉查找树,将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况:
① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空,就意味着"该节点的后继节点"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
删除操作的伪代码《算法导论》
RB-DELETE(T, z)01 if left[z] = nil[T] or right[z] = nil[T] 02 then y ← z // 若“z的左孩子” 或 “z的右孩子”为空,则将“z”赋值给 “y”;03 else y ← TREE-SUCCESSOR(z) // 否则,将“z的后继节点”赋值给 “y”。04 if left[y] ≠ nil[T]05 then x ← left[y] // 若“y的左孩子” 不为空,则将“y的左孩子” 赋值给 “x”;06 else x ← right[y] // 否则,“y的右孩子” 赋值给 “x”。07 p[x] ← p[y] // 将“y的父节点” 设置为 “x的父节点”08 if p[y] = nil[T] 09 then root[T] ← x // 情况1:若“y的父节点” 为空,则设置“x” 为 “根节点”。10 else if y = left[p[y]] 11 then left[p[y]] ← x // 情况2:若“y是它父节点的左孩子”,则设置“x” 为 “y的父节点的左孩子”12 else right[p[y]] ← x // 情况3:若“y是它父节点的右孩子”,则设置“x” 为 “y的父节点的右孩子”13 if y ≠ z 14 then key[z] ← key[y] // 若“y的值” 赋值给 “z”。注意:这里只拷贝z的值给y,而没有拷贝z的颜色!!!15 copy y's satellite data into z 16 if color[y] = BLACK 17 then RB-DELETE-FIXUP(T, x) // 若“y为黑节点”,则调用18 return y
结合伪代码以及为代码上面的说明,先理解RB-DELETE。理解了RB-DELETE之后,接着对 RB-DELETE-FIXUP的伪代码进行说明
RB-DELETE-FIXUP(T, x)01 while x ≠ root[T] and color[x] = BLACK 02 do if x = left[p[x]] 03 then w ← right[p[x]] // 若 “x”是“它父节点的左孩子”,则设置 “w”为“x的叔叔”(即x为它父节点的右孩子) 04 if color[w] = RED // Case 1: x是“黑+黑”节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。05 then color[w] ← BLACK ? Case 1 // (01) 将x的兄弟节点设为“黑色”。06 color[p[x]] ← RED ? Case 1 // (02) 将x的父节点设为“红色”。07 LEFT-ROTATE(T, p[x]) ? Case 1 // (03) 对x的父节点进行左旋。08 w ← right[p[x]] ? Case 1 // (04) 左旋后,重新设置x的兄弟节点。09 if color[left[w]] = BLACK and color[right[w]] = BLACK // Case 2: x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。10 then color[w] ← RED ? Case 2 // (01) 将x的兄弟节点设为“红色”。11 x ← p[x] ? Case 2 // (02) 设置“x的父节点”为“新的x节点”。12 else if color[right[w]] = BLACK // Case 3: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。13 then color[left[w]] ← BLACK ? Case 3 // (01) 将x兄弟节点的左孩子设为“黑色”。14 color[w] ← RED ? Case 3 // (02) 将x兄弟节点设为“红色”。15 RIGHT-ROTATE(T, w) ? Case 3 // (03) 对x的兄弟节点进行右旋。16 w ← right[p[x]] ? Case 3 // (04) 右旋后,重新设置x的兄弟节点。17 color[w] ← color[p[x]] ? Case 4 // Case 4: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的。(01) 将x父节点颜色 赋值给 x的兄弟节点。18 color[p[x]] ← BLACK ? Case 4 // (02) 将x父节点设为“黑色”。19 color[right[w]] ← BLACK ? Case 4 // (03) 将x兄弟节点的右子节设为“黑色”。20 LEFT-ROTATE(T, p[x]) ? Case 4 // (04) 对x的父节点进行左旋。21 x ← root[T] ? Case 4 // (05) 设置“x”为“根节点”。22 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。23 color[x] ← BLACK61阅读请您转载分享:
下面对删除函数进行分析。在分析之前,我们再次温习一下红黑树的几个特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
前面我们将"删除红黑树中的节点"大致分为两步,在第一步中"将红黑树当作一颗二叉查找树,将节点删除"后,可能违反"特性(2)、(4)、(5)"三个特性。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。
为了便于分析,我们假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。为什么呢?
通过RB-DELETE算法,我们知道:删除节点y之后,x占据了原来节点y的位置。 既然删除y(y是黑色),意味着减少一个黑色节点;那么,再在该位置上增加一个黑色即可。这样,当我们假设"x包含一个额外的黑色",就正好弥补了"删除y所丢失的黑色节点",也就不会违反"特性(5)"。 因此,假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。
现在,x不仅包含它原本的颜色属性,x还包含一个额外的黑色。即x的颜色属性是"红+黑"或"黑+黑",它违反了"特性(1)"。
现在,我们面临的问题,由解决"违反了特性(2)、(4)、(5)三个特性"转换成了"解决违反特性(1)、(2)、(4)三个特性"。RB-DELETE-FIXUP需要做的就是通过算法恢复红黑树的特性(1)、(2)、(4)。RB-DELETE-FIXUP的思想是:将x所包含的额外的黑色不断沿树上移(向根方向移动),直到出现下面的姿态:
a) x指向一个"红+黑"节点。此时,将x设为一个"黑"节点即可。
b) x指向根。此时,将x设为一个"黑"节点即可。
c) 非前面两种姿态。
将上面的姿态,可以概括为3种情况。
① 情况说明:x是“红+黑”节点。
处理方法:直接把x设为黑色,结束。此时红黑树性质全部恢复。
② 情况说明:x是“黑+黑”节点,且x是根。
处理方法:什么都不做,结束。此时红黑树性质全部恢复。
③ 情况说明:x是“黑+黑”节点,且x不是根。
处理方法:这种情况又可以划分为4种子情况。这4种子情况如下表所示:
| 现象说明 | 处理策略 | |
| Case 1 | x是"黑+黑"节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。 | (01) 将x的兄弟节点设为“黑色”。 (02) 将x的父节点设为“红色”。 (03) 对x的父节点进行左旋。 (04) 左旋后,重新设置x的兄弟节点。 |
| Case 2 | x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。 | (01) 将x的兄弟节点设为“红色”。 (02) 设置“x的父节点”为“新的x节点”。 |
| Case 3 | x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 | (01) 将x兄弟节点的左孩子设为“黑色”。 (02) 将x兄弟节点设为“红色”。 (03) 对x的兄弟节点进行右旋。 (04) 右旋后,重新设置x的兄弟节点。 |
| Case 4 | x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。 | (01) 将x父节点颜色 赋值给 x的兄弟节点。 (02) 将x父节点设为“黑色”。 (03) 将x兄弟节点的右子节设为“黑色”。 (04) 对x的父节点进行左旋。 (05) 设置“x”为“根节点”。 |
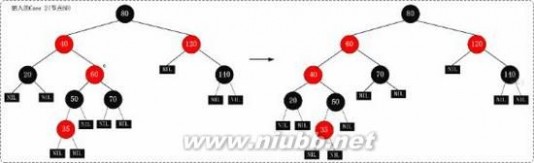
1. (Case 1)x是"黑+黑"节点,x的兄弟节点是红色
1.1 现象说明
x是"黑+黑"节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。
1.2 处理策略
(01) 将x的兄弟节点设为“黑色”。
(02) 将x的父节点设为“红色”。
(03) 对x的父节点进行左旋。
(04) 左旋后,重新设置x的兄弟节点。
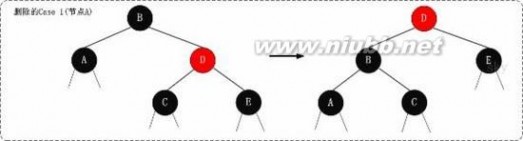
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
这样做的目的是将“Case 1”转换为“Case 2”、“Case 3”或“Case 4”,从而进行进一步的处理。对x的父节点进行左旋;左旋后,为了保持红黑树特性,就需要在左旋前“将x的兄弟节点设为黑色”,同时“将x的父节点设为红色”;左旋后,由于x的兄弟节点发生了变化,需要更新x的兄弟节点,从而进行后续处理。
1.3 示意图
2. (Case 2) x是"黑+黑"节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色
2.1 现象说明
x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。
2.2 处理策略
(01) 将x的兄弟节点设为“红色”。
(02) 设置“x的父节点”为“新的x节点”。
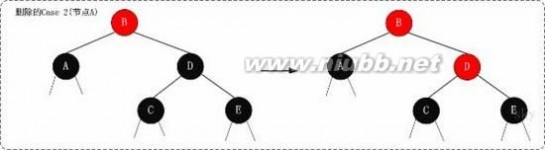
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
这个情况的处理思想:是将“x中多余的一个黑色属性上移(往根方向移动)”。 x是“黑+黑”节点,我们将x由“黑+黑”节点 变成 “黑”节点,多余的一个“黑”属性移到x的父节点中,即x的父节点多出了一个黑属性(若x的父节点原先是“黑”,则此时变成了“黑+黑”;若x的父节点原先时“红”,则此时变成了“红+黑”)。 此时,需要注意的是:所有经过x的分支中黑节点个数没变化;但是,所有经过x的兄弟节点的分支中黑色节点的个数增加了1(因为x的父节点多了一个黑色属性)!为了解决这个问题,我们需要将“所有经过x的兄弟节点的分支中黑色节点的个数减1”即可,那么就可以通过“将x的兄弟节点由黑色变成红色”来实现。
61阅读请您转载分享:
经过上面的步骤(将x的兄弟节点设为红色),多余的一个颜色属性(黑色)已经跑到x的父节点中。我们需要将x的父节点设为“新的x节点”进行处理。若“新的x节点”是“黑+红”,直接将“新的x节点”设为黑色,即可完全解决该问题;若“新的x节点”是“黑+黑”,则需要对“新的x节点”进行进一步处理。
2.3 示意图
3. (Case 3)x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的
3.1 现象说明
x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。
3.2 处理策略
(01) 将x兄弟节点的左孩子设为“黑色”。
(02) 将x兄弟节点设为“红色”。
(03) 对x的兄弟节点进行右旋。
(04) 右旋后,重新设置x的兄弟节点。
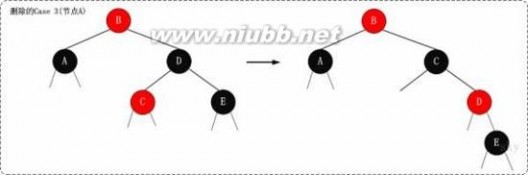
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
我们处理“Case 3”的目的是为了将“Case 3”进行转换,转换成“Case 4”,从而进行进一步的处理。转换的方式是对x的兄弟节点进行右旋;为了保证右旋后,它仍然是红黑树,就需要在右旋前“将x的兄弟节点的左孩子设为黑色”,同时“将x的兄弟节点设为红色”;右旋后,由于x的兄弟节点发生了变化,需要更新x的兄弟节点,从而进行后续处理。
3.3 示意图
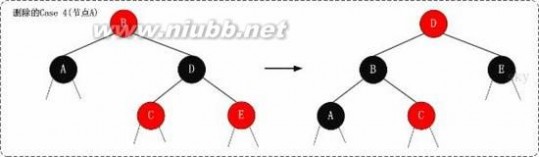
4. (Case 4)x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色
4.1 现象说明
x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。
4.2 处理策略
(01) 将x父节点颜色 赋值给 x的兄弟节点。
(02) 将x父节点设为“黑色”。
(03) 将x兄弟节点的右子节设为“黑色”。
(04) 对x的父节点进行左旋。
(05) 设置“x”为“根节点”。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
我们处理“Case 4”的目的是:去掉x中额外的黑色,将x变成单独的黑色。处理的方式是“:进行颜色修改,然后对x的父节点进行左旋。下面,我们来分析是如何实现的。
为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“兄弟节点的左孩子”为BLS(Brother's Left Son),“兄弟节点的右孩子”为BRS(Brother's Right Son),“父节点”为F(Father)。
我们要对F进行左旋。但在左旋前,我们需要调换F和B的颜色,并设置BRS为黑色。为什么需要这里处理呢?因为左旋后,F和BLS是父子关系,而我们已知BL是红色,如果F是红色,则违背了“特性(4)”;为了解决这一问题,我们将“F设置为黑色”。 但是,F设置为黑色之后,为了保证满足“特性(5)”,即为了保证左旋之后:
第一,“同时经过根节点和S的分支的黑色节点个数不变”。
若满足“第一”,只需要S丢弃它多余的颜色即可。因为S的颜色是“黑+黑”,而左旋后“同时经过根节点和S的分支的黑色节点个数”增加了1;现在,只需将S由“黑+黑”变成单独的“黑”节点,即可满足“第一”。
第二,“同时经过根节点和BLS的分支的黑色节点数不变”。
若满足“第二”,只需要将“F的原始颜色”赋值给B即可。之前,我们已经将“F设置为黑色”(即,将B的颜色"黑色",赋值给了F)。至此,我们算是调换了F和B的颜色。
第三,“同时经过根节点和BRS的分支的黑色节点数不变”。
在“第二”已经满足的情况下,若要满足“第三”,只需要将BRS设置为“黑色”即可。
经过,上面的处理之后。红黑树的特性全部得到的满足!接着,我们将x设为根节点,就可以跳出while循环(参考伪代码);即完成了全部处理。
至此,我们就完成了Case 4的处理。理解Case 4的核心,是了解如何“去掉当前节点额外的黑色”。
4.3 示意图
OK!至此,红黑树的理论知识差不多讲完了。后续再更新红黑树的实现代码!
61阅读请您转载分享:
本文标题:程序猿-IBM报告:七成“程序猿”年龄小于30岁61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1