一 : 杨氏模量的测量

深 圳 大 学 实 验 报 告

课程名称： 大学物理实验（一） 实验名称：学 院：指导教师： 报告人： 组号： 学号 实验地点 实验时间： 年 月 日 提交时间：

1

杨氏模量的测定 杨氏模量的测量

2

杨氏模量的测定 杨氏模量的测量

3

杨氏模量的测定 杨氏模量的测量

4

杨氏模量的测定 杨氏模量的测量

5

杨氏模量的测定 杨氏模量的测量

6

杨氏模量的测定 杨氏模量的测量

实验目的：

a．用伸长法测量金属丝的杨氏模量；

b．用光杠杆测量长度的微小变化；

c．用逐差法处理数据

实验仪器：

杨氏模量测定仪（包括光杠杆、光学望远镜）、米尺、砝码、待测金属丝、游标卡尺、千分尺等 实验原理和方法：

a．测定金属丝杨氏模量

假定长为L、横截面积为S的均匀金属丝，在受到沿长度方向的外力F作用下伸长?L，根据胡克

定律可知，在弹性限度内，应变?L/L与外施压强F/S成正比，即

E?L

L?F

S（E称为该金属的杨氏模量） 由此可得：E?FL S?L

其中F,S和L都比较容易测量；?L是一个很小的长度变化量。（www.61k.com）

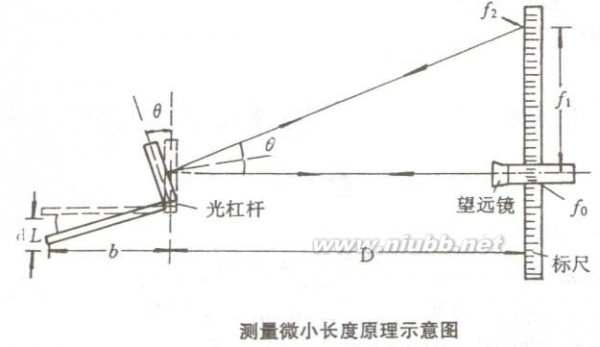
b．光杠杆测量微小长度变化

当金属丝受力伸长?L时，光杠杆后脚

tan?f1也随之下降?L，在?较小（即?L<< b）时，有 ?L/ b = ??……○1

若望远镜中的叉丝原来对准竖尺上的刻度为r0；平面镜转动后，根据广的反射定律，镜面旋转?，反射线将旋转2?，设这时叉丝对准新的刻度为r1。令l = |r1–r0|，则当2?很小（即l<<D）并维持镜面

竖尺面平行时，有l / D = tan2?

1、○2得，?L＝ b l / (2D)。 由○

c．由以上可知，光杠杆的作用在于将微小的伸长量?L放大为竖尺上的位移l。通过l,b,D这些比较容

易准确测量的量间接地测定?L。其中2D/b称为光杠杆的放大倍数。E

?2?……○2 ?8FLD?d2bl

7

杨氏模量的测定 杨氏模量的测量

8

二 : 杨氏模量的测定

杨氏模量的测定

【实验简介】

任何物体在外力作用下都要发生形变，形变可分为弹性形变和范性形变两种。(www.61k.com)如果外力在一定限度以内，当外力撤去后，物体能恢复到原来的形状，这是弹性形变。当外力撤去以后，物体不能恢复到原来的形状，这是范性形变。固体材料弹性形变能利用杨氏弹性模量这一个重要物理量来描述。杨氏弹性模量表征的是材料的自身属性，仅与材料的性质有关，与几何尺寸以及作用力无关，是工程设计中选用材料的重要参数之一。

实验操作过程比较简单，但从望远镜中找到标尺的像有一定的难度，需要一定的实验技巧；实验数据处理比较烦琐，且有一定的难度。

【实验目的】

1. 用伸长法测定金属丝的杨氏模量

2. 学习光杠杆原理并掌握使用方法

【实验仪器】

杨氏模量测定仪，螺旋测微器，游标卡尺，钢卷尺，光杠杆及望远镜直横尺。

【实验原理及设计】

胡克定律指出，在弹性限度内，弹性体的应力和应变成正比。设有一根长为l横截面积为S的钢丝，在外力F作用下伸长了δ，则 F??ESl （1）

杨氏模量的测定 杨氏模量的测定

式中的比例系数E称为杨氏模量，单位为N.m-2。［www.61k.com]设钢丝直径为d，则S?1?d2，将此代入上式并整理后得出 4

E?4Fl

?d2? （2）

上式表明，对于长度l、直径d和所加外力F相同的情况下，杨氏模量大的金属丝的伸长量δ较小，而杨氏模量小的伸长量较大。因而，杨氏模量表达了材料抵抗外力产生拉伸（或压缩）形变的能力。

根据式（2）测杨氏模量时，伸长量δ比较小不易测准，因此，测定杨氏模量的装置，都是围绕如何测准伸长量而设计的。此实验是利用光杠杆装置去测量伸长量δ。

如图1安装光杠杆G及望远镜直横尺。光杠

杆前后足尖的垂直距离为h，光杠杆平面镜到标

尺的距离为R，设加砝码m后金属丝伸长为δ，

加砝码m前后望远镜中直尺的读数差为?d，则由

图2知，tgθ＝δ/h,反射线偏转了2θ，tg2θ=Δd/R, 当θ＜5°时，tg2θ≈2θ, tgθ

≈θ,故有2δ/h＝Δd/R，即ΔL＝Δd h/2R

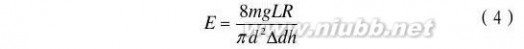
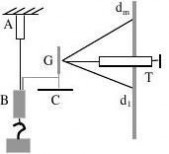
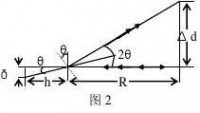
或者 δ＝（d2－d1）h/2R （3）

将F＝mg代入上式，得出用伸长法测金属的杨氏模量E的公式为

杨氏模量的测定 杨氏模量的测定

【实验内容及步骤】

1． 杨氏模量测定仪的调整

（1）调节杨氏模量测定仪底脚螺丝，使立柱处于垂直状态；

（2）将钢丝上端夹住，下端穿过钢丝夹子和砝码相连；

（3）将光杠杆放在平台上，调节平台的上下位置，尽量使三足在同一个水平面上。(www.61k.com)

2．光杠杆及望远镜直横尺的调节（重点掌握要点）

（1）镜面保持垂直状态；

（2）望远镜和平面镜等高（直接比对）；

（3）望远镜筒轴线保持水平；

（4）望远镜与平面镜相距一米左右；

（5）从望远镜上方，调节使得准星与平面镜中标尺的像三者一线；

（6）正反调节望远镜，从望远镜中找到平面镜中直尺的像；

（3）仔细调节望远镜的目镜，使望远镜内的十字线看起来清楚为止。

3．测量

（1）将砝码托盘挂在下端，再放上一个或两个砝码成为本底砝码（无效砝码），拉直钢丝，记下此时望远镜中标尺所对应的刻度读数；

（2）顺次增加砝码（1kg），直至将砝码全部加完为止（奇数），然后再依次减去直至将砝码全部取完为止（不包括本底砝码），分别记录下刻度读数。注意加减砝码要轻放。由对应同一砝码值的两个读数求平均，然后再分组对数据应用逐差法进行处理；

杨氏模量的测定 杨氏模量的测定

（3）用钢卷尺测量钢丝长度L；

（4）用钢卷尺测量标尺到平面镜之间的距离R；

（5）用螺旋测微器测量钢丝直径d ,变换位置测五次（注意不能用悬挂砝码的钢丝），求平均值；

（6）将光杠杆在纸上压出三个足印，用卡尺测量出h。(www.61k.com）

【实验数据处理】

测量钢丝的微小伸长量，记录表格自行设计。

【思考题】

1. 加挂初始砝码（本底砝码）的作用是什么？（铅直钢丝，使系统稳定）。

2. 为什么钢丝长度只测量一次，且只需选用精度较低的测量仪器？而钢丝直径必须用精度较高的仪器多次测量？（由不确定度UE各E分项可知，钢丝直径d和伸长量测量误差对实验的结果影响最大，故钢丝直径d必须用精度较高的仪器多次测量）。

3．如何消除视差:视差是由于目标成像面与十字叉丝面不重合，当眼睛上下移动时，物像与叉丝有相对位移。

消除方法：微调望远镜物镜焦距，使物成像面落在十字叉丝面上。

61阅读提醒您本文地址：

三 : ire：ire-ire，ire-测量的定义

ire_ire -ire

IRE是1个在视频测量中的单位，以创造这个名词的组织——“无线电工程学会”来命名的。
例如在广播级视频电平中规定了任何视频信号在播放时的亮度电平都不能超过100IRE。
测量是按照某种规律，用数据来描述观察到的现象，即对事物作出量化描述。测量是对非量化食物的量化过程。

ire_ire -测量的定义

1.早期的定义：研究地球的形状和大小，确定地面点的坐标的学科。
2.当前的定义：研究三维空间中各种物体的形状、大小、位置、方向和其分布的学科。
测量学的内容包括测定和测设2个部分。测定是指使用测量仪器和工具，通过测量和计算，得到一系列测量数据，或把地球表面的地形缩绘成地形图。测设是指把图纸上规划设计好的建筑物、构筑物的位置在地面上标定出来，作为施工的依据。

ire_ire -测量的工具

长度——刻度尺、游标卡尺
质量——天平
时间——计时器、秒表
体积——液体或形状不规则的固体梯级的测量：量筒&量杯。

ire_ire -注意

1)正确读出刻度尺的零刻度、最小刻度、测量范围；
(2)把刻度尺的刻度尽可能与被测物体接近，不能歪斜；
(3)读数时，视线应垂直于被测物体与刻度尺；
(4)除读出最小刻度以上各位数字外，还应估读最小刻度下一位的数字；
(5)记录的测量数据，包括准确值、估计值以及单位（没有单位的数值是毫无意义的）．
对于精密测量，要注意
（1）要考虑测量温度及湿度对测量结果的影响，量具和被测工件应尽可能放在同一环境温度中，1m以下不少于1.5h，1～3m的为3h，超过3m时应在4h以上。
(2) 要减小测力引起的误差
（3）测量周围环境要求：无震动、无磁场无粉尘等

ire_ire -测量的分类

组合测量：如果被测量有多个，虽然被测量（未知量）与某种中间量存在一定函数关系，但由于函数式有多个未知量，对中间量的一次测量是不可能求得被测量的值。这时可以通过改变测量条件来获得某些可测量的不同组合，然后测出这些组合的数值，解联立方程求出未知的被测量。

四 : 关于杨氏模量测量的几种的讨论

关于杨氏模量测量的几种方法的讨论

帅成久

物理与电子信息学院物理学专业2006级 指导老师：刘自祥

摘 要: 本文讨论了两种测量杨氏模量的方法——自由振动发和非平衡电桥法。(www.61k.com)自由振动法根据振动理论，给出了悬臂梁自由振动的周期与材料杨氏模量的关系，并设计了一种测量杨氏模量的实验装置，改装置的测量精度比传统的静态拉伸法高了一个数量级；非平衡电桥法克服了静态拉伸法中占用空间大和误差大的缺点。 关键词：杨氏模量

任何物体或材料在外力作用下都会发生形变。在弹性限度内，材料的胁强与胁变(即相对形变)之比为一常数，叫弹性模量。条形物体(如钢丝)沿纵向的弹性模量叫杨氏模量,它是表征材料性质的一个物理量，仅与材料的化学结构成分及其加工制造方法有关。某种材料发生一定形变所需的力大，该材料的杨氏模量也就大，杨氏模量的大小标志了材料的刚性。

胡克定理指出，在弹性限度内, 弹性体的应力和应变成正比，设有一根长为??，横截面积为?? 的钢丝，在外力作用下伸长了???，则

?????=?? (1) 设钢丝的直径为??，则S=πd2 4，将此代入上式并整理后得出

4??????= (2) 上式表明，对于长度直径和所加外力相同的情况下，杨氏模量??大的金属丝的伸长量??? 较小，而杨氏模量??小的伸长量??? 较大。因而，杨氏模量表达了材料抵抗外力产生拉伸(或压缩)形变的能力。根据(1)式测杨氏模量时，伸长量??? 比较小不易测准。因此，在测定杨氏模量时，伸长量??? 的测量是整个实验的关键，在很多试验课本上大多是在静态拉伸实验中测量伸长量??? 。由于金属丝的伸长量非常微小, 常规的测量方法很难做到精确测定。本文讨论另外几种测量杨氏模量的方法：

1 自由振动法测量杨氏模量

1.1 实验原理

任何弹性系统在作自由振动时,系统振动的固有频率与系统的内在属性直接相关,这些属性包括系统结构、系统材料、系统振动模态等,下面以梁的弯曲自由

杨氏模量的测定 关于杨氏模量测量的几种的讨论

振动加以说明。［www.61k.com）

1.1.1 弯曲自由振动的运动微分方程

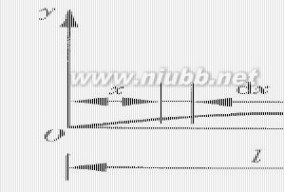
研究均质细长等截面直梁的平面弯曲振动,由于是细长直梁,则梁的运动可用梁轴线上各点的位移表示。梁的??、??、??、??均为常数,其中??为梁的长度，??为梁长度方位的线密度, ??为梁横截面对弯曲中性轴的惯性矩, ??为梁材料的杨氏模量。梁的弯曲振动如图1所示，利用微分方法，将梁分为若干个微元，相邻微元之间的相互作用力如图2所示，即梁的弯矩??，剪力??，而??、?? 是x的函数，即?? =?? ( ??) , ?? =?? ( ??) ,它们与梁轴线的弯曲挠曲线方程?? = ?? ( ??)有直接关系:

图 1 梁的弯曲振动 图 2 梁微元的受力

??2????=???? (3) ??????= (4) 将(3)、(4)两式代入梁作自由振动时微元沿??方位的运动微分方程：

??2????????????==??? ????+?? (5) 得：

??4??????2??+=0 (6) 令??????=??2,则(6)式表示为：

??4??1??2??+=0 (7)

1.1.2 弯曲自由振动的固有频率与振型

运用分离变量法，假定四阶偏微分方程(7)的解有如下形式：

?? ??,?? =?? ?? ?? ?? (8)

将(8)式代入方程(7)，得：

杨氏模量的测定 关于杨氏模量测量的几种的讨论

1??2????2??4???=?? (9) (9)式左端、右端分别仅依赖于变量??与??，要使该式成立，该式的左右端应等于同一常数，设此常数为???2，且令??2=?? ??，则有：

??2?? +??2??=0 (10) ??4?? ???4??=0 (11) 由方程(10)的形式可知：??即是方程(10)所反映的弯曲自由振动系统的固有角频率。（www.61k.com）由微分方程理论，方程(11)的通解可表示为:

?? ?? =??1???????+??2???????+??3??????????+??4?????????? (12)

式(12)称为弯曲自由振动系统的振型函数，??为振型函数的特征值，??值决定固有角频率，??1、??2、??3、??4为与??相对应的系数，各系数间的相对比值决定振型函数的函数图形状，即振型。由系统的边界条件，可确定??与?? ( ??) 。对均质等截面细长直悬臂梁，其固定端边界条件可表示为:

?? 0 =??′ 0 =0 (13) 自由端边界条件可表述为：

??′′ ?? =??′′ ?? =0 (14) 由边界条件(13)、(14)得： ??1=???3 (15) ??2=???4

???????+?????????? ??1+ ???????+?????????? ??2=0

????????sin???? ??1+ ???????+cos???? ??2=0

若将??1、??2看做未知量，方程组(16)有非零解的条件的为：

?????????????????=?1 (17) 用数值解法中的二分法解得式(17)的一阶特征根????=1.875104，从而得：

21.875104????2 ??1=??1???=? (18) (16)

将一阶特征根??1??代入式⒁,可得系数??2 与??1及??3 与??4的一阶比值：

??2??4?????1??+????????1?? = =? (19) 113111对振型而言,若取??1=1，则系统的一阶固有振型函数可取为：

?????1???????????1?? ?????1???????????1?? (20) ??1 ?? =?????1???????????1?11

杨氏模量的测定 关于杨氏模量测量的几种的讨论

类似地,可求出悬臂梁自由振动系统的二阶、三阶固有角频率??2、??3与固有振型函数??2 ?? 、??3 ?? 。[www.61k.com]悬臂梁自由振动系统的前三阶固有振型示意图如图3所示。

图 3 梁的前三阶固有振动 图 4 振动的初始状态

1.1.3 杨氏模量与振动周期的关系

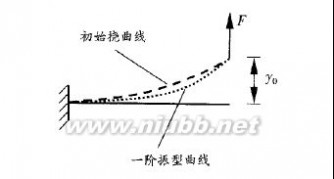
讨论图4均质等截面细长直悬臂梁在小阻尼下的衰减自由振动。初始时施加力??, 使自由端偏离平衡位置??0则梁的初始挠曲线为三次抛物线,撤去??，梁将作自由振动。初始挠曲线接近一阶振型曲线,所以自由振动中主要为一阶固有振型，而一阶固有振型的衰减速度最慢，经过一段时间的衰减后，自由振动就很接近一阶固有振型，又因阻尼较小，则认为实际的振动角频率为一阶固有角频率。

若测出衰减自由振动后期的振动周期??,??即近似为悬臂梁的一阶固有周期??1, ??1=1 ??1=2?? ??1，得悬臂梁材料的杨氏模量：

4??2??4?? ??= (21)

1.2 实验装置的设计

如图5，将一根均质细长圆截面直钢丝铅垂放置，上端用夹头紧固于台座上,下端设置一细光束光电门。

杨氏模量的测定 关于杨氏模量测量的几种的讨论

图 5 实验部分装置

钢丝静止时，仔细调节钢丝与光电门，使钢丝恰好遮住光束。（www.61k.com)经测试，钢丝振动的阻尼?0.1可不考虑阻尼对振动周期的影响。在一个振动周期内, 钢丝会遮断光束2次, 光电门产生的脉冲信号接入TH—4型毫秒计，可将毫秒计设置为：对两个脉冲信号记录一次计数及时刻，则相邻计数的时刻之差即为钢丝的振动周期。实测中，使钢丝初始时作近似于一阶振型的自由振动，控制毫秒计，记录振动后期的若干个记数及对应的时刻，选择其中连续的十个数据计算振动周期。

1.3 测量数据及处理结果

1.3.1 钢丝实验常数

选择合适的量具对钢丝进行多次测量，取平均值得钢丝的实验常数：悬臂长度??：0.1518(m)；线密度??：0.003209(kg/m)；直径??：0.721(mm)。

1.3.2 毫秒计记录

在后期的振动中，所选择的连续10个计数??所对应的时刻??1如表1所示。 表 1 毫秒计记录

?? 1 2 3 4 5 6 7 8 9 ti s 0.5174 0.5625 0.6075 0.6526 0.6976 0.7427 0.7877 0.8327 0.8778

1.3.3 钢丝振动周期 ??

由表1中的数据得：

9??=1（????+1?????）??==0.045056（??） 1.3.4 钢丝杨氏模量 ??:

由(21)式得:

4π2×0.15184×0.003209E==2.0207×1011(N m2) 1.8751044××0.04505621.4 结论

以自由振动法为基础,用悬臂梁为振动体的实验装置所测钢丝的杨氏模量与钢的标准值2.0×1011?? ??2相差很小,对同一根钢丝测量多次的结果相互间也很接近。说明该实验装置具有较高的准确性。该装置的测量原理可靠,仪器设备简单,从影响测量结果的因素分析,如果将钢丝质量、振动时间的测量精度提高,可进一步提高实验装置的测量准确性。

2 用非平衡法测铜丝的杨氏模量

杨氏模量的测定 关于杨氏模量测量的几种的讨论

2.1 实验原理

用电学的方法测力学量。（www.61k.com］如图5所示：??1为铜丝，??2、??3、??4为电阻箱，调

图 5

节??2、??3、??4，使得R1

R2=R3R4??为电源电动势，内阻

为0，??1代表流经??2和??1支路的电流，??2代表流经??3和??4支路的电流，

?? ??1= (22) 12

??2=?? (23) 34

????2 ??1=??? (24) 12

??2=???

由R1

R2????4 (25) 34=R3R4，可得： ??2??4 = (26) 1234

??1=??2 (27) 由(24)、(25)、(26)三式可得： 此电桥即为平衡电桥，电压表读数应为0。

我们给??1施加一拉力 ??，??1的长度增加???，横截面积减小???，电阻改变???,而此时??2、??3、??4的阻值并未改变，则

??1+?????3≠ (28) 24

杨氏模量的测定 关于杨氏模量测量的几种的讨论

此电压表读数应是??1和??2的电压差。［www.61k.com)

下面来研究电压差???与???之间的关系:

应用非平衡电桥法分析，此时

??1=??1 ??1+??? (29)

??2=??2??2 (30)

?? ??1= (31) 12

??2=?? (32) 34

?? ??1+??? ????3? 1234???=??1???2=

?????13 =?? (33) 1++ 1+ 113由于R1

R2=R3R4?RR1

?????1 ???=??? (34) ??1 1+1

在选取铜丝和电阻时，令R1

R2的值接近 1，因此

1??? ???=??? (35) 1

下面讨论???和???之间的关系：

由电阻的决定式可知，

???? ??= (36) 其中??为电阻率，??为导体的横截面，??为导体的长度。设导体的体积为??，则 ??=????,代入式(36)，得

????2 ??= (37) 对式(37)两边微分，得

2????? (38) 由式(35)式(37)，可以推导出???和???间的关系，即 ???=

杨氏模量的测定 关于杨氏模量测量的几种的讨论

???=

将式(39)代入(1)中，得 2??1????? (39) ???? ??=? (40)

2.2 实验数据及结果

选择合适的量具对铜丝进行多次测量，取平均值得铜丝的实验常数：铜丝横截面积的直径：??=0.231mm；铜丝有效长度：??=42.50cm；电阻率：??=1.55×10?6Ω?cm；电动势：??=1.620V。(www.61k.com］

表 2

砝码质量：m (g) 对应的电压表读数：?? (μV)

??0=0 ??0=0.1

??1=300 ??1=13.2

??2=600 ??2=26.8

??3=900 ??3=38.5

??4=1200 ??4=51.9

??5=1500 ??5=67.5 ??6=1800 ??6=79.0

由以上数据可得杨氏模量：

????0.425×9.8????6E=?==5.728×10? 其中，???=???????0，(??=1,2,3,4,5,6)

代入数据，得

?3300×1011 2E1=5.728×106×=1.312×10Nm； ?3600×10E2=5.728×106×=1.287×1011N m2； 900×10?311 2E3=5.728×10×=1.343×10Nm； 6

?31200×10E4=5.728×106×=1.330×1011N m2； 51.9?0.1×10

杨氏模量的测定 关于杨氏模量测量的几种的讨论

?31500×10E5=5.728×106×=1.279×1011N m2； 67.5?0.1×10

?31800×1011 2E6=5.728×106×=1.307×10Nm =1.310×1011?? ??2 取平均值，得 ??

2.3 误差分析

铜丝的杨氏模量理论值为：??=1.43×1011?? ??2, 相对误差

??? ????=×100=8.39% (1)在测铜丝直径时产生一定的误差，使得测量值偏小；

(2)在测铜丝长度时，所测的长度并不一定是有效长度；

(3)电阻箱的精确度不高，使得R1

R2=R3R4计算出的??1值有偏差；

(4)给铜丝施加一定的拉力之后，铜丝的伸长是一个不断变化的过程，并不是瞬间就能完成的，所以读取的数据不是精确数值，加之人眼的误差，最后的计算结果就产生了一定的误差。（www.61k.com］

本文标题：杨氏模量的测定-杨氏模量的测量
本文地址： http://www.61k.com/1184770.html