一 : 七年级下全等三角形练习题经典综合拔高题87

全等三角形综合练习题

1、 三角形全等的条件

（1）边边边公理：如果两个三角形的三条边分别对应相等，那么这两个三角形全等，简记为SSS （2）边角边公理：如果两个三角形的两边及其夹角分别对应相等，那么这两个三角形全等，简记为SAS

（3）角边角公理：如果两个三角形的两个角及其夹边分别对应相等，那么这两个三角形全等，简记为ASA

（4）角角边公理：有两个角和其中一角的对边对应相等的两个三角形全等，简记为AAS 2、直角三角形全等的特殊条件：斜边和一条直角边对应相等的两个直角三角形全等，简写成“斜边、直角边”或“HL”

3、选择证明三角形全等的方法（“题目中找，图形中看”） （1）已知两边对应相等

①证第三边相等，再用SSS证全等 ②证已知边的夹角相等，再用SAS证全等 ③找直角，再用HL证全等 （2）已知一角及其邻边相等

①证已知角的另一邻边相等，再用SAS证全等 ②证已知边的另一邻角相等，再用ASA证全等 ③证已知边的对角相等，再用AAS证全等 （3）已知一角及其对边相等 证另一角相等，再用AAS证全等 (4)已知两角对应相等

①证其夹边相等，再用ASA证全等

②证一已知角的对边相等，再用AAS证全等 4、全等三角形中的基本图形的构造与运用

（1）出现角平分线时，常在角的两边截取相等的线段，构造全等三角形

知识点睛

（2）出现线段的中点（或三角形的中线）时，可利用中点构造全等三角形（常用加倍延长中线） （3）利用加长（或截取）的方法解决线段的和、倍问题（转移线段）

经典例题

1. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.

求证:AC∥DF．

2. 如图,已知: AD是BC上的中线 ,且DF=DE．求证:BE∥CF．

3. 如图, 已知：AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF．求

证：AC=EF．

B

E

D

C

A

G

F

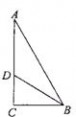
4. 如图，在ΔABC中，AC=AB，AD是BC边上的中线，则AD⊥BC，请说明理由。

A

CB D

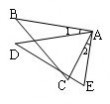
5. 如图，已知AB=DE，BC=EF，AF=DC，则∠EFD=∠BCA，请说明理由。 ADF

6. 如图，在ΔABC中，D是边BC上一点，AD平分∠BAC，在AB上截取AE=AC，连结DE，已知DE=2cm，

BD=3cm，求线段BC的长。

A

C7. 如图，ΔABC的两条高AD、BE相交于H，且AD=BD，试说明下列结论成立的理由。

（1）∠DBH=∠DAC； （2）ΔBDH≌ΔADC。

E

D

C

8. 如图，已知?ABC为等边三角形，D、E、F分别在边BC、CA、AB上，且?DEF也是等边

三角形．

（1） 除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的； （2） 你所证明相等的线段，可以通过怎样的变化相互得到？写出变化过程．

E

B

D

C

9. 已知等边三角形ＡＢＣ中，ＢＤ＝ＣＥ，ＡＤ与ＢＥ相交于点Ｐ，求∠ＡＰＥ的大小。

10. 如图，在矩形ABCD中，F是BC边上的一点，AF的延长线交DC的

延长线于G，DE⊥AG于E，且DE＝DC，根据上述条件，请你在图中找出一对全等三角形，并证明你的结论。

11. 已知：如图所示，BD为∠ABC的平分线，AB=BC，点P在BD上，PM

⊥AD于M，?PN⊥CD于N，判断PM与PN的关系． ADM

C

12. 如图所示，P为∠AOB的平分线上一点，PC⊥OA于C，?∠OAP+∠OBP=180°，若OC=4cm，求AO+BO

的值．

A

BD

13. 如图，∠ABC=90°，AB=BC，BP为一条射线，AD⊥BP，CE⊥PB，若AD=4，EC=2.求DE的长。

i.

14. 如图所示，A，E，F，C在一条直线上，AE=CF，过E，F分别作DE?⊥AC，BF⊥AC，若AB=CD，

可以得到BD平分EF，为什么？若将△DEC的边EC沿AC方向移动，变为如图所示时，其余条件不变，上述结论是否成立？请说明理由． B

EC

CA FA D

D

15. 如图，OE=OF，OC=OD，CF与DE交于点A，求证： AC=AD。

E

C

O

F

16. 已知：如图E在△ABC的边AC上，且∠AEB=∠ABC。 (1) 求证：∠ABE=∠C；

(2) 若∠BAE的平分线AF交BE于F，FD∥BC交AC于D，设AB=5，AC=8，求DC的长。

17. 如图∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D，AD=2、5cm，DE=1.7cm,

求BE的长

18. 如图，在△ABE中，AB＝AE,AD＝AC,∠BAD＝∠EAC, BC、DE交于点O.求证：(1) △ABC≌△AED；

(2) OB＝OE .

19. 如图，D是等边△ABC的边AB上的一动点，以CD为一边向上作等边△EDC，连接AE，找出图中

的一组全等三角形，并说明理由．

E

B C

20. 已知：如图，B、E、F、C四点在同一条直线上，AB＝DC，BE＝CF，∠B＝∠C．

求证：OA＝OD．

七年级下全等三角形练习题经典综合拔高题87_全等三角形习题

21. 如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直

F线于E，直线CE交BA的延长线于F．求证：BD=2CE．

E

CB

22. 如图，AB?AC,AD?BC，请你写出图中三对全于点D，AD?AE，AB平分?DAE交DE于点F．．

等三角形，并选取其中一对加以证明．

B D C

23. 如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，

BD交AC于点M．

（1） 求证：MB=MD，ME=MF

（2） 当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请

给予证明；若不成立请说明理由．

24. 如图，已知在△ABC中，∠BAC为直角，AB=AC，D为AC上一点，CE⊥BD于E．

1

（1） 若BD平分∠ABC，求证CE=BD；

2

（2） 若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，求出它

的度数，并说明理由。

E

A

F

B

E

25、（7分）

在△ABC中，,AB=AC， 在AB边上取点D，在AC延长线上了取点E ，使CE=BD ， 连接DE交BC于点F，求证DF=EF .

B

26、（8分）

如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点， DE⊥DF，交AB于点E，连结EG、EF.

A(1) 求证：EG=EF;

(2) 请你判断BE+CF与EF的大小关系，并说明理由。

F

B C

G

27、 如图△ABC≌△A｀Ｂ｀Ｃ，∠ACB=90°，∠A=25°，点B在A｀Ｂ｀上，求∠ACA｀的度数。

A`B

28、 如图：四边形ABCD中，AD∥BC ，AB=AD+BC ，E是CD的中点，求证：AE⊥BE 。

E

B

29、 如图所示,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE, 垂足为F,过

B作BD⊥BC交CF的延长线于D.

i. 求证:(1)AE=CD;(2)若AC=12cm,求BD的长. A

30、 在正方形ABCD中，E是AB上一点，F是AD延长线上

一点，且DF=BE。

i. 求证：CE=CF。

ii. 在图中，若G点在AD上，且∠GCE=45° ，则GE=BE+GD成

立吗？为什么？

D

B

E

C

E

31、 如图(1), 已知△ABC中, ∠BAC=90, AB=AC, AE是过A的一条直线, 且B、C

在A、E的异侧, BD⊥AE于D, CE⊥AE于E 试说明: BD=DE+CE.

若直线AE绕A点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD与DE、CE的关系如何? 为什么？

若直线AE绕A点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD与DE、CE的关系如何? 请直接写出结果, 不需说明.

归纳前二个问得出BD、DE、CE关系。用简洁的语言加以说明。

32、 如图所示,已知D是等腰△ABC底边BC上的一点,它到两腰AB、AC的距离分别为DE、DF,CM

⊥AB,垂足为M,请你探索一下线段DE、DF、CM三者之间的数量关系, 并给予证明.

A

M

F

E

BC33、 在Rt△ABC中，AB=AC，∠BAC=90°，O为BC的中点.

写出点O 到△ABC的三个顶点A、B、C的距离的大小关系，并说明理由.

若点M、N分别是AB、AC上的点，且BM=AN，试判断△OMN形状，并证明你的结论. 34、 如图，ABCD是正方形，点G是BC上的任意一点，DE⊥AG于E，BF∥DE，交AG于F．求

证：AF=BF+EF．

A

D

35、如图10，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE、BE，BE⊥AE，延长AE交BC

的延长线于点F． 求证：（1）FC＝AD；

（2）AB＝BC＋AD．

G

C

36、如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP． (1)如图②，若M为AD边的中点， ①,△AEM的周长=_____cm；

②求证：EP=AE+DP；

(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．

二 : 全等三角形及判定练习题

全等三角形（1）

一．知识点：

1．能够完全重合的两个三角形叫做全等三角形

含义：形状相同，大小相等.

2．符号：“≌”

3．对应（边、角、顶点）：重合的边、重合的角，重合的顶点

4．全等三角形的性质：

⑴全等三角形的对应边相等. ⑵全等三角形的对应角相等. ⑶全等三角形的周长、面积相等.

二、基础习题

1如图，?ABC≌?ADE，?EAC?30?，求?BAD的度数.

2、如图，?ABC≌?DEF，且A、D、B、E在同一条直线上，试找出图中互相平行的线段，并说明理由.

3、如图，?ABE≌?ACD，?1??2，?B??C.求证：?BAD??CAE

4.如图，?ABC≌?EFC，B、C、E在同一条直线上，且BC?3cm，CE?4cm，?EFC?52?. 求AF的长和?A的度数.

5.如图，长方形ABCD沿AE折叠，使得点D落在BC边上的点F处，且?BAF?50?.求?DAE的度数.

6、如图，点A、E、B、F在同一条直线上，?ABC≌?FED.

⑴判断AC与DF的位置关系，并说明理由；

⑵判断AE与BF的数量关系，并说明理由.

1

三角形全等的判定 全等三角形及判定练习题

全等三角形（2）

一．全等三角形的判定1：三边对应相等的两个三角形全等.简写成“边边边”或“SSS” 几何符号语言：在?ABC和?DEF中

?AB?DE?∵?BC?EF

?AC?DF?

∴?ABC≌?DEF（SSS）

二、基础习题

1如图，点B、E、C、F在同一直线上，BE?CF，AB?DE，AC?DF.求证：?EGC??D

2、如图，点A、C、F、D在同一直线上，AF?DC，AB?DE，BC?EF求证：AB//DE

3、如图，在四边形ABCD中，AB?CD，AD?BC.求证：①AB//CD；②AD//BC．

4、如图，AC与BD交于点O，AD?CB，E、F是BD上两点，且AE?CF，DE?BF． 求证：⑴?D??B；⑵AE//CF

全等三角形（3）

一．全等三角形的判定2：两边和它们的夹角对应相等的两个三角形全等.简写为“边角边”或“SAS” 几何符号语言：在?ABC和?DEF中

?AB?DE?∵??B??E

?BC?EF?

∴?ABC≌?DEF（SAS）

2

三角形全等的判定 全等三角形及判定练习题

二、基础习题

1、如图，D是?ABC中边BC的中点，?ABD??ACD，且AB?AC.

求证：⑴?ABD≌?ACD ⑵EB?EC

2、点A、D、F、B在同一直线上，AD?BF，且AE//BC.

求证：⑴?AEF≌?BCD ⑵EF//CD

3、 如图，CD?DE于D，AB?DB于B，CD?BE，AB?DE.

求证：CE?AE

4、 如图，?ABC和?ECD都是等边三角形，连接BE、AD交于O.

求证：⑴AD?BE ⑵?AOB?60?

全等三角形（4）

一．全等三角形的判定3：有两角和其夹边对应相等的两个三角形全等.简写成“角边角”或“ASA” 全等三角形的判定4：有两角和其一角对边对应相等的两个三角形全等.简写成“角角边”或“AAS” 几何符号语言：在?ABC和?DEF中

??A??D?∵?AB?DE

??B??E?

∴?ABC≌?DEF（ASA）

或：在?ABC和?DEF中

??A??D?∵??B??E

?BC?EF?

∴?ABC≌?DEF（AAS）

二、基础习题

1．已知AB?A?B?，?A??A?，?B??B?，则?ABC≌?A?B?C?的根据是（ ）

A．SAS B．SSA C．ASA D．AAS

2．?ABC和?DEF中，AB?DE，?B??E，要使?ABC≌?DEF ，则下列补充的条件

3

三角形全等的判定 全等三角形及判定练习题

中错误的是（ ）

A．AC?DF B．BC?EF C．?A??D D．?C??F

3．如图，AD平分?BAC，AB?AC，则图中全等三角形的对数是（ ）

A．2对 B．3对 C．4对 D．5对

4．如图，已知AB//CD，欲证明?AOB≌?COD，可补充条件________．（填写一个适合的条件即可）

5．如图，AB?AC，BD?CD，?1??2，欲得到BE?CE，?可先利用_______，证明?ABC≌?DCB，得到______=______，再根据___________?证明________?≌________，即可得到BE?CE．

6．如图，AC平分?DAB和?DCB，欲证明?AEB??AED，?可先利用___________，证明?ABC≌?ADC，得到______=_______，再根据________，证明______≌________，即可得到?AEB??AED.

7．如图，AC?AE，?C??E，?1??2.

求证：?ABC≌?ADE．

8．如图，已知BD?CE，?1??2，那么AB?AC，你知道这是为什么吗？

全等三角形（5）

一．全等三角形的判定5：斜边和一条直角边对应相等的两个直角三角形全等. 简写为“斜边、直角边”或“HL”

几何符号语言：∵?C??F?90?

∴在Rt?ABC和Rt?DEF中

∵??AB?DE ∴?ABC≌?DEF ?AC?DF

二、基础习题

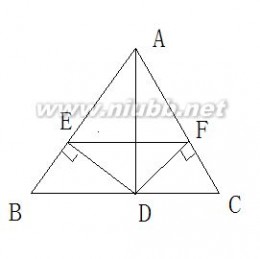
1.如图，AB?AC，AD?BC于D.

求证：AD平分?BAC，BD?CD

2.如图，AB?AC，AE?AF，AE?EC于E，AF?FB于F.

4

三角形全等的判定 全等三角形及判定练习题

求证：?1??2

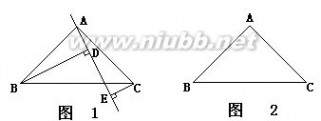
3．在?ABC中，?BAC?90?，AB?AC，AE是过点A的一条直线，且BD?AE于D，CE?AE于E. ⑴当直线AE处于如图1的位置时，猜想BD、DE、CE之间的数量关系，并证明. ⑵请你在图2选择与⑴不同位置进行操作，并猜想⑴中的结论是否还成立？加以证明； ⑶归纳⑴、⑵，请你用简洁的语言表达BD、DE、CE之间的数量关系.

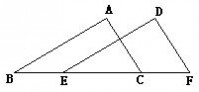
4.如图，在?ABC和?DEF中，B、E、C、F在同一直线上，下面有四个条件，请你从中选三个作为题设，余下的一个作为结论，写出一个正确的命题，并加以证明． ．．

①AB?DE，②AC?DF，③?ABC??DEF，④BE?CF．

5.如图，OA?OB，OC?OD，?AOB??COD?90?.

猜想线段AC、BD的关系，并说明理由.

5

三 : 全等三角形复习练习题

全等三角形复习练习题

一、选择题

1．如图，给出下列四组条件：

①AB?DE，BC?EF，AC?DF；②AB?DE，?B??E，BC?EF； ③?B??E，BC?EF，?C??F；④AB?DE，AC?DF，?B??E．

其中，能使△ABC≌△DEF的条件共有（ ）A．1组 B．2组 C．3组 D．4组

2.如图，D，E分别为△ABC的AC，BC边的中点，将此三角形沿DE折叠，使点C落在AB边上的点P处．若?CDE?48°，则?APD等于（ ）

3.如图（四），点P是AB上任意一点，?ABC??ABD，还应补充一个条件，才能推出△APC≌△APD．从下列条件中补充一个条件，不一定能推出△APC≌△APD的是．．．．（ ） A．BC?BD

B．AC?AD C．?ACB??ADB

D．?CAB??DAB

A．42° B．48° C ．52° D．58°

P

A

D

图（四）

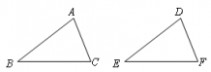
1题图 2题图 4.如图，在△ABC与△DEF中，已有条件AB=DE，还需添加两个条件才能使△ABC≌△DEF，不能添加的一组条件是( )

(A)∠B=∠E,BC=EF（B）BC=EF，AC=DF (C)∠A=∠D，∠B=∠E（D）∠A=∠D，BC=EF 5．如图，△ABC中，∠C = 90°，AC = BC，AD是∠BAC的平分线，DE⊥AB于E， 若AC = 10cm，则△DBE的周长等于( )

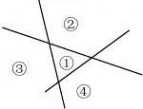
A．10cm B．8cm C．6cm D．9cm 6． 如图所示，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）Ａ．1处 Ｂ．2处 Ｃ．3

C

D

E

B

6题图 4题图 5题图

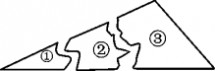
7．某同学把一块三角形的玻璃打碎了3块，现在要到玻璃店去配一块完全一样的玻璃，那 么最省事的方法是（ ）A．带①去 B．带②去 C．带③去 D．带①②③去 8．如图，在Rt△ABC中，?B?90 ，ED是AC的垂直平分线，交AC于点D，交BC 于点E．已知?BAE?10，则?C的度数为（ ）

A．30 B．40 C．50 D．60 9．如图，△ACB≌△A?C?B?，?BCB?=30°，则?ACA?的度数为（ ） A．20°

?

?

?

?

?

?

B．30° C．35° D．40°

10．如图，AC＝AD，BC＝BD，则有（ ）

A．AB垂直平分CD B．CD垂直平分AB 1题图C．AB与CD互相垂直平分

A

D．CD平分∠ACB

?A E

7题图

A

C

B

8题

C BD C 10

题图

11．尺规作图作?AOB的平分线方法如下：

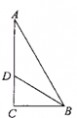
以O为圆心，任意长为半径画弧交OA、OB于

1

C、D，再分别以点C、D为圆心，以大于CD长为半径画弧，两弧交于点P，作射线

2

OP，由作法得△OCP≌△ODP的根据是（ ）A．SAS B．ASA C．AAS D．SSS 12.如图, ∠C=90°,AD平分∠BAC交BC于D,若BC=5cm,BD=3cm,则点D到AB的距离为( )A. 5cm B. 3cm C. 2cm D. 不能确定

13．如图，OP平分?AOB，PA?OA，PB?OB，垂足分别为A，B．下列结论中不一定成立的是（ ）A．PA?PB B．PO平分?APB C．OA?OB D．AB垂直平分OP

14.如图，已知AB?AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是

（ ）

A．CB?CD B．∠BAC?∠DAC C．∠BCA?∠DCA D．∠B?∠D?90? A

B

C

O B

11题图 12题图 13 题图 B

14题图

二、填空题

C

1.如图，已知AB?AD，?BAE??DAC，要使 △ABC≌△ADE，可补充的条件是 （写出一个即可）_______________．

2.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,且AB=5cm,则△DEB的周长为 ________

3.如图，?BAC??ABDOC?OD（只添一个即

可）．

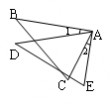
4.如图，在ΔABC中，∠C=90°∠ABC的平分线BD交AC于点D,若BD=10厘米，BC=8厘米，DC=6厘米，则点D到直线AB的距离是__________厘米。

D

BA

D

A

B

D

C

1题图 2题图 3题图 4题图

5.观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形 有 个

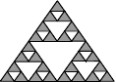
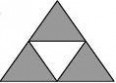
第1个

第2个

第3个

6.已知：如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则∠AEB＝________度. 7如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°.恒成立的结论有_______________________

8.如图所示，AB = AD，∠1 = ∠2，添加一个适当的条件，使△ABC ≌ △ADE，则需要添加的条件是________.

O

B

DACE

6题图 7 题图 8 题图 三、解答题

1.如图，D是等边△ABC的边AB上的一动点，以CD为一边向上作等边△EDC，连接AE，找出图中的一组全等三角形，并说明理由．

2.如图，在△ABC和△DCB中，AB = DC，AC = DB，AC与DB交于点M．

（1）求证：△ABC≌△DCB ；（2）过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．

B

E

C

C

N

3．如图，在△ABC和△ABD中，现给出如下三个论断：①AD?BC；②?C??D； ③?1??2．请选择其中两个论断为条件，另一个论断为结论，构造一个命题．

（1）写出所有的真命题（写成“

?： ?? ”形式，用序号表示） ?Ｄ ．

（2）请选择一个真命题加以证明．

你选择的真命题是：

证明：

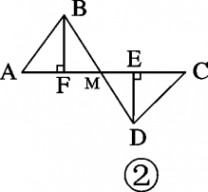
4．如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．

（1）求证：MB=MD，ME=MF

（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．

??? ． ?Ａ1

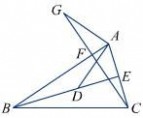
5.如图，已知在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD = AC，在CF的延长线上截取CG = AB，连结AD、AG，则AG与AD有何关系？试证明你的结论

6.如图，在△ABC和△DBC中，∠ACB =∠DBC = 90o，E是BC的中点，EF⊥AB，垂足为F，且AB = DE．

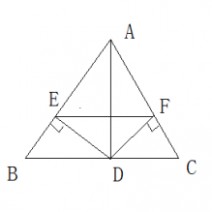
7.如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，连接EF，EF

与AD交于G，AD与EG垂直吗？证明你的结论。

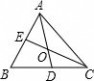
8．如图，在△ABC中，∠B=60°，△ABC的角平分线AD，CE相交于

点O．试说明AE+CD=AC．．如图，在△ABC中，∠B=60°，△ABC的

角平分线AD，CE相交于点O．试说明AE+CD=AC．

9.如图，已知E是正方形ABCD的边CD 的中点，点F在BC上，且∠DAE=∠FAE. 求证：AF=AD+CF。

D

E F C

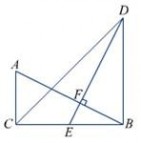
10．已知：在△ABC中，∠BAC=90°，AB=AC,AE是过点A的一条直线，且BD⊥AE于D，CE⊥AE于E,(1)当直线AE处于如图①的位置时，有BD=DE+CE,请说明理由；（2）当直线AE处于如图②的位置时，则BD,DE,CE的关系如何？请说明理由；（3）归纳（1）（2），请用简洁的语言表达BD,DE,CE之间的关系。

D A

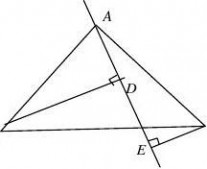
E

C B C

四 : 全等三角形复习练习题

全等三角形复习练习题

一、选择题

1．如图，给出下列四组条件：

①AB?DE，BC?EF，AC?DF；②AB?DE，?B??E，BC?EF； ③?B??E，BC?EF，?C??F；④AB?DE，AC?DF，?B??E．

其中，能使△ABC≌△DEF的条件共有（ ）A．1组 B．2组 C．3组 D．4组

2.如图，D，E分别为△ABC的AC，BC边的中点，将此三角形沿DE折叠，使点C落在AB边上的点P处．若?CDE?48°，则?APD等于（ ）

3.如图（四），点P是AB上任意一点，?ABC??ABD，还应补充一个条件，才能推出△APC≌△APD．从下列条件中补充一个条件，不一定能推出△APC≌△APD的是．．．．（ ） A．BC?BD

B．AC?AD C．?ACB??ADB

D．?CAB??DAB

A．42° B．48° C ．52° D．58°

P

A

D

图（四）

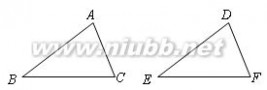
1题图 2题图 4.如图，在△ABC与△DEF中，已有条件AB=DE，还需添加两个条件才能使△ABC≌△DEF，不能添加的一组条件是( )

(A)∠B=∠E,BC=EF（B）BC=EF，AC=DF (C)∠A=∠D，∠B=∠E（D）∠A=∠D，BC=EF 5．如图，△ABC中，∠C = 90°，AC = BC，AD是∠BAC的平分线，DE⊥AB于E， 若AC = 10cm，则△DBE的周长等于( )

A．10cm B．8cm C．6cm D．9cm 6． 如图所示，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）Ａ．1处 Ｂ．2处 Ｃ．3

C

D

E

B

6题图 4题图 5题图

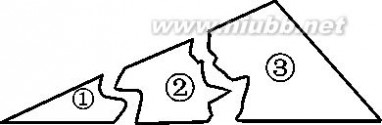
7．某同学把一块三角形的玻璃打碎了3块，现在要到玻璃店去配一块完全一样的玻璃，那 么最省事的方法是（ ）A．带①去 B．带②去 C．带③去 D．带①②③去 8．如图，在Rt△ABC中，?B?90 ，ED是AC的垂直平分线，交AC于点D，交BC 于点E．已知?BAE?10，则?C的度数为（ ）

A．30 B．40 C．50 D．60 9．如图，△ACB≌△A?C?B?，?BCB?=30°，则?ACA?的度数为（ ） A．20°

?

?

?

?

?

?

B．30° C．35° D．40°

全等三角形练习题 全等三角形复习练习题

10．如图，AC＝AD，BC＝BD，则有（ ）

A．AB垂直平分CD B．CD垂直平分AB 1题图C．AB与CD互相垂直平分

A

D．CD平分∠ACB

?A E

7题图

A

C

B

8题

C BD C 10

题图

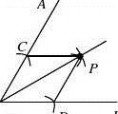
11．尺规作图作?AOB的平分线方法如下：

以O为圆心，任意长为半径画弧交OA、OB于

1

C、D，再分别以点C、D为圆心，以大于CD长为半径画弧，两弧交于点P，作射线

2

OP，由作法得△OCP≌△ODP的根据是（ ）A．SAS B．ASA C．AAS D．SSS 12.如图, ∠C=90°,AD平分∠BAC交BC于D,若BC=5cm,BD=3cm,则点D到AB的距离为( )A. 5cm B. 3cm C. 2cm D. 不能确定

13．如图，OP平分?AOB，PA?OA，PB?OB，垂足分别为A，B．下列结论中不一定成立的是（ ）A．PA?PB B．PO平分?APB C．OA?OB D．AB垂直平分OP

14.如图，已知AB?AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是

（ ）

A．CB?CD B．∠BAC?∠DAC C．∠BCA?∠DCA D．∠B?∠D?90? A

B

C

O B

11题图 12题图 13 题图 B

14题图

二、填空题

C

1.如图，已知AB?AD，?BAE??DAC，要使 △ABC≌△ADE，可补充的条件是 （写出一个即可）_______________．

2.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,且AB=5cm,则△DEB的周长为 ________

3.如图，?BAC??ABDOC?OD（只添一个即

可）．

4.如图，在ΔABC中，∠C=90°∠ABC的平分线BD交AC于点D,若BD=10厘米，BC=8厘米，DC=6厘米，则点D到直线AB的距离是__________厘米。（www.61k.com)

D

BA

D

A

B

D

C

全等三角形练习题 全等三角形复习练习题

1题图 2题图 3题图 4题图

5.观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形 有 个

第1个

第2个

第3个

6.已知：如图，△OAD≌△OBC，且∠O＝70°，∠C＝25°，则∠AEB＝________度. 7如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ.以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°.恒成立的结论有_______________________

8.如图所示，AB = AD，∠1 = ∠2，添加一个适当的条件，使△ABC ≌ △ADE，则需要添加的条件是________.

O

B

DACE

6题图 7 题图 8 题图 三、解答题

1.如图，D是等边△ABC的边AB上的一动点，以CD为一边向上作等边△EDC，连接AE，找出图中的一组全等三角形，并说明理由．

2.如图，在△ABC和△DCB中，AB = DC，AC = DB，AC与DB交于点M．

（1）求证：△ABC≌△DCB ；（2）过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．

B

E

C

C

N

全等三角形练习题 全等三角形复习练习题

3．如图，在△ABC和△ABD中，现给出如下三个论断：①AD?BC；②?C??D； ③?1??2．请选择其中两个论断为条件，另一个论断为结论，构造一个命题．

（1）写出所有的真命题（写成“

?： ?? ”形式，用序号表示） ?Ｄ ．

（2）请选择一个真命题加以证明．

你选择的真命题是：

证明：

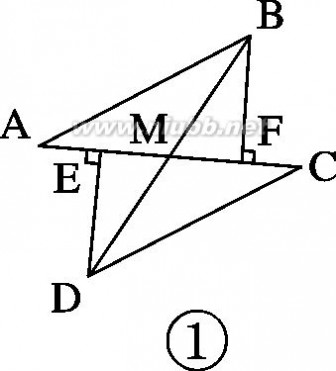
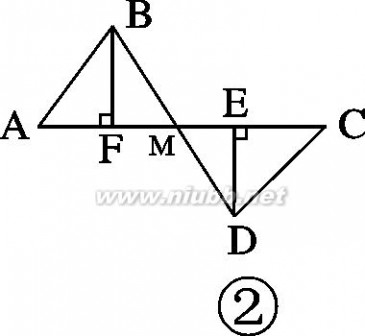
4．如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．

（1）求证：MB=MD，ME=MF

（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．

??? ． ?Ａ1

5.如图，已知在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD = AC，在CF的延长线上截取CG = AB，连结AD、AG，则AG与AD有何关系？试证明你的结论

全等三角形练习题 全等三角形复习练习题

6.如图，在△ABC和△DBC中，∠ACB =∠DBC = 90o，E是BC的中点，EF⊥AB，垂足为F，且AB = DE．

7.如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，连接EF，EF

与AD交于G，AD与EG垂直吗？证明你的结论。(www.61k.com）

8．如图，在△ABC中，∠B=60°，△ABC的角平分线AD，CE相交于

点O．试说明AE+CD=AC．．如图，在△ABC中，∠B=60°，△ABC的

角平分线AD，CE相交于点O．试说明AE+CD=AC．

9.如图，已知E是正方形ABCD的边CD 的中点，点F在BC上，且∠DAE=∠FAE. 求证：AF=AD+CF。

全等三角形练习题 全等三角形复习练习题

D

E F C

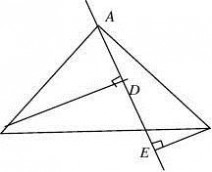
10．已知：在△ABC中，∠BAC=90°，AB=AC,AE是过点A的一条直线，且BD⊥AE于D，CE⊥AE于E,(1)当直线AE处于如图①的位置时，有BD=DE+CE,请说明理由；（2）当直线AE处于如图②的位置时，则BD,DE,CE的关系如何？请说明理由；（3）归纳（1）（2），请用简洁的语言表达BD,DE,CE之间的关系。(www.61k.com］

D A

E

C B C

本文标题：全等三角形练习题-七年级下全等三角形练习题经典综合拔高题87
本文地址： http://www.61k.com/1179352.html