一 : 几种简单证明勾股定理的方法
几种简单证明勾股定理的方法
——拼图法、定理法 江苏省泗阳县李口中学沈正中
据说对社会有重大影响的10大科学发现,勾股定理就是其中之一。(www.61k.com)早在4000多年前,中国的大禹曾在治理洪水的过程中利用勾股定理来测量两地的地势差。迄今为止,关于勾股定理的证明方法已有500余种,各种证法融几何知识与代数知识于一体,完美地体现了数形结合的魅力。让我们动起手来,拼一拼,想一想,娱乐几种,去感悟数学
图

1
的神奇和妙趣吧!
一、拼图法证明(举例12种)
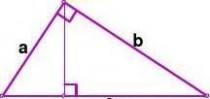
拼法一:用四个相同的直角三角形(直角边为a、b,斜边为c)按图2拼法。
问题:你能用两种方法表示左图的面积吗?对比两种不同的表示方法,你发现了什么?
图

2
2 分析图2:S正方形=(a+b)= c2 + 4×ab 2
化简可得:a2+b2 = c2
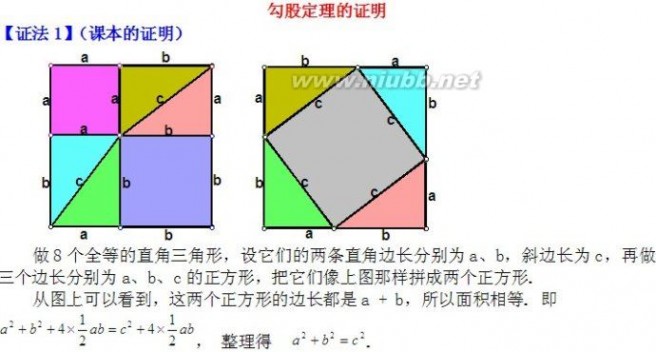
拼法二:做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像左
图那样拼成两个正方形。
从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即
a2+b2+4×ab = c2+4×ab 整理得 a2+b2 = c2 22
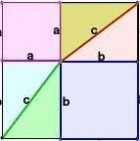
拼法三:用四个相同的直角三角形(直角边为a、b,斜边为c)按图3拼法。
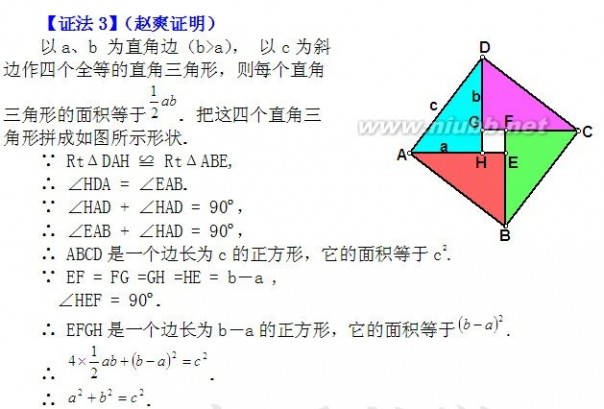
问题:图3是由三国时期的数学家赵爽在为《周髀算经》作注时给出的。在图3中用同样的办法研究,你有什么发现?你能验证a2+b2=c2吗?
图

3
图
4
分析图3:S正方形= c2 =(a-b)2+ 4×ab 2化简可得:a2+b2 = c2
观察图2、图3与图4的关系,并用一句话表示你的观点。

勾股定理的证明 几种简单证明勾股定理的方法
图4为图2与图3面积之和。[www.61k.com]
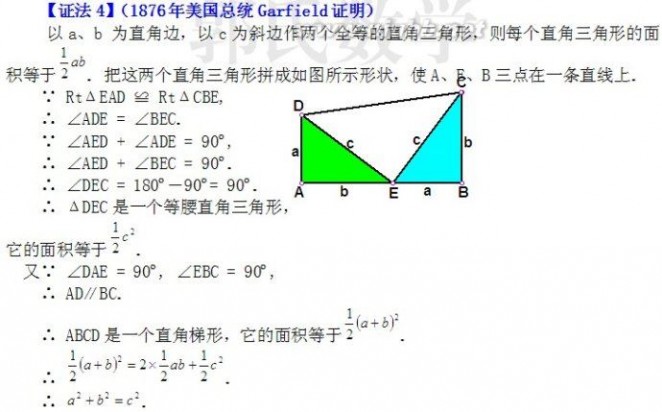
拼法四:用两个完全相同的直角三角形(直角边为a、b,斜边为c)按图5拼法。
背景:在1876年一个周末的傍晚,在美国首都华盛
顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就
B E
图

5 C 是当时美国俄亥俄州共和党议员伽菲尔德(Garfield).他发现附近的一个小石凳上,有两个小孩正在谈论着什么.由于
好奇心的驱使,伽菲尔德向两个小孩走去,想搞清楚两个小
孩到底在干什么.只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形.于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“请问先生,如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答到:“是5呀.”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的斜边长又是多少?”伽菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时语塞,无法解释了,心理很不是滋味。
于是伽菲尔德不再散步,立即回家,潜心探讨小男孩给他留下的难题。他经过反复的思考与演算,终于弄清楚了其中的道理,并给出了简洁的证明方法。
问题: 图5就是伽菲尔德总统的拼法,你知道他是如何验证的吗?你能用两种方法表示图5的面积吗?
伽菲尔德总统是这样分析的:
S梯形ABCD=(a+b)2 2
S梯形ABCD=S△ABE+ S△ECD+ S△AED=ab+ab+c2 222
则有:(a+b)2=ab+ab+c2 2222
化简可得:a2+b2 = c2
比较图5与图2,你有什么发现?
图5面积为图2之半。
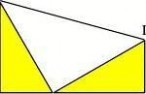
拼法五:用四个相同的直角三角形(直角边为a、b,斜边为c),
拼成图6,得边长分别为a、b、c正方形。
问题:观察图6,你能发现边长分别为a、b、c的正方形吗?你能
通验证到:a2+b2 = c2吗?
图
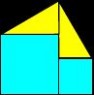
6 分析:其实,图6可以转化为下面两图:
图a的面积可表示为:a2+b2+2×ab 2
图b的面积可表示为:c2+2×ab 2
比较a、b两图,你发现了什么?
图
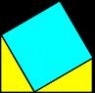
a 图b 2a2+b2+2×ab = c+2×ab
22
勾股定理的证明 几种简单证明勾股定理的方法
化简可得:a2+b2 = c2
D
拼法六:设直角三角形两直角边的长分别为a、b,斜边的长为c. 作边长是a+b的正方形ABCD把正方形ABCD划分成左图所示的几个部
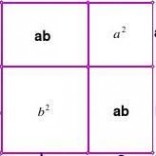
分,则该正方形ABCD的面
2
积为(a+b)=a2+b2+2ab;
再把正方形ABCD划分成右
2
图所示的几个部分,则正方形ABCD的面积为(a+b)=c2+4×ab 2
由两正方形面积相等得 a2+b2+2ab=c2+4×ab 整理得 a2+b2 = c2 2
61阅读请您转载分享:
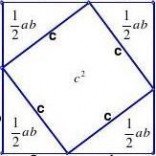
拼法七:用四个相同的直角三角形(直角边为a、b,斜边为c)拼成图7。(www.61k.com)
问题:你能把图7转化为图c吗?通过位置变换,你发现了什么?你能发现边长分别为a、b、c的正方
图7
图c
形吗?能否验证到:a2+b2 = c2呢? 分析:图7的面积可表示为:c2+4×ab 2
图c的面积可表示为:a2+b2+4×ab 2比较图c、图7,你发现了什么?
a2+b2+4×ab = c2+4×ab 化简可得:a2+b2 = c2 22
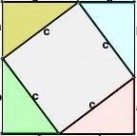
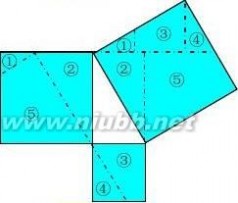
拼法八、九、十、十一、十二:制作一个五巧
板,如图8。
方法:先作一个直角三角形,直角边为a、b,斜边为c,以斜边为边长向内作正方形,并把正方形按图中实线分割为五个部分,这就是一个五巧板。
问题:运用五巧板,拼出图d、图e、图f、图
图8
a2+b2 = c2呢?你还有其它的拼法吗?


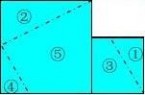
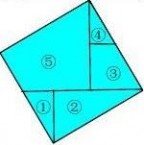
图d
图e

g,并仔细观察、比较,你发现了什么?能否验证到:
勾股定理的证明 几种简单证明勾股定理的方法
图g
图f
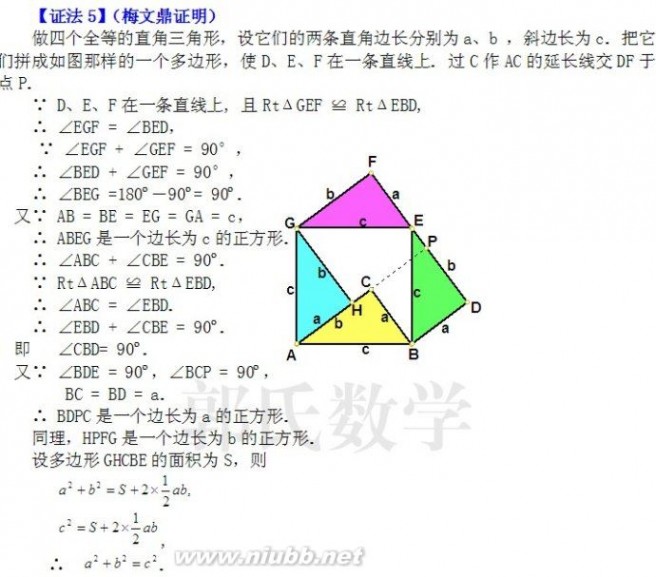
二、定理法证明(举例3种)

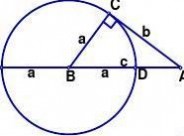
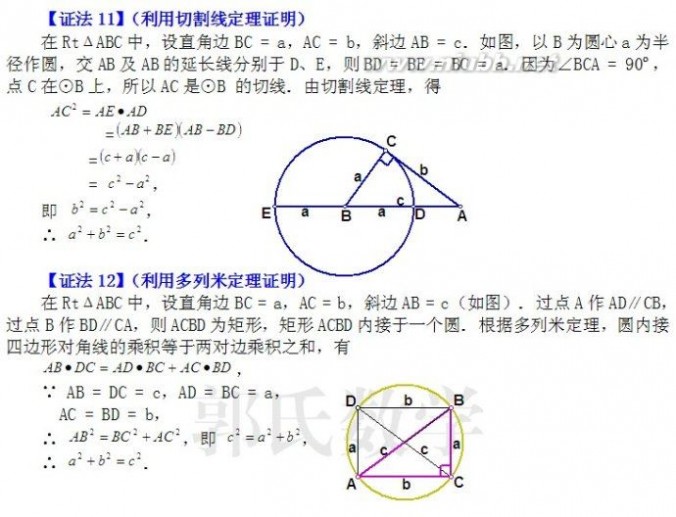
利用切割线定理证明 在RtΔABC中,设直角边BC = a,AC = b,斜边AB = c. 如图,以B为圆心a为半径作圆,交AB及AB的延长线分别于D、E,则BD = BE = BC = a. 因为∠BCA = 90
o,点C在⊙B上,所以AC是⊙B 的切线. 由切割线定
理,得
AC2=AE·AD=(AB+BE) (AB-BD)=(c+a)(c-a)=c2-a2 从而可得 a2+b2 = c2
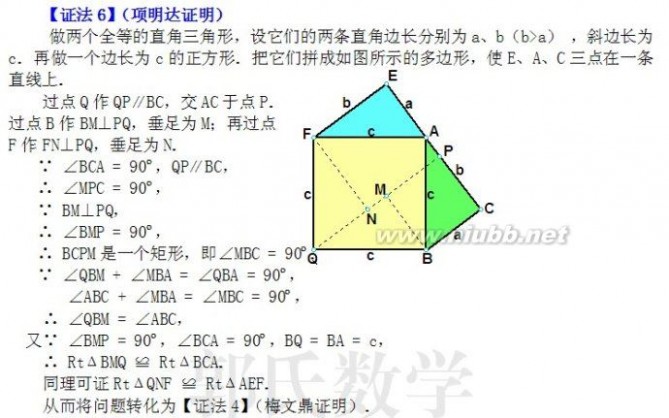
利用托勒密定理证明 在RtΔABC中,设直角边BC = a,AC = b,斜边AB = c(如图). 过点A作AD∥CB,过点B作BD∥CA,则ACBD为矩形,矩形ACBD内接于一个圆. 根据托勒密定理,圆内接四边形对角线的乘积等于两对边乘积之和,有
AB·DC=AD·BC+AC·BD 从而可得a2+b2 = c2
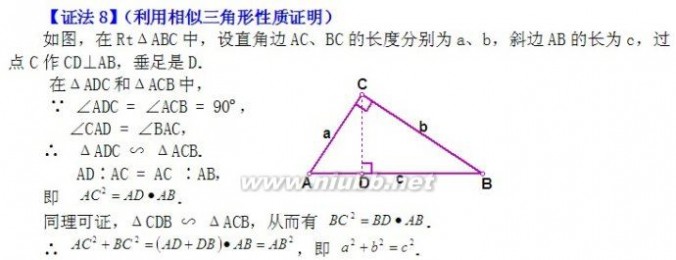
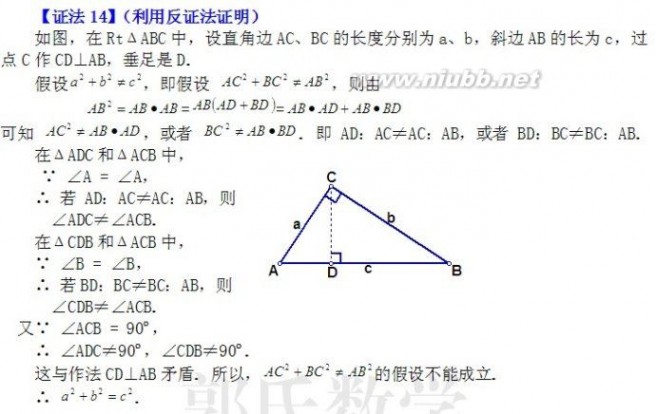
利用射影定理证明
如图,在RtΔABC中,设直角边AC、BC的长度分别为a、b,斜边AB的长为c,过点C作CD⊥AB,垂足是D. 根据射影定理,得
AC2=AD·AB, BC2=BD·BA
即AC2+BC2=AD·AB+BD·BA=AB(AD+BD)=AB2 从而得a2+b2 = c2
品味各种拼图,方法各异,妙趣横生,证明思路别具匠心,极富创新。[www.61k.com]它们充分运用了几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,深刻体现了形数统一、代数和几何紧密结合、互不可分的独特魅力。

61阅读请您转载分享:
二 : 勾股定理的证明问题据说勾股定理有很多种证明方法啊,再次特地请教一
勾股定理的证明问题
据说勾股定理有很多种证明方法啊,再次特地请教一下大家,回答时请附图说明,多谢啦!
勾股定理的证明,常用的有两种方法:
(1).面积法:这种方法用的最多,也最容易理解。现行的初中教材上就是用的面积法,它是根据面积相等,列出算式,化简即可。我国古代数学家都是用面积法来证明勾股定理的。(楼上的勾股圆方图就是一例)
(2).相似法:①射影定理法,在RTΔABC中,CD是斜边AB上的高,则AC^2=AD*AB ,
BC^2 =BD*AB ,所以两式相加得AC^2+BC^2=AD*AB+BD*AB=AB^2 .②托勒密定理法,
其内容为:内接于圆的四边形,其两组对边乘积的和等于两对角线的积。即四边形ABCD内接于圆,则AB*CD + AD*BC = AC*BD (用相似三角形去证明),特别地,当四边形ABCD是矩形时,AB=CD、AD=BC、AC=BD ,代入定理中,则AB^2 +BC^2=AC^2
(传图不易)
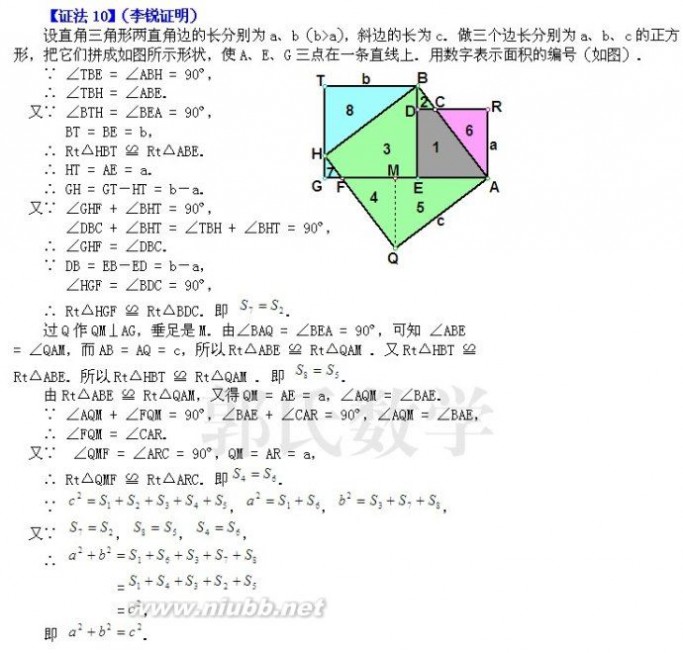
三 : 勾股定理的16种证明方法
勾股定理的证明是论证数学的发端,它是历史上第一个把形与数联系起来的定理,即第一个把几何与代数联系起来的定理,也是数学家认为探索外星文明与外星人沟通的最好“语言”。勾股定理导致希伯索斯无理数的发现,引发了第一次数学危机,加深了人们对数的理解,促进了数学的进步发展。勾股定理是历史上第一个给出不定方程的解答,从而促使费尔玛大定理的提出,这是一只下金蛋的鹅,数学家们经过350年的历程才获得解决,这期间给整个数学界带来了巨大的财富。
我国古代数学家对勾股定理的证明,极富创意,即使在理论方面也占一席之地。以赵爽的“弦图”作为2002年在中国召开世界数学家大会的会徽,可知“弦图”已作为了我国古代数学成就的代表。而在西方,欧几里得在证明勾股定理的同时结合图形分析,以演绎推理的方法获得了一系列的定理和推论,为几何公理体系的完善和发展写下了新的篇章。
中国的数学文化传统反映的是重视应用,数形结合以算为主的务实精神。由于述而不作研究,使勾股定理在中国古代一直没有超越直观经验和具体运算,发展成一套完整的演绎体系,而只是作为一种技艺在传播应用,走的只是解决实际问题的模式化道路。
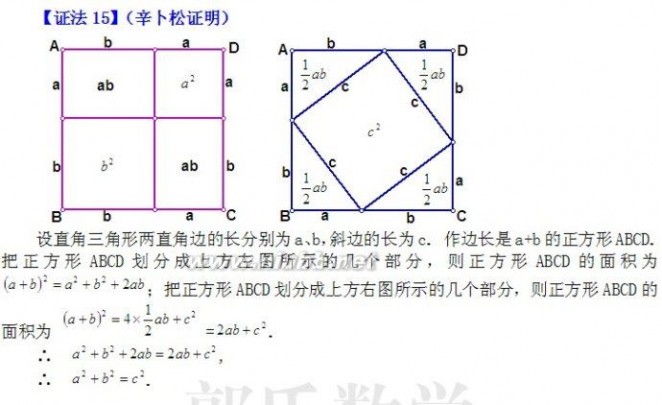
勾股定理有数百种证明方法,下面是最基础的16种证明方法,有兴趣的同学可以研究下。






郭氏数学满分班学习资料邮购
——送初高中语数外、理化生、政史地名校内部资料状元笔记
——在家学到名校内部学习资料,和状元接受一样的教学资源

郭氏数学开创者:郭老师,曾就职于陕西省重点中学西安市高新一中,现就职于河南省某重点中学,郑州市骨干教师、学科带头人,市级教学比赛一等奖。有数十篇教学论文发表于《中学生数理化》、《中学数学杂志》、《数学周报》、《中国数学教育》等。所带学生每年都有中考满分,99%学生成绩有明显提高。
周老师,衡水中学初中数学组组长,“河北省名师”“全国教育系统劳模”“河北省有突出贡献的青年专家”“中考命题专家组成员”。周老师的班级数学平均成绩近110。
为让更多的学生能接受更好的教育考上满意的高中,由郭氏数学名师联盟(包括衡水、北京、上海、南京、郑州五地十位重点学校在职老师)精心编辑状元班全套资料电子版,适合初中各年级学生。让您的孩子在家也能学到名校名师内部资料、和中考状元接受一样的教学资源。比任何一本你在市面上能买到的教辅资料都更权威、翔实、口语化、易学习、易掌握。状元班内部资料里面的考试方法和学习技巧,都是实战化的:从怎么读题到从哪找思路然后如何一步步打通思路、如何写在卷面上,最后如何避免失误、确保正确。从而让学生得到高分甚至满分。
名师团内部学习资料,是各科名师数十年教学经验的结晶,已经有全国近30个省市的学生购买,成绩普遍有明显提升,经常可以收到同学们的感谢信息;许多公办学校和辅导机构老师买了教学用,反响极好。
【教材版本问题】郭氏数学内部资料,有人教版、北师大版、华师版、苏教版、浙教版。
电子版资料由word文档、PPT课件和手稿笔记照片构成,同学们既可以在手机电脑上学习,也可以自由选择打印。包括:
1.【名师课堂】郭氏数学各地名师对初中数学各章节的教学课件(初中数学的每一章每一节都有各地名校名师内部教学课件等资料,让您在自家也能接受名校的教学资源)和指导学生做的学习笔记(笔记以口语化方式记述了各知识点重点解题方法和如何确保正确防范失误的注意要点,相当于名师一对一讲给你听)(★★★★★);
2.【学习方法】为什么有的同学明明很努力,却总是学不好呢?郭氏数学内部学习方法,让你比学霸更高效!
3.【考试技巧】标准化解题方法,名师总结“不失分”技巧,让你的成绩稳步超过班里的学霸,趋于满分(★★★★★);
4.【中考数学命题研究】2013-2015年年全国各地中考试卷数十个专题,研究出题模式与得分技巧(★★★★★);
5.【选择题填空题满分技巧】选择题的特殊解法满分诀窍,填空题高分技巧,针对性练习;
6.【中考一轮二轮三轮复习】知识点全面系统复习、分类梳理强化、各种综合题型详解;
7.【中考专题】分类讨论、易错题、动点问题、折叠问题、压轴大题、开放题、创新题等专题讲解;
8.【中考试卷解析】历年各省市中考真题和名校模拟题名师解析上百套,每一道题都有名师分析、精解与点评总结;
9.【初中各科】初中语文、英语、物理、化学、历史、地理、生物、政治中考高分必备复习资料(名校内部使用)。
10.【高中资料】高考文理科状元高考语文、数学、英语、历史、政治、地理、物理、化学、生物学习笔记和数位高中名师对高考各科知识点、题型的精心总结。
单是其中的数学资料就是郭氏数学各地名师心血的结晶,效果好于一个普通的在职教师一对一每周2小时单独课外辅导。
其他初中科目资料有衡水中学内部教学资料,其效果远远好于在校外花几百块钱每科买6本辅导书。
各科高考状元笔记和名校高中学习资料,比淘宝上卖500一套的全面得多,其内容是淘宝上面高考状元笔记的10倍以上,质量更是远远好于淘宝上面的。
内部资料,我们几位老师一直都在更新。发给你的是下载网址和密码。只要每月重新下载,随时都可以得到最新的状元班内部教学和考试资料【无论将来资料价格涨到多少,购买一次,永远免费】。哪怕你现在是初一,一直到高三都可以一直得到郭氏数学最新资料,永不过时。
以上全部资料,一共998元。为促进教育公平,每周限2名学生,只要498元就可以让孩子拥有初高中六年的名校学习资料!
联系方式:郭老师15838248498QQ2696902349。可以银行汇款或支付宝付款,支付宝账号:15838248498(付款时留邮箱和教材版本即可,郭老师会第一时间把资料发给你)
温馨提示:网上搜到的学习资料,平均每份资料都有8-10处错误。请不要贪便宜,让孩子被这样的资料所害。郭氏数学名师团内部资料,经过各地名师精心总结和多年教学实践,更权威、更实用。




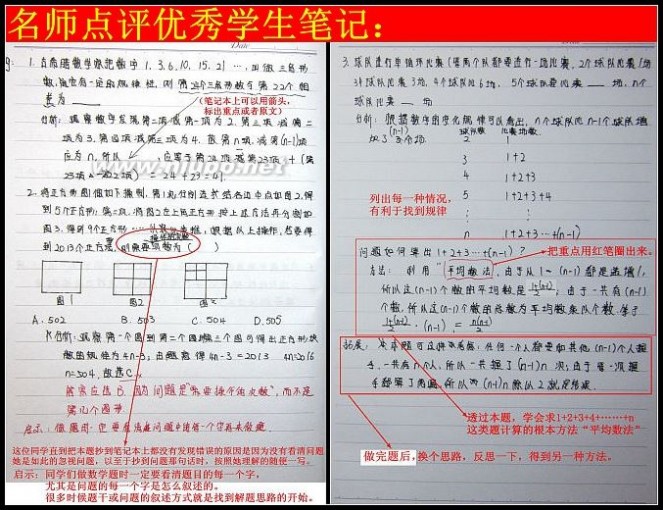


郭氏数学学习法简介:
搜狗百科对于郭氏数学的介绍:
教师评价:
郭老师手稿:
中考考点分析:
教材分析:
《中考数学解题方法与技巧》简介:
本文标题:勾股定理的证明方法-几种简单证明勾股定理的方法61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1