一 : 逆矩阵及其运算
一、概念的引入
在数的运算中,当数a ? 0 时, 有
aa ? a a ? 1,
其中 a ?1 ? 1 为 a 的倒数, (或称 a 的逆); a 在矩阵的运算中, 单位阵 E相当于数的乘法运算中 的1, 那么,对于矩阵 A , 如果存在一个矩阵A?1, 使得
?1
?1
AA?1 ? A?1 A ? E ,
A?1称为 A 的可逆矩阵或逆阵. 则矩阵
二、逆矩阵的概念和性质
定义
,使得
对于 n 阶矩阵 A ,如果有一个 n 阶矩阵 B
AB ? BA ? E ,
?1
则说矩阵A是可逆的,并把矩阵 B 称为 A 的逆矩阵.
A的逆矩阵记作 A .
例
? 1 ? 1? ? 1 2 1 2? ?, B ? ? ?, 设 A?? ?1 1 ? ? ? 1 2 1 2?
? AB ? BA ? E ,
? B是A的一个逆矩阵 .
说明 若 A 是可逆矩阵,则 A 的逆矩阵是唯一的.
若设 B 和 C 是 A 的可逆矩阵,则有
AB ? BA ? E , AC ? CA ? E ,
可得 B ? EB ? ?CA?B ? C ? AB ? ? CE ? C . 所以 A 的逆矩阵是唯一的,即
B ? C ? A ?1 .
例 解 则
? 2 1? ? , 求A的逆阵. 设 A?? ? ? 1 0? ?a b? ? 利用待定系数法 是 A 的逆矩阵, 设 B?? ?c d? ? 2 1 ?? a b ? ? 1 0 ? AB ? ? ?? ??? ? ? ? 1 0 ?? c d ? ? 0 1 ? ? 2a ? c 2b ? d ? ? 1 0 ? ?? ??? ? ? b ? ? 0 1? ? ?a
? 2a ? c ? 1, ? 2b ? d ? 0 , ? ?? ? ? a ? 0, ? ? b ? 1, ?
又因为
? a ? 0, ?b ? ?1, ? ?? ? c ? 1, ? d ? 2. ?
AB
BA
? 2 1 ?? 0 ? 1 ? ? 0 ? 1 ?? 2 1 ? ? 1 0 ? ?, ? ?? ?? ? ?? ? ?? ? ? 1 0 ?? 1 2 ? ? 1 2 ?? ? 1 0 ? ? 0 1 ?
所以
? 0 ? 1? A ?? ?. ?1 2 ?
?1
定理1
矩阵 A 可逆的充要条件是 A ? 0 ,且 1 ? ?1 A ? A, A
其中A?为矩阵A的伴随矩阵.
证明 若 A 可逆,即有A?1使AA ?1 ? E .
故 A ? A?1 ? E ? 1,
所以 A ? 0.
当 A ? 0时,
当 A ? 0时,
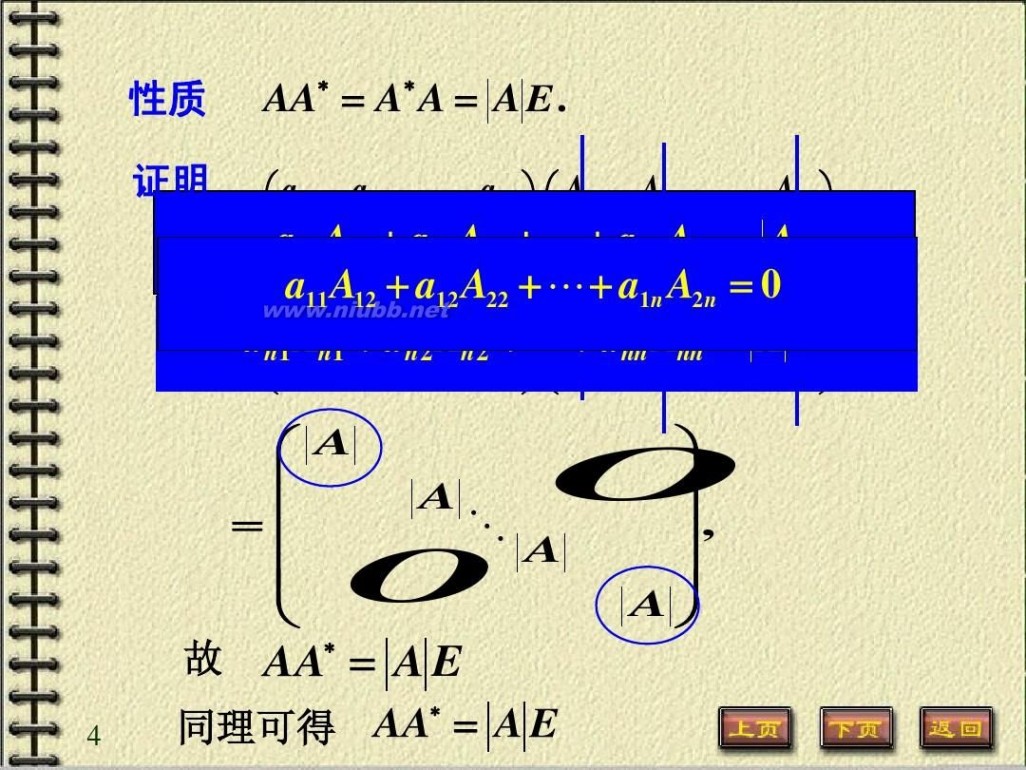
? a11 a12 ? a1n ? ? A11 A21 ? An1 ? ? ?? ? a a22 ? a2 n ? ? A12 A22 ? An 2 ? ? ? 21 AA ? ? a A ? a A ? ? ? ? a A ? A? 11 12 1 1n ? 11 ? ? 12 ? ? ? ?n ? ? ? ?a a ? a ? ? A A ? A ? ?? ? ? n1A n? a A nn ???n a 2 nA ? A ? ? 1? 2 nn a
n1 n1 n2 n2 nn nn
? A ? ? ?? ? ? ?
A
O
?
O
A
? ? ? ?, ? A? ?
A? A? AA? ? A? A ? A E ? A ? A ? E , A A
按逆矩阵的定义得
A A ? . A
?1
?
证毕
奇异矩阵与非奇异矩阵的定义
当 A ? 0时, A称为奇异矩阵,当 A ? 0时, A称为 非奇异矩阵.
由此可得A是可逆阵的充要条件是 为非奇异矩阵 A .
推论 证明
若AB ? E ?或BA ? E ?, 则B ? A?1 .
A ? B ? E ? 1,
故 A ? 0,
因而A?1存在, 于是
B ? EB ? A?1 A B ? A?1 ? AB?
?
?
? A?1. ?A E
?1
证毕
逆矩
阵的运算性质
?1? 若A可逆, 则A 亦可逆, 且?A
?1
?1 ?1
?
? A.
?2? 若A可逆, 数? ? 0, 则?A可逆, 且
??A? ? A?1 .
?1
1
?
?3? 若A, B为同阶方阵且均可逆则AB亦可逆, 且 ,
? A B ?1 ??1 ? B ?1 A
证明
? AB??B?1 A?1 ? ? A?BB?1 ?A?1
?1 ? AEA ?1 ? AA ? E ,
? AB ??1 ? B ?1 A?1 . ?
推广
? ?A1 A2 ?Am??1 ? Am 1 A2?1 A1?.1 ?
?4? 若A可逆, 则A 亦可逆 , 且 ?A
T
T ?1
? ? ?A ? .
?1 T
证明
? A ?A
T
?1 T
? ? ? A A?
?1 ?1 T
T
? E T ? E,
? ?A
T ?1
?
? ?A
?.
A
?k
另外, 当 A ? 0时, 定义 A ? E,
0
? ?A
?1 k
?.
?k为正整数?
当 A ? 0, ? , ?为整数时, 有 A A ?A
? ? ? ??
,
?1
?A ?
? ?
? A?? .
?5? 若A可逆,则有 A ? A .
?1
证明
? AA ?1 ? E
? A A ?1 ? 1
因此 A ? A .
?1
?1
三、逆矩阵的求法
例1
? 1 2 3? ? ? 求方阵 A ? ? 2 2 1 ? 的逆矩阵. ? 3 4 3? ? ? 1 2 3 ? A ? 2 2 1 ? 0, 3 4 3
解
? A?1存在.
2 1 3 3
A11 ?
2 1 4 3
? 2,
A12 ? ?
? ?3,
同理可得
A13 ? 2, A21 ? 6, A22 ? ?6, A23 ? 2,
A31 ? ?4, A32 ? 5, A33 ? ?2,
得
故
6 ? 4? ? 2 ? ? ? A ? ? ? 3 ? 6 5 ?, ? 2 2 ? 2? ? ?
3 ? 2? 6 ? 4? ? 1 ? 2 ? ? ? 1 ? 1? A ?1 ? A ? ? ? 3 ? 6 5 ? ? ? ? 3 2 ? 3 5 2 ? . A 2? ? ? 1 1 ?1? ? 2 ? 2? ? ? 2
例2 下列矩阵A, B是否可逆? 若可逆, 求出其逆 矩阵. ? 2 3 ?1 ? ? 1 2 3? ? ? ? ? B ? ??1 3 5 ?. A ? ? 2 1 2 ?, ? 1 5 ? 11? ? 1 3 3? ? ? ? ?
1 2 3
解
1 0
2 1
3 0
A ? 2 1 2? 0 ? 3 ?4 1 3 3
1 0
2 1
3 0
1 2 3 3 2 1 1 3
? 0 ?3 ?4?
?3 ?4 1 0
? 4 ? 0, 所以A可逆 .
2 2 1 3
? A11 ? A13 ?
? ?3, ? 5,
A12 ? ?
? ?4,
同理可求得
A21 ? 3 , A22 ? 0 , A23 ? ?1, A31 ? 1, A32 ? 4 , A33 ? ?3.
? A11 A21 A31 ? ? A 1? ?1 ? A ? ? ? A12 A22 A32 ? A A? A13 A23 A33 ? ? ?
?
1 ? ?? 3 3 ? 1? ? ??4 0 4 ?. 4? 5 ? 1 ? 3? ? ? 2 1 3 ?1 5 ? 0,
故B不可逆 .
由于 B ? ? 1 3
5 ? 11
例3
? 1 2 3? ? 1 3? ? ? ? ? ? 2 1? ?, C ? ? 2 0 ?, 设 A ? ? 2 2 1 ?, B ? ? ? 5 3? ? 3 4 3? ? 3 1? ? ? ? ?
求矩阵X使满足 AXB ? C .
1 2 3
解 ? A ? 2 2 1 ? 2 ? 0, B ?
2 1 5 3
? 1 ? 0,
3 4 3
? A , B 都存在.
?1
?1
3 ? 2? ? 1 ? ? ?1 且 A ? ? ? 3 2 ? 3 5 2 ?, ? 1 1 ?1? ? ?
? 3 ? 1? B ?? ?, ?? 5 2 ?
?1
? A?1 AXBB ?1 ? A?1CB ?1 又由 AXB ? C E ? X ? A?1CB ?1 . 于是 X ? A?1CB ?1
3 ? 2 ?? 1 3 ? ? 1 ?
?? ?? 3 ? 1 ? ? ? ? 3 2 ? 3 5 2 ?? 2 0 ?? ? ? 1 ?? 3 1 ?? ? 5 2 ? 1 ? 1 ?? ? ?
1 ? ?1 1 ? ? ?2 ? ?? 3 ? 1 ? ? ? ? ? 0 ? 2 ?? ? ? ? 10 ? 4 ? . ? 0 2 ?? ? 5 2 ? ? ? 10 4 ? ? ? ? ?
例4
设方阵A满足方程A2 ? A ? 2 E ? 0, 证明 :
由A2 ? A ? 2 E ? 0,
A, A ? 2 E都可逆, 并求它们的逆矩阵 .
证明
A ?1
A? E ?E 得A? A ? E ? ? 2 E ? A 2 A? E ? A ? 1 ? A ? 0, 故A可逆 . 2
1 ? A ? ? A ? E ?. 2
?1
又由A2 ? A ? 2 E ? 0
? ? A ? 2 E ?? A ? 3 E ? ? 4 E ? 0
? 1? ? ? ? A ? 2 E ??? A ? 3 E ?? ? E ? 4 ?
1 ? A ? 2 E ? ? A ? 3 E ? ? 1, 故A ? 2 E可逆 . 4 1 3E ? A ?1 且 ? A ? 2E ? ? ? ? A ? 3E ? ? . 4 4
? A ? 2E ?
?1
例5
解矩阵方程 ? 1 ? 5? ?3 2? ?1? ? ?X ? ? ?; ? ?1 4 ? ?1 4?
? 1 ? 1 1? ? 1 2 ? 3? ? ? ? ? ?2? X ? 1 1 0 ? ? ? 2 0 4 ?; ? 2 1 1? ? 0 ? 1 5 ? ? ? ? ?
解
?1?
? 1 ? 5? ? 3 2? ? ?X ? ? ? ??1 4 ? ? 1 4?
?1
? 1 ? 5? 给方程两端左乘矩阵 ? ? , ??1 4 ? E ? 1 ? 5? ? 1 ? 5? ? 1 ? 5? ? 3 2? 得 ? ? ? ? X ?? ? ? ? ??1 4 ? ??1 4 ? ? ? 1 4 ? ? 1 4? ? 1 ? 5 ? ? 3 2 ? ? ? 4 ? 5 ?? 3 2 ? ? ? 17 ? 28 ? ? X ?? ? ? ? ?? ?? ??? ?. ? ? 1 4 ? ? 1 4 ? ? ? 1 ? 1 ?? 1 4 ? ? ? 4 ? 6 ?
?1 ?1 ?1
? 1 ? 1 1? ? 1 2 ? 3? ? ? ? ? ?2 ? X ? 1 1 0 ? ? ? 2 0 4 ? ? 2 1 1? ? 0 ? 1 5 ? ? ? ? ?
给方程两端右乘矩阵
? 1 ? 1 1? ? ? ? 1 1 0? , ? 2 1 1? ? ?
?1
?1
得
9 ? 5? ? 1 2 ? 3 ?? 1 ? 1 1 ? ? 2 ? ? ?? ? ? X ? ?2 0 4 ?? 1 1 0 ? ? ? ? 2 ? 8 6 ? . ? 0 ? 1 5 ?? 2 1 1 ? ? ? 4 ? 14 9 ? ? ? ?? ? ?
例6
设三阶矩阵A, B满足关系:
?1 2 ? ? ? ?1 A BA ? 6 A ? BA, 且A ? ? 14 ? 求B . ? 1 7? ? ?
o
o
?1
解
A ?1 BA ? BA ? 6 A
? ?A
?1
? E ?BA ? 6 A ? ?A
?1 ?1
? E ?B ? 6 E
? B ? 6?A ? E ? .
B ? 6? A ? E ?
?1
?1
?? 2 0 0 ? ? 1 0 0 ? ? ? 1 0 0? ? ? ?? 0 4 0 ? ? ? 0 1 0 ? ? ?6 ? ? ? ? ? ? 6? 0 3 0 ? ? ? 0 0 7 ? ? 0 0 1 ?? ? 0 0 6? ?? ? ? ?? ? ? ?
?1
?1
?1
0 ? ? 6 0 0? ? 1 0 0? ?1 0 ? ? ? ? ? ? ? 6? 0 3 0 ? ? 6? 0 1 3 0 ? ? ? 0 2 0 ? . ? 0 0 6? ? 0 0 1 6? ? 0 0 1? ? ? ? ? ? ?
例7
?1 ? ?0 已知A ? ? 0 ? ?0 ?0 ?
因 A ? 5! ? 0,
0 0 0 0? ? 2 0
0 0? ? 求 A ?1 . 0 3 0 0 ? 0 0 4 0? ? 0 0 0 5?
故A?1存在.
解
由伴随矩阵法得 A?1 ? A? A ,
0 0 0 0 ? ?2? 3?4?5 ? ? 1? 3 ? 4 ? 5 0 0 0 ? ? 0 1? ? 0 0 1? 2 ? 4 ? 5 0 0 ? ? 5! ? 0 0 1? 2 ? 3 ? 5 0 ? ? 0 ? 0 0 0 0 1? 2 ? 3 ? 4? ? ?
?1 ? ?0 ? ?0 ? ?0 ?0 ? 0 1 2 0 0 0 0 0 1 3 0 0 0 0 0 14 0 0 ? ? 0 ? 0 ?. ? 0 ? 1 5? ?
四、小结
逆矩阵的概念及运算性质.
逆矩阵 A?1 存在 ? A ? 0. 逆矩阵的计算方法
?3?初等变换法?下一章介绍?.
A? ?2?利用公式A?1 ? ; ?1?待定系数法; A
思考题
若A可逆, 那么矩阵方程AX ? B是否有唯一解 X ? A?1 B ? 矩阵方程 YA ? B 是否有唯一解 Y ? BA?1 ?
思考题解答
答
是的. 这是由于A?1的唯一性决定的 .
二 : 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008
伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008

伴随矩阵 伴随矩阵法求逆矩阵2008
(www.61k.com]伴随矩阵 伴随矩阵法求逆矩阵2008
(www.61k.com)伴随矩阵 伴随矩阵法求逆矩阵2008
(www.61k.com)伴随矩阵 伴随矩阵法求逆矩阵2008
(www.61k.com)伴随矩阵 伴随矩阵法求逆矩阵2008
[www.61k.com)61阅读提醒您本文地址:
三 : 设矩阵(其中a>0,b>0),(Ⅰ)若a=2,b=3,求矩阵M的逆矩阵M
设矩阵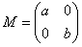 (其中a>0,b>0), (其中a>0,b>0), (Ⅰ)若a=2,b=3,求矩阵M的逆矩阵M-1; (Ⅱ)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′:  ,求a,b的值. ,求a,b的值. |
解:(Ⅰ)设矩阵M的逆矩阵 |
考点:
考点名称:逆变换与逆矩阵逆变换的定义:
一般地,设ρ是一个线性变换,如果存在线性变换σ,使得σρ=ρσ=I,则称变换ρ可逆,并且称σ是ρ的逆变换。
逆矩阵的定义:
对于二阶矩阵A,B,若有AB=BA=E,则称A是可逆的,B称为A的逆矩阵,通常记A的逆矩阵为 。
。
逆矩阵的特点:
1、逆矩阵是唯一的。
2、若二阶矩阵A,B均存在逆矩阵,则AB也存在逆矩阵,且 。
。
矩阵的定义:
由m×n个数排成的m行n列的表
称为m行n列矩阵(matrix),简称m×n矩阵。
特殊形式矩阵:
(1)n阶方阵:在矩阵 中,当m=n时,A称为n阶方阵;
中,当m=n时,A称为n阶方阵;
(2)行矩阵:只有一行的矩阵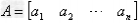 叫做行矩阵;
叫做行矩阵;
列矩阵:只有一列的矩阵, 叫做列矩阵;
叫做列矩阵;
(3)零矩阵:元素都是零的矩阵称作零矩阵。
二阶矩阵与平面图形的变换:
(1)二阶矩阵的定义:由4个数a,b,c,d排成的正方形数表 称为二阶矩阵;
称为二阶矩阵;
(2)几种特殊线性变换:主要有旋转变换、反射变换、伸压变换、投影变换、切变变换这几种。求经矩阵变换后的解析式常采用数形结合的方法,先观察是属于哪一种变换,然后利用解析几何中的相关点法(转移代入法)来解。
矩阵的运算律:
(1)矩阵的和(差):当两个矩阵A、B的维数相同时,将它们各位置上的元素加(减)所得到的矩阵称为矩阵A、B的和(差),记作: 。
。
运算律:加法运算律: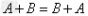 ;
;
加法结合律: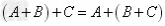 。
。
(2)数乘矩阵:矩阵与实数的积:设 为任意实数,把矩阵A的所有元素与
为任意实数,把矩阵A的所有元素与 相乘得到的矩阵叫做矩阵A与实数
相乘得到的矩阵叫做矩阵A与实数 的乘积矩阵,记作:
的乘积矩阵,记作: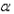 A。
A。
运算律:(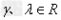 )
)
分配律: ;
;
结合律: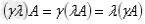 。
。
(3)矩阵的乘积:一般地,设A是m×k阶矩阵,B是k×n阶矩阵,设C为m×n矩阵,如果矩阵C中第i行第j列元素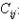 是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
运算律:
分配律: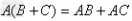 ;
; ;
;
结合律: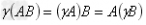 ;
;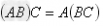 。
。
注:(1)交换律不成立,即:AB≠BA;(2)只有当矩阵A的列数与矩阵B的行数相等时,矩阵之积才有意义。
四 : 设矩阵(其中a>0,b>0),(Ⅰ)若a=2,b=3,求矩阵M的逆矩阵M
设矩阵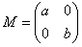 (其中a>0,b>0), (其中a>0,b>0), (Ⅰ)若a=2,b=3,求矩阵M的逆矩阵M-1; (Ⅱ)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′: 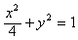 ,求a,b的值. ,求a,b的值. |
解:(Ⅰ)设矩阵M的逆矩阵 |
考点:
考点名称:逆变换与逆矩阵逆变换的定义:
一般地,设ρ是一个线性变换,如果存在线性变换σ,使得σρ=ρσ=I,则称变换ρ可逆,并且称σ是ρ的逆变换。
逆矩阵的定义:
对于二阶矩阵A,B,若有AB=BA=E,则称A是可逆的,B称为A的逆矩阵,通常记A的逆矩阵为 。
。
逆矩阵的特点:
1、逆矩阵是唯一的。
2、若二阶矩阵A,B均存在逆矩阵,则AB也存在逆矩阵,且 。
。
矩阵的定义:
由m×n个数排成的m行n列的表
称为m行n列矩阵(matrix),简称m×n矩阵。
特殊形式矩阵:
(1)n阶方阵:在矩阵 中,当m=n时,A称为n阶方阵;
中,当m=n时,A称为n阶方阵;
(2)行矩阵:只有一行的矩阵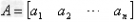 叫做行矩阵;
叫做行矩阵;
列矩阵:只有一列的矩阵,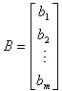 叫做列矩阵;
叫做列矩阵;
(3)零矩阵:元素都是零的矩阵称作零矩阵。
二阶矩阵与平面图形的变换:
(1)二阶矩阵的定义:由4个数a,b,c,d排成的正方形数表 称为二阶矩阵;
称为二阶矩阵;
(2)几种特殊线性变换:主要有旋转变换、反射变换、伸压变换、投影变换、切变变换这几种。求经矩阵变换后的解析式常采用数形结合的方法,先观察是属于哪一种变换,然后利用解析几何中的相关点法(转移代入法)来解。
矩阵的运算律:
(1)矩阵的和(差):当两个矩阵A、B的维数相同时,将它们各位置上的元素加(减)所得到的矩阵称为矩阵A、B的和(差),记作: 。
。
运算律:加法运算律: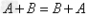 ;
;
加法结合律: 。
。
(2)数乘矩阵:矩阵与实数的积:设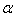 为任意实数,把矩阵A的所有元素与
为任意实数,把矩阵A的所有元素与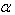 相乘得到的矩阵叫做矩阵A与实数
相乘得到的矩阵叫做矩阵A与实数 的乘积矩阵,记作:
的乘积矩阵,记作: A。
A。
运算律:(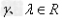 )
)
分配律: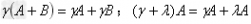 ;
;
结合律: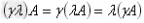 。
。
(3)矩阵的乘积:一般地,设A是m×k阶矩阵,B是k×n阶矩阵,设C为m×n矩阵,如果矩阵C中第i行第j列元素 是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
是矩阵A第i个行向量与矩阵B的第j个列向量的数量积,那么矩阵C叫做A与B的乘积,记作:C=AB。
运算律:
分配律: ;
;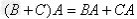 ;
;
结合律: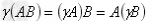 ;
;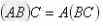 。
。
注:(1)交换律不成立,即:AB≠BA;(2)只有当矩阵A的列数与矩阵B的行数相等时,矩阵之积才有意义。
五 : 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

矩阵的逆 逆矩阵及其运算

61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1