一 : 怎么在Word2010中输入排列组合的数学符号

高中教学中经常有许多符号，尤其是理科，数学、物理、化学多的是符号，那么这些东西怎么在Word2010中输入呢？下面，以数学中比较实用的排列组合公式来举例，教大家怎么在Word2010中输入。

 　　①首先启动Word2010，输入一个大写字母A，如下图所示。

　　②然后，点击菜单栏--开始--双行合一。下图红色方框标记的很清楚。

　　③在文字中输入2 5，注意要空格，下方预览里面可以查看效果。

　　④按下确定键之后，就完成了数学公式的输入。

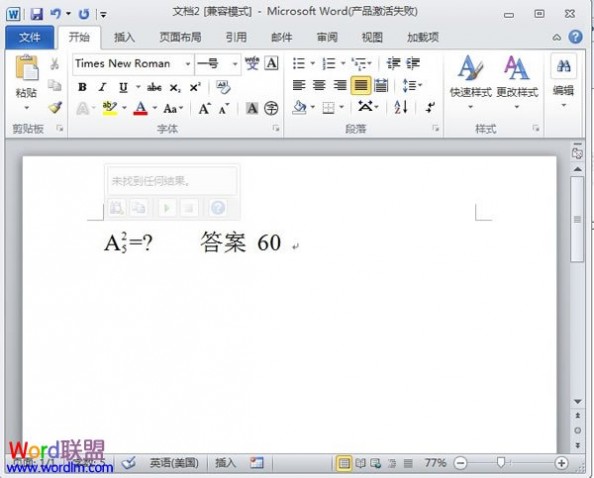
二 : 高中数学排列组合问题七名师生站成一排照相留念,其中老师一人,男生

高中数学排列组合问题

七名师生站成一排留念,其中老师一人,男生四人,女生两人,在下列情况下,有站法多少？
-----若4名男生升高都不等，按从高到低的一种顺序站。（相除的含义？？）

---

关键：插队问题。

7名师生站成一排照相留念，其中老师一人,男生四人,女生两人

若4名男生身高都不等，按从高到低的一种顺序站，站法的可能分情况讨论：

首先4男生从高到低站好，每两名男生中间留空隙，允许其他人站，若没有人站，再靠近即可。

4名男生身边共有5个位置可以站人。

情况1）剩余3人各站一个位置，站法C(5,3)*A(3,3)=A(5,3)=60

理由：任选三个位置C(5,3)，三个人站法全排A(3,3)

情况2）剩余3人站两个位置，站法C(3,1)*A(5,2)*A(2,2)=120

理由：分两组，任选一人单独站，另外两个人站一起，C(3,1)，这两组人

任选两个位置，站法全排C(5,2)A(2,2)=A(5,2),2个人组站法全排A(2,2)

情形3）剩余3人站一起，站法C(5,1)*A(3,3)=30

理由：五个位置任选一个，站进去，C(5,1)，这三个人全排A(3,3)

综上，本题可能站法;60+120+30=210

另解：

七人全排，除以4个男生的全排，因为对此题而言，

男生不能全排，只有一种站法：7!/4!=210

三 : 人教版高中数学《排列组合和概率》全部教案

人教版高中数学全部教案

两个基本原理

一、教学目标

1、知识传授目标：正确理解和掌握加法原理和乘法原理

2、能力培养目标：能准确地应用它们分析和解决一些简单的问题

3、思想教育目标：发展学生的思维能力，培养学生分析问题和解决问题的能力

二、教材分析

1.重点：加法原理，乘法原理。 解决方法：利用简单的举例得到一般的结论．

2.难点：加法原理，乘法原理的区分。解决方法：运用对比的方法比较它们的异同．

三、活动设计

1.活动：思考，讨论，对比，练习．

2.教具：多媒体课件．

四、教学过程正

1．新课导入

随着社会发展，先进技术，使得各种问题解决方法多样化，高标准严要求，使得商品生产工序复杂化，解决一件事常常有多种方法完成，或几个过程才能完成。

排列组合这一章都是讨论简单的计数问题，而排列、组合的基础就是基本原理，用好基本原理是排列组合的关键．

2．新课

我们先看下面两个问题．

(l)从甲地到乙地，可以乘火车，也可以乘汽车，还可以乘轮船．一天中，火车有4班，汽车有 2班，轮船有 3班，问一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法？ 板书：图

因为一天中乘火车有4种走法，乘汽车有2种走法，乘轮船有3种走法，每一种走法都可以从甲地到达乙地，因此，一天中乘坐这些交通工具从甲地到乙地共有 4十2十3=9种不同的走法．

一般地，有如下原理：

加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，??，在第n类办法中有mn种不同的方法．那么完成这件事共有N＝m1十m2十?十mn种不同的方法．

(2) 我们再看下面的问题：

由A村去B村的道路有3条，由B村去C村的道路有2条．从A村经B村去C村，共有多少种不同的走法？

板书：图

这里，从A村到B村有3种不同的走法，按这3种走法中的每一种走法到达B村后，再从B村到C村又有2种不同的走法．因此，从A村经B村去C村共有 3X2=6种不同的走法． 一般地，有如下原理：

乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，??，做第n步有mn种不同的方法．那么完成这件事共有N＝m1 m2?mn种不同的方法．

例1 书架上层放有6本不同的数学书，下层放有5本不同的语文书．

1）从中任取一本，有多少种不同的取法？

人教版高中数学全部教案

2）从中任取数学书与语文书各一本，有多少的取法？

解：（1）从书架上任取一本书，有两类办法：第一类办法是从上层取数学书，可以从6本书中任取一本，有6种方法；第二类办法是从下层取语文书，可以从5本书中任取一本，有5种方法．根据加法原理，得到不同的取法的种数是6十5=11．

答：从书架L任取一本书，有11种不同的取法．

（2）从书架上任取数学书与语文书各一本，可以分成两个步骤完成：第一步取一本数学书，有6种方法；第二步取一本语文书，有5种方法．根据乘法原理，得到不同的取法的种数是 N＝6X5＝30．

答：从书架上取数学书与语文书各一本，有30种不同的方法．

练习： 一同学有4枚明朝不同古币和6枚清朝不同古币

1）从中任取一枚，有多少种不同取法？ 2）从中任取明清古币各一枚，有多少种不同取法？

例2(1)由数字l，2，3，4，5可以组成多少个数字允许重复三位数？

(2)由数字l，2，3，4，5可以组成多少个数字不允许重复三位数？

(3)由数字0，l，2，3，4，5可以组成多少个数字不允许重复三位数？

解：要组成一个三位数可以分成三个步骤完成：第一步确定百位上的数字，从5个数字中任选一个数字，共有5种选法；第二步确定十位上的数字，由于数字允许重复，

这仍有5种选法，第三步确定个位上的数字，同理，它也有5种选法．根据乘法原理，得到可以组成的三位数的个数是N=5X5X5=125．

答：可以组成125个三位数．

练习：

1、从甲地到乙地有2条陆路可走，从乙地到丙地有3条陆路可走，又从甲地不经过乙地到丙地有2条水路可走．

（1）从甲地经乙地到丙地有多少种不同的走法？

（2）从甲地到丙地共有多少种不同的走法？

2．一名儿童做加法游戏．在一个红口袋中装着2O张分别标有数1、2、?、19、20的红卡片，从中任抽一张，把上面的数作为被加数；在另一个黄口袋中装着10张分别标有数1、2、?、9、1O的黄卡片，从中任抽一张，把上面的数作为加数．这名儿童一共可以列出多少个加法式子？

3．题2的变形

4．由0－9这10个数字可以组成多少个没有重复数字的三位数？

小结：要解决某个此类问题，首先要判断是分类，还是分步？分类时用加法，分步时用乘法 其次要注意怎样分类和分步，以后会进一步学习

练习

1．（口答）一件工作可以用两种方法完成．有 5人会用第一种方法完成，另有4人会用第二种方法完成．选出一个人来完成这件工作，共有多少种选法？

2．在读书活动中，一个学生要从 2本科技书、 2本政治书、 3本文艺书里任选一本，共有多少种不同的选法？

3．乘积（a1+a2+a3）（b1+b2+b3+b4）（c1+c2+c3+c4+c5）展开后共有多少项？

4．从甲地到乙地有2条路可通，从乙地到丙地有3条路可通；从甲地到丁地有4条路可通，从丁地到丙地有2条路可通．从甲地到丙地共有多少种不同的走法？

5．一个口袋内装有5个小球，另一个口袋内装有4个小球，所有这些小球的颜色互不相同．

（1）从两个口袋内任取一个小球，有多少种不同的取法？

人教版高中数学全部教案

（2）从两个口袋内各取一个小球，有多少种不同的取法？

作业：（略）

欢迎您进入数学999 http://sx999.k12.net.cn/

排列

【复习基本原理】

1.加法原理 做一件事，完成它可以有n类办法，第一类办法中有m1种不同的方法，第二

办法中有m2种不同的方法??，第n办法中有mn种不同的方法，那么完成

这件事共有

N=m1+m2+m3+?mn

种不同的方法.

2.乘法原理 做一件事，完成它需要分成n个步骤，做第一 步有m1种不同的方法，做第

二步有m2种不同的方法，??，做第n步有mn种不同的方法，.那么完成这

件事共有

N=m1?m2?m3???mn

种不同的方法.

3.两个原理的区别：

【练习1】

1.北京、上海、广州三个民航站之间的直达航线，需要准备多少种不同的机票？

2.由数字1、2、3可以组成多少个无重复数字的二位数？请一一列出.

【基本概念】

1. 什么叫排列？从n个不同元素中，任取m(m?n)个元素（这里的被取元素各不相同）

按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列 ．．．．．．．．．

2. 什么叫不同的排列？元素和顺序至少有一个不同.

3. 什么叫相同的排列？元素和顺序都相同的排列.

4. 什么叫一个排列？

【例题与练习】

1. 由数字1、2、3、4可以组成多少个无重复数字的三位数？

2.已知a、b、c、d四个元素，①写出每次取出3个元素的所有排列；②写出每次取出4个元素的所有排列.

人教版高中数学全部教案

【排列数】

1. 定义：从n个不同元素中，任取m(m?n)个元素的所有排列的个数叫做从n个元素中

m取出m元素的排列数，用符号pn表示.

用符号表示上述各题中的排列数.

m2. 排列数公式：pn=n(n-1)(n-2)?(n-m+1)

123pn? ；pn? ；pn? ；4pn?

242计算：p5 p5p15

【课后检测】

1. 写出：

① 从五个元素a、b、c、d、e中任意取出两个、三个元素的所有排列；

② 由1、2、3、4组成的无重复数字的所有3位数.

③ 由0、1、2、3组成的无重复数字的所有3位数.

2. 计算：

① p

3100 ② p36 ③ p?2p4828 ④ 8p12 7p12

欢迎您进入数学999 http://sx999.k12.net.cn/

排 列

课题：排列的简单应用(1)

目的：进一步掌握排列、排列数的概念以及排列数的两个计算公式，会用排列数公式计算和解决简单的实际问题．

过程：

一、复习：（引导学生对上节课所学知识进行复习整理）

1．排列的定义，理解排列定义需要注意的几点问题；

2．排列数的定义，排列数的计算公式

mm?An?n(n?1)(n?2)?(n?m?1)或Ann! （其中m≤n m,n?Z） (n?m)!

人教版高中数学全部教案

3．全排列、阶乘的意义；规定 0!=1

4．“分类”、“分步”思想在排列问题中的应用．

二、新授：

例1：⑴ 7位同学站成一排，共有多少种不同的排法？

7 解：问题可以看作：7个元素的全排列——A7＝5040

⑵ 7位同学站成两排（前3后4），共有多少种不同的排法？

解：根据分步计数原理：7×6×5×4×3×2×1＝7！＝5040

⑶ 7位同学站成一排，其中甲站在中间的位置，共有多少种不同的排法？

6 解：问题可以看作：余下的6个元素的全排列——A6=720

⑷ 7位同学站成一排，甲、乙只能站在两端的排法共有多少种？

2 解：根据分步计数原理：第一步 甲、乙站在两端有A2种；第二步 余下的5名

55同学进行全排列有A5种 则共有A2A5=240种排列方法 2

⑸ 7位同学站成一排，甲、乙不能站在排头和排尾的排法共有多少种？

解法一（直接法）：第一步 从（除去甲、乙）其余的5位同学中选2位同学站在

2排头和排尾有A5种方法；第二步 从余下的5位同学中选5位进行排列（全排

525列）有A5种方法 所以一共有A5＝2400种排列方法． A5

66 解法二：（排除法）若甲站在排头有A6种方法；若乙站在排尾有A6种方法；若

5甲站在排头且乙站在排尾则有A5种方法．所以甲不能站在排头，乙不能排在

765排尾的排法共有A7－2A6＋A5=2400种．

小结一：对于“在”与“不在”的问题，常常使用“直接法”或“排除法”，对某些特

殊元素可以优先考虑．

例2 ： 7位同学站成一排．

⑴甲、乙两同学必须相邻的排法共有多少种？

解：先将甲、乙两位同学“捆绑”在一起看成一个元素与其余的5个元素（同学）一

6起进行全排列有A6种方法；再将甲、乙两个同学“松绑”进行排列有A2种方法．所

6以这样的排法一共有A6A2＝1440种． 22

⑵甲、乙和丙三个同学都相邻的排法共有多少种？

53 解：方法同上，一共有A5＝720种． A3

⑶甲、乙两同学必须相邻，而且丙不能站在排头和排尾的排法有多少种？

解法一：将甲、乙两同学“捆绑”在一起看成一个元素，此时一共有6个元素，因为

丙不能站在排头和排尾，所以可以从其余的5个元素中选取2个元素放在排头和排

人教版高中数学全部教案

42尾，有A5种方法；将剩下的4个元素进行全排列有A4种方法；最后将甲、乙两个

2422同学“松绑”进行排列有A2种方法．所以这样的排法一共有A5＝960种A4A2

方法．

解法二：将甲、乙两同学“捆绑”在一起看成一个元素，此时一共有6个元素，

5若丙站在排头或排尾有2A5种方法，所以丙不能站在排头和排尾的排法有

652(A6?2A5)?A2?960种方法．

解法三：将甲、乙两同学“捆绑”在一起看成一个元素，此时一共有6个元素，因为

1丙不能站在排头和排尾，所以可以从其余的四个位置选择共有A4种方法，

5 再将其余的5个元素进行全排列共有A5种方法，最后将甲、乙两同学“松绑”，所

5以这样的排法一共有A4A5A2＝960种方法． 12

小结二：对于相邻问题，常用“捆绑法”（先捆后松）．

例3： 7位同学站成一排．

⑴甲、乙两同学不能相邻的排法共有多少种？

762解法一：（排除法）A7?A6?A2?3600

5解法二：（插空法）先将其余五个同学排好有A5种方法，此时他们留下六个位置

2（就称为“空”吧），再将甲、乙同学分别插入这六个位置（空）有A6种方法，

52所以一共有A5A6?3600种方法．

⑵甲、乙和丙三个同学都不能相邻的排法共有多少种？

解：先将其余四个同学排好有A4种方法，此时他们留下五个“空”，再将甲、乙和

33丙三个同学分别插入这五个“空”有A5种方法，所以一共有A4A5＝1440种． 44

小结三：对于不相邻问题，常用“插空法”（特殊元素后考虑）．

三、小结：

1．对有约束条件的排列问题，应注意如下类型：

⑴某些元素不能在或必须排列在某一位置；

⑵某些元素要求连排（即必须相邻）；

⑶某些元素要求分离（即不能相邻）；

2．基本的解题方法：

⑴ 有特殊元素或特殊位置的排列问题，通常是先排特殊元素或特殊位置，称为

人教版高中数学全部教案

优先处理特殊元素（位置）法（优限法）；

⑵ 某些元素要求必须相邻时，可以先将这些元素看作一个元素，与其他元素排

列后，再考虑相邻元素的内部排列，这种方法称为“捆绑法”；

⑶ 某些元素不相邻排列时，可以先排其他元素，再将这些不相邻元素插入空挡，这种方法称为“插空法”；

⑷ 在处理排列问题时，一般可采用直接和间接两种思维形式，从而寻求有效的

解题途径，这是学好排列问题的根基．

四、作业：《课课练》之“排列 课时1—3”

欢迎您进入数学999 http://sx999.k12.net.cn/

排 列

课题：排列的简单应用(2)

目的：使学生切实学会用排列数公式计算和解决简单的实际问题，进一步培养分析问题、解决问题的能力，同时让学生学会一题多解．

过程：

一、复习：

1．排列、排列数的定义，排列数的两个计算公式；

2．常见的排队的三种题型：

⑴某些元素不能在或必须排列在某一位置——优限法；

⑵某些元素要求连排（即必须相邻）——捆绑法；

⑶某些元素要求分离（即不能相邻）——插空法．

3．分类、分布思想的应用．

二、新授：

示例一： 从10个不同的文艺节目中选6个编成一个节目单，如果某女演员的独唱节

目一定不能排在第二个节目的位置上，则共有多少种不同的排法？

15 解法一：（从特殊位置考虑）A9 A9?136080

56 解法二：（从特殊元素考虑）若选：5?A9 若不选：A9

56则共有 5?A9＋A9＝136080

65解法三：（间接法）A10?A9?136080

示例二：

⑴ 八个人排成前后两排，每排四人，其中甲、乙要排在前排，丙要排在后排，

则共有多少种不同的排法？

5 略解：甲、乙排在前排A4；丙排在后排A4；其余进行全排列A5．

5所以一共有A4A4A5＝5760种方法． 2121

⑵ 不同的五种商品在货架上排成一排，其中a, b两种商品必须排在一起，而c, d

本文标题：高中数学排列组合-怎么在Word2010中输入排列组合的数学符号
本文地址： http://www.61k.com/1136312.html