一 : 布施：布施-职业生涯，布施-其它相关

布施,即以慈悲心而施福利与人之义。盖布施原为佛陀劝导优婆塞等之行法，其本义乃以衣、食等物施与大德及贫穷者；至大乘时代，则为六波罗蜜之一，再加上法施、无畏施二者，扩大布施之意义。亦即指施与他人以财物、体力、智慧等，为他人造福成智而求得累积功德，以致解脱之一种修行方法。大乘义章卷十二解释布施之义：以己财事分散与他，称为布；惙己惠人，称为施。小乘布施之目的，在破除个人吝啬与贪心，以免除未来世之贫困，大乘则与大慈大悲之教义联结，用于超度众生。另，指德意志民主共和国演员、歌唱家,生卒：1900～1980,出生于工人家庭。16岁成为社会主义工人青年的成员。

图片

［www.61k.com)无畏布施_布施 -职业生涯

第一次世界大战后学习表演和歌唱。1920年登台演出。1927年到柏林人民舞台当演员，同时从事电影工作，参加嘲讽时弊的小型歌舞演出，结识B.布莱希特、E.皮斯卡托、魏纳特等进步艺术家。1933年希特勒当政后，布施流亡国外。1937年参加西班牙国际纵队，1939年被俘。1942年越狱，又落入法西斯手中。1945年为苏军解放，随即重返舞台。1951年起受聘为柏林德意志剧院和柏林剧团的演员。布施以多才多艺著称，戏路甚广，擅于创造各种不同身份不同性格特征的角色，其中有平民形象厨师（《大胆母亲和她的孩子们》）、喜剧人物阿兹达克（《高加索灰阑记》）、魔鬼形象糜菲斯特(《浮士德》)、反面人物伊阿古(《奥赛罗》)、科学家伽利略（《伽利略传》）。布施曾获民主德国国家奖金、卡尔?马克思勋章、列宁和平奖金

无畏布施_布施 -其它相关

檀越

布施
于日本，信者所属之寺院，称为檀那寺；而道场所属之信者，称为檀家、檀中、檀徒、檀方。施财之人，称为檀越（梵da^napati，布施主之意，意译为施主、檀那主，简称为檀那）；而所施之财物，称为嚫资、嚫财、嚫金、嚫钱、堂嚫（对僧堂之僧施物之于日本，。意）、表嚫（分与于日于日本。施物之意）、信施（信徒施物之意）。此外，献上钱财，称为上嚫；施物供于佛前，称为下嚫。

六念之一

布施乃六念之一（念施），四摄法之一（布施摄），六波罗蜜及十波罗蜜之一（布施波罗蜜、檀波罗蜜）。布施能使人远离贪心，如对佛、僧、贫穷人布施衣、食等物资，必能招感幸福之果报。又向人宣说正法，令得功德利益，称为法施。使人离开种种恐怖，称为无畏施。财施与法施称为二种施；若加无畏施，则称3种施。以上三施系菩萨所必行者。其中法施之功德较财施为大。布施若以远离贪心与期开悟为目的，则称为清净施；反之则称不清净施。至于法施，劝人生于人天之说教，称为世间法施；而劝人成佛之教法（三十七菩提分法及三解脱门），称为出世法施。此外，关于施、施波罗蜜之区别，据优婆塞戒经卷二载，声闻、缘觉、凡夫、外道之施，及菩萨在初二阿僧祇劫所行之施，称为施；而菩萨于第三阿僧祇劫所行之施，则称为施波罗蜜。

8种布施

据菩萨善戒经卷一序品载，在家菩萨行财施与法施；出家菩萨行笔施、墨施、经施、说法施等四施；而得无生忍之菩萨则具足施、大施、无上施等三施。俱舍论卷十八举出8种布施，即：随至施、怖畏施、报恩施、求报施、习先施、希天施、要名施、为庄严心等施。同书卷十八亦举出施客人、施行人、施病人、施侍病者、施园林、施常食、随时施等7种布施。旧译华严经卷十二‘十无尽藏品’则有修习施、最后难施、内施、外施、内外施、一切施、过去施、未来施、现在施、究竟施等十施。上述乃就布施行为之内容、态度、目的等之不同，而有种种分类方式。又施者、受者、施物三者本质为空，不存任何执着，称为三轮体空、三轮清净。[中阿含卷三十福田经、增一阿含经卷四、卷九、卷二十、大般若波罗蜜多经卷四六九、卷五六九、菩萨地持经卷四、布施卷、大智度论卷十四、卷二十九、瑜伽师地论卷三十九]（参阅‘达嚫’5677）

行布施

行布施前，需要有前行发心，即明了要把自己所有的东西给其他众生的目的，乃是为了令自他一切有情众生皆能于未来成佛的缘故，因而发菩提心。
真正行布施时，即正行之际，必须要没有人我执与法我执。也就是在没有“我”及“我的”是真实存在的心念下行布施。世人行施心希果报，是为着相;菩萨行施了达三轮(施者、受者、所施物)体空(虚妄)，能不住于相、不希果报名闻等而行施者。”
而结行是指在行布施之后，为了令自他一切有情众生皆能于未来成佛，而将此布施的功德回向发愿给一切众生。具足此三法的布施才称为布施波罗蜜。一般而言，将财物施舍给贫困的人时，若行布施前没有发菩提心，布施时没有顺便引导众生迈向佛道，行布施后也没有将功德回向给一切众生，这样虽然也有大利益，但不能成为成佛之因，所以不称为布施波罗蜜。

行布施者

出家众主要行无畏布施、法施。在经典中，佛并没有要出家众行广大的财物布施。宗喀巴大师说，这是由于会障碍闻思修，故不许出家众集财宝而行财布施，但若无妨害，由宿生福力多而得的财宝，也当行财布施。
在家众主要行财布施，将钱财或物品布施给众生，或用以供养三宝，譬如到寺院去奉献香火钱或直接以金钱衣物供养法师等，佛家以施主称之，又叫名檀那主、檀越主。[1]

如何布施

布施时若有受施的人相，便会有拣择，有分别心，则心量小，心小福亦小。若布施有所住，有所执着，不管是住于色、声、香、味、触、法等六尘境之任何1种，都是有所住而行布施。这种有所住之布施，只有福德没有功德；只有布施而无布施波罗密，不能到彼岸，不能解脱。有智之人有5种布施：一、至心施。即以至诚心行布施，是故舍掉了傲慢。二、自手施。也就是亲自布施，不假他人之手；若假让他人之手，所得福报也要经过他人才能所得，所以要自手施。三、信心施。相信布施之果报不失，有布施之因，必得其果，如此信心行布施。四、时节施。依时节因缘之需要而行布施，就是时节施。譬如要以对方之所需要而行施，当对方得了重病，所需要的是治病，所以要助他就医，解除他的痛苦，就是时节施。五、如法求物施。这是指布施之物要如法而求，不可用不正当的手段取得而来的财物来布施。

果报

布施能得5种果报，即是色身、寿命、安乐、力气、辩才5种果报。这5种果报，无论施者、受者都可获得，而打坐观想布施之方式，根本不能令人获得这5种果报，所以不算是布施。又观想者本身，也不能获得此5种果报。布施对象不同，所得果报有差异，此可见于《菩萨忧塞戒经》。譬如布施给畜生，得百倍果报；布施给1个破戒者，得千倍报；布施给1个持戒者，得十万倍报。若布施给1个外道的离欲者，得百万倍报；若布施给1个向道者，得千亿报。若布施、供养1个初果人，乃至于成佛，都是无量报。布施之人若有下列三事，则布施后不能得到胜妙果报。一、先多发心，后则少与——本来发心答应要布施多少，事后却未完全做到，譬如已经答应、应承要拿一万元帮助对方，实际上却只拿五千元。这样布施五千元之果报，最后虽然还是会有，却不胜妙，也许得来会很勉强。二、选择恶物，持以施人——有的喜欢把自己不要的东西送给人家，或是把旧的东西送到佛寺去，这是不对的做法，这样所得果报不胜妙。应该把最好的或是对方真正需要的东西送给对方，这才是如法之布施。三、既行施已，心生悔恨常会听到一句话，就是：“我很后悔帮了他！”事实上不需要这样，帮就帮，都已经帮了，因为因缘不同，过去的就让它过去。若心生悔恨，则所得果报必不胜妙。

无畏布施_布施 -10种利益

《月灯三昧经》云布施10种利益：布施乃破悭贪之前阵，入道之初门。菩萨行能此者，则获10种利益也：
一、降伏悭吝　谓修菩萨行者，若能布施，则悭鄙吝惜之心，自然降伏，不复萌动矣。
二、舍心相续　谓修菩萨行者，行于布施，财虽匮乏，而喜舍之心，无有间断也。
三、同其资产　谓修菩萨行者，施心无量，观诸众生，与己无异，所有财产，平等受用，无有彼此也。
四、生豪富家　谓修菩萨行者，于一切财物，常行惠施，心无吝惜，则当来果报，必生豪富之家，财宝具足，受用无穷矣。
五、生处施心现前　谓修菩萨行者，此生既能行于布施，则感后世随其所生之处，而他人施与之者，皆无悭吝之心矣。
六、四众爱乐　谓修菩萨行者，既能常怀惠施，无所悭嫉，则四众之心，常生爱乐，而无嫌恨也。
七、入众不怯　谓修菩萨行者，既能布施，而为四众之所爱乐，故入大众之中，自无畏怯之心也。
八、胜名流布　谓修菩萨行者，能无所求而行布施，则人多称赞，胜妙名闻，流布遐迩也。
九、手足柔软　谓修菩萨行者，好行布施，济人缺乏，能感手足柔软，相好圆满之报也。
十、不离知识　谓修菩萨行者，自初发心行施以来，常得亲近诸佛菩萨善知识等，获闻法要，未尝远离也。

无畏布施_布施 -种类

总的来说，布施分为3大部分：财布施、法布施、无畏布施。修财布施得财富、修法布施得聪明智慧、修无畏布施得健康长寿。
一、财布施：分内财、外财。譬如布施你的体力，帮别人劳动就是内财布施；布施掉你的钱财去帮助别人，这就是外财布施。
二、法布施：讲经、印经并结缘给他人、记录讲经说法的碟片结缘给他人、劝人学佛等均是法布施。
三、无畏布施：无畏布施就是让众生不再感到畏惧。最简单的，吃素就是无畏布施（因为你不吃它们了，它们就不会因为我们的口腹之欲而死亡）。放生也是无畏布施。
<末学才疏学浅、智慧有限，若有不当、不足之处，敬请斧正、添加。>
其他信息
第一、和颜施：对於别人，给予和颜悦色的布施。
第二、言施：向人说好话的布施，存好心、做好事、做好人、说好话，并勉励人应切实力行。
第三、心施：为对方设想的心、体贴众生的心的布施。
第四、眼施：用和气的眼神看人。
第五、身施：身体力行，帮助别人，如帮人拿行李。
第六、座施：让座给人的布施。
第七、察施：不用问对方，就知道对方的心理。如果你身体力行此七项布施，幸运会跟著来。

无畏布施_布施 -扩展

佛说三13种不清净布施

佛告诉毗耶娑，有人虽做了好事，但挟带了功利性的不清净心理，不算真布施。他列举了三13种不清净、不纯净的布施：

1到11

第1种，是以歪曲的心理、颠倒的见解、无纯净心所施的财物，这不是真正的布施。
第二种，有人昨天请我吃过一块蛋糕，今天我要还礼；或者他十几年前帮助过我，投桃报李，礼尚往来，不算布施。
第3种，有人施舍财物，不是出于真正的慈悲、怜悯和同情心，而是为了耍阔气，或纯粹是打发人家了事，这不算布施。
第4种，因为自己有所欲求，比如看到这束花特别喜欢，多付上一毛钱；或上舞厅感到那位姑娘很漂亮，多给2个小费，这都不算布施。
第五和第6种，把财物丢到火中或投进水里，都不能算布施。因为水火都是自然物，你把财物白白扔掉了，却不能使别人受益。
第7种，有人送礼给大人物，指望以后可以有所提拔照顾；或者看在某个大老板、某个大人物的面子上，在慈善救济事上凑上一份，藉以拉个关系，这都不是纯净的布施。
第8种，怕强有力的黑道中人来抢你，赶快送钱消灾，这不是布施。
第9种，送人家鸦片、海洛因、麻醉剂等毒品，这不是布施。但医生见病人太痛苦，打麻醉针以止痛，这是布施。这里有很多道理，要研究。
第10种，送人家武器，不是布施。我儿子前天买了一把防身刀给我，他在刀下面放了一毛钱。我打电话问他这是什么意思，他说美国人的规矩，送刀给人，不是让人自杀，放上一毛钱，表示吉利的意思。这个我不懂，他还算是真布施哦！
第11种，送肉与人，那是杀生而施舍给人家，这不算布施。

12到22

第12种，你收养了许多孤儿，保护他们，把他们养育成人。但你指望以后可以使唤他们，做你的帮手，这就带上先决条件了，就不能说是纯净的布施。
第13种，为了出名而施舍，不是纯净的布施。
第14种，为了捧歌星、戏子而出钱，比如1个歌星开赈灾歌唱会，一天收到几千万捐款，这个歌星做了好事，可出钱者未必是净布施。歌星不唱之际，你为什么不布施？有些人是为捧歌星的场，这里面有差别。
第15种，有些人破产了，财物转到别人手里，这并非出自自愿，所以不是布施。
第16种，比如说，这个屋子因闹鬼，不敢住下去了，送给出家人做寺庙；或者因为打官司，自己的屋子有麻烦，干脆送给社会慈善机构，这都不算净布施。

第17种，有人因学佛或受了教育，知道帮助人家是好事，但自己没有钱，就拿人家的财物做人情，这也不算布施。
第18种，谷麦在田地、仓屋中被鼠鸟等所食，并非有意送与它们吃，不能说是布施。讲到这里，想起前两天报上揭露一批送往大陆灾区的大米，在码头搬运中发现是发霉的。这就不是布施，相反，人吃了霉米会中毒，送的人反在造恶业了。
第19种，假使我电脑坏了，我请这方面的行家来修理，请他吃饭，送他钱。这是你想学东西是应该付的酬劳，而不是布施，布施是没有条件的。
第20种，比如病人怕自己要死，送医师1个大红包，以为医生就会对他尽心了。这是有求于人而给钱，不是布施。
第21种，打了人家，骂了人家，自己觉得难为情，然后送东西给他谢罪，这个不算布施。
第22种，有人布施了之后，心中疑虑人家是否在骗他，或在想人家以后是否会报答他，这都不算布施。

23到33

第23种，有人施舍了之后心痛懊悔，这就不是布施。我年轻时在四川学佛，人家有困难，我站出来说要帮助他，大家比较买我的面子。后来有个老前辈劝我不要再替人家去化缘了，为什么呢，他说四川人有句老话，“劝人出钱，如钝刀割肉”，人家虽然给了你面子，但那个人心里难过啊！他还给我讲了个笑话：有个大魔王在地方上作怪，连孙悟空都降服不了。后来从西天佛祖那里派了个小和尚，魔王根本不把他放在眼里，小和尚说此行不是来收服他的，只是给他看个东西。说着，从背上黄布包袱里拿出一本化缘簿，“居士，请你多少写一笔吧！”那魔王一看，“哇！”就跑掉了。
所以，平时在人家谈布施时，我就不轻易谈。有些人把钱送出去以后，越想越后悔，越后悔越睡不着，“如是施者，非净布施”。
第二十四，还有的人，送了东西给人家，好像这个人从此就卖给他了，今后定要人家报答他。这个就不是净布施。
第二十五，有些阿公阿婆，念咒、布施都有账可查，你看他们念什么《心经》、《白衣咒》，念一段经，在黄裱纸上戳1个印，“我念了多少卷，死后带到阴间去，也不知一卷是二十八块还是三十五块。”这等于在投资，将来连本带利得多少好报。“如是施者，非净布施”。
第二十六，人到衰老、重病临死之时，感到痛苦了，晓得时间不长了，不把财产传给子女，却布施出去。这也不算净布施，因为你已晓得财产把握不住了，你不布施也不属于你了。没有清净心，还是不行。
第27种，为了名誉而施舍。希望在电视上露面，希望在报纸上广而告之，希望一切人都感激我，这不是净布施。
第28种，好比说看到黄医师都出了十块，我就出十五块，蔡老板不服气，出二十块，把我们2个都盖了。出于攀比心、嫉妒心而送财物的，不是布施。
第29种，为贪女色而摆阔气，送种种金银珠宝、绫罗绸缎等贵重东西，那是你为了追求漂亮女人，不是布施。
第30种，有些人因为自己没有儿女，所以才愿意拿出家产送人，这是做好事，固然不错，但从佛法的布施学来看，还不算是纯净布施。
第三11种，以有无福德来挑选布施对象，这样的布施不是净布施。
第三12种，布施首先要雪中送炭，周济穷苦者，若看上不看下，只做锦上添花的事，那也不算净布施。
第三13种，就是为了鲜花果品而舍物与人，这也不是布施。这是很轻的一条了。
佛教的布施学，这里每一条研究起来，都是戒律。

评述

上述三13种不净布施只是大概而言，经典上记载的还有许多。佛告诉毗耶娑，这些不净布施，不会得到真正佛道的果报，最多也就是修到仙道的果报而已。佛用种子作比喻，布施作为1种业力行为，等于播种，挟带不纯动机的“垢染布施”，就像种子下到盐碱地里，不会有好的收成。而且，这种子本身的功能（“种子界”），不但与土地的品质（“地界”）处在1种相依相存的关系中，还须有阳光、空气和雨水，才能使种子发芽。种子放在玻璃瓶中，固然不会发芽，但播种在贫瘠的土地上，若得不到雨水的滋润，也是不能开花结果的。

无畏布施_布施 -利益

《大智度论》是龙树菩萨为我们这个时代所讲的一部妙典。论中说：“出家重持戒，居家重布施”。菩萨的语言以作为我们后学的印证，布施中分为3种。
一、财施
以财物金钱送给贫穷之人，使其能养活色身治疗疾病。以培养我们舍掉贪心的念头。《地藏经》说：“舍一得万报”。并且我们财施生生世世能得大富贵。
二、法施
以印造佛经法物送给大众并为人演说，使其能养活智慧之命。以培养我们大慈的精神，了《法华经》说：“诸供养中，法供养最”。并且我们法施能得大智慧。
三、无畏施
以善巧方便开示心里不安烦恼之人，使其能心无怖畏而得自在，以培养我们大悲的精神。《普贤菩萨行愿品》说：“菩萨以方便力为我们在怖畏急难中，能施无畏”。并且我们学习菩萨无畏施能得现生健康和快乐。
以上3种布施，加戒杀放生利益六道众生，所得果报说不能尽。——方海权著
布施

无畏布施_布施 -德国元帅

布施（1885-1945），陆军元帅。1904年毕业于普鲁士武备学校。参加过第一次世界大战。战后，1919年起在国防军中任职，历任师长、军长。1939年任第十六集团军司令。布施认为军人就是应该服从。参加侵略波兰、法国和苏联的战争。以作战手段顽强（实际上可以说是残酷）著称。1943年晋升元帅，出任东线中央集团军群司令。1944年7月，因所部在白俄罗斯地区遭围歼而解职。1945年3月，复任西线德军集群司令，防守北海沿岸和石勒苏益格-荷尔斯泰因。德国投降后被英军俘虏，在战俘营中死于心脏病。
德国纳粹陆军元帅布施

无畏布施_布施 -关于布施的诗歌

布施·七绝
并非修德必施钱，
世上常人穷缚缠；
福祸皆从心内造，
长生善念吉祥联。

无畏布施_布施 -所属分类

著名音乐家
外国音乐

二 : 宿舍：宿舍-词语概念，宿舍-其它相关

“宿舍”是住宿的房屋，外延大，包括寝室、卫生间、洗浴间、阳台等。宿舍住的人数不同，有单人间，双人间，多人间等。宿舍不仅仅是学习和睡觉的地方，更是你的另一个家。《史记·张仪列传》：“﹝苏秦﹞乃言赵王，发金币车马，使人微随 张仪 ，与同宿舍，稍稍近就之。”曹禺《献给周总理的八十诞辰》：“总理来到史家胡同人艺的宿舍，学员们从睡梦中醒来，看到总理站在床头，揉了揉眼睛，再揉揉眼睛，他们才相信这是真的。十、不准私自留宿外来人员，须住宿者在门卫处办理登记手续。

寝室新闻联播_宿舍 -词语概念

［www.61k.com）基本信息

校园宿舍

【词目】宿舍

【拼音】sù shè

【英译】[Dormitory；Hostel]

【五笔输入】PWWF

【解释】

1.住宿停留。

2.指旅店。

3.机关﹑企业﹑学校等供职工﹑学员等住宿的房屋。

基本解释

宿舍

(1) [hotel]∶旅舍。

使人微随张仪,与同宿舍。——《史记·张仪传》

(2) [domitory;hostel]∶学校、机关等供学生、工作人员及其家属住的房屋。

学生宿舍。

引证解释

1. 住宿停留。

《史记·张仪列传》：“﹝苏秦﹞乃言赵王，发金币车马，使人微随 张仪 ，与同宿舍，稍稍近就之。”

2. 指旅店。

宋陈鹄《耆旧续闻》卷六：“﹝ 施逵 ﹞及出狱，赂防送卒，使缓其行。买一获（婢）自随，所至宿舍，纵其通淫。”

3. 机关、企业、学校等供职工、学员等住宿的房屋。

洪深《劫后桃花》：“这是督办公署职员第三宿舍，里面正在收拾屋子呢，不能进去。”曹禺《献给周总理的八十诞辰》：“总理来到史家胡同人艺的宿舍，学员们从睡梦中醒来，看到总理站在床头，揉了揉眼睛，再揉揉眼睛，他们才相信这是真的。”1989年《睢县志·古建筑》：“袁家山（袁可立别业），……1966年‘文化大革命’时，曾改作县第二机械厂宿舍。”

4、在大陆，宿舍一般指学校学生或企业员工居住的地方。但在香港大学，宿舍这个概念是远远不同于大陆的。在那里，宿舍被称为“舍堂”，不仅仅是居住的地方，更多是发展自我的环境。舍堂的入住是要经过申请，并且要面试，成员来自不同的年级和专业，只要你愿意为舍堂的发展贡献一份力量（金钱），那么欢迎你的加入。

宿舍不仅仅是学习和睡觉的地方，更是你的另1个家。

寝室新闻联播_宿舍 -其它相关

宿舍与寝室区别

词义

寝,卧也。——东汉·许慎《说文》

无东西厢有室曰寝。——《尔雅·释宫》

1、寝室 【qǐnshì】

宿舍

（1）[Bedroom]∶设有床、主要供睡觉用的房间;卧室。

学生寝室

（2）[Dormitory]∶集体寝室,主要作睡觉用、通常住很多人的大房间。又如：寝庙(宗庙)

使人微随张仪,与同宿舍。——《史记·张仪传》

2、宿舍 【sùshè】

学校、机关等供学生、工作人员及其家属住的房屋。

相同之处：

1、词性相同，空间（处所）名词，都表示1个概念；

2、词义相近，都是休息的场所。

不同之处：

1、词义不同：“宿舍”是住宿的房屋，“寝室”是睡觉的地方；

2、概念的外延不同：“宿舍”，住宿的房屋，外延大，包括“寝室”、卫生间、洗浴间、厨房等；“寝室”，卧室，外延小，包含于“宿舍”，包括床、衣柜、洗漱用品等。

例子：

（1）学校给新来的老师安排了宿舍（？寝室）

宿舍

（2）公司在旁边的居民楼租了两套房，用作临时的宿舍（？寝室）

（3）职工宿舍（？职工寝室）

（4）宿舍管理科（？寝室管理科）

（5）东部第五宿舍（？东部第五寝室）

宿舍管理制度

为了加强规范管理，搞好2个文明建设，特制管理制度如下：

一、不准倒床吸烟、乱丢烟头。

二、不准乱拉搭设电线，灯泡限60W以下。

三、不准使用电炒锅、电炉、电饭煲及用明火做饭取暖。

四、不准随地吐痰或大小便。

五、不准乱倒脏水和各种杂物，室内生活用具摆放整齐，室外做好卫生环境，每星期六集中室内外消毒一次，并由专人检查卫生工作。

六、不准乱拆乱搭房子和铺位，按指定位置住宿。

七、不准赌博、不准打架斗殴、酒后闹事。

八、不准男女混住及民工带家属小孩进入施工现场。

九、不准损坏公共设施，如有损坏必须赔偿。

十、不准私自留宿外来人员，须住宿者在门卫处办理登记手续。

三 : 斯伟江：斯伟江-相关经历，斯伟江-其它信息

斯伟江（1970年-），浙江诸暨人，大邦律师事务所合伙人，知识产权律师。华政毕业，曾游学美国，思想囿于旧儒家和自由主义之中，律师执业位于商业和法律援助之间。中央电视台《为您服务》法律版块嘉宾、上海电视台《撞击》嘉宾、《夜线约见》嘉宾。

斯伟江_斯伟江 -相关经历

[www.61k.com]斯伟江，1970 年出生，浙江诸暨人。高级律师，擅长诉讼仲裁、知识产权、其他民商事法律事务等，为公司、个人提供常年或专项法律服务（知识产权方向为主）。

上海大邦律师事务所合伙人。曾任浙江协力律师事务所律师、浙江矛盾律师事务所创设合伙人、星韵律师事务所上海分所执行主任、国浩律师事务所合伙人。

华东政法大学兼职教授，同济大学兼职讲习（案例教学）。

1992 年7 月毕业于华东政法学院法律系，法学士学位。

1992年起执业，高级律师。

全国律师协会知识产权委员会副秘书长、执行委员。

上海市律师协会业务研究和职业培训委员会副主任。

上海市律师协会知识产权委员会副主任。

《上海律师》杂志编委。

上海投资咨询公司特聘知识产权专家。

中央电视台《为您服务》法律版块嘉宾、上海电视台《撞击》嘉宾、《夜线约见》嘉宾。

2011年4月19日斯伟江接受李庄家属的委托将出庭为李庄辩护。

斯伟江_斯伟江 -其它信息

斯伟江律师“心思缜密，旧学深沉”，他博览群书，目光高远，对中国律师及律师业所处的环境有着独到的见解和清醒的认识,是中国律师观察中心的积极推动者和支持者。曾游学美国，思想囿于旧儒家和自由主义之中，律师执业位于商业和法律援助之间。爱读书，爱运动，爱小孩。

七律—斯人伟江 文 /老街味道

闻道儒冠多误身，而今点检信斯人。穷途正义非当下，击鼓悲情缘太真。

伟业千秋槐国梦，江流万载太宗臣。广陵散绝无寻处，孟母何方择比邻。

斯伟江_斯伟江 -解除合同

2015年6月6日，应复旦投毒案被告人林森浩爸爸林尊耀的要求，上海大邦律师事务所与林尊耀先生解除了《委托协议》，至此，斯伟江律师不再担任林森浩案件死刑复核阶段的辩护人。在此之前的复核阶段，辩护人已经前后向最高法院提交了5万字的法律意见，及若干新证据、医学专家会诊意见、申请等，也到北京当面向复核的合议庭法官陈述了辩护意见，会见了林森浩，已经基本完成了该阶段的工作。虽然得知，林森浩本人不同意解除对斯伟江律师的委托，但鉴于委托协议系林尊耀先生与本所签署，委托合同基于信任，专业人士需知进退，不给委托人留遗憾，也考虑到辩护人的工作已经基本完成，退出不至于对林森浩产生不利后果，故同意解除合同。

斯伟江_斯伟江 -其他资料

斯伟江律师“新思缜密，旧学深沉”，他博览群书，目光高远，对中国律师及律师业所处的环境有着独到的见解和清醒的认识,是中国律师观察中心的积极推动者和支持者。曾游学美国，思想囿于旧儒家和自由主义之中，律师执业位于商业和法律援助之间。爱读书，爱运动，爱小孩。

辩护词

李庄再次被控辩护人妨害作证罪一审辩护词

审判长、审判员：

依据我国《刑事诉讼法》等的相关规定，本律师为依法维护李庄合法权益，特发表如下辩护意见。

【特别申明】：本次出庭辩护，并不意味律师承认贵院对本案有管辖权，只是为了避免李庄的合法权益受到二次伤害，从而依法出庭辩护。

辩护人认为：本案从侦查、到起诉，再到审理，程序屡屡违法，漏洞百出。俗话说，强扭的瓜不甜，强管的案子，程序上千疮百孔。程序正义犹如交通规则，如果今天江北区公检法可以这样不顾交通规则，把李庄撞回监狱，明天任何1个老百姓也可以被撞进监狱，甚至包括在座各位，谁也不能幸免。我国文革才过去30来年，殷鉴不远，眼下重来，岂非悲哀。

有人对李庄说，专政机器很强大，对谁，谁都抗拒不了。专政机器依法开动，当然强大。但是，如果专政机器不顾交通规则，法定程序，程序正义，最后恐怕，也是要掉到沟里去的。始作俑者，其无后乎？维护法律规定的程序，才能让民众权利受到保护，齐家而平天下，这就是，为什么我们要为李庄辩护，既为李庄个人，也是为了这个国家的长治久安。以下是具体辩护意见：

第一部分：本案程序严重违法

【案件时间节点】从本案程序上的关键时间节点，即可看出本案程序上的诸多严重违法之处：

根据卷宗显示本案程序上的具体时间表如下：

2010年1月16日，江北区检察院收到徐丽军的举报。

2010年1月27日，江北区检察院将举报材料移送江北区公安局

2010年1月28日，江北区公安局接受刑事案件，并进行登记，领导批示是初查。

2010年2月9日，李庄涉嫌辩护人妨害罪证罪（龚刚模案）二审宣判。

2010年2月9日，龚刚模的表弟龚云飞向江北区公安局举报李庄代理龚刚模案中涉嫌合同诈骗，公安局批示初查。

2010年2月10日，重庆市公安局指定江北区公安局管辖李庄涉嫌合同诈骗罪一案。

2010年2月10日，重庆市江北区公安局决定对李庄涉嫌合同诈骗罪立案侦查。

2010年2月10日，重庆市第二看守所将李庄带到南川监狱，同日接江北区公安局通知带出。李庄未能在监狱服刑。

2010年2月11日，江北区公安局对李庄涉嫌（上海孟英案）妨害作证罪决定立案侦查。

2011年3月28日，江北区公安局对李庄涉嫌合同诈骗，妨害作证罪，侦查终结，移送江北区检察院。

2011年4月2日，江北区检察院将李庄涉嫌辩护人妨害作证罪起诉到江北区人民法院。

根据以上毫无疑问时间节点，辩护人对程序上提出如下意见：

一，江北区公安局无权管辖本案，本案从侦查开始程序上就违法。

【先后顺序】从来没有1个案子是因为法院有管辖权，即可推断公安局有侦查权，因为法院永远在公安局之后，中间还有1个检察院，这等于孙子先出世，再生出祖父，既违反自然规律，也违反法定程序。任何法院无侦查权，本案也不例外。因此，不能因为法院有管辖权而推定公安机关有管辖权。

【检察院规则】江北区检察院2010年1月17日接到举报时，应按照刑诉法的24条的规定，应当将本案移送到犯罪行为地上海市徐汇区公安局。我国刑事诉讼法对管辖的规定非常清楚，第18条规定，刑事案件的侦查由公安机关进行，法律另有规定的除外。本案应该由公安机关侦查。

《人民检察院刑事诉讼规则》（以下简称《检察刑诉规则》）第一百二十四条第1款第一项关于“举报中心对于所收到的举报线索，应当及时审查，并根据举报线索的不同情况和管辖规定，在七日以内分别作出如下处理：（一）不属于人民检察院管辖的，移送有关主管机关处理，并且通知报案人、控告人、举报人、自首人。……”

【公安规则】《公安刑案规定》第十五条“刑事案件由犯罪地的公安机关管辖。如果由犯罪嫌疑人居住地的公安机关管辖更为适宜的，可以由犯罪嫌疑人居住地的公安机关管辖”。根据《刑诉法》第八十四条第3款关于“公安机关、人民检察院或者人民法院对于报案、控告、举报，都应当接受。对于不属于自己管辖的，应当移送主管机关处理，……”。

【审判管辖】刑诉法第24条明确规定，刑事案件由犯罪地的人民法院管辖。如果被告人居住地的人民法院审判更为合适的，可以由居住地人民法院管辖。第83条规定，公安机关或人民检察院发现犯罪事实或者犯罪嫌疑人，应当按照管辖范围，立案侦查。人民检察院《刑事诉讼规则》第124条，对于举报，不属于不属于人民检察院管辖的，移送有关主管机关处理，并通知报案人。本案犯罪地在上海徐汇区，被告人居住地在北京。重庆江北区检察院应当将本案举报线索移送给徐汇区公安局。

综上，以上是一环扣一环，法律规定是严谨的。无论从那个环节，本案都不应有重庆江北区公安局侦查、江北区检察院起诉、江北区法院审判，江北区公安局对本案无任何管辖的法律依据，检察院起诉也无依据，法院审判也没有依据。

第二，所谓合同诈骗重罪吸收妨害作证的轻罪，以此并案侦查也没有法律依据。

【没有重罪，何来吸收？】从控方提供的材料看，李庄宣判当日，既发送龚刚模表弟举报李庄李庄涉嫌合同诈骗，次日，重庆市公安局指定江北区公安局立案侦查。似乎江北区公安局试图以重罪吸收轻罪的方法来行使对李庄涉嫌妨害作证案的管辖。然后，所谓的合同诈骗案，江北区检察院都没有起诉，皮之不存毛将焉附，案都不成立，根本就无案可并，不能以1个不成立的案件来实际行驶1个对此本无管辖权案件的管辖。要借力也得有力可接，不可能凭空来1个借案管辖。如此玩弄法律，法律岂是失足妇女？如此可以，按照逻辑，全中国任何1个人都可以被虚构在重庆有1个重罪，然后把其他地方的案件吸收过来，再撤销重罪，重庆公安局成了全国的公安部，甚至，可以把全世界的人，包括美国总统都管辖进来。这种荒唐的逻辑，如成立，刑诉法的地域管辖的规定还需要吗？

第三，法院以最高法院刑诉法司法解释第14条行使原审法院管辖权，前提不成立。

贵院宣称依据最高法院《关于执行<中华人民共和国刑事诉讼法>若干问题的解释》（下称最高法院刑诉法司法解释）第14条规定行使对本案的管辖权。最高法院刑诉法司法解释第14条规定，发现正在服刑的罪犯在判决宣告前还有其他犯罪没有受到审判的，由原审人民法院管辖；如果犯罪服刑地或者新发现罪的主要犯罪地的人民法院管辖更为合适的，可以由服刑地或者新发现罪的主要犯罪地的人民法院管辖。

【发现犯罪时间】依照前面所列时间表，本案“发现所谓漏罪”在二审宣判前，不存在服刑期间发现的事实，贵院援引的法条前提不成立。

魔鬼藏在细节中。虽然我国现行法律对“发现犯罪”定义无相关司法解释，然后，不管以哪种解释，都无法证明贵院对本案有管辖权。

【举报时间在宣判前】

如发现所谓漏罪时间为本案接受举报时间，则2010年2月9日之前对李庄妨害作证案的判决应予撤销。

如果将“发现漏罪”定义为发现犯罪线索如举报，那么本案发现李庄涉嫌漏罪应当在二审宣判前，那么，根据最高人民法院司1993年给江西高院的批复（1993）3号规定，当时的二审法院应当将本案发回重审，将两案合并处理，由于所谓漏罪是同种罪，对李庄不实行数罪并罚，（详见最高法院的批复）。江北区公安局、检察院，没有理由不知道李庄案当时为二审期间，因此，江北区检察院把案子藏起来，违背现行法律规定，是1种涉嫌渎职行为。即使构成犯罪，李庄也只要受一次审判，检察院凭空把李庄变成两次审判，不也是1种涉嫌违法行为吗？

【合同诈骗不是漏罪】

如果把“发现漏罪定义为龚刚模合同诈骗案，那么该罪实际并不成立，无法依据合同诈骗罪的依据来管辖辩护人妨害作证罪。这等于张冠李戴，能套得上吗？法律依据何在？

【公安局立案没有证据】

如将发现漏罪时间定为本案公安立案侦查时间，也是无稽之谈，公安都没有任何证据，凭什么立案？通过查阅本案案件可以发现，本案江北区公安局立案调查李庄涉嫌辩护人妨害作证罪时，就是李庄原妨害作证案二审宣判的次日，当时，除举报材料之外，并无其他任何证据。什么证据都没有的立案，违反公安部《关于办理刑事案件的程序规定》第159条，甚至162条。

立案侦查。首先必须有发现“犯罪事实”，在只有徐丽军的举报，江北区公安局就能断定李庄有犯罪事实？提审李庄关于涉嫌妨害作证都在2010年11月之后，公安2月11日就立案，岂不是神仙？如国际歌所言，世上没有神仙，江北区公安局如果这种做法，只能推定，公安机关不不择手段，违法管辖。如是，如以立案时间定发现漏罪时间，变成公安机关可以随时界定发现犯罪时间。

退1步讲，即使依据本条规定，江北法院有管辖权，也不意味着江北公安局有侦查权。不能倒因为果。法院的是审判管辖权，而公安是立案侦查管辖权。两者不同。如果李庄案，江北区公安局、检察院、法院能管，那么，徐丽军涉嫌构成伪证罪，谁来管辖？如果徐丽军归上海管辖，上海管辖了吗？重庆公安局移送犯罪线索了吗？

第四，其他程序严重违法的事实

【服刑地违法】本案中，李庄在2010年2月9日宣判后，次日被送到南川监狱，蜻蜓点水，手续都没办完，就回到重庆市第二看守所，根据我国法律规定，超过1年的有期徒刑应当送到监狱。本案李庄实际服刑地在重庆市第二看守所，根据案卷在2010年8月之前，公安机关没有任何侦查材料。实际上是强行把李庄从应当服刑的监狱放到看守所服刑，剥夺了其在环境相对宽松监狱服刑的权利。这是严重违法的。

【侦查期限超长违法】

本案侦查期限长达一年多，中间没看到任何合法延长法律文书，江北区公安局严重违反刑诉法的期限规定。作为法律监督机关的检察院，对此没有任何片言只语的监督。法律监督职能何在？

【剥夺侦查期间请律师的权利】

李庄在长达一年多的侦查过程中，没有享受接受律师提供法律帮助的权利。卷宗之中，只有涉嫌合同诈骗罪的会见。李庄在本案中，没有受到法律规定侦查阶段请律师的权利。这个违法，检察院有没有进行监督？

【本案变相不公开审理】本案看似100多号人来旁听，但是，法官对家属要求有派出所证明才能进去，这样的要求完全没有法律依据，请法官出示法律依据。其他公民申请旁听，也被拒绝，而法庭上，从开庭开始，第一排的座位就只有2个法警坐。这样的审判完全违背了公开审判的规定。

【法庭不接受录像证据违法】辩方提供的李庄和徐丽军的录像，是为了反驳控方提供徐丽军笔录中，涉及所谓李庄教唆其在朱立岩死刑案件中作伪证，录像显示，李庄让其客观，实事求是，在同一份笔录中，徐丽军会诬陷李庄在朱立岩案件作伪证，可想而知，徐丽军指控李庄在孟英案的伪证，是靠不住的。这样的证据是反驳控方证据的，法庭说与本案无关，显然是违法的。

结论：

1个本来就无管辖权的案件，非得强拿到重庆来管辖，所以，才会有拼凑，才有强词夺理，千疮百孔。辩护人不谈有什么目的和动机，我们只是强调，这样的侦查、起诉、审判一点合法性都没有。合议庭做出的任何判决，都将是枉法裁判，为历史所耻笑，同时，也必将承担相应的法律责任。

第二部分：李庄并没有引诱、教唆的证人改变证言。

实体上，李庄并无引诱证人改变证言的事实，公诉机关起诉证据严重不足。

一：本案的取证程序违法和证人可信度极低

1，取证程序严重违法

【侦查主体违法】由于本案重庆市公安局、江北公安分局都没有管辖权，侦查主体全部违法。所作的侦查笔录和取的证据全部系违法无效证据。

【侦查何时终结】本案的较多证据系2011年3月28日公安侦查终结后再行调查取得，有部分甚至在法院审判阶段取证，这类证据没有法律效力。辩护人诧异的是，公诉机关居然还敢拿到法庭上来出示，如果这可以，什么叫侦查终结？有完没完？公诉人居然说，依据刑事诉讼法第140条第1款，真是令人大跌眼镜。

【侦查地点】本案证人的侦查地点多在证人的家里，侦查人员住的宾馆，茶楼，辩护人奇怪为什么如此强势的侦查机关如此迁就证人，难道是有求于证人？我国《刑事诉讼法》97条明文规定，侦查人员询问证人，可以到证人的所在单位或者住处进行，必要之际，也可以通知证人到人民检察院或者公安机关提供证言。侦查机关如此在茶楼，宾馆取证，做个说明是证人提出的要求，那么试问证人要边洗桑拿边做笔录行吗？

【侦查人员】侦查人员李军身份，一会儿是江北分局，一会儿是重庆市公安局。虽然公诉人说本案情况特殊，市局宏观上指导，这已经远远超出宏观，已经在微观上插手了，这是违法的。

2，证人可信度极低。

【徐丽军不是证人而是伪证主犯】如果本案对李庄指控成立，徐丽军涉嫌在出庭作证时公开进行伪证行为，触犯刑法305条，构成伪证罪，且属于主犯。本罪不对其进行逮捕起诉而追究李庄，明显系恶意执法报复性执法。对徐以不起诉换取的证言，明显是胁迫证言，不真实证言，无效证言。

【主要证人系直系亲属】本案指控被告人李庄涉嫌辩护人妨害作证的证人，主要是举报人徐丽军及其家人，（儿子苏文龙和妈妈），这种一家人本身利害关系明显，其证言证据效力有限。

【证人吸毒、反复无常】本案主要证人和举报人徐丽军，吸毒多年，四次进过戒毒所，在公安、法院、律师处的证言多处反复，在上海表演多次跳楼秀，在上海徐汇检察院表演跳楼秀，其今天的书面证言根本就不可信。

【证人徐丽军说谎】辩方提供的录像证据显示，徐丽军在本案笔录中，说李庄在朱立岩案中让其做为证，完全是虚假的。虽然，法庭违法不让出示，但仍无法掩盖。

二， 徐丽军投入金汤城的确实不是投资款，是借款或类似性质款项，其出庭作证所述并不虚假。

本案焦点事实，起诉书指控李庄引诱证人徐丽军违背事实改变证言，把投资款说成借款，证据表明，所谓徐丽军投入金汤城在100万确实不是投资款，是借款。

1，首先，请查清楚100万元到底是谁的？

【公诉机关指控事实不清】

公诉机关起诉书指控，徐丽军投入的100万元是投资款，李庄让其违背事实改变证言，辩护人认为这个事实存在疑问。

首先，上海徐汇区法院的民事判决认定这个款项所有权是王德伟的。

其次，证人笔录显示所谓王德伟和徐丽军是夫妻，并没有结婚证、离婚证等婚姻登记材料印证。结婚不是光凭两人说是夫妻即可的，这一点法律常识无需辩护人多言，本案，公诉机关指控缺乏证据。

2，退1步讲，徐丽军（王德伟）投入金汤城的100万元，也确实不是投资款，是借款或者其他。

【徐丽军的录音证据】李庄接受孟英案之前，金汤城的法律顾问，上海欧阳法律服务所的两位法律工作者和徐丽军的录音证据显示，徐丽军承认这个不是投资款，只是和孟玲之间个人的有口头约定，是借款或其他，朱立岩不同意她在金汤城投资，嫌100万元太少。盖财务章的收据可能是财务陈芳英私自给的。即便个人之间的隐名投资，需要其他股东同意，才能转化为股权，在其他股东同意之前，这个款项只能是借款或其他，并未转化为投资款。法律性质的认定并不以口供确定，而是要根据法律概念、实然形态来确定。本案只能认定为债权性质款项，而不可以判断为投资。徐丽军2008年7月30日在上海徐汇区法院所作证言，并非虚假。

【王德伟取回款项17万】李庄在接受孟英案之钱，王德伟从所谓的投资款100万元已经取回17万元，根据法律常识，投资款是要共担风险的，不能抽回。能抽回的只能是借款。因此，李庄更有理由断定该款是借款。

【孟英供述】孟英在开庭认定该100万元是私人借款。孟英在公安笔录中也认为，徐丽军和其约定对外该款称为私人借款。

【金汤城否认其为投资】从辩方提供的徐汇法院民事卷宗看，金汤城大部分股东不同意该款为投资款。

【金汤城律师认为是借款】金汤城在民事诉讼中的任律师认为该100万元可以以借款处理，因为不是投资款，大部分股东不同意徐丽军投资。

【控方提供的周恩奇证言】其中就提到徐丽军的钱，朱立岩认为是借款。

【法院判决驳回其股东请求】徐汇区人民法院民事判决确定，王德伟（所谓徐丽军的丈夫）投入到金汤城的100万元资金不是股本金。判决驳回王德伟要求确认股东名份及出资份额所占注册资本比例，并办理工商登记的请求，这种情况下，公诉人居然还认为这是投资，却无法回答辩护人的问题，投资的回报率多少？风险是什么？是什么类型的投资？辩护人多次问公诉人，你在银行存入了多少钱，这有投资风险吗？公诉人至今不回答。

【借款协议是强力证据】在徐丽军出庭作证前15天，徐丽军和孟英的家属签订还款协议，这个还款协议充分表明了徐丽军和孟玲之间的款项性质。起诉书指控徐丽军违背事实，依据何在？即使此协议是李庄支持下达成，李庄也没有强迫各方的能力。徐丽军也没有去撤销这个协议，反而依据这个协议向孟家要钱，说明她是尊重这个还款协议的。

【100万的真实性质】按照现在最高法院的司法解释，这100万元，在获得50%股东同意之前，既可以理解徐丽军和孟英之间的信托关系，之前也有法律人士理解是待转化的借款法律关系。在出庭作证时，金汤城的股东仍未同意，也永不可能同意其为股东。因此，这100万元的款项，只能是孟英和徐丽军之间的法律关系，不是投资款。后来双方签订还款协议，更是确定了款项的性质为借款。

三，李庄没有引诱证人改变证言的事实。

【李庄的主观判断】李庄在想徐汇法院提供证人出庭时，手头有这些证据材料，律师只能根据自己的法律知识和掌握事实，因此，李庄作为法律人士认为该款是借款，符合其认知的事实。

【指控证据不足】光凭徐丽军、苏文龙等的证言是无法证实李庄明知是投资款，而让徐丽军改变证言。

首先，李庄自己不承认有引诱、教唆行为，其一直说要求徐丽军事实就是，而且，庭前对100万元的性质进行分析，也完全是依法进行的。

其次，徐丽军吸毒多年，多次进过戒毒所，每次公安询问完毕都要问她，头脑是否清醒，正如问1个醉汉是否喝醉，他肯定说自己没喝醉。这样的问话，岂不是笑话。请侦查人员去精神病院问精神病人，他们肯定也认为自己精神很正常。今天徐丽军不出庭，本身就说明了问题。精神是否正常，是否可以作为证人，应该出庭接受双方质询。正如辩护人在质证阶段回复公诉人，公诉人认为如果徐丽军的精神状态差，为什么李庄还让她作证。李庄是让徐丽军出庭，让大家质证检验其精神状态，李庄做到的，今天的公诉人敢吗？

第三，苏文龙的证言不可信，苏文龙是徐丽军的儿子。几年前的1个饭局，坐哪里的细节居然还记得，不符合常理。而且，苏文龙只在关于李庄的片言只语中，说“我只听到几句，现在能记清楚的就是李庄让我妈妈放心，黄说把她投资的钱说成是借给孟英的”。其他都记不清楚了，这样选择性记忆证人，可信度极差。

第四，徐丽军的妈妈杨盛梅的证言只是传闻证据，而且，取证地点在其卧室，这样的取证，让辩护人大开眼界。1个70几岁的老太太，动辄说作伪证，法言法语，令人咂舌。

第五，公安机关在侦查终结之后所取证据，完全违反刑诉法规定，这些证据，法院绝对不能采信。

我国刑诉法第129条规定，“公安机关侦查终结的案件，应当做到犯罪事实清楚，证据确实充分，并且写出起诉意见书，连同案卷、证据一并移送同级人民检察院审查决定”。

首先，本案案卷中没有起诉意见书。起诉意见书不提供，检察院是否应该法律监督？

其次，既然，事实清楚，证据确实充分了，你为什么还要继续调查，取证？反过来是否正好证明你事实不清，证据不足？

第三公安机关的侦查权到了侦查终结后，就没有了，凭什么在起诉阶段，甚至法院审理阶段，都还在侦查，这种证据，如果法院能采信，那么，公安机关是否在开庭后，还可以继续取证？

第六，最重要的是，根据最高人民法院（法发2010）20号通知：“办理其他刑事案件，参照《关于办理死刑案件审查判断证据若干问题的规定》（下次死刑案件证据规定）执行”。而《死刑案件证据规定》第十五条规定，“具有下列情形的证人，人民法院应当通知出庭作证；经依法通知不出庭作证证人的书面证言经质证无法确认的，不能作为定案的根据：（一）人民检察院、被告人及其辩护人对证人证言有异议，该证人证言对定罪量刑有重大影响的”；在庭审之前，辩护人即对证人证言有异议，要求法院通知证人出庭，现在证人不出庭，上述证据，不应该被作为定案的证据。

第七，公安机关存在明显的诱供行为

如2011年3月24日桂学武、李军对孟玲的询问笔录，第2页，没有由来地，直接问：你是否听到李庄教唆徐丽军把投资款说成是借款？正常的话应当问，你听到李庄和徐丽军说什么？

同页：侦查人员问，李庄有没有教唆徐丽军把投资款说成借款，他是怎样教的？这种诱供，非常露骨。

本案如果依法排除了不出庭的主要证人徐丽军、苏文龙之后，并无其他有力证据。据证人王辽的说法：李庄和徐丽军说话，徐丽军提到她投资金汤城的钱的事，李庄就用法律方面的规定告诉徐丽军，什么算借钱，什么算投资款，具体内容我说不出来。然后，李庄就对徐丽军说了些话，意思是要徐丽军把这个钱说成借款。

从这段证言看，李庄实际上是在分析徐丽军投入款项的法律性质，这和徐汇法院的判决是一致的，也和金汤城的律师意见一致，也和徐丽军录音说的一致。如果这是事实，那么这样的法律分析，是完全合法的。以上的证据，充分表明了对于徐丽军（王德伟）投入到金汤城的款项性质，绝对不是简单的投资款，从各项证据来看，是1种待转化的债权，在没有其他股东确认之前，只是1个借款或者类似借款的债权而已。徐丽军在法庭上所作证言符合事实，不管李庄如何说，都不构成妨害作证罪。

审判长、审判员：

各位坐在法庭上，头戴国徽，身穿法袍，手握法槌，行使法律授予的权力，无一不需要法律上的授权，如果没有程序法上的授权，今天的庭审将寸步难行。同为法律人，辩护人和法官、公诉人都应该如同珍惜自己的职业声誉一样，尊重法定程序，依照程序法来，仔细判断有没有管辖权，侦查取证时间、地点是否符合刑诉法，是否超期，综合的证据是否内心确证事实清楚，证据确凿，只有这样，步步为营，环环相扣，逻辑严密，得出的结论，才会赢得大家的尊重，这也是法治的精髓所在。反其道而行之，得到的判决，只会带来羞辱。

今天的开庭如此引人瞩目，不是因为被告人是李庄，李庄只是1个非常普通的人，只是性格比较倔强而已。本案引人瞩目，只是因为李庄是1个在执业中的律师，这个职业本来是该保护犯罪嫌疑人合法权益的，律师不是国家专政机器的对立面，而恰恰是为了保证公民在国家机器面前有人依法保护他，毕竟公检法未必全是对的，否则，也不需要立国家赔偿法了。这种在履行职务过程中无辜被入罪。这和殴打，拘禁1个正在看病的医生一样，是1种双重伤害。因为，同时受伤的，是任何公民的律师辩护权。而今天的李庄案，是双重的双重伤害，所以，才更让人同情，也更让人担心中国犯罪嫌疑人能否得到律师真正的帮助。

1个律师在给死刑犯辩护时，第一次被306条，已经引起国人瞩目，今天，他又一次被同1个罪名，在同1个地方受审，审理的内容却是在上海做的事，单单程序上的不公，已经可以说是，决嘉陵之波，流恶难尽。罄歌乐之竹，难书其罪。之后，恐怕，不管实体如何判，如何文字构陷，罪轻罪重，已难堵天下，悠悠之口。

最后，鹦鹉学舌，学下公诉人的警示教育。对于李庄，最大的教训就是，在中国如此险恶的刑事辩护环境下，居然还敢提交数十份无罪证据，居然还敢向法庭申请证人出庭，居然还敢对权力机关叫板，你赢得了死刑犯朱立岩及其妈妈的尊敬，然后，夜路走多终于见到鬼，自己身陷囹圄，亲人都见不到。这才是最需要接受教训的事情。沉痛的是，李庄最也不可能吸取教训，重做律师，只能让其他刑事辩护律师吸取自己的教训，当事人的罪与非罪是第二位的，律师自身安全是第一位的，如李庄般傻，一再入罪，值得吗？

从公诉人口中讲到李庄案的特殊，和本案管辖上，程序上的诸多违法之处，辩护人和李庄早就预测到本案的结果，将会是有罪，也不指望有奇迹发生。对于这种既定结果的判决面前，似乎辩护人是无力的，然后，在历史审判面前，谁都无法逃脱。违背法律的人，必将被法律所严惩。天理昭昭，李庄必有昭雪的一天。这句话，送给李庄，也送给所有的法律人。正义虽然不在当下，但，我们等得到！

谢谢！

上海大邦律师事务所

律师：斯伟江

2011年4月20日

四 : 对称：对称-词语简介，对称-其它相关

对称英文：symmetry ，指图形或物体两对的两边的各部分,在大小、形状和排列上具有一一对应的关系对称，指物体或图形在某种变换条件（例如绕直线的旋转、对于平面的反映，等等）下，其相同部分间有规律重复的现象，亦即在一定变换条件下的不变现象。对称性的扩张是通过联合对称性操作实现的，从简单到复杂，对称性的扩张也都是由几种对称性操作而组成。再查看有无一个n≥2的Cn轴，n个C2轴，垂直Cn轴的σh，平分C2轴的σd，以区分Dn，Dnh，Dnd；进一步区分只有一个In轴的点群Sn和Cni；区分只有一个Cn轴的Cn，Cnh和Cn v等。

对称_对称 -词语简单介绍

基本资料

词目：对称

拼音：duì chèn

英文：symmetry

基本释义

[symmetry;symmetrical] 指图形或物体两对的两边的各部分,在大小、形状和排列上具有一一对应的关系。

我国的建筑,…绝大部分是对称的。

引证解释

1. 指第二人称。

朱自清《你我》：“利用呼位，将他称与对称拉在一块儿。”

2. 物体或图象对某一点、直线或平面而言，在大小、形状和排列上相互对应。

洪深《戏剧导演的初步知识》：“画面构成的第一条原则是‘对称’：左右相等，不偏不倚。”

对称_对称 -其它相关

守恒律与对称性的联系

可以肯定的是，杨振宁1962年出版的《原子物理中某些发现的小史》（中译本为《基本粒子发现简史》，上海科学技术出版社1963年出版）引用过（译名为凡尔），杨先生引的那句话“不对称很少仅仅由于对称的不存在”，已成为深刻的哲理名言。我写《分形艺术》时，也装潢门面，把外尔和杨先生的话一并引了。在自然科学和数学上，对称意味着某种变换下的不变性，即“组元的构形在其自同构变换群作用下所具有的不变性”，通常的形式有镜像对称（左右对称或者叫双侧对称）、平移对称、转动对称和伸缩对称等。物理学中守恒律都与某种对称性相联系。

生物形态的对称

一般指图形和形态被点、线或平面区分为相等的部分而言。在生物形态上主要的对称分为下列各种：（1）辐射对称：与身体主轴成直角且互为等角的几个轴（辐射轴）均相等，如果通过辐射轴把含有主轴的身体切开时，则常可把身体分为显镜像关系的2个部分。例如海星可见有5个辐射轴。另外在高等植物的茎和花等，也常具有辐射对称的结构；

（2）双辐射对称：只有2个辐射轴，彼此互成直角，形式上可以把它看成是从辐射对称向左右对称的过渡型（例如栉水母）；

（3）左右对称：或称两侧对称，是仅通过1个平面（正中矢面）将身体分为互相显镜像关系的2个部分（例如脊椎动物的外形）。在正中矢面内由身体前端至后端的轴称为头尾轴或纵轴，这个轴与身体长轴大都一致。在正中矢面内与头尾轴成直角并通过背腹的轴为背腹轴或矢状轴。还有与正中矢面成直角的轴称正中侧面轴（或内外轴）、该轴夹着正中矢面，彼此相等且具有方向相反的极性，如果将两侧的正中侧面轴合起来看成为一轴时，则称为横轴。在辐射对称中，如相当于海星的一根足的同型部分，称为副节（paramere），副节其本身成两侧对称。一般两侧对称的每一半为与同一轴相关而极向相反的同型部分，此称为对节或体辐。副节、对节等的同型部分，一般来看，仅相互方向不同，可认为这是与对外界的关系相同有着密切的联系。所以在个体发生或系统发生过程中其生活方式变化时，而与之相关的对称类型也时有变化。例如棘皮动物在自由运动的幼体期具有左右对称的体制，在接近静止生活的成体，则显有辐射对称的体制。再如比目鱼等左右体侧可成为二次的背腹关系。把无对称的关系称为非对称（asy－metry），其中具有规则形态的在生物界可广泛见到的有螺旋性。此外还有即使外形上表现对称，但与外界无直接关系的内脏，基本既可表现为对称的，也有不少由于形态变形而表现为不对称的。

中心对称

概念

把1个图形绕着某一点旋转180°，如果它能与另1个图形重合，那么就说这2个图形关于这个点对称或中心对称（central symmetry），这个点叫做对称中心，这2个图形的对应点叫做关于中心的对称点。

中心对称和中心对称图形是2个不同而又紧密联系的概念．它们的区别是：中心对称是指2个全等图形之间的相互位置关系，这2个图形关于一点对称，这个点是对称中心，2个图形关于点的对称也叫做中心对称．成中心对称的2个图形中，其中1个上所有点关于对称中心的对称点都在另1个图形上，反之，另1个图形上所有点的对称点，又都在这个图形上；而中心对称图形是指1个图形本身成中心对称．中心对称图形上所有点关于对称中心的对称点都在这个图形本身上．如果将中心对称的2个图形看成1个整体（1个图形），那么这个图形就是中心对称图形；1个中心对称图形，如果把对称的部分看成是2个图形，那么它们又是关于中心对称．

也就是说：

① 中心对称图形：如果把1个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形。

②中心对称：如果把1个图形绕着某一点旋转180度后能与另1个图形重合，那么我们就说，这2个图形成中心对称。

中心对称图形

正（2N）边形（N为大于1的正整数）、线段、圆、平行四边形、直线等。

实际上，除了直线外，所有中心对称图形都只有1个对称点。

既不是轴对称图形又不是中心对称图形：不等腰三角形，直角梯形，普通四边形

中心对称的性质

①关于中心对称的2个图形是全等形。

②关于中心对称的2个图形，对称点连线都经过对称中心，并且被对称中心平分。

③关于中心对称的2个图形，对应线段平行（或者在同一直线上）且相等。

识别1个图形是否是中心对称图形就是看是否存在一点，使图形绕着这个点旋转180°后能与原图形重合。

中心对称是指2个图形绕某1个点旋转180°后，能够完全重合，称这2个图形关于该点对称，该点称为对称中心.二者相辅相成，两图形成中心对称，必有对称中点，而点只有能使2个图形旋转180°后完全重合才称为对称中点.

辐射对称动物

辐射对称动物Radiata是左右对称动物的对应词。顾维尔（G.L.Cuv－ier）把大部分的棘皮动物、腔肠动物、海绵动物、扁形动物及滴虫类命名为辐射对称动物。冯·西波德（K.T.von Siebold）把棘皮动物、腔肠动物、海绵动物总称为辐射对称动物。以后，被命名为腔肠动物（有时也包括棘皮动物）。

科学与艺术

科学和艺术都很重视对称性。对于科学，对称性决定了各种可能的守恒定律，因而具有更根本性的意义。在艺术中，对称性常与平衡、形状、形式、空间等一同讨论。人们通常从静态表现上理解对称性，有一定意义，但更重要的是从操作意义上、从生成过程上理解对称性。

一在科学中，对称性是指某种操作下的不变性或者守恒性，对称性常与守恒定律相联系。与空间平移不变性对应的是动量守恒定律；与时间平移不变性对应的是能量守恒定律；与转动变换不变性对应的是角动量守恒；与空间反射（镜像）操作不变性对应的是宇称守恒。在弱相互作用中，“宇称”不守恒，自然界在C或P下不是对称的，在CP下也不是对称的，但却是CPT对称的。这里C表示电荷变号操作，相当于反转变换，如由底片洗出照片，电子变正电子，物质变反物质；P表示镜像反射操作，如人照镜子；T表示时间反演操作，如微观可逆过程。也就是说，当同时把粒子与反粒子互变（C）、左与右互变（P）、过去与未来互变（T），自然界又是对称的。

但把物质的宇称、超荷、同位旋等所有物理性质都加起来考虑，会发现它们总体上并不守恒，即对称性有破缺。人们假设，这是只考虑“物质”的结果，如果把“真空”也算在内，就有可能找回“失去的对称性”，总体上这世界仍然是对称的、守恒的。问题是，到目前为止，科学家对真空的了解还不够多。为什么CP不守恒，而CPT就守恒？CPT守恒意味着什么？CPT真的永远守恒吗？这都是些非常重要而艰难的问题，还有很大一部分需要科学家进1步研究来解答。

对称性是第一世界固有的，还是第二世界强加于其上的？是自然界的属性，还是自然科学中物理定律的属性？或者问，对称性是客观的，还是主观的？1种简便的而肯定的回答是，对称性是客观的、自然世界固有的属性。这也是过去流行的观点，但此观点对于解决问题并不比相反的观点更具有优势。如果把认识世界视为1个复杂的、不断进步的过程，理解对称性也要放在1个过程之中进行，在此认识系统中，“属性”的词汇是不恰当。如果仍然保留“属性”一词，它也只能指对象在某种条件下表现出来的功能，这也可以称作“条件主义”科学哲学。条件也即约束，可对应于某种操作，标示某种认识层次。对称性原理均根植于“不可观测量”的理论假设上；不可观测就意味着对称性，任何不对称性的发现必定意味着存在某种可观测量。（李政道）那么“不可观测”是不是由于我们认识能力而导致的1种假相呢？

李政道说：“这些‘不可观测量’中，有一些只是由于我们目前测量能力的限制。当我们的实验技术得到改进时，我们的观测范围自然要扩大。因而，完全有可能到某种时候，我们能够探测到某个假设的‘不可观测量’，而这正是对称破坏的根源。然而，当确实发生这样的破坏时，1个更深入的问题是，我们怎么能够确信这不是意味着世界不对称呢？是否有可能，自然界基本规律仍然是对称的？是自然规律不对称，还是世界不对称？这2种观点究竟有什么区别呢？”此论述概括了理论物理学的认识过程，更涉及一些基本的哲学问题。

二

当年数学家魏尔（H．Weyl）在讨论艺术作品中的对称性时，提到西方艺术像其生活一样，倾向于缓解、放宽、修正，甚至打破严格的对称性，接着有一名句：“但是不对称很少是仅仅由于对称的不存在。”（《对称》，商务1986，第11页）杨振宁引用了魏尔的话，并加上一句评论：“这句话有物理学中似乎也是正确的。”（《基本粒子发现简史》，上海科技1979，第58页）我们则又加一句，无论对于科学还是艺术，“同样，找到对称也绝对不是仅仅由于非对称的不存在。”

科学和艺术都是讲究对称性的，对称性意味着某种规则，很难想象像科学与艺术如此宏大而不断积累的人类文明会没有规则，杂乱无章。那么是否可以推论出，科学与艺术只关注规则、对称性，并且只有对称的东西才称得上科学与艺术呢？答案是否定的。李政道1996年5月23日在中央工艺美术学院的演讲中曾指出：“艺术与科学，都是对称与不对称的巧妙组合。”这无疑是正确的。对称是美，不对称也是美，准确说，对称与对称破缺的某种组合才是美。“单纯对称和单纯不对称都是单调。1个对称的建筑只有放在不对称的环境空间中才显得美，反之亦然。”

无论对于科学还是对于艺术，对称性都涉及不同的方面和不同的层次。不同方面指对称的多样性：平移对称（连续装饰花纹、花布）、旋转对称（穹窿、五角星、伞、晶体）、左右对称性（建筑立面、人体）及联合操作对称性（埃舍尔的《骑士图》，类似CP操作）。不同方面还涉及局部与整体的关系，对称性有长程整体对称（如晶体），也有局部短程对称（如准晶、凯尔特装饰艺术），这些在科学与艺术作品中都有许多实例。不同层次指对称性依赖于物质层次或者观念层次，在不同的层次上对称性可以很不相同，以人体为例，外表是左右对称的，但内脏则不是，心脏通常靠近左侧，肾等还是对称的。凯尔特艺术（Celticart）有很强的规则性，可以明显地发现少数基本结构在不同的层次上重复出现，不同层次的对称性与对称性破缺相互照应，细节丰富、层次分明，给予人以较强的装饰效果。可以肯定地说，凯尔特艺术有意识地利用了伸缩变换不变性，即标度变换下的不变性，也就是自相似对称性。特别有趣的是，在分形科学与艺术中，能够观察到各种对称性，既有不同方面的也有不同层次的，通过复函数计算机迭代，非常容易地展示这些对称性。

“对称案”重现江湖

《李政道传》

近日，杨振宁或将与《李政道传》上法庭打官司。主要是围绕季羡林之子、李政道助手季承撰写的《李政道传》。杨振宁称《李政道传》有诸多不实之处，并再次强调，半个多世纪以来，他和李政道决裂的责任在李政道。昨日，季承表示，欢迎杨振宁“质疑”。因为回应越多，才能越有助于相关研究者和学界找到事情的真相。季承还表示，如果杨振宁要起诉他，他愿意应诉。

据杨振宁说，《李政道传》中，季承引用李政道的说法，认为宇称不守恒的突破思想是李政道先提出的。对此，杨振宁表示，突破思想是2个人在研究中“顿悟”的，而顿悟的是“杨”还是“李”，他也没有铁证，但他又称“80%~90%的可信度是自己”，因为发现该定律最重要的是与对称有关的系数，而对称是他的专业，“所以才能想到这不寻常的一面”。

《对称》小册子

《对称》是举世闻名的大手笔小册子，是作者大学退休前“唱出的一支天鹅曲”，它由普林斯顿大学出版社将外尔（C.H.H.Weyl，曾译作魏尔或者凡尔）退休前的系列讲座汇编而成书。据说许多百科全书的“对称”条目都将外尔的这部小书列为主要参考文献。

对称_对称 -图书一

图书信息

作者：（德）外尔着，冯承天，陆继宗译

出 版 社：上海科技教育出版社

出版时间：2005-4-1版次：1页数：171字数：106000

印刷时间：2005-4-1开本：纸张：胶版纸

印次：I S B N：9787542837882包装：平装

内容简单介绍

遵循现代人文教育和公民教育的理念，秉承通达民情，化育人心的中国传统教育精神，大学经典依据中西文明传统的知识谱系及其价值内涵，将人类历史上具有人文内涵的经典作品编辑成为大学教育的基础读本，应时代所需，顺时势所趋，为塑造现代中国人的人文素养，公民意识和国家精神倾力尽心。开放人文旨在提供全景式的人文阅读平台，从文学、历史、艺术，科学等多个面向调动读者的阅读愉悦，寓学于乐，寓乐于心，为广大读者陶冶心性，培植情操。

目录

图书对称

序言及文章评注

双侧对称性

平移对称性、旋转对称性和有关的对称性

装饰对称性

晶体·对称性的一般数学观念

附录A 确定三维空间中由真旋转构成的所有有限群

附录B 计入非真旋转

致谢

对称_对称 -图书二

图书信息

书名：Symmetries(对称)

ISBN：9787302214786

作者：Johnson, D.L.着

定价：34元

出版日期：2009-11-1

出版社：清华大学出版社

图书简单介绍

本书研究空间几何中的各种对称，介绍相关的对称群；以通俗易懂的方式讲述几何与群的本质，以及两者之间的联系（即对称）。书中有大量习题并附部分习题答案或提示。本书是一本优秀的数学教材，适用于数学系本科生和其他专业对数学有兴趣的本科生用作数学参考书或课外读物。

目录

Contents1. Metric Spaces and their Groups ............................ 11.1 Metric Spaces............................................ 1-1.2- Isometries ...............................................-41.3 Isometries of the Real Line ................................ 51.4 Matters Arising .......................................... 71.5 Symmetry Groups........................................ 102. IsometriesofthePlane..................................... 152.1 Congruent Triangles ...................................... 152.2 IsometriesofDifferentTypes............................... 182.3 The Normal Form Theorem................................ 202.4 Conjugationoflsometries ................................. 213. Some Basic Group Theory.................................. 273.1 Groups.................................................. 28A~m~3.2 Subgroups ............................................... 503.3 Factor Groups ........................................... 333.4 Semidirect Products ...................................... 364. Products of Reflections ..................................... 454.1 The Product of Two Reflections............................ 454.2 Three Reflections......................................... 474.3 Four or More ............................................ 505. Generators and Relations................................... 555.1 Examples................................................ 565.2 Semidirect Products Again ................................ 60eoeXlllxiv Contents~ I ~ ~ I I I _ II I I I I I II I III ~ ~ I I I I I15.3 Change of Presentation.................................... 615,5.4 Triangle Groups.......................................... 6[)15.5 Abelian Groups .......................................... 706. Discrete Subgroups of the Euclidean Group ................ 7[)-15.-1- -Leonardo's Theorem ......................................-~Su6.2 ATrichotomy............................................ 816.3 Friezes and Their Groups.................................. 836.,1 The Classification ........................................ 8157 Plane Crystallographic Groups' OP Case 897.1 The Crystallographic Restriction ........................... 807.2 TheParametern......................................... Ol7.3 The Choice of b .......................................... 027.4 Conclusion .............................................. 048. Plane Crystallographic Groups: OR Case................... 97-8.-1--A Useful----Dichotomy ......................................--978.2 The Case n - 1 .......................................... 10083 The Case n - 2 1008 4 The Case n - 4 1018 5 The Case n - 3 1028 6 The Case n - 6 1049. Tessellations of the Plane................................... 107O.1 Regular Tessellations...................................... 1079.2 Descendants of (4, 4) ..................................... 1109.3 Bricks................................................... 1129.4 Split Bricks.............................................. 1139.5 Descendants of (3, 6) ..................................... 11610. Tessellations of the Sphere.................................. 123dMm~10.1 Spherical Geometry....................................... 12310.2 The Spherical Excess ..................................... 125-1--0.3 Tessellations of- the--Sphere.................................-1--281-0.-4 The-Platonic Solids.......................................-1-~3010.5 Symmetry Groups........................................ 13311. Triangle Groups ............................................ 13911.1 The Euclidean Case....................................... 14011.2 The Elliptic Case......................................... 14211.3 The Hyperbolic Case...................................... 144Contents xvI I I I I I I __ I II Ilml11.4 Coxeter Groups . ......................................... 14612. Regular Polytopes.......................................... 15512.1 The Standard Examples................................... 15612.2 The Exceptional Types in Dimension Four................... 15812.8 Three Concepts and a Theorem ............................ 16012.4 Schliifli's Theorem ........................................ 1ogSolutions ....................................................... 167Guide to the Literature......................................... 187Index of Notation .............................................. 1OlIndex........................................................... 105

对称_对称 -对称群

无法区别上下脚标理解起来比较麻烦

群的基本概念

1个分子具有的全部对称元素构成1个完整的对称元素系，和该对称元素系对应的全部对称操作形成1个对称操作群，群是按照一定规律相互联系着的一些元(又称元素)的集合，这些元可以是操作、数字、矩阵或算符等。连续做2个对称操作即和这2个元的乘法对应。 若对称操作A,B,C,…的集合G={A,B,C,…}同时满足下列4个条件，这时G形成1个群。

(1)封闭性：指A和B若为同一群G中的对称操作，则AB=C，C也是群G中的1个对称操

作。

(2)主操作：在每个群G中必有1个主操作E，它与群中任何1个操作相乘给出AE=EA=A

(3)逆操作：群G中的每1个操作A均存在逆操作A-1，A-1也是该群中的1个操作。逆操作

是按原操作途径退回去的操作。AA-1=A-1A=E

分子点群及分类

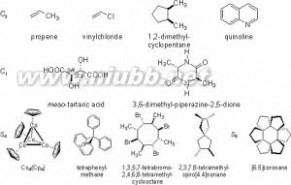
在分子中，原子固定在其平衡位置上，其空间排列是对称的图象，利用对称性原理探讨分子的结构和性质，是人们认识分子的结构和 性质的重要方法。分子对称性是联系分子结构和分子性质的重要桥梁。分子点群大致可分为几类：Cn、Cnv、CNH、Dn、Dnh、Dnd及高阶群。

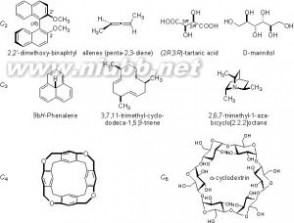对称

1.Cn点群

Cn群只有一个Cn旋转轴。独立对称操作有n个，阶 次为n。若分子只有n重旋转轴，它就属于Cn群，群元素为{E，Cn，Cn 2…Cnn-1}。这是n阶循环群。最简单的点群C1只含1个主操作E， 它包括所有不对称分子和分子构型，所以这类分子都有手性。比如：CH3CH2CHBrCH3，葡萄糖等。

2.Cnh点群

Cnh点群分子

Cnh群中有一个Cn轴，垂直于此轴有一个σh。阶次为2n。C1h点群用Cs记号。若分子有1个n重旋转轴和1个垂直于轴 的水平对称面就得到Cnh群，它有2n个对称操作，{E，Cn，CN2……Cnn-1，σn，Sn2……Snn-1}包括（n-1）个旋转、1个反映面， 及旋转与反映结合的（n-1）个映转操作。当n为偶次轴时，S2nn即为对称中心。

反式二氯乙烯

以反式二氯乙烯分子说明C2h点群，C=C键中点存在垂直于分子平面的C2 旋转轴；分子所在平面即为水平对称面σh；C=C键中点还是分子的对称中心i。 所以C2h点群的对称操作有4个：{E，C2，σh，i}，若分子中有偶次旋转轴及垂直于该轴的水平平面，就会产生1个对称中心。

3.Cnv点群

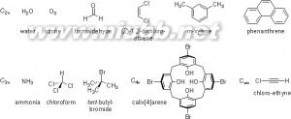Cnv 点群分子示例

Cnv群中有一个Cn轴,通过此轴有n个σv。阶次为2n。若分子有 n重旋转轴和通过Cn轴的对称面σ，就生成1个Cnv群。由于Cn轴的存在，有1个对称面，必然产生（n-1）个对称面。2个平面交角为π/n。它也是2n阶群。

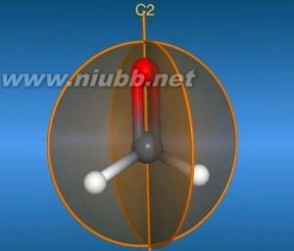C2 点群的H2O 分子

水分子属C2v点群，C2轴经过O原子、平分∠HOH，分子所在平面是1个σv平面，另1个σv平面经过O原子且与分子平面相互垂直。与水分子类似的V 型分子，如SO2、NO2、ClO2、H2S,船式环已烷、N2H4等均属C2v点群。其它构型的C2v分子如稠环化合物菲（C14H10），茚，杂环化合物呋喃(C4H4O)吡啶 (C5H5N)等。NH3分子是C3v点群典型例子。C3轴穿过N原子和三角锥的底心， 3个垂面各包括1个N-H键。其它三角锥型分子PCl3、PF3、PSCl3、CH3Cl、 CHCl3等，均属C3v点群，P4S3亦属C3v点群。CO分子是C∞v点群典型例子。 C∞v轴穿过了C原子和O原子所在的直线，任何1个经过C原子和O原子所在的面都是其σv平面。

4.Sn和Cni点群

对称

分子中有一个In轴，当n为奇数时，属Cni群；当n为偶数但不为4的整数倍时，属Cn/2h点群；当n为4的整数倍时，属Sn点群。分子中只含有1个映转轴Sn的点群属于这1类。映转轴所对应的操作的绕 轴转2π/n，接着对垂直于轴的平面进行反映。

S1=Cs群：S1=σ、C11=σ即S1为对称面反映操作，故S1群相当于Cs 群。即对称元素仅有1个对称面。亦可记为C1h=C1v=Cs：{E，σ}。这样的 分子不少。如TiCl2(C5H5)2，Ti形成四配位化合物，两个Cl原子和环戊烯基成对角。又如的六元杂环化合物N3S2PCl4O2亦是属于Cs对称性。

Ci群：S2=σ、C2=Ci为绕轴旋转180°再进行水平面反映，操作结果相当于1个对称心的反演。故S2群亦记为Ci群。例如Fe2(CO)4(C5H5)2，每个Fe与1个羰基，1个环戊烯基配位，再通过2个桥羰基与另1个Fe原子成键，它属于Ci对称性。S3=σC3=C3+σ

S4点群：只有S4是独立的点群。例如：1,3,5,7-四甲基环辛四烯，有1个S4映转轴，没有其它独立对称元素，一组甲基基团破坏了所有对称面及C2轴。

5.Dn点群

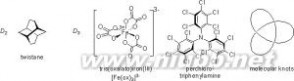Dn点群和三叶草环，该点群分子都具有手性。

Dn群由一个Cn轴和垂直于此轴的n个C2轴组成，阶次为2n。 如果某分子除了1个主旋转轴Cn(n≥2)之外，还有n个垂直于Cn轴的二次 轴C2，则该分子属Dn点群。

6.Dnh点群Dnh群

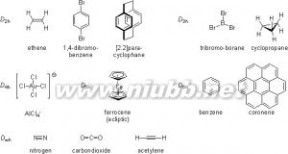对称

由Dn群的对称元素系中加入垂直于Cn轴的σh组成。若Cn奇数轴，将产生I2n和n个σv，注意这时对称元素系中不含对称中心i。若Cn 为偶数轴，对称元素系中含有In，n个σv和i。Dnh分子含有1个主旋转轴Cn （n>2），n个垂直于Cn轴的二次轴C2，还有1个垂直于主轴Cn的水平对称面σh；由此可产生4n个对称操作：{E，Cn，Cn2，Cn 3…Cnn-1；C1(1)，C2(2)…C2(n)；σh，Sn1，Sn2，…Snn-1；σv(1)，σv(2)…σv(n)｝Cn旋转轴产生n个旋转操作，n个C2 (i)轴旋转产生n个旋转操作，还有对称面反映及（n-1）个映转操作，n个通过Cn主轴的垂面σv的反映操作。故Dnh群为4n阶群。

D2h对称性的分子亦很多，如常见的乙烯分子，平面型的对硝基苯分子 C6H4(NO2)2，草酸根离子[C2O4]2-等。

D3h：平面三角形的BBr3、CO32－、NO3 －或三角形骨架的环丙烷均属D3h点群。三角双锥PCl5、三棱柱型的Tc6Cl6(图VI)金属簇合物等也是D3h对称性。

D4h：[Ni(CN)4]2－、[PtCl4]2－等平面四边形分子属D4h对称性，典型的金属四重键分子Re2Cl8 2－，2个Re各配位4个Cl原子，两层Cl原子完全重叠，故符合D4h对称性要求。

D5h：重叠型的二茂铁属D5h对称性(平行的)，IF7、UF7离子为五角双锥构 型，也属D5h对称性。

D6h：点群以苯分子为例，苯的主轴位于苯环中心垂直于分子平面，六个二 次轴，三个分别经过两两相对C-H键，三个分别平分六个C－C键。分子平面 即σh平面，六个σv垂面分别经过六个C2轴且相交于C6轴。苯环属于D6h对 称群，共有4×6＝24阶对称操作，是对称性很高的分子。二苯铬（重叠型）也是D6h对称性。

D∞h：同核双原子分子H2、N2、O2等，或中心对称的线型分子CO2、CS2、 C2H2、Hg2Cl2等属于D∞h对称性。在分子轴线存在1个C∞轴，过分子中心又有 1个垂直于分子轴的平面，平面上有无数个C2轴⊥C∞轴，还有无数个垂面σv 经过并相交于C∞轴。

7.Dnd点群Dnd群

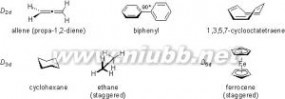Dnd 点群示例

由Dn群的对称元素系和通过Cn有平分两个C2轴的夹角的n个σd组成。若Cn奇数轴，对称元素系中含有Cn，n个C2，n个σd，i和In，若Cn为偶数轴，对称元素系中含有Cn，n个C2，n个σd和I2n，注 意这时不包含对称中心i。1个分子若含有1个n重旋转轴Cn及垂直于Cn轴n个2次轴，即满足Dn群要求后，要进1步判断是Dnh或Dnd，首先要寻找有否 垂直于Cn主轴的水平对称面σh。若无，则进1步寻找有否通过Cn轴并平分C2轴的n个σd垂直对称面，若有则属Dnd点群，该群含4n个对称操作。以丙二烯为例说明。沿着C=C=C键方向有C2主轴，经过中心C原子垂直于C2轴的两个C2轴，与2个平面成45°交角。但不存在1个过中心D、垂直于主轴的平面，故丙二烯分子属D2d而不是D2h。D4d：一些过渡金属八配位化合物， ReF8 2－、 TaF8 3－和Mo(CN)8 3+等均形成四方反棱柱构型，它的对称性属D4d。

8.T，Th和Td点群

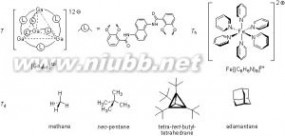T，Th 和Td 点群示例

这些是四面体群，其特点是都含有四个C3轴，按立方体体对角线排列。T点群由四个C3，和三个C2组成。Th点群由四个C3和三个C2，三个σh（它们分别和三个C2轴垂直）和i组成。Td点群由四个C3，和三个I4（其中含有C2）和六个σd（分别平分四个C3轴的夹角）组成，注意其中不包含对称中心i。

T群：当1个分子具有四面体骨架构型，经过每个四面体顶点存在1个C3 旋转轴，四个顶点共有四个C3轴，联结每两条相对棱的中点，存在一个C2轴，六条棱共有三个C2轴，可形成十二个对称操作：｛E，4C3，4C32，3C2｝。这些对称操作构成T群，群阶为12。T群是纯旋转群,不含对称面,这样的分子很少。

Th群：当某个分子存在T群的对称元素外，在垂直C2轴方向有一对称面，三个C2轴则有三个对称面，C2轴与垂直的对称面又会产生对称心。这样共有二十四个对称操作｛E，4C3，4C32，3C2，I，4S6，4S65，3σh｝，这个群称Th群，群阶为24。

Td群：若1个四面体骨架的分子，存在四个C3轴，三个C2轴，同时每个C2轴还处在2个互相垂直的平面σd的交线上，这2个平面还平分另外两个C2轴（共有六个这样的平面）则该分子属Td对称性。对称操作为｛E，3C2，8C3，6S4，6σd｝共有24阶。这样的分子很多。四面体CH4、CCl4对称性属Td群，一些含氧酸根SO4 2－、PO4 3－等亦是。在CH4 分子中，每个C－H键方向存在一个C3轴，两个氢原子连线中点与中心C原子间是C2轴， 还有六个σd平面。

9.O和Oh点群

这些是八面体群，其特点是都含有三个C4轴，O群由三个C4，和四个C3和六个C2组成。Oh群由三个C4，和四个 C3和六个C2，三个σh（分别和三个C4轴垂直），六个σd（分别平分四个C3轴的夹角）和i等组成。分子几何构型为立方体、八面体的， 其对称性可属于O或Oh点群。

Oh 点群示例

O群：立方体与八面体构型可互相嵌套，在立方体的每个正方形中心处取1个顶点,把这6个顶点连接起来就形成八面体。经过立方体2个平行面的中心，存在一个C4旋转轴，共有3组平行面，所以有三个C4轴。通过相距最远的2个顶点有一个C3轴，共有四个C3轴，三个C4轴与四个C3轴构成了二十四个对称操作，{E，6C4，3C2 '，6C2，8C3}，构成纯旋转群O群。O群的C4轴对八面体构型来说，存在于2个对立顶点之间。六个顶点就有三个C4轴，联结2个平行的三角面的中心，则为一个C3轴，共有八个三角面，就有四个C3轴.。 对称性为O群的分子较少。

Oh群：1个分子若已有O群的对称元素（四个C3轴，三个C4轴），再有1个垂直于C4轴的对称面σh，同理存在三个σh对称面，有C4轴与垂直于它的水平对称面，将产生1个对称心I，由此产生一系列的对称操作，共有4八个：{E，6C4，3C2，6C2'，8C3，I，6S4，3σh，6σv，8S6}这就形成了Oh群，它包括八面体和立方体。属于Oh群的分子有八面体构型的SF6、WF6、Mo(CO)6，立方体构型的OsF8、立方烷C8H8，还有一些金属簇合物对称性属Oh点群。例如Mo6Cl8

4+或Ta6Cl12 2+，这2个离子中，六个金属原子形成八面体骨架，Cl原子在三角面上配位，或在棱桥位置与M配位，还有1种立方八面体构型的分子对称性也属Oh群。

10.I和Ih点群

这些是二十面体群，其特点是都含有六个C5轴。I点群由六个C5，十个C3 或十五个C2组成。Id点群由六个C5，十个C3或十五个C2，十五个σ和i组成。Id点群有时又称Ih 点群。正二十面体与正十二面体具有完全相同的对称操作。（将正十二面体的每个正五边形的中心取为顶点，联结起来就形成严格正二十面体。反之，从正二十面体每个三角形中心取1个顶点，联结起来就形成1个正十二面体。）

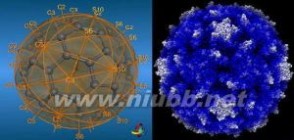Ih 群的C60 和I 群的脊髓灰质炎病毒

I群：现以十二面体为例说明；联结十二面体2个平行五边形的中心，即是多面体的1个C5 对称轴，共有十二个面，即有六个C5轴，联结十二面体相距最近的2个顶点，则为C3轴，共有20 个顶点，故有十个C3轴。经过一对棱的中点，可找到一个C2轴，共有30条棱，所以有十五个C2 轴。六个C5轴、十个C3轴、十五个C2轴共同组成了I群的60个对称操作：{E，12C5，12C5 2，20C3，15C2}，I群的1个60阶的纯旋转群。属于I群的分子很少，典型的是脊髓灰质炎病毒。

Ih群：在I群对称元素基础上，增加1个对称心，就可以再产生60个对称操作，形成1二十个对 称操作的Ih点群：{E，12C5，12C5 2，20C3，15C2，i，12S10，12S10 3，20S6，15σ}。正十二面体 和正二十面体的构结属于这个点群，C60也属Ih点群。

分子所属点群的判别

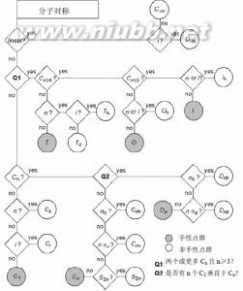要确定1个对称分子属于那种点群可以根据这张图的步骤来判断

1个分子的对称性一定属于上述十类点群中的1种。首先查看是否是线性的，再查看有无多个高次轴Cn：注意有无六个C5，或三个C4，或四个C3，以区分二十面体群，八面体群，四面体群。再查看有无1个n≥2的Cn轴，n个C2轴，垂直Cn轴的σh，平分C2轴的σd，以区分Dn，Dnh，Dnd；进1步区分只有1个In轴的点群Sn和Cni；区分只有1个Cn轴的Cn，Cnh和Cn v等。

所有分子都可以归纳为这些对称点群的分类，用群论的方法来处理这样的对称性是在分子的尺度上忽略了原子的差异性的。这些分子又构成了大分子体系以及细胞和生物体，对称性并没有因为系统的非线性叠加而消失；由于系统的自相似性存在，这样的对称性在将一直延伸到 宏观世界。比如：Ih点群正二十面体的噬菌体，I点群的脊髓灰质炎病毒等都有着类似分子的对称性（忽略病毒各个面分子的差异性）。

雪花总是呈现六边形严格对称

还有水分子由于氢键链接形成的对称结构，由于空间平移的不变性在宏观表现为对称六边形的雪花；六边形结构是稳定性与对外接触吸收更多水分相 妥协结果。因为雪花的形成过程是混沌的，所以世界上没有两片完全相同的雪花，但雪花都是对称的。当然，宏观的事物相对微观的角度来观察，差异性是必然存在的；而微观的事物相对宏观的角度来观察，则是忽略这样的差异性，而表现出来的紧密对称性。

对称_对称 -对称性的扩张（symmetryexpanded）

很多自然界的形状又都包含着诸多对称性操作的扩张。事物的对称性，并不仅仅是1种点 群的归纳，事物的的发展往往伴随对称性的扩张。1952年外尔（H.Weyl）提出用数学处理相似 对称的方法。他定义了2个相似变换的平面E2：1个中心扩张（简称扩张）和扩张旋转，且限 制扩张系数k>0，他使空间等距、平移和扭转分别建立了联系。即平移对称和旋转对称的迭代， 这种操作无限迭代构成Σ群。他的分析是基于满足自然界的相似性。像鹦鹉螺那样按照对数螺 旋（位矢与切线间的夹角保持恒定）其形状始终保持不变,鹦鹉螺的螺旋中暗含了菲波纳切数列， 而菲波纳切数列的两项间比值也是无限接近黄金分割数的。

鹦鹉螺的螺旋中暗含了菲波纳切数列

在平面相似对称理论的进1步发展是许勃尼科夫(A.V.Shubnikov)，他指出所有的相似性变换平面E2：中心扩张k，膨胀旋转L和扩张反映M，都源于旋转和反映；并衍生出5种相似对称群，CnK,CnL,CnM,DnK,DnL,；DnL与DnM是一致的。更多内容可以参见SlavikV.Jablan的《对称性和装饰》、KlausMainzer的《对称性与复杂性——热情而美丽的非线性科学》以及Hermann Weyl的《对称性》。

艺术与对称

埃舍尔

荷兰画家埃舍尔（M.C.Escher）的骑士图对镜象反射加上黑白置换和必要的平移操作才构成对称操作。对称性的扩张是通过联合对称性操作实现的，从简单到复杂，对称性的扩张也都是由几种对称性操作而组成。简单的对称点群，通过对称操作形成了复杂的对称图案，而这样的对称性扩张不仅仅是在几何意义上的。在经济学中对称性是1个功能原则；在社会学中是1个动态原则。

在社会学中对称性扩张的结果就 是平衡，例如民主与划分力量平衡的洛克自由主义影响了美国和法国的宪法。

音乐必要成分的创作是另1种艺术，这包括：结构、形式、组织、和谐、比例、平衡。是否有1个创作音乐的普遍原理，即音乐的部分组织成为1个整体？拉里·所罗门(LarryJ.Solomon)在他的博士论文中提出1个观点，对称性就是这样的1个普遍原则。音乐的关系组成在不同国家文化、历史、种族中，大部分是基于对称性建立的。

对称性的观念并不只限于基础数学、物理，他还包括艺术，文化和经济等；对称性原则是一般性原则的决定原则。对称群中的反映、旋转和平移操作一样可以应用于其他领域。在乐谱中时间代表水平线，如果关于轴对称其结果是与原来全等，而满足了反射对称的条件。在三维轴（或3个层面，音高、时间、动态）反映成为平面，大多数音乐剧的形式只限于2个变量，我们可以在二维空间中参考他们的图样，音乐符号在音调轴和音高轴同样可以对称，音高在音符代表垂直。

五 : 中年：中年-词语概念，中年-其它相关

“中年”是介于“青少年”和“老年”之间的年龄，没有明确的年龄划分，一般是指四、五十岁的年龄。《晋书·王羲之传》：“谢安尝谓羲之曰：‘中年以来，伤于哀乐。’”陆游《闲游》诗：“老躯健似中年日，乡俗淳如太古时。”《晋书·后妃传序》：“爰自（）古，是谓元妃；降及中年，乃称皇后。”。

人到中年万事休_中年 -词语概念

基本信息

词目：中年
拼音：zhōngnían

释义

刘江46岁的照片
（1）指四、50岁的年纪。
《晋书·王羲之传》：“谢安尝谓羲之曰：‘中年以来，伤于哀乐。’”
陆游《闲游》诗：“老躯健似中年日，乡俗淳如太古时。”
（2）指中世。
《晋书·后妃传序》：“爰自（）古，是谓元妃；降及中年，乃称皇后。”

基本解释

1.[middleage]∶人生的1个时期，指40—59岁
人到中年
2.[mediumterm]∶中期

详细解释

崔久峰46岁的照片
1.中等收成的年岁。

《周礼·地官·均人》：“丰年则公旬用三日焉，中年则公旬用二日焉。”《管子·治国》：“中年，亩二石，一夫为粟二百石。”
2.犹隔年。
《礼记·学记》：“比年入学，中年考校。”郑玄注：“中，犹闲也。乡遂大夫，闲岁则考。”
3.指四50岁的年龄。
《列子·周穆王》：“宋阳里华子中年病忘。”《晋书·王羲之传》：“谢安尝谓羲之曰：‘中年以来，伤於哀乐。’”元孟汉卿《魔合罗》楔子：“月过十五光明少，人到中年万事休。”谌容《人到中年》：“中年人，正是大显身手之际。”

闫怀礼45岁的留影
4.犹言中世，中期。
《晋书·后妃传序》：“爰自夐古，是谓元妃；降及中年，乃称王后。”《北齐书·魏兰根传》：“缘边诸镇，控摄长远，昔时初置，地广人稀……中年以来，有司乖实，号曰府户，役同厮养。”清龚景潮《平凉新乐府》：“平凉民，耕何田，赋籍沿自明中年。”

人到中年万事休_中年 -其它相关

鲁迅46岁
养生用语
汉·王充《论衡·论死》：“若中年夭亡，以亿万数。”中年是社会的顶梁柱，上有老下有小，心理压力极大，是亟需社会各界关心的1个群体。
1980年作家谌容创作的小说《人到中年》和1983年出品的电影《人到中年》是描写关注中年群体的优秀文艺作品，引起极大反响。该片荣获1983年电影金鸡奖和百花奖。 本文标题：其它相关-布施：布施-职业生涯，布施-其它相关
本文地址： http://www.61k.com/1111408.html