一 : 三角形内角和教案
《三角形的内角和》教案
西藏山南扎囊县吉汝乡第一小学一小:达瓦
教学内容:
人教版小学数学四年级下册《三角形内角和》
教学目标:
1、知识目标:知道三角形内角和是180度 。(www.61k.com]
2、能力目标:(1)、通过学生猜、测、拼、折、观察等活动,培养学生的探索、发现能力、观察和动手操作能力。(2)、能运用三角形内角和这一规律解决实际问题。
3、情感目标:(1)、让学生在探索活动中产生对数学的好奇心,发展学生的空间观念;(2)、体验探索的乐趣和成功的快乐,增强学好数学的信心。
教学重点:引导学生发现三角形内角和是180°
教学难点:用不同方法验证三角形的内角和是180°
教具学具准备:课件、学生准备不同类型的三角形各一个,长方形。剪刀、量角器。
教学过程:
创设情景,引出问题
1、引出课题
(课件出示)看来三角形的角之间一定存在有一些奥秘在里面,这节课我们就来研究有关三角形角的知识“三角形内角和”。
三角形的内角、内角和
1
三角形内角和教学设计 三角形内角和教案
(1)三角形内角(课件)
三角形里面的三个角都是三角形的内角。(www.61k.com]
(2)三角形内角和
师:内角和指的是什么?
生:三角形的三个角的度数的和,就是三角形的内角和。
(多让几个学生说一说)
猜一猜
师:这个三角形的内角和是多少度?
生:180°
师:是不是所有的三角形的内角和都是180°呢?你能肯定吗? 生:是。 生:不是
预设1师:有的同学确定了,有的同学没有把握。大家意见不统一,我们得想个办法验证三角形的内角和是多少?可以用什么方法验证呢? 预设2师:可以用什么方法验证三角形的内角和是180度。 生:量一量。(量角器)
师:用量角器度量,你能说的更明白一些吗?
量一量
(1)量一量、算一算
量一量、算一算不同类型三角形内角和各是多少度?
(2)小组合作探究
(大部分的同学已经量好了。没有量好的小组,先停下来。让我们一起来分享其他同学的测量成果。请你给大家介绍你们组测量的三角形的形 2
三角形内角和教学设计 三角形内角和教案
状,每个角的度数和内角和是多少?)学生汇报的时候教师板书。[www.61k.com]
(3)汇报交流
学生的汇报中可能会出现答案不是惟一的情况。如180°179°181°等 师:观察这些测量结果你能发现什么?
生:都在180°左右。
师:为什么会出现这种情况?
剪拼、折拼
剪拼、撕拼
预设1师:用度量的方法验证,得到的结果不统一,有没有比度量更精确的验证方法?(让学生多思考),也就是不用度量你能用别的方法验证吗?
预设2师:不着急,看黑板(板书),内角和就是(~~)
生:就是把内角合并在一起。
度量的验证方法是分别量出每个角的度数,分成单个研究。
如果把三个角合在一起考虑呢?你还有什么验证方法?
求三角形内角和就是把三角形的三个角和起来考虑问题,三个角和起来是什么角?三个角和起来是多少度的角,你有办法吗?
预设3师:如果三角形的内角和是180度,180度的角就是我们以前学过的平角
把三角形的三个角拼起来是不是一个平角?
有什么方法能把三角形的三个内角合并在一起?
预设4师:我在电脑里收索一个验证方法。(课件演示)
3
三角形内角和教学设计 三角形内角和教案
生:把三角形的三个角剪下来,再拼成一个角。(www.61k.com)
师:你能说的更明白一些吗?
师:你们觉得他得方法可行吗?
全班小组操作
大部分小组已经拼好了,还没拼好的小组先停一停。我们一起来分享其他小组的验证结果。
汇报交流
预设1师:(把学生的作品展示)把三个角拼在一起你们有什么发现? (你能看出这是用什么三角形拼成的?为什么?三个角拼在一起你有什么发现?)
预设2让学生上来介绍
师:你怎么做?发现了什么?让学生展示不同类型的三角形拼成一个平角。说明三角形的内角和是180°(板书:剪拼 一个平角) 师:这种验证方法是谁第一个发现的,我们用掌声来祝贺他。 师课件演示拼的过程。
折拼
师:用剪拼的方法是比较精确,美中不足就是把三角形给剪了或是撕了,有没有更好验证方法?
预设1生:用折的方法
师:老师也收集了一种方法请看演示
师:要把三角形的三个角折成一个平角靠我们现在的经验是有点难。看电脑是怎样折的。(课件演示)
4
三角形内角和教学设计 三角形内角和教案
师:先要找到两条边的中点,用线连接起来,再按这条线折起来。[www.61k.com]再把另外的两个角折起来就可以了。
预设2学生不会想到用折的方法。
师:我在电脑里收索到折的方法,请同学们看一看他是怎么折的(课件演示)
计算,推理(看学生基础选用)
将一个长方形按对角线剪成两个完全一样的直角三角形。因为长方形的四个角都是直角,长方形的内角和是360°,所以剪成后的直角三角形的内角和是180°
师:你发现了什么?
生:直角三角形的内角和是180°

师:你能说得更明白一些吗?

师:你能算出这个直角三角形的内角和吗?
生:90°乘4等于360°,在把360°除以2就等于180°(板书) 师:我们给这种验证方法取个名字?(推算)
师:这个直角三角形可以用推算的方法验证,是不是所有的直角三角形都可以用这种方法推算呢?
师:推算的验证方法是谁先发现的,我们也对他表示祝贺。
6、通过这么多的方法我们验证了三角形的内角和是180度,(板书:是180度)现在让我们用肯定的口气读一遍“三角形的内角和是180度”
7、现在让我们看看教材上是如何说的。
8、解疑
5
三角形内角和教学设计 三角形内角和教案
为什么在一个三角形中不可有两个角是直角或两个角是钝角?
9、一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度?
三、应用三角形的内角和解决问题
我们就用这个结论来解决问题
1. (1) 看图求出未知角的度数。(www.61k.com](课件出示)

180°-55°-65° 180°-(55°+65°)
=125°-65° =180°-120°
=60° =60°
刚才是已知两个内角的度数,求另一个内角的度数。如果只告诉你一个内角的度数,你会求出另外两个内角的度数吗?如果一个内角的度数也不告诉你,你能知道三个内角的度数吗?
(2)三角形中,∠1=750,∠2=390,∠3=( )0
2、请说出下列每个三角形每个角的度数。(课件出示)

180°÷3=60° 180°-96°=84° 180°-90°-40=50° 84°÷2=42° 90°-40°=50° 6
三角形内角和教学设计 三角形内角和教案
3、发现性作业:
(1)数学趣事
今天一大早,数学王国的两个三角形就在那儿争吵不休。[www.61k.com]一个大三角形说“我的内角和大”,另一个小的三角形说“我的内角和才大呢!”同学们,你们说一说到底谁的内角和大呢?
(2)市政问题:
问题:由于市政需要,需要测量电视塔各角的度数,由于电视塔很高很高,只能测量两个底角的度数,要想知道顶角的度数,应该没么办呢?
(3)走向生活:
“啪——”地一声响起,学校花架上的一块三角形玻璃被突然飞来的小球击碎了(见下图),一下子围上了许多同学。小勇看着地上的碎玻璃着急地说:“是我不小心打碎的,我想赶紧去配一块,可是,玻璃已被打碎,尺寸大小都不知道,该怎么办,真急人!”同学小聪的眼睛盯上了其中的一块碎玻璃,高兴地说:我有办法了,只要拿一块碎玻璃,就可以去配上与原先完全相同的玻璃。同学们,你认为应该拿哪一块呢? 四:全课小结
师:这节课你有什么收获?我们是怎样研究三角形的内角和是180°? 师:这节课通过我们班同学共同合作,我们用了几种验证方法。 师:撕拼和折拼方法有什么相同点?(注意说话有说服力)
生:都是把三角形的三个角拼成一个平角。
板书
7
三角形内角和教学设计 三角形内角和教案
三角形内角和 180°
猜想 实验


验证
度量 180° 179° 181° 182° 183° 剪拼 一个平角
折拼 8
二 : 三角形内角和教学反思_吕正云
<<三角形内角和>>教学反思
实验小学吕正云
学生在学习了三角形的特征以及三角形分类的基础上,进1步研究三角形3个角的关系。根据教学目标和学生掌握知识的情况,课堂上我围绕以下几点去完成教学目标:
一、创设情境,营造研究氛围
怎样提供1个良好的研究平台,使学生有兴趣去研究三角形内角的和呢?为此我抛出大、小2个三角形争吵的情境,让学生评判谁说的对?为什么争吵?导入课引出研究问题。“三角形的内角指的是什么?”“三角形的内角和是多少?”激发学生求知的欲望,引起探究活动。我在研究三角形内角和时,没有按教材设计的量角求和环节进行,而是从学生熟悉的正方形纸的内角和是360°入手,再把正方形纸沿着对角线剪开后会怎样呢?猜想一下其中的一个三角形的内角和是几度?学生很快得出1个直角三角形内角和是180°。猜测以下是不是各种形状、大小不同的三角形内角和都是180°呢?再组织学生去探究,动手验证,并得出结论。生在不断的发现中很自然地得到“三角形内角和是180°”的猜想。这样既使学生在这个探究过程中得到快乐的情感体验,又使学生有高度的热情去继续深入地研究“是否任何三角形内角和都是180°”。
二、小组合作,自主探究
任何一项科学研究活动或发明创造都要经历从猜想到验证的过程。“是否任何三角形内角和都是180°”,这个猜想如何验证,这正是小组合作的契机。通过小组内交流,使学生认识到可以通过多种途径来验证,可以量一量、拼一拼、折一折,让学生在小组内完成从特殊到一般的研究过程。然后再小组汇报研究结果以及存在问题。教师根据学生实际情况充分把握好生成性资源,让学生认识到有些客观原因会影响到研究的结果的准确性。例如,有些小组的学生量出内角和的度数要高于180°或低于180°,先让学生讨论一下有哪些因素会影响到研究结果的准确性。
三、练习设计,由易到难
研究是为了应用,在应用“三角形内角和是180°”这一结论时,第一层练习是已知三角形中2个内角的度数,求另1个角。第二层练习是已(www.61k.com)知等腰三角形中顶角或底角的度数,让学生应用结论求另外的内角度数。第三层练习是让学生用学过的知识解决四边形、五边形、六边形的内角和。练习设计提问体现开放性,“你还知道了什么”,让学生根据计算结果运用已有经验去判断思索。
四、教学中存在不足
在教学中,由于我对学生了解的不够充分,让学生自己想其它的验证方法,难度较大,浪费了大量时间,使教学任务不能完成,练习较少,新知没有得到充分巩固,以后应引起重视。在设计教案时要了解学生,深入教材,精心设计。
三 : 《三角形的内角和》教学反思

《三角形的内角和》教学反思
《三角形的内角和》是人教版数学四年级下册第五单元的一节课,是在学生学习了三角形的特征以及三角形分类的基础上,进1步研究三角形3个角的关系。课堂上我注意留给学生充分进行自主探究和交流的空间,让学生探索、实验、发现、讨论交流、推理归纳出三角形的内角和是180°。
一、创设情境,营造探究氛围。
怎样提供1个良好的探究平台,使学生有兴趣去研究三角形内角的和呢?这节课在复习旧知“三角形的特征”后,我引出了研究问题“三角形的内角指的是什么?”“三角形的内角和是多少?”。而画1个有2个内角是直角的三角形却无法画出这一问题的出现,使学生萌生了想了解其中奥秘的想法,激发了学生探究新知的欲望。由于学生对三角尺上每个角的度数比较熟悉,新知的探究就从这里入手。我先让学生分别算出每块三角尺3个内角的和都是180°,由此引发学生的猜想:其它三角形的内角和也是180°吗?
二、小组合作,自主探究。
“是否任何三角形的内角和都是180°呢?”,我趁势引导学生小组合作,动手验证。通过小组内交流,使学生认识到可以通过多种途径来验证,可以量一量、撕一撕、拼一拼、折一折、算一算。在明确验证方法后,学生在小组内通过动手操作、记录、观察,验证三角形的内角和是否为180°。之后我组织学生在全班汇报交流,有的小组通过量一量、算一算的方法,得出三角形的内角和是180°或接近180°(测量误差);有的小组通过撕一撕、拼一拼的方法发现:各类三角形的3个内角可以拼成1个平角。还有的小组通过折一折、拼一拼的方法也发现:各类三角形的3个内角都可以拼成1个平角。此时我利用课件进行动态演示,在演示中进1步验证,使学生在小组合作、自主探究、全班交流中获得了三角形的内角和的确是180°的结论。这一系列活动潜移默化地向学生渗透了“转化”的数学思想,为后继学习奠定了必要的基础。
三、练习设计,由易到难。
探究新知是为(www.61k.com)了应用,这节课在练习的安排上,我注意把握练习层次,共安排3个层次,由易到难,逐步加深。在应用“三角形的内角和是180°”这一结论时,第一层练习是已知三角形2个内角或1个内角的度数,求另1个角。练习内容的安排从知识的直接应用到间接应用,数学信息的出现从比较显现到较为隐藏。第二层练习是判断题,让学生应用结论思考分析,检验语言的严密性。第三层练习是让学生用学过的知识解决四边形、六边形的内角和,使学生的思维得到拓展。这些练习顾及到了智力水平不同的学生,形式上具有趣味性,激发了学生主动解题的积极性。
本着“学贵在思,思源于疑”的思想,这节课我不断创设问题情境,让学生去猜想、去探究、去发现新知识的奥妙,从而让学生在动手操作、积极探索的活动中掌握知识,积累数学活动经验,发展空间观念。
四 : 三角形的内角和教学反思
三角形的内角和是180°是三角形的一个重要性质。它有助于学生理解三角形的三个内角之间的关系,也是进一步学习的基础。
成功之处:
1.教学中注意了两点:一是让学生理解“内角”“内角和”的含义;二是让学生为了使所得的结论具有普遍性,对锐角三角形、直角三角形、钝角三角形进行操作实验。
2.教学中采用让学生课前剪出锐角三角形、直角三角形、钝角三角形,然后量出每个角的度数,初步感知三角形的内角和的特征。课上让学生汇报三角形的内角和的度数有180°、178°182°等。由于学生在量、画三角形的过程中出现误差,导致出现三角形的内角和是180°左右,在此情形下,让学生通过小组合作交流,探索验证三角形内角和的特征。通过学生间的合作交流、智慧碰撞、思维火花闪现,出现了剪一剪、折一折两种验(www.61k.com]证方法,从而得出三角形的内角和是180°这一三角形重要性质。
3.在解决问题中,明确应用三角形内角和是180°,可以解决在一个三角形中,已知两个角的度数,可以求第三个角的度数。
不足之处:
在对于直角三角形中,可以引导学生采用简便方法求出其中一个角的度数,对于直角三角形的特点加以分析。
再教设计:
重视对直角三角形、等腰三角形中,求其中一个角度数的方法的对比练习,让学生比较清晰的解决特殊三角形的一个角的度数。
五 : 三角形内角和教案
《三角形的内角和》教案
西藏山南扎囊县吉汝乡第一小学一小:达瓦
教学内容:
人教版小学数学四年级下册《三角形内角和》
教学目标:
1、知识目标:知道三角形内角和是180度 。
2、能力目标:(1)、通过学生猜、测、拼、折、观察等活动,培养学生的探索、发现能力、观察和动手操作能力。(2)、能运用三角形内角和这一规律解决实际问题。
3、情感目标:(1)、让学生在探索活动中产生对数学的好奇心,发展学生的空间观念;(2)、体验探索的乐趣和成功的快乐,增强学好数学的信心。
教学重点:引导学生发现三角形内角和是180°
教学难点:用不同方法验证三角形的内角和是180°
教具学具准备:课件、学生准备不同类型的三角形各一个,长方形。剪刀、量角器。
教学过程:
创设情景,引出问题
1、引出课题
(课件出示)看来三角形的角之间一定存在有一些奥秘在里面,这节课我们就来研究有关三角形角的知识“三角形内角和”。
三角形的内角、内角和
1
(1)三角形内角(课件)
三角形里面的三个角都是三角形的内角。
(2)三角形内角和
师:内角和指的是什么?
生:三角形的三个角的度数的和,就是三角形的内角和。
(多让几个学生说一说)
猜一猜
师:这个三角形的内角和是多少度?
生:180°
师:是不是所有的三角形的内角和都是180°呢?你能肯定吗? 生:是。 生:不是
预设1师:有的同学确定了,有的同学没有把握。大家意见不统一,我们得想个办法验证三角形的内角和是多少?可以用什么方法验证呢? 预设2师:可以用什么方法验证三角形的内角和是180度。 生:量一量。(量角器)
师:用量角器度量,你能说的更明白一些吗?
量一量
(1)量一量、算一算
量一量、算一算不同类型三角形内角和各是多少度?
(2)小组合作探究
(大部分的同学已经量好了。没有量好的小组,先停下来。让我们一起来分享其他同学的测量成果。请你给大家介绍你们组测量的三角形的形 2
状,每个角的度数和内角和是多少?)学生汇报的时候教师板书。
(3)汇报交流
学生的汇报中可能会出现答案不是惟一的情况。如180°179°181°等 师:观察这些测量结果你能发现什么?
生:都在180°左右。
师:为什么会出现这种情况?
剪拼、折拼
剪拼、撕拼
预设1师:用度量的方法验证,得到的结果不统一,有没有比度量更精确的验证方法?(让学生多思考),也就是不用度量你能用别的方法验证吗?
预设2师:不着急,看黑板(板书),内角和就是(~~)
生:就是把内角合并在一起。
度量的验证方法是分别量出每个角的度数,分成单个研究。
如果把三个角合在一起考虑呢?你还有什么验证方法?
求三角形内角和就是把三角形的三个角和起来考虑问题,三个角和起来是什么角?三个角和起来是多少度的角,你有办法吗?
预设3师:如果三角形的内角和是180度,180度的角就是我们以前学过的平角
把三角形的三个角拼起来是不是一个平角?
有什么方法能把三角形的三个内角合并在一起?
预设4师:我在电脑里收索一个验证方法。(课件演示)
3
生:把三角形的三个角剪下来,再拼成一个角。
师:你能说的更明白一些吗?
师:你们觉得他得方法可行吗?
全班小组操作
大部分小组已经拼好了,还没拼好的小组先停一停。我们一起来分享其他小组的验证结果。
汇报交流
预设1师:(把学生的作品展示)把三个角拼在一起你们有什么发现? (你能看出这是用什么三角形拼成的?为什么?三个角拼在一起你有什么发现?)
预设2让学生上来介绍
师:你怎么做?发现了什么?让学生展示不同类型的三角形拼成一个平角。说明三角形的内角和是180°(板书:剪拼 一个平角) 师:这种验证方法是谁第一个发现的,我们用掌声来祝贺他。 师课件演示拼的过程。
折拼
师:用剪拼的方法是比较精确,美中不足就是把三角形给剪了或是撕了,有没有更好验证方法?
预设1生:用折的方法
师:老师也收集了一种方法请看演示
师:要把三角形的三个角折成一个平角靠我们现在的经验是有点难。看电脑是怎样折的。(课件演示)
4
师:先要找到两条边的中点,用线连接起来,再按这条线折起来。再把另外的两个角折起来就可以了。
预设2学生不会想到用折的方法。
师:我在电脑里收索到折的方法,请同学们看一看他是怎么折的(课件演示)
计算,推理(看学生基础选用)
将一个长方形按对角线剪成两个完全一样的直角三角形。因为长方形的四个角都是直角,长方形的内角和是360°,所以剪成后的直角三角形的内角和是180°
师:你发现了什么?
生:直角三角形的内角和是180°
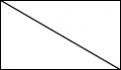
师:你能说得更明白一些吗?
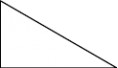
师:你能算出这个直角三角形的内角和吗?
生:90°乘4等于360°,在把360°除以2就等于180°(板书) 师:我们给这种验证方法取个名字?(推算)
师:这个直角三角形可以用推算的方法验证,是不是所有的直角三角形都可以用这种方法推算呢?
师:推算的验证方法是谁先发现的,我们也对他表示祝贺。
6、通过这么多的方法我们验证了三角形的内角和是180度,(板书:是180度)现在让我们用肯定的口气读一遍“三角形的内角和是180度”
7、现在让我们看看教材上是如何说的。
8、解疑
5
为什么在一个三角形中不可有两个角是直角或两个角是钝角?
9、一块三角尺的内角和是180度,用两块完全一样的三角尺拼成一个三角形,这个三角形的内角和是360度?
三、应用三角形的内角和解决问题
我们就用这个结论来解决问题
1. (1) 看图求出未知角的度数。(课件出示)
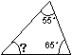
180°-55°-65° 180°-(55°+65°)
=125°-65° =180°-120°
=60° =60°
刚才是已知两个内角的度数,求另一个内角的度数。如果只告诉你一个内角的度数,你会求出另外两个内角的度数吗?如果一个内角的度数也不告诉你,你能知道三个内角的度数吗?
(2)三角形中,∠1=750,∠2=390,∠3=( )0
2、请说出下列每个三角形每个角的度数。(课件出示)

180°÷3=60° 180°-96°=84° 180°-90°-40=50° 84°÷2=42° 90°-40°=50° 6
3、发现性作业:
(1)数学趣事
今天一大早,数学王国的两个三角形就在那儿争吵不休。一个大三角形说“我的内角和大”,另一个小的三角形说“我的内角和才大呢!”同学们,你们说一说到底谁的内角和大呢?
(2)市政问题:
问题:由于市政需要,需要测量电视塔各角的度数,由于电视塔很高很高,只能测量两个底角的度数,要想知道顶角的度数,应该没么办呢?
(3)走向生活:
“啪——”地一声响起,学校花架上的一块三角形玻璃被突然飞来的小球击碎了(见下图),一下子围上了许多同学。小勇看着地上的碎玻璃着急地说:“是我不小心打碎的,我想赶紧去配一块,可是,玻璃已被打碎,尺寸大小都不知道,该怎么办,真急人!”同学小聪的眼睛盯上了其中的一块碎玻璃,高兴地说:我有办法了,只要拿一块碎玻璃,就可以去配上与原先完全相同的玻璃。同学们,你认为应该拿哪一块呢? 四:全课小结
师:这节课你有什么收获?我们是怎样研究三角形的内角和是180°? 师:这节课通过我们班同学共同合作,我们用了几种验证方法。 师:撕拼和折拼方法有什么相同点?(注意说话有说服力)
生:都是把三角形的三个角拼成一个平角。
板书
7
三角形内角和 180°
猜想 实验


验证
度量 180° 179° 181° 182° 183° 剪拼 一个平角
折拼 8
本文标题:三角形内角和教学反思-三角形内角和教案61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1