一 : 完全平方数举例说明

完全平方数举例说明

完全平方数举例说明的参考答案

（一）完全平方数的性质

一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数,也叫做平方数.例如：

0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,…

观察这些完全平方数,可以获得对它们的个位数、十位数、数字和等的规律性的认识.下面我们来研究完全平方数的一些常用性质：

性质1：完全平方数的末位数只能是0,1,4,5,6,9.

性质2：奇数的平方的个位数字为奇数,十位数字为偶数.

证明 奇数必为下列五种形式之一：

10a+1, 10a+3, 10a+5, 10a+7, 10a+9

分别平方后,得

(10a+1)=100+20a+1=20a(5a+1)+1

(10a+3)=100+60a+9=20a(5a+3)+9

(10a+5)=100+100a+25=20 (5a+5a+1)+5

(10a+7)=100+140a+49=20 (5a+7a+2)+9

(10a+9)=100+180a+81=20 (5a+9a+4)+1

综上各种情形可知：奇数的平方,个位数字为奇数1,5,9；十位数字为偶数.

性质3：如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.

证明 已知=10k+6,证明k为奇数.因为的个位数为6,所以m的个位数为4或6,于是可设m=10n+4或10n+6.则

10k+6=(10n+4)=100+(8n+1)x10+6

或 10k+6=(10n+6)=100+(12n+3)x10+6

即 k=10+8n+1=2(5+4n)+1

或 k=10+12n+3=2(5+6n)+3

∴ k为奇数.

推论1：如果一个数的十位数字是奇数,而个位数字不是6,那么这个数一定不是完全平方数.

推论2：如果一个完全平方数的个位数字不是6,则它的十位数字是偶数.

性质4：偶数的平方是4的倍数；奇数的平方是4的倍数加1.

这是因为 (2k+1)=4k(k+1)+1

(2k)=4

性质5：奇数的平方是8n+1型；偶数的平方为8n或8n+4型.

在性质4的证明中,由k(k+1)一定为偶数可得到(2k+1)是8n+1型的数；由为奇数或偶数可得(2k)为8n型或8n+4型的数.

性质6：平方数的形式必为下列两种之一：3k,3k+1.

因为自然数被3除按余数的不同可以分为三类：3m,3m+1, 3m+2.平方后,分别得

(3m)=9=3k

(3m+1)=9+6m+1=3k+1

(3m+2)=9+12m+4=3k+1

同理可以得到：

性质7：不能被5整除的数的平方为5k±1型,能被5整除的数的平方为5k型.

性质8：平方数的形式具有下列形式之一：16m,16m+1, 16m+4,16m+9.

除了上面关于个位数,十位数和余数的性质之外,还可研究完全平方数各位数字之和.例如,256它的各位数字相加为2+5+6=13,13叫做256的各位数字和.如果再把13的各位数字相加：1+3=4,4也可以叫做256的各位数字的和.下面我们提到的一个数的各位数字之和是指把它的各位数字相加,如果得到的数字之和不是一位数,就把所得的数字再相加,直到成为一位数为止.我们可以得到下面的命题：

一个数的数字和等于这个数被9。嫑_犇。除的余数.

下面以四位数为例来说明这个命题.

设四位数为,则

= 1000a+100b+10c+d

= 999a+99b+9c+(a+b+c+d)

= 9(111a+11b+c)+(a+b+c+d)

显然,a+b+c+d是四位数被9除的余数.

对於n位数,也可以仿此法予以证明.

关於完全平方数的数字和有下面的性质：

性质9：完全平方数的数字之和只能是0,1,4,7,9.

证明 因为一个整数被9除只能是9k,9k±1, 9k±2, 9k±3, 9k±4这几种形式,而

(9k)=9(9)+0

(9k±1)=9(9±2k)+1

(9k±2)=9(9±4k)+4

(9k±3)=9(9±6k)+9

(9k±4)=9(9±8k+1)+7

除了以上几条性质以外,还有下列重要性质：

性质10：为完全平方数的充要条件是b为完全平方数.

证明 充分性：设b为平方数,则

==(ac)

必要性：若为完全平方数,=,则

性质11：如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.

证明 由题设可知,a有质因数p,但无因数,可知a分解成标准式时,p的次方为1,而完全平方数分解成标准式时,各质因数的次方均为偶数,可见a不是完全平方数.

性质12：在两个相邻的整数的平方数之间的所有整数都不是完全平方数,即若

n^2

则k一定不是完全平方数.

性质13：一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n本身).

(二)重要结论

1.个位数是2,3,7,8的整数一定不是完全平方数；

2.个位数和十位数都是奇数的整数一定不是完全平方数；

3.个位数是6,十位数是偶数的整数一定不是完全平方数；

4.形如3n+2型的整数一定不是完全平方数；

5.形如4n+2和4n+3型的整数一定不是完全平方数；

6.形如5n±2型的整数一定不是完全平方数；

7.形如8n+2, 8n+3, 8n+5, 8n+6,8n+7型的整数一定不是完全平方数；

8.数字和是2,3,5,6,8的整数一定不是完全平方数.

二 : 高等数学：判断极限不存在的方法高数请举例说明，非常感谢！

高等数学：判断极限不存在的方法

高数请举例说明，非常感谢！

---

判断当x→x0时的极限，只要考察左、右极限，如果两者相等，则极限存在，否则极限不存在。

例如f(x)=arctan(1/x)，在x=0处的左极限为-π/2，右极限为π/2，两者不相等，所以当x→0时，arctan(1/x)的极限不存在。

判断当x→∞时的极限，只要考察x→-∞与x→+∞时的极限，如果两者相等，则极限存在，否则极限不存在。

例如f(x)=e^x，当x→-∞时的极限为0，当x→+∞时的极限为+∞，两者不相等，所以当x→∞时，e^x的极限不存在。

三 : 16进制：16进制-表示方法，16进制-举例说明

16进制：数学、计算机算法名词术语。十六进制(简写为hex或下标16)在数学中是一种逢16进1的进位制，一般用数字0到9和字母A到F表示(其中:A~F即10~15)。例如十进制数79，在二进制写作01001111，在16进制写作4F(4=0100，F=1111)。在历史上，中国曾经在重量单位上使用过16进制，比如，规定16两为一斤。现在的16进制则普遍应用在计算机领域，这是因为将4个位元(Bit)化成单独的16进制数字不太困难。1字节可以表示成2个连续的16进制数字。可是，这种混合表示法容易令人混淆,因此需要一些字首、字尾或下标来显示。

16进制_16进制 -表示方法

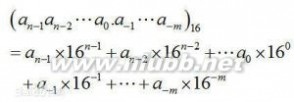
16进制十六进制照样采用位置计数法，位权是16为底的幂。对于n位整数，m位小数的十六进制数用加权系数的形式表示。

16进制_16进制 -举例说明

6进制的20表示成10进制就是：2×161+0×16o=32
10进制的32表示成16进制就是：20
十进制数可以转换成十六进制数的方法是：十进制数的整数部分“除以16取余”，十进制数的小数部分“乘16取整”，进行转换。
比如说十进制的0.1转换成八进制为0.0631463146314631。就是0.1乘以8=0.8，不足1不取整，0.8乘以8=6.4，取整数6，0.4乘以8=3.2，取整数3，依次下算。
编程中，我们常用的还是10进制.毕竟C/C++是高级语言。
比如：
inta=100,b=99;
不过，由于数据在计算机中的表示，最终以二进制的形式存在，所以有的时候使用二进制，可以更直观地解决问题。
C，C++没有提供在代码直接写二进制数的方法。用16进制或8进制可以解决这个问题。因为，进制越大，数的表达长度也就越短。2、8、16，分别是2的1次方、3次方、4次方。这一点使得3种进制之间可以非常直接地互相转换。8进制或16进制缩短了二进制数，但保持了二进制数的表达特点。

16进制_16进制 -转换

二进制转换十进制

二进制数第0位的权值是2的0次方，第1位的权值是2的1次方
所以，设有1个二进制数：101100100，转换为10进制为：356
用横式计算
0×20+0×21+1×22+0×23+0×24+1×25+1×26+0×27+1×28=356
0乘以多少都是0，所以我们也可以直接跳过值为0的位：
1×22+1×25+1×26+1×28=356
4+32+64+256=356

八进制转换十进制

八进制就是逢8进1。
八进制数采0～7这八数来表达1个数。
八进制数第0位的权值为8的0次方，第1位权值为8的1次方，第2位权值为8的2次方
所以，设有1个八进制数：1507，转换为十进制为：839，具体方法如下：
可以用横式直接计算：
7×80+0×81+5×82+1×83=839
也可以用竖式表示
第0位7×80=7
第1位0×81=0
第2位5×82=320
第3位1×83=512

十六进制转换十进制

16进制就是逢16进1，但我们只有0~9这10个数字，所以我们用A，B，C，D，E，F这6个字母来分别表示10，11，12，13，14，15。字母不区分大小写。
十六进制数的第0位的权值为16的0次方，第1位的权值为16的1次方，第2位的权值为16的2次方
所以，在第N（N从0开始）位上，如果是数β（β大于等于0，并且β小于等于15，即：F）表示的大小为β×16的N次方。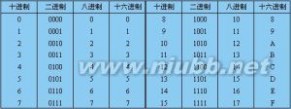

16进制_16进制 -表达方法

16进制程序的表达方法环境格式备注URL%hex无XML,XHTML&#xhex无HTML,CSS#hex6位，表示颜色UnicodeU+hex6位,表示字符编码MIME=hex无Modula-2#hex无Smalltalk,ALGOL6816rhex无CommonLisp#xhex或#16rhex无IPv6八个hex用:分隔无
CC++的表达方法
如果不使用特殊的书写形式，16进制数也会和10进制相混。随便1个数：9876，就看不出它是16进制或10进制。
C，C++规定，16进制数必须以0x开头。比如0x1表示1个16进制数。而1则表示1个十进制。另外如：0xff,0xFF,0X102A，等等。其中的x也不区分大小写。（注意：0x中的0是数字0，而不是字母O)
以下是一些用法示例：
inta=0x100F;
intb=0x70+a;
至此，我们学完了所有进制：10进制，8进制，16进制数的表达方式。最后一点很重要，C/C++中，10进制数有正负之分，比如12表示正12，而-12表示负12，；但8进制和16进制只能表达无符号的正整数，如果你在代码中写：-078，或者写：-0xF2,C,C++并不把它当成1个负数。
在转义符中的使用
转义符也可以接1个16进制数来表示1个字符。如\'?\'字符，可以有以下表达方式：
\'?\'//直接输入字符
\'\77\'//用八进制，此时可以省略开头的0
\'\0x3F\'//用十六进制
同样，这一小节只用于了解。除了空字符用八进制数\'\0\'表示以外，我们很少用后2种方法表示1个字符。

16进制_16进制 -标准表示

十六进制在数制使用时，常将各种数制用简码来表示：如十进制数用D表示或省略；二进制用B来表示；十六进制数用H来表示。
如：十制数123表示为：123D或者123；二进制数1011表示为：1011B；十六进制数3A4表示为：3A4H。
另外在编程中十六进制数也用“0x”作为开头。

16进制_16进制 -意义

用于计算机领域的1种重要的数制。
对计算机理论的描述，计算机硬件电路的设计都是很有益的。比如逻辑电路设计中，既要考虑功能的完备，还要考虑用尽可能少的硬件，十六进制就能起到一些理论分析的作用。比如四位二进制电路，最多就是16种状态，也就是1种十六进制形式，只有这16种状态都被用上了或者尽可能多的被用上，硬件资源才发挥了尽可能大的作用。
十六进制更简短，因为换算的时候一位16进制数可以顶4位2进制数。
你可以在二进制前加几个0，意义不变。

二进制八进制十进制十六进制010101011022211333100444101555110666111777100010881001119910101210A10111311B11001412C11011513D11101614E11111715F100002016101000121171110010221812100112319131010024201410101252115101102622161011127231711000302418110013125191101032261A1101133271B1110034281C1110135291D1111036301E1111137311F10000040322010000141332110001042342210001143352310010044362410010145372510011046382610011147392710100050402810100151412910101052422A10101153432B10110054442C10110155452D10111056462E10111157472F11000060483011000161493111001062503211001163513311010064523411010165533511011066543611011167553711100070563811100171573911101072583A11101173593B11110074603C11110175613D11111076623E11111177633F100000010064401000001101654110000101026642100001110367431000100104684410001011056945100011010670461000111107714710010001107248100100111173491001010112744A1001011113754B1001100114764C1001101115774D1001110116784E1001111117794F101000012080501010001121815110100101228252101001112383531010100124845410101011258555101011012686561010111127875710110001308858101100113189591011010132905A1011011133915B1011100134925C1011101135935D1011110136945E1011111137955F11000001409660110000114197611100010142986211000111439963110010014410064

四 : 蒙太奇手法：蒙太奇手法-蒙太奇手法，蒙太奇手法-举例说明

五 : 说明的方法－举例法

举例法是运用典型事例说明事物特征的一种方法。它能够将一些复杂的事物或事理说得更具 体明白，易于为人理解。例如：?

《书籍的未来?》

从甲骨金石到蔡伦造纸，从石碑墨拓到毕升发明的活字印刷术，书本几番换装，终 于形成了今天这样的面貌：白纸黑字，1000多年过去了，其貌依然。现在，变革已经开始， 迅猛发展的新技术正创造着书的新形象。?70年代末激光录像盘面世。它的外形和一张普通唱片差不多。别看其貌不扬，本事可不小— —能够记录10?8万张图象。如果一本书有300页，那它就能贮存120本这样的书。后来进一 步采用数字化技术，每张录像盘竟能记录3200本书的内容。这种惊人的贮存信息的本领，令 普通的书本望尘莫及，在古代更是梦想。值得一提的是，录像盘带有双声道录音，可以提供 不同的信息，满足不同水平读者的要求，例如讲解一次外科手术过程，医生与护士，各听不 同声道，各取所需而互不干扰。?

电子计算机和电子技术的结合更是别开生面。我们把家里的电脑通过出版公司的发行通讯网 络和作者的电脑联结起来，就可随时读到作者刚刚写完的章节。如果用通讯卫星把各国的出 版发行网络接通，那么坐在家中就能博览世界图书，大开眼界了。?

新技术不仅使信息的传播速度更快，面更广，而且有利于信息的收集。你需要某一专题的资 料 ，启动电脑，所需的信息一览无遗展现在荧光屏上。这样，我们就不必逐本逐本地翻书，一 个个图书馆地跑了。?将来还会出现一种内容灵活可变的书。人们常常对某篇小说的结局持不同意见，争论不休。 未来的书的内容和形式将依各人心愿，提供多种选择。现在已有初步尝试：一部名为《你的 化名是乔纳》的侦探小说，编排了41种结局，读者就是小说里的侦探，情节发展到关键时 刻，就要读者自行设置条件并将其输入电脑，由于所设条件不同，结局当然也就不同。?

传统的印刷术将要被先进的电子技术取代，纸书将被各式各样的“电子书”取代，这大概是 书的未来发展方向，但这决不意味着纸书会消失殆尽，或者成为案头摆设。因为纸书也有一 些“电子书”无法比拟的优点：便于携带，价钱低廉，阅读方便，既不需要辅助设备，也不 用消耗能源。另外从人的心理和美学的角度来看，荧光屏出现的字体单一，而印刷书刊的字 体则多样化，特别是汉字，楷隶行草，风韵各异，为书刊添色不少。凡此种种，足见在未来 的书刊之中，纸书还会占有一席之地。?

书，是人类文明的重要标志。它的未来，为我们展现了一个无比广阔的知识海洋，召唤着我 们扬帆远航。? 在这篇例文中，作者运用一个个生动的例子，把“未来的书”给具体化了，体现出了 作者丰富的想象力

本文标题：举例子的说明方法-完全平方数举例说明
本文地址： http://www.61k.com/1106487.html