一 : 《微积分》公式大全

《微积分》公式大全

二 : 微积分公式大全

高等数学微积分公式大全

一、基本导数公式

⑴(c)′=0 ⑵x=μx

μ

μ?1

⑶(sinx)′=cosx

⑷(cosx)′=?sinx ⑸(tanx)′=sec2x ⑹(cotx)′=?csc2x ⑺(secx)′=secx?tanx ⑻(cscx)′=?cscx?cotx ⑼e

()′=e

x

x

⑽a

()′=a

x

x

1

lna ⑾(lnx)′=

x

⑿logax

(

1

⒀(

arcsinx)′=)′=xlna

⒁(

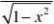
arccosx)′=⒂(arctanx)′=

1′=?1⒄ ⒃arccotx()1+x21+x2

(x)′=

1⒅

=′

二、导数的四则运算法则

?u?′u′v?uv′′′(u±v)=u′±v′ (uv)=u′v+uv′ ??=2

v?v?

三、高阶导数的运算法则 （1）??u(x)±v(x)??（3）??u(ax+b)??

(n)(n)

=u(x)

n

(n)

±v(x) （2）??cu(x)??

(n)

(n)(n)

=cu(

n

n)

(x)

(x)v(k)(x)

=au

(n)

(ax+b) （4）??u(x)?v(x)??

(n)

k(=∑cnuk=0

n?k)

四、基本初等函数的n阶导数公式 （1）xn

()

(n)

=n! （2）(eax+b)

(n)

=an?eax+b (3)(ax)

(n)

=axlnna

(4)??sin(ax+b)??

(n)π?π???n

cosax+b?=acosax+b+n?=ansin?ax+b+n?? (5) ?()?? ??2?2???

n

?1?

(6)???ax+b?

(n)

=(?1)

an?n!

(ax+b)

n+1

(7) ??ln(ax+b)??

(n)

=(?1)

n?1

an?(n?1)!

(ax+b)

n

五、微分公式与微分运算法则

⑴d(c)=0 ⑵dxμ=μxμ?1dx ⑶d(sinx)=cosxdx ⑷d(cosx)=?sinxdx ⑸d(tanx)=secxdx ⑹d(cotx)=?cscxdx

2

2

()

⑺d(secx)=secx?tanxdx ⑻d(cscx)=?cscx?cotxdx ⑼de

()=edx ⑽d(a)=a

x

x

x

x

lnadx ⑾d(lnx)=

1

dx x

积分公式大全 微积分公式大全

⑿dlogax=()1 ⒁d(

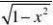
arccosx)= dx

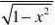
⒀d(arcsinx)=xlna11 ⒃darccotxdxdx =?()221+x1+x⒂d(arctanx)=

六、微分运算法则

⑴d(u±v)=du±dv ⑵d(cu)=cdu

⑶d(uv)=vdu+udv ⑷d?

七、基本积分公式 ?u?vdu?udv ?=2v?v?

xμ+1dx+c ⑶∫⑴∫kdx=kx+c ⑵∫xdx==lnx+c μ+1xμ

ax

+c ⑸∫exdx=ex+c ⑹∫cosxdx=sinx+c ⑷∫adx=lnax

⑺sinxdx=?cosx+c ⑻12dxsec=∫∫cos2x∫xdx=tanx+c 112⑼∫ ⑽csccot=xdx=?x+c∫1+x2dx=arctanx+c

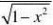
sin2x∫

⑾=arcsinx+c

八、补充积分公式

∫tanxdx=?lncosx+c ∫cotxdx=lnsinx+c ∫secxdx=lnsecx+tanx+c ∫cscxdx=lncscx?cotx+c

11xdx=arctan+c ∫a2+x2aa11x?adxln=+c ∫

x2?a22ax+a

+c

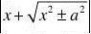
dx=ln+c

九、下列常用凑微分公式

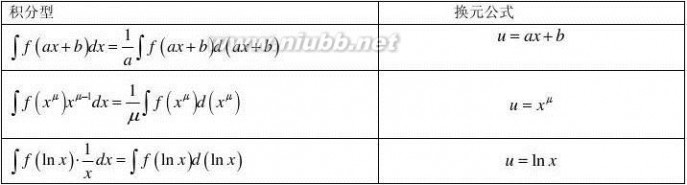
积分公式大全 微积分公式大全

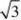
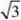
十、分部积分法公式

⑴形如xneaxdx，令u=x

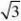
n，dv=eaxdx ∫

∫∫

∫

∫

∫形如xnsinxdx令u=xn，

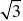
dv=sinxdx 形如xncosxdx令u=xn，dv=cosxdx ⑵形如xnarctanxdx，令u=arctanx，dv=xndx 形如xnlnxdx，令u=lnx，dv=xndx ⑶形如eaxsinxdx，eaxcosxdx令u=e,sinx,cosx均可。[www.61k.com] ∫ax

十一、第二换元积分法中的三角换元公式

x=asint x=atant x=asect

【特殊角的三角函数值】

（1）sin0=0 （2）sinπ

6=1ππ （3）sin= （4）sin=1） （5）sinπ=0 2322

π1π （3）cos= （4）cos=0） （5）cosπ=?1 2322

ππ （3）tan=（4）tan不存在 （5）tanπ=0 332（1）cos0=1 （2）cosπ6=（1）tan0=0 （2）tanπ

6=

积分公式大全 微积分公式大全

（1）cot

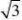
0不存在 （2）cot

十二、重要公式 π6=（3

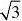
）cotπ3=π（4）cot=0（5）cotπ不存在 32

1sinx（1）lim=1 （2）lim(1+x)x=e （3

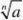
）a>o)=1 x→0nx→0x

（4

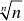
）lim=1 （5）limarctanx=nx→∞π2 （6）limarctanx=?x→?∞π2

（7）limarccotx=0 （8）limarccotx=π （9）lime=0 x→∞x→?∞xx→?∞

x=1 （10）lime=∞ （11）lim+x→+∞x→0xx

?a0?b0a0xn+a1xn?1++an??=?0（12）limx→∞bxm+bxm?1+L+b01m?∞???

十三、下列常用等价无穷小关系（xn=mn<m （系数不为0的情况） n>m→0）

12x 2

sinx??x tanx??x arcsinx??x arctanx??x 1?cosx??ln(1+x)??x ex?1??x ax?1??xlna (1+x)?1???x

十四、三角函数公式

1.两角和公式 ?

sin(A+B)=sinAcosB+cosAsinB sin(A?B)=sinAcosB?cosAsinB cos(A+B)=cosAcosB?sinAsinB cos(A?B)=cosAcosB+sinAsinB

tanA+tanBtanA?tanB tan(A?B)= 1?tanAtanB1+tanAtanBcotA?cotB?1cotA?cotB+1 cot(A?B)= cot(A+B)=cotB+cotAcotB?cotAtan(A+B)=

2.二倍角公式

sin2A=2sinAcosA cos2A=cos2A?sin2A=1?2sin2A=2cos2A?1 tan2A=2tanA 21?tanA

3.半角公式

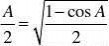
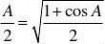
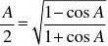
sinAsinA

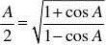
==1+cosA1?cosA

积分公式大全 微积分公式大全

4.和差化积公式

sina+sinb=2sina+ba?ba+ba?b sina?sinb=2cos ?sin?cos2222

a+ba?ba+ba?b cosa?cosb=?2sin ?sincosa+cosb=2cos?cos2222

tana+tanb=sin(a+b) cosa?cosb

5.积化和差公式

11 sinasinb=??cosa+b?cosa?b?cosacosb=?cos(a+b)+cos(a?b)?()()?? 2?2?

11 sinacosb=?sina+b+sina?b?cosasinb=sin(a+b)?sin(a?b)??()()????22

6.万能公式

a1?tan2

cosa=sina=a1+tan21+tan2

22tan

7.平方关系 aa2tan tana= aa1?tan222

sin2x+cos2x=1 sec2x?tan2x=1 csc2x?cot2x=1

8.倒数关系

tanx?cotx=1 secx?cosx=1 cscx?sinx=1

9.商数关系

tanx=sinxcosx cotx= cosxsinx

dy=f(x)g(y) ， f1(x)g1(y)dx+f2(x)g2(y)dy=0 dx十五、几种常见的微分方程 1.可分离变量的微分方程：

2.齐次微分方程：

dy?y?=f?? dx?x?

3.一阶线性非齐次微分方程：dy+p(x)y=Q(x) 解为： dx

?p(x)dx?p(x)dx? ∫y=e∫Qxedxc+()???∫?

三 : 《微积分》公式大全

《微积分》公式大全

微积分公式大全 《微积分》公式大全

微积分公式大全 《微积分》公式大全

微积分公式大全 《微积分》公式大全

本文标题：微积分公式大全-《微积分》公式大全
本文地址： http://www.61k.com/1093055.html