一 : logistic回归分析

第十六章 logistic回归分析

logistic回归为概率型非线性 回归模型，是研究分类观察 结果(y)与一些影响因素(x) 之间关系的一种多变量分析 方法

问题提出： 医学研究中常研究某因素存在条件下某结果是否 发生？以及之间的关系如何？ 因素（X） 疾病结果（Y） x1，x2，x3…XK 发生 Y=1 不发生 Y=0 例：暴露因素 高血压史(x1)：有 或无 高血脂史(x2)： 有 或 无 吸烟(x3)： 有或无 冠心病结果 有 或 无

研究问题可否用多元线性回归方法？

? y ? a ? b1x1 ? b2 x2 ?bm xm
1.多元线性回归方法要求 Y 的取值为计量 的连续性随机变量。 2.多元线性回归方程要求Y与X间关系为线 性关系。 ? 3.多元线性回归结果 Y 不能回答“发生 与否” logistic回归方法补充多元线性回归的不足

Logistic回归方法
该法研究是 当 y 取某值（如y=1）发生的概率（p）与 某暴露因素（x）的关系。

p( y ? 1/ x) ? f ( x),即p ? f ( x)
P（概率）的取值波动0～1范围。 基本原理：用一组观察数据拟合Logistic模型， 揭示若干个x与一个因变量取值的关系，反映y 对x的依存关系。

第一节 logistic回归 一、基本概念
1.变量的取值 logistic回归要求应变量（Y）取值为分类变量 （两分类或多个分类）
?1 Y ?? ?0 出现阳性结果 (发病、有效、死亡等） 出现阴性结果 (未发病、无效、存活等）

自变量（Xi）称为危险因素或暴露因素，可为连续变 量、等级变量、分类变量。 可有m个自变量X1， X2，… Xm

2.两值因变量的logistic回归模型方 程
一个自变量与Y关系的回归模型 如：y：发生=1,未发生=0 x ： 有=1， 无=0， 记为p（y=1/x）表示某暴露因素状态下， 结果y=1的概率（P）模型。x ?0 ? ?

或

e P( y ? 1 / x) ? ? 0 ? ?x 1? e

1 p( y ? 1 / x) ? 1 ? exp[ ?( ? 0 ? ?x)]
模型描述了应变量p与x的关系

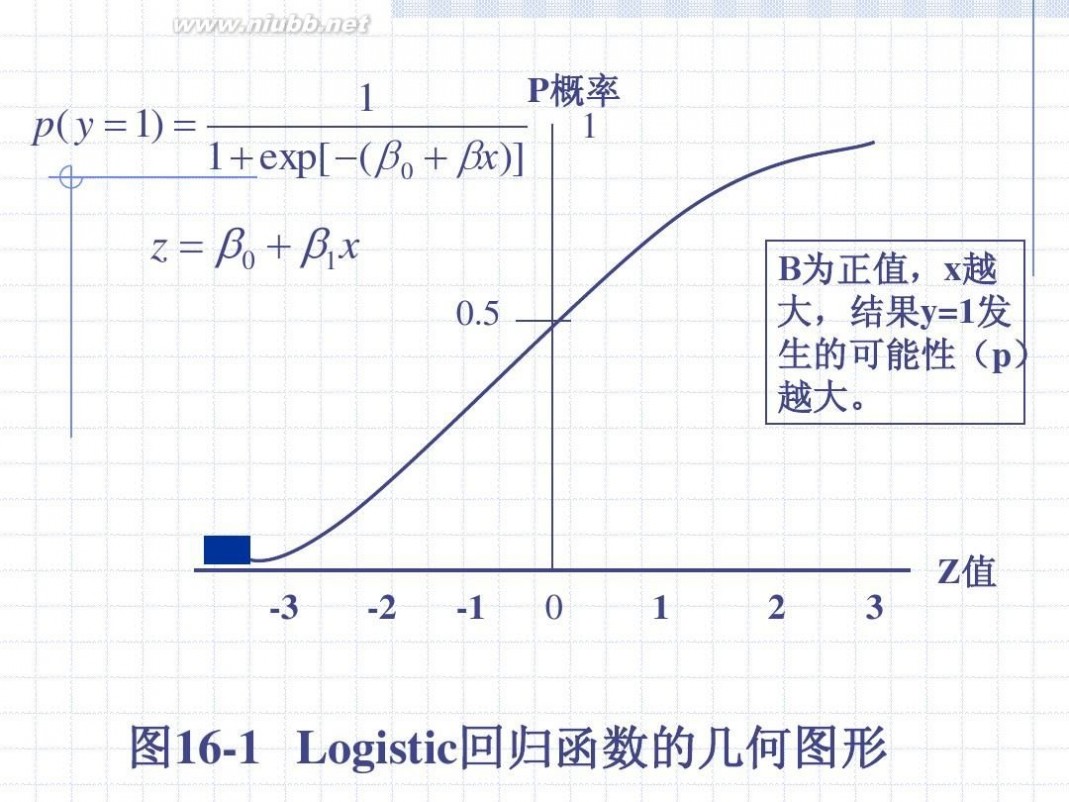
P概率 1 p( y ? 1) ? 1 1 ? exp[ ?( ? 0 ? ?x)]

z ? ? 0 ? ?1 x
0.5

Β为正值，x越 大，结果y=1发 生的可能性（p） 越大。

Z值 -3 -2 -1 0 1 2 3

图16-1 Logistic回归函数的几何图形

几个logistic回归模型方程
e p1 ? P( y ? 1/ x ? 1) ? ?0 ? ? x 1? e
?0 ? ? x

e P( y ? 0 / x ? 1) ? 1 ? ? 1 ? p1 ?0 ? ? x 1? e e p0 ? P( y ? 1/ x ? 0) ? ?0 1? e ?0 e P( y ? 0 / x ? 0) ? 1 ? ? 1 ? p0 ?0 1? e
?0

?0 ? ? x

logistic回归模型方程的线性表达
对logistic回归模型的概率（p）做logit变 换，

p log it ( p) ? ln( ) 1? p

方程如下：
线形 关系

y ? log it ( p) ? ? 0 ? ?1 x1

Y～（-∞至+∞）

截距（常数）

回归系数

在有多个危险因素（Xi）时
多个变量的logistic回归模型方程的线性表达： 公式16-2

? P ? logit(p) ? ln ? ? = ? 0 ?

?1 X 1 ? ? 2 X 2 ? ? ? ? m X m ?1? P ?
或

p( y ? 1/ x1 , x2 ? xk ) ?

1 1? e
? ( ? 0 ? ?1 xk ?.... ? k xk )

2.模型中参数的意义
? P ? ln ? ? = ? 0 ? ?1 X 1 ?1? P ?
Β0（常数项）：暴露因素Xi=0时，个体发病 概率与不发病概率之比的自然对数比值。

? P( y ? 1 / x ? 0) ? ? = ?0 ln ? ? 1 ? P( y ? 0 / x ? 0) ? ? ?

Xi=1与Xi=0相比，发生某结果（如发病）优势 比的对数值。

?i

的含义：某危险因素，暴露水平变化时，即

? P /(1 ? P ) ? 1 ln OR ? ln ? 1 ? ? P0 /(1 ? P0 ) ? ? log itP ? log itP0 1

P1（y=1/x=1）的概率 P0（y=1/x=0）的概率

? ( ? 0 ? ?1 x1 ) ? ( ? 0 ? ? x0 ) ? ?1 x1

OR ? e

?

P /(1 ? P ) odds1 1 OR ? 1 ? P0 /(1 ? P0 ) odds0

Y 发病=1 不发病=0

危险因素 x= 1 x= 0 30（a） 10（ b） 70（c） 90（d） a+c b+d 危险因素 x= 1 x= 0 p1 p0 1-p1 1-p0

Y 发病=1 不发病=0

a p1 ? a?c

有暴露因素人群中发病的比例

多元回归模型的的

?i

概念

? P ? logit(p) ? ln ? ? =? 0 ? ?1 X 1 ? ? ? ? m X m ? 1? P ?

? i 反映了在其他变量固定后，X=1与x=0相
比发生Y事件的对数优势比。 回归系数β与OR X与Y的关联 β=0，OR=1， 无关 β＞1，OR＞1 ， 有关，危险因素 β＜1，OR＜1， 有关，保护因子
?i

事件发生率很小，OR≈RR。

二、logistic回归模型的参数估计
1. 模型中的参数（βi）估计
，

? P ? ln? ? = ? 0 ? ?1 X 1 ? ? 2 X 2 ? ? ? ? m X m ?1? P ?

通常用最大似然函数 (maximum likelihood estimate， MLE)估计β， 由统计软件包完成。(讲义259页）

OR ? e

?

如X=1，0两分类，则OR的1-α可信区间 估计公式

e

(b j ?u? / 2 Sb j )

Sb j

为回归系数 的标准误

（公式16-10）

例：讲义表16-1资料
一个研究吸烟、饮酒与食道癌关系的病例－对 照资料（886例），试作logistic回归分析。 变量的赋值

?1 Y ?? ?0
?1 X1 ? ? ?0

食管癌患者 对照：非食管癌
吸烟 不吸烟
?1 X2 ? ? ?0 饮酒 不饮酒

经logistic回归计算后得 b0 =-0.9099， b1 =0.8856， b2 =0.5261， 方程表达：

p ln( ) ? ?0.9099 ? 0.8856 x1 ? 0.5261x 2 1? p

exp( ? ) ? OR
exp( 0.8856) ? OR ? 2.4244

控制饮酒因素后， 吸烟与不吸烟相比 患食管癌的优势比 为2.4倍

exp( 0.5261) ? OR ? 1.6923

OR的可信区间估计
吸烟与不吸烟患食管癌OR的95%可信区间：

exp(b1 ? u? / 2 Sb1 ) ? exp(0.8856 ? 1.96 ? 0.15) ? (1.81,3.25)
饮酒与不饮酒OR的95%可信区间：

exp(b2 ? u? / 2 Sb2 ) ? exp(0.5261 ?1.96 ?0.1572) ? (1.24, 2.30)

1.检验一：对建立的整个模型做检验。
说明自变量对Y的作用是否有统计意义。

三、Logistic 回归模型的假设检验

H1 :

各?（j ? 1， ???，m)不全为0 2， j
? P ? ln? ? = ? 0 ? ?1 X 1 ? ? 2 X 2 ? ? ? ? m X m ?1? P ?
检验方法（讲义260-261页） 1）似然比检验 (likelihood ratio test) 2）Wald检验

H 0 : ?1 ? ? 2 ? ? ? ? m ? 0

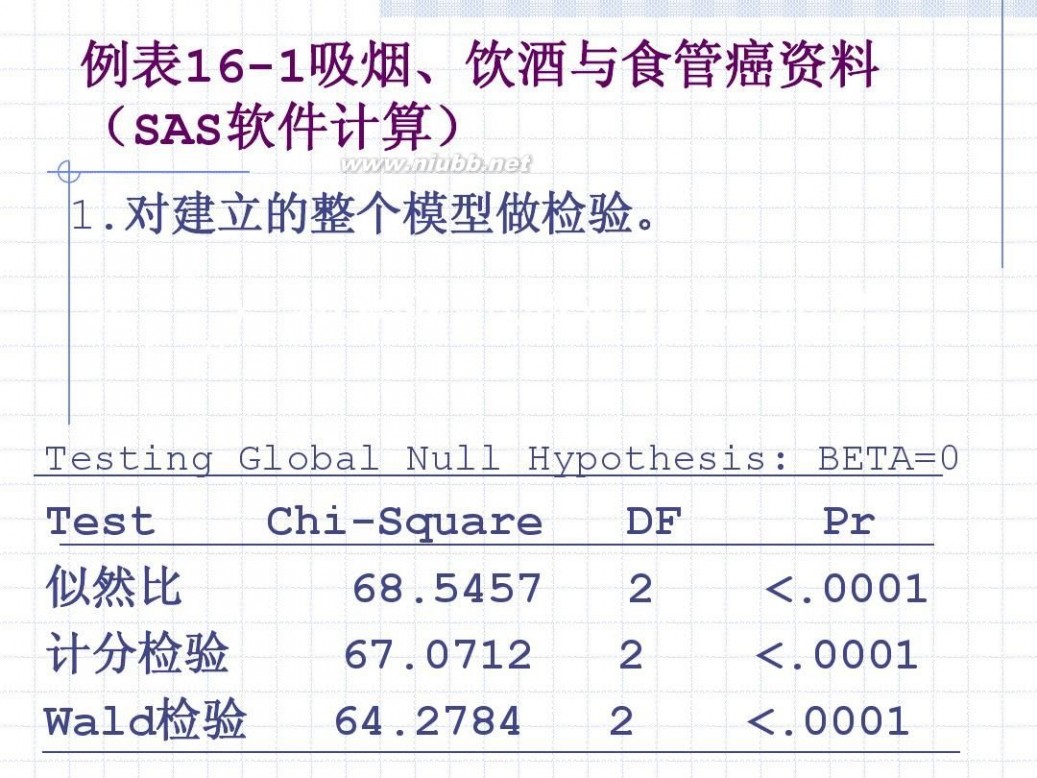
例表16-1吸烟、饮酒与食管癌资料 （SAS软件计算）
1.对建立的整个模型做检验。 p ln( ) ? ?0.9099 ? 0.8856 x1 ? 0.5261x2 1? p
Testing Global Null Hypothesis: BETA=0

Test Chi-Square 似然比 68.5457 计分检验 67.0712 Wald检验 64.2784

DF 2 2 2

Pr <.0001 <.0001 <.0001

2.检验二：
检验模型中某β是否对Y有作用。 检验假设：

H0 : ? j ? 0
bj Sb j
2

H1 : ? j ? 0

检验统计量：主要为Wald检验（SAS软件）

? ?(
2

)

2

ν=1的χ2

公式16-13

例；

0.8856 2 ? ?( ) ? 在大样本时，三方法结果一致。 33.86 0.15

例表16-1资料，对各x的β做检验（wald检验）
参数 β估计值 常数-0.9099 吸烟 0.8856 标准误 0.1358 0.1500 Chi-Squa 44.8699 34.8625 Pr .0001 .0001

饮酒 0.5261

0.1572

11.2069

.0008

Odds Ratio Estimates

Point
Effect 吸烟x1 饮酒x2 Estimate 2.424 1.692

95% Wald
Confidence Limits 1.807 1.244 3.253 2.303

似然比检验（讲义）
对某个β做检验，检验统计量（G）

G ? 2(ln L1 ? ln L0 )

ln L1 ln L0

包括p个自变量的对 数似然函数 包括 l 个自变量的 对数似然函数

G服从自由度（d）=p-l的χ2分布

例：X1为吸烟，X2为饮酒，检验饮酒与食

似然比检验对β做检验

管癌关系，H0：β2=0，H1：β2≠0

ln L1 ( X1 , X 2 ) ? ?579.711

log it ( p) ? ?0 ? ?1 x1 ? ?2 x2

ln L0 ( X1 ) ? ?585.326

log it ( p) ? ?0 ? ?1 x1

G ? 2[ln L( X1 , X 2 ) ? ln L ( X1 ) ? 2(?579.711? (? 585.326)] ? 11.23
G ＞3.84，p＜0.05，说明调整吸烟因素 后，饮酒与食管癌有关系。

四、变量筛选
目的；将回归系数有显著意义的自变量选入 模型中，作用不显著的自变量则排除在外。 变量筛选算法有：前进法、后退法和 逐步法（stepwise）。 例：讲义例16-2，用逐步法 选入变量的显著水准为0.10，变量保留在方 程的水准为0.15 例：16-2讲义261-263页

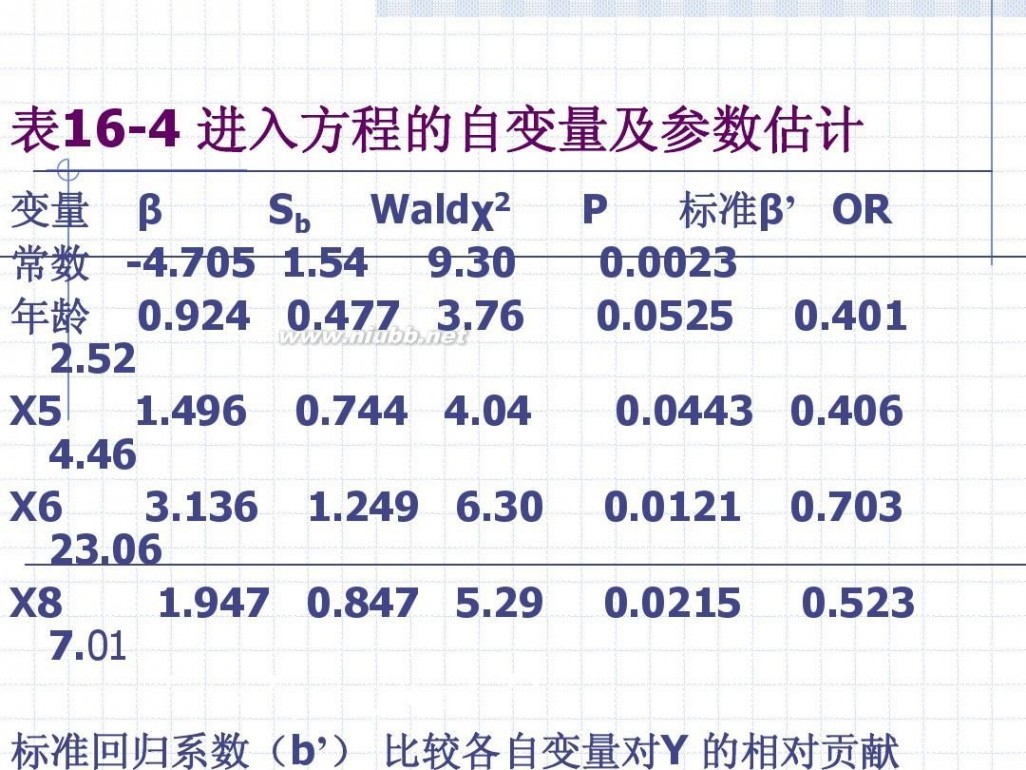
表16-4 进入方程的自变量及参数估计
变量 β Sb Waldχ2 P 标准β’ OR 常数 -4.705 1.54 9.30 0.0023 年龄 0.924 0.477 3.76 0.0525 0.401 2.52 X5 1.496 0.744 4.04 0.0443 0.406 4.46 X6 3.136 1.249 6.30 0.0121 0.703 23.06 X8 1.947 0.847 5.29 0.0215 0.523 7.01

b j ' ? b j ? s j /(? / 3)

标准回归系数（b’） 比较各自变量对Y 的相对贡献

第二节 条件Logistic回归
概念： 用配对设计获得病例对照研究资料，计算的 Logistic回归模型为条件Logistic回归。

成组（未配对）设计的病例对照研究资料，计算的 Logistic回归模型为非条件Logistic回归。 例：见265页 区别： 条件Logistic回归的参数估计无常数项（β0

），主 要用于危险因素的分析。

项 一、logistic回归的应用
1.疾病（某结果）的危险因素分析和筛选

用回归模型中的回归系数（β i）和OR说明 危险因素与疾病的关系。例：讲义例16-1， 16-2，16-3
适用的资料：

前瞻性研究设计、病例对照研究设计、 横断面研究设计的资料。
三类研究计算的logistic 回归模型的β意义是一致。仅常 数项不同。（证明略）

Logistic回归的应用
2.校正混杂因素，对疗效做评价 在临床研究和疗效的评价，组间某些因素构 成不一致干扰疗效分析，通过该法可控制 非处理因素，正确评价疗效。 3.预测与判别 预测个体在某因素存在条件下，发生某事件 （发病）的概率，为进一步治疗提供依据。

例1

例：

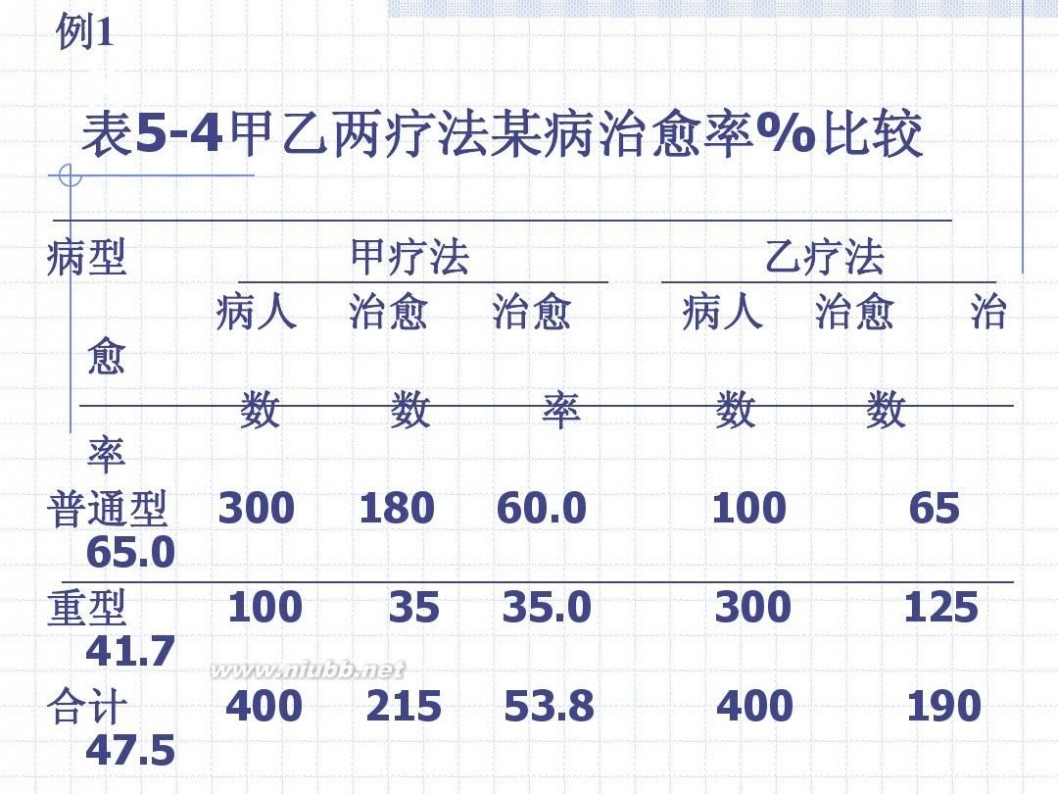
表5-4甲乙两疗法某病治愈率%比较
病型 病人 愈 甲疗法 治愈 治愈 乙疗法 病人 治愈 治

数
率 普通型 65.0 重型 41.7 合计 47.5 300 100

数
180 35

率
60.0 35.0

数
100 300

数
65 125

400

215

53.8

400

190

表5-5直接法计算标准化治愈率
病型 标准 治疗 人数 400 400 800 甲疗法 原治 预期 愈率 治愈数 60.0 240 35.0 140 380 乙疗法 原治 预期 愈率 治愈数 65.0 260 41.7 167 427

普通型 重型 合计

调整率（标准化率）：

?N i Pi 380 P '? ? ? 47.5% 甲 ?N i 800

427 P '? ? 53.4% 乙 800

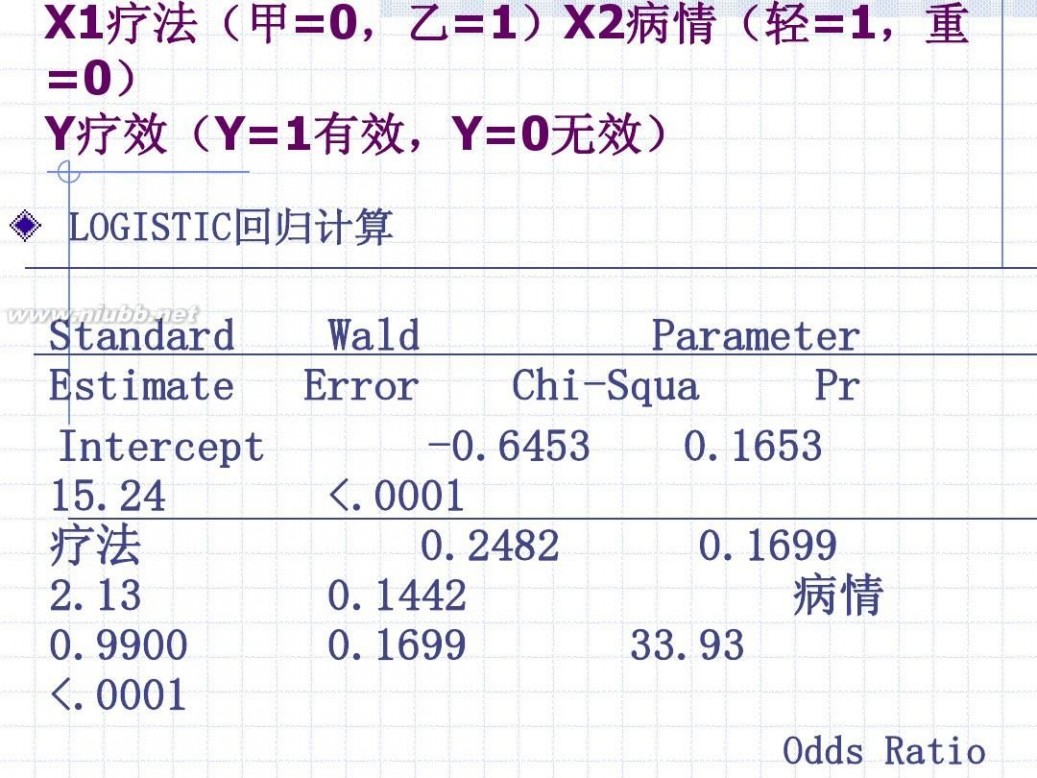
X1疗法（甲=0，乙=1）X2病情（轻=1，重 =0） Y疗效（Y=1有效，Y=0无效）
LOGISTIC回归计算

Standard Wald Parameter Estimate Error Chi-Squa Pr Intercept -0.6453 0.1653 15.24 <.0001 疗法 0.2482 0.1699 2.13 0.1442 病情 0.9900 0.1699 33.93 <.0001
Odds Ratio

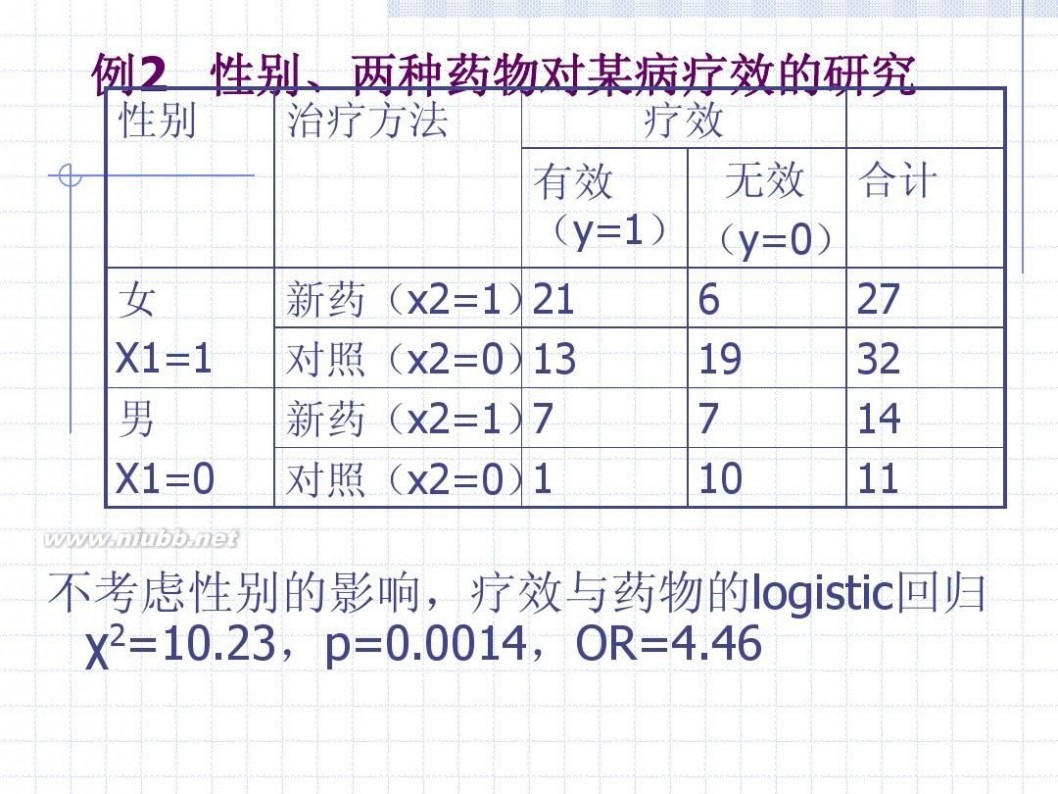
例2 性别、两种药物对某病疗效的研究
性别 治疗方法 疗效 无效 合计 有效 （y=1） （y=0） 21 6 27 新药（x2=1） 13 19 32 对照（x2=0） 7 7 14 新药（x2=1） 1 10 11 对照（x2=0）

女 X1=1 男 X1=0

不考虑性别的影响，疗效与药物的logistic回归 χ2=10.23，p=0.0014，OR=4.46

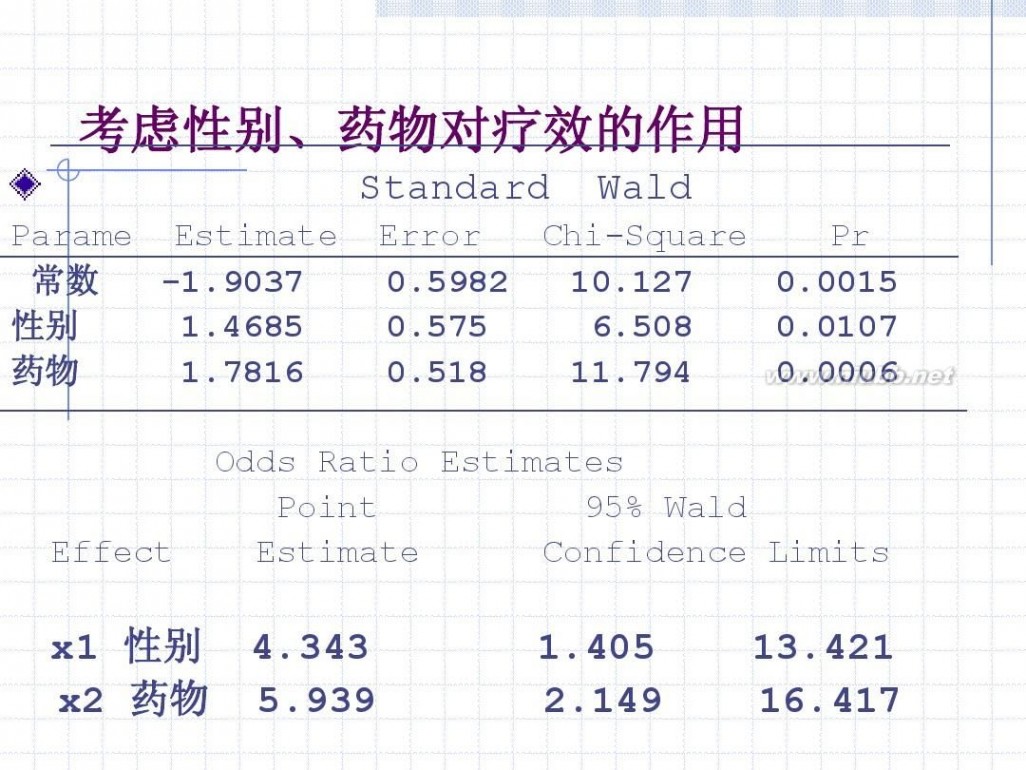
考虑性别、药物对疗效的作用
Standard
Parame Estimate 常数 -1.9037 性别 1.4685 药物 1.7816

Wald

Error Chi-Square Pr 0.5982 10.127 0.0015 0.575 6.508 0.0107 0.518 11.794 0.0006

Effect

Odds Ratio Estimates Point 95% Wald Estimate Confidence Limits

x1 性别 x2 药物

4.343 5.939

1.405 2.149

13.421 16.417

结论：性别和药物的回归系数都均有统计意义。 说明女性或用新药的疗效较优。 用Logistic模型方程对个体的疗效做预测 ：

p( y ? 1/ x) ?

1 1? e
? ( ?1.9037 ?1.4685 x1?1.7816 x 2)

设如女性病人，x1=1，用新药x2=1，有效的概率p=0.79
如男性病人x1=0，用新药x2=1， 有效的概率p=0.4695

二、Logistic回归应用的注意事项
1.模型中自变量的取值 自变量（X）可为计量数据、分类数据和 等级数据。 计量数据常重新划为有序组段，OR的实际 意义较大。 p ) ? a ? 0.04 x1 例：年龄（岁，x1

） ln( 1? p

OR ? exp(0.04) ? 1.0408

数据的几种赋值形式
1）两分类变量，赋值为：有=1，无=0 2）有序变量，赋值；无=0，少=1，中=2，多=3 例；年龄 ＜45=1 45-54=2 55-64=3 ≥65=4 3.）多分类无序变量： 赋值为：哑变量（dummy variable）形式 见例： 注：变量取值不同，方程的系数和符号将发生变化。

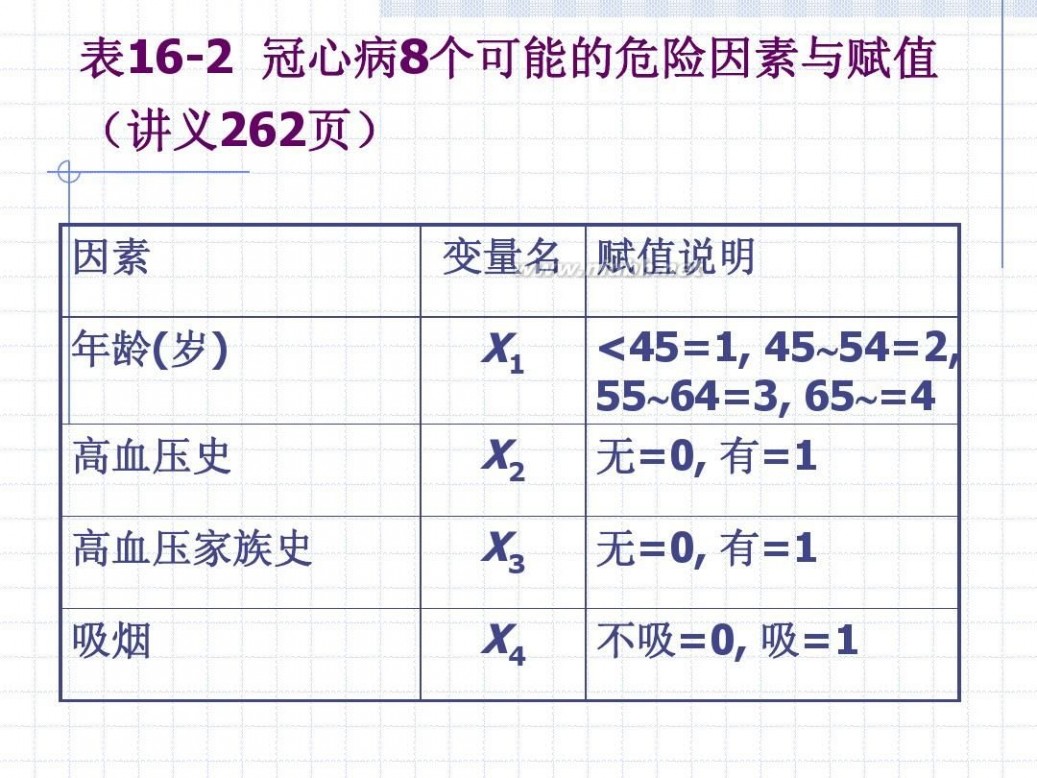
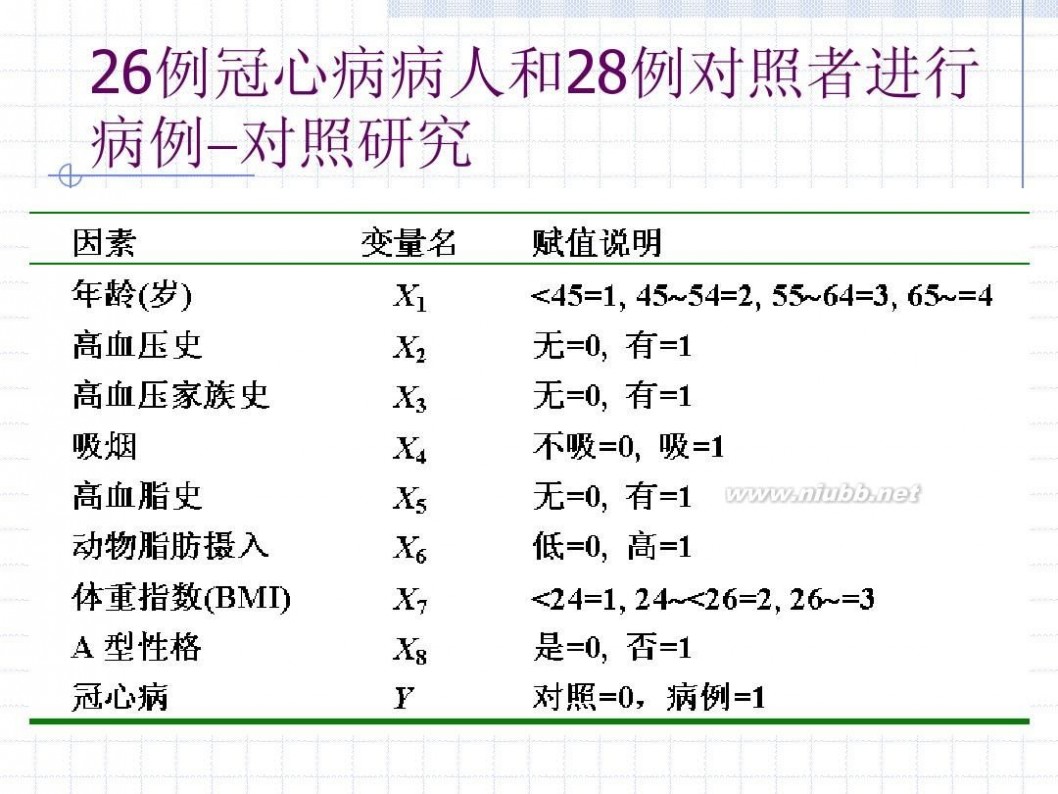
表16-2 冠心病8个可能的危险因素与赋值 （讲义262页）
因素 年龄(岁) 高血压史 高血压家族史 吸烟 变量名 赋值说明

X1 X2 X3 X4

<45=1, 45?54=2, 55?64=3, 65?=4 无=0, 有=1 无=0, 有=1 不吸=0, 吸=1

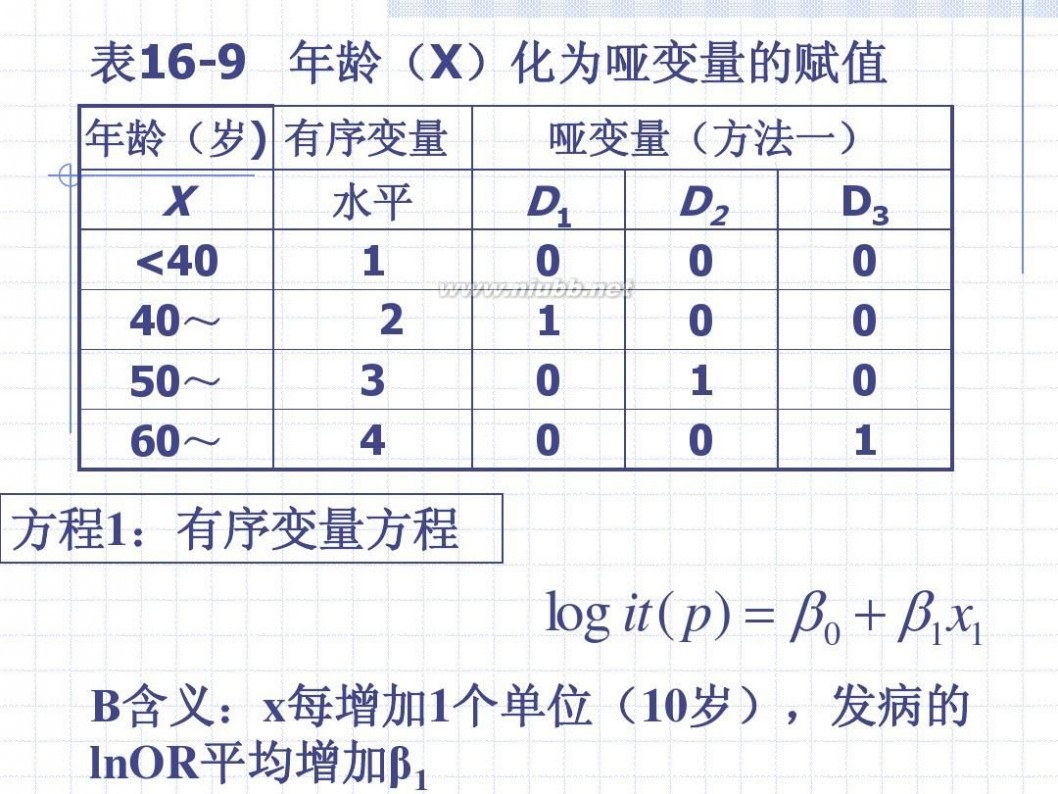
表16-9 年龄（X）化为哑变量的赋值
年龄（岁) 有序变量 哑变量（方法一）

X
<40 40～ 50～ 60～

水平 1 2 3 4

D1
0 1 0 0

D2
0 0 1 0

D3 0 0 0 1

方程1：有序变量方程

log it ( p) ? ? 0 ? ?1 x1
Β含义：x每增加1个单位（10岁），发病的 lnOR平均增加β1

方程2：哑变量方程（哑变量个数=分类数－1）

log it ( p) ? ? 0 ? ?1 D1 ? ? 2 D2 ? ? 3 D3
方程系数的解释：

?1 ?2 ?3

表示40-岁/＜40岁相比的对数优势比 表示50-岁/＜40岁相比的对数优势比 表示60-岁/＜40岁相比的对数优势比

哑变量的赋值方法
血型 （X） X1 A 0 B 1

例2：研究某结果与血型的关系
哑变量 X2 X3 0 0 0 0
变量规定某个 分类为对照， 对照组在哑变 量的赋值均为 0

O
AB

0
0

1
0

0
1

log it ( p) ? ? 0 ? ?1 x1 ? ? 2 x2 ? ? 3 x3
式中回归系数表示各对比组与对照组（A型）相 比的变化值。

270页分析题2
变量X4的哑变量的赋值方法 规定治疗11周=X4-1，是=1，否=0 规定治疗21周=X4-2，是=1，否=0 规定治疗1周为对照组。 哑变量的赋值 X4-1 X4-2 0 0 1 0 0 1

周 1～ 11～ 21～

2.样本含量：
1）病例和对照组的例数可相等或不等。 2）样本例数的估计 原则：自变量个数越多，例数越多。各 组样本例数（对照组和病例组）至少 为自变量个数的5-20倍。

3.模型的评价（讲义269页）

对所建立的回归方程做拟合优度检验。检 查模型估计与实际数据的符合情况。 检验统计量： 1.剩余差（deviance，记为D） 2.Pearson χ 2 （16-26）

（16-25）

统计量的概率值P＞0.05，认为模型拟合较好 例：表16-10 （讲义表16-10）

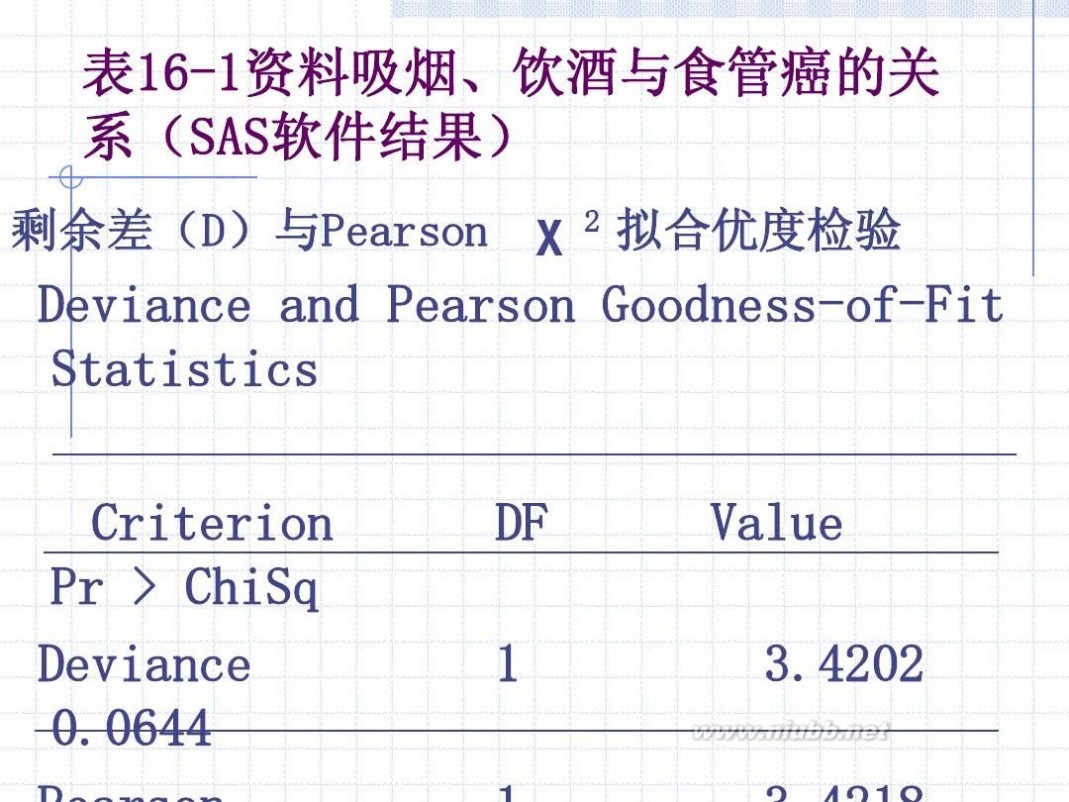
表16-1资料吸烟、饮酒与食管癌的关 系（SAS软件结果）
剩余差（D）与Pearson χ
2

拟合优度检验

Deviance and Pearson Goodness-of-Fit Statistics

Criterion Pr > ChiSq Deviance 0.0644

DF 1

Value 3.4202

4.多分类的Logistic回归
Logistic回归可处理： 1）应变量（Y）为有序的多分类资料 如结果为：治愈、显效、好转、无效

2）应变量（Y）为无序的多分类资料 例： 研究阑尾炎类型与危险因素关系 阑尾炎类型有：卡他型、坏疽型、腹膜炎型
多分类Logistic回归方法（略）

结果的

表达
一般logistic 回归分析报告内容： 1.危险因素的回归系数及标准误、p值 2.标准化的回归系数。 ' 讲义264页 bj ? bj ? S j / ? / 3

?

?

3.危险因素对应的OR和可信区间 4.Logistic回归方程

本节重点掌握内容和作业
一、问答题 1.Logistic回归与线性回归有什么不同？ 2. Logistic回归可解决哪些问题？ 3.自变量可以有哪些类型，应用时应如何 赋值？ 4. Logistic回归中β的含义和方程的表达。 二、计算分析题的第2题的第（1）题。

Logistic回归
Logistic regression

第一节.非条件logistic回归 第二节.条件logistic回归 第三节. 应用及其注意事项

什么情况下采用Logistic回归
医学研究中常碰到应变量的可能取值 仅有两个（即二分类变量），如发病与未 发病、阳性与阴性、死亡与生存、治愈与 未治愈、暴露与未暴露等，显然这类资料 不满足多重回归的条件

实例
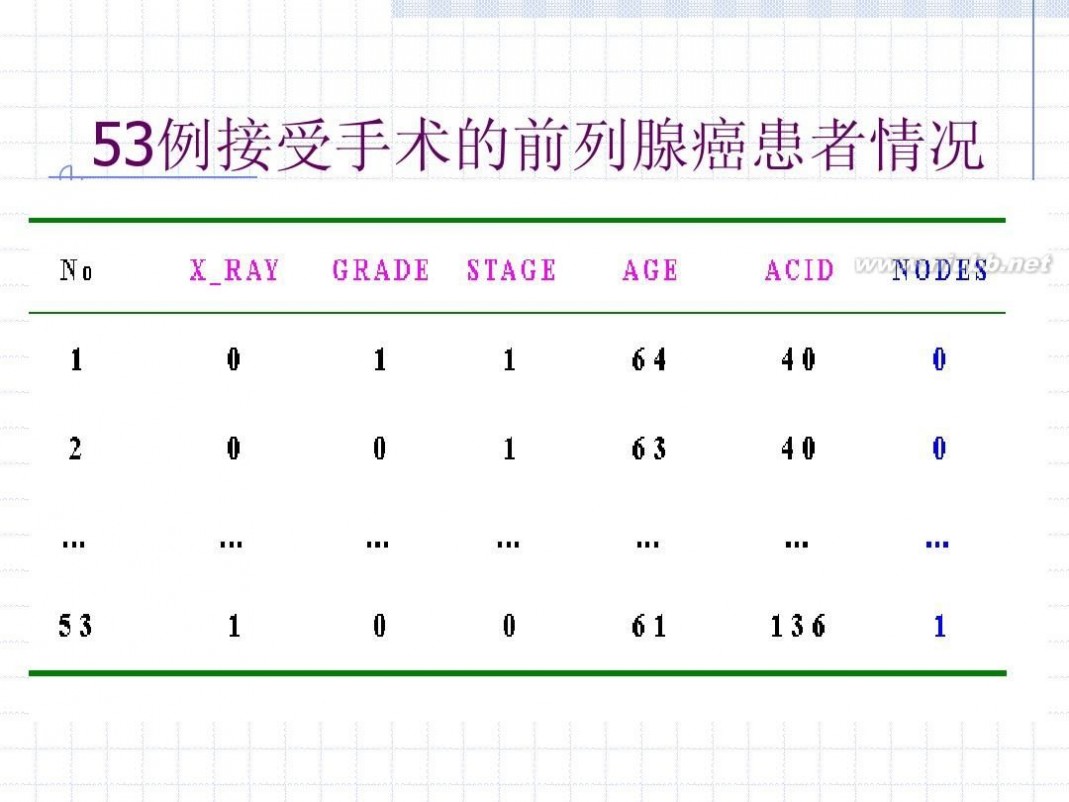
Brown(1980)在术前检查了53例前列腺 癌患者，拟用年龄(AGE)、酸性磷酸酯酶 (ACID)两个连续型的变量，X射线(X_RAY)、 术前探针活检病理分级(GRADE)、直肠指检 肿瘤的大小与位置(STAGE)三个分类变量与 手术探查结果变量NODES（1、0分别表示癌 症的淋巴结转移与未转移 ）建立淋巴结转 移的预报模型。

53例接受手术的前列腺癌患者情况

26例冠心病病人和28例对照者进行 病例?对照研究

26例冠心病病人和28例对照者进行 病例?对照研究

一、logistic回归模型

概率预报模型
??

exp( ? 0 ? ?1 X 1 ? ? ? ? p X p )

1 ? exp( ? 0 ? ?1 X 1 ? ? ? ? p X p )

1 ? 1 ? exp[ ?( ? 0 ? ?1 X 1 ? ? ? ? p X p )] ? 1 1? e
? ( ? 0 ? ?1 X 1 ??? ? p X p )

二、模型的参数估计
Logistic回归参数的估计通常采 用最大似然法(maximum likelihood， ML)。最大似然法的基本思想是先建 立似然函数与对数似然函数，再通过 使对数似然函数最大求解相应的参数 值，所得到的估计值称为参数的最大 似然估计值。

参数估计的公式

三、回归参数的假设检验

优势比及其可信区间

标准化回归参数

P262表16-3资料计算的SAS程序

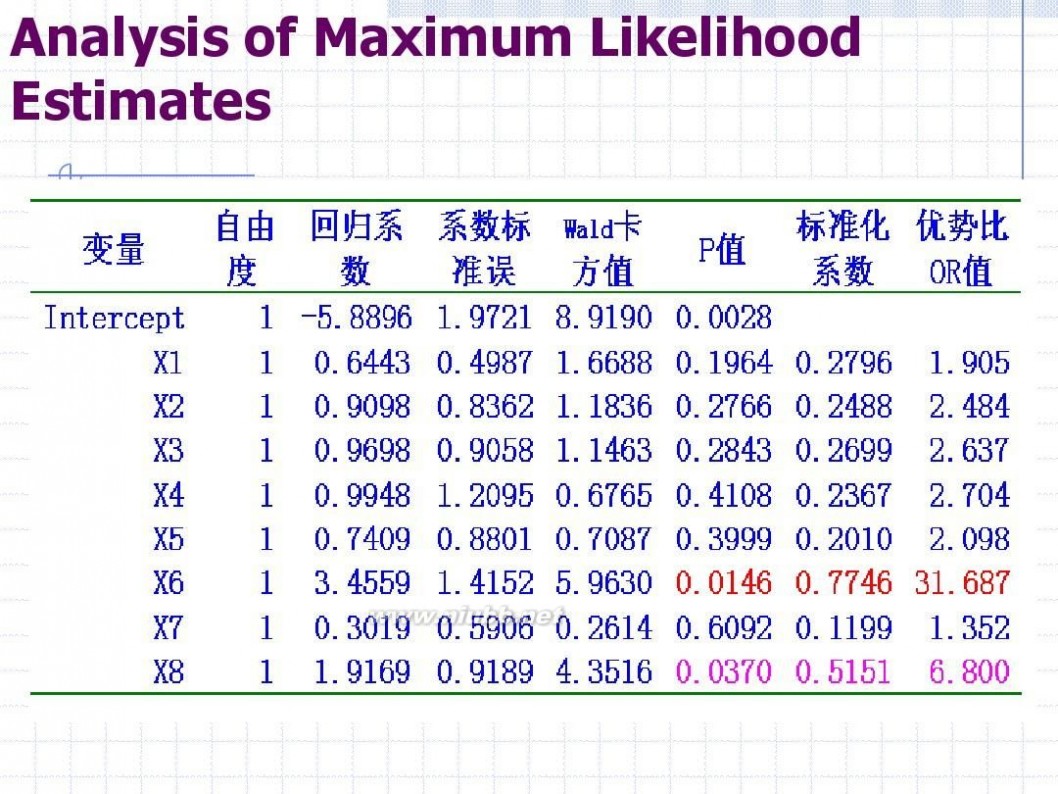
Analysis of Maximum Likelihood Estimates

预报模型
exp( ?5.8896 ? 0.6443 X 1 ? ? ? 1.9169 X 8 ) ?? 1 ? exp( ?5.8896 ? 0.6443 X 1 ? ? ? 1.9169 X 8 ) 1 ? 1 ? exp ?? (?5.8896 ? 0.6443 X 1 ? ? ? 1.9169 X 8 )? ? 1 1? e
? ( ?5.8896? 0.6443X 1 ???1.9169X 8 )

四、回归参数的意义

当只有一个自变量时，以相应的预报概率 ? 为纵轴，自变量 X 为横轴，可绘制出一条 S形曲线。回归参数的正负符号与绝对值大 小，分别决定了S形曲线的形状与方向 1
0.8

预报概率

0.6 0.4 0.2 0 -2.5 -1.5 -0.5 0.5 1.5
X

Logistic回归曲线 中心线

2.5

3.5

五

、整个回归模型的假设检验

似然比检验（likelihood ratio test）

六、logistic逐步回归（变量筛选）
MODEL语句加入选项“ SELECTION=STEPWISE SLE=0.10 SLS=0.10;” 常采用似然比检验：
2 ? LR ? ?2(ln L0 ? ln L1 ) ? (?2 ln L0 ) ? (?2 ln L1 )

决定自变量是否引入或剔除。

模型中有X5、X6、X8， 看是否引入X1
模型含X5、X6、X8的模型的负二倍 对数似然为： (?2 ln L ＝50.402 0) 模型含X1、X5、X6、X8的模型的负二倍 对数似然为： (?2 ln L1 ) ＝46.224
2 ? LR

? 50 .402 ? 40 .224 ? 4.178 ,

? ? 1, P ? 0.0410 ? 0.10,引入变量 X1

第二节.条件logistic回归

条件似然函数

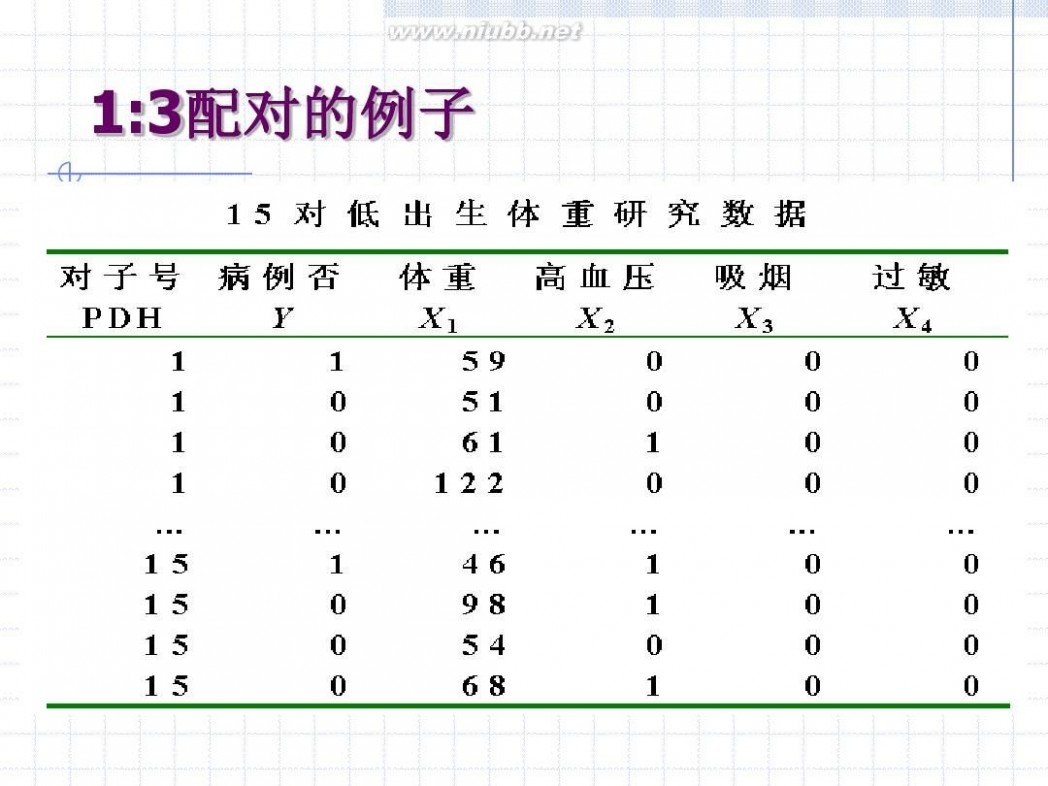
1:3配对的例子

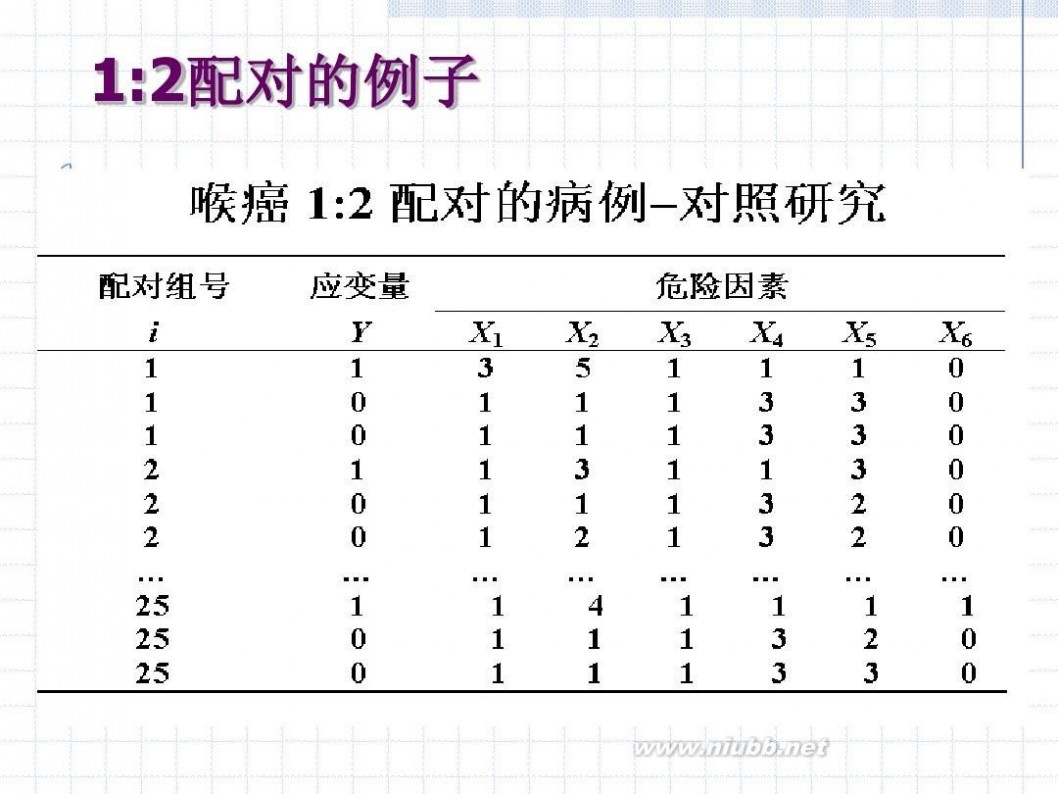
1:2配对的例子

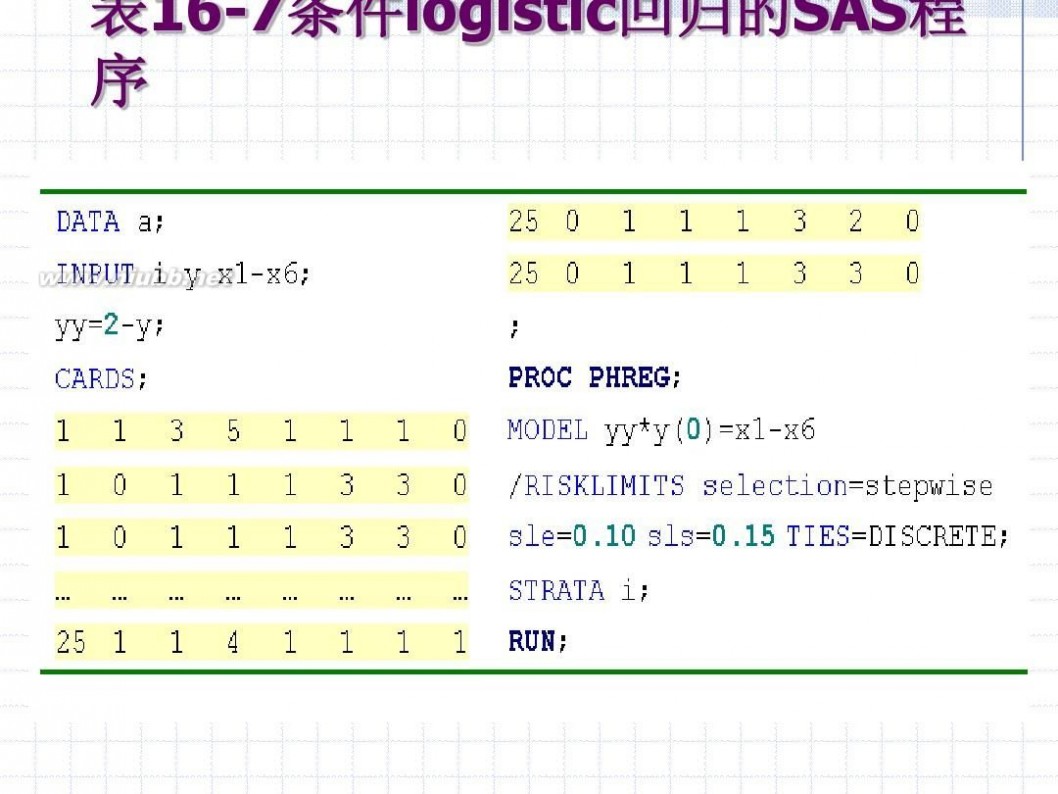
表16-7条件logistic回归的SAS程 序

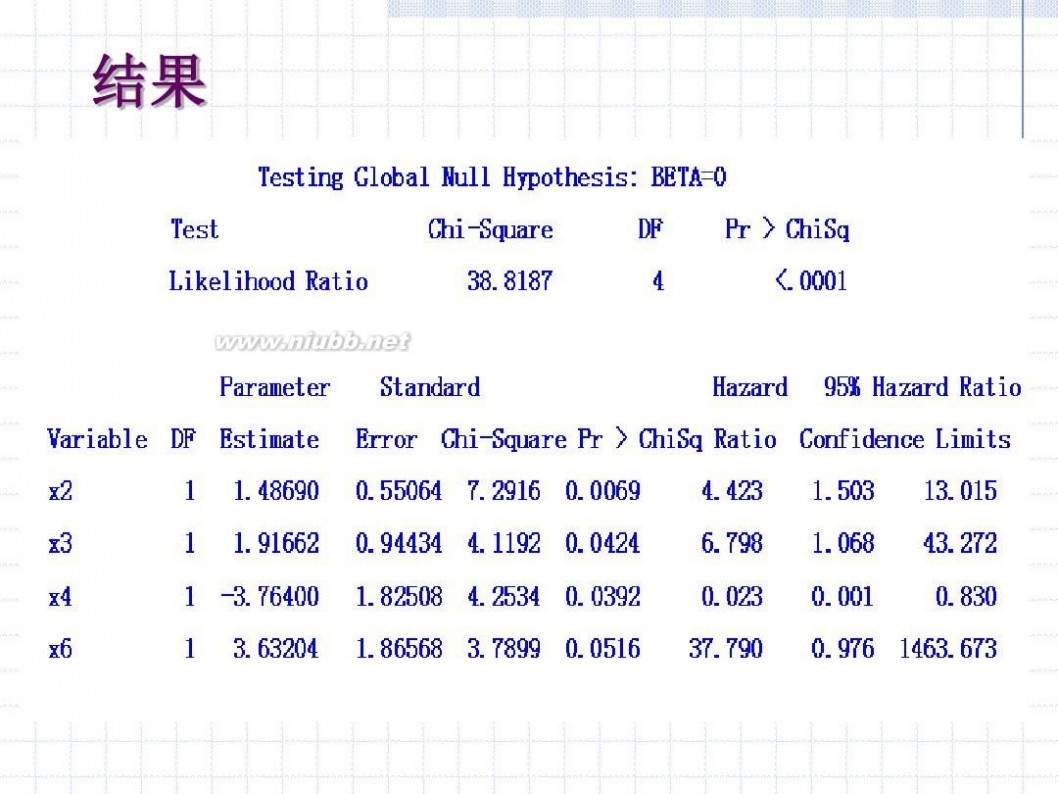
结果

第三节

应用及其注意事项

应变量为（二项）分类的资料 （预测、判别、危险因素分析等等）

注意事项
1. 分类自变量的哑变量编码

为了便于解释，对二项分类变量一 般按0、1编码，一般以0表示阴性或较 轻情况，而1表示阳性或较严重情况。 如果对二项分类变量按+1与-1编码，那 么所得的 OR ? exp( 2? )，容易造成错误的 解释。

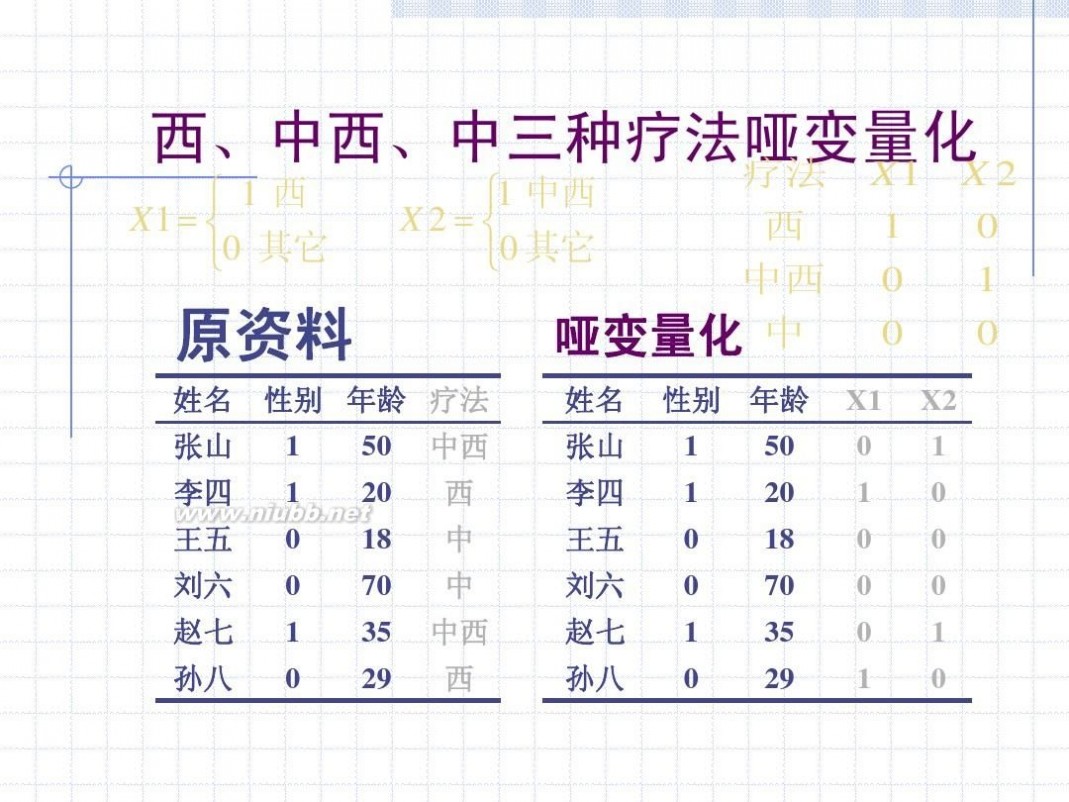
? 1西 X1 ? ? ?0 其它

西、中西、中三种疗法哑变量化 2 疗法 X 1 X
?1 中西 X2?? ?0 其它
西 中西 中
50 20 18 70 35 0 1 0 0 0 性别 年龄 1 1 0 0 1

1 0 0
X1 X2 1 0 0 0 1

0 1 0

原资料
姓名 张山 李四 王五 刘六 赵七 性别 年龄 疗法 1 1 0 0 1 50 20 18 70 35 中西 西 中 中 中西

哑变量化
姓名 张山 李四 王五 刘六 赵七

孙八

0

29

西

孙八

0

29

1

0

注意事项
2.自变量的筛选 不同的筛选方法有时会产生不同的模 型。实际工作中可同时采用这些方法，然 后根据专业的可解释性、模型的节约性和 资料采集的方便性等，决定采用何种方法 的计算结果。

注意事项
3.交互作用 交互作用的分析十分复杂，应 根据临床意义与实际情况酌情使用。

注意事项
4. 多分类logistic回归

心理疾病分为精神分裂症、抑郁症、神 经官能症等（名义变量nominal variables) ；疗效评价分为无效、好转、显效、痊愈( 有序变量ordinal variables)。
参见“余松林主编。医学统计学（七年制 全国规划教材，第17章， 2002年3月 ）”

二 : logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

logistic logistic回归分析

三 : spss二分类的logistic回归的操作和分析方法

[logistic]spss二分类的logistic回归的操作和分析方法——简介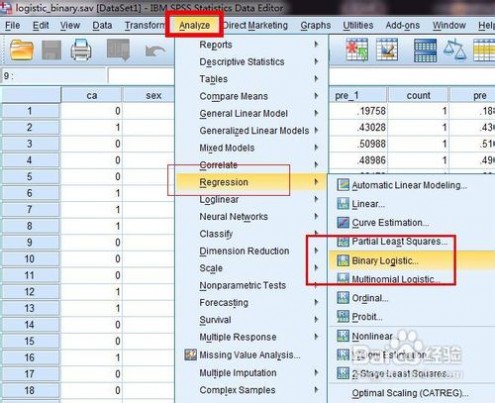

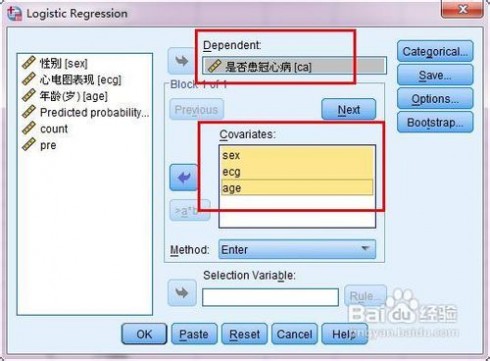
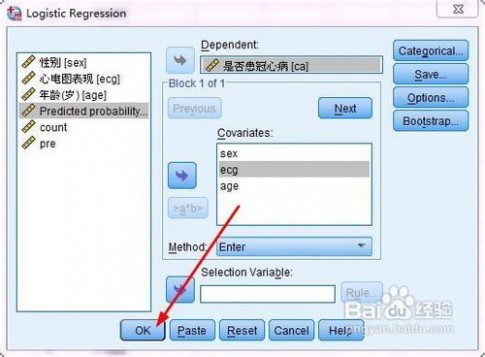
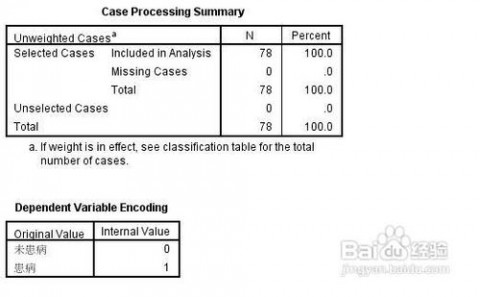
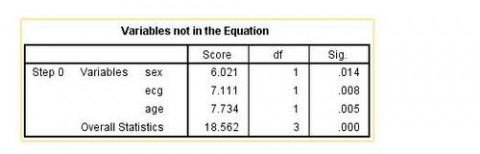
二分类指的是因变量的数据只有两个值，代表事物的两种类别，典型的二分类变量如性别、是否患病等。因变量为二分变量原则上是无法做回归的，在回归方程中的因变量实质上是概率，而不是变量本身。在理解二分类变量以后，我们看看如何做二分类变量的logistic回归。
[logistic]spss二分类的logistic回归的操作和分析方法——知识点
spss20.0

[logistic]spss二分类的logistic回归的操作和分析方法——详细知识

[logistic]spss二分类的logistic回归的操作和分析方法 一

打开数据以后，菜单栏上依次点击：analyse--regression--binary logistic，打开二分回归对话框

[logistic]spss二分类的logistic回归的操作和分析方法 二

将因变量和自变量放入格子的列表里，如图所示，上面的是因变量，下面的是自变量，我们看到这里有三个自变量

[logistic]spss二分类的logistic回归的操作和分析方法 三

设置回归方法，这里选择最简单的方法：enter，它指的是将所有的变量一次纳入到方程。其他方法都是逐步进入的方法，在前面的文章中有介绍，这里就不再熬述。

[logistic]spss二分类的logistic回归的操作和分析方法 四

点击ok，开始处理数据并检验回归方程，等待一会就会弹出数据结果窗口

[logistic]spss二分类的logistic回归的操作和分析方法 五

看到的第一个结果是对case的描述，第一个列表告诉你有多少数据参与的计算，有多少数据是缺省值；第二个列表告诉你因变量的编码方式，得分为1代表患病，得分为0代表没有患病

[logistic]spss二分类的logistic回归的操作和分析方法 六

这个列表告诉你在没有任何自变量进入以前，预测所有的case都是患病的正确率，正确率为%52.6

[logistic]spss二分类的logistic回归的操作和分析方法 七

下面这个列表告诉你在没有任何自变量进入以前，常数项的预测情况。B是没有引入自变量时常数项的估计值，SE它的标准误，Wald是对总体回归系数是否为0进行统计学检验的卡方。

[logistic]spss二分类的logistic回归的操作和分析方法 八
下面这个表格结果，通过sig值可以知道如果将模型外的各个变量纳入模型，则整个模型的拟合优度改变是否有统计学意义。 sig值小于0.05说明有统计学意义

[logistic]spss二分类的logistic回归的操作和分析方法 九

这个表格是对模型的全局检验，为似然比检验，供给出三个结果：同样sig值<0.05表明有统计学意义。

[logistic]spss二分类的logistic回归的操作和分析方法 十
下面的结果展示了-2log似然值和两个伪决定系数。两个伪决定系数反应的是自变量解释了因变量的变异占因变量的总变异的比例。他们俩的值不同因为使用的方法不同。


[logistic]spss二分类的logistic回归的操作和分析方法 1一

分类表，这里展示了使用该回归方程对case进行分类，其准确度为%71.8。

[logistic]spss二分类的logistic回归的操作和分析方法 1二

最后是输出回归方程中的各变量的系数和对系数的检验额值，sig值表明该系数是否具有统计学意义。到此，回归方程就求出来了。
本文标题：logistic回归spss-logistic回归分析
本文地址： http://www.61k.com/1081035.html