一 : 已知A，B，C是椭圆W：x24+y2=1上的三个点，O是坐标原点．（Ⅰ）当

已知A，B，C是椭圆W： x2 4 +y2=1上的三个点，O是坐标原点． （Ⅰ）当点B是W的右顶点，且四边形OABC为菱形时，求此菱形的面积； （Ⅱ）当点B不是W的顶点时，判断四边形OABC是否可能为菱形，并说明理由．

题型：解答题难度：中档来源：北京

（I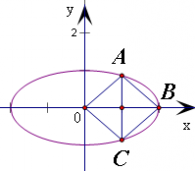） ∵四边形OABC为菱形，B是椭圆的右顶点（2，0） ∴直线AC是BD的垂直平分线，可得AC方程为x=1 设A（1，t），得 12 4 +t2=1，解之得t= 3 2 （舍负） ∴A的坐标为（1， 3 2 ），同理可得C的坐标为（1，- 3 2 ） 因此，|AC|= 3 ，可得菱形OABC的面积为S= 1 2 |AC|?|B0|= 3 ； （II）∵四边形OABC为菱形，∴|OA|=|OC|， 设|OA|=|OC|=r（r＞1），得A、C两点是圆x2+y2=r2 与椭圆W： x2 4 +y2=1的公共点，解之得 3x2 4 =r2-1 设A、C两点横坐标分别为x1、x2，可得A、C两点的横坐标满足 x1=x2= 2 3 3 ? r2-1 ，或x1= 2 3 3 ? r2-1 且x2=- 2 3 3 ? r2-1 ， ①当x1=x2= 2 3 3 ? r2-1 时，可得若四边形OABC为菱形，则B点必定是右顶点（2，0）； ②若x1= 2 3 3 ? r2-1 且x2=- 2 3 3 ? r2-1 ，则x1+x2=0， 可得AC的中点必定是原点O，因此A、O、C共线，可得不存在满足条件的菱形OABC 综上所述，可得当点B不是W的顶点时，四边形OABC不可能为菱形．

考点：

考点名称：椭圆的性质（顶点、范围、对称性、离心率）

椭圆的离心率：

椭圆的焦距与长轴长之比叫做椭圆的离心率。

椭圆的性质：

1、顶点：A（a，0），B（-a，0），C（0，b）和D（0，-b）。
2、轴：对称轴：x轴，y轴；长轴长|AB|=2a，短轴长|CD|=2b，a为长半轴长，b为短半轴长。
3、焦点：F₁（-c，0），F₂（c，0）。
4、焦距：。
5、离心率：；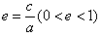
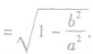
离心率对椭圆形状的影响：e越接近1，c就越接近a，从而b就越小，椭圆就越扁；e越接近0，c就越接近0，从而b就越大，椭圆就越圆；
6、椭圆的范围和对称性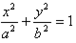：（a＞b＞0）中-a≤x≤a，-b≤y≤b，对称中心是原点，对称轴是坐标轴。
。

利用椭圆的几何性质解题：

利用椭圆的几何性质可以求离心率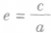及椭圆的标准方程．要熟练掌握将椭圆中的某些线段长用a，b，c表示出来，例如焦点与各顶点所连线段的长，过焦点与长轴垂直的弦长等，这将有利于提高解题能力。

椭圆中求最值的方法：

求最值有两种方法：
(1)利用函数最值的探求方法利用函数最值的探求方法，将其转化为函数的最值问题来处理．此时应充分注意椭圆中x，y的范围，常常是化为闭区间上的二次函数的最值来求解。
(2)数形结合的方法求最值解决解析几何问题要注意数学式子的几何意义，寻找图形中的几何元素、几何量之间的关系．

椭圆中离心率的求法：

在求离心率时关键是从题目条件中找到关于a，b，c的两个方程或从题目中得到的图形中找到a，b，c的关系式，从而求离心率或离心率的取值范围．

二 : 几何画板坐标系中怎么绘制一个椭圆形?

在直角坐标里画椭圆可以使用两种方法，一种是画函数图像的方法，另一种是直接利用椭圆工具，再调整长半轴和短半轴还有中心位置，今天我教大家使用第二种方法画椭圆。

软件名称：

nb几何画板软件 v1.0.1 中文官方安装版

软件大小：

23.7MB

更新时间：

2015-09-21

1、建立一个新的几何画板文件，单击自定义工具，建立一个微型坐标系。我要画的椭圆长半轴是4，短半轴为3.

2、单击自定义工具，迷你坐标系，选择无参数版。

3、单击初始化坐标系，建立一个新的小型坐标系。注意，初始化前要先单击一下箭头工具。

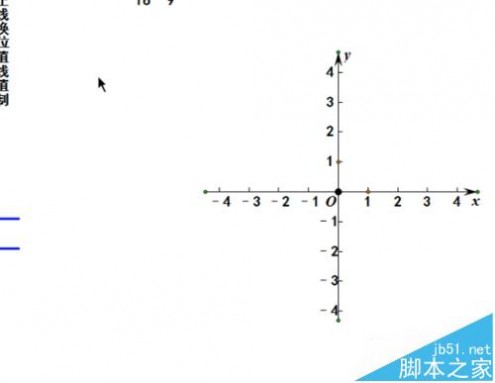
4、单击自定义工具，圆锥曲线，选择椭圆。

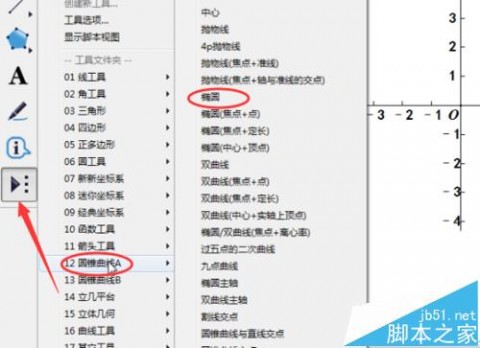
5、在原点处单击一下，向右拖曳可画出一个椭圆。

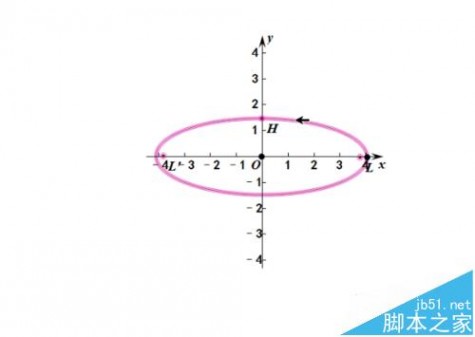
6、注意右边的黑色控制点，拉动它，使椭圆的长半轴为4.

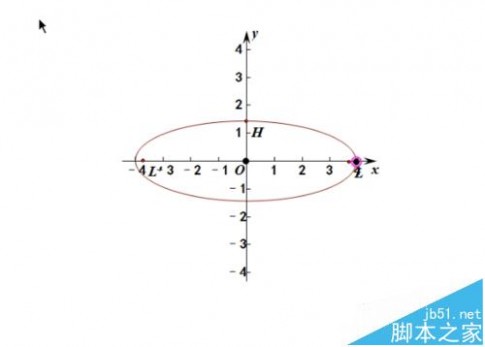
7、上面也有一个控制点，用来调整短半轴长度，适当移动位置，使短半轴为3，这样椭圆就画好了。如果中心不在原点，先按这样调整好长、短半轴后，再移动中心的位置。

相关推荐：

几何画板如何使用多边形工具?

几何画板怎么画几何图形的阴影部分?

几何画板怎么绘制两个外相切的圆并标注?

三 : CDR用椭圆和贝赛尔工具绘制两只可爱北极熊教程

效果图：

主要过程：

1、矩形工具绘制一个矩形，大小自定，填充颜色

2、把矩形复制一个等比例缩小，取消填充颜色，把轮廓填充白色加粗点，如图

3、开始绘制熊，椭圆工具绘制一个椭圆大小自定，填充颜色如图

4、绘制耳朵，椭圆绘制一个小点的椭圆，填充之前一样的颜色，把小椭圆复制一份等例缩小，居中填充颜色，把两个小椭圆群组复制一层放到右边置于步骤3下面，如图

5、开始绘制眼睛，椭圆绘制一个小椭圆填充黑色，复制一个放到右边，如图

6、椭圆绘制腮红放到眼睛下面，再复制一个放大点填充黑色作鼻子，如图

7、用贝赛尔工具绘制一段曲线作嘴巴，轮廓加粗点，如图

8、椭圆工具绘制一个椭圆作身子，填充和头一样的颜色置于头的下层，如图

9、用贝赛尔工具绘制手，注意调圆滑点，填充颜色，如图，再复制一个水平镜像放到右边

10、再绘制一个放到上面，填充和身子一样的颜色，复制一个放到右边，如图

11、用贝赛尔工具绘制脚，填充和身子一样的颜色，再复制一个放到右边，如图

12、用贝赛尔工具绘制脚部阴影，填充颜色，如图

13、绘制帽子放上面，矩形工具绘制一个矩形转曲，用形状工具把两边的线往里缩调成有点弧度，填充黑色

14、用贝赛尔工具绘制帽沿填充黑色，用矩形工具绘制一个长条矩形填充颜色用形状工具调成有点弧度放到帽子上面如图

15、绘制围巾，贝赛尔工具绘制围巾形状填充颜色，如图

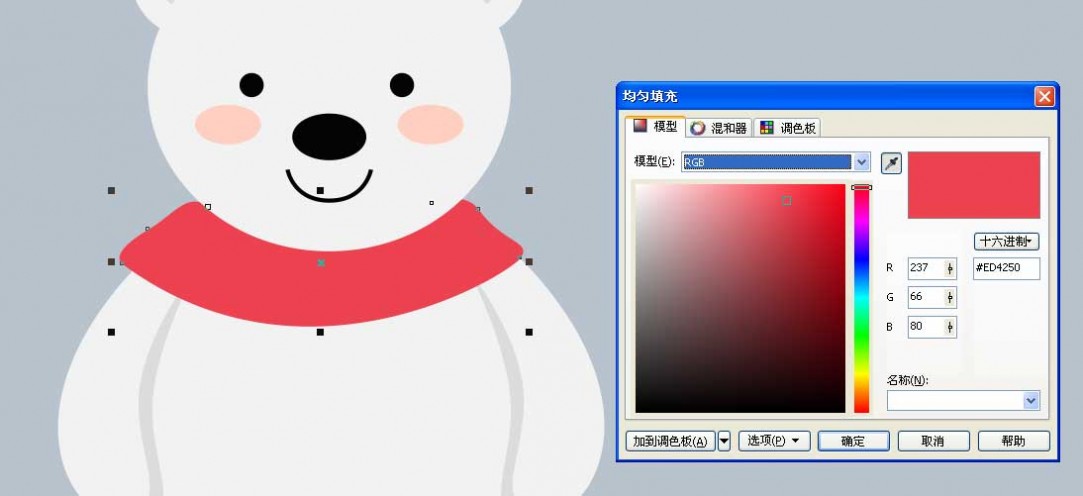
16、再用贝赛尔工具绘制下面两条，如图

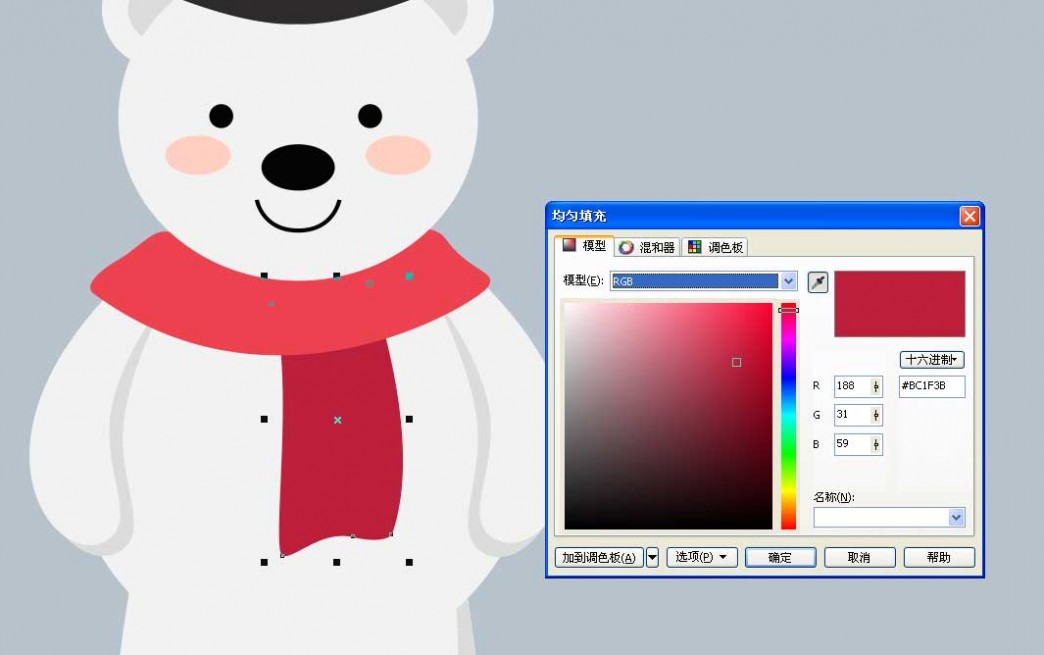
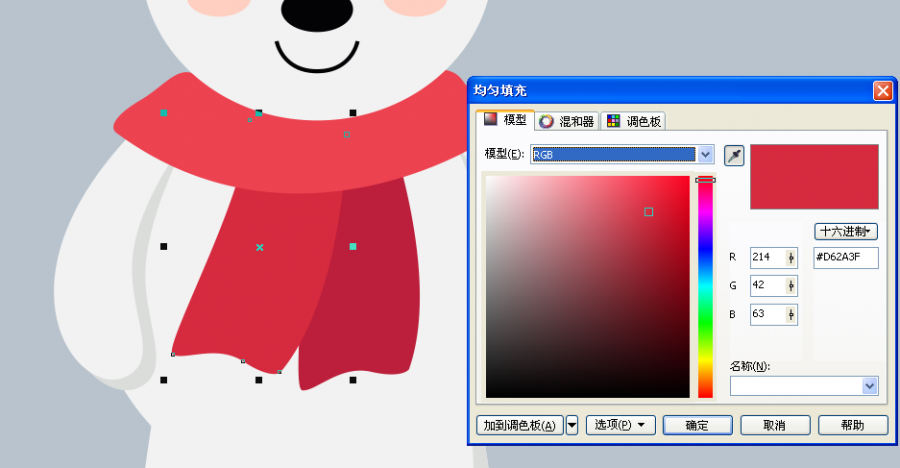
17、椭圆工具绘制一个阴影，绘制椭圆填充颜色置于熊的下层，如图

教程结束，以上就是CDR绘制两只可爱的卡通北极熊实例教程的全部内容，希望大家喜欢！

相关教程推荐：

CDR绘制可爱的卡通熊实例教程

CDR绘制可爱卡通的米老鼠教程

 Coreldraw(CDR)利用贝塞尔工具和交互式填充工具模仿绘制逼真的迪斯尼小熊维尼实例教程

四 : 已知椭圆方程怎样求椭圆的焦点坐标

已知椭圆方程怎样求椭圆的焦点坐标

已知椭圆方程怎样求椭圆的焦点坐标的参考答案

已知椭圆方程 x²/a²+y²/b²=1

焦点坐标是F1(-c,0) F2(c,0)

则 c²=a²-b²

本文标题：椭圆的极坐标方程-已知A，B，C是椭圆W：x24+y2=1上的三个点，O是坐标原点．（Ⅰ）当
本文地址： http://www.61k.com/1072382.html