一 : iOS应用中常用的临时层归纳
很多组件功能有重叠,使用的规则边界不甚明显,有些可替换使用。具体使用何种形式,需要结合自己的产品和业务目的决定。

《支付宝体验设计精髓》中根据页面元素的稳定性,将页面元素归纳为5个不同的层级,临时层指那些在页面中默认隐藏,需要时再展示的元素。

临时层包含弹窗、Toast提示、浮层弹窗、操作列表、全屏弹窗等,每种组件都有其适用的使用场景,合理的使用,能提高用户效率和使用体验。作为新接触 app 端设计的小白,为了规范自己的设计,总结了部分自己的理解,与大家交流。错误之处还请指正。因为工作以 iOS 端为主,故本文仅梳理了部分iOS应用中常用的临时层,并不仅限于iOS的规范组件。
弹窗(Alerts)Alerts 属于模态弹窗,用户必须处理后才可以继续原操作。弹窗是一种比较强的反馈形式,弹出时会阻断用户原操作,对用户任务的打断性很强。但频繁的打断用户会带给用户挫败感,同时也影响用户完成任务的效率,所以需要慎重使用。
弹窗由标题、内容、操作组成。内容描述文字并非必要,可以省略。一个好的弹窗要告知用户当前发生了什么及怎么解决。

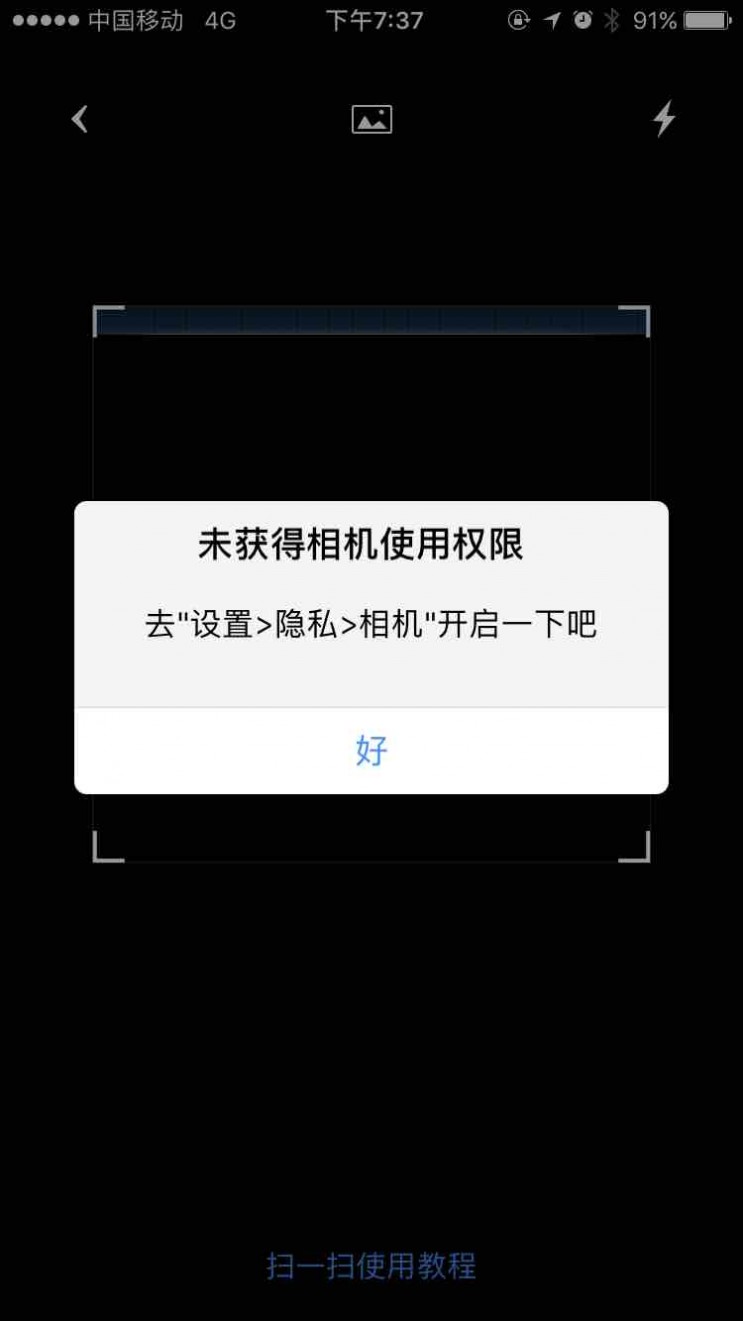
1.告知信息:弹窗用于告知用户一些会影响到他们使用 应用的重要信息,比如当使用扫一扫功能时,告知用户“没有开启相机权限”。关于重要信息的定义,不同产品可能有不同的理解,我认为大概需要满足 必要、重要、与当前任务相关这几个条件。
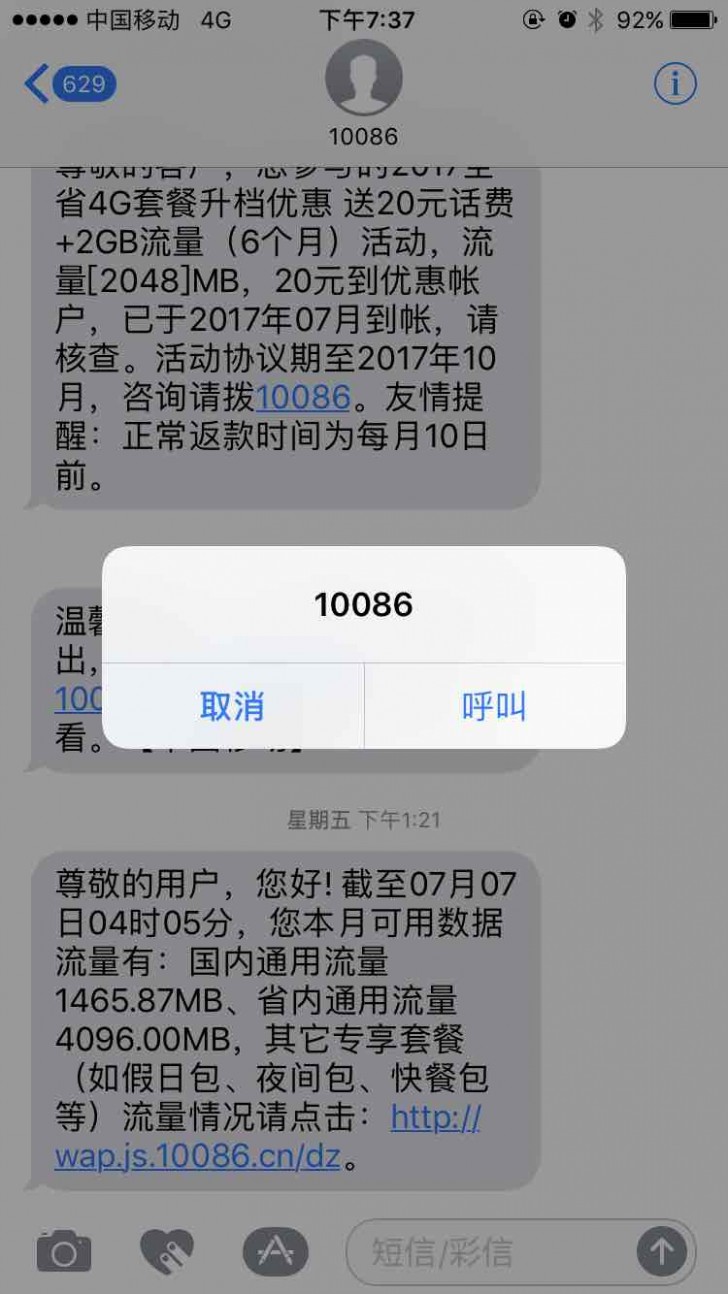
必要:当任务有前提条件需要满足时。比如使用扫一扫需要开启手机相机权限。 重要:当有重要信息需要告知用户,会对用户任务造成影响时。比如用户扫描失效二维码时,系统告知二维码已经失效,需要更换二维码。与当前任务相关:即在合理的时间展示,不要显示与当前任务无关的提示,保证用户专注于当前任务。2.快速操作:弹窗也用户执行一些可以快速执行的小任务,比如拨打电话。
操作列表展示了与用户触发操作直接相关的一系列选项。和弹窗相比操作列表对用户的干扰性稍弱,并支持点击页面空白区域关闭,一般是由用户主动操作触发。

在承载操作方便,和弹窗功能有重合,当操作大于3个时,改用操作列表。关于Alerts和操作列表的关系,可以理解成:严重且操作较少时使用alert,其他情况使用操作列表。
限制操作列表不支持滚动,需控制操作总数量,当操作过多时,可以使用网格式等其他自定义样式。
浮层弹窗从页面底部弹出的浮层,覆盖部分页面。弹出层相较于打开新页面,更轻量,用户可以更快速的完成任务,更快的返回修改。浮层里支持滚动操作。
关于浮层的收起,浮层应该有单独的关闭按钮,也支持点击浮层外区域收起。
当允许用户点击浮层外区域收起时,可以使用户快速切换浮层状态,但也会带来误触问题。所以,当浮层内有用户耗费精力完成的内容时,收起时要记录用户完成的工作,方便用户再次打开浮层时可以继续。
有时,比如支付环节,我们不希望用户轻易跳出,或用户退出后不保存浮层内结果时,可以仅允许用户点击关闭按钮才能退出。
使用情景和当前内容相关的小体量的任务:如选择支付宝付款码页,选择付款方式。任务和当前页面需要频繁切换以便校验或修改信息时:如淘宝的添加购物车浮层、查看物流信息等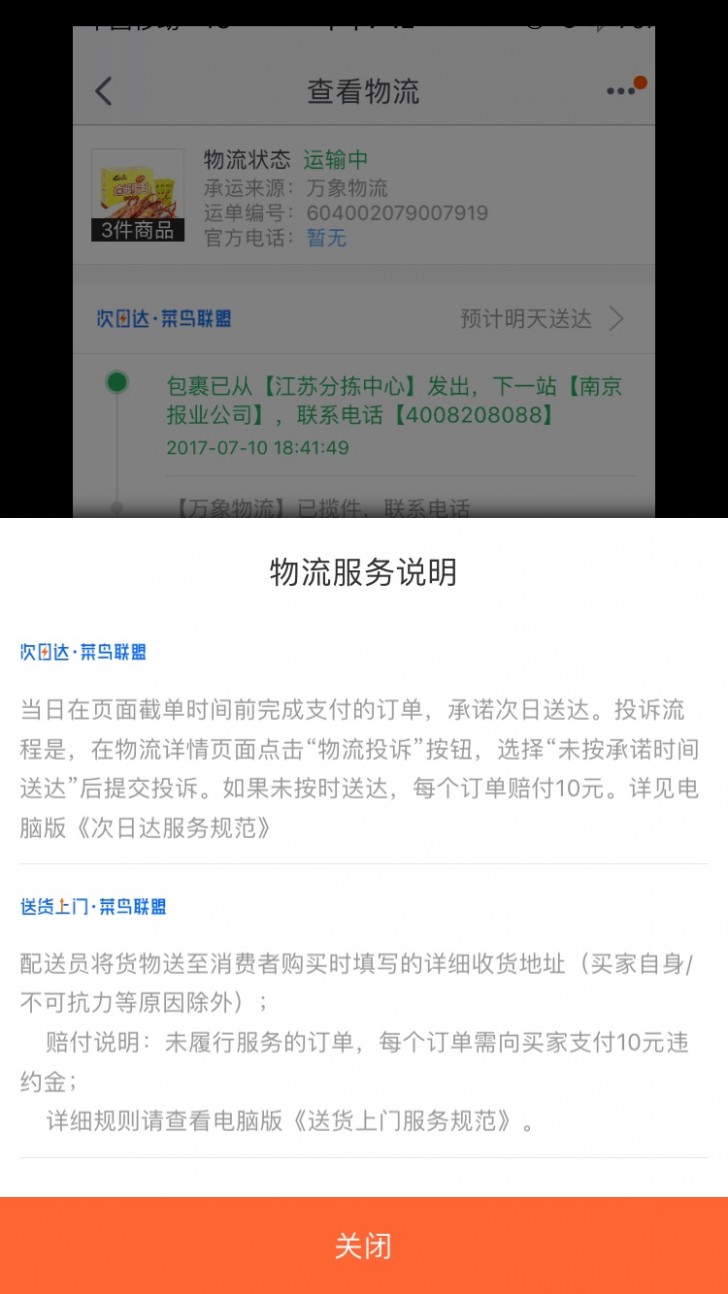
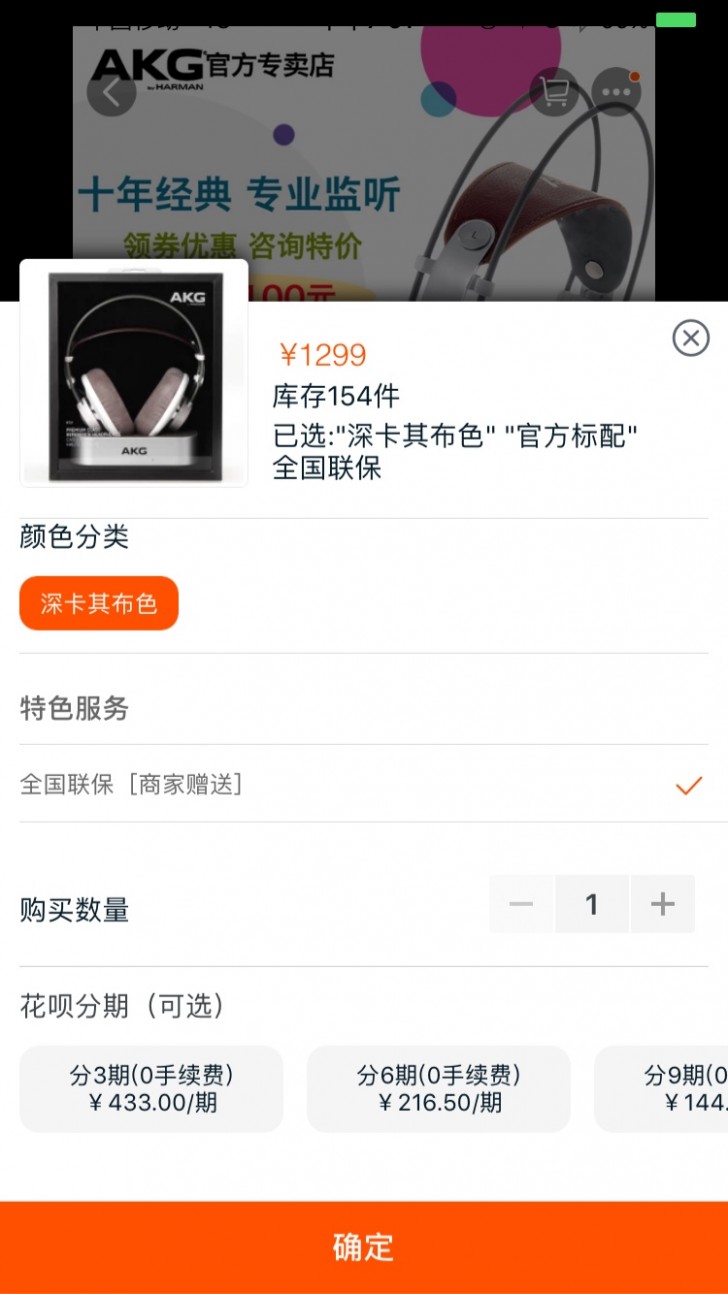
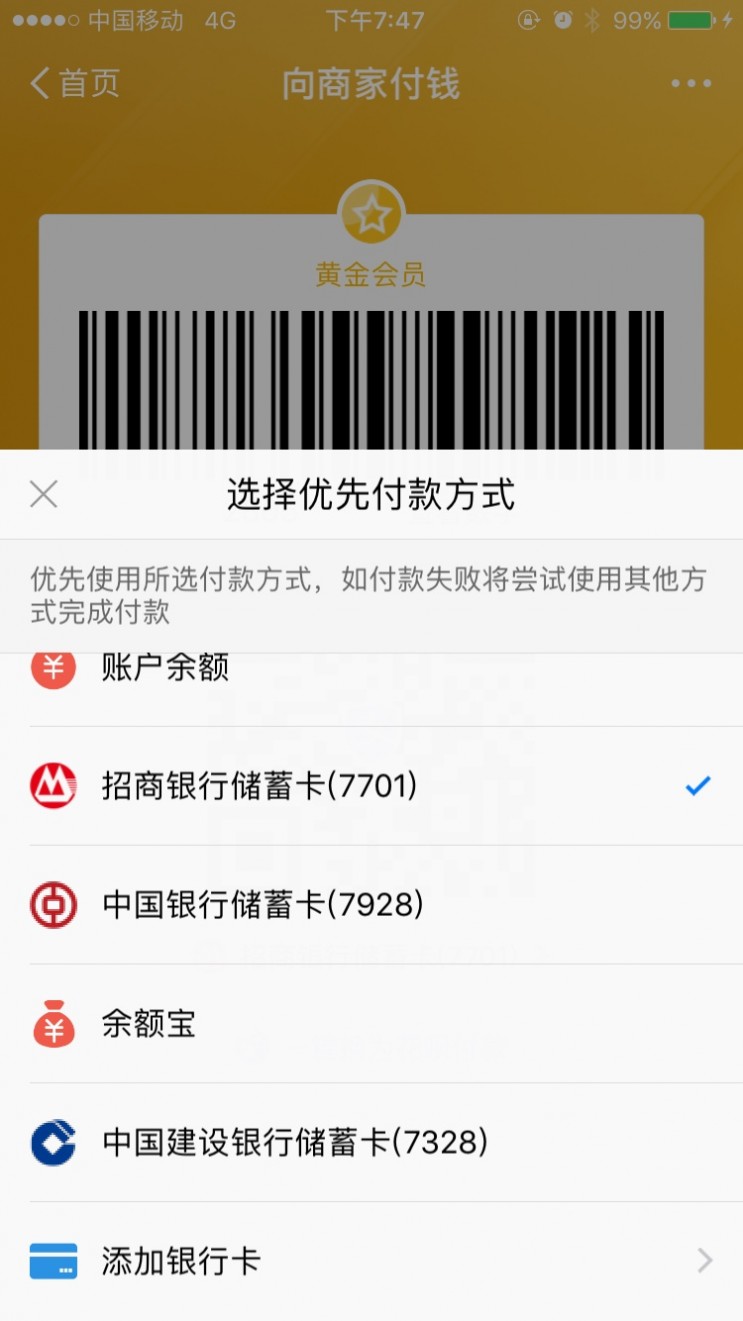
浮层空间较小,不适合承载复杂任务。
全屏弹窗在MATERIAL DESIGN 中被称为全屏弹窗,在iOS规范中被称为模态视图。和浮层弹窗相比,面积更大,可以完成更复杂的任务。全屏弹窗由页面底部向上弹出,退出时,向下收起。
使用全屏弹窗和新页面执行任务,一个明显区别是回到原页面的方式,全屏弹窗通过点击左上角的关闭,子级新页面通过点击左上角的“返回”。在iOS应用中,关于全屏弹窗的使用,似乎没有统一规范可循,比如同样是切换城市,美团使用全屏弹窗,支付宝使用子页面。
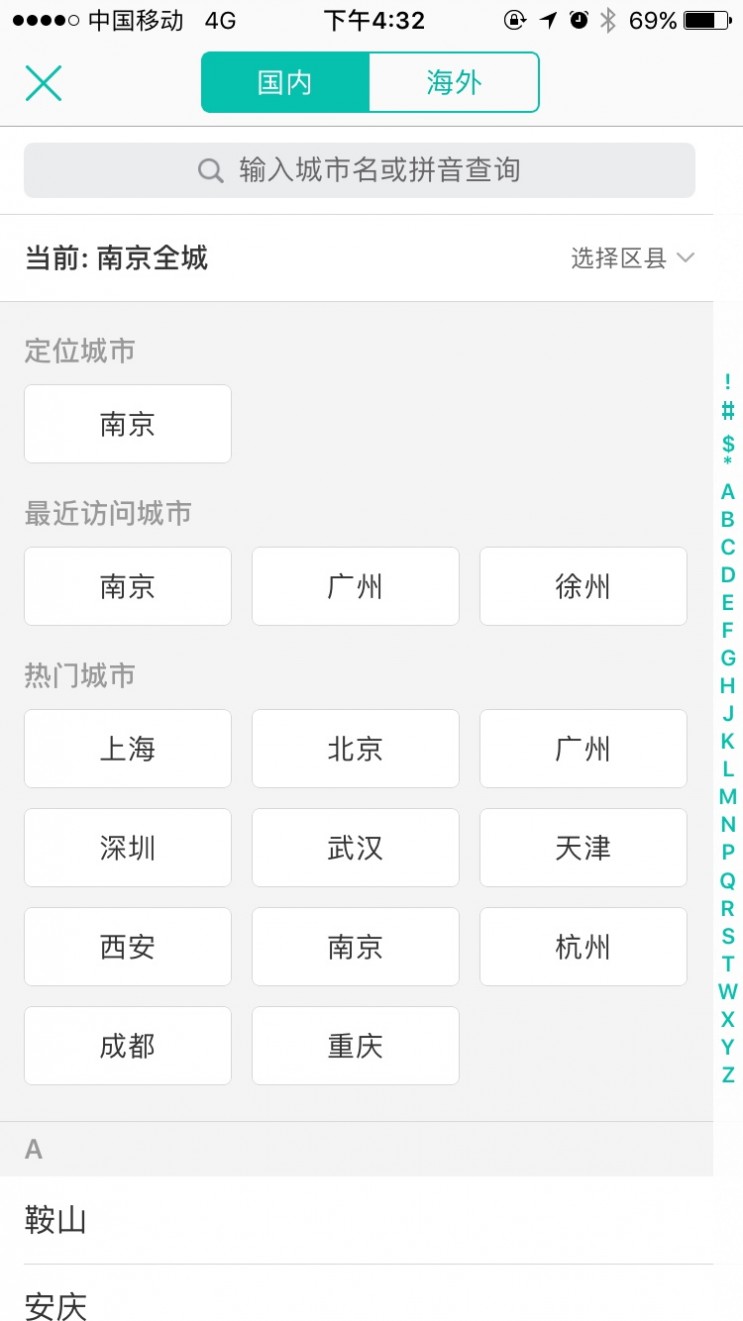
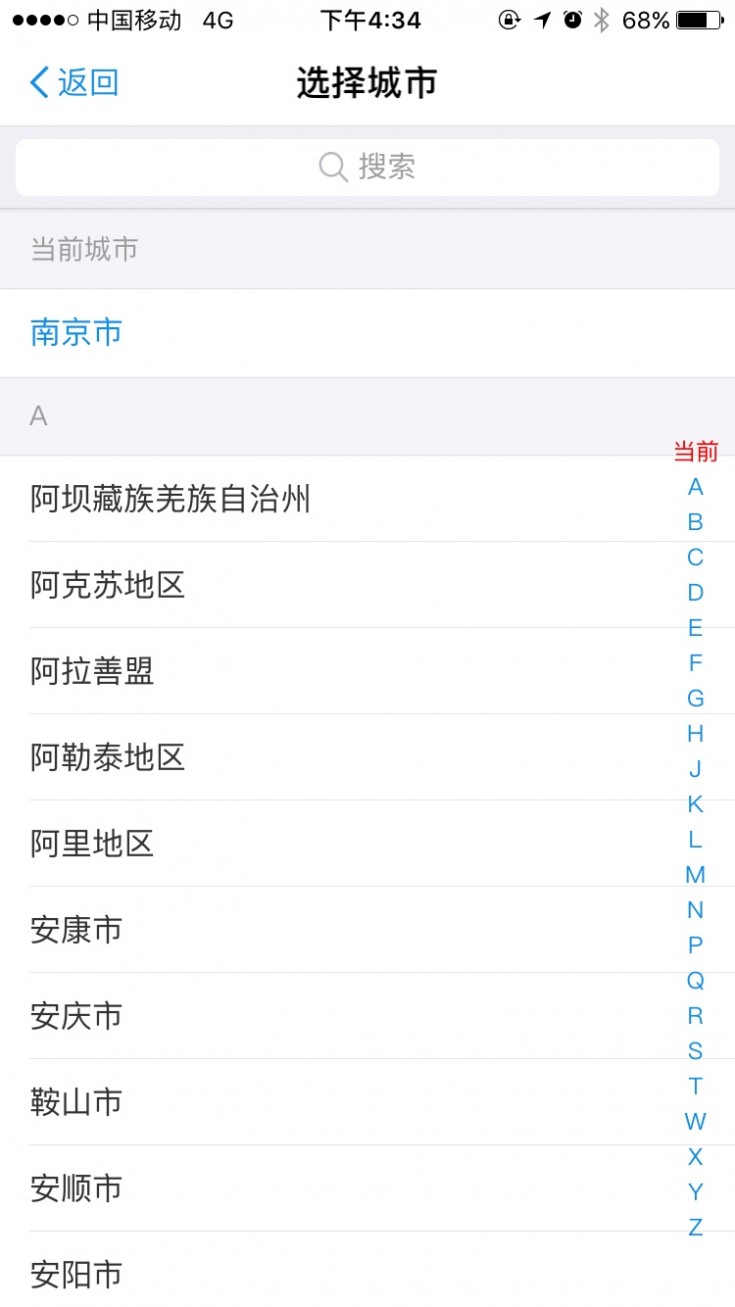
必须点击“保存”,页面内容才能生效。
ToastsToasts 是一种干扰性更弱的信息反馈方式,短暂出现后会自动消失,不会打断用户任务流程。

和 Alerts 相比,toasts适用于一些不严重的信息的反馈,比如发送成功、表单项校验等
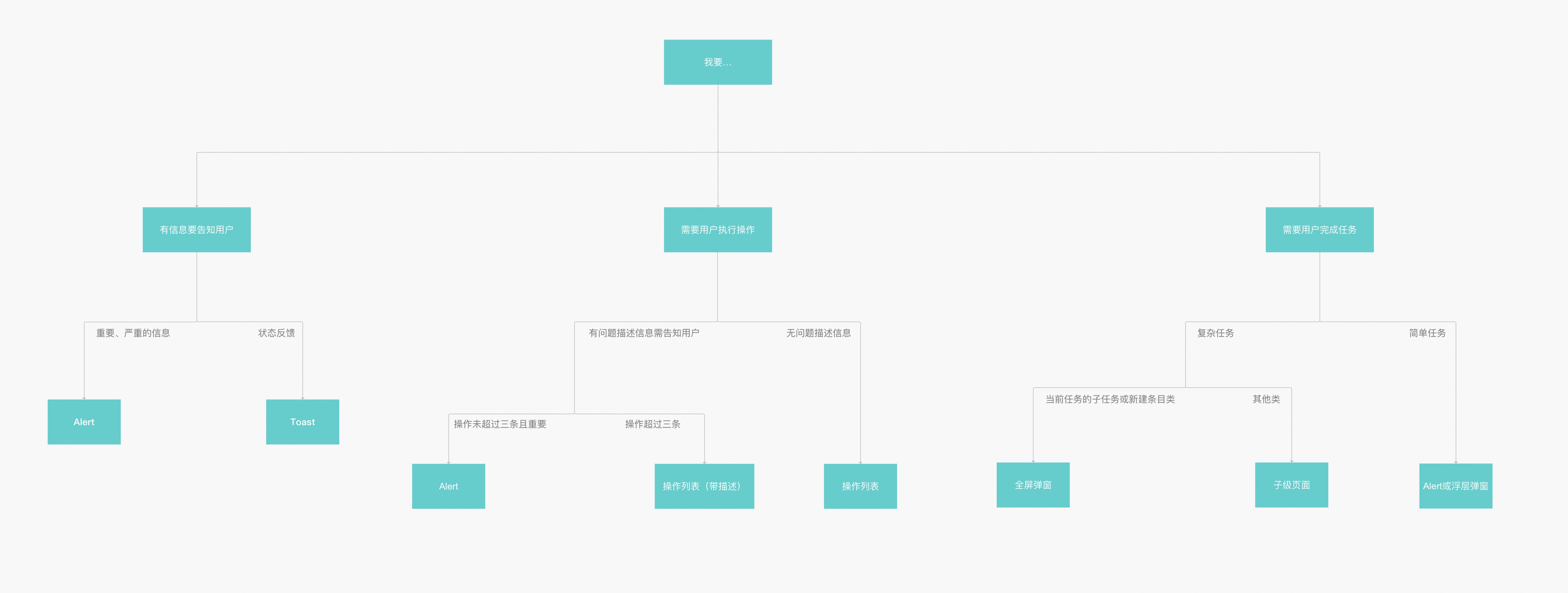
总结综上分析,很多组件功能有重叠,使用的规则边界不甚明显,有些可替换使用。具体使用何种形式,需要结合自己的产品和业务目的决定。从任务情景出发,我将上面的内容归于下面的图,方便判断该使用何种形式。
文章作者系 @m. 未经许可,禁止转载。
二 : 谈量词“个”的用法
“个”作为一个量词,它的使用范围十分广泛。它可以修饰没有专用量词的名词,如人、馒头、国家、苹果等等;同时,一些有专用量词的事物,如“一只耳朵”、“一所学校”、“一家工厂”等也都可以用“个”来修饰,成为“一个耳朵”、“一个学校”、“一个工厂”,因此,有人称“个”为“万能量词”。但是任何一个量词都有它的适用范围,“个”也不可能是万能的,哪儿都适用,有些事物就不能用“个”作量词。这可以分为以下几种事物:
1.细长条的事物
“一根绳子”、“一条蛇”、“一条路”,这里的量词“根”、“条”都是表现了一种细长的形体,不能用“个”来替代。这种细长的形状可以指较实在的物体,也可以指较虚的一些事物,如“一线光明”、“一绺头发”、“一丝细雨”等。
这些事物也不能用“个”来作量词。另外,在指称植物时,我们常常用“棵”和“株”这两个量词来体现植物的那种修长、向上的特点,故此,我们也不能说成“一个树”、“一个草”。
2.能够在平面上展开,且较薄的事物
我们说“一张纸”、“一面红旗”、“一幅画”,但不能说“一个纸”、“一个红旗”、“一个画”。当“片”用于某种较抽象事物时,如“一片欢腾”、“一
片歌声”也不能用“个”。这是因为在这里“片”在一定程度上表现出一个“面”的概念来。
3.立体的且表现出一定形状的事物
“一块砖”、“一团面”、“一坨泥”,不能说成“一个砖”、“一个面”、“一个泥”。
4.有些事物形状不固定,具有一定的流动性,如水、油等,而有的事物虽有一定的形状,但由于其颗粒细小,在实际使用中常常不能以颗粒计数,如米、沙等。这些事物,我们一般用容器或度量衡来计量,如“一杯水”、“一壶油”、“一
斤米”、“一碗沙子”等,这些我们也不能用“个”来替换。
5.有些事物只是属于一个整体事物中的一部分,适用于它们的量词有“层”、“重”、“级”、“节”、“段”、“截”等。用这些量词来修饰的事物,如“(一层)楼”、“(一重)山”、“(一级)台阶”、“(一节)甘蔗”、“(一段)木头”、“(一截)电线”也不能用“个”来修饰。
由动词转化过来的量词不能用“个”代替。如“一捆柴”、“一把米”、“一撮毛”、“一抱草”、“一包糖”、“一任县长”、“一束花”、“一串糖葫芦”、“一堵墙”、“一服药”、“一堆土”、“一封信”、“一滴水”,中的量词都不能用“个”来代替。这又可分成两种情况:一类如捆、抱、把、撮、包、串、束、堆等,它们本身就具有集合义,“个”是个体量词,所以不适用。封、服这类词在由动词转化过来时,仍带有一定的动量性,如:“一封信”,是指“一个封了口的信”,“一服药”是指“一次服用的药”,用“个”这个量词来代替,意义就不一样了。
由名词转化过来的量词,也不能用“个”来代替,如“一朵花”、“一本书”、“一篇文章”、“一瓣花瓣”中的“朵、本、篇、瓣”实际上是由名词“花朵、书本、篇章、花瓣”等转过来的,也是为了突出这些事物的特征,因此转为量词后,一般不能用“个”来代替。
我们也要看到,“个”在作一些有专用量词的事物的量词时,往往会改变话语的感情色彩,如我们可以说“一位老先生”,也可以说“一个老先生”,但二者的感情色彩却不一样,“位”表示尊敬之意,而“个”则不带任何感情。“个”也不能体现出事物的形状,如“一颗珍珠”,我们能够从量词“颗”知道珍珠的形状应该是圆而小的东西,如果说“一个珍珠”就很难想象珍珠的形状了。
三 : 浅谈BroadcastReceiver的用法
最近看了下关于广播方面的东西,加深了理解,也纠正了自己以前的不正确的看法。(www.61k.com)
关于广播有2中注册方式,一种是在代码中注册,也叫动态注册,另一种是在AndroidManifest里面注册,也叫静态注册。
不管在哪个里面注册,都需要发送广播sendBroadcast()。广播发送的是一个Intent,intent里面一般是action。
如果是在代码里面注册,一般在onResume()方法里面注册。
1 @Override
2 protected void onResume() {
3 // TODO Auto-generated method stub
4
5 myReceiver = new MyReceiver();
6 IntentFilter filter = new IntentFilter();
7 //向过滤器中添加action
8 filter.addAction("com.android.shang");
9 //注册广播
10 registerReceiver(myReceiver, filter);
11
12 Intent intent = new Intent();
13 intent.setAction("com.android.xiang");
14 //发送广播
15 sendBroadcast(intent);
16 super.onResume();
17 }
在onPause()方法里面要取消注册。
1 @Override
2 protected void onPause() {
3 // TODO Auto-generated method stub
4 unregisterReceiver(myReceiver);
5 super.onPause();
6 }
当然,也可以在xml文件中注册:
1 <receiver
2 android:name=".MyBrocastReceiverTest">
3 <intent-filter>
4 <action android:name="com.android.xiang"></action>
5 </intent-filter>
6 </receiver>
如果发送的广播的action已经注册了,那么在onReceive()方法中就会接收到发过来的广播,继而做出一些处理。
你可以写出一个内部类:
1 class MyReceiver extends BroadcastReceiver {
2
3 @Override
4 public void onReceive(Context context, Intent intent) {
5 // TODO Auto-generated method stub
6 //从这里的log中可以看到是否接受到了广播
7 System.out.println("intent = " + intent);
8 }
9
10 }
当然也可以单独写一个类:
package com.android.TestBrocastReceiver;
import android.content.BroadcastReceiver;
import android.content.Context;
import android.content.Intent;
public class MyBrocastReceiverTest extends BroadcastReceiver {
@Override
public void onReceive(Context context, Intent intent) {
// TODO Auto-generated method stub
System.out.println("intent = " + intent);
}
}
一般如果在代码里面注册,就把广播写在代码里面,在xml文件中注册就单独写一个类。
注册在代码里面:
1 package com.android.TestBrocastReceiver;
2
3 import android.app.Activity;
4 import android.content.BroadcastReceiver;
5 import android.content.Context;
6 import android.content.Intent;
7 import android.content.IntentFilter;
8 import android.os.Bundle;
9
10 public class TestBrocastReceiver extends Activity {
11
12 MyReceiver myReceiver;
13
14 @Override
15 public void onCreate(Bundle savedInstanceState) {
16 super.onCreate(savedInstanceState);
17 setContentView(R.layout.main);
18 }
19
20 @Override
21 protected void onPause() {
22 // TODO Auto-generated method stub
23 unregisterReceiver(myReceiver);
24 super.onPause();
25 }
26
27 @Override
28 protected void onResume() {
29 // TODO Auto-generated method stub
30
31 myReceiver = new MyReceiver();
32 IntentFilter filter = new IntentFilter();
33 //向过滤器中添加action
34 filter.addAction("com.android.shang");
35 //注册广播
36 registerReceiver(myReceiver, filter);
37
38 Intent intent = new Intent();
39 intent.setAction("com.android.xiang");
40 //发送广播
41 sendBroadcast(intent);
42 super.onResume();
43 }
44
45 class MyReceiver extends BroadcastReceiver {
46
47 @Override
48 public void onReceive(Context context, Intent intent) {
49 // TODO Auto-generated method stub
50 //从这里的log中可以看到是否接受到了广播
51 System.out.println("intent = " + intent);
52 }
53 }
54 }
注册在xml文件中:
在xml文件中注册,写上一个广播类,然后在activity中发送广播就可以了。
有时系统会发出一些广播,比如说时间的变化等,时间走一秒就会发一个广播,这时我们可以监听这个广播,然后在接收器中做处理就可以了,而不需要在发广播了。
四 : 数学归纳法在中学数学中的应用
摘要:文章详尽阐述了数学归纳法在高中数学中的一些相关应用,通过对它基本形式的学习和理解,对数学归纳法在解决和正整数相关的类型题中的作用做出肯定。[www.61k.com)对与正整数有关的恒等式、不等式、整除性问题和几何问题等,用相应的实例进行解析说明在各类型中数学归纳法的具体应用。在很多时候学生的错误就是在于不能真正理解数学归纳法和存在的一些数学归纳法应用的思维定势。我们应该去除学生在学习归纳法时的这些弊端,充分了解它的好处和局限,更好的去应用它来帮助我们解决相应的问题。
关键词:归纳法;应用数学;教学
中图分类号:FG633.6 文献标志码:A 文章编号:1673-291X(2011)14-0304-02
数学归纳法是高中数学中一种常用的论证方法,它虽然有一定的局限性,只适用和正整数有关的命题,但它在中学数学中的作用是不可或缺的。因此,它不仅是高考数学的一个考点,也是一个难点。在看似简单易懂,形式固定的外表下,它却使得很多学生不能真正掌握,难以理解其实质。有些同学仅仅只是生硬的记忆和牵强的套用,没有真正体会到数学归纳法的核心思想。我们应该怎样理解数学归纳法,在高中数学中又有哪些方面的应用?在哪些类型题上使用可以更加方便?数学归纳法又有哪些局限性?我们应该怎样具体问题具体分析,更好的学习和利用数学归纳法呢?
在本文中通过对数学归纳法基本形式理解的基础上,进一步论述了在解决很多和自然数函数有关的整式、不等式、整除和几何等问题时数学归纳法的应用。当然数学归纳法,在很多时候也会使解题变的复杂繁琐,因此我们要理解其实质,真正掌握正确运用数学归纳法的能力。
数学归纳法的基本形式:
(1)验证当n取第一个值时,命题正确:
(2)假设n=k时命题正确,证明n=k+1时命题也正确:
(3)根据(1) (2)断定命题对于全体自然数都正确。
例1: 证明n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2(n∈N*)
证明:(1)当n=1时,左边=1=右边,等式显然成立。
(2)假设n=k时等式成立,即k+(k+1)+(k+2)+…+(3k-2)=(2k-1)2
那么,当n=k+1时,有
(k+1)+(k+2)+…+(3k-2)+(3k-1)+3k+(3k+1)
=[k+(k+1)+(k+2)+…+(3k+2)]
=(2k-1)2+8k=(2k+1)2=[2(k+1)-1]2
即当n=k+1时,等式也成立。故对于任意正整数n等式都成立。
通过数学归纳法基本形式和例题可以看出其原理就是递推思想,其中(1)是递推的基础,没有它归纳假设就失去了依据,后面递推就没有了奠基。(2)是递推的依据是数学归纳法证明最根本的一步,是整个数学归纳法证明的核心,只有通过它无限次递推成为可能,人们的认识才达到了质的飞越——通过有限认识无限,所以数学归纳法的两个步骤缺一不可。
数学归纳证题的两个步骤虽然都很重要,但在证题时第一步较易,第二步较难。学生往往感到很困难,绞尽脑汁都难以完成这一步,到底我们应该怎样转化,不同的问题我们又应该怎样去解决?下面我们来探讨一下数学归纳法在中学数学中的应用。
一、应用数学归纳法证明恒等式
应用数学归纳法证明的恒等式,包括与正整数有关的代数恒等式、三角恒等式、组合数公式及其恒等式等,证明过程中只要实现等式左右两边相等即可。
例1:用数学归纳法证明: n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2(n∈N*)
证明:(1)当n=1时,左边=1=(2×1-1)2=右边,等式成立。
(2)假设n=k时,等式成立,即k+(k+1)+(k+2)+…+(3k-2)=(2k-1)2
那么,当n=k+1时有
(k+1)+(k+2)+…+(3k-2)+(3k-1)+3k+(3k+1)
=[k+(k+1)+(k+2)+…+(3k+2)]+8k
=(2k-1)2+8k
=4k2+4k+1
=(2k+1)2
=[2(k+1)-1]2
即当n=k+1时,等式也成立,故对于任意正整数n,等式都成立。
二、应用数学归纳法证明不等式
应用数学归纳法证明不等式,分为严格不等式和非严格不等式两种,严格不等式的证明,只要保证原不等式中的“>”或“<”成立即可。对于非严格不等式而言,情况略显复杂。
例2:已知x1,x2,x3,…,xn都是正数,试证:
+++…≥x1,x2,x3…,xn
证明:(1)当n=1时,因为=x1,所以原不等式成立(取等号)
(2)假设当n=k时原不等式成立,即
+++…≥x1,x2,x3…,xk
那么,当n=k+1时,不等式的左边
+++…+=(+++…)-++≥x1+x2+x3+…+xk++(*)
显然,只要证明
+≥xk-1
原不等式即可得证。但此式难以直接证明,经仔细观察发现,原不等式关于变量x1,x2,x3…,xn是轮换对称的,于是不妨设xk-1=max{x1,x2,x3,…,xk,xk-1},则xk-12-xk2>0。
+≥+==xk-1
故当n=k+1时,不等式也成立。即原不等式对于所有自然数都成立。
三、应用数学归纳法证明整除问题
应用数学归纳法证明整除性问题,是数学归纳法的重要应用之一。这类问题涉及到整除性的知识,如果a能被c整除,那么a的倍数ma也能被c整除,如果a,b都被c整除,那么它们的和或差a±b也能被c整除,从整数的基本入手,通过添项去项进行”配凑“,使之能够获证。
例3:证明f(n)=5n+2•3n+1能被8整除。
证明:(1)当n=1时,f(n)=5n+2•3n+1=8显然能被8整除,命题成立。
(2)假设当n=k时,原命题成立,即f(k)=5k-1+2•3k+1能被8整除,那么,当n=k+1时,f(k+1)=5k-1+2•3k+1
=5•5k+6•3k+1+4•3k-1-4•3k-1
=5•5k+10•3k-1+5-4•3k-1-4
=5•f(k)-4(3k-1+1)
这里第一项由归纳假设能被8整除,第二项中3k-1是奇数,则3k-1+1是偶数。故第二4(3k-1+1)能被8整除,由整除性质可知,它们的差也能被8整除,这就是说:当n=k+1时命题也成立。即原命题对所有自然数n都成立。
四、应用数学归纳法证明几何问题
应用数学归纳法证明几何问题是数学归纳法的一个重要应用。数学归纳法是证明与正整数有关的命题的重要方法,但是运用它只能证明命题的正确性,而不能指望由它发现命题。有很多与正整数有关的几何问题,可以用数学归纳法证明,但在证明之前要找出规律,获得公式,而后才能应用数学归纳法证明结论。
例4:证明凸n边形的对角线的条数f(n)=n(n-3).(n≥3)
证明:(1)当n=3时,f(3)=0,因三角形没有对角线,所以原命题成立。
(2)假设:当n=k(n≥3)时命题成立,即凸k边形的对角线条数为f(k)=k(k-3)。那么当n=k+1,凸k边形的k个顶点增加一个顶点Ak-1成为凸k+1边形时,由顶点Ak-1与它不相邻的另外k-2个顶点A2,A3,A4,…,Ak-1可画出k-2条对角线,同时原来凸k边形的一条边A1Ak变成一条对角线。这样从凸k边形到凸k+1边形一共增加了k-1条对角线。由此凸 边形的对角线条数为:
f(k+1)=f(k)+(k+1)
=k(k-3)+(k-1)
=(k2-k-2)
=(k+1)(k-2)
=(k+1)[(k+1)-3]
这就是说,当n=k+1时,命题也成立。
需要指出,虽然数学归纳法是一种论证与自然数有关的命题的重要方法,但并非结论是自然数的函数的命题都适合用数学归纳法证明。有些题目应用数学归纳法进行证明,过程相当繁琐,尤其是由n=k到n=k+1的变化过程很多,不易操作。事实上,很多与正整数有关的命题,若能避开数学归纳法的思维定势,利用其命题本身的特点,采用非数学归纳法的证明,则能避繁就简。
例5:n∈N*,求证1+++…+<2。
证:令bn=2,则bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)
当n≥2时,bn-bn-1=2(-)=>=,从而1+++…+<b1+(b2-b1)+…+(bn-bn-1)=bn=2
即1+++…+<2。
通过以上例题,只是想说明对于有关自然数的命题的证明,不一定都采用数学归纳法这一种方法而应该针对题目本身的特点,选择适当的方法达到简化证明过程的目的。从另一个角度来讲也能克服学习中的思维定势,使知识融会贯通,灵活运用。
以上我们对数学归纳法的基本形式,及在中学数学中和自然数函数有关的整式、不等式、整除问题和几何问题等,一些常见题型中的应用做了简单的举例,并通过相应的例题对这几种方法进行了解析,使学生对数学归纳法有了更进一步的了解。纵观科学技术迅猛发展的当今时代,我们对数学归纳法的研究已经取得了很大的进步,对于它的更加优越的性质和更广泛的应用仍需要我们继续努力钻研。深入探讨数学归纳法的相关性质,究竟何时使用归纳法何时不使用,中学数学归纳法还有哪些应用,还有待同学仔细研究和探索。
论文联盟 www.61k.com
参考文献:
[1] 刘世泽.数学归纳法的另外两种形式[J].数学通报,1994,(1).
[2] 杨玉声.归纳法与数学归纳法及其应用[J].中学理科,1999,(Z2).
[3] 朱华伟,史亮.高中数学新课程标准中的归纳法[J].数学通讯,2005,(13).
五 : 浅谈awk的基本用法
awk
1.域和记录:
取第一域,并在开头和结尾加字符begin和end
通常使用BEGIN来显示变量和预置变量,使用END来输出最终结果。[www.61k.com]
awk ' BEGIN {print "being"} {print $1} END {print "end"}' file
2.条件操作符:
第一字域,包含expect,就打印整行
awk '{if($1~/expect/) print $0}' c.sh 或者 awk '$1~/expect/{print $0}' file
精确匹配:,只打印第3 域等于"48"的记录
awk '$3=="48" {print $0}' file
不等于: awk '$1 != "asima"' temp
不匹配: 打印整条不包含ASIMA 的记录
awk '$0 !~ /ASIMA/' temp
小于: awk '{if ($1<$2) print $1 "is smaller"}' temp
设置大小写: awk '/[Gg]reen/' temp 打印整条包含Green,或者green 的记录
任意字符: awk '$1 ~/^...a/' temp 打印第1 域中第四个字符是a 的记录,符号’^’
代表行首,符合’.’代表任意字符
AND 与关系: awk '{if ( $1=="a" && $2=="b" ) print $0}' temp
OR 或关系: awk '{if ($1=="a" || $1=="b") print $0}' temp
for循环
awk -F "," '{for (i=1;i<=NF;i++) if($i~/a=/) {print $i}}'
3.awk内置变量:

例: awk 'END {print NR}' temp 在最后打印已读记录条数
awk '{print NF,NR,$0} END {print FILENAME}' temp
awk '{if (NR>0 && $4~/Brown/) print $0}' temp 至少存在一条记录且包含Brown
NF 的另一用法: echo $PWD | awk -F/ '{print $NF}' 显示当前目录名
4. awk操作符:
在awk 中使用操作符,基本表达式可以划分成数字型、字符串型、变量型、域及数组元素
设置输入域到变量名:
awk '{name=$1;six=$3; if (six=="man") print name " is " six}' temp
域值比较操作:
awk 'BEGIN {BASE="27"} {if ($4<BASE) print $0}' temp
修改数值域取值:(原输入文件不会被改变)
awk '{if ($1=="asima") $6=$6-1;print $1,$6,$7}' temp
修改文本域:
awk '{if ($1=="asima") ($1="desc");print $1}' temp
只显示修改记录:(只显示所需要的,区别上一条命令,注意{})
awk '{if ($1=="asima") {$1="desc";print$1}}' temp
创建新的输出域:
awk '{$4=$3-$2; print $4}' temp
统计列值:
awk '(tot+=$3);END {print tot}' temp 会显示每列的内容
awk '{(tot+=$3)};END {print tot}' temp 只显示最后的结果
awk '{total+=$1}END{print total}' a.txt 只显示最后的结果
文件长度相加:
ls -l|awk '/^[^d]/ {print $8"\t"$5} {tot+=$5} END{print "totKB:" tot}'
只列出文件名:ls -l|awk '{print $9}' 常规情况文件名是第8域
5.awk打印除了第二列外所有列
cat /etc/passwd|awk -F: '{$2=null;print $0}' 就是把某一列制空
61阅读请您转载分享:
本文标题:浅谈数学归纳法的应用-iOS应用中常用的临时层归纳61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1