一 : 今天，奋斗的起点

　　昨天带着回忆默默的逝去，今天携着希望悄悄来临，而明天，又闪烁着光辉等待着人们。有沉浸在回忆中，他们依恋明天；有的人只迷醉在梦幻中，他们企盼着明天。这两种人，都忘了最应该珍惜的今天。

　　今天不就是短短的一天吗？我从明天开始勤奋学习，有些人是这样的想，也是这样的做。朋友，不觉不怀疑你的真诚，但为什么要把事情放到明天呢？日月匆匆，到了明天，明天又变成了今天，而每个今天之后都有无穷无尽的明天。那么，你的决心，你的力量理想，哪一天才能变成行动呢？变为现实呢？

　　莎士比亚说：“抛弃时间的人，时间也回抛弃他。”我说：“抛弃今天的人，今天也会抛弃他，而被今天抛弃的人，他也就没有了明天。”

　　“明日复明日，明日何其多，我生待明日，万事成蹉跎。”短短的几句诗，是先辈千折百曲历经磨难的生活体验的结晶啊！古人有感于此，于是有了“悬梁刺股”、“囊虫映雪”、“凿壁偷光”的勤学佳话。现在我们条件优越了，不是更应该珍惜，抓紧今天的分分秒秒吗？

　　抓住了今天，就是抓住了掌握获取知识的机会；抓住了今天，就是抓住发明创造的可能。聪明、勤奋、有志的人，他们深深懂得时间就是生命，甚至比生命还宝贵，他们决不会把今天宝贵时光虚掷给明天。

　　相反，对有些人来说，时间就像代表它的那本日历，撕了这张，还有下一张，撕完了这一本，还有下一本，却不知道在洁白如雪的日历上留下自己辛勤奋斗的汗水和学习、工作的收获。那样，他们从呱呱落地到长眠地下，都是在闲散和观望，等待之中度过的，如果人的一生如此度过，那么消逝的岁月将如一场凄凉的悲剧，留在个人生命史上的回忆，将拌和着悔恨、痛惜和哀伤的泪水……

　　朋友，不要沉湎昨天，不要观望明天，一切从现在开始，从今天开始吧！

　　今天，是奋斗的起点！

本文地址：

二 : 我奋斗了18年不是为了和你一起喝咖啡PK我奋斗了18年才和你坐在一起喝咖

编者语：大概5年前，编者在网上看到“我奋斗了18年才和你坐在一起喝咖啡”的贴子时，不甚唏嘘；5后，又偶尔看到“我奋斗了18年不是为了和你一起喝咖啡”一文，又顿生感慨之情。而网友都市隐士评论“其实我们都应该感恩，因为不论贫贱，我们都来到了这个世界，都在品味这个世界的生活，我们都生存着，并会平等的迈入坟墓”之精彩深隧，以及网友赌侠说“我们出生的时候，上帝已发好了牌，抓的牌好与不好，我们已无法抗拒，我们唯一能做的，就是把手中的牌出好，哪怕是一把烂牌”之积极进取，让编者不禁有“奇文共欣赏”之念，遂编辑成文，以飨读者。我奋斗了18年才和你坐在一起喝咖啡□文|麦子我的白领、金领、黑领朋友们，如果我是一个初中没毕业就来沪打工的民工，你会和我坐在“星巴克”一起喝咖啡吗？不会，肯定不会。比较我们的成长历程，你会发现，为了一些在你看来唾手可得的东西，我却需要付出18年的努力。从我出生的一刻起，我的身份就与你有了天壤之别，因为我只能报农村户口，而你是城市户口。如果我长大以后一直保持农村户口，那么我就无法在城市中找到一份正式工作，无法享受养老保险、医疗保险。你可能会问我：“为什么非要到城市来？农村不很好吗？空气新鲜，又不像城市这么拥挤。”可是农村没有好的医疗条件，那年SARS好像让大家一夜之间发现农村的医疗保健体系竟然如此落后，物质供应也不丰富，因为农民挣的钱少，贵一点儿的东西就买不起，所以商贩也不会进太多货。春节联欢晚会的小品中买得起等离子彩电的农民毕竟是个别现象，绝大多数农民还在为基本的生存而奋斗，于是我要进城，要通过自己的奋斗获得你生下来就拥有的大城市户口以及户口带来的相关待遇。考上大学是我跳出农门的唯一机会。我要刻苦学习，小学升初中，初中升高中，高中考大学，我在独木桥上奋勇搏杀，眼看着周围的同学一批批落马，前面的道路越来越窄，我这个佼佼者心里不知是喜是忧。激烈的竞争让我不敢疏忽，除了学习功课，我无暇顾及业余爱好，学校也没有这些发展个人特长的课程。进入高中的第一天，校长就告诉我们这三年只有一个目标——高考。于是我披星戴月，早上5：30起床，晚上11：00睡觉，就连中秋节的晚上，我还在昏暗的路灯下背政治题。而你的升学压力要小得多，竞争不是那么激烈，功课也不是很沉重，你可以有充足的时间去发展个人爱好，去读课外读物，去球场挥汗如雨，去野外享受蓝天白云。如果你不想那么辛苦去参加高考，只要成绩不是太差，你可以在高三时有机会获得保送名额，哪怕成绩忒差，也会被“扫”进一所本地三流大学，而那所三流大学我可能也要考到很高的分数才能进去，因为按地区分配的名额中留给上海本地的名额太多了。我们的考卷一样我们的分数线却不一样，但是当我们都获得录取通知书的时候，所交的学费是一样的。每人每年6000元，四年下来光学费就要2.4万元，再加上住宿费每人每年1500元，还有书本教材费每年1000元、生活费每年4000元（只吃学校食堂），四年总共5万元。2003年上海某大学以“新建的松江校区环境优良”为由，将学费提高到每人每年1万元，这就意味着仅学费一项四年就要4万元，再加上其他费用，总共6.6万元。6.6万元对于一个上海城市家庭来说也许算不上沉重的负担，可是对于一个农村的家庭，这简直是一辈子的积蓄。我的家乡在东部沿海开放省份，是一个农业大省，相比西部内陆省份应该说经济水平还算比较好，但一年辛苦劳作也剩不了几个钱。以供养两个孩子的四口之家为例，除去各种日常必需开支，一个家庭每年最多积蓄3000元，那么6.6万元上大学的费用意味着22年的积蓄！前提是任何一个家庭成员都不能生大病，而且另一个孩子无论学习成绩多么优秀，都必须剥夺他上大学的权利，因为家里只能提供这么多钱。我属于比较幸运的，东拼西凑加上助学贷款终于交齐了第一年的学费，看着那些握着录取通知书愁苦不堪全家几近绝望的同学，我的心中真的不是滋味。教育产业化时代的我终于可以如愿以偿地在大学校园里汲取知识的养分！努力学习获得奖学金，假期打工挣点生活费，我实在不忍心多拿父母一分钱，那每一分钱都是一滴汗珠掉在地上摔成八瓣挣来的血汗钱啊！来到上海这个大都市，我发现与我的同学相比我真是土得掉渣。我不会作画，不会演奏乐器，不认识港台明星，没看过武侠小说，不认得MP3，不知道什么是walkman，为了弄明白营销管理课上讲的“仓储式超市”的概念，我在“麦德隆”好奇地看了一天，我从来没见过如此丰富的商品。我没摸过计算机，为此我花了半年时间泡在学校机房里学习你在中学里就学会的基础知识和操作技能。我的英语是聋子英语、哑巴英语，我的发音中国人和外国人都听不懂，这也不能怪我，我们家乡没有外教，老师自己都读不准，怎么可能教会学生如何正确发音？基础没打好，我只能再花一年时间矫正我的发音。我真的很羡慕大城市的同学多才多艺，知识面那么广，而我只会读书，我的学生时代只有学习、考试、升学，因为只有考上大学，我才能来到你们中间，才能与你们一起学习，所有的一切都必须服从这个目标。我可以忍受城市同学的嘲笑，可以几个星期不吃一份荤菜，可以周六周日全天泡在图书馆和自习室，可以在周末自习回来的路上羡慕地看着校园舞厅里的成双成对，可以在寂寞无聊的深夜在操场上一圈圈地奔跑。我想有一天我毕业的时候，我能在这个大都市挣一份工资的时候，我会和你这个生长在都市里的同龄人一样——做一个上海公（www.61k.com）民，而我的父母也会为我骄傲，因为他们的孩子在大上海工作！终于毕业了，在上海工作难找，回到家乡更没有什么就业机会。能幸运地在上海找到工作的应届本科生只有每月2000元左右的工资水平，也许你认为这点钱应该够你零花的了，可是对我来说，我还要租房，还要交水电煤电话费还要还助学贷款，还想给家里寄点钱让弟妹继续读书，剩下的钱只够我每顿吃盖浇饭，我还是不能与你坐在“星巴克”一起喝咖啡！如今的我在上海读完了硕士，现在有一份年薪七八万的工作。我奋斗了18年，现在终于可以与你坐在一起喝咖啡。我已经融入到这个国际化大都市中了，与周围的白领、金领朋友没有什么差别。可是我无法忘记奋斗历程中那些艰苦的岁月，无法忘记那些曾经的同学和他们永远无法实现的夙愿。于是我以第一人称的方式写下了上面的文字，这些是典型的中小县城和农村平民子弟奋斗历程的写照。每每看到正在同命运抗争的学子，我的心里总是会有一种说不出的辛酸与欣慰之情。写这篇文章不是为了怨天尤人，这个世界上公平是相对的，这并不可怕，但是对不公平视而不见是非常可怕的。我在上海读硕士的时候，曾经讨论过一个维达纸业的营销案例，我的一位当时曾有三年工作经验，现任一家中外合资公司人事行政经理的同学，提出一个方案：应该让维达纸业开发高档面巾纸产品推向9亿农民市场。我惊讶于她提出这个方案的勇气，当时我问她是否知道农民兄弟吃过饭后如何处理面部油腻时，她疑惑地看着我，我用手背在两侧嘴角抹了两下，对如此不雅的动作她投以鄙夷神色。在一次宏观经济学课上，我的另一同学大肆批判下岗工人和辍学务工务农的少年：“80%是由于他们自己不努力，年轻的时候不学会一门专长，所以现在下岗活该！那些学生可以一边读书一边打工嘛，据说有很多学生一个暑假就能赚几千元，学费还用愁吗？”我的这位同学忒不了解贫困地区农村了。我是70年代中期出生的人，我的同龄人正在逐渐成为社会的中流砥柱，我们的行为将影响社会和经济的发展。把这篇文章送给那些在优越环境中成长起来的年轻人和很久以前曾经吃过苦现在已经淡忘的人，关注社会下层，为了这个世界更公平些，我们应该做些力所能及的事情，让“老吾老以及人之老，幼吾幼以及人之幼”的人文情怀驻留我们的头脑。我花了18年时间才能和你坐在一起喝咖啡。
网友评论：井底蛙：我也是一个在农村苦苦奋斗拼搏走出来的女孩，以前家里没钱供我读书，我在高中三年都没拿学校的课本，四处向别人借书来读，暑假就到外面城市的工厂打工挣学费。现在我已经是一名公务员了，回首往事，觉得不胜辛酸，希望广大农村的孩子能够不畏艰难勇敢地去追求自己的理想！夜归人：世界本没有什么公平可言，一生过得怎么样，主要还是取决于我们对生活的热忱。做自己认为对、值得的事，开心就好。二代豪侠：当我们骂官二代，骂富二代的时候，可以顺便了解一下他们的父母，他们的父母都是特别努力特别优秀的人，能有现在的成就绝大部分是他们年轻时候艰苦努力得来的。红尘过客：为了一个目标不懈努力，不论结果如何都值得尊重。无论未来如何，至少现在，笔者值得尊重。人生是可以选择的，关键是看你是否为了你的选择奋斗。愿每个人都可以赢得自己人生的成功，都可以为此感到骄傲和满足。都市隐士：有人就有江湖，江湖大了，就什么鸟都有。原来的地主和长工正如现在的富人和穷人。农民是很淳朴的，也辛苦的为自己及后代奋斗着，但当他们甩下汗水收获粮食后，财富却大多被商人剥削了。当周围的人因为放高利贷而每天锦衣玉食时，当同事因为父母的余荫而前途一片光明时，你是否曾抱怨父母没给你留下积蓄或人脉，是否曾幻想如果我是富二代或官二代。其实我们都应该感恩，因为不论贫贱，我们都来到了这个世界，都在品味这个世界的生活，我们都生存着，并会平等的迈入坟墓。北漂一族：我已大学毕业16个年头了，可以说这16年当中有10多年全部都是为了报答父母的养育之恩，我把我所有赚来的钱为家里买了一套房子，房主是家人的名字。直到去年才把贷款还清了，现在才真正的为自己以后的生活作打算，有时想想真的很辛苦，我城市的同学，一生下来就有房子车子，我不但没有还要帮家里，呵呵，不过我乐意去扛，或许这是我这辈子活着的意义了！

我奋斗了18年不是为了和你一起喝咖啡□文|优游几年前，麦子的一篇《我奋斗了18年才和你坐在一起喝咖啡》引起多少共鸣，一个农家子弟经过18年的奋斗，才取得和大都会里的同龄人平起平坐的权利，一代人的真实写照。然而，几年过去，我恍然发觉，他言之过早。18年又如何？再丰盛的年华叠加，我仍不能和你坐在一起喝咖啡。那年我25岁，无数个夙兴夜寐，换来一个硕士学位，额上的抬头纹分外明显，脚下却半步也不敢停歇。如果不想让户口打回原籍，子子孙孙无穷匮地修地球，得赶紧地找份留京工作。你呢？你不着急，魔兽世界和红色警报早玩腻了！你野心勃勃地筹划着“创业创业”。当时李彦宏、陈天桥、周云帆，牛人们还没有横空出世，百度、Google、完美时空更是遥远的名词，可青春所向披靡不可一世，你在校园里建起配送网站，大张旗鼓地招兵买马，大小媒体的记者蜂拥而至。我们寝室很快名噪一时，小姑娘们从天南地北寄来粉粉的信纸，仰慕地写道：“从报上得知你的精彩故事……”得空，我们爬上楼顶吹吹风，你眉飞色舞地转向我，以照顾自己人的口气说，兄弟，一起发财如何？好呀，可惜，我不能。创业于你，是可进可退可攻可守的棋，启动资金有三姑六眷帮忙筹集，就算铩羽而归，父母那三室一厅、温暖的灶台也永不落空。失败于我，意味着覆水难收一败涂地，每年夏天，为了节省两三百块钱的机械收割钱，爹娘要扛着腰肌劳损在大日头下收割5亩农田。我穿着借来的西服完成了第一次面试，戴着借来的手表与心爱的女孩进行了第一次约会。当你拿到了第一笔投资兴奋地报告全班时，我冷静地穿越大半个北京城，去做最后一份家教。没错，“这活儿技术含量忒低”，但在第一个月工资下发前，我租来的立锥之地与口粮全靠它维持。不多久，互联网就遭遇了寒流，你也对创业意兴阑珊，进了家国有性质的通信公司，我被一家外企聘用。坐井观天的我，竟傻傻地以为扳回了一局。明面上的工资，我比你超出一截，税后8000，出差住5星级宾馆，一年带薪休假10天。玩命一样地投入工作，坚信几年后也有个童话般的结尾，“和公主过上幸福的生活”。好景不长，很快，我明白了为什么大家说白领是句骂人的话。写字楼的工作套餐，标价35，几乎没人搭理它。午餐时间，最抢手的是各层拐角处的微波炉，“白领”们端着带来的便当，排起了长长的队伍。后来，物业允许快餐公司入住，又出现了“千人排队等丽华”的盛况。这些月入近万的人士节约到抠门的程度。一位同事，在脏乱差的火车站耗上3个小时，为的是18：00后返程能多得150元的晚餐补助。这幕幕喜剧未能令我发笑，我读得懂，每个数字后都凝结着加班加点与忍气吞声，俯首帖耳被老板盘剥，为的是一平米一平米构筑起自己的小窝。白手起家的过程艰辛而漫长，整整3年，我没休过一次长假没吃过一回山珍海味；听到“华为25岁员工胡新宇过劳死”的新闻，也半点儿不觉得惊讶，以血汗、青春换银子的现象在这个行业太普遍了。下次，当你看见一群人穿着西装革履拎着IBM笔记本奋力挤上公交车，千万别奇怪，我们就是一群IT民工。惟一让人欣慰的是，我们离理想中的目标一步步靠近。突如其来地，你的喜讯从天而降：邀请大家周末去新居暖暖房。怎么可能？你竟比我快？可豁亮的100多平方米、红苹果家具、42寸液晶大彩电无可质疑地摆在眼前。你轻描淡写地说，老头子给了10万，她家里也给了10万，老催着我们结婚……回家的路上，女朋友郁郁不说话，她和我一样，来自无名的小山村。我揽过她的肩膀，鼓励她也是鼓励自己，没关系，我们拿时间换空间。蜜月你在香港过的，轻而易举地花掉了半年的工资，回来说，意思不大，不像TVB电视里拍的那样美轮美奂；我的婚礼，在家乡的土路、乡亲的围观中巡游，在低矮昏暗的老房子里拜了天地，在寒冷的土炕上与爱人相拥入眠。幸运的是，多年后黯淡的图景化作妻子博客里光芒四射的图画，她回味：“有爱的地方，就有天堂。”我们都想给深爱的女孩以天堂，天堂的含义却迥然不同。你的老婆当上了全职太太，每天的主题是享受；我也想这么来着，老婆不同意，说你养我，谁养我爸妈？不忍心让你一个人养7个人。当你的女人敷着倩碧面膜舒服地翘起脚，我的女人却在人海中顽强地搏杀。2004年年底，我们也攒到了人生中第一个10万，谁知中国的楼市在此时被魔鬼唤醒，海啸般狂飙突进，摧毁一切渺小虚弱的个体。2005年3月，首付还够买西四环的楼盘，到7月，只能去南城扫楼了。我们的积蓄本来能买90平方米的两居来着，9月中旬，仅仅过去2个月，只够买80多平米。没学过经济学原理？没关系。生活生动地阐释了什么叫资产泡沫与流动性泛滥。这时专家跳出来发言了，“北京房价应该降30%，上海房价应该降40%。”要不，再等等？我险些中招了，是你站出来指点迷津：赶快买，房价还会涨。买房的消息传回老家，爹娘一个劲儿地唏嘘。在他们看来，7500元一平方米是不可思议的天价。3年后的2008，师弟们纷纷感叹，你赚大发了，四环内均价1万4，已无楼可买。几天前，我看见了水木年华论坛上的一句留言，颇为感慨：“工作5年还没买房真活该，2003年正是楼市低迷与萧条之时。等到今天，踏空的不仅是黄金楼市，更是整个人生。”真要感谢你，在我不知理财为何物之时，你早早地告诉我什么叫消费什么叫投资。并非所有人都拥有前瞻的眼光和投资的观念。许多和我一样来自小地方、只知埋头苦干的兄弟们，太过关注脚下的麦田，以至于错过一片璀璨的星空。你的理论是，赚钱是为了花，只有在流通中才能增值，买到喜爱的商品，让生活心旷神怡。而我的农民兄弟——这里特指是出身农家毕业后留在大城市的兄弟，习惯于把人民币紧紧地捏在手中。存折数字的增长让他们痴迷。该买房时，他们在租房；该还贷时，他们宁可忍受7%的贷款利率，也要存上5年的定期。辛苦赚来的银子在等待中缩水贬值。他们往往在房价的巅峰处，无可奈何地接下最后一棒。也曾天真地许愿，赚够50万就回家买房。可等到那一天真的到来，老家的房价，二线、三线城市甚至乡镇的都已疯长。这便是我和你的最大差别，根深蒂固的分歧、不可逾越的鸿沟也在于此。我曾经以为，学位、薪水、工作环境一样了，我们的人生便一样了。事实上，差别不体现在显而易见的符号上，而是体现在世世代代的传承里，体现在血液里，体现在头脑中。18年的积累，家庭出身、生活方式、财务观念，造就了那样一个你，也造就了这样一个我，造就了你的疏狂与我的保守持重。当我还清贷款时，你买了第二套住房；上证指数6000点，当我好容易试水成为股民，你清仓离场，转投金市；我每月寄1000元回去，承担起赡养父母的责任，你笑嘻嘻地说，养老，我不啃老就不错了；当我思考着要不要生孩子、养孩子的成本会在多大程度上折损生活品质时，4个老人已出钱出力帮你抚养起独二代；黄金周去一趟九寨沟挺好的了，你不满足，你说德国太拘谨美国太随意法国才是你向往的时尚之都……我的故事，是一代“移民”的真实写照——迫不得已离乡背井，祖国幅员辽阔，我却像候鸟一样辗转迁徙，择木而栖。现行的社会体制，注定了大城市拥有更丰富的教育资源、医疗资源、生活便利。即便取得了一纸户口，跻身融入的过程依然是充满煎熬，5年、10年乃至更长时间的奋斗才获得土著们唾手可得的一切。曾经愤慨过，追寻过，如今，却学会了不再抱怨，在一个又一个缝隙间心平气和。差距固然存在，但并不令人遗憾，正是差距和为弥补差距所付出的努力，加强了生命的张力。可以想见的未来是，有一天我们的后代会相聚于迪斯尼(这点自信我还是有的)，讲起父亲的故事，我的那一个，虽然不一定更精致更华彩，无疑曲折有趣得多。那个故事，关于独立、勇气、绝地反弹、起死回生，我给不起儿子名车豪宅，却能给他一个不断成长的心灵。我要跟他说，无论贫穷富贵，百万家资或颠沛流离，都要一样地从容豁达。至此，喝不喝咖啡又有什么打紧呢？生活姿态的优雅与否，不取决于你所坐的位置、所持的器皿、所付的茶资。它取决于你品茗的态度。我奋斗了18年，不是为了和你一起喝咖啡。
网友评论：农民工二代：“工作5年还没买房真活该，2003年正是楼市低迷与萧条之时。等到今天，踏空的不仅是黄金楼市，更是整个人生。”——太他妈经典了，我顶！王谢人家：唉，我本无心求富贵，偏偏生在帝王家！乡里巴人：这两篇文章我都看过，给我的感触很大，我感觉自己算是不努力的一类人，我无法用言语来表达现在内心深处的思想，这并不是我不想表达，而是我当初没努力，没学好知识，无法用言语表达……三角猫美女：当一字一字记录下过去的岁月时，是泪水是微笑？一切都已经不重要了，生活给了我们太多太多，而所有这一切都已成为我们宝贵的财富。不需要多么强硬的家庭背景，拥有一个强大的内心足以。东方智叟：没错，各种资源都集中在了大城市，不过，同样各种肮脏的东西也集中在这里。不用羡慕，上帝对你关上一扇门的同时，一定也会为你打开另一扇窗。赌侠：我们出生的时候，上帝已发好了牌，抓的牌好与不好，我们已无法抗拒，我们唯一能做的，就是把手中的牌出好，哪怕是一把烂牌。会飞的鱼：不错，正如题所说“我奋斗了18年，不是为了和你一起喝咖啡”，你有你的金汤匙，我也有奋斗的精彩！编辑 倚天《商道》杂志QQ⑤群号：184484127

三 : 蓝莲花咖啡~我和小伙伴们在一起

空虚寂寞的时候你会干什么？我一个好朋友现在每天晚上都在粘钻画，长达一米九的钻画啊，一颗钻一颗钻粘下去，眼睛要累瞎了。而且这东西也没个技术含量，反正无聊时我是不会做这个，喝咖啡去多好啊，多小资多休闲啊，哈哈。我住的地方离工大超近，作为黑龙江省内排名第一的大学，留学生是相当多的，学校周围咖啡简餐也是相当多的，一天换个地方，一个月你都不带重复的。咖啡简餐不好做啊，反正我眼见着旧的咖啡馆倒下去，新的咖啡馆如雨后春笋般的冒出来，能坚持下来的真没几家。我今天去的蓝莲花算是桥东街的老店了，11年开业，坚持到现在不能说不是奇迹啊。今天借着哈馆的光我们去涨知识去了。

蓝莲花咖啡馆，桥东街53号，很朴素的门面。蓝莲花是许巍很著名的一首歌，我一直很喜欢，曾经放在我博客首页好一阵子，蓝莲花代表着在路上，也代表着追求梦想。

我去的时候小伙伴们已经到了，真是小伙伴，每个人都要比我小十岁以上，你们说我心有多大，这么大岁数了还跟小朋友一起吃吃喝喝呢，方方球啊，你长点心吧。

美女老板先给我们普及了一下咖啡知识，防止我们错把珍珠当鱼目。就我这一生不羁放纵爱自由的性格，当时真是强挺着正襟而坐，其实我这个人挨上沙发就想出溜下去，淑女不是我的风格啊。

我能说我根本没好好听老板讲什么了，只关注她的玉手了吗。回到家里我还长久地看了这张照片，老肖说我明白你的意思---镯子。多年夫妻成亲人，老肖你真懂我，不过你不用卖血攒钱给我买镯子了，我的胳膊短，手指头也粗，配不上这么美貌的镯子。

她家的菜单呀杯子呀很多都是蓝色的，大概是为了配合蓝莲花的这个蓝字。我大概看了一下价格，都在20左右，比较亲民。

沙发也是蓝色的，看来店主装修的时候还是下了一番功夫的。

这个店在整个桥东街的咖啡馆里算是大的，下午的阳光也很好。而且还有包间，因为里面有客人就没拍上。

店里的吊灯都不错。

我比较偏爱这个，尤其在阳光下晶莹剔透的样子。亲们，店里有wifi的呀。

阳光很好，心情很好

谁不想拥有这样的小店，我真的很想。

从书架上我发现了一本很邪恶的书，我拍了一页让大家也跟着邪恶一下，哈哈。
也不知道那个糖需不需要付费，反正我偷吃了一块，韩国糖啊，自从看上了星星，我对韩国的一切都感兴趣了。

这是老板为了让我们学习分辨好咖啡特意上的基础咖啡。拿铁咖啡啊，卡布奇诺啊，都是在这个咖啡的基础上添加东西做出来的。因为没好好听课也不知道说得对不对，不对的地方请大家告诉我，随时改，方球虽然岁数大，但一点也没影响她谦虚，哈哈。

这个透明的杯子可以看出咖啡的品质很好，上面是油质。说到这里心都虚了，也不知道说的对不对，再次哈哈~咖啡杯的正确拿法，应是拇指和食指捏住杯把儿再将杯子端起，我经常满把握杯的喝法是不对的。


我的榛果拿铁咖啡，主要成分是牛奶还有基础咖啡。奶味很浓郁。店主说她家的奶都是进口的德国牛奶，成本很高的。

吃饭不拍照臣妾做不到啊，喝咖啡之前先用镜头消一下毒.你们想认识照片里的美女帅哥吗，如果她们同意我就把名字告诉你们，学历都很高啊，博士啊，硕士啊，我想正是这些好吃的给了他们上进的力量。

男士点的美式咖啡，我想问没有奶的咖啡好喝吗？

卡布奇诺，请问拉花能不能拉出个叫兽？原谅我吧，弱智少年问题多啊！

热巧克力可可，据说很甜很香。对了喝咖啡的时候转动杯子，吹气，发出声响，用小勺喝，给别人加糖这些行为都是违反礼仪的，我也是现学现卖哈哈。

巧克力摩卡

苏小苏同学不敢喝咖啡怕晚上失眠，店主贴心的给她上了一杯木瓜牛奶。

这个是啥嘞，我忘了

店主额外赠送的芒果冰沙，很好吃，很大杯，我喜欢芒果。

主食来了。番茄肉酱意粉。因为屋子不是很热，所以这个意粉上来很快就凉了，于是我就吃了一口。

味道还是不错的，番茄味道很浓，还加了香草。

太不环保了，我占用了这么多勺子叉子。

意大利肉酱焗饭

可以拉丝，奶酪分量很足，这个我很喜欢，吃了很多，热乎乎的真给力。

金枪鱼三明治，在家可以给孩子做，很简单的

黑椒牛柳焗饭。我喜欢吃里面的青豆，牛肉很大片，味道特别好，有点辣，好吃，用我们淘宝店主的话就是全五分！

咖喱牛腩饭，咖哩味道不是很大，土豆是刚煮熟的，很绵软，她家的焗饭个个我都很满意。

胡萝卜蛋糕来了，颜色好，营养足，里面还有很多核桃肉呢，香，实惠，能吃饱的蛋糕。

附近景一张。

芝士蛋糕，除了饼底有点坚硬别的无缺点，而且我认为的缺点也只是我个人的观点，哈哈。

巧克力熔岩蛋糕，很香很腻很甜，可惜照片没拍好，影响了它的美貌。

送给大家一只萌兔子，什么时候都保持好心情是最重要的。

四 : 在天才和疯子之间奋斗的一生--JohnNash--博弈论

最近看了关于博弈论的公开课，受益匪浅。约翰.纳什1994年获得诺贝尔经济学奖的时候已经66岁。

晚上无意中观赏了《A beautifulmind》这不电影，讲述了约翰.纳什这个高智商的孤独男人奋斗的一生，从心理学的角度看完了整部电影，可歌可泣的是，当白发苍苍的老人站在瑞典国的领奖台上的时候，他的视界里、感言中始终是台下容颜不再的妻子，这个用一生的青春、爱与命运博弈，成就纳什博弈均衡理论的智慧大爱的女人。

作为应用数学1个分支，孤独的天才数学家John Nash的gametheory被无数次引经据典的是他的非合作博弈，也就是Nash均衡:

以下Nashequilibrium转自wikipedia(http://en.wikipedia.org/wiki/Nash_equilibrium)

In game theory, the Nash equilibrium (namedafter John Forbes Nash) is a solution concept of a game involving two or more players, inwhich each player is assumed to know the equilibriumstrategies of the other players, and no player has anything togain by changing only his own strategy unilaterally.^[1]:14If each player has chosen a strategy and no player can benefit bychanging his or her strategy while the other players keep theirsunchanged, then the current set of strategy choices and thecorresponding payoffs constitute a Nash equilibrium.

Stated simply, Amy and Phil are in Nash equilibrium if Amy ismaking the best decision she can, taking into account Phil'sdecision, and Phil is making the best decision he can, taking intoaccount Amy's decision. Likewise, a group of players are in Nashequilibrium if each one is making the best decision that he or shecan, taking into account the decisions of the others.

Applications:

Game theorists use the Nash equilibrium concept to analyze theoutcome of the strategic interaction of several decision makers. In other words, it providesa way of predicting what will happen if several people or severalinstitutions are making decisions at the same time, and if theoutcome depends on the decisions of the others. The simple insightunderlying John Nash's idea is that we cannot predict the result ofthe choices of multiple decision makers if we analyze thosedecisions in isolation. Instead, we must ask what each player woulddo, taking into account the decision-making of theothers.

Nash equilibrium has been used to analyze hostile situationslike warand arms races^[2](see Prisoner's dilemma), and also howconflict may be mitigated by repeated interaction (see Tit-for-tat). It has also been used to study towhat extent people with different preferences can cooperate (seeBattle of the sexes),and whether they will take risks to achieve a cooperative outcome(see Stag hunt). It has been used to study the adoptionof technical standards^{[citationneeded]}, and also the occurrence of bankruns and currency crises (see Coordination game). Other applicationsinclude traffic flow (see Wardrop's principle), how to organizeauctions (see auction theory), the outcome of effortsexerted by multiple parties in the education process,^[3]regulatory legislation such as environmental regulations (seeTragedy of theCommons),^[4]and even penalty kicks in soccer(see Matching pennies).^[5]

History:

A version of the Nash equilibrium concept was first used byAntoine Augustin Cournot inhis theory of oligopoly (1838). In Cournot's theory, firms choosehow much output to produce to maximize their own profit. However,the best output for one firm depends on the outputs of others. ACournot equilibrium occurs when eachfirm's output maximizes its profits given the output of the otherfirms, which is a pure strategy Nash Equilibrium.

The modern game-theoretic concept of Nash Equilibrium is insteaddefined in terms of mixed strategies, where players choose aprobability distribution over possible actions. The concept of themixed strategy Nash Equilibrium was introduced by John von Neumann and Oskar Morgenstern in their 1944 book TheTheory of Games and Economic Behavior. However, their analysiswas restricted to the special case of zero-sum games. They showed that a mixed-strategyNash Equilibrium will exist for any zero-sum game with a finite setof actions. The contribution of John Forbes Nash in his 1951 articleNon-Cooperative Games was to define a mixed strategy NashEquilibrium for any game with a finite set of actions and provethat at least one (mixed strategy) Nash Equilibrium must exist insuch a game.

Since the development of the Nash equilibrium concept, gametheorists have discovered that it makes misleading predictions (orfails to make a unique prediction) in certain circumstances.Therefore they have proposed many related solution concepts (also called 'refinements'of Nash equilibrium) designed to overcome perceived flaws in theNash concept. One particularly important issue is that some Nashequilibria may be based on threats that are not 'credible'. Therefore, in 1965 Reinhard Selten proposed subgame perfect equilibrium as arefinement that eliminates equilibria which depend on non-credible threats. Other extensionsof the Nash equilibrium concept have addressed what happens if agame is repeated, or what happens if a game is playedin the absence of perfect information. However,subsequent refinements and extensions of the Nash equilibriumconcept share the main insight on which Nash's concept rests: allequilibrium concepts analyze what choices will be made when eachplayer takes into account the decision-making of others.

Informal definition

Informally, a set of strategies is a Nash equilibrium if noplayer can do better by unilaterally changing his or her strategy.To see what this means, imagine that each player is told thestrategies of the others. Suppose then that each player askshimself or herself: "Knowing the strategies of the other players,and treating the strategies of the other players as set in stone,can I benefit by changing my strategy?"

If any player would answer "Yes", then that set of strategies isnot a Nash equilibrium. But if every player prefers not to switch(or is indifferent between switching and not) then the set ofstrategies is a Nash equilibrium. Thus, each strategy in a Nashequilibrium is a best response to all other strategies in thatequilibrium.^[6]

The Nash equilibrium may sometimes appear non-rational in athird-person perspective. This is because it may happen that a Nashequilibrium is not Pareto optimal.

The Nash equilibrium may also have non-rational consequences insequential games because players may "threaten" each other withnon-rational moves. For such games the subgame perfect Nashequilibrium may be more meaningful as a tool of analysis.

Formal definition

Let (S, f) be a game with n players, whereS_i is the strategy set for player i,S=S₁ × S₂ ... × S_n is theset of strategy profiles andf=(f₁(x), ..., f_n(x)) is the payofffunction for x S. Let x_i be a strategy profile of playeri and x_-i be a strategy profile of allplayers except for player i. When each player i {1, ..., n} chooses strategy x_i resulting instrategy profile x = (x₁, ..., x_n)then player i obtains payoff f_i(x). Notethat the payoff depends on the strategy profile chosen, i.e., onthe strategy chosen by player i as well as the strategieschosen by all the other players. A strategy profilex^* S is a Nash equilibrium (NE) if no unilateral deviation instrategy by any single player is profitable for that player, thatis

A game can have either a pure-strategy or a mixed Nash Equilibrium, (in the latter a purestrategy is chosen stochastically with a fixed frequency). Nash proved that if we allow mixed strategies, then everygame with a finite number of players in which each player canchoose from finitely many pure strategies has at least one Nashequilibrium.

When the inequality above holds strictly (with instead of ) for all players and all feasible alternative strategies, thenthe equilibrium is classified as a strict Nash equilibrium.If instead, for some player, there is exact equality between and some other strategy in the set , then the equilibrium is classified as a weak Nashequilibrium.

Nash均衡最浅显易懂的例子就是"囚徒困境":

Prisoner's dilemma

中文描述如下:　
一天，一位富翁在家中被杀，财物被盗。警方抓到2个犯罪嫌疑人，斯卡尔菲丝和那库尔斯，并从他们的住处搜出被害人家中丢失的财物。但是，他们矢口否认曾杀过人，辩称是先发现富翁被杀，然后只是顺手牵羊偷了点儿东西。于是警方将两人隔离，分别关在不同的房间进行审讯。由地方检察官分别和每个人单独谈话。检察官说，“由于你们的偷盗罪已有确凿的证据，所以可以判你们一年刑期。但是，我可以和你做个交易。如果你单独坦白杀人的罪行，我只判你3个月的监禁，但你的同伙要被判十年刑。如果你拒不坦白，而被同伙检举，那么你就将被判十年刑，他只判3个月的监禁。但是，如果你们两人都坦白交代，那么，你们都要被判5年刑。”斯卡尔菲丝和那库尔斯该怎么办呢？他们面临着两难的选择——坦白或抵赖。显然最好的策略是双方都抵赖，结果是大家都只被判一年。但是由于两人处于隔离的情况下无法串供。所以，按照亚当·斯密的理论，每1个人都是从利己的目的出发，他们选择坦白交代是最佳策略。因为坦白交代可以期望得到很短的监禁———三个月，但前提是同伙抵赖，显然要比自己抵赖要坐10年牢好。这种策略是损人利己的策略。不仅如此，坦白还有更多的好处。如果对方坦白了而自己抵赖了，那自己就得坐10年牢。太不划算了！因此，在这种情况下还是应该选择坦白交代，即使两人同时坦白，至多也只判5年，总比被判10年好吧。所以，两人合理的选择是坦白，原本对双方都有利的策略(抵赖)和结局(被判1年刑)就不会出现。这样两人都选择坦白的策略以及因此被判5年的结局被称为“纳什均衡”，也叫非合作均衡。因为，每一方在选择策略时都没有“共谋”(串供)，他们只是选择对自己最有利的策略，而不考虑社会福利或任何其他对手的利益。也就是说，这种策略组合由所有局中人(也称当事人、参与者)的最佳策略组合构成。没有人会主动改变自己的策略以便使自己获得更大利益。“囚徒的两难选择”有着广泛而深刻的意义。个人理性与集体理性的冲突，各人追求利己行为而导致的最终结局是1个“纳什均衡”，也是对所有人都不利的结局。他们两人都是在坦白与抵赖策略上首先想到自己，这样他们必然要服长的刑期。只有当他们都首先替对方着想时，或者相互合谋(串供)时，才可以得到最短时间的监禁的结果。
见Main article: Prisoner's dilemma

Example PD payoffmatrix

	Cooperate	Defect
Cooperate	3, 3	0, 5
Defect	5, 0	1, 1

The Prisoner's Dilemma has a similar matrix as depicted for theCoordination Game, but the maximum reward for each player (in thiscase, 5) is only obtained when the players' decisions aredifferent. Each player improves his own situation by switching from"Cooperating" to "Defecting," given knowledge that the otherplayer's best decision is to "Defect." The Prisoner's Dilemma thushas a single Nash Equilibrium: both players choosing to defect.

What has long made this an interesting case to study is the factthat this scenario is globally inferior to "Both Cooperating." Thatis, both players would be better off if they both chose to"Cooperate" instead of both choosing to defect. However, eachplayer could improve his own situation by breaking the mutualcooperation, no matter how the other player possibly (or certainly)changes his decision.

还有信号灯的博弈协调控制:

Coordination game

Main article: Coordination game

A sample coordination gameshowing relative payoff for player1 / player2 with eachcombination

	Player 2 adopts strategy A	Player 2 adopts strategy B
Player 1 adopts strategy A	4 / 4	1 / 3
Player 1 adopts strategy B	3 / 1	2 / 2

The coordination game is a classic (symmetric) two player, two strategy game, with an examplepayoff matrix shown to the right. The playersshould thus coordinate, both adopting strategy A, to receive thehighest payoff; i.e., 4. If both players chose strategy B though,there is still a Nash equilibrium. Although each player is awardedless than optimal payoff, neither player has incentive to changestrategy due to a reduction in the immediate payoff (from 2 to1).

A famous example of this type of game was called the Staghunt; in the game two players may choose to hunt a stag or arabbit, the former providing more meat (4 utility units) than thelatter (1 utility unit). The caveat is that the stag must becooperatively hunted, so if one player attempts to hunt the stag,while the other hunts the rabbit, he will fail in hunting (0utility units), whereas if they both hunt it they will split thepayload (2, 2). The game hence exhibits two equilibria at (stag,stag) and (rabbit, rabbit) and hence the players' optimal strategydepend on their expectation on what the other player may do. If onehunter trusts that the other will hunt the stag, he should hunt thestag; however if he suspects that the other will hunt the rabbit,he should hunt the rabbit. This game was used as an analogy forsocial cooperation, since much of the benefit that people gain insociety depends upon people cooperating and implicitly trusting oneanother to act in a manner corresponding with cooperation.

Another example of a coordination game is the setting where twotechnologies are available to two firms with compatible products,and they have to elect a strategy to become the market standard. Ifboth firms agree on the chosen technology, high sales are expectedfor both firms. If the firms do not agree on the standardtechnology, few sales result. Both strategies are Nash equilibriaof the game.

Driving on a road, and having to choose either to drive on theleft or to drive on the right of the road, is also a coordinationgame. For example, with payoffs 100 meaning no crash and 0 meaninga crash, the coordination game can be defined with the followingpayoff matrix:

The drivinggame

	Drive on the Left	Drive on the Right
Drive on the Left	100, 100	0, 0
Drive on the Right	0, 0	100, 100

In this case there are two pure strategy Nash equilibria, whenboth choose to either drive on the left or on the right. If weadmit mixed strategies (where a pure strategy ischosen at random, subject to some fixed probability), then thereare three Nash equilibria for the same case: two we have seen fromthe pure-strategy form, where the probabilities are (0%,100%) forplayer one, (0%, 100%) for player two; and (100%, 0%) for playerone, (100%, 0%) for player two respectively. We add another wherethe probabilities for each player is (50%, 50%).

以及基于网络的Nash均衡:

Network traffic

See also: Braess's ParadoxSample network graph. Values on edges are the travel timeexperienced by a 'car' travelling down that edge. is the number of cars travelling via that edge.

An application of Nash equilibria is in determining the expectedflow of traffic in a network. Consider the graph on the right. Ifwe assume that there are "cars" traveling from A to D, what is the expected distribution oftraffic in the network?

This situation can be modeled as a "game" where every travelerhas a choice of 3 strategies, where each strategy is a route from Ato D (either , , or ). The "payoff" of each strategy is the travel time of each route.In the graph on the right, a car travelling via experiences travel time of 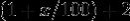, where is the number of cars traveling on edge . Thus, payoffs for any given strategy depend on the choices ofthe other players, as is usual. However, the goal in this case isto minimize travel time, not maximize it. Equilibrium will occurwhen the time on all paths is exactly the same. When that happens,no single driver has any incentive to switch routes, since it canonly add to his/her travel time. For the graph on the right, if,for example, 100 cars are travelling from A to D, then equilibriumwill occur when 25 drivers travel via , 50 via , and 25 via . Every driver now has a total travel time of 3.75.

Notice that this distribution is not, actually, sociallyoptimal. If the 100 cars agreed that 50 travel via and the other 50 through , then travel time for any single car would actually be 3.5 whichis less than 3.75. This is also the Nash equilibrium if the pathbetween B and C is removed, which means that adding an additionalpossible route can decrease the efficiency of the system, aphenomenon known as Braess's Paradox.

Competition game

A competitiongame

	Player 2 chooses '0'	Player 2 chooses '1'	Player 2 chooses '2'	Player 2 chooses '3'
Player 1 chooses '0'	0,0	2, -2	2, -2	2, -2
Player 1 chooses '1'	-2, 2	1, 1	3,-1	3, -1
Player 1 chooses '2'	-2, 2	-1,3	2,2	4, 0
Player 1 chooses '3'	-2, 2	-1, 3	0, 4	3, 3

This can be illustrated by a two-player game in which bothplayers simultaneously choose an integer from 0 to 3 and they bothwin the smaller of the two numbers in points. In addition, if oneplayer chooses a larger number than the other, then he/she has togive up two points to the other.

This game has a unique pure-strategy Nash equilibrium: bothplayers choosing 0 (highlighted in light red). Any other choice ofstrategies can be improved if one of the players lowers his numberto one less than the other player's number. In the table to theright, for example, when starting at the green square it is inplayer 1's interest to move to the purple square by choosing asmaller number, and it is in player 2's interest to move to theblue square by choosing a smaller number. If the game is modifiedso that the two players win the named amount if they both choosethe same number, and otherwise win nothing, then there are 4 Nashequilibria (0,0...1,1...2,2...and 3,3).

Nash equilibria in a payoff matrix

There is an easy numerical way to identify Nash equilibria on apayoff matrix. It is especially helpful in two-person games whereplayers have more than two strategies. In this case formal analysismay become too long. This rule does not apply to the case wheremixed (stochastic) strategies are of interest. The rule goes asfollows: if the first payoff number, in the duplet of the cell, isthe maximum of the column of the cell and if the second number isthe maximum of the row of the cell - then the cell represents aNash equilibrium.

A Payoff Matrix - NashEquilibria in bold

	Option A	Option B	Option C
Option A	0, 0	25, 40	5, 10
Option B	40, 25	0, 0	5, 15
Option C	10, 5	15, 5	10, 10

We can apply this rule to a 3×3 matrix:

Using the rule, we can very quickly (much faster than withformal analysis) see that the Nash Equilibria cells are (B,A),(A,B), and (C,C). Indeed, for cell (B,A) 40 is the maximum of thefirst column and 25 is the maximum of the second row. For (A,B) 25is the maximum of the second column and 40 is the maximum of thefirst row. Same for cell (C,C). For other cells, either one or bothof the duplet members are not the maximum of the corresponding rowsand columns.

This said, the actual mechanics of finding equilibrium cells isobvious: find the maximum of a column and check if the secondmember of the pair is the maximum of the row. If these conditionsare met, the cell represents a Nash Equilibrium. Check all columnsthis way to find all NE cells. An N×N matrix may have between 0 andN×N pure strategy Nash equilibria.

Stability

The concept of stability, useful in the analysis of manykinds of equilibria, can also be applied to Nash equilibria.

A Nash equilibrium for a mixed strategy game is stable if asmall change (specifically, an infinitesimal change) inprobabilities for one player leads to a situation where twoconditions hold:

1. the player who did not change has no better strategy in the newcircumstance
2. the player who did change is now playing with a strictly worsestrategy.

If these cases are both met, then a player with the small changein his mixed-strategy will return immediately to the Nashequilibrium. The equilibrium is said to be stable. If condition onedoes not hold then the equilibrium is unstable. If only conditionone holds then there are likely to be an infinite number of optimalstrategies for the player who changed. John Nash showed that the latter situationcould not arise in a range of well-defined games.

In the "driving game" example above there are both stable andunstable equilibria. The equilibria involving mixed-strategies with100% probabilities are stable. If either player changes hisprobabilities slightly, they will be both at a disadvantage, andhis opponent will have no reason to change his strategy in turn.The (50%,50%) equilibrium is unstable. If either player changes hisprobabilities, then the other player immediately has a betterstrategy at either (0%, 100%) or (100%, 0%).

Stability is crucial in practical applications of Nashequilibria, since the mixed-strategy of each player is notperfectly known, but has to be inferred from statisticaldistribution of his actions in the game. In this case unstableequilibria are very unlikely to arise in practice, since any minutechange in the proportions of each strategy seen will lead to achange in strategy and the breakdown of the equilibrium.

The Nash equilibrium defines stability only in terms ofunilateral deviations. In cooperative games such a concept is notconvincing enough. Strong Nash equilibrium allows fordeviations by every conceivable coalition.^[7]Formally, a Strong Nash equilibrium is a Nashequilibrium in which no coalition, taking the actions of itscomplements as given, can cooperatively deviate in a way thatbenefits all of its members.^[8]However, the Strong Nash concept is sometimes perceived as too"strong" in that the environment allows for unlimited privatecommunication. In fact, Strong Nash equilibrium has to be Pareto efficient. As a result of theserequirements, Strong Nash is too rare to be useful in many branchesof game theory. However, in games such as elections with many moreplayers than possible outcomes, it can be more common than a stableequilibrium.

A refined Nash equilibrium known as coalition-proof Nashequilibrium (CPNE)^[7]occurs when players cannot do better even if they are allowed tocommunicate and make "self-enforcing" agreement to deviate. Everycorrelated strategy supported by iterated strict dominance and on thePareto frontier is a CPNE.^[9]Further, it is possible for a game to have a Nash equilibrium thatis resilient against coalitions less than a specified size, k. CPNEis related to the theory of the core.

Finally in the eighties, building with great depth on such ideasMertens-stable equilibriawere introduced as a solution concept. Mertens stable equilibria satisfy bothforward induction and backward induction. In a Gametheory context stable equilibria now usually refer toMertens stable equilibria.

Occurrence

If a game has a unique Nash equilibrium and is played amongplayers under certain conditions, then the NE strategy set will beadopted. Sufficient conditions to guarantee that the Nashequilibrium is played are:

1. The players all will do their utmost to maximize their expectedpayoff as described by the game.
2. The players are flawless in execution.
3. The players have sufficient intelligence to deduce thesolution.
4. The players know the planned equilibrium strategy of all of theother players.
5. The players believe that a deviation in their own strategy willnot cause deviations by any other players.
6. There is common knowledge that all playersmeet these conditions, including this one. So, not only must eachplayer know the other players meet the conditions, but also theymust know that they all know that they meet them, and know thatthey know that they know that they meet them, and so on.

Where the conditions are not met

Examples of game theory problems in which theseconditions are not met:

1. The first condition is not met if the game does not correctlydescribe the quantities a player wishes to maximize. In this casethere is no particular reason for that player to adopt anequilibrium strategy. For instance, the prisoner’s dilemma is not adilemma if either player is happy to be jailed indefinitely.
2. Intentional or accidental imperfection in execution. Forexample, a computer capable of flawless logical play facing asecond flawless computer will result in equilibrium. Introductionof imperfection will lead to its disruption either through loss tothe player who makes the mistake, or through negation of thecommon knowledge criterionleading to possible victory for the player. (An example would be aplayer suddenly putting the car into reverse in the game of chicken, ensuring a no-loss no-winscenario).
3. In many cases, the third condition is not met because, eventhough the equilibrium must exist, it is unknown due to thecomplexity of the game, for instance in Chinese chess.^[10]Or, if known, it may not be known to all players, as when playingtic-tac-toe with a small child who desperatelywants to win (meeting the other criteria).
4. The criterion of common knowledge may not be met even if allplayers do, in fact, meet all the other criteria. Players wronglydistrusting each other's rationality may adopt counter-strategiesto expected irrational play on their opponents’ behalf. This is amajor consideration in “Chicken” or an armsrace, for example.

Where the conditions are met

Due to the limited conditions in which NE can actually beobserved, they are rarely treated as a guide to day-to-daybehaviour, or observed in practice in human negotiations. However,as a theoretical concept in economics and evolutionary biology, the NE hasexplanatory power. The payoff in economics is utility (or sometimesmoney), and in evolutionary biology gene transmission, both are thefundamental bottom line of survival. Researchers who apply gamestheory in these fields claim that strategies failing to maximizethese for whatever reason will be competed out of the market orenvironment, which are ascribed the ability to test all strategies.This conclusion is drawn from the "stability" theory above. In these situationsthe assumption that the strategy observed is actually a NE hasoften been borne out by research^{[citationneeded]}.^{[verificationneeded]}

NE and non-credible threats

Extensive and Normal form illustrations that show the differencebetween SPNE and other NE. The blue equilibrium is not subgameperfect because player two makes a non-credible threat at 2(2) tobe unkind (U).

The Nash equilibrium is a superset of the subgame perfect Nashequilibrium. The subgame perfect equilibrium in addition to theNash Equilibrium requires that the strategy also is a Nashequilibrium in every subgame of that game. This eliminates allnon-credible threats, that is,strategies that contain non-rational moves in order to make thecounter-player change his strategy.

The image to the right shows a simple sequential game thatillustrates the issue with subgame imperfect Nash equilibria. Inthis game player one chooses left(L) or right(R), which is followedby player two being called upon to be kind (K) or unkind (U) toplayer one, However, player two only stands to gain from beingunkind if player one goes left. If player one goes right therational player two would de facto be kind to him in that subgame.However, The non-credible threat of being unkind at 2(2) is stillpart of the blue (L, (U,U)) Nash equilibrium. Therefore, ifrational behavior can be expected by both parties the subgameperfect Nash equilibrium may be a more meaningful solution conceptwhen such dynamic inconsistencies arise.

Proof of existence

Proof using the Kakutani fixed point theorem

Nash's original proof (in his thesis) used Brouwer's fixed pointtheorem (e.g., see below for a variant). We give a simpler proofvia the Kakutani fixed point theorem,following Nash's 1950 paper (he credits DavidGale with the observation that such a simplification ispossible).

To prove the existence of a Nash Equilibrium, let be the best response of player i to the strategies of all otherplayers.

Here, , where , is a mixed strategy profile in the set of all mixed strategiesand is the payoff function for player i. Define a set-valued function such that . The existence of a Nash Equilibrium is equivalent to having a fixed point.

Kakutani's fixed point theorem guarantees the existence of afixed point if the following four conditions are satisfied.

1. is compact, convex, and nonempty.
2. is nonempty.
3. is convex.
4. is upper hemicontinuous

Condition 1. is satisfied from the fact that is a simplex and thus compact. Convexity follows from players'ability to mix strategies. is nonempty as long as players have strategies.

Condition 2. is satisfied because players maximize expectedpayoffs which is continuous function over a compact set. TheWeierstrass Extreme Value Theorem guarantees thatthere is always a maximum value.

Condition 3. is satisfied as a result of mixed strategies.Suppose , then . i.e. if two strategies maximize payoffs, then a mix between thetwo strategies will yield the same payoff.

Condition 4. is satisfied by way of Berge's maximum theorem. Because is continuous and compact, is upper hemicontinuous.

Therefore, there exists a fixed point in and a Nash Equilibrium.^[11]

When Nash made this point to John von Neumann in 1949, von Neumannfamously dismissed it with the words, "That's trivial, you know.That's just a fixed point theorem." (See Nasar,1998, p.94.)

Alternate proof using the Brouwer fixed-pointtheorem

We have a game where is the number of players and is the action set for the players. All of the action sets are finite. Let denote the set of mixed strategies for the players. The finitenessof the s ensures the compactness of .

We can now define the gain functions. For a mixed strategy , we let the gain for player on action be

The gain function represents the benefit a player gets byunilaterally changing his strategy. We now define where

for . We see that

We now use to define as follows. Let

for . It is easy to see that each is a valid mixed strategy in . It is also easy to check that each is a continuous function of , and hence is a continuous function. Now is the cross product of a finite number of compact convex sets,and so we get that is also compact and convex. Therefore we may apply the Brouwerfixed point theorem to . So has a fixed point in , call it .

I claim that is a Nash Equilibrium in . For this purpose, it suffices to show that

This simply states the each player gains no benefit byunilaterally changing his strategy which is exactly the necessarycondition for being a Nash Equilibrium.

Now assume that the gains are not all zero. Therefore, , , and such that . Note then that

So let . Also we shall denote as the gain vector indexed by actions in . Since we clearly have that . Therefore we see that

Since we have that is some positive scaling of the vector . Now I claim that

.To see this, we first note that if then this is true by definition of the gain function. Now assumethat . By our previous statements we have that

and so the left term is zero, giving us that the entireexpression is as needed.

So we finally have that

where the last inequality follows since is a non-zero vector. But this is a clear contradiction, so allthe gains must indeed be zero. Therefore is a Nash Equilibrium for as needed.

Computing Nash equilibria

If a player A has a dominant strategy then there exists a Nash equilibrium in which A plays . In the case of two players A and B, there exists a Nashequilibrium in which A plays and B plays a best response to . If is a strictly dominant strategy, A plays in all Nash equilibria. If both A and B have strictly dominantstrategies, there exists a unique Nash equilibrium in which eachplays his strictly dominant strategy.

In games with mixed strategy Nash equilibria, the probability ofa player choosing any particular strategy can be computed byassigning a variable to each strategy that represents a fixedprobability for choosing that strategy. In order for a player to bewilling to randomize, his expected payoff for each strategy shouldbe the same. In addition, the sum of the probabilities for eachstrategy of a particular player should be 1. This creates a systemof equations from which the probabilities of choosing each strategycan be derived.^[6]

Examples

Matchingpennies

	Player B plays H	Player B plays T
Player A plays H	−1, +1	+1, −1
Player A plays T	+1, −1	−1, +1

In the matching pennies game, player A loses a point to B if Aand B play the same strategy and wins a point from B if they playdifferent strategies. To compute the mixed strategy Nashequilibrium, assign A the probability p of playing H and (1−p) ofplaying T, and assign B the probability q of playing H and (1−q) ofplaying T.

E[payoff for A playing H] = (−1)q + (+1)(1−q) = 1−2q

E[payoff for A playing T] = (+1)q + (−1)(1−q) = 2q−1

E[payoff for A playing H] = E[payoff for A playing T] ⇒ 1−2q =2q−1 ⇒ q = 1/2

E[payoff for B playing H] = (+1)p + (−1)(1−p) = 2p−1

E[payoff for B playing T] = (−1)p + (+1)(1−p) = 1−2p

E[payoff for B playing H] = E[payoff for B playing T] ⇒ 2p−1 =1−2p ⇒ p = 1/2

Thus a mixed strategy Nash equilibrium in this game is for eachplayer to randomly choose H or T with equal probability.

关于Nash的生平:From Wikipedia, the freeencyclopedia

JohnForbes Nash, Jr.

John Forbes Nash, Jr.
Born	June13, 1928 (age84) Bluefield, West Virginia,U.S.
Residence	United States
Nationality	American
Fields	Mathematics, Economics
Institutions	MassachusettsInstitute of Technology Princeton University
Alma mater	Princeton University, Carnegie Institute ofTechnology (now part of Carnegie Mellon University)
Doctoral advisor	Albert W. Tucker
Knownfor	Nash equilibrium Nash embedding theorem Algebraic geometry Partialdifferential equations
Notable awards	Nobel MemorialPrize in Economic Sciences (1994)
Spouse	Alicia Lopez-Harrison de Lardé (m. 1957–1963;2001–present)

John Forbes Nash, Jr. (born June 13, 1928) is an Americanmathematician whose works in gametheory, differential geometry, and partialdifferential equations have provided insight into the forcesthat govern chance and events inside complex systems in daily life.His theories are used in market economics,computing, evolutionary biology, artificial intelligence, accounting,politics and military theory. Serving as a Senior ResearchMathematician at Princeton University during the latterpart of his life, he shared the 1994 Nobel MemorialPrize in Economic Sciences with game theorists Reinhard Selten and John Harsanyi.

Nash is the subject of the Hollywood movie A Beautiful Mind. The film,loosely based on the biography of the same name, focuseson Nash's mathematical genius and struggle with paranoidschizophrenia.^[1][2]

In his own words, he states,

I later spent times of the order of five to eight months inhospitals in New Jersey, always on an involuntary basis and alwaysattempting a legal argument for release. And it did happen thatwhen I had been long enough hospitalized that I would finallyrenounce delusional hypotheses and revert to thinking of myself asa human of more conventional circumstances and return tomathematical research. In these interludes of, as it were, enforcedrationality, I did succeed in doing some respectable mathematicalresearch. Thus there came about the research for "Le problème de Cauchy pour les équationsdifférentielles d'un fluide général"; the idea that Prof. Hironakacalled "the Nash blowing-up transformation"; and those of "ArcStructure of Singularities" and "Analyticity of Solutions ofImplicit Function Problems with Analytic Data".

But after my return to the dream-like delusional hypotheses inthe later 60's I became a person of delusionally influencedthinking but of relatively moderate behavior and thus tended toavoid hospitalization and the direct attention ofpsychiatrists.

Thus further time passed. Then gradually I began tointellectually reject some of the delusionally influenced lines ofthinking which had been characteristic of my orientation. Thisbegan, most recognizably, with the rejection ofpolitically-oriented thinking as essentially a hopeless waste ofintellectual effort.^[3]

Early lifeand career

Nash was born on June 13, 1928, in Bluefield, West Virginia. Hisfather, after whom he is named, was an electrical engineer for theAppalachian Electric PowerCompany. His mother, born Margaret Virginia Martin and known asVirginia, had been a schoolteacher before she married. Both parentspursued opportunities to supplement their son's education,providing him with encyclopedias and even allowing him to takeadvanced mathematics courses at a local college while still in highschool. After attending Carnegie Institute ofTechnology (now Carnegie Mellon University) andgraduating in 1948 with bachelor's and master's degrees inmathematics, he accepted a scholarship to Princeton Universitywhere he pursued his graduate studies in Mathematics.^[3]

Post-graduate career

Nash's advisor and former Carnegie Tech professor R.J. Duffinwrote a letter of recommendation consisting of a single sentence:"This man is a genius."^[4]Nash was accepted by Harvard University, but the chairman ofthe mathematics department of Princeton, Solomon Lefschetz, offered him the John S. Kennedyfellowship, which was enough to convince Nash that Harvard valuedhim less.^[5]Thus he went to Princeton where he worked on his equilibrium theory. He earned a doctorate in 1950 with a 28-pagedissertation onnon-cooperative games.^[6]The thesis, which was written under the supervision of Albert W. Tucker, contained the definitionand properties of what would later be called the "Nash equilibrium". These studies led to fourarticles:

Nash did ground-breaking work in the area of real algebraic geometry:

His work in mathematics includes the Nash embedding theorem, which showsthat any abstract Riemannian manifold can be isometrically realized as a submanifold of Euclidean space. He also made significantcontributions to the theory of nonlinear parabolic partialdifferential equations and to singularity theory.

In the book A Beautiful Mind, author Sylvia Nasarexplains that Nash was working on proving a theorem involving ellipticpartial differential equations when, in 1956, he suffered a severedisappointment when he learned of an Italian mathematician,Ennio de Giorgi, who had published a proof acouple of months^[vague]before Nash achieved his proof. Each took different routes to getto their solutions. The two mathematicians met each other at theCourant Institute of Mathematical Sciences of New York University during the summer of1956. It has been speculated that if only one of them had solvedthe problem, he would have been given the Fields Medal for the proof.^[3]

In 2011, the National Security Agencydeclassified letters written by Nash in 1950s, in which he hadproposed a new encryption-decryption machine.^[8]The letters show that Nash had anticipated many concepts of moderncryptography, which are based on computationalhardness.^[9]

Personallife

In 1951, Nash went to the MassachusettsInstitute of Technology as a C. L. E. Moore Instructor in themathematics faculty. There, he met Alicia Lopez-Harrison de Lardé(born January 1, 1933), a physicsstudent from El Salvador, whom he married in February1957 at a Catholic ceremony, although Nash was an atheist.^[10]She admitted Nash to a mental hospital in 1959for schizophrenia; their son, John Charles MartinNash, was born soon afterward, but remained nameless for a yearbecause his mother felt that her husband should have a say in thename.

Nash and de Lardé divorced in 1963, though after his finalhospital discharge in 1970 Nash lived in de Lardé's house. Theywere remarried in 2001.

Nash has been a longtime resident of West Windsor Township,New Jersey.^[11]

Mentalillness

Schizophrenia

Nash began to show signs of extreme paranoia and his wife later described his behavioras erratic, as he began speaking of characters like Charles Hermanand William Parcher who were putting him in danger. Nash seemed tobelieve that all men who wore red ties were part of a communistconspiracy against him. Nash mailed letters to embassies inWashington, D.C., declaring that they wereestablishing a government.^[12][13]

He was admitted to the McLean Hospital, April–May 1959, where he wasdiagnosed with paranoidschizophrenia. The clinical picture is dominated by relativelystable, often paranoid, fixed beliefs that are either false,over-imaginative or unrealistic, usually accompanied by experiencesof seemingly real perception of something not actuallypresent— particularly auditory and perceptionaldisturbances, a lack of motivation for life, and mild clinicaldepression.^[14]Upon his release, Nash resigned from MIT, withdrew his n,and went to Europe, unsuccessfully seeking political asylum inFrance and East Germany. He tried to renounce his U.S.citizenship. After a problematic stay in Parisand Geneva, he was arrested by the French police anddeported back to the United States at the request of the U.S.government.

In 1961, Nash was committed to the New Jersey State Hospital at Trenton. Over thenext nine years, he spent periods in psychiatric hospitals, where, aside fromreceiving antipsychotic medications, he was administered insulin shock therapy.^[14][15][16]

Although he sometimes took prescribed medication, Nash laterwrote that he only ever did so under pressure. After 1970, he wasnever committed to the hospital again and he refused anymedication. According to Nash, the film A Beautiful Mind inaccuratelyimplied that he was taking the new atypical antipsychotics during thisperiod. He attributed the depiction to the screenwriter (whosemother, he notes, was a psychiatrist), who was worried aboutencouraging people with the disorder to stop taking theirmedication.^[17]Others, however, have questioned whether the fabrication obscured akey question as to whether recovery from problems like Nash's canactually be hindered by such drugs,^[18]and Nash has said they are overrated and that the adverse effectsare not given enough consideration once someone is deemed mentally ill.^[19][20][21]According to Sylvia Nasar, author of the book A Beautiful Mind, on which themovie was based, Nash recovered gradually with the passage of time.Encouraged by his then former wife, de Lardé, Nash worked in acommunitarian setting wherehis eccentricities were accepted. De Lardé said of Nash, "it's justa question of living a quiet life".^[13]

Nash in November 2006 at a game theory conference in Cologne.

Nash dates the start of what he terms "mental disturbances" tothe early months of 1959 when his wife was pregnant. He hasdescribed a process of change "from scientific rationality ofthinking into the delusional thinkingcharacteristic of persons who are psychiatrically diagnosed as'schizophrenic' or 'paranoid schizophrenic'"^[22]including seeing himself as a messenger or having a specialfunction in some way, and with supporters and opponents and hiddenschemers, and a feeling of being persecuted, and looking for signsrepresenting divine revelation.^[23]Nash has suggested his delusional thinking was related to hisunhappiness and his striving to feel important and be recognized,and to his characteristic way of thinking such that "I wouldn'thave had good scientific ideas if I had thought more normally." Hehas said, "If I felt completely pressureless I don't think I wouldhave gone in this pattern".^[24]He does not see a categorical distinction between terms such asschizophrenia and bipolar disorder.^[25]Nash reports that he did not hear voices until around 1964, laterengaging in a process of rejecting them.^[26]He reports that he was always taken to hospitals against his will,and only temporarily renounced his "dream-like delusionalhypotheses" after being in a hospital long enough to decide tosuperficially conform - to behave normally or to experience"enforced rationality". Only gradually on his own did he"intellectually reject" some of the "delusionally influenced" and"politically-oriented" thinking as a waste of effort. However, by1995, although he was "thinking rationally again in the style thatis characteristic of scientists," he says he also felt morelimited.^[22][27]

Recognition and latercareer

At Princeton, campus legend Nash became "The Phantom of FineHall" (Princeton's mathematics center), a shadowy figure who wouldscribble arcane equations on blackboards in the middle of thenight. The legend appears in a work of fiction based on Princetonlife, The Mind-Body Problem, by Rebecca Goldstein.

In 1978, Nash was awarded the John von Neumann Theory Prizefor his discovery of non-cooperative equilibria, now calledNash equilibria. He won the Leroy P. Steele Prize in 1999.

In 1994, he received the Nobel MemorialPrize in Economic Sciences (along with John Harsanyi and Reinhard Selten) as a result of his gametheory work as a Princeton graduate student. In the late 1980s,Nash had begun to use email to gradually link with workingmathematicians who realized that he was the John Nash andthat his new work had value. They formed part of the nucleus of agroup that contacted the Bank of Sweden's Nobelaward committee and were able to vouch for Nash's mental healthability to receive the award in recognition of his earlywork.^{[citationneeded]}

As of 2011 Nash's recent work involves ventures in advanced gametheory, including partial agency, which show that, as in his earlycareer, he prefers to select his own path and problems. Between1945 and 1996, he published 23 scientific studies.

Nash has suggested hypotheses on mental illness. He hascompared not thinking in an acceptable manner, or being "insane"and not fitting into a usual social function, to being "on strike" from an economic point of view. He hasadvanced evolutionary psychology views aboutthe value of human diversity and the potential benefits ofapparently nonstandard behaviors or roles.^[28]

Nash has developed work on the role of money in society. Withinthe framing theorem that people can be so controlled and motivatedby money that they may not be able to reason rationally about it,he has criticized interest groups that promote quasi-doctrinesbased on Keynesian economics that permitmanipulative short-term inflation and debt tacticsthat ultimately undermine currencies. He has suggested a global"industrial consumption price index" system that would support thedevelopment of more "ideal money" that people could trust ratherthan more unstable "bad money". He notes that some of his thinkingparallels economist and political philosopher Friedrich Hayek's thinking regarding moneyand a nontypical viewpoint of the function of theauthorities.^[29][30]

Nash received an honorary degree, Doctor of Science andTechnology, from Carnegie Mellon University in1999, an honorary degree in economics from the University of NaplesFederico II on March 19, 2003,^[31]an honorary doctorate in economics from the University ofAntwerp in April 2007, and was keynote speaker at a conferenceon Game Theory. He has also been a prolific guest speaker at anumber of world-class events, such as the Warwick Economics Summit in 2005held at the University of Warwick.

Nash has an Erdős number of 3.^[32][33][34]

博弈论大师：约翰·福布斯·纳什（John Forbes Nash Jr.）

(from:http://forum.e2002.com/forum.php?mod=viewthread&tid=325578)

约翰·纳什1928年出生在美国西弗吉尼亚州工业城布鲁菲尔德的1个富裕家庭。他的爸爸是受过良好教育的电子工程师，妈妈则是拉丁语教师。纳什从小就很孤僻，他宁愿钻在书堆里，也不愿出去和同龄的孩子玩耍。但是那个时候，纳什的数学成绩并不好，小学老师常常向他的家长抱怨纳什的数学有问题，因为他常常使用一些奇特的解题方法。而到了中学，这种情况就更加频繁了，老师在黑板上演算了整个黑板的习题，纳什只用简单的几步就能解出答案。
　　

中学毕业后，约翰·纳什进入了匹兹堡的卡耐基技术学院化学工程系。1948年，大学三年级的纳什同时被哈佛大学、普林斯顿大学、芝加哥大学和密执安大学录取，而普林斯顿大学则表现得更加热情，当普林斯顿大学的数学系主任莱夫谢茨感到纳什的犹豫时，就立即写信敦促他选择普林斯顿，这促使纳什接受了一份1150美元的奖学金。

　　当时的普林斯顿已经成了全世界的数学中心，爱因斯坦等世界级大师均云集于此。在普林斯顿自由的学术空气里，纳什如鱼得水，他21岁博士毕业，不到三十岁已经闻名遐迩。1958年，纳什因其在数学领域的优异工作被美国《财富》杂志评为新一代天才数学家中最杰出的人物。

　　约翰·纳最重要的理论就是现在广泛出现在经济学教科书上的“纳什均衡”。而“纳什均衡”最著名的1个例子就是“囚徒困境”，大意是：1个案子的2个嫌疑犯被分开审讯，警官分别告诉2个囚犯，如果两人均不招供，将各被判刑一年；如果你招供，而对方不招供，则你将被判刑3个月，而对方将被判刑十年；如果两人均招供，将均被判刑五年。于是，两人同时陷入招供还是不招供的两难处境。2个囚犯符合自己利益的选择是坦白招供，原本对双方都有利的策略不招供从而均被判刑１年就不会出现。这样两人都选择坦白的策略以及因此被判５年的结局被称为“纳什均衡”，也叫非合作均衡。“纳什均衡”是他21岁博士毕业的论文，也奠定了数十年后他获得诺贝尔经济学奖的基础。

　　那时的纳什“就像天神一样英俊”，1.85米的个子，体重接近77公斤，手指修长、优雅，双手柔软、漂亮，还有一张英国贵族的容貌。他的才华和个人魅力吸引了1个漂亮的女生——艾里西亚，她是当时麻省理工学院物理系仅有的两名女生之一。1957年，他们结婚了。之后漫长的岁月证明，这也许正是纳什一生中比获得诺贝尔奖更重要的事。

　　就在事业爱情双双得意的时候，纳什也因为喜欢独来独往，喜欢解决折磨人的数学问题而被人们称为“孤独的天才”。他不是1个善于为人处世并受大多数人欢迎的人，他有着天才们常有的骄傲、自我中心的毛病。他的同辈人基本认为他不可理喻，他们说他“孤僻，傲慢，无情，幽灵一般，古怪，沉醉于自己的隐秘世界，根本不能理解别人操心的世俗事务。”
普林斯顿的幽灵
　　1958年的秋天，正当艾里西亚半惊半喜地发现自己怀孕时，纳什却为自己的未来满怀心事，越来越不安。系主任马丁已答应在那年冬天给他永久教职，但是纳什却出现了各种稀奇古怪的行为：他担心被征兵入伍而毁了自己的数学创造力，他梦想成立1个世界政府，他认为《纽约时报》上每1个字母都隐含着神秘的意义，而只有他才能读懂其中的寓意。他认为世界上的一切都可以用1个数学公式表达。他给联合国写信，跑到华盛顿给每个国家的大使馆投递信件，要求各国使馆支持他成立世界政府的想法。他迷上了法语，甚至要用法语写数学论文，他认为语言与数学有神秘的关联……

　　终于，在孩子出生以前，纳什被送进了精神病医院。

　　几年后，因为艾里西亚无法忍受在纳什的阴影下生活，他们离婚了，但是她并没有放弃纳什。离婚以后，艾里西亚再也没有结婚，她依靠自己作为电脑程序员的微薄收入和亲友的接济，继续照料前夫和他们惟一的儿子。她坚持纳什应该留在普林斯顿，因为如果1个人行为古怪，在别的地方会被当作疯子，而在普林斯顿这个广纳天才的地方，人们会充满爱心地想，他可能是1个天才。

　　于是，在上世纪70和80年代，普林斯顿大学的学生和学者们总能在校园里看见1个非常奇特、消瘦而沉默的男人在徘徊，他穿着紫色的拖鞋，偶尔在黑板上写下数字命理学的论题。他们称他为“幽灵”，他们知道这个“幽灵”是1个数学天才，只是突然发疯了。如果有人敢抱怨纳什在附近徘徊使人不自在的话，他会立即受到警告：“你这一生都不可能成为像他那样杰出的数学家！”

　　正当纳什本人处于梦境一般的精神状态时，他的名字开始出现在70年代和80年代的经济学课本、进化生物学论文、政治学专著和数学期刊的各领域中。他的名字已经成为经济学或数学的1个名词，如“纳什均衡”、“纳什谈判解”、“纳什程序”、“德乔治－纳什结果”、“纳什嵌入”和“纳什破裂”等。

　　纳什的博弈理论越来越有影响力，但他本人却默默无闻。大部分曾经运用过他的理论的年轻数学家和经济学家都根据他的论文发表日期，想当然地以为他已经去世。即使一些人知道纳什还活着，但由于他特殊的病症和状态，他们也把纳什当成了1个行将就木的废人。
传奇仍在继续
　　有人说，站在金字塔尖上的科学家都有1个异常孤独的大脑，纳什发疯是因为他太孤独了。但是，纳什在发疯之后却并不孤独，他的妻子、朋友和同事们没有抛弃他，而是不遗余力地帮助他，挽救他，试图把他拉出疾病的深渊。

　　尽管纳什决心辞去麻省理工学院教授的职位，但他的同事和上司们还是设法为他保全了保险。他的同事听说他被关进了精神病医院后，给当时美国著名的精神病学专家打电话说：“为了国家利益，必须竭尽所能将纳什教授复原为那个富有创造精神的人。”越来越多的人聚集到纳什的身边，他们设立了1个资助纳什治疗的基金，并在美国数学会发起1个募捐活动。基金的设立人写到：“如果在帮助纳什返回数学领域方面有什么事情可以做，哪怕是在1个很小的范围，不仅对他，而且对数学都很有好处。”对于普林斯顿大学为他做的一切，纳什在清醒后表示，“我在这里得到庇护，因此没有变得无家可归。”

　　守得云开见月明，妻子和朋友的关爱终于得到了回报。80年代末的1个清晨，当普里斯顿高等研究院的戴森教授像平常一样向纳什道早安时，纳什回答说：“我看见你的女儿今天又上了电视。”从来没有听到过纳什说话的戴森仍然记得当时的震惊之情，他说：“我觉得最奇妙的还是这个缓慢的苏醒，渐渐地他就越来越清醒，还没有任何人曾经像他这样清醒过来。”

　　纳什渐渐康复，从疯癫中苏醒，而他的苏醒似乎是为了迎接他生命中的一件大事：荣获诺贝尔经济学奖。当1994年瑞典国王宣布年度诺贝尔经济学奖的获得者是约翰·纳什时，数学圈里的许多人惊叹的是：原来纳什还活着。

　　纳什没有因为获得了诺贝尔奖就放弃他的研究，在诺贝尔奖得主自传中，他写道：从统计学看来，没有任何1个已经66岁的数学家或科学家能通过持续的研究工作，在他或她以前的成就基础上更进1步。但是，我仍然继续努力尝试。由于出现了长达25年部分不真实的思维，相当于提供了某种假期，我的情况可能并不符合常规。因此，我希望通过目前的研究成果或以后出现的任何新鲜想法，取得一些有价值的成果。”

　　而在2001年，经过几十年风风雨雨的艾里西亚与约翰·纳什复婚了。事实上，在漫长的岁月里，艾里西亚在心灵上从来没有离开过纳什。这个伟大的女性用一生与命运进行博弈，她终于取得了胜利。而纳什，也在得与失的博弈中取得了均衡。

　　2005年6月1日晚，诺贝尔北京论坛在故宫东侧菖蒲河公园内的东苑戏楼闭幕。热闹的晚宴结束后，纳什没有搭乘主办方安排的专车，而是1个人夹着文件夹走出了东苑戏楼。他像1个普通老人一样步行穿过菖蒲河公园，然后绕到南河沿大街路西的人行横道上等待红绿灯。绿灯亮起，老人隅隅独行的背影在暮色中渐行渐远，终于消失不见。

本文标题：我奋斗了18年才和你坐在一起喝咖啡-今天，奋斗的起点
本文地址： http://www.61k.com/1187608.html