一 : 2014年秋电大高等数学基础形成性考核册答案

高等数学基础作业1

第1章 函数

第2章 极限与连续

（一） 单项选择题

⒈下列各函数对中，（C ）中的两个函数相等．

A. f(x)?(x)2，g(x)?x B. f(x)?x2，g(x)?x

x2?13 C. f(x)?lnx，g(x)?3lnx D. f(x)?x?1，g(x)? x?1

⒉设函数f(x)的定义域为(??,??)，则函数f(x)?f(?x)的图形关于（C）对称．

A. 坐标原点 B. x轴

C. y轴 D. y?x

⒊下列函数中为奇函数是（B）．

A. y?ln(1?x2) B. y?xcosx

ax?a?x

1?x) C. y? D. y?ln(2

⒋下列函数中为基本初等函数是（C）．

A. y?x?1 B. y??x

C. y?x2??1,x?0 D. y?? 1,x?0?

⒌下列极限存计算不正确的是（D）．

x2

?1 B. limln(1?x)?0 A. lim2x?0x??x?2

sinx1?0 D. limxsin?0 C. limx??x??xx

⒍当x?0时，变量（C）是无穷小量．

sinx1 A. B. xx

1 C. xsin D. ln(x?2) x

⒎若函数f(x)在点x0满足（A），则f(x)在点x0连续。(www.61k.com)

A. limf(x)?f(x0) B. f(x)在点x0的某个邻域内有定义 x?x0

f(x)?f(x0) D. limf(x)?limf(x) C. lim???x?x0x?x0x?x0

（二）填空题 x2?9⒈函数f(x)??ln(1?x)的定义域是?x|x?3? x?322⒉已知函数f(x?1)?x?x，则f(x)? 1x)?． ⒊lim(1?x??2x

高等数学基础形成性考核册答案 2014年秋电大高等数学基础形成性考核册答案

11x12x?1

lim(1?)?lim(1?)2?e2 x??x??2x2x

1?x?⒋若函数f(x)??(1?x),x?0，在x?0处连续，则k? e ．

?x?0?x?k,

?x?1,x?0⒌函数y??的间断点是x?0 sinx,x?0?

⒍若limf(x)?A，则当x?x0时，f(x)?A称为x?x0时的无穷小量 ． x?x0

（二） 计算题

⒈设函数

?ex,x?0f(x)?? ?x,x?0

求：f(?2),f(0),f(1)．

解：f??2???2，f?0??0，f?1??e?e 1

2x?1的定义域． x

?2x?1??x?0??2x?11?解：y?lg有意义，要求?解得?x?或x?0 x2?x?0????x?0?1?? 则定义域为?x|x?0或x?? 2??

⒊在半径为R的半圆内内接一梯形，梯形的一个底边与半圆的直径重合，另一底边的两个端⒉求函数y?lg点在半圆上，试将梯形的面积表示成其高的函数．

解：

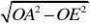
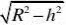
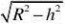
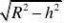
A

O h

B

C

设梯形ABCD即为题中要求的梯形，设高为h，即OE=h，下底CD＝2R

直角三角形AOE中，利用勾股定理得

AE?

则上底＝2AE?h2R??hR? 2

sin3x⒋求lim． x?0sin2x故S???

高等数学基础形成性考核册答案 2014年秋电大高等数学基础形成性考核册答案

sin3xsin3x?3xsin3x3133解：lim?lim?lim?＝?? x?0sin2xx?0x?02122?2x2x2x

x2?1⒌求lim． x??1sin(x?1)

x2?1(x?1)(x?1)x?1?1?1?lim?lim???2 解：limx??1sin(x?1)x??1sin(x?1)x??11

x?1

tan3x⒍求lim． x?0x

tan3xsin3x1sin3x11?lim?lim??3?

1??3?

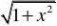
3

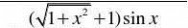
解：limx?0x?

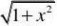
0xxcos3xx?03xcos3x1

?x2?1

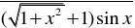
⒎求lim． x?012

??解：limx?0x?0x?0sinx

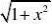
?limx?0 x1)x?0?0 1?1?1⒏求lim(x??x?1x)． x?3

111(1?)x[(1?)?x]?1x?1xe?1

x?4解：lim( )?lim()?lim?lim??ex3x??x?3x??x??xx??e11?(1?)[(1?)3]3

xx3

x2?6x?8⒐求lim2． x?4x?5x?4

x2?6x?8?x?4??x?2??limx?2?4?2?2 解：lim2?limx?4x?5x?4x?4x?4x?1x?4x?14?131?⒑设函数

?(x?2)2,x?1?f(x)??x,?1?x?1

?x?1,x??1?

讨论f(x)的连续性，并写出其连续区间．

解：分别对分段点x??1,x?1处讨论连续性

（1）

x??1?

x??1?limf?x??limx??1x??1?x??1?limf?x??lim?x?1???1?1?0

高等数学基础形成性考核册答案 2014年秋电大高等数学基础形成性考核册答案

(www.61k.com)

二 : 2015电大高等数学基础形成性考核手册答

高等数学基础形考作业

第1章 函数

第2章 极限与连续

（一） 单项选择题

⒈下列各函数对中，（C）中的两个函数相等．

A. f(x)?(x)2，g(x)?x B. f(x)?x2

f(x)?lnx3，g(x)?x C. ，g(x)?3lnx D. x2?1 f(x)?x?1，g(x)?x?1

⒉设函数f(x)的定义域为(??,??)，则函数f(x)?f(?x)的图形关于（C）对称．

A. 坐标原点 B.

⒊下列函数中为奇函数是（B）．

A. x轴 y?x C. y轴 D. y?ln(1?x2) B. y?xcosx

ax?a?x

y?2 D. C. y?ln(1?x)

⒋下列函数中为基本初等函数是（C）．

A. y?x?1 B. y??x

C. y?x2 D. ??1,x?0 y??x?0?1,

⒌下列极限存计算不正确的是（D）．

A. x2lim2?1 B. limln(1?x)?0 x?0x??x?2

limsinx1?0 D. limxsin?0 x??x??xx

⒍当x?0时，变量（C）是无穷小量．

sinx1 A. B. xx

1 C. xsin D. ln(x?2) x C.

⒎若函数

A.

C. f(x)在点x0满足（A），则f(x)在点x0连续。 x?x0limf(x)?f(x0) B. f(x)在点x0的某个邻域内有定义 x?x0x?x0?x?x0limf(x)?f(x0) D. limf(x)?limf(x) ??

（二）填空题

1

⒈函数f(x)?x2?9?ln(1?x)的定义域是?3,???． x?3

⒉已知函数f(x?1)?x2?x，则f(x)?2． 11x)?e2． ⒊lim(1?x??2x

1?x?f(x)??(1?x),x?0，在x?0处连续，则k?

?x?0?x?k,⒋若函数e ．

?x?1,x?0⒌函数y??的间断点是x?0．

?sinx,x?0

⒍若x?x0limf(x)?A，则当x?x0时，f(x)?A称为x?x0时的无穷小量。

（三）计算题

⒈设函数

?ex,x?0f(x)?? x,x?0?

求：

解：f(?2),f(0),f(1)． f??2???2，f?0??0，f?1??e1?e y?lg2x?1的定义域． x⒉求函数

?2x?1??x?0??2x?11?解：y?lg有意义，要求?解得?x?或x?0 x2?x?0????x?0? 则定义域为?x|?

?1?x?0或x?? 2?

⒊在半径为R的半圆内内接一梯形，梯形的一个底边与半圆的直径重合，另一底边的两个端点在半圆上，试将梯形的面积表示成其高的函数．

解： O h E

C

设梯形ABCD即为题中要求的梯形，设高为h，即OE=h，下底CD＝2R

2

直角三角形AOE中，利用勾股定理得

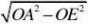
AE?则上底＝2AE

故S

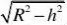
?h2R??hR 2

sin3x⒋求lim． x?0sin2xsin3xsin3x?3xsin3x3133解：lim?lim?lim?＝?? x?0sin2xx?0x?02122?2x2x2x??

?x2?1⒌求lim． x??1sin(x?1)x2?1(x?1)(x?1)x?1?1?1?lim?lim???2 解：limx??1sin(x?1)x??1sin(x?1)x??11

x?1

tan3x． x?0x

tan3xsin3x1sin3x11?lim?lim??3?

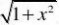
1??3?

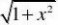
3

解：limx?0x?

0xxcos3xx?03xcos3x1⒍求lim

?x2?1

⒎求lim． x?0sinx

12

??解：limx?0x?0x?0sinx

?limx?0x1)sinxx?0?0 1?1?1⒏求lim(x??x?1x)． x?3

111(1?)x[(1?)?x]?1x?1xe?1

x解：lim()?lim()?lim?lim?3?e?4 xx??x?3x??x??x??33e11?(1?)x[(1?)3]3

xx31?x2?6x?8⒐求lim2． x?4x?5x?4

x2?6x?8?x?4??x?2??limx?2?4?2?2 解：lim2?limx?4x?5x?4x?4x?4x?1x?4x?14?13

⒑设函数

3

?(x?2)2,x?1?f(x)??x,?1?x?1

?x?1,x??1?

讨论f(x)的连续性。

??1,x?1处讨论连续性 解：分别对分段点x

（1）

x??1?

x??1?limf?x??limx??1x??1?limf?x??lim?x?1???1?1?0x??1?

x??1?x??1? 所以

（2）

x?1?

x?1?limf?x??limf?x?，即f?x?在x??1处不连续 limf?x??lim?x?2???1?2??1x?1?x?1?22limf?x??limx?1

f?1??1

所以limx?1? f?x??limf?x??f?1?即f?x?在x?1处连续 x?1?

由（1）（2）得

f?x?在除点x??1外均连续

高等数学基础作业2答案：

第3章 导数与微分

（一）单项选择题

⒈设

A.

C. f(0)?0且极限limx?0f(x)f(x)?（C）． 存在，则limx?0xxf(0) B. f?(0) f?(x) D. 0cvx

f(x)在x0可导，则limh?0 ⒉设f(x0?2h)?f(x0)?（D）． 2h

A.

C. ?2f?(x0) B. f?(x0) 2f?(x0) D. ?f?(x0) ⒊设

A. f(x)?ex，则lim?x?0e B. 2e C. f(1??x)?f(1)?（A）． ?x11e D. e 24 ⒋设

f(x)?x(x?1)(x?2)?(x?99)，则f?(0)?（D）． 4

A. 99 B. ?99 C. 99! D. ?99!

⒌下列结论中正确的是（C）．

A. 若

C. 若f(x)在点x0有极限，则在点x0可导． B. 若f(x)在点x0连续，则在点x0可导． f(x)在点x0可导，则在点x0有极限． D. 若f(x)在点x0有极限，则在点x0连续．

（二）填空题

⒈设函数1?2xsin,x?0?，则f?(0)?f(x)??x?x?0?0,

⒉设f(ex)?e2x?5ex，则df(lnx)2lnx5??xxdx

1。 2。 ⒊曲线f(x)?x?1在(1,2)处的切线斜率是k? ⒋曲线f(x)?sinx在(,1)处的切线方程是y?1。 π2

⒌设y?x2x，则y??2x2x(1?lnx)

y?xlnx，则y??? ⒍设1。 x

（三）计算题

⒈求下列函数的导数y?： ⑴y?(xx?3)ex

31

x 解:y??xx?3e?xx?3?e? ?(x?3)e?x2e 2???x??x?3

2x

⑵y?cotx?x2lnx

??2?22??解：y??cotx??x?lnx?x?lnx???cscx?x?2xlnx

x2

⑶y? lnx

??x?lnx?x?lnx?解：y??22?

ln2x?2xlnx?x ln2x

5

三 : 2014年秋电大高等数学基础形成性考核册

高等数学基础作业1

第1章 函数

第2章 极限与连续

（一） 单项选择题

⒈下列各函数对中，（C ）中的两个函数相等．

A. f(x)?(x)2，g(x)?x B. f(x)?x2，g(x)?x

x2?13 C. f(x)?lnx，g(x)?3lnx D. f(x)?x?1，g(x)? x?1

⒉设函数f(x)的定义域为(??,??)，则函数f(x)?f(?x)的图形关于（C）对称．

A. 坐标原点 B. x轴

C. y轴 D. y?x

⒊下列函数中为奇函数是（B）．

A. y?ln(1?x2) B. y?xcosx

ax?a?x

1?x) C. y? D. y?ln(2

⒋下列函数中为基本初等函数是（C）．

A. y?x?1 B. y??x

C. y?x2??1,x?0 D. y?? 1,x?0?

⒌下列极限存计算不正确的是（D）．

x2

?1 B. limln(1?x)?0 A. lim2x?0x??x?2

sinx1?0 D. limxsin?0 C. limx??x??xx

⒍当x?0时，变量（C）是无穷小量．

sinx1 A. B. xx

1 C. xsin D. ln(x?2) x

⒎若函数f(x)在点x0满足（A），则f(x)在点x0连续。

A. limf(x)?f(x0) B. f(x)在点x0的某个邻域内有定义 x?x0

f(x)?f(x0) D. limf(x)?limf(x) C. lim???x?x0x?x0x?x0

（二）填空题 x2?9⒈函数f(x)??ln(1?x)的定义域是?x|x?3? x?322⒉已知函数f(x?1)?x?x，则f(x)? 1x)?． ⒊lim(1?x??2x

11x12x?1

lim(1?)?lim(1?)2?e2 x??x??2x2x

1?x?⒋若函数f(x)??(1?x),x?0，在x?0处连续，则k? e ．

?x?0?x?k,

?x?1,x?0⒌函数y??的间断点是x?0 sinx,x?0?

⒍若limf(x)?A，则当x?x0时，f(x)?A称为x?x0时的无穷小量 ． x?x0

（二） 计算题

⒈设函数

?ex,x?0f(x)?? ?x,x?0

求：f(?2),f(0),f(1)．

解：f??2???2，f?0??0，f?1??e?e 1

2x?1的定义域． x

?2x?1??x?0??2x?11?解：y?lg有意义，要求?解得?x?或x?0 x2?x?0????x?0?1?? 则定义域为?x|x?0或x?? 2??

⒊在半径为R的半圆内内接一梯形，梯形的一个底边与半圆的直径重合，另一底边的两个端⒉求函数y?lg点在半圆上，试将梯形的面积表示成其高的函数．

解：

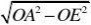
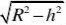
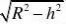
A

O h

B

C

设梯形ABCD即为题中要求的梯形，设高为h，即OE=h，下底CD＝2R

直角三角形AOE中，利用勾股定理得

AE?

则上底＝2AE?h2R??hR? 2

sin3x⒋求lim． x?0sin2x故S???

sin3xsin3x?3xsin3x3133解：lim?lim?lim?＝?? x?0sin2xx?0x?02122?2x2x2x

x2?1⒌求lim． x??1sin(x?1)

x2?1(x?1)(x?1)x?1?1?1?lim?lim???2 解：limx??1sin(x?1)x??1sin(x?1)x??11

x?1

tan3x⒍求lim． x?0x

tan3xsin3x1sin3x11?lim?lim??3?

1??3?

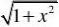
3

解：limx?0x?

0xxcos3xx?03xcos3x1

?x2?1

⒎求lim． x?012

??解：limx?0x?0x?0sinx

?limx?0 x1)x?0?0 1?1?1⒏求lim(x??x?1x)． x?3

111(1?)x[(1?)?x]?1x?1xe?1

x?4解：lim( )?lim()?lim?lim??ex3x??x?3x??x??xx??e11?(1?)[(1?)3]3

xx3

x2?6x?8⒐求lim2． x?4x?5x?4

x2?6x?8?x?4??x?2??limx?2?4?2?2 解：lim2?limx?4x?5x?4x?4x?4x?1x?4x?14?131?⒑设函数

?(x?2)2,x?1?f(x)??x,?1?x?1

?x?1,x??1?

讨论f(x)的连续性，并写出其连续区间．

解：分别对分段点x??1,x?1处讨论连续性

（1）

x??1?

x??1?limf?x??limx??1x??1?x??1?limf?x??lim?x?1???1?1?0

所以limf?x??limf?x?，即f?x?在x??1处不连续 x??1?x??1?

（2）

x?1?

x?1?limf?x??lim?x?2???1?2??1x?1?x?1?22limf?x??limx?1

f?1??1

所以limf?x??limf?x??f?1?即f?x?在x?1处连续 x?1?x?1?

由（1）（2）得f?x?在除点x??1外均连续

故f?x?的连续区间为???,?1?

第3章 导数与微分

（一）单项选择题 ??1,??? 《高等数学基础》第二次作业

f(x)f(x)?（C ）． 存在，则limx?0x?0xx

A. f(0) B. f?(0)

C. f?(x) D. 0cvx

f(x0?2h)?f(x0)?（D ）． ⒉设f(x)在x0可导，则limh?02h

A. ?2f?(x0) B. f?(x0)

C. 2f?(x0) D. ?f?(x0) ⒈设f(0)?0且极限lim

f(1??x)?f(1)?（A ）． ?x?0?x

A. e B. 2e

11 C. e D. e 24

⒋设f(x)?x(x?1)(x?2)?(x?99)，则f?(0)?（D ）． ⒊设f(x)?ex，则lim

A. 99 B. ?99

C. 99! D. ?99!

⒌下列结论中正确的是（ C ）．

A. 若f(x)在点x0有极限，则在点x0可导．

B. 若f(x)在点x0连续，则在点x0可导．

C. 若f(x)在点x0可导，则在点x0有极限．

D. 若f(x)在点x0有极限，则在点x0连续．

（二）填空题

1?2?xsin,x?0 ⒈设函数f(x)??，则f?(0)? x?x?0?0,

df(lnx)2lnx5． ??xxdx

1 ⒊曲线f(x)?x?1在(1,2)处的切线斜率是k? 2

π22? ⒋曲线f(x)?sinx在(,1)处的切线方程是y?x?(1?) 4224

⒌设y?x2x，则y??2x2x(1?lnx)

1 ⒍设y?xlnx，则y??? x ⒉设f(ex)?e2x?5ex，则

（三）计算题

⒈求下列函数的导数y?： 3x⑴y?(xx?3)e y??(x?3)e?x2e 2

⑵y?cotx?x2lnx y???csc2x?x?2xlnx xx321

2xlnx?xx2

⑶y? y?? 2lnxlnx

cosx?2xx(?sinx?2xln2)?3(coxs?2x)⑷y? y?? 3xx4

1sinx(?2x)?(lnx?x2)cosx2lnx?x⑸y? y?? 2sinxsinx

sinx3?cosxlnx ⑹y?x4?sinxlnx y??4x?x

sinx?x23x(cosx?2x)?(sinx?x2)3xln3⑺y? y?? 32x3x

ex1xxx??⑻y?etanx?lnx y??etan 2cosxx

⒉求下列函数的导数y?： ⑴y?e1?x2

?x

⑵y?lncosx3 y??e?x2x2

?sinx3

223y??3x??3xtanx 3cosx

⑶y?

7

8xxx ?17y?x y??x8 8⑷y?x?x

1?2?111y??(x?x2)3(1?x2) 32

2x⑸y?cose

y???exsin(2ex)

⑹y?cose

x2x2 x2y???2xesine

⑺y?sinnxcosnx

y??nsinn?1xcosxcosnx?nsinnxsin(nx) ⑻y?5sinx2

y??2xln5cosx5⑼2sinx2 y?esin2x

y??sin2xe

⑽sin2x y?x?e

x2x2x2 y??x(x?2xlnx)?2xe⑾

x2 y?x

exex?eex y??xex

xex(?elnx)?eex

x

2y ⒊在下列方程中，y?y(x)是由方程确定的函数，求y?： ⑴ycosx?e

y?cosx?ysinx?2e2yy?

ysinxy?? 2ycosx?2e

⑵y?cosylnx

1y??siny.y?lnx?cosy. x

cosyy?? x(1?sinylnx)

x2

⑶2xsiny? y

2yx?x2y?x22yx? 2xcosy.y??2siny?y(2xcosy?)??2siny y2y2y22xy?2ysinyy?? 2xy2cosy?x2

⑷y?x?lny

y??1 y

y y??y?1

⑸lnx?ey?y2 1?eyy??2yy? x

1 y??x(2y?ey)y??

⑹y2?1?exsiny

2yy??excosy.y??siny.ex

exsiny y??x2y?ecosy

⑺ey?ex?y3 eyy??ex?3y2y?

ex

y??y?3y2 e

⑻y?5x?2y

y??5xln5?y?2yln2

5xln5y?? y1?2ln2

⒋求下列函数的微分dy： ⑴y?cotx?cscx

?1cosx?)dx 22cosxsinx

lnx⑵y? sinx

1sinx?lnxcosxxdy?dx 2sinx

1?x⑶y?arcsin 1?xdy?(

dy?1

1?x2?()1?x?(1?x)?(1?x)?x21dx??dx 22x(1?x)(1?x)

⑷y?1?x 1?x

1?ln(1?x)?ln(1?x)? 3两边对数得：lny?y?1?11?(?) y31?x1?x

y???

1?x11(?) 31?x1?x1?x

⑸y?sin2ex

dy?2sinexexexdx?sin(2ex)exdx

⑹y?tanex 33

dy?sec2ex3x2dx?3x2exsec2xdx

⒌求下列函数的二阶导数：

⑴y?xlnx 33

y??1?lnx

1y??? x

⑵y?xsinx

y??xcosx?sinx

y????xsinx?2cosx

⑶y?arctanx

y??1 1?x2

2x y????22(1?x)

2⑷y?3x

y??2x3ln3 y???4x3ln3?2ln3?3

（四）证明题

设f(x)是可导的奇函数，试证f?(x)是偶函数． 证：因为f(x)是奇函数 所以f(?x)??f(x)

两边导数得：f?(?x)(?1)??f?(x)?f?(?x)?f(x) 所以f?(x)是偶函数。

x22x22x2

《高等数学基础》第三次作业

第4章 导数的应用

（一）单项选择题

⒈若函数f(x)满足条件（D），则存在??(a,b)，使得f?(?)? A. 在(a,b)内连续 B. 在(a,b)内可导

C. 在(a,b)内连续且可导 D. 在[a,b]内连续，在(a,b)内可导 ⒉函数f(x)?x2?4x?1的单调增加区间是（D ）． A. (??,2) B. (?1,1) C. (2,??) D. (?2,??) ⒊函数y?x2?4x?5在区间(?6,6)内满足（A ）． A. 先单调下降再单调上升 B. 单调下降 C. 先单调上升再单调下降 D. 单调上升 ⒋函数f(x)满足f?(x)?0的点，一定是f(x)的（C ）．

A. 间断点 B. 极值点 C. 驻点 D. 拐点

⒌设f(x)在(a,b)内有连续的二阶导数，x0?(a,b)，若f(x)满足（ C ），则f(x)在x0取到极小值．

A. f?(x0)?0,f??(x0)?0 B. f?(x0)?0,f??(x0)?0 C. f?(x0)?0,f??(x0)?0 D. f?(x0)?0,f??(x0)?0

⒍设f(x)在(a,b)内有连续的二阶导数，且f?(x)?0,f??(x)?0，则f(x)在此区间内是（ A ）．

A. 单调减少且是凸的 B. 单调减少且是凹的 C. 单调增加且是凸的 D. 单调增加且是凹的

（二）填空题

⒈设f(x)在(a,b)内可导，x0?(a,b)，且当x?x0时f?(x)?0，当x?x0时

f(b)?f(a)

．

b?a

f?(x)?0，则x0是f(x)的

⒉若函数f(x)在点x0可导，且x0是f(x)的极值点，则f?(x0)? ⒊函数y?ln(1?x2)的单调减少区间是(??,0)．

⒋函数f(x)?ex的单调增加区间是(0,??)

⒌若函数f(x)在[a,b]内恒有f?(x)?0，则f(x)在[a,b]上的最大值是f(a)． ⒍函数f(x)?2?5x?3x3的拐点是

（三）计算题

⒈求函数y?(x?1)(x?5)的单调区间和极值． 令y??(x?1)2(x?5)?2(x?5)(x?2)

2

2

2

?驻点x?2,x?5

列表：

极大值：f(2)?27

极小值：f(5)?0

⒉求函数y?x2?2x?3在区间[0,3]内的极值点，并求最大值和最小值．

令：y??2x?2?0?x?1(驻点）

f(0)?3

f(3)?6

f(3)?6

f(1)?2 f(1)?2 ?最大值?最小值

⒊试确定函数y?ax3?bx2?cx?d中的a,b,c,d，使函数图形过点(?2,44)和点(1,?10)，且x??2是驻点，x?1是拐点．

?44??8b?4b?2x?d??10?a?b?c?d?解：? 0?12a?4b?c??0?6a?2b??a?1?b??3? ??c?16???d??24

⒋求曲线y2?2x上的点，使其到点A(2,0)的距离最短．

解：设p(x,y)是y2?2x上的点，d为p到A点的距离，则：

d?(x?2)2?y2?(x?2)2?2x

令d??2(x?2)?2

2(x?2)?2x2?x?1(x?2)?2x2?0?x?1

?y2?2x上点(1,2)到点A(2,0)的距离最短。

⒌圆柱体上底的中心到下底的边沿的距离为L，问当底半径与高分别为多少时，圆柱体的体积最大？

设园柱体半径为R，高为h，则体积

V??R2h??(L2?h2)h

令：V???[h(?2h)?L2?h2]??[L2?3h2]?0?L?hh?L3R?2L3?当h?2,R?L时其体积最大。 33

⒍一体积为V的圆柱体，问底半径与高各为多少时表面积最小？

设园柱体半径为R，高为h，则体积

V??R2hS表面积?2?Rh?2?R2?2V?2?R2 R

令：S???2VR?2?4?R?0

h?4V ?VV ?R3?R?2?2??

答：当R?V4V h?时表面积最大。 2??

⒎欲做一个底为正方形，容积为62.5立方米的长方体开口容器，怎样做法用料最省？

解：设底连长为x，高为h。则：

62.5?x2h

2?h?62.5 2x2侧面积为：S?x?4xh?x?

令S??2x?250 x250?02x?x3?125?x?5

答：当底连长为5米，高为2.5米时用料最省。

（四）证明题

⒈当x?0时，证明不等式x?ln(1?x)． 证：由中值定理得：ln(1?x)ln(1?x)?ln11???1x(1?x)?11??

?x?ln(1?x)(当x?0时） (???0) ?ln(1?x)?1x

x⒉当x?0时，证明不等式e?x?1．

设f(x)?ex?(x?1)

f?(x)?ex?1?0(当x?0时）?当x?0时f(x)单调上升且f(0)?0 ?f(x)?0,即ex?(x?1)证毕

《高等数学基础》第四次作业

第5章 不定积分

第6章 定积分及其应用

（一）单项选择题

1，则f?(x)?（D ）． x

112 A. lnx B. ?2 C. D. 3 xxx ⒈若f(x)的一个原函数是

⒉下列等式成立的是（D ）．

A?f?(x)dx?f(x) B. ?df(x)?f(x)C. d?f(x)dx?f(x) D. df(x)dx?f(x) ?dx

⒊若f(x)?cosx，则?f?(x)dx?（B ）．

A. sinx?c B. cosx?c C. ?sinx?c D. ?cosx?c

⒋d23xf(x)dx?（ B）． ?dx

323 A. f(x) B. xf(x) C.

⒌若?f(x)dx?F(x)?c，则?11f(x) D. f(x3) 331f(x)dx?（B ）． x

A. F(x)?c B. 2F(x)?c C. F(2x)?c D. 1

xF(x)?c

⒍由区间[a,b]上的两条光滑曲线y?f(x)和y?g(x)以及两条直线x?a和x?b所

围成的平面区域的面积是（C ）．

A. ?b

a[f(x)?g(x)]dx B.?[g(x)?f(x)]dx ab

C. ?b

af(x)?g(x)dx D. ?ba[f(x)?g(x)]dx

（二）填空题

⒈函数f(x)的不定积分是?f(x)dx．

⒉若函数F(x)与G(x)是同一函数的原函数，则F(x)与G(x)之间有关系式F(x)?G(x)?c(常数）．

⒊dedx?e

⒋(tanx)?dx?tanx?c

⒌若

⒍3?x2x2??f(x)dx?cos3x?c，则f?(x)??9cos(3x) 15(sinx?)dx?3 ??32

??1dx收敛，则p?0 ⒎若无穷积分?1xp

（三）计算题 cos

⒈

⒉??e1dx??cos1d(1)??sin1?c ?xxxx2x

x

11dx??d(lnx)?ln(lnx)?c ⒊?xlnxlnx

1111⒋?xsin2xdx??xcos2x??cos2xdx??xcos2x?sin2x?c 2224

e3?lnxe11edx??(3?lnx)d(3?lnx)?(3?lnx)1? ⒌?11x2211?2x111?2x1?21?2x11?21?2x⒍?xedx??ex??edx??e?ee? 0?002224440

eex21ee21⒎?xlnxdx?lnx??xdx?? 1122241

eelnxe1111e?2⒏?dx??lnx??2dx?????1 1x21xxex1e1

（四）证明题

⒈证明：若f(x)在[?a,a]上可积并为奇函数，则

证:令x??tdx?2?edx?2e?c ?a?af(x)dx?0． a

?a?a?af(x)dx????aaf(?t)dt??f(?t)dt???f(t)dt ?aa

??aa

?af(x)dx????af(x)dx??a?af(x)dx?0 证毕

⒉证明：若f(x)在[?a,a]上可积并为偶函数，则?a

?af(x)dx?2?a0f(x)dx．

证：?a

?af(x)dx??0a?af(x)dx??0f(x)dx

令x??t,则?0

?af(x)dx???0af(?t)dt??a0f(t)dt?f(x)是偶函数

?a0aa

?af(x)dx??f(x)dx??f(x)dx??f(x)dx??af(x)dx?2?a?a0000f(x)dx⒊证明：?aa

?af(x)dx??0[f(x)?f(?x)]dx

证：?a0a0a

?af(x)dx???af(x)dx??0f(x)dx???af(?x)dx??0f(x)dx =?a)dx??af(x)dx??a

0f(?x00[f(x)?f(?x)]dx 证毕 证毕

四 : 2015电大高等数学基础形成性考核手册答案

高等数学基础形考作业

第1章 函数

第2章 极限与连续

（一） 单项选择题

⒈下列各函数对中，（C）中的两个函数相等．

A. f(x)?(x)2，g(x)?x B. f(x)?x2

f(x)?lnx3，g(x)?x C. ，g(x)?3lnx D. x2?1 f(x)?x?1，g(x)?x?1

⒉设函数f(x)的定义域为(??,??)，则函数f(x)?f(?x)的图形关于（C）对称．

A. 坐标原点 B.

⒊下列函数中为奇函数是（B）．

A. x轴 y?x C. y轴 D. y?ln(1?x2) B. y?xcosx

ax?a?x

y?2 D. C. y?ln(1?x)

⒋下列函数中为基本初等函数是（C）．

A. y?x?1 B. y??x

C. y?x2 D. ??1,x?0 y??x?0?1,

⒌下列极限存计算不正确的是（D）．

A. x2lim2?1 B. limln(1?x)?0 x?0x??x?2

limsinx1?0 D. limxsin?0 x??x??xx

⒍当x?0时，变量（C）是无穷小量．

sinx1 A. B. xx

1 C. xsin D. ln(x?2) x C.

⒎若函数

A.

C. f(x)在点x0满足（A），则f(x)在点x0连续。（www.61k.com］ x?x0limf(x)?f(x0) B. f(x)在点x0的某个邻域内有定义 x?x0x?x0?x?x0limf(x)?f(x0) D. limf(x)?limf(x) ??

（二）填空题

1

高等数学基础形成性考核册答案 2015电大高等数学基础形成性考核手册答案

⒈函数f(x)?x2?9?ln(1?x)的定义域是?3,???． x?3

⒉已知函数f(x?1)?x2?x，则f(x)?2． 11x)?e2． ⒊lim(1?x??2x

1?x?f(x)??(1?x),x?0，在x?0处连续，则k?

?x?0?x?k,⒋若函数e ．

?x?1,x?0⒌函数y??的间断点是x?0．

?sinx,x?0

⒍若x?x0limf(x)?A，则当x?x0时，f(x)?A称为x?x0时的无穷小量。(www.61k.com]

（三）计算题

⒈设函数

?ex,x?0f(x)?? x,x?0?

求：

解：f(?2),f(0),f(1)． f??2???2，f?0??0，f?1??e1?e y?lg2x?1的定义域． x⒉求函数

?2x?1??x?0??2x?11?解：y?lg有意义，要求?解得?x?或x?0 x2?x?0????x?0? 则定义域为?x|?

?1?x?0或x?? 2?

⒊在半径为R的半圆内内接一梯形，梯形的一个底边与半圆的直径重合，另一底边的两个端点在半圆上，试将梯形的面积表示成其高的函数．

解： O h E

C

设梯形ABCD即为题中要求的梯形，设高为h，即OE=h，下底CD＝2R

2

高等数学基础形成性考核册答案 2015电大高等数学基础形成性考核手册答案

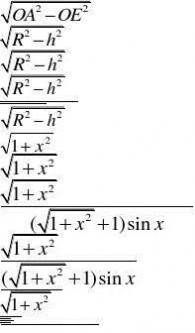
直角三角形AOE中，利用勾股定理得

AE?则上底＝2AE

故S

?h2R??hR 2

sin3x⒋求lim． x?0sin2xsin3xsin3x?3xsin3x3133解：lim?lim?lim?＝?? x?0sin2xx?0x?02122?2x2x2x??

?x2?1⒌求lim． x??1sin(x?1)x2?1(x?1)(x?1)x?1?1?1?lim?lim???2 解：limx??1sin(x?1)x??1sin(x?1)x??11

x?1

tan3x． x?0x

tan3xsin3x1sin3x11?lim?lim??3?

1??3?

3

解：limx?0x?

0xxcos3xx?03xcos3x1⒍求lim

?x2?1

⒎求lim． x?0sinx

12

??解：limx?0x?0x?0sinx

?limx?0x1)sinxx?0?0 1?1?1⒏求lim(x??x?1x)． x?3

111(1?)x[(1?)?x]?1x?1xe?1

x解：lim()?lim()?lim?lim?3?e?4 xx??x?3x??x??x??33e11?(1?)x[(1?)3]3

xx31?x2?6x?8⒐求lim2． x?4x?5x?4

x2?6x?8?x?4??x?2??limx?2?4?2?2 解：lim2?limx?4x?5x?4x?4x?4x?1x?4x?14?13

⒑设函数

3

高等数学基础形成性考核册答案 2015电大高等数学基础形成性考核手册答案

[www.61k.com)

五 : 2014年7月高等数学基础形成性考核册答案

2013高等数学基础形成性考核册答案：

第1章 函数极限与连续

一、单项选择题

1.C 2.C 3.B 4.C 5.D 6.C 7.A

二、填空题

1．?3，+??； 2．x2?x； 3

4．e； 5．x＝0； 6．无穷小量.

三、计算题

1．解：f?2???2,f?0??0,f?1??e1?e.

2．解：要使lg2x?1

x 有意义，必须 ?2

?x?1

?x?0, 解得：x?0或x?1,

??x?02 ?函数y?lg2x?1

x的定义域为?-?,0????1?

?2,????.

3．解：如图，梯形ABCD为半圆O的内接梯形，ABDC，AB＝2R，高DE＝

x 连接OD,则DEO为直角三角形，

DC?2OC?

?梯形的面积S=1

2DE?

DC?AB??1

2x?

2R?C

?

即S?xR?,?其中0?x?R?E O B

4．解：原式＝limsin3x2x33sin3x

x?03x?sin2x?2?2limx?03x?lim2x

x?0sin2x?3

2. A

5．解：原式＝limx?1x?1

sinx?1??x?1??limx??1sinx?1?limx??1?x?1???2 x??1

6．解：原式＝limsin3x3sin

x?03x?cos3x?3lim3x

x?03x?lim1

x?0cos3x?3.

11

7

．解：原式＝

2

x?0

0.

?x?0??x?3?4

?3

8．解：原式＝lim???4??4???

x????1???x?1???e?4.

??x?3????x?3?

1

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

9．解：原式＝lim?x?4??x?2?

x?1?limx?2

x?4x?4x?4x?1?2

3.

高等数学基础】作业2答案：

导数与微分

一、 单项选择题

1.B 2.D 3.A 4.D 5.C

二、填空题

1．0； 2．2lnx?5

x； 3．1

2； 4．y?1?0； 5．2x2x?lnx?1?；

三、计算题

1.求下列函数的导数y?：

(1)解：y??3

?x2?3?13

?ex,?y??3x2ex???x2?3??ex

??2?? 即 y??1

2ex?2.

?2?解：y???1

sin2x?2xlnx?x2?11

x??sin2x?2xlnx?x.

?3?解：y??1?

ln2x??2xlnx?x2?1?x

x???ln2x?2lnx?1?.

?4?解：y??1x

x6????sinx?2ln2?x3?3x2?cosx?2x???

?2x

xln2?3??1

4?xx4?xsinx?3cosx?.

?5?解：y???1??

sin2x???1

?x?2x???sinx??lnx?x2?cosx??? 22

?1?2xx?lnx

xsinx?sin2x?cosx.

?6?解：y??4x3?cosxlnx?sinx

x.

?7?解：y??1

??

3x?2?3x?cosx?2x??3xln3?sinx?x2???

?1cosx?2x?sinxln3?x2

3x?ln3?.．1x.

2 6

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

?8?解：y??extanx?ex?1

cos2x?1

x

?ex???tanx?1?

cos2x???1

x.

2.求下列函数的导数y?：

?

1?解：y???

??

?2?解：y??1

cosx??cosx????sinx

cosx??tanx.

1

?1?2

?1

3?解：y??xx?x2

???2??71

???x8,?y??7x?8.

??????8

?4?解：y??2sinx??sinx???2sinx?cosx?sin2x. ?5?解：y??cosx2??x2???2xcosx.

?6?解：y?=-sinex??ex????ex?sinex. ?7?解：y??nsinn?1x?cosx?cosnx?sinnx???sinnx??n?nsinn?1x??cosxcosnx?sinxsinnx??nsinn?1x?cos?n?1?x. ?8?解：y??5sinx?ln5??sinx???5sinxcosxln5. ?9?解：y??ecosx??cosx????sinxecosx.

3. 在下列方程中，y?y?x?是由方程确定的函数，求y?： ?1?解：y?cosx?y??sinx??e2y?2y?,

y??cosx?e2y??ysinx,

?y??ysinx

cosx?e2y.

?2?解：y???siny?y?lnx?cosy

x,

?1?sinylnx?y??cosy

x,

?y??cosy

x1?sinylnx.

3

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

?3?解：ysiny?x

2,两边求导，得

y?siny?ycosy?y??1

2,

?y??1

2siny?ycosy.

?4?解：y?=1+1y?

y?y??1?y.

?5?1

x?ey?y??2y?y?,

?2y?ey?y??1

x,

?y??1

x2y?ey.

?6?解：2y?y??exsiny?ex?cosy?y?,?2y?excosy?y??exsiny, ?y??exsiny

2y?excosy.

?7?解：ey?y??ex?3y2?y?,?ey?3y2?y??ex, y??ex

?ey?3y2.

?8?解：y??5xln5?2yln2?y?,?1?2yln2?y??5xln5, ?y??5xln5

1?2yln2.

4.求下列函数的微分dy： ?1?解：y???csc2x?cot2xcscx??cscx?cotx?cscx?,?dy?y?dx??cscx?cotx?cscx?dx.

1sinx?

?cosxlnx2?解：y??xsinx?xcosxlnxsin2x?xsin2x,

?dy?sinx?xcosxlnx

xsin2xdx.

4

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

?3?解：y??2sinxcosx?sin2x,

?dy?sin2xdx.

?4?解：y??sec2ex?ex?exsec2x,

x ?dy?esec2xdx.

5.求下列函数的二阶导数：

?

1?解：y??1?1

?2x2,

1?1?1

?y??3?3

??22

2????2x????4x.

x

?2?解：y??3ln3,

?y???3xln23.

?3?解：y??1

x,

?y????1

x2.

?4?解：y??sinx?xcosx,?y???cosx??cosx?xsinx??2cosx?xsinx.

四、证明题

证：由题设，有f??x???f?x?,

???f??x????????f?x????,

即f???x????1???f??x?,

f???x??f??x?

?f??x?是偶函数.

【高等数学基础】作业3答案 第四章 导数的应用

一、 单项选择题

1.D 2.D 3.A 4.C 5.C 6.A

二、 填空题

1．极小值； 2．0； 3．???,0?； 4．?0,???； 5．f?a?； 6．?0,2?.

三、 计算题

1.解：令y???x?5?2?2?x?1??x?5??3?x?5??x?1??0，

得：x1?1,x2?5.

列表如下

5

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

?函数 y 的单调增区间为?-?,1?,?5,???,单调减区间为?1，5?.

当x=1时，函数取得极大值32；当x=5时，函数取得极小值0.

2.解：令y?

?2x

?2?2?x?1??

0, 得 x?1.

当 x??0,1?时，y??

0;当 x

??1,3?时，y??0.

?函数y?x2?2x?3在区间?0,3?上的极值点为x?

1.

又y

?0??3,y?1??2,y?3??6,

?函数y?x2-2x+3在?0

，3?上的最大值为6，最小值为0.

3.解： 设所求的点P?x,y?,PA?d, 则y2?2x,(x?0)

d??令d??

得x?1??0,

易知，x?1是函数d的极小值点，也是最小值点.

此时， y2?2?1?2,y??所求的点为P或P1,.

4.解：如图所示，圆柱体高h与底半径r满足

h?r?L

圆柱体的体积公式为

V??rh

将r?L?h代入得

V??(L?h)

h

求导得

V???(?2h?(L?h))??(L?3h)

令V

??0得h?2

22222222

2222??2，并由此解出r?.即当底半径r?L，高h?L时，圆柱体的体积最大.

5.解：设圆柱体半径为R，高为h，则

6

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

h?V,?R2S表面积

?2?Rh?2?R2?2V?2?R2 R令

S??4?R?2V?02得R??h ??R??时，S?0,

???时，S??0 ??R??R?S的极小值点，也是最小值点.

此时答：当R?V2? h?4V?时表面积最大.

6.解：设长方体的底边长为x米，高为h米. 则 由62.5?x2h得h?62.5

x2

用料的面积为：S?x2?4xh?x2?250

x，?x?0?

令S??2x?2503

x2?0得x?125，x?5

易知，x?5是函数S的极小值点，也是最小值点.

答：当该长方体的底边长为5米，高为2.5米时用料最省。（www.61k.com)

证明题

1.证：令f?x??x?ln?1?x?,则

当x?0时，f??x??1?1x

1?x?1?x?0,

?函数f?x?在区间?0，+??为增函数 .

又f?0??0,

?当x?0时，f?x??f?0??0,

x?ln?1?x??0,

于是 x?ln?1?x?.?7 四、

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

2.证：令f?x??ex??x?1?, 则

当x?0时，f??x??ex?1?0,

?函数f?x?=ex??x?1?在区间?0，+??为增函数 .

又f?0??0,

?当x?0时，f?x??f?0??0,

ex??x?1??0,

于是 ex?x?1.

【高等数学基础】作业4答案：第五章 不定积分

第六章 积分及其应用

一、 单项选择题

1.D 2.D 3.B 4.B 5.B 6.D

二、填空题

1．?f?x?dx； 2．F?x??G?x??c； 3．ex2dx； 4．tanx?c； 5．?9cos3x；

7.?1.

三、计算题 1.解：原式＝??cos1

x??1?

?x????sin1

x?c.

2.解：原式＝2??2?c. 3.解：原式＝?1

lnx?lnx??ln?lnx??c. 4.解：原式＝1

2?sin2xd?2x???1

2cos2x?c.

5.解：原式＝?e

1?3?lnx?d?lnx?

e

???1?

?3lnx?2ln2x??1

????3?1?

2???0

?7

2.．3.

8 6

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

6.解：原式＝?1?1?2x

20xde

??1xe?2x1

20?11

2?0e?2xdx

??11

e?2?1?

2????4e?2x??

??111

2e2?4e2?4

?1

4?3

4e2.

7.解：原式＝1?e2

21lnxdx

?1

2x2lnxe1e

1?2?1x2dlnx

?121e

2e?2?1xdx

?1

2e2?1

4x2e

1

?1

2e2?1

2e2?1

4

?1

4?e2?1?.

8.解：原式＝??e?1?

1lnxd??x??

??1

xlnxee1

1??1x?lnx?

??1e1

e??1x2??1

e?1e

x1

??11

e?e?1

?1?2

e.

1.证：由题设，f??x???f?x?,x???a,a???aa

?af?x?dx??0?af?x?dx??0f?x?dx

???a?f??x??a

0???d??x???0f?x?dx

???a

0f?x?dx??a0f?x?dx

?0.

9 四、证明题

高等数学基础形成性考核册答案 2014年7月高等数学基础形成性考核册答案

2.证：由题设，f??x??f?x?,x???a,a???a

?a

?af?x?dx??0?af?x?dx??f?x?dx0aa?

???

0a??f??x???d??x???0f?x?dxa0 0f?x?dx??f?x?dxa0?2?f?x?dx.

10

本文标题：高等数学基础形成性考核册答案-2014年秋电大高等数学基础形成性考核册答案
本文地址： http://www.61k.com/1064621.html