一 : 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
数学中国 中国数学名人
二 : 中国古代著名数学家及其贡献
刘徽
刘徽(生于公元250年左右)，三国后期魏国人，是中国古代杰出的数学家，也是中国古典数学理论的奠基者之一．其生卒年月、生平事迹，史书上很少记载。据有限史料推测，他是魏晋时代山东邹平人。终生未做官。他在世界数学史上，也占有杰出的地位．他的杰作《九章算术注》和《海岛算经》，是我国最宝贵的数学遗产．
《九章算术》约成书于东汉之初，共有246个问题的解法．在许多方面：如解联立方程，分数四则运算，正负数运算，几何图形的体积面积计算等，都属于世界先进之列，但因解法比较原始，缺乏必要的证明，而刘徽则对此均作了补充证明．在这些证明中，显示了他在多方面的创造性的贡献．他是世界上最早提出十进小数概念的人，并用十进小数来表示无理数的立方根．在代数方面，他正确地提出了正负数的概念及其加减运算的法则；改进了线性方程组的解法．在几何方面，提出了"割圆术"，即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法．他利用割圆术科学地求出了圆周率π=3.14的结果．刘徽在割圆术中提出的"割之弥细，所失弥少，割之又割以至于不可割，则与圆合体而无所失矣"，这可视为中国古代极限观念的佳作．
《海岛算经》一书中， 刘徽精心选编了九个测量问题，这些题目的创造性、复杂性和富有代表性，都在当时为西方所瞩目．
刘徽思想敏捷，方法灵活，既提倡推理又主张直观．他是我国最早明确主张用逻辑推理的方式来论证数学命题的人．
刘徽的一生是为数学刻苦探求的一生．他虽然地位低下，但人格高尚．他不是沽名钓誉的庸人，而是学而不厌的伟人，他给我们中华民族留下了宝贵的财富．
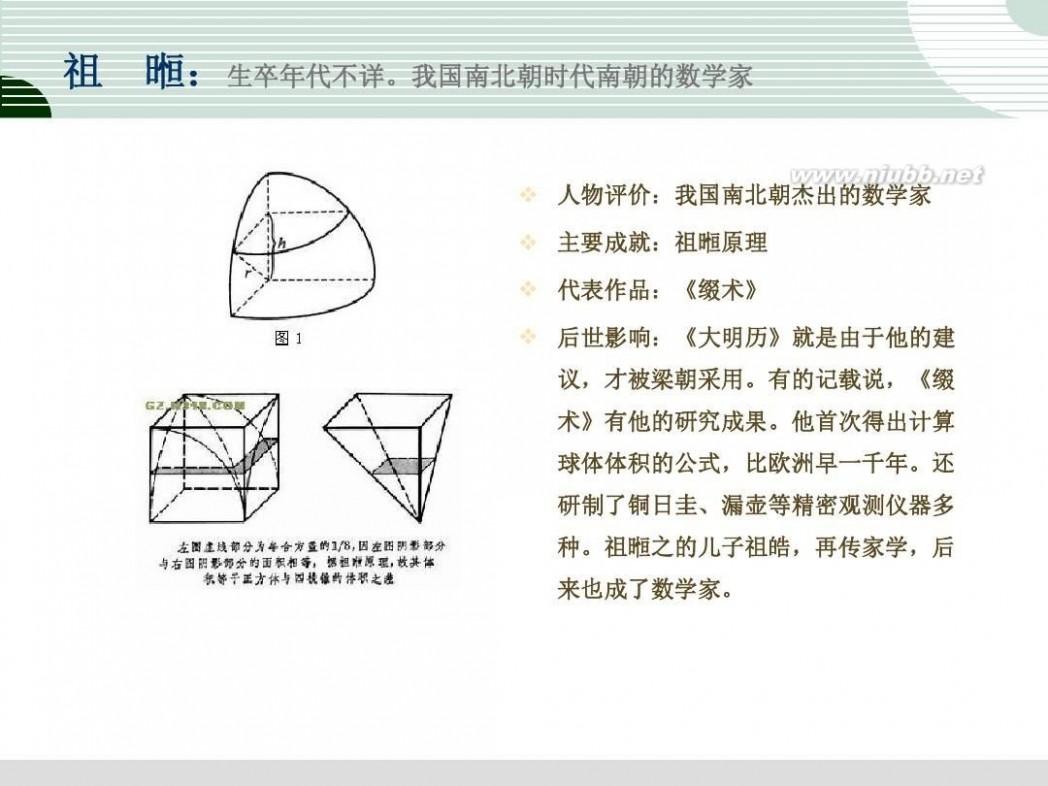
祖冲之
祖冲之（公元429年─公元500年）是我国杰出的数学家，科学家。南北朝时期人，汉族人，字文远。生于未文帝元嘉六年，卒于齐昏侯永元二年。祖籍范阳郡遒县（今河北涞水县）。其主要贡献在数学、天文历法和机械三方面。在数学方面，他写了《缀术》一书，被收入著名的《算经十书》中，作为唐代国子监算学课本，可惜后来失传了。祖冲之还和儿子祖暅一起圆满地利用「牟合方盖」解决了球体积的计算问题，得到正确的球体积公式。在机械学方面，他设计制造过水碓磨、铜制机件传动的指南车、千里船、定时器等等。此外，对音乐也研究。他是历史上少有的博学多才的人物。
祖冲之在数学上的杰出成就，是关于圆周率的计算．秦汉以前，人们以"径一周三"做为圆周率，这就是"古率"．后来发现古率误差太大，圆周率应是"圆径一而周三有余"，不过究竟余多少，意见不一．直到三国时期，刘徽提出了计算圆周率的科学方法--"割圆术"，用圆内接正多边形的周长来逼近圆周长．刘徽计算到圆内接96边形，求得π=3.14，并指出，内接正多边形的边数越多，所求得的π值越精确．祖冲之在前人成就的基础上，经过刻苦钻研，反复演算，求出π在3.1415926与3.1415927之间．并得出了π分数形式的近似值，取22/7为约率，取355/113为密率，其中355/113取六位小数是3.141592，它是分子分母在16604以内最接近π值的分数．祖冲之究竟用什么方法得出这一结果，现在无从考查．若设想他按刘徽的"割圆术"方法去求的话，就要计算到圆内接12288边形，这需要花费多少时间和付出多么巨大的劳动啊！由此可见他在治学上的顽强毅力和聪敏才智是令人钦佩的．祖冲之计算得出的密率，外国数学家获得同样结果，已是一千多年以后的事了．为了纪念祖冲之的杰出贡献，有些外国数学史家建议把π=叫做"祖率"．
祖冲之博览当时的名家经典，坚持实事求是，他从亲自测量计算的大量资料中对比分析，发现过去历法的严重误差，并勇于改进，在他三十三岁时编制成功了《大明历》，开辟了历法史的新纪元．
祖冲之还与他的儿子祖暅（也是我国著名的数学家）一起，用巧妙的方法解决了球体体积的计算．他们当时采用的一条原理是："幂势既同，则积不容异．"意即，位于两平行平面之间的两个立体，被任一平行于这两平面的平面所截，如果两个截面的面积恒相等，则这两个立体的体积相等．这一原理，在西文被称为卡瓦列利原理，但这是在祖氏以后一千多年才由卡氏发现的．为了纪念祖氏父子发现这一原理的重大贡献，大家也称这原理为"祖暅原理"．
▲张丘建--<张丘建算经>
《张丘建算经》三卷，据钱宝琮考，约成书于公元466～485年间.张丘建,北魏时清河(今山东临清一带)人,生平不详。最小公倍数的应用、等差数列各元素互求以及“百鸡术”等是其主要成就。“百鸡术”是世界著名的不定方程问题。13世纪意大利斐波那契《算经》、15世纪阿拉伯阿尔•卡西<<算术之钥》等著作中均出现有相同的问题。
▲朱世杰：《四元玉鉴》
朱世杰（1300前后），字汉卿，号松庭，寓居燕山（今北京附近），“以数学名家周游湖海二十余年”，“踵门而学者云集”。朱世杰数学代表作有《算学启蒙》（1299）和《四元玉鉴》（1303）。《算学启蒙》是一部通俗数学名著，曾流传海外，影响了朝鲜、日本数学的发展。《四元玉鉴》则是中国宋元数学高峰的又一个标志，其中最杰出的数学创作有“四元术”（多元高次方程列式与消元解法）、“垛积法”（高阶等差数列求和）与“招差术”（高次内插法）
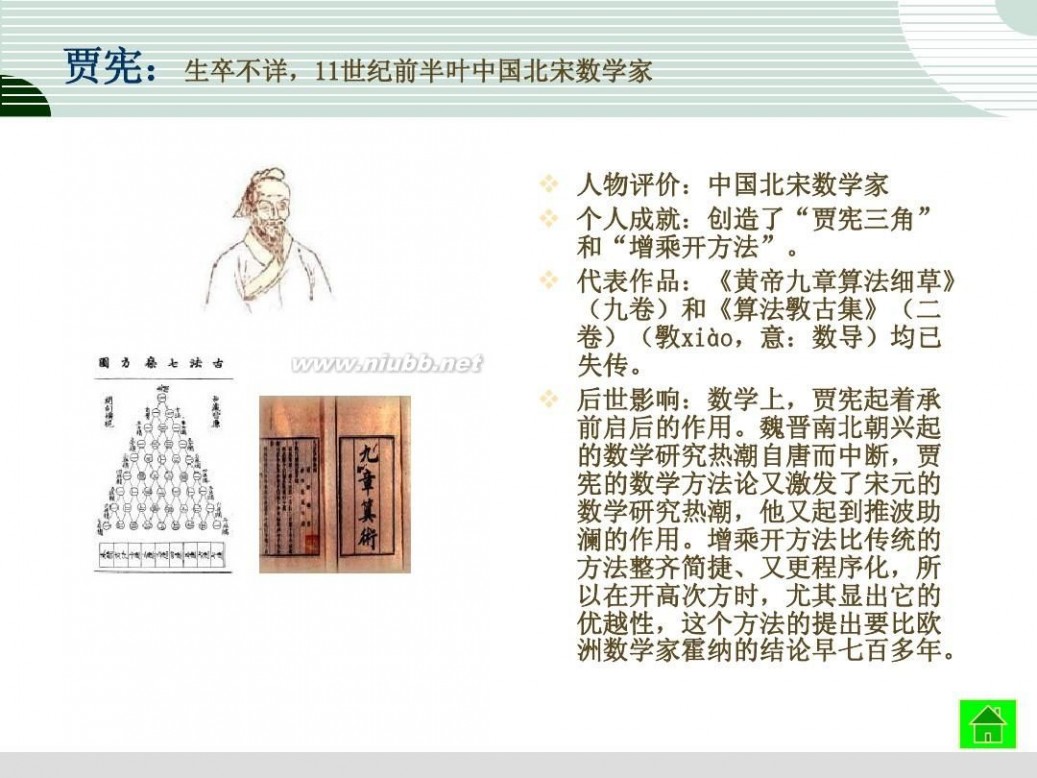
▲贾宪：〈〈黄帝九章算经细草〉〉
中国古典数学家在宋元时期达到了高峰，这一发展(www.61k.com）的序幕是“贾宪三角”（二项展开系数表）的发现及与之密切相关的高次开方法（“增乘开方法”）的创立。贾宪，北宋人，约于1050年左右完成〈〈黄帝九章算经细草〉〉，原书佚失，但其主要内容被杨辉（约13世纪中）著作所抄录，因能传世。杨辉〈〈详解九章算法〉〉（1261）载有“开方作法本源”图，注明“贾宪用此术”。这就是著名的“贾宪三角”，或称“杨辉三角”。〈〈详解九章算法〉〉同时录有贾宪进行高次幂开方的“增乘开方法”。
贾宪三角在西方文献中称“帕斯卡三角”，1654年为法国数学家 B•帕斯卡重新发现。
▲秦九韶：〈〈数书九章〉〉
秦九韶（约1202～1261），字道吉，四川安岳人，先后在湖北、安徽、江苏、浙江等地做官，1261年左右被贬至梅州（今广东梅县），不久死于任所。秦九韶与李冶、杨辉、朱世杰并称宋元数学四大家。他早年在杭州“访习于太史，又尝从隐君子受数学”，1247年写成著名的〈〈数书九章〉〉。〈〈数书九章〉〉全书共18卷，81题，分九大类（大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易）。其最重要的数学成就——“大衍总数术”（一次同余组解法）与“正负开方术”（高次方程数值解法），使这部宋代算经在中世纪世界数学史上占有突出的地位。
▲李冶：《测圆海镜》——开元术
随着高次方程数值求解技术的发展，列方程的方法也相应产生，这就是所谓“开元术”。在传世的宋元数学著作中，首先系统阐述开元术的是李冶的《测圆海镜》。
李冶（1192～1279）原名李治，号敬斋，金代真定栾城人，曾任钧州（今河南禹县）知事，1232年钧州被蒙古军所破，遂隐居治学，被元世祖忽必烈聘为翰林学士，仅一年，便辞官回家。1248年撰成《测圆海镜》，其主要目的就是说明用开元术列方程的方法。“开元术”与现代代数中的列方程法相类似，“立天元一为某某”，相当于“设x为某某”，可以说是符号代数的尝试。李冶还有另一部数学著作《益古演段》（1259），也是讲解开元术的。
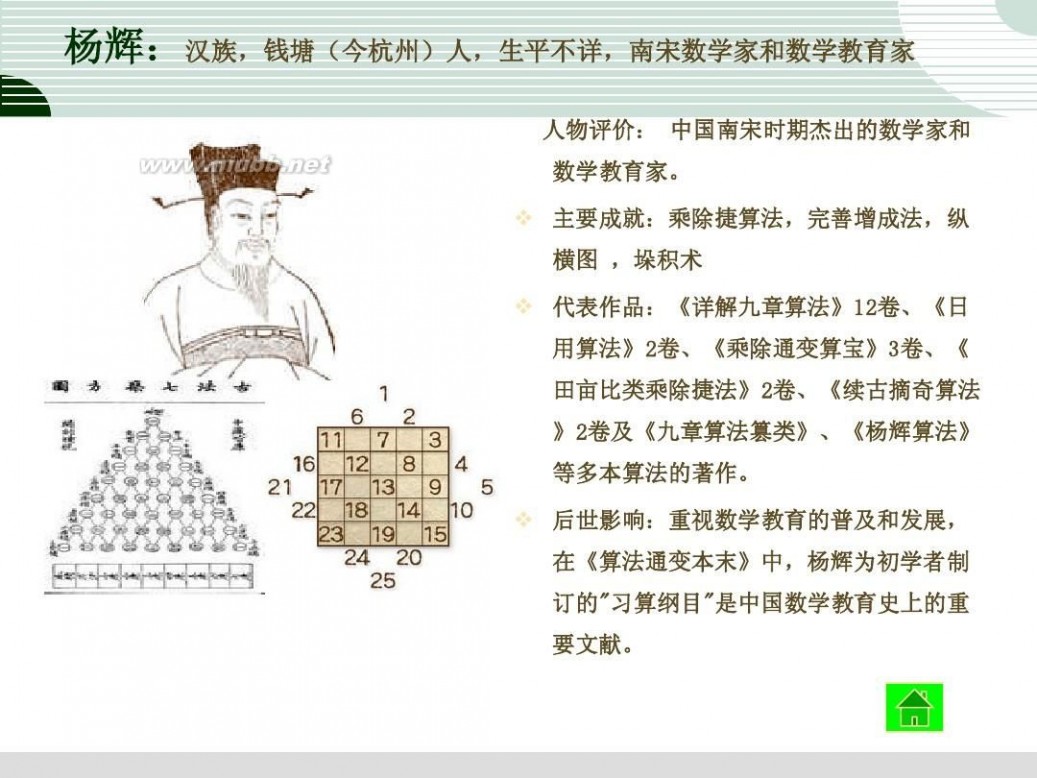
杨 辉
杨辉，中国南宋时期杰出的数学家和数学教育家。在13世纪中叶活动于苏杭一带，其著作甚多。
他著名的数学书共五种二十一卷。著有《详解九章算法》十二卷（1261年）、《日用算法》二卷（1262年）、《乘除通变本末》三卷（1274年）、《田亩比类乘除算法》二卷（1275年）、《续古摘奇算法》二卷（1275年）。
宋元数学四大家之一的杨辉，他是世界上第一个排出丰富的纵横图和讨论其构成规律的数学家。杨辉可以说是世界上第一个给出了如此丰富的纵横图和讨论了构成规律的数学家。杨辉除此成就之外，还有一项重大贡献，就是“杨辉三角”。
杨辉的数学研究与教育工作的重点是在计算技术方面，他对筹算乘除捷算法进行总结和发展，有的还编成了歌决，如九归口决。他在《续古摘奇算法》中介绍了各种形式的"纵横图"及有关的构造方法，同时"垛积术"是杨辉继沈括"隙积术"后，关于高阶等差级数的研究。杨辉在"纂类"中，将《九章算术》246个题目按解题方法由浅入深的顺序，重新分为乘除、分率、合率、互换、二衰分、叠积、盈不足、方程、勾股等九类。
他非常重视数学教育的普及和发展，在《算法通变本末》中，杨辉为初学者制订的"习算纲目"是中国数学教育史上的重要文献。
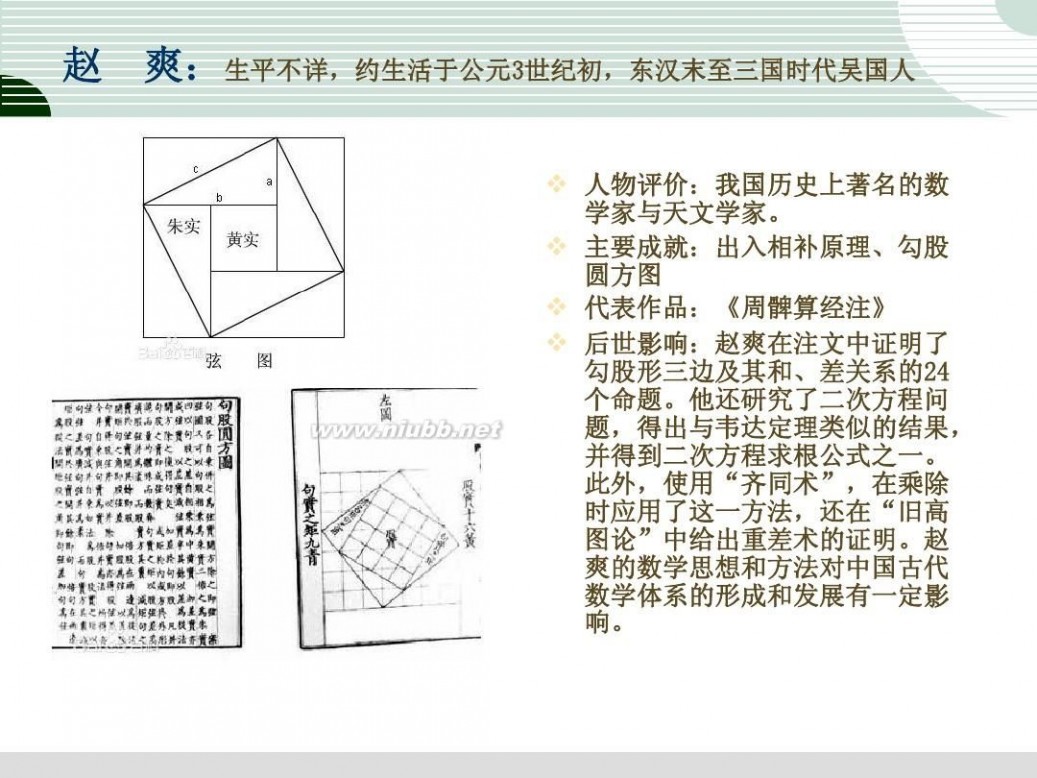
赵 爽
赵爽，又名婴，字君卿，东汉末至三国时代的吴国数学家。他在数学上的最大贡献是研究《周髀算经》中取得的成就。他所作的《周髀算经注》中有一篇《勾股圆方图注》全文五百余字，并附有云幅插图（已失传），这篇注文简练地总结了东汉时期勾股算术的重要成果，最早给出并证明了有关勾股弦三边及其和、差关系的二十多个命题，他的证明主要是依据几何图形面积的换算关系。
赵爽还在《勾股圆方图注》中推导出二次方程(其中a>0,A>0)的求根公式
在《日高图注》中利用几何图形面积关系，给出了“重差术”的证明。（汉代天文学家测量太阳高、远的方法称为重差术）。
黄宗宪
黄宗宪，字玉屏，号小谷，中国清代湖南新化人。他是丁取忠的学生，亦是以丁取忠为首的白芙堂数学学术团体的重要成员。在他多部著作中以《求一术通解》（1874）最为重要，由左潜参定。在该书中，黄宗宪对秦九韶的「求一术」作了进一步的阐述，他不仅解答了一次同余式组问题，还用「求一术」解决了二元一次不定方程问题。
徐光启
徐光启（1562.4.24—1633.11.8），字子先，号玄扈，上海人。他在介绍西方自然科学和发展我国农业、水利、天文、数学等方面都有相当大的贡献，是我国明末杰出的科学家。
徐光启在数学方面的重要贡献是翻译了欧几里得的《几何原本》前六卷。他的译文质量很高，许多数学上的专门名词和术语，如几何、点、线、面、平行线、钝角、锐角、三角形、四边形等等，都是由他首先使用，并沿用至今。另外，他还有《测量异同》和《勾股义》等数学著作。他把中西测量方法和数学方法进行了一些比较，并运用《几何原本》中的定理把我国古代一些证明方法严格化。还创造了一些新的证明系统，为我国后来的数学研究作出了很大的贡献。
三 : 中国古代数学家
）」时说：「然。此皆算术之所及。」提出数学方法（术）是「言约而用博」，作到「问一类而以万事达者」，才能「谓之知道」。学习数学要「同术相学，同事相观」，能「通类」，作到「类以合类」。这是当时存在的数学的总结，也规范了后来中国传统数学著作的特点与风格。他还提出了用比例与勾股定理测望日之远近、大小的方法，用到开方术。
《九章算术》
）历「最为微近」，决定使用此历。「汉家言律历者，本之张苍。」（《史记》）先秦以「九数」为主体的《九章算术》因秦始皇焚书而散坏，他收集秦火遗存，删补而成《九章算术》，是为影响中国传统数学二千余年的经典著作。
《九章算术》 《海岛算经》
）乡（今山东省邹平县）人，魏晋数学家。生平不详，约生于3世纪20年代后期或其后。自述「幼习《九章》，长再详览。观阴阳之割裂，总算术之根源，探赜（小老师）之暇，遂悟其意。是以敢竭顽鲁，采其所见，为之作注。」时在公元263年。《九章算术注》原10卷。后第10卷「重差」以《海岛算经》为名单行。他还著《九章重差图》1卷，已佚。他受到以「析理」为主要方法的辩难之风的影响，「析理以辞，解体用图」，发展了出入相补原理、齐同原理与率理论，首创用极限思想和无穷小分割方法进行数学证明，以演绎逻辑为主要方法全面证明了《九章算术》的算法，奠定了中国传统数学的理论基础。刘徽认为数学方法是「规矩度量可得而共」，概括了中国传统数学的特点。他将数学知识比喻为「枝条虽分而同本干」的大树，使当时的数学知识形成了一个完整的理论体系。他在中国首创了求圆周率的科学方法，求出两个圆周率值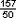
与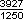
；指出并纠正了《九章算术》某些错误或不精确的公式；设计了牟合方盖（小知识
），指出了解决球体积的正确途径，并对截面积原理有相当理性的认识；创造了解线性方程组的互乘相消法与方程新术；在开方不尽时，创造了求「微数」的思想，用十进分数逼近无理根，开十进小数之先河；他发展了两汉以来的重差术，总结了重表、连索、累矩三种方法，设计了二望、三望、四望等题目，西方数学传入之前，再无大的突破。
）（今河北省涞（小老师）水县）人。南朝宋、齐间数学家、天文学家、机械制造家、文学家。在宋主持华林学省，后任南徐州（今江苏省镇江市）从事史。创制《大明历》，首先将岁差引入历法，其他历法常数也比以前的历法精确。撰《驳议》，不畏权贵，批驳他人对《大明历》的攻击，反对「信古而疑今」，敢于捍卫科学真理。撰《缀术》（一作《缀述》，一说祖暅之撰），因隋唐算学馆学官「莫能究其深奥」而失传。他推算的圆周率值精确到8位有效数字，提出密率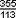
，领先世界约千年。「又设开差幂、开差立，兼以正负参之」，一般认为是负系数三次方程的解法。他还造千里船、水碓（小老师）磨，改造指南车、木牛流马等，对《论语》、《易经》、《老子》、《庄子》等都有研究，还撰《安边论》、《述异记》。其子祖暅之在刘徽的基础上，提出祖暅之原理，彻底解决了球体积问题。
《详解九章算术》
）古集》2卷（亡佚）。前者进一步抽象《九章算术》的术文，提出了若干新的解法，在刘徽之后，进一步提高了《九章算术》的理论水平。创造「开方作法本源」即贾宪三角，成为开方问题的纲领。又创造增乘开方法，并用于开四次方。以增乘开方法为主导的求解高次方程正根是宋元最发达的分支。贾宪是宋元数学高潮的主要推动者之一。
《数书九章》
《测图海镜》
）城（今河北省）人，生于大兴（今北京市），金元数学家、历史学家。其父为官清廉正直，李冶自幼受到良好教育，爱好数学，青年时便是「经为通儒，文为名家」的著名学者。1230年中金词赋科进士，被任命为钧州（今河南省禹州市）代理知事。1232年元军破钧州，李冶微服北渡，长期隐居在忻（小老师）、崞（小老师）（今山西省北部）一带，饥寒几至不能自存，却「聚书环堵」，潜心研究数学与其他学问。1248年在「洞渊九容」的基础上，使用天元术，撰《测圆海镜》12卷。是为现今了解天元术的最早著作，也是集中国传统数学勾股形与圆的关系知识大成的著作。1251年他回到少年求学的元氏县，主持封龙书院。1257年，在开平（今内蒙古正蓝旗）接受元主忽必烈的召见，他表达了有法度、减刑狱、止征伐、不妄杀、进君子、退小人、反对种族歧视的政治主张。1259年在封龙书院撰《益古演段》3卷。1261年元世祖忽必烈在燕京（今北京）聘李冶为翰林学士，同修国史。一年后，他因「翰林视草，唯天子命之；史馆秉笔，以宰相监之」，羞于做御用文人，便以老病为由辞职回封龙山。李冶反对将数学视为「九九贱技」的世俗观念，表示不计悯笑，献身于数学。他主张「推自然之理，以明自然之数」而研究数学。他的文史著作也很多，传世的仅有《敬斋古今黈》。该书阐发了李冶不拘一格的议论之学。
《详解九章算法》
《则古昔斋算学》
四 : 中国著名数学家资料
中国著名数学家资料
工作到最后一天的华罗庚(1910—1985)
1985年6月12日，在东京一个国际学术会议上，75岁的华罗庚教授用流利的英语，作了十分精彩的报告。当他讲完最后一句话，人们还在热烈鼓掌时，他的身子歪倒了。 华罗庚出生于江苏省金坛县一个小商人家庭，从小喜欢数学，而且非常聪明。一天老师出了一道数学题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何?”“23!”老师的话音刚落，华罗庚的答案就脱口而出，老师连连点头称赞他的运算能力。可惜因为家庭经济困难，他不得不退学去当店员，一边工作，一边自学。18岁时，他又染上伤寒病，与死神搏斗半年，虽然活了下来，但却留下终身残疾——右腿瘸了。 1930年，19岁的华罗庚写了一篇《苏家驹之代数的五次方程不成立的理由》，发表在上海《科学》杂志上。清华大学数学系主任熊庆来从文章中看到了作者的数学才华，便问周围的人，“他是哪国留学的?在哪个大学任教?”当他知道华罗庚原来是一个19岁的小店员时，很受感动，主动把华罗庚请到清华大学。华罗庚在清华四年中，在熊庆来教授的指导下，刻苦学习，一连发表了十几篇论文，后来又被派到英国留学，获得博士学位。他对数论有很深的研究，得出了著名的华氏定理。
抗日战争时期，华罗庚白天在西南联大任教，晚上在昏暗的油灯下研究。在这样艰苦的环境中，华罗庚写出了20多篇论文和厚厚的一本书《堆垒素数论》。他特别注意理论联系实际，1958年以后，他走遍了20多个省市自治区，动员群众把优选法用于农业生产。记者在一次采访时问他：“你最大的愿望是什么?”他不加思索地回答：“工作到最后一天。”他的确为科学辛劳工作到最后一天，实现了自己的诺言。
获沃尔夫奖唯一华人数学家——陈省身
(1911～2004)
在数学领域，沃尔夫奖与菲尔兹奖是公认的能与诺贝尔奖相媲美的数学大奖。菲尔兹奖主要奖励在现代数学中做出突出贡献的年轻数学家，而沃尔夫奖主要奖励在数学上做出开创性工作、具有世界声誉的数学家。到1990年为止，世界上仅有24位数学家获得过沃尔夫奖，而陈省身教授就是其中之一。他由于在整体微分几何上的杰出工作获得1984年度沃尔夫奖，成为唯一获此殊荣的华人数学家。
陈省身教授是浙江嘉兴人，现定居美国。他15岁就考入了天津南开大学，后进 入清华大学研究生院，1934年完成学业并赴德国留学，仅用了1年零3个月便获得了汉堡大学博士学位。之后又赴法国师从微分几何学泰斗嘉当，由此开始了他在整体微分几何领域的开创性工作。
除了在数学上做出巨大成就，陈省身教授还培养了一大批世界级的科学家，其中包括诺贝尔物理学奖获得者杨振宁，菲尔兹奖获得者丘成桐，中国国家自然科学奖一等奖获得者吴文俊等。
近年来，陈省身教授积极致力于中国数学研究的开展，多次回国讲学，举办讨论班，指导各种学术活动，并于1985年创办南开大学数学研究所，亲自担任所长。展望21世纪，陈省身教授预言中国将成为世界数学大国。
丘成桐
(1949～ )
1983年，国际数学会议决定将1982年的数学界的诺贝尔奖——菲尔兹奖颁发给 一位年仅34的华人数学家，这位才能非凡的年轻人就是丘成桐。
丘成桐原籍中国广东，后来迁居香港，1966年进入香港中文大学数学系。他自 幼迷恋数学，经过不懈的努力，在大学三年级时就由于出众的才华被一代几何学宗 师陈省身发现，破格成为美国加州大学伯克利分校的研究生。在陈省身教授的亲自 指导下，年仅22岁的丘成桐获得了博士学位。28岁时，丘成桐成为世界著名学府斯 坦福大学的教授，并且是普林斯顿高级研究所的终身教授。
丘成桐的第一项重要研究成果是解决了微分几何的著名难题—卡拉比猜想，从 此名声鹊起。他把微分方程应用于复变函数、代数几何等领域取得了非凡成果，比
如解决了高维闵考夫斯基问题，证明了塞凡利猜想等。这一系列的出色工作终于使 他成为菲尔兹奖得主。
刘徽
刘徽（生于公元250年左右），是中国数学史上一个非常伟大的数学家，在世界数学史上，也占有杰出的地位．他的杰作《九章算术注》和《海岛算经》，是我国最宝贵的数学遗产．
《九章算术》约成书于东汉之初，共有246个问题的解法．在许多方面：如解联立方程，分数四则运算，正负数运算，几何图形的体积面积计算等，都属于世界先进之列，但因解法比较原始，缺乏必要的证明，而刘徽则对此均作了补充证明．在这些证明中，显示了他在多方面的创造性的贡献．他是世界上最早提出十进小数概念的人，并用十进小数来表示无理数的立方根．在代数方面，他正确地提出了正负数的概念及其加减运算的法则；改进了线性方程组的解法．在几何方面，提出了"割圆术"，即将圆周用内接或外切正多边形穷竭的一种求圆面积和圆周长的方法．他利用割圆术科学地求出了圆周率π=3.14的结果．刘徽在割圆术中提出的"割之弥细，所失弥少，割之又割以至于不可割，则与圆合体而无所失矣"，这可视为中国古代极限观念的佳作．
《海岛算经》一书中， 刘徽精心选编了九个测量问题，这些题目的创造性、复杂性和富有代表性，都在当时为西方所瞩目．
刘徽思想敏捷，方法灵活，既提倡推理又主张直观．他是我国最早明确主张用逻辑推理的方式来论证数学命题的人．
刘徽的一生是为数学刻苦探求的一生．他虽然地位低下，但人格高尚．他不是沽名钓誉的庸人，而是学而不厌的伟人，他给我们中华民族留下了宝贵的财富．
秦九韶
（公元1202~1261年）
南宋，数学家。他在1247年（淳佑七年）著成『数书九章』十八卷．全书共81道题，分为九大类：大衍类、天时类、田域类、测望类、赋役类、钱谷类、营建类、军旅类、市易类。这是一部划时代的巨着，它总结了前人在开方中所使用的列筹方法，将其整齐而有系统地应用到高次方程的有理或无理根的求解上去，其中对「大衍求一术」﹝一次同余组解法）和「正负开方术」﹝高次方程的数值解法）等有十分深入的研究。其中的”大衍求一术”﹝一次同余组解法），在世界数学史上占有崇高的地位。在古代＜孙子算经＞中载有”物不知数”这个问题，举例说明：有一数，三三数之余二，五五数之余二，七七数之余二，问此数为何？这一类问题的解法可以推广成解一次同余式组的一般方法．奏九韶给出了理论上的证明，并将它定名为”大衍求一术”。
杨辉——宋代著名的数学教育家
杨辉，字谦光，中国南宋（1127～1279）末年钱塘（今杭州市）人。其生卒年月及生平事迹均无从详考。据有关著述中的字句推测，杨辉大约于13世纪中叶至末叶生活在现今浙江杭州一带，曾当过地方官，到过苏州、台州等地。是当时有名的数学家和数学教育家，他每到一处都会有人慕名前来请教数学问题。
杨辉一生编写的数学书很多，但散佚也很严重。据史料记载，他至少有以下书，曾在国内或国外刊行：《详解九章算法》12卷（1261）
《详解算法》若干卷
《日用算法》（1262）
《乘除通变算宝》3卷（1274）
《续古摘奇算法如卷（1275）
《田亩比类乘除捷法如卷（1275）其中《详解九章算法》残缺不全，《详解算法》、《日用算法》迄今未见传本。而后3种共7卷合刊在一起，被称为《杨辉算法》。
杨辉继承中国古代数学传统，他广征博引数学典籍，引用了现已失传的宋代的许多算书，使我们才得知其部分内容。其中，刘益的“正负开方术”，贾宪的“增乘开方法”与“开方作法本源”图（即误传为“杨辉三角”），就是极其宝贵的数学史料。
杨辉继沈括研究“隙积术”之后，研究了“垛积术”，即关于高阶等差数列的研究。他
本文标题：中国古代著名数学家-中国数学名人61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1