一 : 为什么物体二力平衡时还会匀速直线运动
为什么物体二力平衡时还会匀速直线运动
问题是这样：一个小男孩推箱子作匀速直线运动,那就是说合力为零了,为什么箱子还会动?(箱子一开始是静止的)
还有力的示意图为什么作用点可以移到中间?
1.二力平衡是一个概念.
定义：一个物体在受到两个力作用时,如果能保持静止或匀速直线运动状态,我们就说物体处于平衡状态.（也就是说此时二力平衡,合力为0）
2.你的问题有一点点小矛盾,一个小男孩推箱子作匀速直线运动,箱子当然会动啦~（物体在静止和匀速直线运动都是合力为0,参考定义）
3.作用点在中间是必须的,我们定义那一点为重心,代表着这个物体受力是均匀的.如果实在搞不懂就抢记.初三要加油,所有的努力都为了中考.不懂及时问老师.GOOD LUCK
二 : 高一年级物理第一学期——第一章匀变速直线运动
第一章匀变速直线运动
A.质点 位移和时间
1.质点(mass point)
质点：在某些条件下，把整个物体看作1个有质量的点，这种用来替代物体的、有质量的点叫做质点。
对于“某些条件”的解释：有时物体各点的运动情况相同，或者物体的形状、大小与所研究的运动无关。
2.坐标系(coordinate system)
坐标系：为了定量地描述物体的位置及其变化，需要在参考系上建立1个坐标系，常用的是平面直角坐标系。
位置(position)：质点在坐标系中的坐标就表示它所在的位置。
参考系：初中这样描述参照物，我们把用来判断物体A是否运动的物体B叫做参照物。高中将这种参照的物体也叫做参考系。参考系的选取对运动的研究是非常重要的。特别在1个完整的研究过程中，所选取的参照系不能改变，否则就可能导致无法获得正确的结果。
研究对象：参考系和研究对象往往是一对概念。这1个看似简单的问题，但是在实际研究问题的时候我们往往会犯错。
对于“坐标系”的解释：我们生活的空间是1个三维空间。当然，当运动只局限于平面内，也就是说，运动只在两维空间里发生的时候，我们当然只要选取1个两维的坐标系就能研究。两维空间的坐标系不只有平面直角坐标系，比如极坐标也可以是两维的坐标系。如何选取坐标系，其目的只是为了研究问题的方便，比如在研究圆周运动的时候，有时极坐标将更方便与研究问题。
3.位移(displacement)和路程(path)
位移：质点的位置变化叫做位移，通常用s表示。
路程：质点运动所经历的轨迹长度叫做路程。
位移的大小：位移的大小等于起点到终点的直线距离，位移的方向从起点指向终点。
位移和路程是2个完全不同的物理量。位移是矢量，既有大小又有方向；路程是标量，只有大小而没有方向。我们知道英文中的path也有“路径”的意思，通俗地说，位移只关心的是起点和终点，并不关心中间的实际过程如何，而路程则必须和实际过程相结合。用不恰当的比喻：你什么时间能到家，这只关心结果；而你怎么回家，回家路上要经过哪些地方，逗留多少时间，这就是对过程的了解了。
4.标量和矢量
标量：物理学中把只有大小没有方向的物理量叫做标量。
矢量：物理学中把既有大小又有方向的物理量叫做矢量。
高中阶段第一次明确矢量的概念。在一维坐标系中，也就是在一根数轴上，我们可以用“+”和“-”来表示矢量的方向。但是我们不能把有正负的物理量就叫做是矢量。最典型的就是初中学过的摄氏温标，零下20摄氏度我们可以书写成“-20oC”，虽然温度也有负值，但是温度是标量而不是矢量。再次明确矢量的概念：既有大小又有方向的物理量。
5.时刻和时间
时钟、手表上指针指示的某一位置表示时刻，前后两时刻之差为时间。
时刻是没有间隔的时间点，是时间轴上的一点，当你刚确定这1个时刻的时候，它已经过去了。时刻在时间轴上起到区分各个时间段的作用。时间则是2个时刻之间的间隔。
B.匀速直线运动的图像
1.匀速直线运动
匀速直线运动：在相等的时间里，物体的位移都相同的直线运动叫做匀速直线运动。
在匀速直线运动的概念中，切记是“位移相同”。位移是矢量，也就是说，不仅路程相同，还要方向相同。
高中对于匀速直线运动概念的表述还存在着一定的问题，严格地说，应该是在任何相等的时间里，物体的位移都相同的直线运动。加上“任何”2个字使得对时间段的取样更具有随机性，使概念的表述更为准确。但是目前的学习以课本为准。
根据匀速直线运动的定义讨论：静止状态是不是属于匀速直线运动？静止状态符合在相等的时间里，物体的位移都相同(位移一直为零)。但是静止状态不符合概念中的直线运动这个状态。所以根据上述概念来说，静止状态不属于匀速直线运动。
2.速度(velocity)
速度：速度是描述质点运动快慢和方向的物理量。
速度等于质点的位移s跟发生这一位移所用的时间t之比。速度用v表示，则有： 。
速度单位是m/s。
对于1个物理量的定义，一般有3个方面的要求：第一是这个物理量的概念(比如速度是描述质点运动快慢和方向的物理量)。第二是1个物理量的计算方式。第三是这个物理量的单位。有了这三方面的规定才是1个完整的物理量的定义。
速度是矢量，它的方向跟运动方向相同。
匀速直线运动是速度不变的运动。这句话点出了匀速直线运动的本质，但是不是匀速直线运动的定义。
概念中用了“质点运动快慢和方向”，而不是用“物体运动快慢和方向”，不明白如此用词的含义。
速率：匀速直线运动的速度大小叫速率。
速率是标量，只有大小，没有方向。
3.匀速直线运动的位移公式
匀速直线运动的位移公式： 。
上式表明：匀速直线运动中位移与所用的时间成正比。
如果以t为自变量，s为函数值，那么：
这是1个典型的截距为零的一次函数，对于匀速直线运动而言，v是不变的，也就是说v是常数，在一次函数中，相当于斜率的意义。4.匀速直线运动的位移-时间图像(s-t图)
匀速直线运动的s-t图是一条倾斜的直线。它表明在任何相等的时间Δt内位移的变化量Δs是相等的，直线的斜率表示速度的大小。
“Δt”中的Δ是在物理量中经常用到的1种数学表达方式，在物理量前加上Δ，表示该物理量的变化量。
一次函数的图像按照斜率可分为3类：第1类斜率为正；第二类斜率为负；第3类斜率为零。按照截距也可分成正、负和零3类。分别对上述的各种分类方式描述匀速直线运动的运动状态。
5.匀速直线运动的速度-时间图像(v-t图)
匀速直线运动的v-t图是一条平行于时间轴线的直线。图中的阴影部分的面积(v1 x t1)表示在一段运动时间内质点的位移。
面积在几何学中是标量，但是在v-t图中，时间轴上的面积和时间轴下的面积所表达的意义是不相同的。在v-t图中，只是借用了几何学中面积的概念，但是要明确地是，速度和时间的积(也就是v-t图中的面积)，其真实含义是位移(根据位移公式s=vt)，位移是矢量，矢量是有方向的。所以如果在v-t图中时间轴上和下所表示的位移方向是不相同的。
如果对于其他运动形式，v-t图不是一条平行于时间轴的直线的话，那么v-t图中的面积又有什么意义呢？
C.快慢变化的运动 平均速度和瞬时速度
1.变速直线运动
变速直线运动：在相等的时间里，物体的位移不相等的直线运动叫做变速直线运动。
对于变速直线运动的表述，不必要在相等前加“任何”2个字。这体现了逻辑的法则，要证明1个判断正确，就必须保证所有的情况都符合该判断；但是要证明1个判断的错误，只要能找出1个错误的例子就可。
2.平均速度(average velocity)
平均速度：做变速直线运动的物体所经过的位移s与所用的时间t之比，叫做这一位移或这一时间内的平均速度。
常用 来表示，则有： 。平均速度也是有方向的。
如果选取的位移(或时间)不同，平均速度的大小也不同，所以平均速度是某段位移或某段时间内，对变速直线运动快慢的粗略的描述。
从概念的表述和说明中，可以明确：平均速度和速度一样，都是矢量。
从概念的表述中，我们发觉平均速度和速度的概念区别不大，但是我们要明确：我们研究的对象的运动状态是不相同的。在匀速直线运动中，我们也可以用平均速度的概念来描述匀速直线运动的运动状态，对于匀速直线运动来说，无论你怎么选取位移段或时间段，所求得或测得平均速度都应该是相同的。但是对于变速直线运动来说，选取不同的位移段或时间段，所获得的平均速度不一定相同。也正因为这个原因，用平均速度来描述物体的运动，必须说明该平均速度是对那一段运动过程的描述，也就是说，必须说明是哪一段位移或者哪一段时间内的平均速度。
如果我们选取的位移越小或者时间间隔越短，同时我们测量的次数越多，那么我们对于该运动的描述就越精确。这种取样间隔越小、取样次数越多，结果越精确的方式不仅是1种实验方式，更是1种思维方式。
平均速率：路程与时间之比，叫做平均速率。
平均速率是标量。只有大小，没有方向。
这里要区分的是，在匀速直线运动中，我们定义速率为：速度的大小叫做速率。在平均速率的定义中，是用路程与时间的比叫做平均速率。这2个速率的定义是不同的。从这个概念的定义出发，平均速度的大小只能成为平均速度的大小，而不能称为平均速率。事实上按照课本中对平均速率的定义，在讨论变速直线运动中某段位移或某段时间内的平均速度和平均速率时，就它们的数值而言，也完全可能是不相同的。
3.瞬时速度(instantaneous velocity)
瞬时速度：运动物体在某一时刻的速度，或经过某一位置时的速度，叫做瞬时速度。
瞬时速度能描述做变速运动(注：这里用的是“变速运动”，而非“变速直线运动”)的物体在任何时刻(或任一位置)的运动快慢和运动方向。
某位置(或某时刻)的瞬时速度，就是无限逼近该位置(或该时刻)附近的位移(或时间)内的平均速度。
瞬时速度是矢量。它既有大小又有方向。
前面平均速度的解释中讲到越小越精确的思维方式。那么如果能达到时间间隔“要多小就多小”的程度，我们就能说对这么1个“要多小就多小”的时间内，我们的描述就是准确的。对于要多小就多小的时间间隔，我们可以把它等同于时刻。对于要多小就多小的位移，我们也可以把它等同于位置。这种思维方式不仅在实验中可行，并且在数学中同样也是可行的。
瞬时速度是在物体运动过程中，对运动速度的精确描述。
瞬时速度更关心的是物体运动到某一时刻或者某一位置上它的运动状态，而与该物体整个运动过程的关系并不大。因此瞬时速度并不关心运动的整个过程。
如果我们同时提出瞬时速率的概念，那么对于瞬时速率，无论我们采取前面2种速率的定义中的哪1种，对于瞬时速率而言，这2种定义方式的结果是相同的。
D.现代实验技术——数字化信息系统(DIS)
1.DIS实验
DIS是我们对数字化信息系统的简称，它是运用现代信息技术进行学习的1种手段。
DIS：Digital Information System
2.DIS的基本结构
DIS由传感器、数据采集器和计算机组成。
3.练习使用DIS
用DIS位移传感器测量距离。
4.用DIS研究变速直线运动的s-t图
5.用DIS测变速直线运动的平均速度
6.用DIS测变速直线运动的瞬时速度
E.速度变化的快慢 加速度
1.加速度(acceleration)
加速度：加速度是描述物体速度变化快慢的物理量。
速度的变化量Δv与发生这一变化所需时间Δt的比叫做加速度，用字母a表示，则有：
加速度的单位是m/s2。
加速度是矢量。不仅有大小，而且有方向。
2.加速度的测量
3.加速度的方向
加速度也是矢量。加速度的方向即速度变化量的方向。物体在一直线上运动，速度增大，加速度为正值；速度减小，加速度为负值。
上述表述是存在问题的。对于直线运动而言，正负表示的是方向。如果运动的速度和规定的正方向相反，那么该速度的数学表达就应该是负值，这种情况下，加速度的方向如果和速度的方向相同，也就是说加速度也是负值，那么速度的大小是在增加，而非减小。
对于直线运动而言，如果加速度的方向和速度的方向相同，那么速度的大小会逐渐增加；相反，如果加速度的方向和速度的方向相反，那么速度的大小会逐渐减小，直到速度变成零以后，速度又会向另1个方向逐渐增大。
F.匀加速直线运动
1.匀变速直线运动
匀变速直线运动：速度随时间均匀变化的直线运动叫做匀变速直线运动。
匀变速直线运动是加速度大小和方向均不随时间变化的运动。
对于匀变速直线运动的定义，也可以参照匀速直线运动的定义方式：在任何相等时间内，速度的变化都相等的直线运动。
2.初速度为零的匀加速直线运动
瞬时速度与时间的关系：
位移与时间的关系：
由上面2个公式可得到，瞬时速度与加速度、位移的关系：位移与时间关系的公式推导，是使用了v-t图中，v的变化曲线和时间轴之间围成的面积而得到的。
我们仍然采用“要多小就多小”的思维方式。我们知道对于匀速直线运动来说，v-t图中v随时间变化的曲线和时间轴围成的面积就是位移。那么我们在研究匀变速直线运动的时候把时间间隔Δt取得要多小就多小，这时速度v在Δt时间间隔内和时间轴之间围成的小梯形就成了1个小矩形，也就是说，在要多小就多小的Δt时间间隔内，我们可以把这一小段匀变速直线运动看成是匀速直线运动，此时的小矩形面积就是位移。如果我们把随时间变化的所有的这些要多小就多小的小矩形的面积全部加起来，就是匀变速直线运动的总位移。所以对于匀变速直线运动来说，v-t图中速度v的变化曲线和时间轴之间围成的面积仍然是位移。由此可以得到初速度为零的匀加速直线运动，它的位移就是1个三角形的面积，即：
G.学习包——自由落体运动
1.自由落体运动
课本中没有给出自由落体运动的定义。我们根据课本中对此运动的描述给出定义：物体在只受到重力的作用下，由初速度零开始做自由下落的运动。
根据我们的经验，当物体的体积或者速度较大的时候，我们都会感觉到空气会对物体的运动产生阻力。比如羽毛的下落，我们明显可以看到，羽毛的下落过程会受到空气对羽毛的作用。那么从我们的定义和我们在初中曾经学过的知识来看，羽毛的下落不过不仅受到了重力的作用，同时也受到了空气对它产生的作用，这种情况下，羽毛的下落过程就不能称为自由落体运动。相反，如果1个小铁球的下落过程，我们知道空气同样也会对小铁球产生作用，但是相比重力对小铁球的作用力，空气阻力非常小，因此在很多情况下我们可以忽略空气阻力的作用，从而我们可以认为小铁球只受到了重力的作用。
从本节的内容设计和高中课本的教程安排来看，自由落体运动中物体下落时的加速度数据只能从实验中获得。我们把物体自由落体时的加速度称为重力加速度，用符号g表示。
既然重力加速度g是加速度的1种，它也应该符合加速的所有特征。所以，重力加速度的单位同样也是m/s2。
重力加速度g的大小一般为9.8m/s2，并且在地球上的不同地方，重力加速度的大小有些微小的变化。
加速度是矢量，所以重力加速度也是矢量。重力加速度的方向和重力的方向相同，也是竖直向下的。
重力加速度是由重力对物体的作用所引起的，并且重力加速度的大小和物体的大小、质量和形状等物理特性没有关系。重力加速度的大小只和地球表面上的位置和高度不同而不同，但是在地球上的同1个位置上，重力加速度俄大小是相同的。
为什么重力加速度的大小和初中所学的重力和质量之间的比例系数的大小相同，我们会在以后的课程中得到解释。
三 : 某同学为了研究做匀速直线运动的物体的快慢情况，分别对行
| 某同学为了研究做匀速直线运动的物体的快慢情况，分别对行驶在高速公路上的三辆汽车进行观察，记录了有关数据，如表一、表二、表三所示．该同学观察到小轿车运动得最快，大客车其次，卡车运动得最慢． 表一：小轿车
（2）分析比较观察序号______的数据及观察到的现象，可以得到初步结论是：当运动物体所用时间相同时，通过的路程越长，物体运动得越快． （3）请进一步综合分析表一、表二、表三中的数据及观察到的现象，并归纳得出结论． （a）分析比较表一、表二或表三中的数据及观察到的现象，可初步得出：______； （b）分析比较表一、表二和表三中的数据及观察到的现象，可初步得出：______． |
| （1）比较观察序号1与4（或2与5，3与6）的数据可知，运动路程相同，时间不同，且运动时间越短的小轿车运动的越快，所以得出的结论是：运动相同的路程，时间越短的物体运动越快； （2）要得出“当运动物体所用时间相同时，通过的路程越长，物体运动得越快”的结论，应控制运动物体所用时间相同而通过路程不同，由表中实验数据可知，符合要求的实验序号为：4和7或5和8或6和9； （3）（a）由表一、或表二、或表三的实验数据可知，路程与时间的比值相同，物体运动快慢相同，由此可知：当物体通过的路程与时间的比值相同时，物体运动得快慢相同； （b）由表一、二、三的实验数据可知，物体的路程与所用时间的比值越大，物体运动越快，由此可知：当物体通过的路程与时间的比值越大时，则物体运动得越快． 故答案为：（1）运动相同的路程，时间越短的物体运动越快； （2）4和7（或5和8，6和9）； （3）（a）当物体通过的路程与时间的比值相同时，物体运动得快慢相同； （b）物体通过的路程与时间的比值越大时，则物体运动得越快． |
考点：
考点名称：匀速直线运动定义：
物体沿着直线运动，方向不变且在任何相等的时问里路程都相等，或者说速度的大小和方向都不改变的运动，称为匀速直线运动。
匀速直线运动是状态不变的运动，是最简单的机械运动。
匀速直线运动的特征：
一是运动的路径是直线；二是运动的快慢保持不变，即它的速度是一个恒量，即任一时刻都相同。但路程与时间成正比。
对概念的理解：
（1）速度是表示物体运动快慢的物理量，速度可以用符号V来表示。在国际单位制（SI）中，速度的主单位是m/s，读作：米每秒。常用的单位有km/h，m/min等等。
（2）做匀速直线运动的物体其速度是保持不变的，因此，如果知道了某一时刻（或某一距离）的运动速度，就知道了它在任意时间段内或任意运动点上的速度。
（3）一个物体在受到两个或两个以上力的作用时，如果能保持静止或匀速直线运动，我们就说物体处于平衡状态。
（4）不能从数学角度把公式s=vt理解成物体运动的速度与路程成正比，与时间成反比。匀速直线运动的特点是瞬时速度的大小和方向都保持不变，加速度为零，是一种理想化的运动。
（6）匀速直线运动仅为理想状态。
图像法解决匀速直线运动的问题：
匀速直线运动的路程一时间图像，如图所示：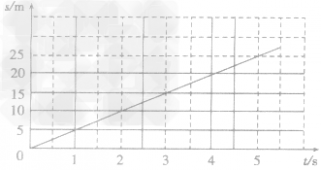
图像中可以获取的信息：
(1)该图像是过原点的直线，它说明做匀速直线运动的物体通过的路程与时间成正比。
(2)该图像的纵坐标表示路程，横坐标表示运行时问，利用一组对应的时间和路程值，可求出该物体的运动速度大小。
(3)可以通过图像，查某段时间内通过的路程。
(4)可以通过图像查该物体通过某段路程需要的时间。
(5)如果是两条线段在同一个图中，可以比较两个物体运动的速度快慢。
(6)如果某段时间内线段是水平的，就说明这段时间内物体是静止的。另外，匀速直线运动的速度一时问(v一t)图像如图所示，它是与时间轴平行的直线，它可以直接查得物体的速度，同一物体的s—t图像和v一t图像形状不同。
例1甲、乙、丙三辆小车同时、同地向同一方向运动，它们运动的图像如图所示，由图像可知：运动速度相同的小车是__和__；经过5s，跑在最前面的小车是__。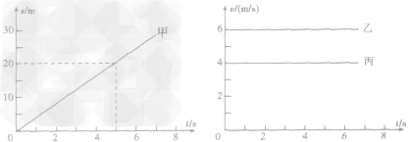
解析：由图像可知，甲、乙、丙都在做匀速直线运动，其中
4m／s，所以运动速度相同的小车是甲和丙。当甲、乙、丙同时、同地、同向运动时，经过5s后，
4rn／s×5s=20m，
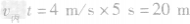，故跑在最前面的小车是乙。
答案：甲 丙 乙
四 : 物体做匀加速直线运动，已知1秒末速度为6m/s，2秒末速度为8m/s
物体做匀加速直线运动，已知1秒末速度为6m/s，2秒末速度为8m/s．下列说法中正确的是（ ）
|
A、物体的加速度a=
C、△v=at=2m/s，知任意1s内速度变化2m/s．故C正确． D、根据
故选ABC． |
考点：
考点名称：匀变速直线运动的速度与时间的关系匀变速直线运动：
物体在一条直线上运动，如果在相等的时间内速度的变化相等，这种运动就叫做匀变速直线运动。也可定义为：沿着一条直线，且加速度不变的运动，叫做匀变速直线运动。
匀变速直线运动的速度公式：
Vt=V0+at。
公式说明：
速度公式是匀变速直线运动速度的一般表示形式。它所表明瞬时速度与时刻t的对应关系。通常取初速度v0方向为正方向，加速度a可正可负（正、负表示方向），在匀变速直线运动中a恒定。
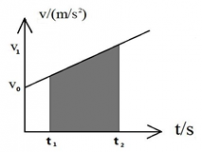
3. 速度图象是对速度公式的直观体现．图象斜率表示加速度，图象与时间轴所围的面积表示位移。
五 : 从静止开始做匀加速运动的物体[]A.第1s、第2s、第3s末的
| 从静止开始做匀加速运动的物体 |
| [ ] |
| A.第1s、第2s、第3s末的瞬时速度之比是1:2:3 B.第1s、第2s、第3s内的平均速度之比是1:2:3 C.前1s、前2s、前3s内的平均速度之比是1:2:3 D.前1s、前2s、前3s的中间时刻的瞬时速度之比是1:2:3 |
| ACD |
考点：
考点名称：匀变速直线运动的导出公式平均速度公式：
V=
。
某段时间的中间时刻的瞬时速度等于该段时间内的平均速度：
。
某段位移的中间位置的瞬时速度公式：
。无论匀加速还是匀减速，都有
。
匀变速直线运动中，在任意两个连续相等的时间T内的位移差值是恒量，即ΔS=Sn+l–Sn=aT2=恒量。
初速度为零的匀加速直线运动的几个比例关系推导：
初速度为零的匀加速直线运动(设其为等分时间间隔)：
① t秒末、2t秒末、……nt秒末的速度之比：(Vt=V0+at=0+at=at)V1：V2：V3……Vn=at：a2t：a3t…：ant=1：2：3…：n
②前一个t秒内、前二个t秒内、……前N个t秒内的位移之比：S1=v0t+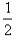
at2=0+
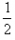at2=
at2；S2=v0t+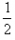
a(2t)2=2at2；S3=v0t+
at2=
a(3t)2=
at2；Sn=v0t+
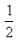at2=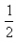
a(nt)2=
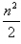at2。S1：S2：S3…….Sn=
at2：2at2：
at2……
at2=1：22：32….N2
③第1个t秒内、第2个t秒内、……-第n个t秒内的位移之比：
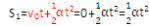（初速度为0）
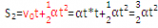（初速度为at）
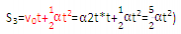（初速度为2at）
Sn=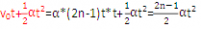
（初速度为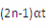
）
所以第一个t内、第二个t内、第三个t内……的位移之比为：sⅠ：sⅡ：sⅢ：……：sN=1：3：5：……：(2N-1)；
④前一个s、前两个s、前三个s……所用的时间之比为：
因为初速度为0，所以
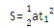
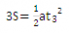
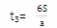
因此前一个s、前两个s、前三个s……所用的时间之比为：t1：t2：t3：……：tn=1：……：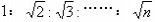
⑤第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ：……：
第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ：……：tN=1：……：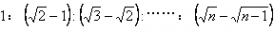 
。
初速为零的匀变速直线运动中的比例关系（设T为相等的时间间隔，s为相等的位移间隔）：
①T末、2T末、3T末……的瞬时速度之比为：v1：v2：v3：……：vn=1：2：3：……：n；
②T内、2T内、3T内……的位移之比为：s1：s2：s3：……：sn=1：4：9：……：n2；
③第一个T内、第二个T内、第三个T内……的位移之比为：sⅠ：sⅡ：sⅢ：……：sN=1：3：5：……：(2N-1)；
④前一个s、前两个s、前三个s……所用的时间之比为：t1：t2：t3：……：tn=1：
……：
；
⑤第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ：……：tN=1：
……：
。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1