一 : 统计学中非参数检验包括什么假设检验
统计学中非参数检验包括什么假设检验
非参数检验是指在总体方差未知或知道甚少的情况下,利用样本数据对总体分布形态等进行推断的方法.由于非参数检验方法在推断过程中不涉及有关总体分布的参数,因而得名为“非参数”检验.
从分析变量的属性类型上来说,非参检验主要包括:有序分类变量非参检验和无序分类变量非参检验.
从分析的的方法上来看,非参检验主要包括:配对样本非参数检验、独立样本非参数检验、相关样本非参数检验和卡方检验.其中,
x09(1)配对样本非参数检验方法主要有:符号检验、Wilcoxon符号秩检验等.x09(2)独立样本非参数检验方法主要有:Mann-WhitneyU检验、Kolmogorov-SmirnovZ检验、Mosesextremereactions检验等.x09
x09(3)独立样本非参数检验方法主要有:Kruskal-W allisH 检验、Median:中位数检验、onckheere-Terpstr检验等.
x09(4)相关样本非参数检验方法主要有:Friedman检验、Kendall协和系数检验、Cochran检验等.
x09此外,还有秩和检验.
x09
以上几种都属于有序分类变量非参检验方法,而对于无序分类变量非参检验最常用的方法则为卡方检验.
都是手打的,
二 : 经典非参数假设检验方法全
非参数假设检验
在前面的课程中,我们已经了解了假设检验的基本思 想,并讨论了当总体分布为正态时,关于其中未知参数的 假设检验问题 .
然而可能遇到这样的情形,总体服从何种理论分布并 不知道,要求我们直接对总体分布形式提出种种假设,然 后利用样本信息对假设进行检验。 在统计学中把不依赖于分布形式的统计方法称为非参数 统计。对总体的分布形式的检验就是非参数检验。
例如,从1500到1931年的432年间,每年爆发战争的 次数可以看作一个随机变量,椐统计,这432年间共爆发 了299次战争,具体数据如下: 战争次数X 0 1 2 3 4 发生 X次战争的年数 223 142 48 15 4
在概率论中,大家对泊松分布产生的一般条件已有所了 解,容易想到,每年爆发战争的次数,可以用一个泊松随机 变量来近似描述 . 也就是说,我们可以假设每年爆发战争次 数分布X近似泊松分布. 现在的问题是:上面的数据能否证实X 具有泊松分布的假设 是正确的?
又如,某钟表厂对生产的钟进行精确性检查,抽取100 个钟作试验,拨准后隔24小时以后进行检查,将每个钟的 误差(快或慢)按秒记录下来.
问该厂生产的钟的误差是否服从正态分布?
再如,某工厂制造一批骰子,声称 它是均匀的. 也就是说,在投掷中,出现1点,2 点,…,6点的概率都应是1/6.
为检验骰子是否均匀,要把骰子实地投掷若干次,统 计各点出现的频率与1/6的差距. 问题是:得到的数据能否说明“骰子均匀”的假设是可信的?
解决这类问题的工具是英国统计学家K.皮尔逊在1900年
发表的一篇文章中引进的所谓 ?2检验法. 这是一项很重要的工作,不少人把它视 为近代统计学的开端.
?2检验法是在总体X 的分布未知时,
根据来自总体的样本,检验关于总体分布 的假设的一种检验方法 K.皮尔逊
本章只介绍?2拟合优度检验、柯尔莫哥洛夫以及
斯米尔诺夫检验、独立性检验方法。
除此还有:符号检验、游程检验、秩和检验等等。
为什么用非参数方法?
? 经典统计的多数检验都假定了总体的背景 分布。 ? 在那里,总体的分布形式或分布族往往是 给定的或者是假定了的。所不知道的仅仅 是一些参数得知或它们的范围。于是,人 们的主要任务就是对一些参数,比如均值 和方差(或标准差)进行估计或检验。 ? 如检验正态分布的均值是否相等或等于零 等等。最常见的检验是和正态总体有关的 t-检验、F-检验、X2检验和最大似然比检 验等。
为什么用非参数方法?
? 非参数检验是针对参数检验而言的。从检验步 骤上讲,二者是一致的:它们都是对总体的某 种数量特征建立相应的原假
设和备择假设,都 是在给定的显著性水平下,根据实际统计量来 判断对原假设的取舍。 ? 二者的不同之处在于:参数检验需要对总体分 布作限制性的假定。这种假定实际就是要求总 体的分布类型已知,所不知道的只是其中的某 个参数,如均值或方差。而非参数检验并不要 求已知总体的分布信息,而是根据数据本身来 推断总体参数。
为什么用非参数方法?
? 在实际生活中,总体的分布信息并不是容 易得到的。有时,数据并不是来自所假定 的总体;或者,数据根本不是来自同一个 总体;还有可能,数据因为种种原因被严 重“污染”。这样,在假定总体分布的情 况下进行推断的做法就可能产生错误的或 者甚至灾难性的结论。 ? 于是,人们希望在不假定总体分布的情况 下,尽量从数据本身来获得所需要的信息, 这就是非参数统计的宗旨。
为什么用非参数方法?
? 正是由于非参数检验要求的信息少,检验 条件比较宽松,因此它具有很强的适应性, 应用的范围比起参数检验更宽广。非参数 检验不仅可以应用于定距、定比数据的检 验而且也适用于定类、定序数据的假设检 验。对于那些不能直接进行加减乘除四则 运算的数据,运用符号检验、秩和检验都 能起到比较好的效果。
为什么用非参数方法?
? 非参数检验同样也有其缺点。由于它对总体的 分布没有严格的要求,因此在检验过程中会失 去许多有用的信息,在方法上就缺乏针对性。 而且非参数检验是通过处理样本数据的秩或等 级来检验假设的,而不是利用原始数据,这又 会失去一些信息,因而检验的有效性有时会比 较差。 ? 当然,如果我们事先对总体的分布信息一无所 知或难下定论,那么建立在数据本身基础上的 非参数检验结果要比建立在一个可疑的总体分 布基础上得到的参数检验结果要可靠的多。
为什么用非参数方法?
? 但是在总体分布形式已知时,非参数检验 就不如传统方法效率高。这是因为非参数 方法利用的信息要少些。往往在传统方法 可以拒绝零假设的情况,非参数检验无法 拒绝。 ? 但非参数统计在总体未知时效率要比传统 方法要高,有时要高很多。是否用非参数 统计方法,要根据对总体分布的了解程度 来确定。
为什么用非参数方法?
? 那么,如何在不知道总体分布的情况下利用数据 本身的信息来进行假设检验呢? ? 我们知道,一组数据最基本的信息就是次序。我 们把样本中各个数据按从小到大的顺序排列起来, 则每个数据都会在这个顺序数列中有它的位置或 次序,这个位置或次序就叫做秩。数据有多少个 观察值,就有多少个秩
。 ? 在一定的假设下,这些秩和它们的统计量的分布 是可以求出来的,而且和原来的总体分布无关。 这样就可以进行所需要的统计推断了。这就是本 节所讲的非参数假设检验的基本思想。
为什么用非参数方法?
? 根据样本又分成
单样本检验 两独立样本检验
? 非参数检验 多个独立样本检验
多个相关样本检验 列联表某一变量各水平比例检验
在本节我们将介绍几种最常用的非参数检验方法: 符号检验、秩和检验和游程检验。
非参数检验
? ? ? ? ? ? ? ? ? ? 非参数检验的方法有很多种,如下几种检验: 正态慨率纸检验; 皮尔逊(Pearson)χ2拟合检验; 柯尔莫哥洛夫与斯米尔诺夫检验; Shapiro-Wilk W检验; D’Agostion’s D检验; Wilcoxon秩和检验。 符号检验 秩和检验 游程检验。
非参数假设检验方法
一、?2拟合优度检验 二、柯尔莫哥洛夫 三、斯米尔诺夫检验 四、独立性检验
一、?2拟合优度检验
适用范围广:一个离散、连续、正态总体都适用。
1、多项分布的?2检法
离散总体
对一次抽样来说,
现在对总体X进行假设,即对X的分布律进行假设
由于频率是概率的近似表现,
那么当容量 n 较大时,
类似于以前的检验方法,取一个标准化的度量。
为此在1900年,英国统计学家 Karl Pearson 首先提出
从该统计量直观上判断有,
另外,用该统计量对总体分布律进行检验,还必须知道 其分布。 Pearson给出了其渐近分布。
定理1
由此可以建立 H0 的拒绝域
只要给定一组样本观察值,代入检验统计量计算后,就 能得出结论。
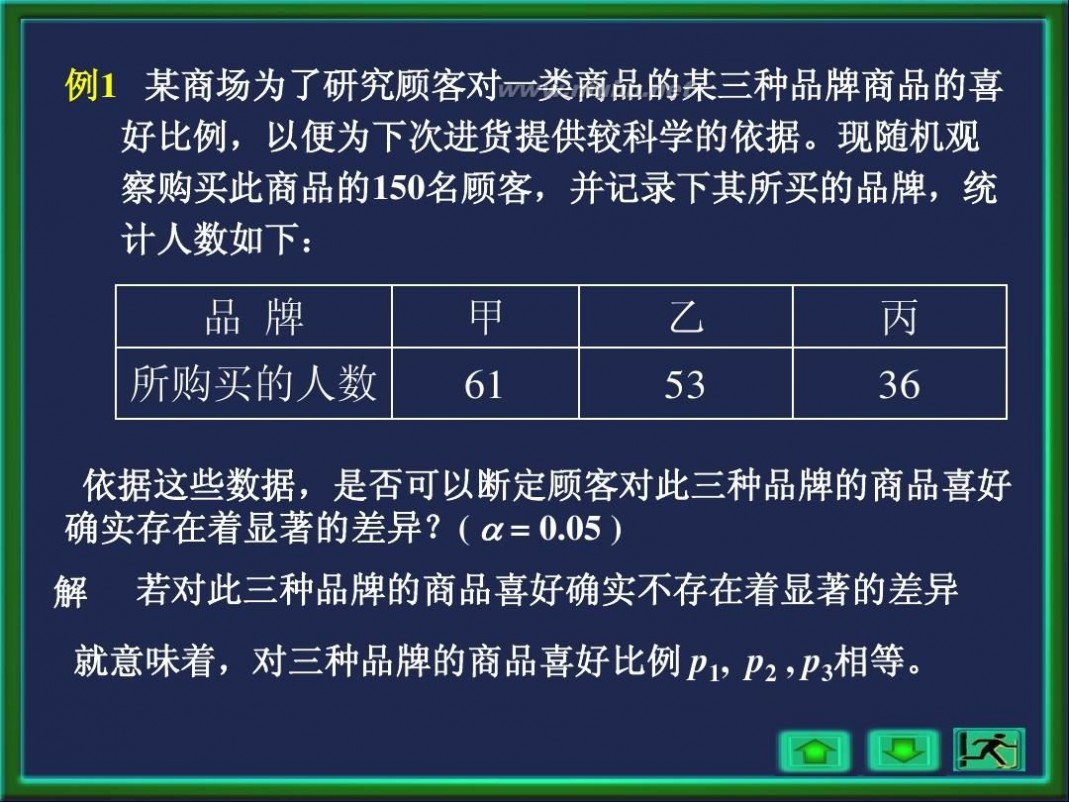
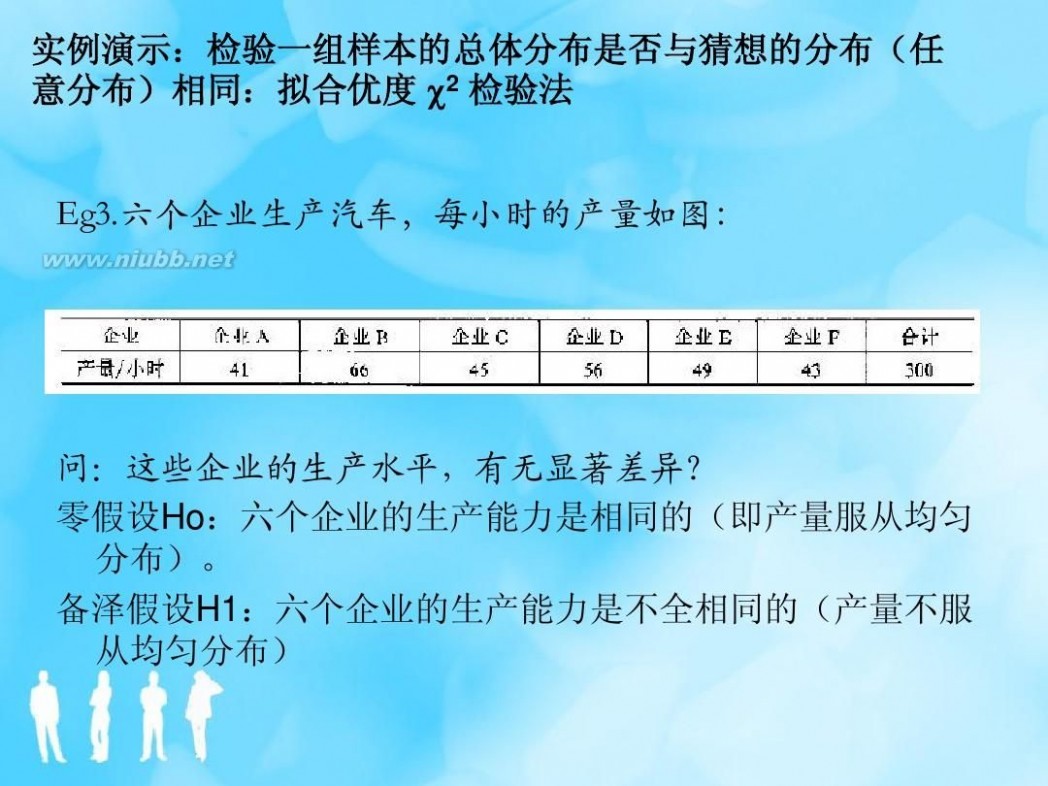
例1 某商场为了研究顾客对一类商品的某三种品牌商品的喜 好比例,以便为下次进货提供较科学的依据。现随机观 察购买此商品的150名顾客,并记录下其所买的品牌,统 计人数如下:
品 牌
甲
乙
丙
所购买的人数
61
53
36
依据这些数据,是否可以断定顾客对此三种品牌的商品喜好 确实存在着显著的差异?( ? = 0.05 )
解
若对此三种品牌的商品喜好确实不存在着显著的差异
就意味着,对三种品牌的商品喜好比例 p1, p2 , p3相等。
此是 m = 3, n1 = 61, n2= 53, n3 = 36,n=150
由于6.52 > 5.991
故有理由拒绝H0
认为顾客对此三种品牌的商品喜好确实存在着显著的差异.
例2 64只某种杂交的几内亚猪的后代,其中34只红色,10只 黑色,20只白色,根据遗传模型,它们之间的比例应为 9:3:4,问以上数据在0.05的水平下体现的与遗传模型是否 吻合。 认为基本吻合 解 若基本吻合,则p1=9/16, p2 =3/16 ,p3 =4/16
此是 m = 3, n1 = 34, n2= 10, n3 = 20,n=64
例3 验证一枚骰子是否均匀。 电话号码的数字出现的概率等等问题。 采
用分组离散化方法 若X的分布函数F(x)的具有明确表达式F0(x),不含未知参数。 根据样本信息推断X的分布函数是否为F0(x).
第一步:
第二步:计算
第三步:记数
第四步:检验
其中m为分组数 H0的拒绝域为
一般有 n > 50,npi > 5最好 npi >10,否则应重新分组。 使得npi > 5最好 npi >10.
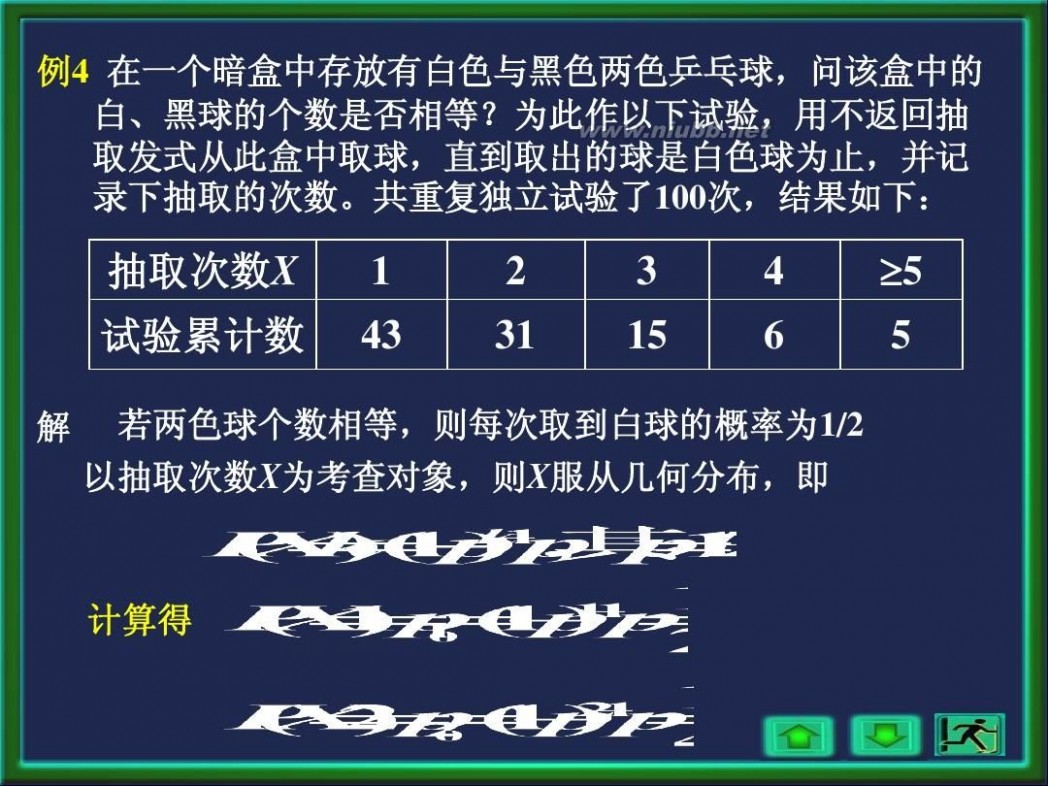
例4 在一个暗盒中存放有白色与黑色两色乒乓球,问该盒中的 白、黑球的个数是否相等?为此作以下试验,用不返回抽 取发式从此盒中取球,直到取出的球是白色球为止,并记 录下抽取的次数。共重复独立试验了100次,结果如下:
抽取次数X 试验累计数
解
1 43
2 31
3 15
4 6
?5 5
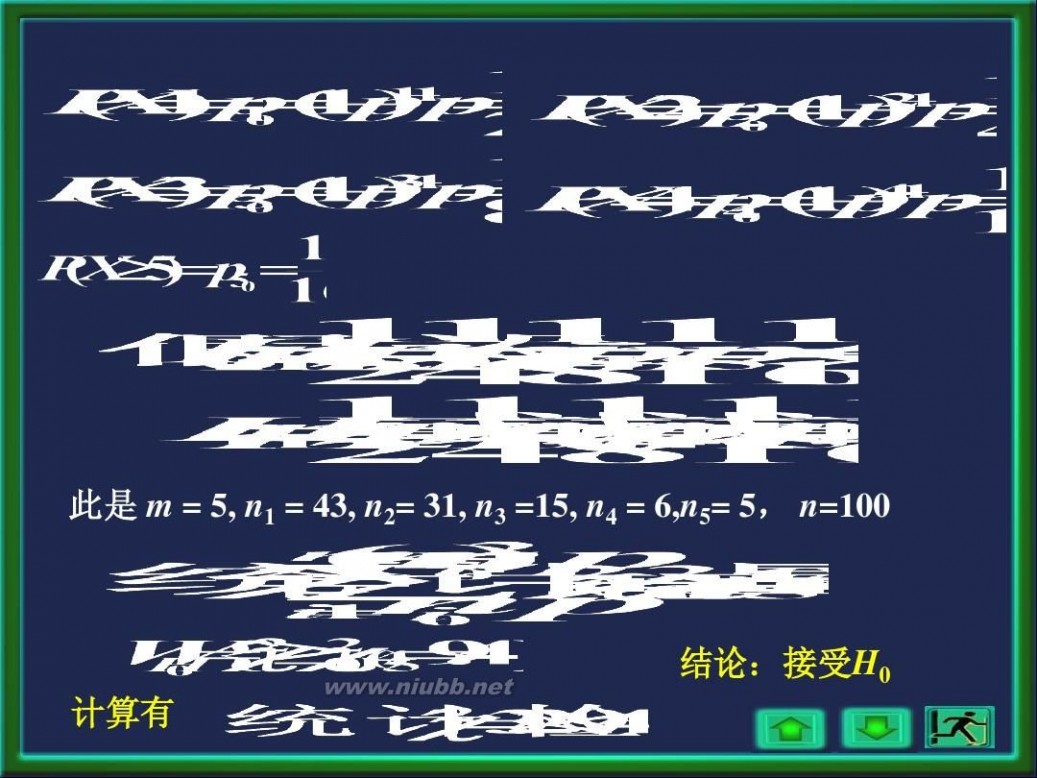
若两色球个数相等,则每次取到白球的概率为1/2 以抽取次数X为考查对象,则X服从几何分布,即
计算得
此是 m = 5, n1 = 43, n2= 31, n3 =15, n4 = 6,n5= 5, n=100
结论:接受H0
计算有
(3) 若X的分布函数F(x)的具有明确表达式F0(x;?),但含 r 个 未知参数。根据样本信息推断X的分布函数是否为F0(x).
第一步: 由样本进行参数的点估计后,将参数估计值代入分 布函数中,使得分布函数成为已知函数F0(x;?) 。 第二步: 仿造情形 (2) 分组离散。令
第三步: 其中 m 为分组数,r 为分布函数中待估参数数.
一般有 n > 50,npi > 5最好 npi >10,否则应重新分组。 使得npi > 5最好 npi >10.
第四步:检验 H0的拒绝域为 定理2 (R.A.Fisher)
让我们回到检验每年爆发战争次数分布是否服从泊松分布. 假设H0: X~P(?)
根据观察结果,得参数 ? 的极大似然估计为 ,i=0,1,2,3,4
=0.69
按参数为? =0.69的泊松分布,计算事件X= i 的概率 pi , pi的估计是 将有关计算结果列表如下:
战争次数 x 实测频数 fi pi npi
0 1 2 223 142 48 0.58 0.31 0.18 216.7 149.5 51.6
3 4 15 4 0.01 0.02 12.0 2.16
?
14.16 ( f i ? npi )2 0.183 0.376 0.251 1.623 npi 因H0所假设的理论分布中有一个未知参数,
按?=0.05,自由度为4-1-1=2查?2分布表得 由于统计量的实测值
2.43
<5的要合并,即将发生3次及4次战争的组归并为一组.
?2 =2.43<5.991, 未落入否定域.
故认为每年发生战争的次数X服从参数为0.69的泊松分布.
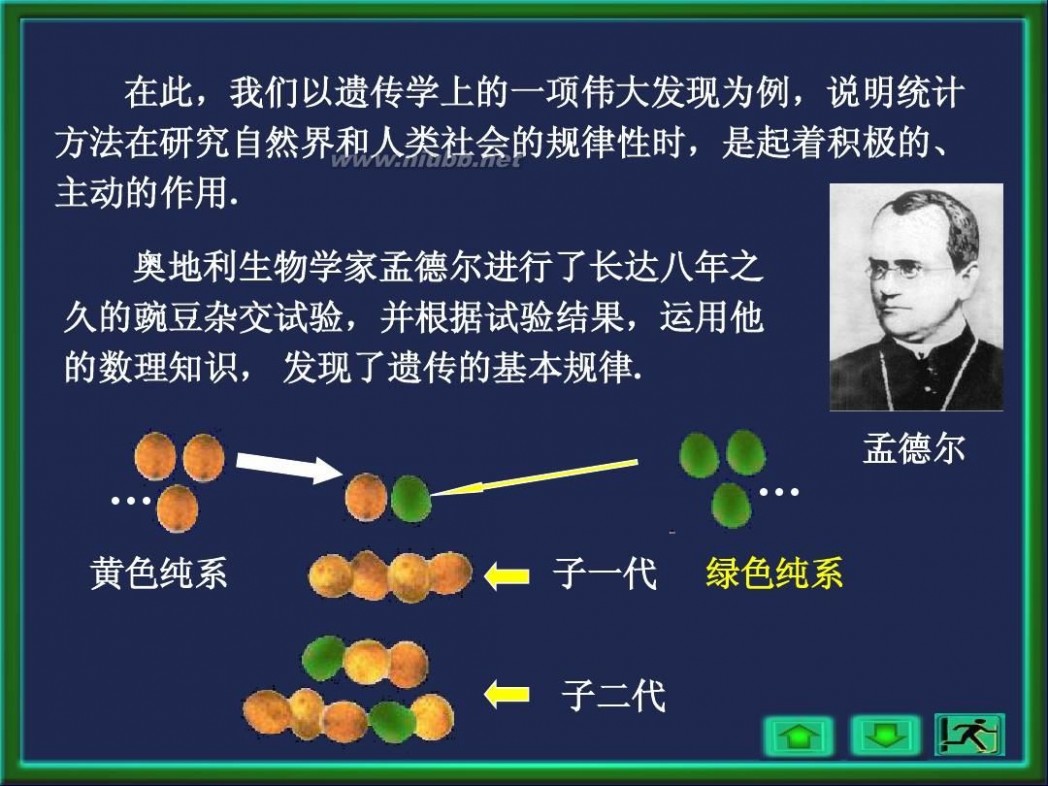
在此,我们以遗传学上的一项伟大发现为例,说明统计 方法在研究自然界和人类社会的规律性时,是起着积极的、 主动的作用. 奥地利生物学家孟德尔进行了长达八年之 久的豌豆杂交试验,并根据试验结果,运用他 的数理知识, 发现了遗传的基本规律.
…
黄色纯系 子一代
…
绿色纯系
孟德尔
子二代
根据他的理论,子二代中, 黄、绿之比 近似为3:1, 他的一组观察结果为: 黄70,绿27 近似为2.59:1,与理论值相近. 由于随机性,观察结果与3:1总有些差距,因此有 必要去考
察某一大小的差异是否已构成否定3:1理论的 充分根据,这就是如下的检验问题. 检验孟德尔的3:1理论:
假设H0: p1=3/4, p2=1/4 ? H1: p1=3/4, p2=1/4至少一不成立
这里,n=70+27=97, k=2, 理论频数为: np1=72.75, np2=24.25 实测频数为70,27.
( fi ? npi )2 统计量 ? ?? ?? 2 ( 2 ? 1) npi i ?1 按? =0.05,自由度为1,查?2分布表得
2 2
自由度为m-1=1
?20.05(1) =3.841
由于统计量?2的实测值
?2=0.4158<3.841, 未落入否定域.
故认为试验结果符合孟德尔的3:1理论. 这些试验及其它一些试验,都显 示孟德尔的3: 1理 论与实际是符合的. 这本身就是统计方法在科学中的一 项重要应用.
用于客观地评价理论上的某个结论是否与观察结果相符, 以作为该理论是否站得住脚的印证.
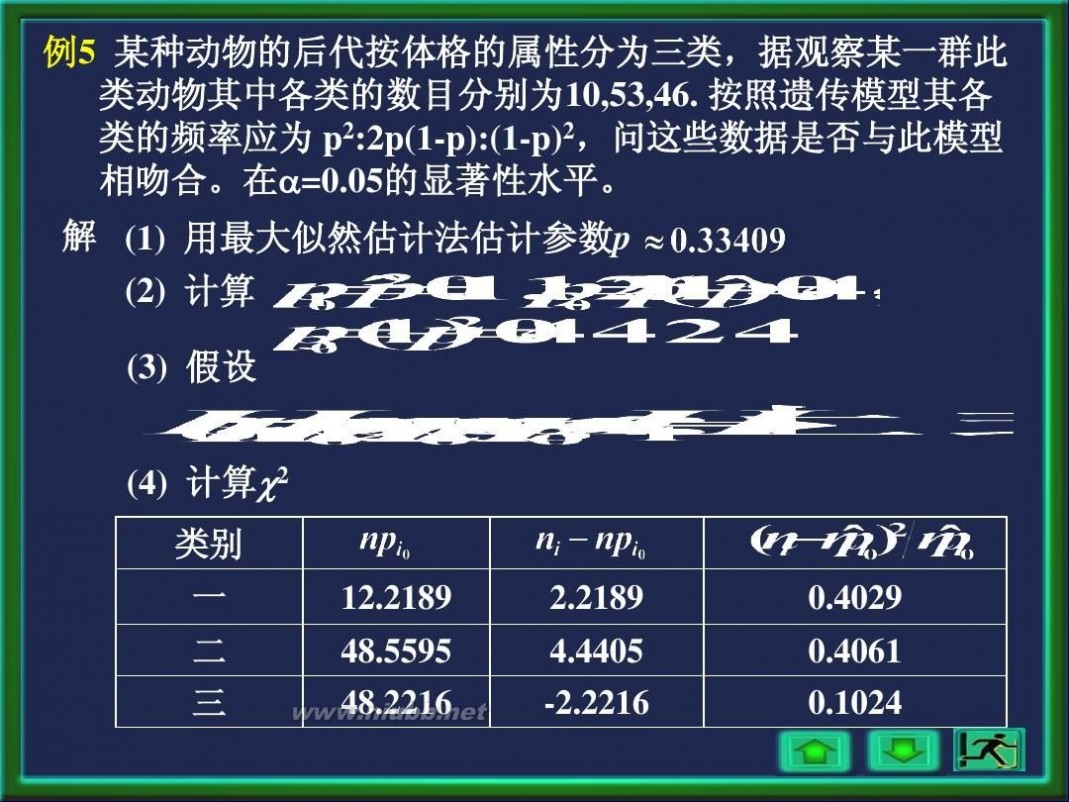
例5 某种动物的后代按体格的属性分为三类,据观察某一群此 类动物其中各类的数目分别为10,53,46. 按照遗传模型其各 类的频率应为 p2:2p(1-p):(1-p)2,问这些数据是否与此模型 相吻合。在?=0.05的显著性水平。 解 (1) 用最大似然估计法估计参数p.
例5 某种动物的后代按体格的属性分为三类,据观察某一群此 类动物其中各类的数目分别为10,53,46. 按照遗传模型其各 类的频率应为 p2:2p(1-p):(1-p)2,问这些数据是否与此模型 相吻合。在?=0.05的显著性水平。 解 (1) 用最大似然估计法估计参数p (2) 计算 (3) 假设 (4) 计算?2
类别 一 12.2189 2.2189 0.4029
二
三
48.5595
48.2216
4.4405
-2.2216
0.4061
0.1024
例5 某种动物的后代按体格的属性分为三类,据观察某一群此 类动物其中各类的数目分别为10,53,46. 按照遗传模型其各 类的频率应为 p2:2p(1-p):(1-p)2,问这些数据是否与此模型 相吻合。在?=0.05的显著性水平。 解 (1) 用最大似然估计法估计参数p. (2) 计算 (3) 假设 (4) 计算?2 (5) H0的拒绝域 (6) 结论 接受H0,认为此数据基本符合模型的。
(4) ?2拟合优度检验法的特点
1) 适用面广,离散和连续总体均可以使用,是考察实测 频率与理论频率的差异。 2) 此法从本质上看,只是检验了理论分布函数的 而未真正检验
然而虽然样本与分组情况都具有随机性,但是当分布函 数较为光滑时,即使F(x)与F0(x)有差异,也不应该太大。 故此法虽有误差,但是常用的方法之一。
3) ?2拟合优度检验法依赖于区间的划分,即依赖与分组情况。 即使 ,但若恰好在分组点处的两函数值相 差不大,即便H0是不真,但?2的检验统计值不改变。从而 ?2拟合优度检验法的精度不高,容易范取伪错误。
二、柯尔莫哥洛夫检验
为了进一步提高精度,柯尔莫哥洛夫针对一个总体的分 布函数,在采用分组离散化后利用经验分布函数的性质的方 法,较完整的考察了
经验分布函数Fn(x)与理论分布函数F(x) 的差异。提高了检验的精度。但假定分布函数是连续的。 设总体X的分布函数F(x)连续,
故可以选用
定理3 设分布函数F(x)连续,则
定理4 设分布函数F(x)连续,则
1、选用Dn为检验统计量,假设H0的拒绝域为:
2、当n>40或100时,可得一近似求Dn,?值方法
假设H0的拒绝域仍为: 即 此种方法虽较精确,但计算量较大。
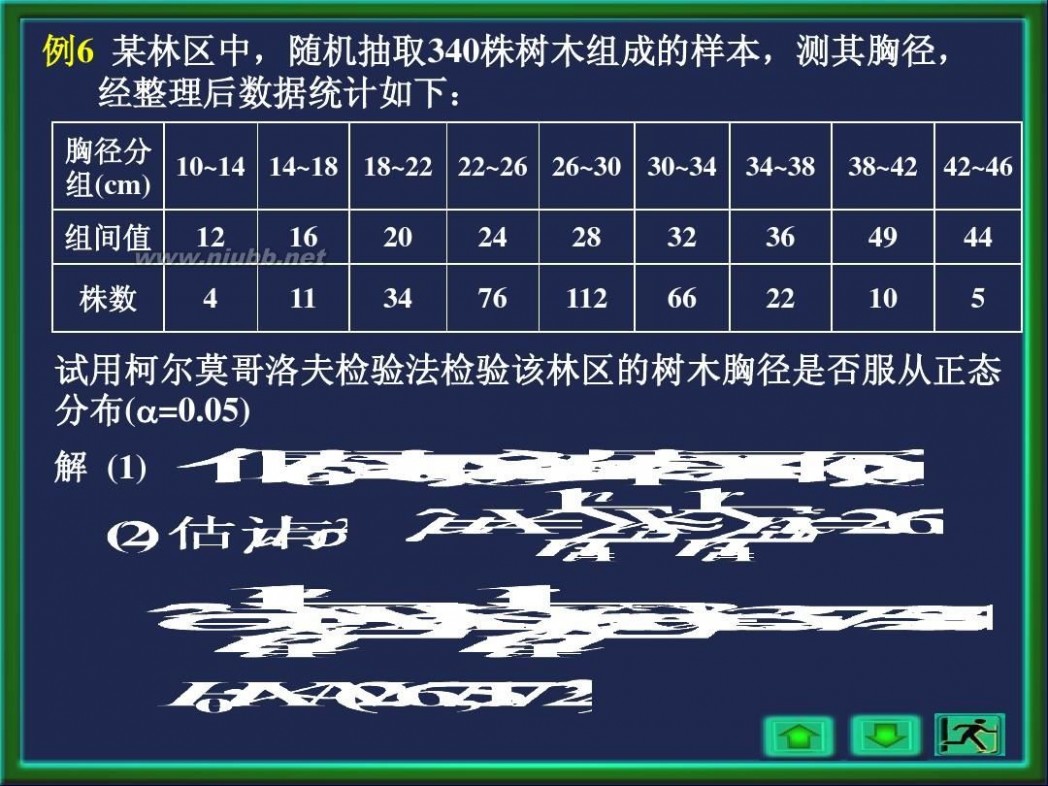
例6 某林区中,随机抽取340株树木组成的样本,测其胸径, 经整理后数据统计如下:
胸径分 10~14 14~18 18~22 22~26 26~30 30~34 34~38 组(cm)
38~42 42~46
组间值
株数
12
4
16
11
20
34
24
76
28
112
32
66
36
22
49
10
44
5
试用柯尔莫哥洛夫检验法检验该林区的树木胸径是否服从正态 分布(?=0.05) 解 (1)
解
频率 组号 分组值 组上限 标准化 经验函数 理论函数
1 2 3 4 5 6 7 8 9
10~14 14~18 18~22 22~26 26~30 30~34 34~38 38~42 42~46
0.0118 0.032 0.100 0.2235 0.3294 0.1941 0.0647 0.0294 0.0151
14 18 22 26 30 34 38 42 46
-2.2388 -1.6798 -0.9807 -0.2817 0.4173 1.1164 1.8154 2.5144 3.2134
0.0118 0.0438 0.1438 0.3673 0.6967 0.8906 0.9555 0.9845 1.0000
0.0126 0.0465 0.1635 0.3897 0.6628 0.8686 0.9656 0.9940 0.9993
0.0008 0.0027 0.0197 0.0224 0.0339 0.022 0.0101 0.0095 0.0007
(4) 求 (5) 检验 接受H0
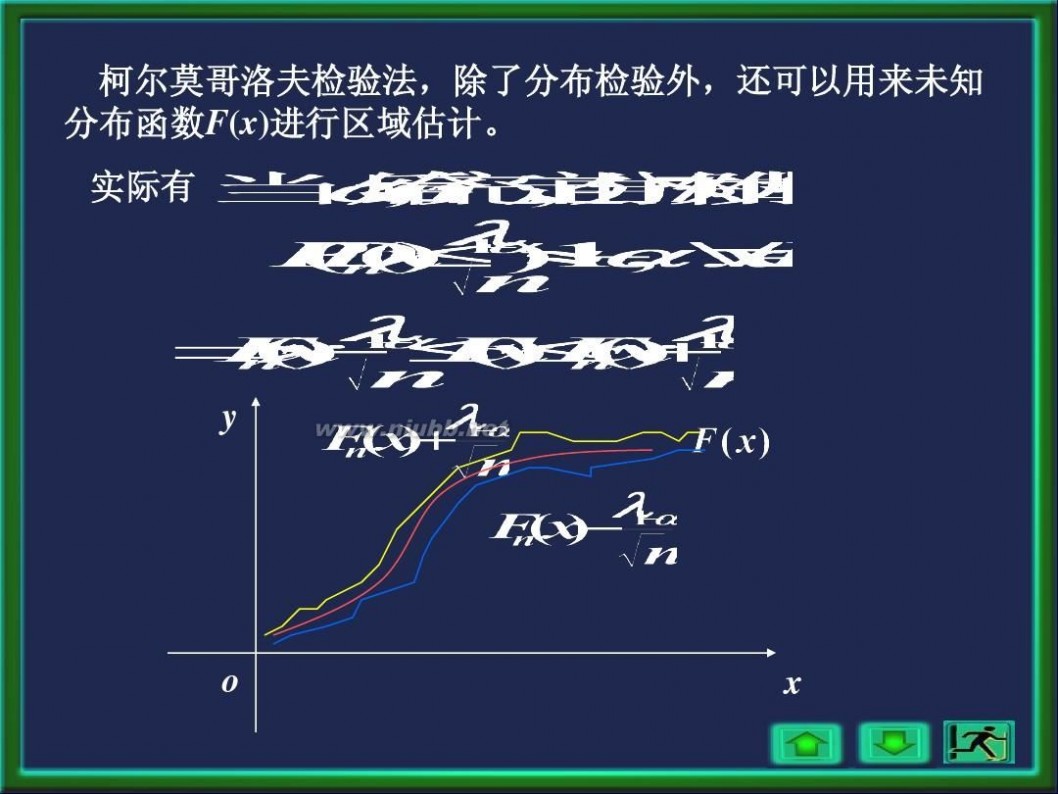
柯尔莫哥洛夫检验法,除了分布检验外,还可以用来未知 分布函数F(x)进行区域估计。
实际有
y
o
x
一、符号检验法
? 在许多实际应用场合,我们关心的不是总体的分 布是什么形状,而是关心(多个)总体是否相同 或者(单个)总体的位置(如均值、中位数)有 没有发生变化。这时就可采用最为简单的检验方 法——符号检验法。 ? 在单样本检验中,符号检验法可以有效地检验总 体的中位数是否等于某一个特定数值;而在配对 样本的检验中,符号检验法可以检验两个总体是 否相同,或者两个样本是否来自于同一总体。
(1) 单样本的符号检验
? 我们知道,反映一个总体分布位置的参数主要 有平均数和中位数。平均数反映的是总体分 布的重心位置,而中位数则是反映分布数据上 下两半观察值次数相等的中央位置。当总体呈 对称分布时,二者的位置是一致的,当分布为 不对称时,而这就有差别了。 当偏斜度较大时,由于中位数对极端值不敏感, 往往比平均数更有实际意义。因此,中位数相 对于平均数来讲适应性更强。在总体分布形态 未知的时候,使用中位数作为总体的未知参数 进行检验很有意义。
?
(1) 单样本的符号检验
单样本的中位数检验的基本思路是:假设总体的中位 数真值是 M e ? A ,并且从实际抽取容量为 n 的样本,观察值 为 x1 , x2 ,?, xn 。每个观察值都减去中位数 A ,并记录下各自 差数的
符号。不难理解,如果原假设 M e ? A 成立,那么所 得的为正的差数个数 n ? 应该与为负的差数个数 n 相差不
?
多,如果二者相差较远的话,则有理由拒绝原假设。
(1) 单样本的符号检验
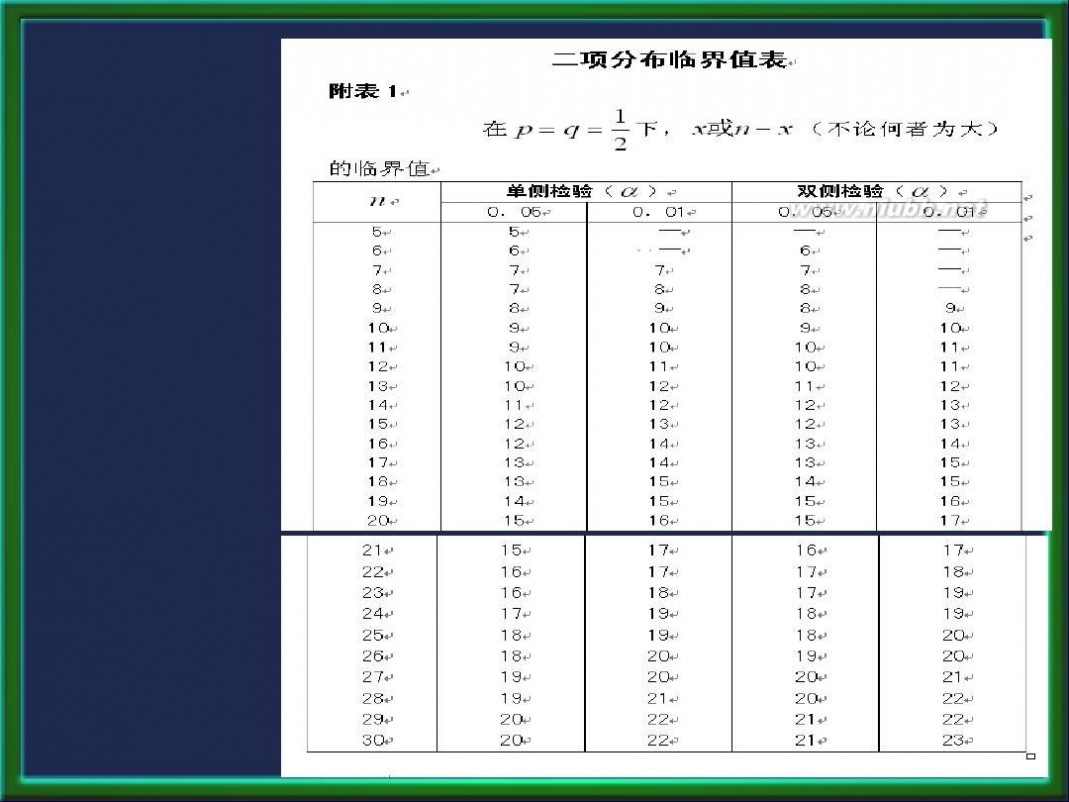
由于用总体中位数来表示中间位置, 这意味 着观察值 x1 , x 2 , ? , x n 取大于 M e 的值的概率应 该等于取小于 M e 值的概率,都为 0.5。 如果有相等的情况,则把这些观察值去掉, 同时相应减少检验过程中样本量 n 的值。这样, 如果 M e ? A 的确是总体的中位数(零假设成立) 则每一个观察值都以 0.5 的概率小于 A ,也以 0.5 的 概 率 大 于 A , 这 显 然 是 一 系 列 伯 努 力 (Bernoulli)试验。 因此, 所用的判别标准是由二项分布临界值提供 的(见附表) ,在大样本下可由正态分布来逼近
(1) 单样本的符号检验
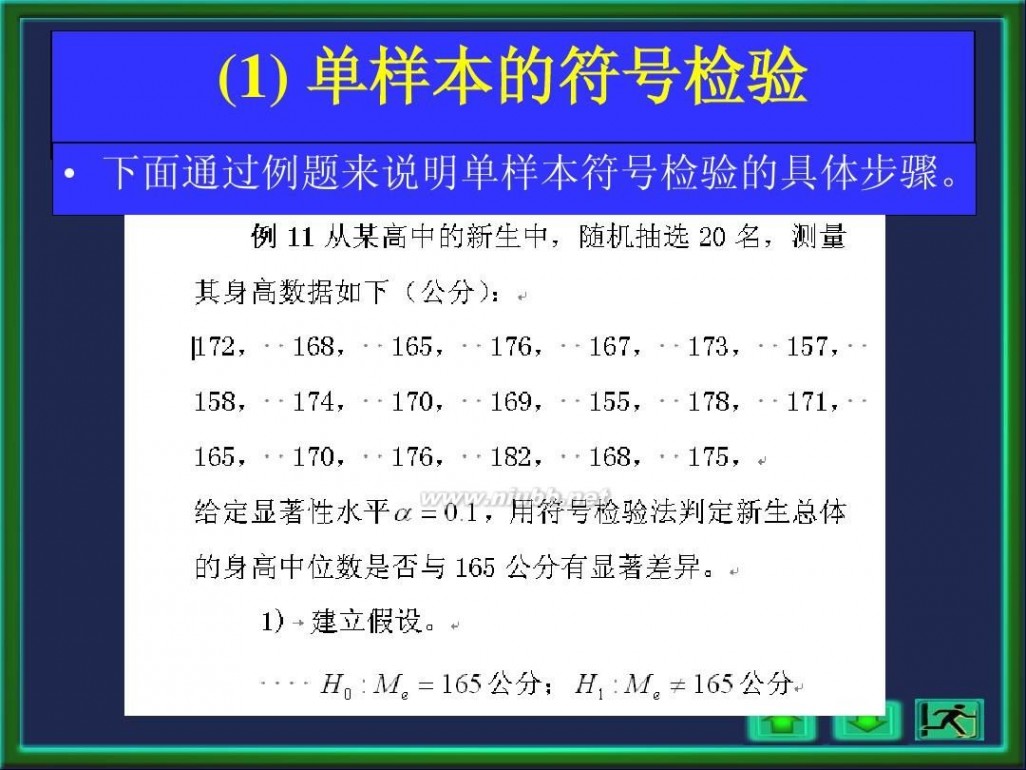
? 下面通过例题来说明单样本符号检验的具体步骤。
(1) 单样本的符号检验
(1) 单样本的符号检验
(1) 单样本的符号检验
(1) 单样本的符号检验
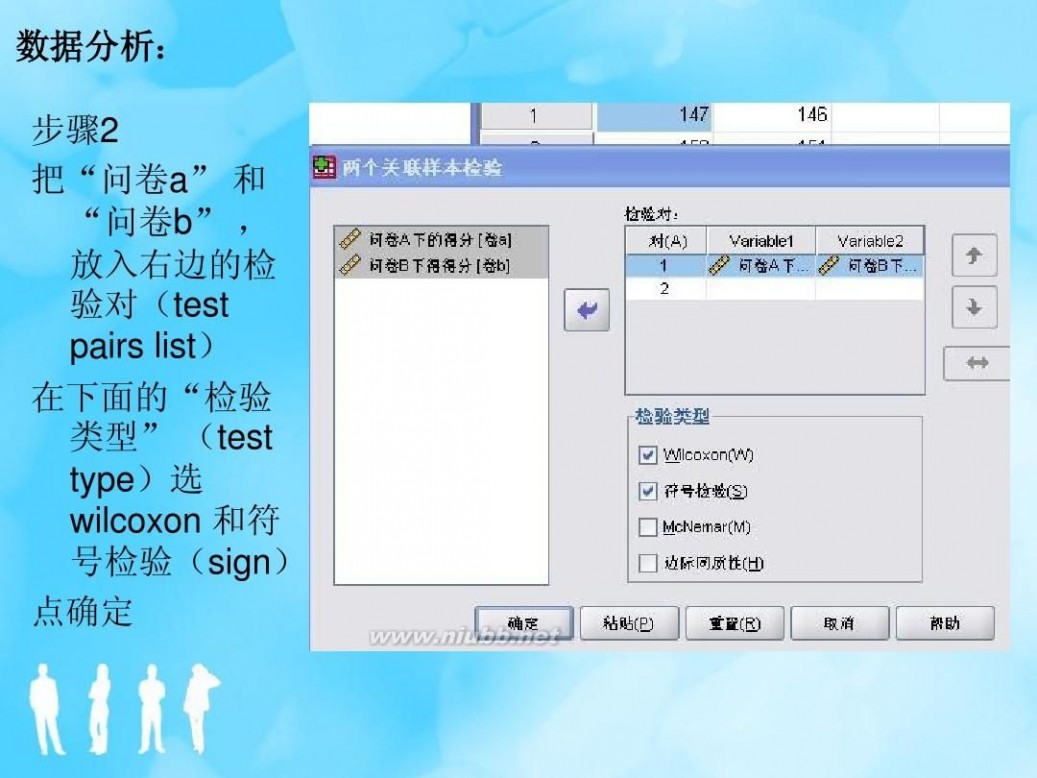
(2)配对样本的符号检验
? 在许多实际工作和科学研究中,往往要检 验两个独立的样本是否来自同一总体或者 是否存在显著性差异。在不知总体分布信 息的情况下,就需要利用配对样本的符号 检验法来检验假设。
(2)配对样本的符号检验
? 基本思路是:将两样本的数据按某一规则 配对,然后将各组配对值相减得到一系列 差值,如果两组样本来自同一总体或者不 存在显著性差异,则所得的为正的差值个 数n+应该与为负的差值个数n-相差不多,如 果二者相差较远的话,则有理由拒绝原假 设。 ? 下面通过例题来介绍配对样本符号检验法 的具体步骤。
(2)配对样本的符号检验
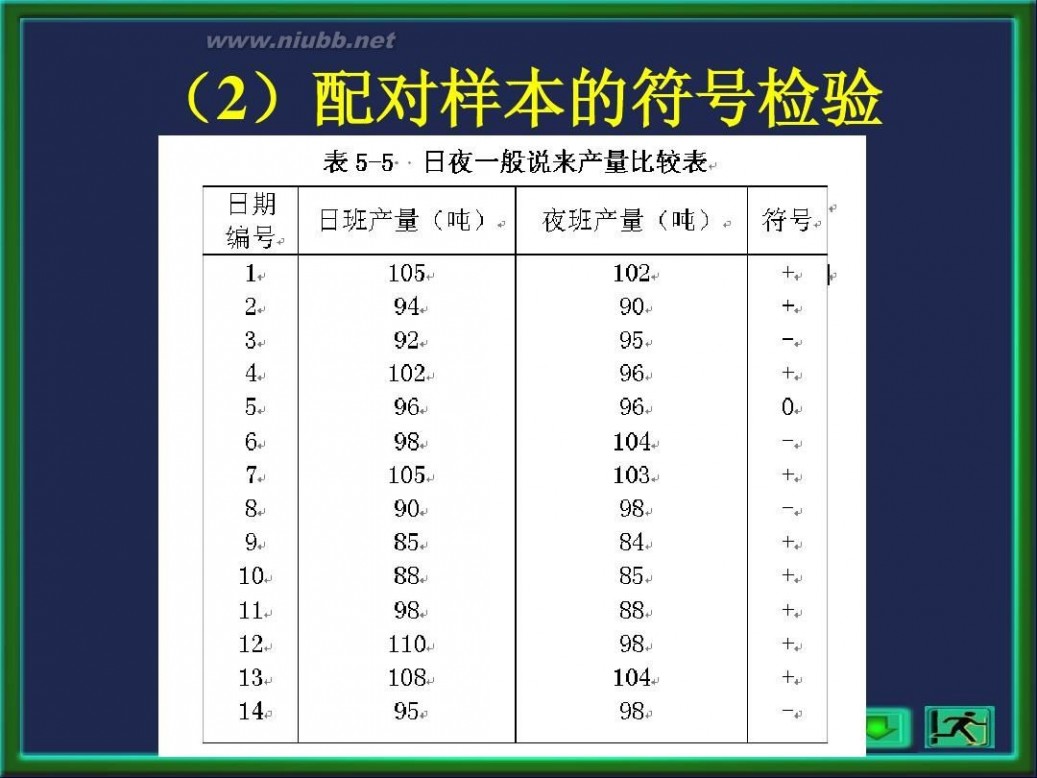
? 例13某工厂为比较日班生产与夜班生产的 效率是否有显著差异,随机抽取两星期进 行观察,各日产量比较如下表5-5所示。试 在显著性水平下,判断日、夜班生产是否 存在显著性的差异。
(2)配对样本的符号检验
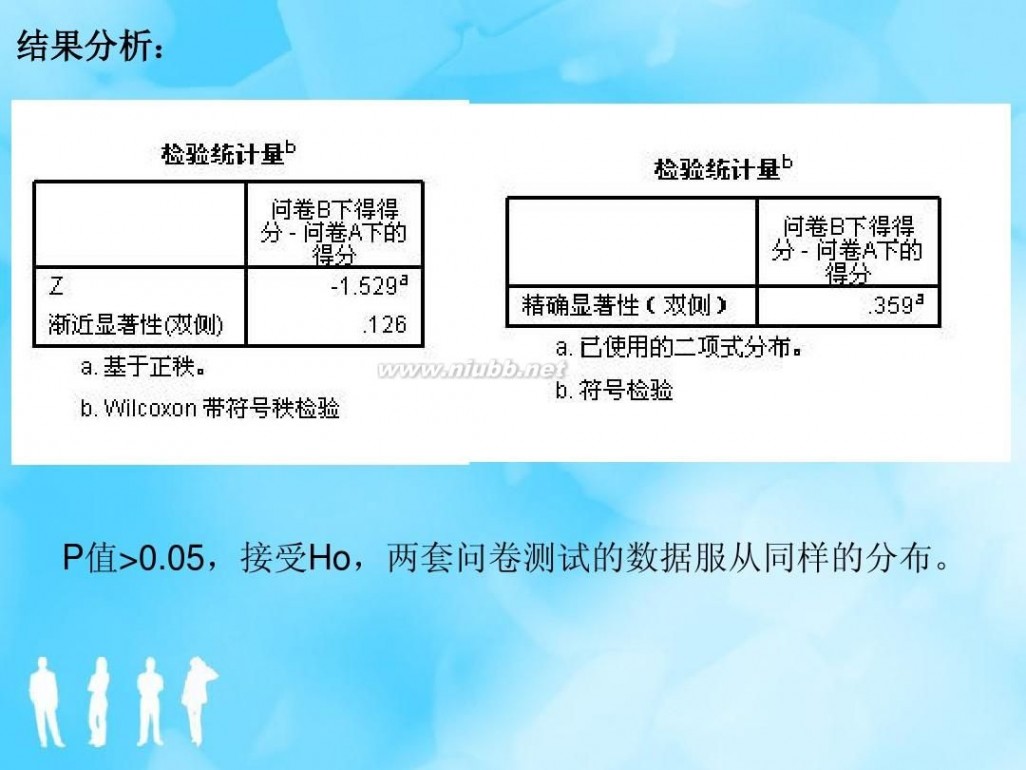
(2)配对样本的符号检验
(2)配对样本的符号检验
(2)配对样本的符号检验
(2)配对样本的符号检验
(2)配对样本的符号检验
(2)配对样本的符号检验
? 符号检验法的最大优点是简单、直观,并 且不要求知道被检验量所服从的分布。 ? 缺点就是精确程度较差,没有充分利用样 本所提供的信息,而且要求数据搭配成对。 ? 下面介绍的秩和检验法在一定程度上弥补 了上述缺陷。
二、秩和检验法
? 在运用符号检验法检验两总体分布是否相同时, 其基本条件之一就是两总体的样本是可以根据某 一规则配对的。 ? 而在实际问题中,两总体样本是独立调查的,并 不总是可以配对,在
这种情况下,符号检验法就 不能使用了。 ? 而秩和检验法可以用于两总体非配对样本是否有 显著差异的检验。秩和检验法不仅考虑样本差值 的符号信息,而且同时考虑了样本差值的出现顺 序。 ? 因此他在利用样本的信息方面比符号检验更充分, 所以效力也更强。
秩(rank)
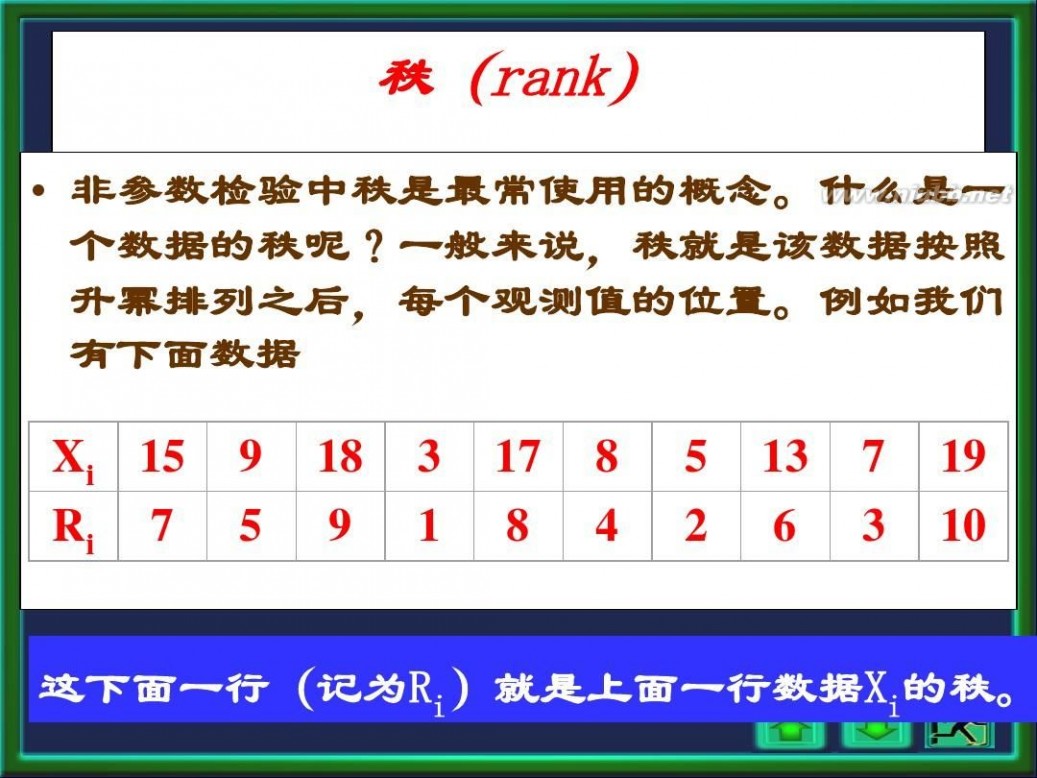
? 非参数检验中秩是最常使用的概念。什么是一 个数据的秩呢?一般来说,秩就是该数据按照 升幂排列之后,每个观测值的位置。例如我们 有下面数据 Xi 15 Ri 7 9 5 18 9 3 1 17 8 8 4 5 2 13 6 7 3 19 10
这下面一行(记为Ri)就是上面一行数据Xi的秩。
秩(rank)
? 利用秩的大小进行推断就避免了不知 道背景分布的困难。这也是大多数非 参数检验的优点。 ? 多数非参数检验明显地或隐含地利用 了秩的性质;但也有一些非参数方法 没有涉及秩的性质。
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
二、秩和检验法
三、关于随机性的游程检验 (run test)
? 游程检验方法是检验一个取两个值的变量的,这两个 值的出现是否是随机的。假定下面是由0和1组成的 一个这种变量的样本(数据run1.sav): ? 0 0 0 0 1 1 1 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 ? 其中相同的0(或相同的1)在一起称为一个游程 (单独的0或1也算)。 ? 这个数据中有4个0组成的游程和3个1组成的游程。 一共是R=7个游程。其中0的个数为m=15,而1的个数 为n=10。
关于随机性的游程检验
? 出现0和1的这样一个过程可以看成是参数 为某未知p的Bernoulli试验。 ? 但在给定了m和n之后,在0和1的出现是随 机的零假设之下,R的条件分布就和这个参 数无关了。根据初等概率论,R的分布可以 写成(令N=m+n)
关于随机性的游程检验
? m ? 1?? n ? 1? 2? ?? ? k ? 1 ?? k ? 1? P ( R ? 2k ) ? ? , ?N? ? ? ?n? ? m ? 1?? n ? 1? ? m ? 1?? n ? 1? 2? ?? ? ? 2? ?? ? ? k ? 1 ?? k ? ? k ?? k ? 1? P( R ? 2k ? 1) ? ?N? ? ? ?n?
关于随机性的游程检验
? 于是就可以算出在零假设下有关R的概率, 以及进行有关的检验了。利用上面公式可 进行精确检验;也可以利用大样本的渐近 分布和利用Monte Carlo方法进行检验。利 用上面数据的结果是
三、游程检验(run test)
利用上面数据的结果是
Runs Test x Test Value a Total Cases Number of Runs Z Asymp. Sig. (2-tailed) Exact Sig. (2-tailed) Point Probability a. User-speci
fied. .5000 25 7 -2.345 .019 .017 .006
这里精确检验的p-值等于0.017,而渐近检验的p-值等于0.019(其渐近正态的统计量 为Z)。因此对于显著性水平0.05,可以拒绝零假设,即认为这个数据的0和1的出 现不是随机的。
关于随机性的游程检验
? 当然,游程检验并不仅仅用于只取两个值的变量, 它还可以用于某个连续变量的取值小于某个值及大 于该值的个数(类似于0和1的个数)是否随机的问 题。看下面例子。 ? 例 (run2.sav): 从某装瓶机出来的30盒化妆品的 重量如下(单位克) ? 71.6 71.0 71.8 70.3 70.5 72.9 71.0 71.0 70.1 71.8 71.9 70.3 70.9 69.3 71.2 67.3 67.6 67.7 67.6 68.1 68.0 67.5 69.8 67.5 69.7 70.0 69.1 70.4 71.0 69.9
关于随机性的游程检验
? 为了看该装瓶机是否工作正常,首先 需要验证是否大于和小于中位数的个 数是否是随机的(零假设为这种个数 的出现是随机的)。 ? 如果把小于中位数的记为0,否则记为 1,上面数据变成下面的0-1序列 ?1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0
三、游程检验(run test)
直接利用这个数据,通过SPSS,得到下面游程检验结果的输出。
Runs Test length Test Value
a
70.20 15 15 30 8 -2.787 .005 .005 .002
Cases < Test Value Cases >= Test Value Total Cases Number of Runs Z Asymp. Sig. (2-tai led) Exact Si g. (2-tailed) Point Probability a. Median
从这个输出可以看出精确检验的p-值等于0.005,而渐近检验的p-值也等 于0.005。因此对于大于0.005的显著性水平,可以拒绝零假设,即有理 由认为这30盒化妆品的重量小于中位数和大于中位数的情况的出现不 是随机的。
三、游程检验软件使用说明
使用我们的数据。选项为 Analyze-Nonparametric Tests-Runs。然后 把变量(这里是 length)选入 Variable List。再在下面 Cut Point 选中 位数 (Median) 当然, 。 也可以选其他值, 如均值 (Mean) 众数 , (Mode) 或任何你愿意的数目(放在 Custom) 。注意在对前面的由 0 和 1 组成的 序列(数据进行随机性检验时,要选任何 0 和 1 之间的数目(不包括 0 和 1) 在点 Exact 时打开的对话框中可以选择精确方法 。 (Exact) Monte , Carlo 抽样方法(Monte Carlo)或用于大样本的渐近方法(Asymptotic only) 。最后 OK 即可。
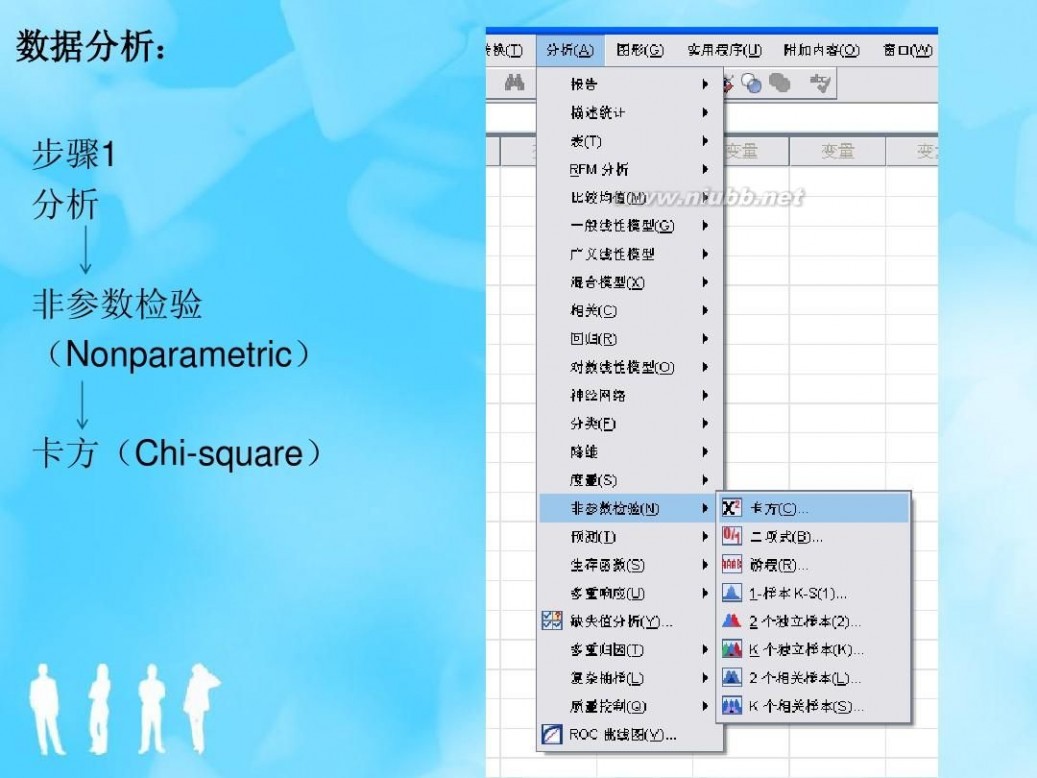
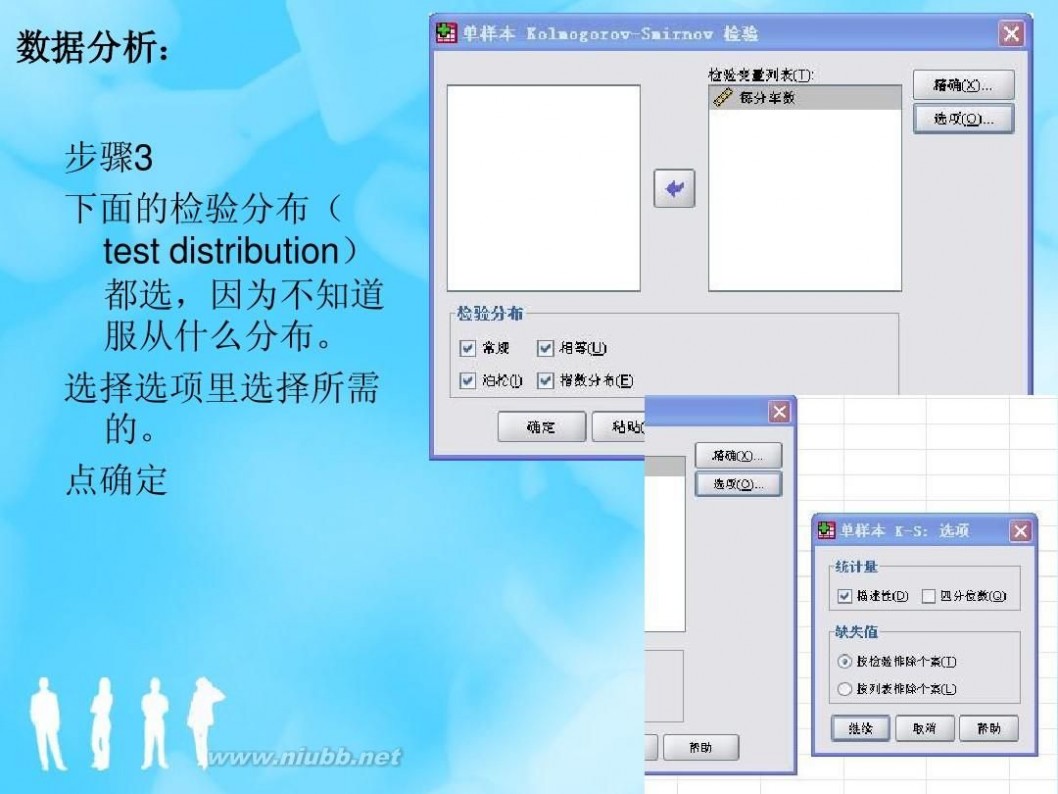
四、单样本KolmogorovSmirnov检验
? 单样本的Kolmogorov-Smirnov检验(K-S检 验)是用来检验一个数据的观测累积分布 是否是已知的理论分布。 ? 这些作为零假设的理论分布在SPSS的选项 中有正态分布,Poisson分布,均匀分布和 指数分布。在SPSS软件中对于是否是正态 分布或均匀分布的检验统计量为
Z ? n max ? S ( X i ?1 ) ? F0 ( X i ) , S ( X i ) ? F0 ( X i ) ?
i
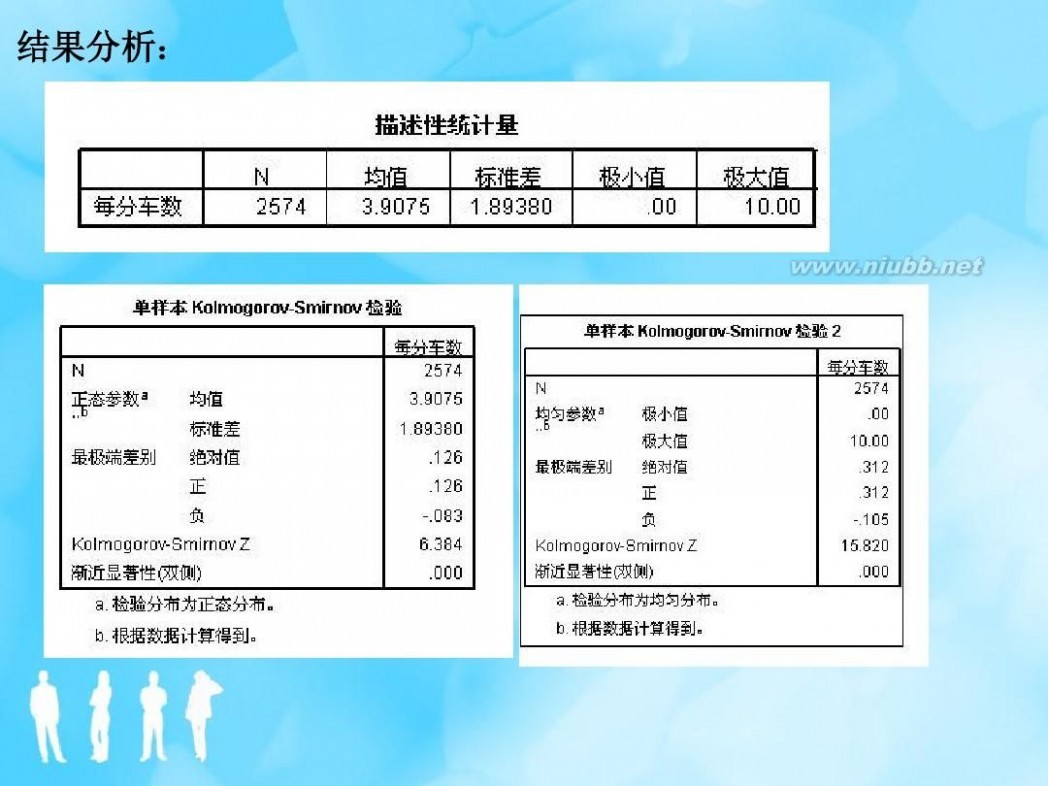
正态分布的检验结果
One -Samp le Ko lmogor ov-Sm irnov
Test X N a,b Normal Parameters Most Extreme Differences Mean Std. Deviation Absolute Positive Negative 50 1.0021 1.07647 .182 .173 -.182 1.284 .074 .069 .000
Kolmogorov-Smirnov Z Asymp. Sig. (2-tailed) Exact Sig. (2-tailed) Point Probability a. Test distribution is Normal. b. Calculated from data.
正态分布的检验结果
? 从检验的结果可知: ? 单边检验的P-值等于0.074/2=0.037(渐进检 验)和0.069/2=0.0345(精确检验)。 ? 因此,如果按照显著性水平为0.05的标准, 可以拒绝产生数据的总体为正态分布。
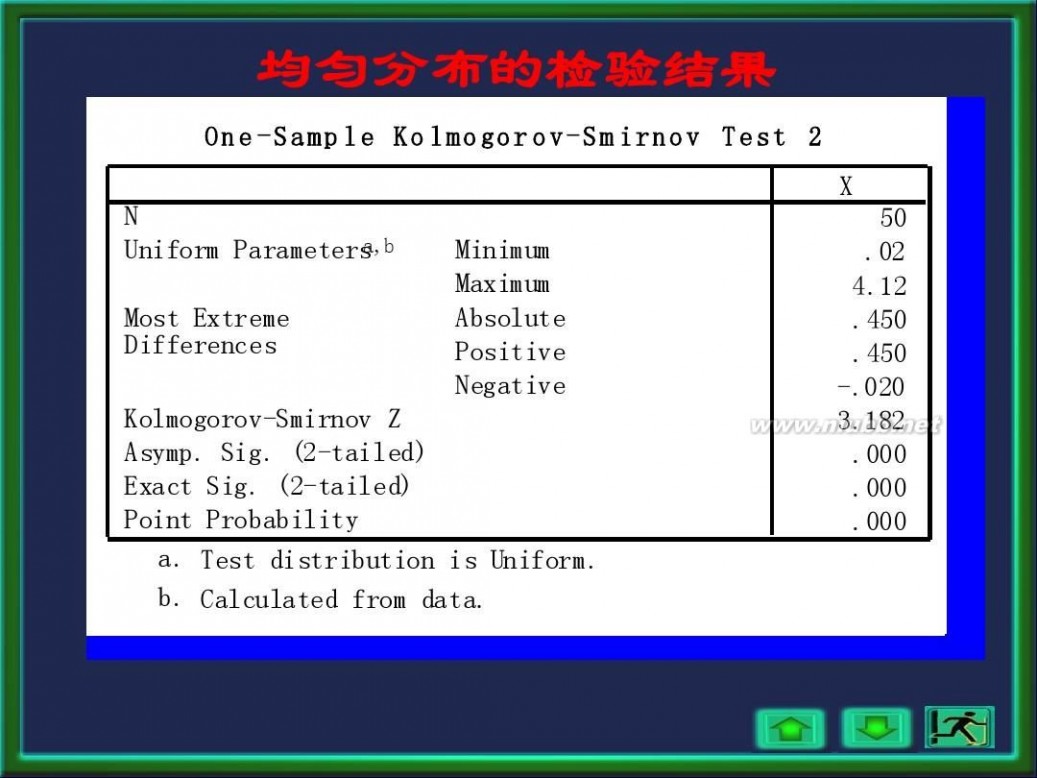
均匀分布的检验结果
One -Samp le Ko lmogor ov-Sm irnov Test 2 X N a,b Uniform Parameters Most Extreme Differences Minimum Maximum Absolute Positive Negative 50 .02 4.12 .450 .450 -.020 3.182 .000 .000 .000
Kolmogorov-Smirnov Z Asymp. Sig. (2-tailed) Exact Sig. (2-tailed) Point Probability a. Test distribution is Uniform. b. Calculated from data.
指数分布的检验结果
One -Samp le Ko lmogor ov-Sm irnov Test 4 X N a,b Exponential parameter. Mean Most Extreme Absolute Differences Positive Negative Kolmogorov-Smirnov Z Asymp. Sig. (2-tailed) Exact Sig. (2-tailed) Point Probability a. Test Distribution is Exponential. b. Calculated from data. 50 1.0021 .103 .103 -.052 .728 .664 .662 .000
SPSS软件使用说明
? SPSS选项为Analyze-Nonparametric Tests- 1 Sample K-S。 ? 然后把变量(这里是x)选入Variable List。再 在下面Test Distribution选中零假设的分布 (Normal、Poisson、Uniform和Exponential) 作为零假设。 ? 在点Exact时打开的对话框中可以选择精确方 法(Exact),Monte Carlo抽样方法(Monte Carlo ) 或 用 于 大 样 本 的 渐 近 方 法 (Asymptotic only)。最后OK即可。
三 : 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

61阅读请您转载分享:
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

61阅读请您转载分享:
非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

61阅读请您转载分享:
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全
非参数假设检验 经典非参数假设检验方法全

非参数假设检验 经典非参数假设检验方法全

61阅读请您转载分享:
四 : 非参数假设检验

非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
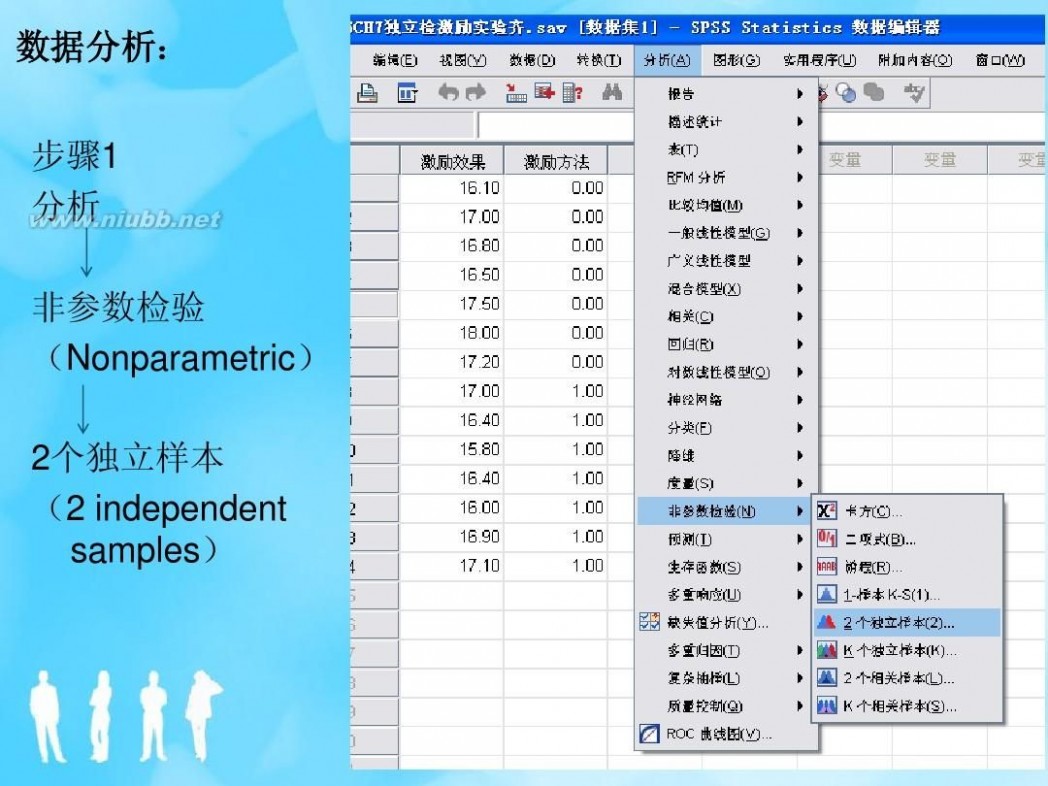
非参数假设检验 非参数假设检验
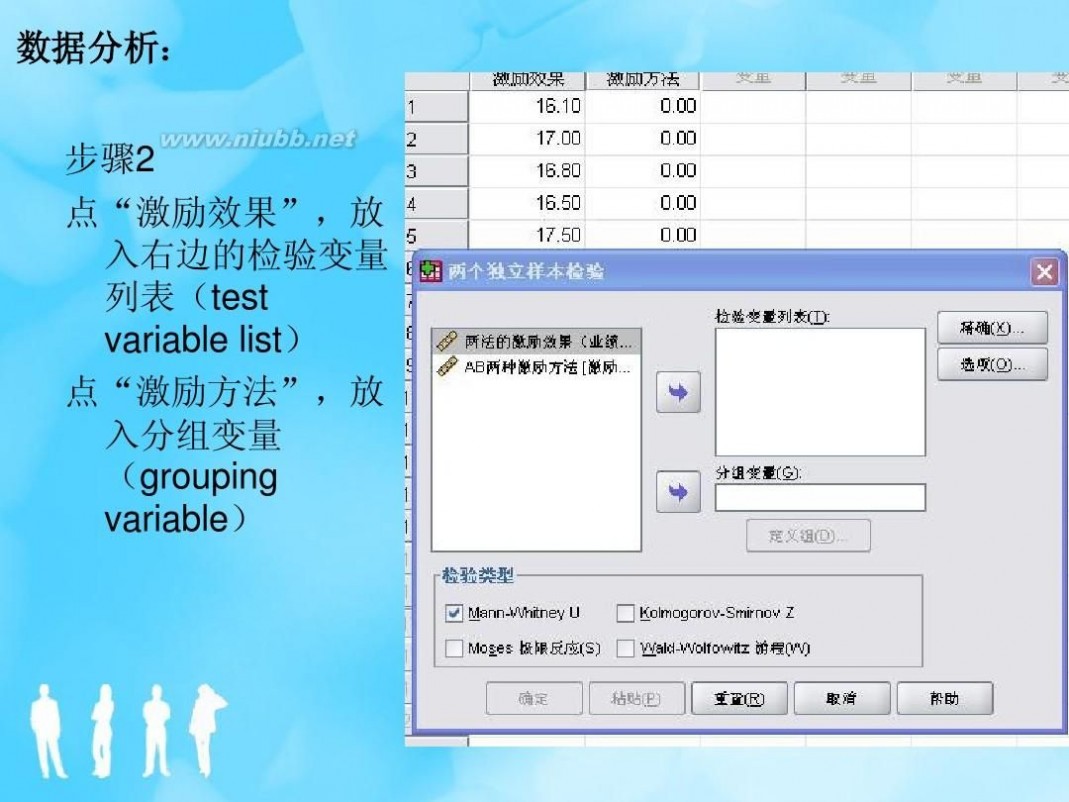
非参数假设检验 非参数假设检验
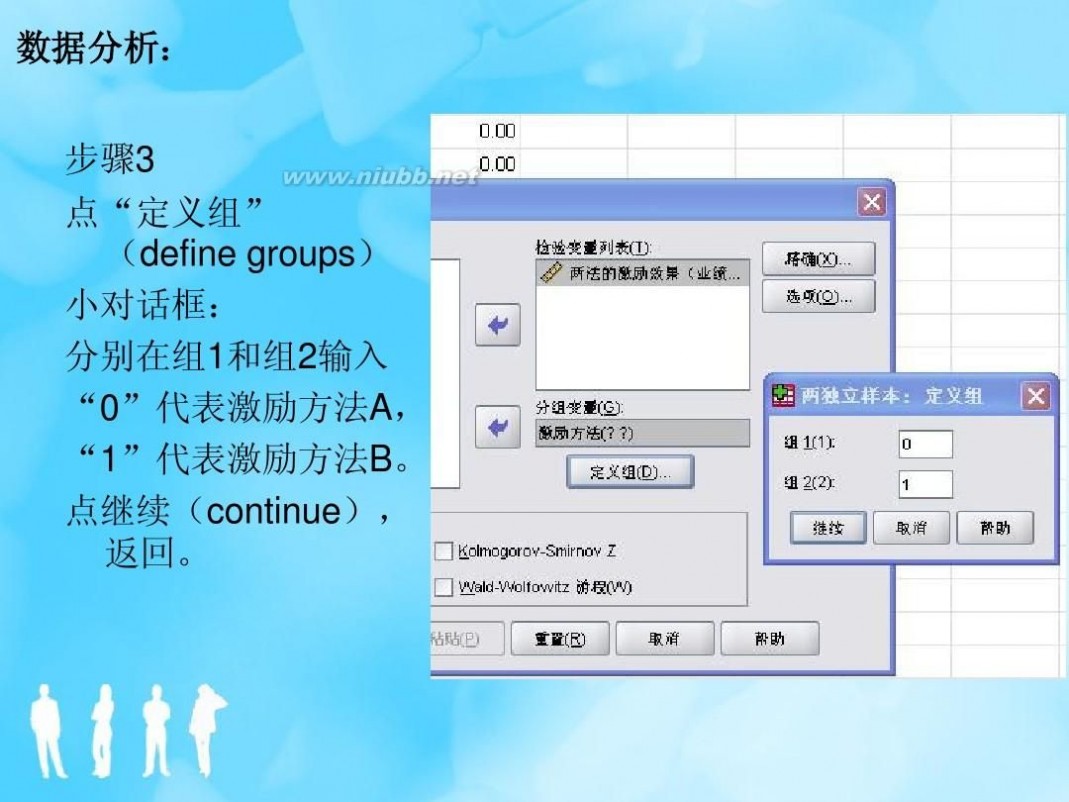
非参数假设检验 非参数假设检验
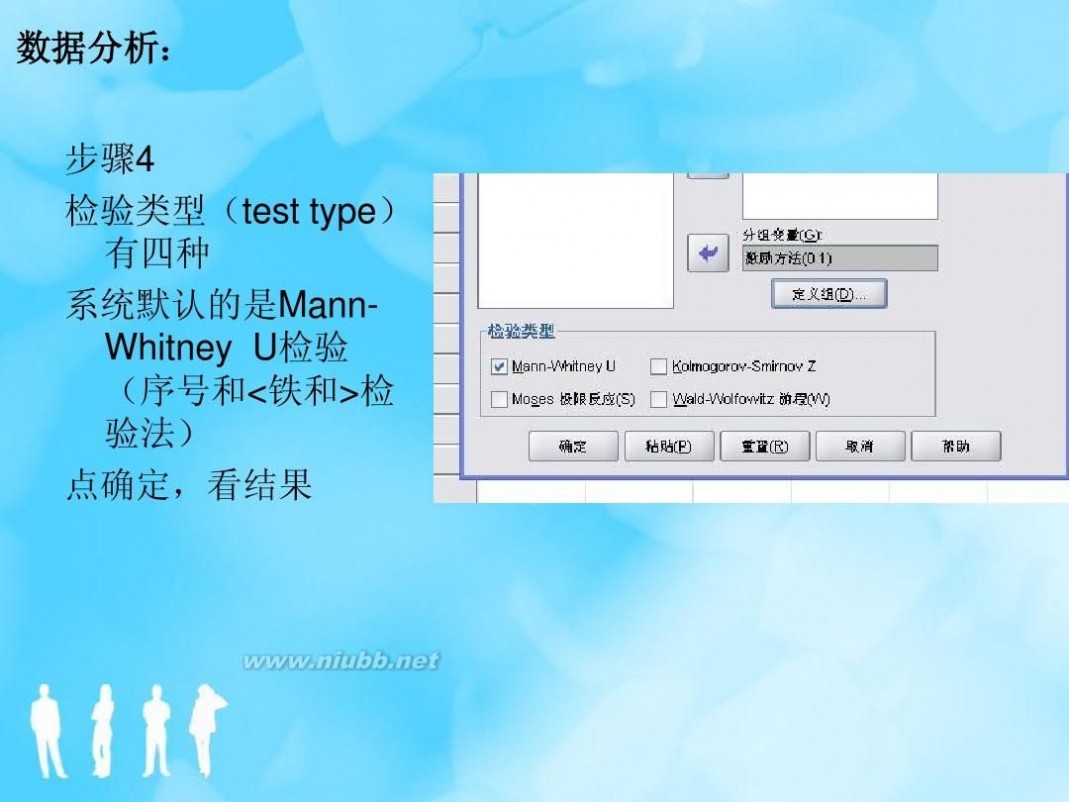
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验
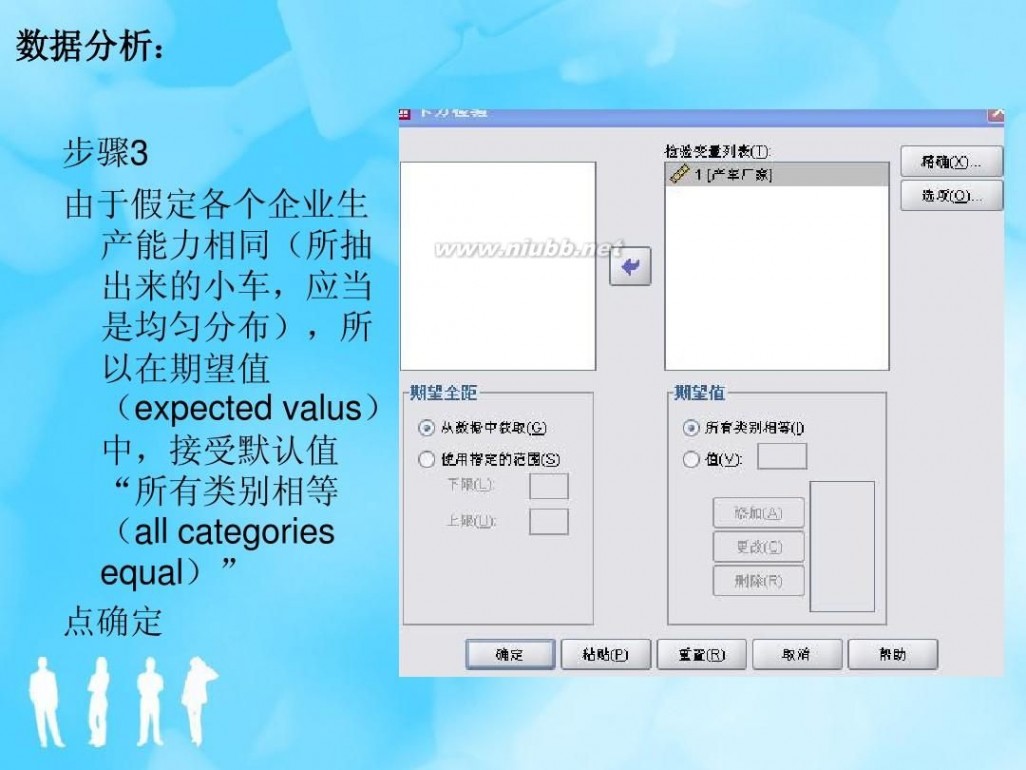
非参数假设检验 非参数假设检验
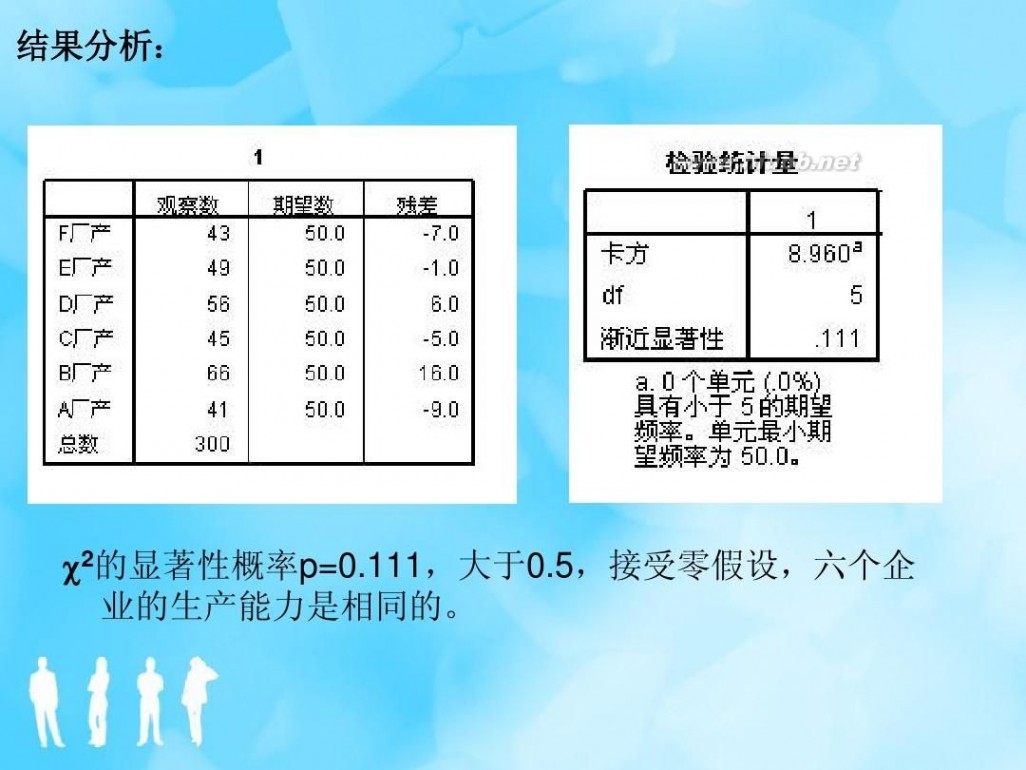
非参数假设检验 非参数假设检验
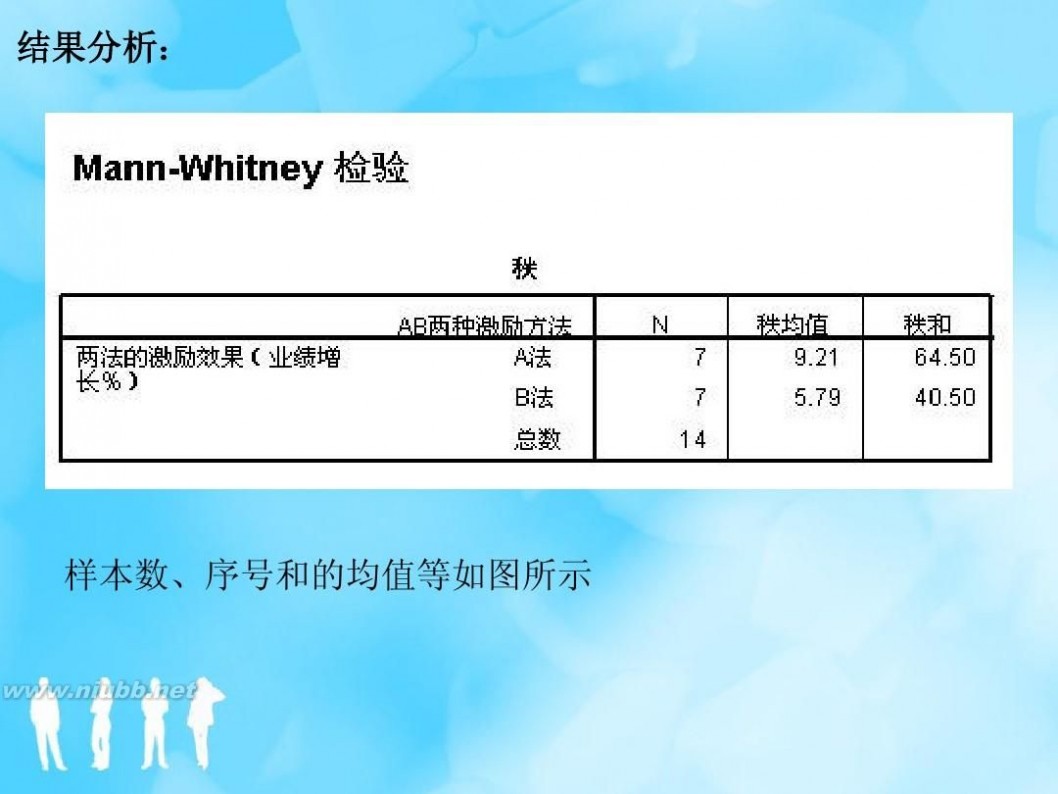
非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验
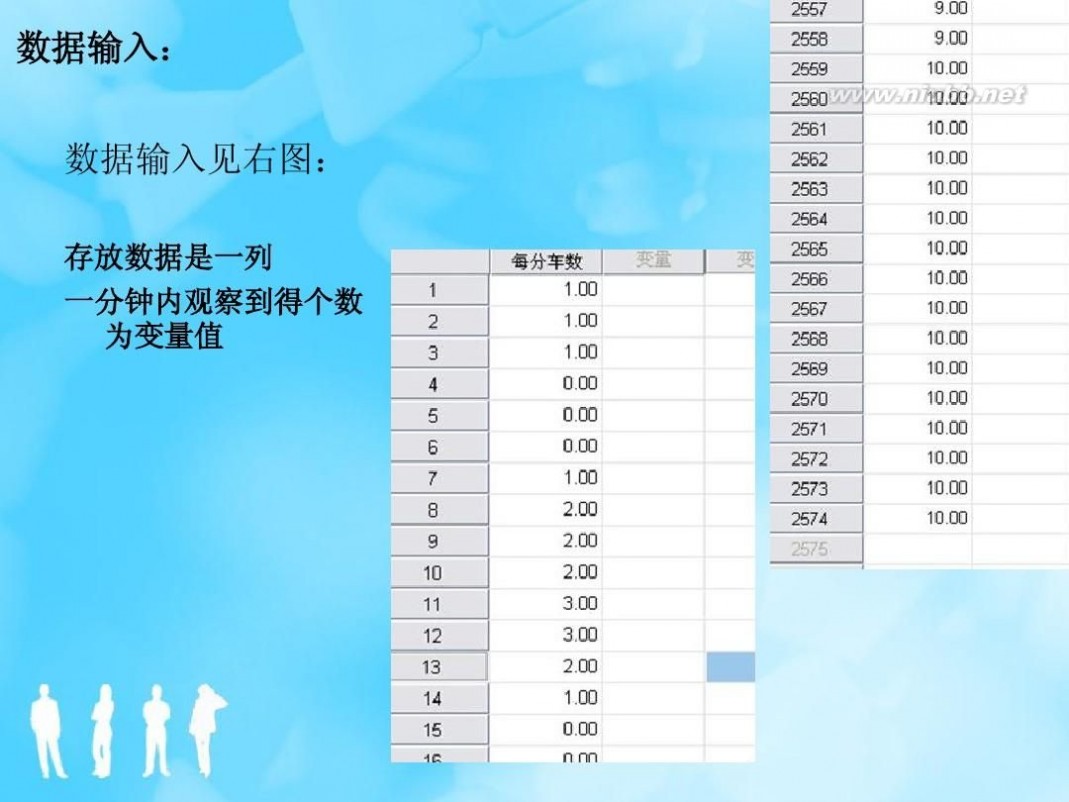
非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验
非参数假设检验 非参数假设检验

非参数假设检验 非参数假设检验

61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1