一 : 中学数学1.05的-3次方怎么计算？请列式。

中学数学

1.05的-3次方怎么计算？请列式。

---

很简单，请看下面（点击放大）：

二 : 行列式的计算方法及应用毕业论文

山西师范大学现代文理学院本科毕业论文

行列式的计算方法及应用

姓 名

系 别

专 业

班 级

学 号

指导教师

答辩日期

成 绩

张建民 数学与计算机科学 数学与应用数学 1004 1090110403 王翠红

行列式的计算方法及应用

内容摘要

科学研究、工程技术和经济活动中有许多问题可归结为线性方程组，行列式正是由研究线性方程组产生的，并成为一种重要的数学工具，因此懂得解行列式就非常重要。本文总结了行列式的十一种计算方法，并对每种方法进行例题跟踪。另外还叙述了行列式在初中代数和解析几何两个方面的应用。

【关键词】线性方程组 行列式 初中代数 解析几何

Calculating methods of determinant and its application

Abstract

Scientific research, engineering and economic activities and there are a lot of problems can be formulated as linear equations, the determinant is generated by a system of linear equations, and become an important mathematical tool, so it is very important to know the solution determinant. This paper summarizes eleven methods of calculating the determinant, and each method are examples of tracking. Also describes the determinant in the application of the two aspects of junior high school algebra and analytic geometry 【Key Words】linear equations Determinant junior high school algebra analytic Geometry

3

前言 .............................................................. 1

一、行列式的计算方法 ......................................... 3

（一）利用行列式定义计算 ........................................ 3

（二）利用行列式的性质计算 ...................................... 4

（三）化三角形法 ................................................ 4

（四）降阶法 .................................................... 5

（五）递推公式法 ................................................ 5

（六）利用范德蒙行列式 .......................................... 7

（七）加边法 .................................................... 8

（八）数学归纳法 ................................................ 8

（九）连加法 .................................................... 9

（十）拆项发 .................................................... 9

（十一）析因子法 ............................................... 10

二、行列式的应用 ............................................. 10

（一）行列式在代数中的应用 ..................................... 11

（二）行列式在几何中的应用 ..................................... 12 参考文献 ........................................................ 14 致谢 ............................................................. 15

行列式的计算方法及应用

学生姓名：张建民 指导老师：王翠虹

前言

解方程是代数中一个基本问题，特别是在中学所学代数中，解方程占有重要地位。比如说，如果一段导线的电阻为R,它两端的点位差为V,那么通过这段导线的电流强度为I,就可以用关系式表示IR?V求出来。这就是通常所谓解一元一次方程的问题。在中学所学代数中，我们解过一元、二元、三元以至四元一次方程组。下面讨论一般的多元一次方程组，即线性方程组。

对于二元线性方程组

?ax?a12x2?b1, ?111

?a21x1?a22x2?b2,

当a11a22?a12a21?0时，此方程组有唯一解，即 x1?b1a22?a21b2ab?a12b1，x2?112. a11a22?a12a21a11a22?a12a21

称a11a22?a12a21为二级行列式，用符号表示为 a11a22?a12a21?

当二级行列式 a11

a21a1222?0 a11a21a12a22.

时，该方程组有唯一解，即 b1a12a11b1

b2a22ab2,x2?21. a11a12a11a12

a21a22a21a22 x1?

对于三元线性方程组有相仿的结论。设有三元线性方程组

?a11x1?a12x2?a13x3?b1,? ?a21x1?a22x2?a23x3?b2,

?ax?ax?ax?b.3223333?311

1

称代数式a11a22a33?a12a23a31?a13a21a32?a11a23a32?a12a21a33?a13a22a31为三级行列式，用符号表示为：

a11a22a33?a12a23a31?a13a21a32?a11a23a32?a12a21a33?a13a22a31 a11a12

a22

a32a13a23. a33

a11a12

a22

a32a13a23?0 a33=a21a31 我们有：当三级行列式 d?a21a31

时，上述三元线性方程组有唯一解，解为 x1?

b1a12

a22

a32a13a11d1d2d3dd1d,x2?2,x3?3, ddda13a11a12a22a32d1d2 d3其中d1?b2b3a23 d2?a21a33a31a23 d3?a21a33a31

把这个结果推广到n元线性方程组

?a11x1?a12x2???a1nxn?b1,?ax?ax???ax?b,?2112222nn2 ? ?????an1x1?an2x2???annxn?bn

的情形。为此将要给出n级行列式的定义及计算方法。 定义?1? n级行列式 a11

a21 ?

an1a12?a1na22?a2n ??an2?ann

等于所有取自不同行不同列的n个元素的乘积

a1j1a2j2?anjn (5)

的代数和，这里j1j2?jn是1,2,?,n的一个排列，每一项(5)都按下列规则带有符号：当j1j2?jn是偶排列时，(5)带有正号，当j1j2?jn是奇排列时，(5)带负号。这一定义可以写成

2

a11

a21

?

an1a12a22??a1n?a2n??j1j2?jn?(?1)?(j1j2?jn)a1j1a2j2?anjn, an2?ann

j1j2?jn这里?表示对所有n级排列求和。

n级行列式性质：?2?

(1)把行列式的各行变为相应的列，所得行列式与原行列式相等。

(2)把行列式的两行（两列）对调，所得行列式与原行列式绝对值相等，符号相反。

(3)把行列式的某一行（或一列）的所有元素乘以某个数k，等于用数k乘原行列式。

(4)如果行列式某两行（或两列）的对应元素成比例，那么行列式等于零。

(5)如果行列式的某一行（一列）的元是二项式，那么这个行列式等于把这些二项式各取一项作成相应行（或列）而其余行（或列）不变的两个行列式的和。

(6)把行列式某一行（或列）的所有元同乘以一个数k，加到另一行（或一列）的对应元上，所得行列式与元行列式相等。

(7)行列式某一行（或一列）的各元与另一行（或一列）对应元的代数余子式的乘积的和等于零。

(8)行列式等于它的任意一行（或一列）的所有元与它们各自对应的代数余子式的乘积的和。

一、 行列式的计算方法

(一)、利用行列式定义计算

例1 计算行列式 0

0 D?0

5

解：展开式中项的一般形式是 0040030020 00

a1j1a2j2a3j3a4j4.

显然，如果j1?5，那么a1j1?0，从而这个项都等于零。因此只需考虑j1?5的 3

那些项；同理，只需考虑j2?4,j3?3,j4?2这些列指标的项。这就是说行列式不为零的项只有a14a23a32a41这一项，而?(3421)?6这一项前面的符号应该是正的。所以

D?2?3?4?5?120

（二）、利用行列式的性质计算

例2 计算n级行列式 cd

dc

d?dd

??

ddd?dd?dc?d ??d?c

解：这个行列式的特点是每一行有一个元素是c，其余n?1个是d。根据性质6，把行列式第二列加到第一列，行列式不变，再把第三列加到第一列，行列式不变??直到第n列也加到第一列，即得 c?(n?1)ddd?d

c?(n?1)dcd?d

d?c?(n?1)ddc?d

????

c?(n?1)ddddc

d

c

=?c?(n?1)d?d

??

dddc?dddddddd dc

把第二行到第n行都分别加上第一行的-1倍，就有

1dd?d

0c?dd?d

c?d?d d??c?(n?1)d?0

????

000?c?d

根据例1得 d??c?(n?1)d?(c?d)n?1

（三）、化三角形法

化三角形法是利用行列式的性质将原行列式化为上（下）三角形行列式计算的一种方法，它是计算行列式的重要方法之一。因为利用行列式的定义容易计算上（下）三角形行列式。因此，在许多情况下，总是先利用行列式的性质将其作保值变形，再将其化为三角形行列式。

例3 计算行列式

4

01

1?1 D?1?2

21

r3?r2r4?2r2

r1?r2103132 00解 D?1?1020113 ?0?13?2

031?4

1?102

r3?r20113 ?? 0041r4?3r2

00?2?r3?2r4

r3?r4 ?1?10?40113=50 00?2?13

000?25

（四）、降阶法

降阶法是按某一行（或一列）展开行列式，这样可以降低一阶，更一般地是用拉普拉斯定理，这样可以降低多阶，为了使运算更加简便，往往是先利用列式的性质化简，使行列式中有较多的零出现，然后再展开.

例5 计算行列式 3

1 D?2

2

c1?c3

c4?2c31?101342102 74解 D?40?2

11?12412010?(?1)2?323?1 34?1122212

7

23??(?1)23?1 ?0r2?2r31r1?4r30?7?6??7?673??21

（五）、递推公式法

应用行列式的性质，把一个n阶行列式表示为具有相同结构的较低阶行列式（比如，n-1阶或n-1阶与n-2阶等）的线性关系式，这种关系式称为递推关系式。根据递推关系式及某个低阶初始行列式（比如二阶或一阶行列式）的值，便 5

可递推求得所给n阶行列式的值，这种计算行列式的方法称为递推法。

例6 计算n阶行列式 41

341

??? Dn?

341

34

解 按第一列展开 31

041

4

314

314????4Dn?1?3Dn?2 3 Dn?4Dn?1?

于是有

Dn?3Dn?1?Dn?1?3Dn?2?Dn?2?3Dn?3

=??D2?3D1?1

及

Dn?Dn?1?3(Dn?1?Dn?2)?32(Dn?2?Dn?3)

=??3n?2(D2?D1)?3n

从上两式削去Dn?1，得Dn?1n?1(3?1) 2

对于形如?的所谓三角行列式，可直接展开得两项递推公式

Dn??Dn?1??Dn?2，然后采用如下一些方法求解。

方法1 如果n较小，则直接递推计算。

方法2 用第二数学归纳法：即验证n?1时结论成立，设n?k结论成立，若证明n?k?1时结论也成立，则对任意自然数结论相应也成立。

方法3 将Dn??Dn?1??Dn?2变形为Dn?pDn?1?q(Dn?1?pDn?2)，其中p?q??，?pq??

由韦达定理知p和q是一元二次方程x2??x???0的两个根。确定p和q后，令f(x)?Dn?pDn?1，利用f(n)?qf(n?1)递推求出f(n)，再由Dn?pDn?1?f(n) 6

递推求出Dn。

方法4 设Dn?xn.代入Dn??Dn?1??Dn?2?0得xn??xn?1??xn?2?0因此有x2??x???0（称为特征方程），求出其根x1和x2（假设x1?x2），则

Dn?k1x1?k2x2.这里k1,k2可通过取n?1和n?2来确定。 例4 求n阶行列式的值

0110

10

11

01

10

???1

nn

Dn?

解 按第一行展开得Dn??Dn?2，即Dn?Dn?2?0.作特征方程x2?1?0解得

x1?i,x2??i，则

Dn?a?in?b?(?i)n (1)

当n?1时，D1?0，代入(1)式得ia?ib?0;当n?2时，D2??1，代入(1)得

?a?b??1 联立求解得a?b?

11

，故Dn?in?(?i)n. 22

??

（六）、利用范德蒙行列式 例7 计算行列式

1

1x2?12

x2?x2

?

n?2

???

1xn?12

xn?xn

?

n?1

D?

x1

x1?12

x1?x1

?

n?1

?x1x2

n?1

?x2

n?2

?xn

?xn?2

解 把第1行的－1倍加到第2行，把新的第2行的－1倍加到第3行，以此类推直到把新的第n?1行的－1倍加到第n行，便得范德蒙行列式

11?1x1x2?xn222

x2?xn=?(ai?aj) D?x1

1?j?i?n

???n?1n?1n?1x1x2?xn其中“?”表示连乘号。

7

（七）、加边法

计算某些行列式有时特意把原行列式加上一行一列再进行计算，这种计算行列式的方法叫做加边法。当然，加边后要保证行列式的值不变，并且要使所得的高一阶行列式容易计算。要根据需要和原行列式的特点选取所加的行和列。加法适用于某一行（列）有一个相同的字母外，也可用于其列（行）的元素分别为n?1个元素的倍数的情况。

例8 计算行列式

?a

1

1

D?

111?b1 11?d

解 给原行列式加边

111101?a11

D?

011?b10111?d

1?1?1?1

1a0010b0100d

1

c2?c1a1

c3?c1b1

c3?c1d

?

?r1?ri

?

i?1

?

111??abd000

111a00 0b000d

=(1?（八）、数学归纳法

111

??)abd abd

首先利用不完全归纳法寻找出行列式的猜想值，再用数学归纳法给出猜想的证明。但给定一个行列式要猜想其值是比较困难的，因此数学归纳法一般是用来证明行列式等式。 例9 计算n阶行列式

x

?1x?0an?1

0?1?0

???

00?x

00??1a1?x

Dn??

0an

an?2?a2

解 用数学归纳法 当n?2时 D2?

xa2

?1x?a1

?x(x?a1)?a2

=x2?a1x?a2

8

假设n?k时，有

Dk?xk?a1xk?1?a2xk?2???ak?1x?ak

则当n?k?1时，把Dk?1按第一列展开，得

Dk?1?xDk?Dk?1

=x(xk?a1xk?1???ak?1x?ak)?ak?1 =xk?1?a1xk???ak?1x2?akx?ak?1

（九）、连加法

如果行列式中某列（行）加上其余各列（行），使该列（行）元素均相等或出现较多零，进而简化行列式的计算方法称为连加法。

例10 计算行列式

xaaa

axaa D? aaxa

aaax

解 它的特点是各列元素之和为(3a?x),因此把各行都加到第一行，然而第一行再提出(3a?x) ,得

1111

axaa D?(3a?x) aaxa

aaax

将第一行乘以(?a)分别加到其余各行，化为三角形行列式，则 11

0x?a D?(3a?x)00

0010x?a010=(3a?x)(x?a)3 0x?a

（十）、拆项发

把行列式的某一行（或列）的元素写成两数和的形式，然后利用行列式的性质5将原行列式写成两行列式之和，进而使行列式简化以便计算。 例11 算行列式

9

a1??1a2a2??2

a2

a3a3 a3??3a2a2??2

a2

a3a3 a3??3

D?

a1a1

a3

a1a2a2??2

a2

?1

解 D?a1

a1a3?0a3??30

=a1?2?3??1?(a2??2)(a3??3)?a2a3?

（十一）、析因子法

例12 算行列式

11

12?x2

D?

232323

23

1419?x2

解 由行列式D定义知为x的4次多项式，

又，当x??1时，1,2行相同，有D?0, 所以x??1为D的根。

当x??2时，3,4行相同，有D?0

所以x??2为D的根。

故D有4个1次因式：x?1,x?1,x?2,x?2 设D?a(x?1)(x?1)(x?2)(x?2)令x?0，则

11D?

221233221133

??12 即，a?1?(?1)(?2)??12，所以a??3 59

所以D??3(x?1)(x?1)(x?2)(x?2)

小结 以上是行列式计算常用的方法，在实际计算中，不同的方法适应于不同特征的行列式，如定义法一般适用于0比较多的行列式，利用性质分为直接利用和利用性质化三角形行列式，降阶法主要是利用按行（列）展开公式，一般某行或某列含有较多的零元素。每一种方法都有其各自的优点及其独特之处，因此研究行列式的解法有非常重要的意义。

二、行列式的应用

行列式是研究数学的重要工具之一，下面主要介绍行列式在代数和几何两

10

个方面的应用。

(一)、行列式在代数中的应用

（1）用行列式解线性方程组

如果线性方程组

?a11x1?a12x2???a1nxn?b1?ax?ax???ax?b?2112222nn2 ? ??????????an1x1?an2x2???annxn?bn

（其中x1,x2,?,xn代表未知量，aij(i?1,2,?,m;i?1,2,?,n)代表未知量的系数，b1,b2,?,bm带表常数项。）的系数行列式D?0,那么，这个方程组有解，并且解事唯一的，可表示为

x1?DD1D,x2?2,?,xn?n DDD

（2）用行列式因式分解

利用行列式分解因式的关键, 是把所给的多项式写成行列式的形式, 并注意行列式的排列规则. 下面列举几个例子来说明.

例13 分解因式 ab2c3?bc2a3?ca2b3?cb2a3?ba2c3?ac2b3.

解 原式=abc(bc2?b2c)?(a2c?ac2)?(ab2?a2b) =bc(c?b)?ac(a?c)?ab(c?b) =bcc1

b1?aca1

c1?ab

bcab a1bca1

=abc1?ab?bcc?a0 acb1ac?bcb?a0

=(ab?bc)(b?a)?(ac?bc)(c?a) =b(a?c)(b?a)?c(a?b)(c?a)

=abc(a?b)(c?a)(b?c)

(3)用行列式证明恒等式

我们知道, 把行列式的某一行（列）的元素乘以同一数后加到另一行（列） 11

的对应元素上, 行列式不变; 如果行列式中有一行（列）的元素全部是零, 那么这个行列式等于零. 利用行列式的这些性质, 我们可以构造行列式来证明等式和不等式.

例14 已知a?b?c?0, 求证a3?b3?c3?3abc 证明 令D?a3?b3?c3?3abc，则

ab

c

a?b?ca?b?ca?b?cc

b

ac

ba

111

?(a?b?c)cab?0

bca

D?cab?

bca

命题得证。

（二）、行列式在几何中的应用 （1）用行列式表示三角形的面积

以平面内三点P(x1,y1)，Q(x2,y2)，R(x3,y3)为顶点的?PQR的面积S是

1x22x3

x1

y11y21 y31

证明 将平面P(x1,y1),Q(x2,y2),R(x3,y3)三点扩充到三维空间，其坐标分别为(x1,y1,k)，(x2,y2,k)，(x3,y3,k)，其中k为任意常数。由此可得

?(x2?x1,y2?y1,0)，?(x3?x1,y3?y1,0)

??(0,0,

?PQR面积为

x2?x1x3?x1

y2?y1y3?y1

)

S?

?,?

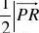
1

?

2

1x2?x1

=

2x3?x1

x2?x1x3?x1

y2?y1y3?y1

2

y2?y1

y3?y1

12

x11

=x2

2x3

y11y21 y31

（2）用行列式表示直线方程

直线通过两点P(x1,y1)和Q(x2,y2)的直线方程为

x1

y1y2?0. (1) y

x2

x证明 由两点式，我们的直线PQ 方程为

x?x2y?y2

?.

x1?x2y1?y2

将上式展开并化简，得

xy1?xy2?x1y?x2y?x2y1?xy2?0 此式可进一步变形为 x

y1y2?y

x11x21

?

x1x2

y1y2

?0

此式为行列式(1)按第三行展开所得结果，原式得证。 （3）三线共点

平面内三条互不平行的直线

a1L1,a1x?b1y?c1?0

L2,a2x?b2y?c2?0相交于一点的充要条件是a2

a3L3,a3x?b3y?c3?0

b1b2

b3

c1

c2?0. c3

（4）三点共线

平面内三点P(x1,y1)，Q(x2,y2)，R(x3,y3)在一直线的充要条件是

x1

y11y21?0. y31

x2

x3

13

参考文献

[1]北京大学数学系几何与代数教研室代数小组. 高等代数(第三版)[M]. 北京: 高等教育出社, 2003.

[2]、江苏师范学院数学系编写组编. 解析几何（第四版）[M].北京：高等教育出版社，2003

[3]、许甫华.高等代数解题方法[M].北京：清华大学出版社，2003

[4]、胡乔林.关于行列式的定义及其计算方法[M],科技信息,2007，25

[5]、张贤科,许浦华 高等代数学[M].北京 清华大学出版社，2003

[6]、毛纲源.线性代数解题方法技巧归纳[M].武汉：华中科技大学出版社，2000

[7]、万广龙. 行列式的计算方法与技巧[J]. China's Foreign Trade , 2011,(04)

[8]、周宁, 夏益斌. 行列式在解析几何中的应用[J]. 昆明冶金高等专科学校学报 , 2011,(01)

[9]、杨鹏辉.行列式的计算技巧[J]. 宜春学院学报 , 2011,(04)

[10]彭丽清. 行列式的应用[J]. 忻州师范学院学报, 2005(5), 40-41.

[11]钱吉林. 高等代数题解精粹[M]. 北京: 中央民族大学出版社, 2002.

14

致谢

本文是在王翠红老师精心指导和大力支持下完成的。王老师以其严谨求实的治学态度、高度的敬业精神、兢兢业业、孜孜以求的工作作风和大胆创新的进取精神对我产生重要影响。王老师渊博的知识、开阔的视野和敏锐的思维给了我深深的启迪。同时，在此次毕业设计过程中我也学到了许多的关于行列式方面的知识，视野得到了极大的开阔。同时我还要感谢我们班的同学，是他们的督促与指导给了我好大的动力。

另外，我还要特别感谢学校为我完成这篇论文提供了巨大的帮助，使我得以顺利完成论文。最后，再次对关心、帮助我的老师和同学表示衷心地感。

15

三 : 行列式的计算方法及应用 23

摘 要

行列式是高等代数课程里基本而重要的内容之一，在数学中有着广泛的应用，懂得如何计算行列式显得尤为重要，本文归纳了行列式的几种计算方法，并通过一些典型的例题介绍计算行列式的一些技巧。

关键词：行列式 计算方法 范德蒙行列式 解析 应用

济南大学泉城学院毕业论文

ABSTRACT

The determinant is higher algebra course in one of the important and basic content, in mathematics in a wide range of applications, know how to calculate the determinant appears especially important, this paper summarizes the determinant of several calculation method, and through some typical examples of some of the techniques introduced calculation determinant.

Key words：determinant;calculation method;vandermonde determinant;analytical;application

III

目 录

摘要………………………………………………………………………………………III ABSTRACT…………………………………………………………………………………IV 1.前言………………………………………………………………………………1 2.行列式的概念及性质……………………………………………………………………1

2.1 行列式概念……………………………………………………………………12.2 行列式性质…………………………………………………………………1 3.1化三角形法………………………………………………………………………3 3.2利用递推关系法………………………………………………………………3 3.3提取公因式法………………………………………………………………5 3.4利用拉普拉斯（Laplace）定理法…………………………………………5 3.5利用范德蒙（Vandermonde）行列式法…………………………………………6 3.6利用乘法定理法……………………………………………………7 3.7裂项法……………………………………………………………………………8 3.8升阶法…………………………………………………………………8 3.9公式法……………………………………………………………………10 3.10规律缺损补足法……………………………………………………………11 3.11特征根法 ………………………………………………………………12 3.12数学归纳法………………………………………………………………13 3.13利用行列式乘法规则…………………………………………………………14 4.应用…………………………………………………………………………………15 结论......................………….………….……………………..….……...…..….………...15参考文献......................…………….…………………..….…..……………….………….15 致谢......................………………….……………………..…….…………...…………….15

3.方法解析………………………………………………………………………………3

一、前言

行列式的计算，高等代数中重要内容之一，最常用的是利用行列式的性质和展开定理，需要熟练的掌握，根据其具体特点采用不同的计算方法，本文对行列式的解题方法进行了总结归纳。将一个行列式化为三角形行列式，是行列式计算的一个基本思想，也是化三角形法的思想精髓。行列式的另一特征便是它的递归性，即一个行列式可以用比它低阶的一系列行列式表示，于是对行列式降阶从而揭示其内部规律也是我们的一个基本想法，即递推法。这两种方法也经常一起使用。而其它方法如：提取公因式法、利用拉普拉斯（Laplace）定理法、利用范德蒙（Vandermonde）行列式法、利用乘法定理法、裂项法、升阶法、公式法、规律缺损补足法、特征根法、数学归纳法、利用行列式乘法规则等可以看成是它们衍生出的具体方法。

二、行列式的概念及性质

2.1行列式的概念

n级行列式

a11a21?an1

a12?

?a1n

?

a22?a2nan2?ann

等于所有取自不同行不同列的个元素的乘积a1j1a2j2?anjn的代数和，这里的j1j2?jn是1，2，?，n的一个排列，每一项都按下列规则带有符号：当j1j2?jn是偶排列时，带有正号；当j1j2?jn是奇排列时，带有负号。这一定义可写成

a11a21?an1

这里

j1j2?jn

a12a22?an2

?a1n?a2n

??ann

?

j1j2?jn

?(?1)

r(j1j2?jn)

a1j1a2j2?anjn

，

?

表示对所有n级排列的求和。

2.2行列式的性质

性质1 行列互换，行列式值不变，即

- 1 -

a11a21?an1

即

a11?kai1?an1

a12?

?a1n

??

a11a12?a1n

a21?an1a22?an2?

?

a2n?ann

a22?a2nan2?ann

性质2 行列式中某一行（列）元素有公因子k，则k可以提到行列式记号之外，

a11?

a12?ai2?

?a1n

??ain

?

a12?

?

a1n?

kai2?kain?kai1

???an2

?

ann

an1an2?ann

这就是说，一行的公因子可以提出去，或者说以一数乘以行列式的一行就相当于用这个数乘以此行列式。 事实上，

a11?kai1?an1

a12??an2

?

a1n??

kai2?kain=kai1Ai1+kai2Ai2+??kainAin

?

ann

=k(ai1Ai2+ai2Ai2+??ainAin)

a11??kai1

?an1

a12?ai2?

?a1n

??ain ，

?

an2?ann

令k=0，如果行列式中任一行为零，那么行列式值为零。

性质3 如果行列式中某列（或行）中各元素均为两项之和，即

aij?bij?cij(i?1,2,?,n)，则这个行列式等于另两个行列式之和。

即

a11?b1j?c1ja21?b2j?c2j?an1?

?bnj?cnj

?a1n?a2n

??ann

?

a11?b1ja21?b2j?

?

an1?bnj

?a1n?a2n

??ann

?

a11?c1ja21?c2j?

?

an1?cnj

?a1n?a2n

??ann

这就是说，如果某一行是两组数的和，那么这个行列式就等于两个行列式的和，而这两个行列式除这一行以外全与原来行列式的对应的行一样。

- 2 -

行列式的计算方法及应用 23_行列式的应用

性质4 如果行列式中有两行（列）相同，则行列式等于零。所谓的两行相同就是说两行的对应元素都相等。

性质5 如果行列式中两行（列）成比例，则行列式等于零。

性质6 如果行列式中的某一行（列）的各元素同乘数k后加到另一行（列）的对应元素上去，则行列式不变。

性质7 对换行列式中两行（列）的位置，行列式反号。

三、方法解析

3.1化三角形法

此种方法是利用行列式的性质把给定的行列式表示为一个非零数与一个三角形行列式之积，所谓三角形行列式是位于对角线一侧的所有元素全部等于零的行列式。三角形行列式的值容易求得，涉及主对角线的三角形行列式等于主对角线上元素之积，涉及次对角线的N阶三角形行列式等于次对角线上元素之积且带符号。

a

例1计算N阶行列式Dn?

bab

???

bba

n?1

???

bba

1

b?0

??

b0?

00

a?b?

bb

???

1bab

解

D??a??n?1?bn

11

???

??a??n?1?b

?a?b

???a??n?1?b???a?b? 3.2利用递推关系法

所谓利用递推关系法，就是先建立同类型n阶与n-1阶（或更低阶）行列式之间的关系——递推关系式，再利用递推关系求出原行列式的值。

a

例2 计算n阶行列式

bac

???

bba

，其中b?c,bc?0

Dn?

cc

???

解 将Dn的第一列视为（a-c）+c,0+c,……,0+c,据行列式的性质，得

- 3 -

a?c?cbac

???

bba?

a?c0?0

bac

???

bba?

ccc

bac

???

bba

Dn?

0?c?0?c

?????????

?Dn??a?c?Dn?1?ca?b

??

n?1

(1)

n?1

由b与c的对称性，不难得到Dn??a?b?Dn?1?b?a?c?联立（1），(2）解之，得

(2)

Dn??b?c?

a?b10

?1

nn

?b?c?a?b?? a?c??????

aba?b1?00

0ab?00

????

10

000?0

ab?00

???

000?aba?b

00?1

00? aba?b

例3 计算n阶行列式

Dn??

00

a?b?

?a?b

a?b?

解 将Dn按第一行展开，得Dn??a?b?Dn?1?ab00

?a?b

于是得到一个递推关系式

Dn??a?b?Dn?1?abDn?2

，变形得

Dn?bD?n1

易知

?a?

D?n1

2

?b

?? n2 ， D

3

Dn?bDn?1?a

????a

n?2

?D

2

?bDn?3??an?2

n?2

?D

n?3

?bDn?4?

?D?bD1??a

2n??

?ab?ba?b???a?b??a

??

??

所以

Dn?a?bDn?1，据此关系式再递推，有

n

n

Dn?a?b

?a

n?1

?bDn?2?a?ab?b

?

nn?12

Dn?2

n1n1

?an?a?b??a?b?

2n?2n?1

???an?an?1b????abbD1

?b

n

如果我们将

Dn的第一列元素看作a+b,1+0,……0+0,按第一列拆成两个行列式的和，

- 4 -

那么可直接得到递推关系式

Dn?a?bDn?1，同样可Dn 的值。

n

3.3提取公因式法

若行列式满足下列条件之一，则可以用此法：（1）有一行（列）元素相同，称为“a,a,?,a型”；（2）有两行（列）的对应元素之和或差相等，称为“邻和型”；（3）各行（列）元素之和相等，称为“全和型”。满足条件（1）的行列式可直接提取公因式a变为“1，1，…，1型”，于是应用按行（列）展开定理，使行列式降一阶。满足（2）和（3）的行列式都可以根据行列式的性质变为满足条件（1）的行列式，间接使用提取公因式法。

x?a1

例4计算N阶行列式

Dn?

aa

1

a

x?a

2

?

2

??

aa

nn

?

1

??

a

ni?1

2

?x?an

解 该行列式各行元素之和都等于 x+?ai，属于“全和型”，所以

1

n

??1?x??ai?Dn?

i?1??1

n

???x??ai?

i?1??

a

x?a

2

?

2

???

aa

n

1

n

a

2

?

a

n

n

??x?an

a

2

??0x?0

??x??ai?

i?1?????

00?x

?

x

n?1

3.4利用拉普拉斯（Laplace）定理法

首先，让我们先来看看拉普拉斯定理的内容：设在行列式D中任意取定了

k(1<=k<=n-1) 行，由这k 行元素所组成的一切k级子式与它们的代数余子式的乘积之和等于行列式D。

拉普拉斯定理，在计算行列式时，主要应用k=1的情形，而很少用一般形式，不过当行列式里零元素很多时，运用一般情形的拉普拉斯定理，往往会给行列式的计算带来方便。

例5 计算2n阶行列式

- 5 -

a?

?

b

ab??ba?

?

a

a

b

?

ba?b

a?ab??

解

D2n???1?

1?2n?1?2n

abba

?

?n?1?

b

?

??1?

1?21?1?n?2??n???

a1bba

2

?n?2?

???

abba

n?1

?

abba

?a?b

?

22

?

n

3.5利用范德蒙（Vandermonde）行列式法

著名的范德蒙行列式，在线性代数中占有重要地位，研究它的应用引起了一些数学家的兴趣，因此在计算行列式时，可直接用其结果。

1

1

?

2

1

例6 计算n阶行列式Dn?

x?x?1?

x1?x?1?

1

12

1x?x?1?x2?x?1?

22

2

???

x?x?1?xn?x?1?

n

n2

n

?

n?1

1

?

n?1

2

?

x1?x?1?x2?x

x??x?1?,x??x

1

1

2

?1??

xn?x

n?1

n

?1?

分析：由题目观察知，行列式除第一行外每一行具有相同的形式，第一行可视为

2

?1?,?,xn??xn?1?，再由行列式的性质，将其化为两个行

列式的和，再来计算。 解 原不等式可化为：

Dn?

xx?x?1?

11

1xx?x

2n?1

22

??1?

??

2

xx?x

nn?1

nn

?1??1?

?

n?1

1

??

x1?x?1?x2?x

?1??

xn?x

- 6 -

n

?

x?1x?x?1?

11

1n?1

1

x?1x?x?1?

22

2n?1

2

x?1x?x?1?

nn

n

x1?x?1?x2?x

?1?

xn?x

n?1

n

?1把第一个行列式从第一行起依次将i行加到i+1行；第二个行列式的第i列提取xi?1

（i=1，2，3……n），得Dn?

xx

x1x2

12

22

???

xxnxn

n2

?

n

?

n

?

n

x1x2

1

1

n

1

1

2

2

i

?????

?x?1?x?x?1?x???x?1??

x1?x?1?x2?x?1?

i?1

n?1

n?1

1

2

n

?n?

???xi???xi?1????xi?xj

i?1?i?1?1?j?i?n

x?x

nn?1

1

n

?1??1xn?x

?

n

??

3.6利用乘法定理法

在计算行列式时，有时可以用乘法定理，将给定的行列式表为两个容易计算的或已知的行列式的乘积，从而求出给定行列式的值；有时不直接计算给定的行列式，而是选一个适当的与给定行列式同阶的行列式，计算两行列式的乘积，由此求出给定行列式的值，这样也可使问题简单。

1?a1b11?a1b2?1?a1bn?a2b11?a2b2?1?a2bn

?

?

?

?

?anb11?anb2?1?anbn

例7计算n阶行列式Dn?

111

解 Dn?

???

a1a2

000

?0?0?0

1??0

100

????

1

b1b2bn

0 0

an

????

所以，当n>2时，Dn?0；

- 7 -

行列式的计算方法及应用 23_行列式的应用

当n=2时，D2??a2?a1??b2?b1?； 当n=1时，D1?1?a1b1

3.7裂项法

此法多用于将行列式某一行或某一列拆分后，行列式具有某种特殊算法

x

例8 计算Dn=

1

?...

2

??

x

?

.........

??

...

......

x

n

x

解：Dn=

1

?...?

2

??

x

?

x

+

1

?...?

2

00...

...?.........?

??

x

?

...?.........?

............

x

n

??

x??

1

=(xn??)Dn?1+

0...

???...0x2??...0

...

.........?

?

n?1i?1

?

=(xn??)Dn?1+??(xi??) （1）

同理

Dn=(xn??)Dn?1???(xj??)

i?1n?1

（2）

若???，由（1），（2）组成的方程组解得

nn

1

(xi??)???(xi??)] Dn????[??i?1i?1

若???，利用（1）递推得到：

Dn?x1?(xi??)???[?(xj??)]

i?2

i?1

j?1

j?i

n

n

n

3.8升阶法

在计算行列式时，我们往往先利用行列式的性质变换给定的行列式，再用展

添行加列使其升阶构造一个容易计算的新行列式，进而求出原行列式的值。这种 计算行列式的方法称为升阶法。凡可利用升阶法计算的行列式具有的特点是：除 主对角线上的元素外，其余的元素都相同，或任两行（列）对应元素成比例。升 阶时，新行（列）由哪些元素组成？添加在哪个位置？这要根据原行列式的特点 作出选择。

c?a1

2

a1a2

c?a2

?

2

???

a1ana2an

?

2

例9计算n阶行列式

Dn?

a2a1

?

，其中c?0

ana1ana2?c?an

分析：观察行列式可知，除主对角线外，行列式的其它元素形式都相同，于是想到用升阶法，对原行列式添加一行一列，运用行列式的性质再来求解。

10

解

Dn?

00

a1a2

2

c?a1

a1a2

2

a2a1c?a2

?

?

????

ana1ana2an

?

2

1?a1

a1a2

c

??

an

c?0 ??a20

??????an

?

c

ana1ana2?c?an

?1

将最后一个行列式的第j列的ca

j?1

倍加到第一列（j=2,3……,n+1），就可以变为上

?1

三角形行列式，其主对角线上的元素为1?c故

?ai,c,c,??,c

i?1

n

2

Dn?c?c?ai

i?1

nn?1

n

2

11

2

??????

2

1

例10 计算n阶行列式Dn??

x1x1x2x2

?

xnxnxn

2

?

n?2

x1

n?2

x2

n?2

x1

n

x2

n

xn

n

解 原行列式看似范德蒙行列式，但并不是，为了利用范德蒙行列式的结果，可以

11

????

2

11

x1x1

2

x2x2x

2n?1

xnxn

2

yy

2

Dn?

??

n?2

?

n?2

?

x1

x1

n?2

?xn??

yy

n?2

n?1

x2xn

n?1n?1

x1

n

x2

n

xn

n

y

n

按第n+1列展开，则得到一个关于y的多项式，

y

n

n?1

的系数为

??1?

n?1?n

?xDn??Dn，另外，Dn?1?1??i?xj????y?xi? j?i?ni?1

n?1

显然，Dn?1中y

n

的系数为

1?j?i?n

??x?x????x?x

i

j

1

j

2

???xn?，

?

所以Dn??xi?

i?1

1?j?i?n

??x?x

i?

3.9公式法

根据分块矩阵的知识，不难证明如下结论：

（1） 设A为n阶可逆矩阵,?,?为n维列向量，则有A????A1??（2） 设A为n阶可逆矩阵,?,?为n维列向量，则有

'

?

'

A

?1

?

?

??

?

A

AC

?A???A

BD

?

?1

?

?1

'

?

（3） 设A，B，C，D都是n阶方阵，且A可逆，则有

?AD?CAB

有些行列式可应用上述结论计算，用上述结论计算行列式的方法，我们称为公式法

11000

2?1

30

?n?1?

00?

n00?0

例11 计算n阶行列式

Dn?

?2?2?00

00

????

?2?n

?n?11?n

?12000

0?2300

00

??

00

00

?2??1?????

0030?'

??? ,?,??

?????????

????

2?n0n???0?n?11?n?

'

解 令 A=

?3?00

??

????

则由结论（2），得Dn?

1

?

A

?A1??A?

?

?1

'

?

???10

?1?

?1???2??n?11

??1?n?1?!?1??2,3,?,n???1?

?2?

????

?1??1???2??

00?

??

??

??0??1??

??0????0????

????????0??1??????n?1???0

??

n?1

1?3??1??3

?

??1?

1

?n?1?! 2

3.10规律缺损补足法

此法多用于除去某些行列或对角线的元素后行列式的各元素具有规律性，此时就须补足规律，而后再减去某些元素。

?1

例12 计算 D?

a1b2...a1bn...a2bn...

...

a2b1...

?2

...

anb1anb2...

解：（1）若 ?(?i?atbt)?0 时

i?1n

?n

???ab11?1

?D=?????

?2?a2b2

...

??a1b1????ab???21??...????n?anbn???anb1

a1b2...

...a1bn?...

a2b2...anb2...

?

a2bn?

? ...?

?anbn??

=A???'=A(1??'A?1?) (*)

?a1??b1???1?a1b1?

??????a??ab?2??b2?222??这里A?, ????, ????

??.........

???????????n?anbn??an??bn??所以(*)式

=?(?i?aibi)?a1b1?(?i?aibi)?a2b2?(?I?aibi)?...?anbn???i?aibi?

i?1

i?2

i?1

i?2

i?1

n

n

n

n?1

????????（?） （2）若存在?i?aibi ，则D?aibi???j?ajbj?

j?1j?in

这时（?）同样适用，因而（?）为计算公式.

3.11特征根法

此法用于行列式所对应矩阵的特征根已知或易求的情况下，利用A??1?2...?n，其中?i为A的特征根.

例13 已知I?A的特征根之模长均小于1，求证0?detA?2n.

证明:首先A没有零特征根，否则存在可逆阵P，使得

?0???

?2??

P?1AP??? ...

????n???

?0???

1??2?2??

所以，P?1(I?A)P=I??= ?......

????n?1??n??

所以，1为I?A的特征根矛盾.

??1?

??

?2??

设P?1AP??， ?...

????n???

行列式的计算方法及应用 23_行列式的应用

??1

所以，P?1(I?A)P?

1??2

...

1??n

所以，??i<1即1>?i-1即?i<2,所以，?1?2...?n<2n即0<detA<2n.

3.12数学归纳法

a11

例14用数学归纳法证明：Dn?1?0

01?0

a2?an

????

00?1

0b1

nn?1

b2?(?1)?aibi

i?1

?bn

解：当n?1时有：D2?

a11

0b1

?(?1)1?1a1b1 命题成立。

假设n?k时，命题成立，要证n?k?1时，等式成立。

a11

Dn?1?Dk?2?

000

a2?ak0100

????

0010

ak?100?01

0b1b2?bkbk?1

???

b按最后一行展开得：

a11

Dk?2?(?1)k?2?k?2bk?10

a11

a2?ak010

???

001

ak?10

0按最后一列展开 =(?1)1?k?1ak?1=(?1)k?2ak?1 ?0

a2?ak010

???

001

ak?10

a11

a2?ak0

?

0b1

????

0?(?1)k?1?k?2?1?01?0b2

?????0

?

1

bk

将0

???

a11

a2?ak010

???

001

0b1

b2 前k?1列?(?bi)加到最后一列 bk

(?1)?aibi

i?1k

将 0

0a1

????

a2?ak010

???

001

=

100

00?01

010

???

2k?3

按最后一列展开得：

???

000

aibi?(?1)=(?1)i??1

k

1?k?1

00

???

=(?1)

k?3

i?1

?aibi

k

所以Dk?2?(?1)

3k?6

ak?1bk?1?(?1)

?(?1)

ki?1k

k?3

i?1

?aibi

k

?(?1)?(?1)

3(k?2)

ak?1bk?1?(?1)

3(k?2)

?aibi

(k?2)

ak?1bk?1?(?1)

ki?1

(k?2)

i?1

?aibi

?(?1) ?(?1)

(k?2)

(ak?1bk?1??aibi)

k?1i?1

(k?2)

?aibi

(n?1)

i?1

因为n?k?1，所以：Dk?2?Dn?1 ?(?1)?aibi故本题得证！

n

注：本题可按行列式定义展开，也可按行或者列展开，还可将第

i?1行(i?1,2,?,n?1)乘以(?ai)都加到第1行，再按第1行展开。同

样可证得此式 3.13利用行列式乘法规则

?

例13 设D?

?2?3?4

?2?3

?4?52

,??1,但??1.求D之值。 4

???3?2

解：由??1，?5?1，有?4??3??2???1?0.

??4

??4??3??4?

??4??34?2??

??44?3??2??

???

10

111

11?41

1?411?125.

所以D?

2

??3??2??

?4

四、应用

行列式是数学研究中的一类重要的工具之一, 在线性方程组，初等代数的行列式分解因式、行列式证明不等式和恒等式，解析几何中在平面几何中的一些应用等，应用非常广泛。

总结

以上总共给出了计算行列式的13种方法，其中有一些是常见的基本的方法，还有一些是特殊的方法。在课外书中还有一些其他方法，如极限法、换元法、导数法、差分法、积分法等，因为用途不广，所以不加以介绍。

我认为只要理解和掌握以上13种方法，不管哪 种行列式的计算，都可以迎刃而解。而且一个题目有时候要由多种解法并用，或一个题可由多种方法独自解出，这就需看大家的灵活应用程度，找出一个最简便的方法解出其值。

参考文献

[1] 姚慕生.吃等代数.复旦大学出版社，2002； [2] 王萼芳 石生明.高等代数. 高等教育出版社，2003；

[3] 孙丽君. 行列式计算的几种常见的方法 河北能源职业技术学院学报[J] 2005年01期； [4] 陈会平. 浅谈N阶行列式计算方法的研究[J]. 黑龙江科技信息，2010年03期； [5] 张学茂. 行列式计算的几种新方法[J] 中国校外教育 2008

[6] 张福阁 磨晓丽 一个行列式的计算与应用[J] 齐齐哈尔大学学报 2006 [7] Bo Peng .The Determinant: a Means to Calculate Volume[J] August 16,2007

[8] Wang Quanlong The Exact Value of detV(x1,x2,x3,...,xn) and Its Applications[J] November 1998

致谢

四年的读书生活在这个季节即将划上一个句号，而于我的人生却只是一个逗号，我将

面对又一次征程的开始。四年的求学生涯在师长、亲友的大力支持下，走得辛苦却也收获满囊，在论文即将付梓之际，思绪万千，心情久久不能平静。 伟人、名人为我所崇拜，可是我更急切

地要把我的敬意和赞美献给一位平凡的人，我的导师——张长温老师。我不是您最出色的学生，而您却是我最尊敬的老师。您治学严谨，学识渊博，思想深邃，视野雄阔，为我营造了一种良好的精神氛围。授人以鱼不如授人以渔，置身其间，耳濡目染，潜移默化，使我不仅接受了全新的思想观念，树立了宏伟的学术目标，领会了基本的思考方式，从论文题目的选定到论文写作的指导,经由您悉心的点拨,再经思考后的领悟,常常让我有“山重水复疑无路,柳暗花明又一村”的感觉。

在论文即将完成之际，我的心情无法平静，从开始进入课题到论文的顺利完成，有多少可敬的师长、同学、朋友给了我无言的帮助，在这里请接受我诚挚谢意！ 同时也感谢学院为我提供良好的做毕业设计的环境。

最后再一次感谢所有在毕业设计中曾经帮助过我的良师益友和同学，以及在设计中被我引用或参考的论著的作者。

四 : 行列式的计算方法及应用毕业论文

山西师范大学现代文理学院本科毕业论文

行列式的计算方法及应用

姓 名

系 别

专 业

班 级

学 号

指导教师

答辩日期

成 绩

张建民 数学与计算机科学 数学与应用数学 1004 1090110403 王翠红

行列式的应用 行列式的计算方法及应用毕业论文

行列式的计算方法及应用

内容摘要

科学研究、工程技术和经济活动中有许多问题可归结为线性方程组，行列式正是由研究线性方程组产生的，并成为一种重要的数学工具，因此懂得解行列式就非常重要。（www.61k.com］本文总结了行列式的十一种计算方法，并对每种方法进行例题跟踪。另外还叙述了行列式在初中代数和解析几何两个方面的应用。

【关键词】线性方程组 行列式 初中代数 解析几何

行列式的应用 行列式的计算方法及应用毕业论文

Calculating methods of determinant and its application

Abstract

Scientific research, engineering and economic activities and there are a lot of problems can be formulated as linear equations, the determinant is generated by a system of linear equations, and become an important mathematical tool, so it is very important to know the solution determinant. This paper summarizes eleven methods of calculating the determinant, and each method are examples of tracking. Also describes the determinant in the application of the two aspects of junior high school algebra and analytic geometry 【Key Words】linear equations Determinant junior high school algebra analytic Geometry

3

行列式的应用 行列式的计算方法及应用毕业论文

前言 .............................................................. 1

一、行列式的计算方法 ......................................... 3

（一）利用行列式定义计算 ........................................ 3

（二）利用行列式的性质计算 ...................................... 4

（三）化三角形法 ................................................ 4

（四）降阶法 .................................................... 5

（五）递推公式法 ................................................ 5

（六）利用范德蒙行列式 .......................................... 7

（七）加边法 .................................................... 8

（八）数学归纳法 ................................................ 8

（九）连加法 .................................................... 9

（十）拆项发 .................................................... 9

（十一）析因子法 ............................................... 10

二、行列式的应用 ............................................. 10

（一）行列式在代数中的应用 ..................................... 11

（二）行列式在几何中的应用 ..................................... 12 参考文献 ........................................................ 14 致谢 ............................................................. 15

行列式的应用 行列式的计算方法及应用毕业论文

行列式的计算方法及应用

学生姓名：张建民 指导老师：王翠虹

前言

解方程是代数中一个基本问题，特别是在中学所学代数中，解方程占有重要地位。[www.61k.com)比如说，如果一段导线的电阻为R,它两端的点位差为V,那么通过这段导线的电流强度为I,就可以用关系式表示IR?V求出来。这就是通常所谓解一元一次方程的问题。在中学所学代数中，我们解过一元、二元、三元以至四元一次方程组。下面讨论一般的多元一次方程组，即线性方程组。

对于二元线性方程组

?ax?a12x2?b1, ?111

?a21x1?a22x2?b2,

当a11a22?a12a21?0时，此方程组有唯一解，即 x1?b1a22?a21b2ab?a12b1，x2?112. a11a22?a12a21a11a22?a12a21

称a11a22?a12a21为二级行列式，用符号表示为 a11a22?a12a21?

当二级行列式 a11

a21a1222?0 a11a21a12a22.

时，该方程组有唯一解，即 b1a12a11b1

b2a22ab2,x2?21. a11a12a11a12

a21a22a21a22 x1?

对于三元线性方程组有相仿的结论。设有三元线性方程组

?a11x1?a12x2?a13x3?b1,? ?a21x1?a22x2?a23x3?b2,

?ax?ax?ax?b.3223333?311

1

行列式的应用 行列式的计算方法及应用毕业论文

称代数式a11a22a33?a12a23a31?a13a21a32?a11a23a32?a12a21a33?a13a22a31为三级行列式，用符号表示为：

a11a22a33?a12a23a31?a13a21a32?a11a23a32?a12a21a33?a13a22a31 a11a12

a22

a32a13a23. a33

a11a12

a22

a32a13a23?0 a33=a21a31 我们有：当三级行列式 d?a21a31

时，上述三元线性方程组有唯一解，解为 x1?

b1a12

a22

a32a13a11d1d2d3dd1d,x2?2,x3?3, ddda13a11a12a22a32d1d2 d3其中d1?b2b3a23 d2?a21a33a31a23 d3?a21a33a31

把这个结果推广到n元线性方程组

?a11x1?a12x2???a1nxn?b1,?ax?ax???ax?b,?2112222nn2 ? ?????an1x1?an2x2???annxn?bn

的情形。［www.61k.com)为此将要给出n级行列式的定义及计算方法。 定义?1? n级行列式 a11

a21 ?

an1a12?a1na22?a2n ??an2?ann

等于所有取自不同行不同列的n个元素的乘积

a1j1a2j2?anjn (5)

的代数和，这里j1j2?jn是1,2,?,n的一个排列，每一项(5)都按下列规则带有符号：当j1j2?jn是偶排列时，(5)带有正号，当j1j2?jn是奇排列时，(5)带负号。这一定义可以写成

2

行列式的应用 行列式的计算方法及应用毕业论文

a11

a21

?

an1a12a22??a1n?a2n??j1j2?jn?(?1)?(j1j2?jn)a1j1a2j2?anjn, an2?ann

j1j2?jn这里?表示对所有n级排列求和。（www.61k.com)

n级行列式性质：?2?

(1)把行列式的各行变为相应的列，所得行列式与原行列式相等。

(2)把行列式的两行（两列）对调，所得行列式与原行列式绝对值相等，符号相反。

(3)把行列式的某一行（或一列）的所有元素乘以某个数k，等于用数k乘原行列式。

(4)如果行列式某两行（或两列）的对应元素成比例，那么行列式等于零。

(5)如果行列式的某一行（一列）的元是二项式，那么这个行列式等于把这些二项式各取一项作成相应行（或列）而其余行（或列）不变的两个行列式的和。

(6)把行列式某一行（或列）的所有元同乘以一个数k，加到另一行（或一列）的对应元上，所得行列式与元行列式相等。

(7)行列式某一行（或一列）的各元与另一行（或一列）对应元的代数余子式的乘积的和等于零。

(8)行列式等于它的任意一行（或一列）的所有元与它们各自对应的代数余子式的乘积的和。

一、 行列式的计算方法

(一)、利用行列式定义计算

例1 计算行列式 0

0 D?0

5

解：展开式中项的一般形式是 0040030020 00

a1j1a2j2a3j3a4j4.

显然，如果j1?5，那么a1j1?0，从而这个项都等于零。因此只需考虑j1?5的 3

行列式的应用 行列式的计算方法及应用毕业论文

那些项；同理，只需考虑j2?4,j3?3,j4?2这些列指标的项。(www.61k.com］这就是说行列式不为零的项只有a14a23a32a41这一项，而?(3421)?6这一项前面的符号应该是正的。所以

D?2?3?4?5?120

（二）、利用行列式的性质计算

例2 计算n级行列式 cd

dc

d?dd

??

ddd?dd?dc?d ??d?c

解：这个行列式的特点是每一行有一个元素是c，其余n?1个是d。根据性质6，把行列式第二列加到第一列，行列式不变，再把第三列加到第一列，行列式不变??直到第n列也加到第一列，即得 c?(n?1)ddd?d

c?(n?1)dcd?d

d?c?(n?1)ddc?d

????

c?(n?1)ddddc

d

c

=?c?(n?1)d?d

??

dddc?dddddddd dc

把第二行到第n行都分别加上第一行的-1倍，就有

1dd?d

0c?dd?d

c?d?d d??c?(n?1)d?0

????

000?c?d

根据例1得 d??c?(n?1)d?(c?d)n?1

（三）、化三角形法

化三角形法是利用行列式的性质将原行列式化为上（下）三角形行列式计算的一种方法，它是计算行列式的重要方法之一。因为利用行列式的定义容易计算上（下）三角形行列式。因此，在许多情况下，总是先利用行列式的性质将其作保值变形，再将其化为三角形行列式。

例3 计算行列式

4

行列式的应用 行列式的计算方法及应用毕业论文

01

1?1 D?1?2

21

r3?r2r4?2r2

r1?r2103132 00解 D?1?1020113 ?0?13?2

031?4

1?102

r3?r20113 ?? 0041r4?3r2

00?2?r3?2r4

r3?r4 ?1?10?40113=50 00?2?13

000?25

（四）、降阶法

降阶法是按某一行（或一列）展开行列式，这样可以降低一阶，更一般地是用拉普拉斯定理，这样可以降低多阶，为了使运算更加简便，往往是先利用列式的性质化简，使行列式中有较多的零出现，然后再展开.

例5 计算行列式 3

1 D?2

2

c1?c3

c4?2c31?101342102 74解 D?40?2

11?12412010?(?1)2?323?1 34?1122212

7

23??(?1)23?1 ?0r2?2r31r1?4r30?7?6??7?673??21

（五）、递推公式法

应用行列式的性质，把一个n阶行列式表示为具有相同结构的较低阶行列式（比如，n-1阶或n-1阶与n-2阶等）的线性关系式，这种关系式称为递推关系式。[www.61k.com]根据递推关系式及某个低阶初始行列式（比如二阶或一阶行列式）的值，便 5

行列式的应用 行列式的计算方法及应用毕业论文

可递推求得所给n阶行列式的值，这种计算行列式的方法称为递推法。[www.61k.com]

例6 计算n阶行列式 41

341

??? Dn?

341

34

解 按第一列展开 31

041

4

314

314????4Dn?1?3Dn?2 3 Dn?4Dn?1?

于是有

Dn?3Dn?1?Dn?1?3Dn?2?Dn?2?3Dn?3

=??D2?3D1?1

及

Dn?Dn?1?3(Dn?1?Dn?2)?32(Dn?2?Dn?3)

=??3n?2(D2?D1)?3n

从上两式削去Dn?1，得Dn?1n?1(3?1) 2

对于形如?的所谓三角行列式，可直接展开得两项递推公式

Dn??Dn?1??Dn?2，然后采用如下一些方法求解。

方法1 如果n较小，则直接递推计算。

方法2 用第二数学归纳法：即验证n?1时结论成立，设n?k结论成立，若证明n?k?1时结论也成立，则对任意自然数结论相应也成立。

方法3 将Dn??Dn?1??Dn?2变形为Dn?pDn?1?q(Dn?1?pDn?2)，其中p?q??，?pq??

由韦达定理知p和q是一元二次方程x2??x???0的两个根。确定p和q后，令f(x)?Dn?pDn?1，利用f(n)?qf(n?1)递推求出f(n)，再由Dn?pDn?1?f(n) 6

行列式的应用 行列式的计算方法及应用毕业论文

递推求出Dn。(www.61k.com)

方法4 设Dn?xn.代入Dn??Dn?1??Dn?2?0得xn??xn?1??xn?2?0因此有x2??x???0（称为特征方程），求出其根x1和x2（假设x1?x2），则

Dn?k1x1?k2x2.这里k1,k2可通过取n?1和n?2来确定。 例4 求n阶行列式的值

0110

10

11

01

10

???1

nn

Dn?

解 按第一行展开得Dn??Dn?2，即Dn?Dn?2?0.作特征方程x2?1?0解得

x1?i,x2??i，则

Dn?a?in?b?(?i)n (1)

当n?1时，D1?0，代入(1)式得ia?ib?0;当n?2时，D2??1，代入(1)得

?a?b??1 联立求解得a?b?

11

，故Dn?in?(?i)n. 22

??

（六）、利用范德蒙行列式 例7 计算行列式

1

1x2?12

x2?x2

?

n?2

???

1xn?12

xn?xn

?

n?1

D?

x1

x1?12

x1?x1

?

n?1

?x1x2

n?1

?x2

n?2

?xn

?xn?2

解 把第1行的－1倍加到第2行，把新的第2行的－1倍加到第3行，以此类推直到把新的第n?1行的－1倍加到第n行，便得范德蒙行列式

11?1x1x2?xn222

x2?xn=?(ai?aj) D?x1

1?j?i?n

???n?1n?1n?1x1x2?xn其中“?”表示连乘号。

7

行列式的应用 行列式的计算方法及应用毕业论文

（七）、加边法

计算某些行列式有时特意把原行列式加上一行一列再进行计算，这种计算行列式的方法叫做加边法。(www.61k.com)当然，加边后要保证行列式的值不变，并且要使所得的高一阶行列式容易计算。要根据需要和原行列式的特点选取所加的行和列。加法适用于某一行（列）有一个相同的字母外，也可用于其列（行）的元素分别为n?1个元素的倍数的情况。

例8 计算行列式

?a

1

1

D?

111?b1 11?d

解 给原行列式加边

111101?a11

D?

011?b10111?d

1?1?1?1

1a0010b0100d

1

c2?c1a1

c3?c1b1

c3?c1d

?

?r1?ri

?

i?1

?

111??abd000

111a00 0b000d

=(1?（八）、数学归纳法

111

??)abd abd

首先利用不完全归纳法寻找出行列式的猜想值，再用数学归纳法给出猜想的证明。但给定一个行列式要猜想其值是比较困难的，因此数学归纳法一般是用来证明行列式等式。 例9 计算n阶行列式

x

?1x?0an?1

0?1?0

???

00?x

00??1a1?x

Dn??

0an

an?2?a2

解 用数学归纳法 当n?2时 D2?

xa2

?1x?a1

?x(x?a1)?a2

=x2?a1x?a2

8

行列式的应用 行列式的计算方法及应用毕业论文

假设n?k时，有

Dk?xk?a1xk?1?a2xk?2???ak?1x?ak

则当n?k?1时，把Dk?1按第一列展开，得

Dk?1?xDk?Dk?1

=x(xk?a1xk?1???ak?1x?ak)?ak?1 =xk?1?a1xk???ak?1x2?akx?ak?1

（九）、连加法

如果行列式中某列（行）加上其余各列（行），使该列（行）元素均相等或出现较多零，进而简化行列式的计算方法称为连加法。[www.61k.com］

例10 计算行列式

xaaa

axaa D? aaxa

aaax

解 它的特点是各列元素之和为(3a?x),因此把各行都加到第一行，然而第一行再提出(3a?x) ,得

1111

axaa D?(3a?x) aaxa

aaax

将第一行乘以(?a)分别加到其余各行，化为三角形行列式，则 11

0x?a D?(3a?x)00

0010x?a010=(3a?x)(x?a)3 0x?a

（十）、拆项发

把行列式的某一行（或列）的元素写成两数和的形式，然后利用行列式的性质5将原行列式写成两行列式之和，进而使行列式简化以便计算。 例11 算行列式

9

行列式的应用 行列式的计算方法及应用毕业论文

a1??1a2a2??2

a2

a3a3 a3??3a2a2??2

a2

a3a3 a3??3

D?

a1a1

a3

a1a2a2??2

a2

?1

解 D?a1

a1a3?0a3??30

=a1?2?3??1?(a2??2)(a3??3)?a2a3?

（十一）、析因子法

例12 算行列式

11

12?x2

D?

232323

23

1419?x2

解 由行列式D定义知为x的4次多项式，

又，当x??1时，1,2行相同，有D?0, 所以x??1为D的根。[www.61k.com）

当x??2时，3,4行相同，有D?0

所以x??2为D的根。

故D有4个1次因式：x?1,x?1,x?2,x?2 设D?a(x?1)(x?1)(x?2)(x?2)令x?0，则

11D?

221233221133

??12 即，a?1?(?1)(?2)??12，所以a??3 59

所以D??3(x?1)(x?1)(x?2)(x?2)

小结 以上是行列式计算常用的方法，在实际计算中，不同的方法适应于不同特征的行列式，如定义法一般适用于0比较多的行列式，利用性质分为直接利用和利用性质化三角形行列式，降阶法主要是利用按行（列）展开公式，一般某行或某列含有较多的零元素。每一种方法都有其各自的优点及其独特之处，因此研究行列式的解法有非常重要的意义。

二、行列式的应用

行列式是研究数学的重要工具之一，下面主要介绍行列式在代数和几何两

10

行列式的应用 行列式的计算方法及应用毕业论文

个方面的应用。［www.61k.com]

(一)、行列式在代数中的应用

（1）用行列式解线性方程组

如果线性方程组

?a11x1?a12x2???a1nxn?b1?ax?ax???ax?b?2112222nn2 ? ??????????an1x1?an2x2???annxn?bn

（其中x1,x2,?,xn代表未知量，aij(i?1,2,?,m;i?1,2,?,n)代表未知量的系数，b1,b2,?,bm带表常数项。）的系数行列式D?0,那么，这个方程组有解，并且解事唯一的，可表示为

x1?DD1D,x2?2,?,xn?n DDD

（2）用行列式因式分解

利用行列式分解因式的关键, 是把所给的多项式写成行列式的形式, 并注意行列式的排列规则. 下面列举几个例子来说明.

例13 分解因式 ab2c3?bc2a3?ca2b3?cb2a3?ba2c3?ac2b3.

解 原式=abc(bc2?b2c)?(a2c?ac2)?(ab2?a2b) =bc(c?b)?ac(a?c)?ab(c?b) =bcc1

b1?aca1

c1?ab

bcab a1bca1

=abc1?ab?bcc?a0 acb1ac?bcb?a0

=(ab?bc)(b?a)?(ac?bc)(c?a) =b(a?c)(b?a)?c(a?b)(c?a)

=abc(a?b)(c?a)(b?c)

(3)用行列式证明恒等式

我们知道, 把行列式的某一行（列）的元素乘以同一数后加到另一行（列） 11

行列式的应用 行列式的计算方法及应用毕业论文

的对应元素上, 行列式不变; 如果行列式中有一行（列）的元素全部是零, 那么这个行列式等于零. 利用行列式的这些性质, 我们可以构造行列式来证明等式和不等式.

例14 已知a?b?c?0, 求证a3?b3?c3?3abc 证明 令D?a3?b3?c3?3abc，则

ab

c

a?b?ca?b?ca?b?cc

b

ac

ba

111

?(a?b?c)cab?0

bca

D?cab?

bca

命题得证。［www.61k.com]

（二）、行列式在几何中的应用 （1）用行列式表示三角形的面积

以平面内三点P(x1,y1)，Q(x2,y2)，R(x3,y3)为顶点的?PQR的面积S是

1x22x3

x1

y11y21 y31

证明 将平面P(x1,y1),Q(x2,y2),R(x3,y3)三点扩充到三维空间，其坐标分别为(x1,y1,k)，(x2,y2,k)，(x3,y3,k)，其中k为任意常数。由此可得

?(x2?x1,y2?y1,0)，?(x3?x1,y3?y1,0)

??(0,0,

?PQR面积为

x2?x1x3?x1

y2?y1y3?y1

)

S?

?,?

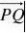
1

?

2

1x2?x1

=

2x3?x1

x2?x1x3?x1

y2?y1y3?y1

2

y2?y1

y3?y1

12

行列式的应用 行列式的计算方法及应用毕业论文

x11

=x2

2x3

y11y21 y31

（2）用行列式表示直线方程

直线通过两点P(x1,y1)和Q(x2,y2)的直线方程为

x1

y1y2?0. (1) y

x2

x证明 由两点式，我们的直线PQ 方程为

x?x2y?y2

?.

x1?x2y1?y2

将上式展开并化简，得

xy1?xy2?x1y?x2y?x2y1?xy2?0 此式可进一步变形为 x

y1y2?y

x11x21

?

x1x2

y1y2

?0

此式为行列式(1)按第三行展开所得结果，原式得证。[www.61k.com］ （3）三线共点

平面内三条互不平行的直线

a1L1,a1x?b1y?c1?0

L2,a2x?b2y?c2?0相交于一点的充要条件是a2

a3L3,a3x?b3y?c3?0

b1b2

b3

c1

c2?0. c3

（4）三点共线

平面内三点P(x1,y1)，Q(x2,y2)，R(x3,y3)在一直线的充要条件是

x1

y11y21?0. y31

x2

x3

13

行列式的应用 行列式的计算方法及应用毕业论文

参考文献

[1]北京大学数学系几何与代数教研室代数小组. 高等代数(第三版)[M]. 北京: 高等教育出社, 2003.

[2]、江苏师范学院数学系编写组编. 解析几何（第四版）[M].北京：高等教育出版社，2003

[3]、许甫华.高等代数解题方法[M].北京：清华大学出版社，2003

[4]、胡乔林.关于行列式的定义及其计算方法[M],科技信息,2007，25

[5]、张贤科,许浦华 高等代数学[M].北京 清华大学出版社，2003

[6]、毛纲源.线性代数解题方法技巧归纳[M].武汉：华中科技大学出版社，2000

[7]、万广龙. 行列式的计算方法与技巧[J]. China's Foreign Trade , 2011,(04)

[8]、周宁, 夏益斌. 行列式在解析几何中的应用[J]. 昆明冶金高等专科学校学报 , 2011,(01)

[9]、杨鹏辉.行列式的计算技巧[J]. 宜春学院学报 , 2011,(04)

[10]彭丽清. 行列式的应用[J]. 忻州师范学院学报, 2005(5), 40-41.

[11]钱吉林. 高等代数题解精粹[M]. 北京: 中央民族大学出版社, 2002.

14

行列式的应用 行列式的计算方法及应用毕业论文

致谢

本文是在王翠红老师精心指导和大力支持下完成的。(www.61k.com］王老师以其严谨求实的治学态度、高度的敬业精神、兢兢业业、孜孜以求的工作作风和大胆创新的进取精神对我产生重要影响。王老师渊博的知识、开阔的视野和敏锐的思维给了我深深的启迪。同时，在此次毕业设计过程中我也学到了许多的关于行列式方面的知识，视野得到了极大的开阔。同时我还要感谢我们班的同学，是他们的督促与指导给了我好大的动力。

另外，我还要特别感谢学校为我完成这篇论文提供了巨大的帮助，使我得以顺利完成论文。最后，再次对关心、帮助我的老师和同学表示衷心地感。

15

五 : 行列式的计算方法和技巧大总结

计算n阶行列式的若干方法举例

1．利用行列式定义直接计算

例 计算行列式 ?010?200??? Dn??

n?1?000

0?00n

解 Dn中不为零的项用一般形式表示为 a1n?1a2n??an?1an. 21n?n!

(n?1)(n?2)

该项列标排列的逆序数t（n－1 n－2…1n）等于， 2故Dn?(?1)(n?1)(n?2)

2n!.

x?2x?1x?2x?3

2x?22x?12x?22x?3

3x?33x?24x?53x?5

4x4x?35x?74x?32．利用行列式的性质计算 （1999数二（5）题）记行列式为f(x)，则方程f(x)?0的根的个数为

（ ）

(A)1. (B)2. (C)3. (D)4.

求解：

x?2x?1x?2x?3

2x?22x?12x?22x?3 f(x)?3x?33x?24x?53x?5

4x4x?35x?74x?3

x?210?1

2x?210?1 ?3x?31x?2?2

4x?3x?7?3

x?2100

2x?2100x?2x?2?1??3x?31x?2?12x?2x?7?64x?3x?7?6

? xx?2?1?(?x)(?5)(x?2?1)?5x(x?1) 2x?5?5

1

行列式的计算方法 行列式的计算方法和技巧大总结

故

f(x)?5x(x?1)?0有两个根，故应选(B).

a10

四阶行列式

0b4

0a2b300b2a30

b100a4

的值等于 （ ）

(A)a1a2a3a4?b1b2b3b4. (B)a1a2a3a4?b1b2b3b4. (C)(a1a2?b1b2)(a3a4?b3b4). (D)(a2a3?b2b3)(a1a4?b1b4).

求解：

a2

原式?

b2a30

0a4

0b4

a2b30

b2

a3?a1a40

a1b3

0?b10

a2b3

b2a3

?b1b4

a2b3

b2a3

?(a2a3?b2b3)(a1a4?b1b4)。(www.61k.com］

故选(D)。

（1999西安电子科大） 计算n?1阶行列式

Dn?1

1?11

其中，ai求解：

第一列提取?1，第i列提取ai(i

1a100

1?100

0?a2?0

????

?an

?0，i?1,2,?,n。

?1,2,?,n)，得

1a1

?110?1?1

00??

1a2010

1an

?0???

01

Dn?1??a1a2?an

???

再将第2,3,?,n?1列都加到第1列，然后按第1列展开得

n

Dn?1??a1a2?an?

i?1

1ai

。

（2005数一（6）题）设?1，?2，?3均为维列向量，记矩阵

A?(?1,?2,?3)，B?(?1??2??3,?1?2?2?4?3,?1?3?2?9?3)。

2

行列式的计算方法 行列式的计算方法和技巧大总结

如果

A?1，那么B?_____。（www.61k.com］

B转化为A计算，或将B的每个列向量用A的列向量现行表示。

利用行列式的性质将求解： 方法一： 利用行列式性质

B?1??2??3,?1?2?2?4?3,?1?3?2?9?3

?1??2??3,?2?3?3,2?2?8?3

?1??2??3,?2?3?3,2?3?2?1??2??3,?2?3?3,?3

?2?1??2,?2,?3?21,?2,?3

因

例： 一个n阶行列式反对称行列式为零. 证明：由aij

A??1,?2,?3?1，故B?2。

Dn?aij

的元素满足

aij??aji,i,j?1,2,?,n, 则称Dn为反对称行列式， 证明：奇数阶

??aji知aii??aii，即aii?0,i?1,2,?,n

0?a12

a120?a23??a2n

a13a230?

?a1n?a2n?a3n??

，由行列式的性质

故行列式

Dn可表示为

Dn??a13

??a1n

A?A?

，

?a3n?

0a12

Dn?a13

?a1n

?a120a23?a2n

?a13??a1n?a23??a2n0?a3n

0?a12

a120?a23??a2n

a13a230?

?a1n?a2n?a3n??

??a3n?(?1)n?a13????0?a1n

?(?1)nDn

?a3n?

当n为奇数时，得Dn =－Dn，因而得Dn = 0. 1．试证明

b?cb1?c1b2?c2

c?ac1?a1c2?a2

a?ba2?b2

aa2

bb1b2

cc1c2

证明：先用行列式的加法性质拆第一列，再用初等变换化简得

a1?b1?2a1

3

行列式的计算方法 行列式的计算方法和技巧大总结

b左?b1

b2

b?b1

b2

b?b1

b2

c?ac1?a1c2?a2

cc1c2cc1c2

a

a?ba2?b2

ca1?c1a2c2a

ba1?b1a2b2

cc2aa1a2cc1c2

c?ac1?a1c2?a2bb1b2a

a?ba1?b1a2?b2

b?b1

b2

c?ac1?a1c2?a2

aa2

cc2

aa1a2

a?ba1?b1a2?b2

a1?b1?c1a1?c1

bcc1c2

aa1a2

=右

a1 ?2b1

b2a2

2．计算n阶行列式

a1?b1

Dn?

a2?b1

a1?b2?a1?bn

a2?b2?a2?bn

??

an?b1an?b2?an?bn

解：当n=1时，D1=a1+b1 ，

当n=2时，D2=（a1+b1）（a2+b2）-（a1+b2）（a2+b1） =（a1-a2）（b1-b2）

当n≥3时,将第一行乘（-1）加到其余各行后，可得这些行对应成比例，即

a1?b1

a2?a1

Dn?a3?a1

?an?a1

综上所述

a1?b2?a1?bna2?a1?a2?a1

a3?a1?a3?a1?0 ?

?

an?a1?an?a1

a1?b1,n?1??

Dn??(a1?a2)(b1?b2),n?2 。［www.61k.com）

?0,n?3?

3． n阶行列式D中每一个元素aij分别用数bi-j(b≠0)去乘得到另一个行列式D1 ，试证明D1=D 。 证明： 首先将行列式D的每行分别提出b1,b2…,bn，再由每列分别提出b-1,b-2…,b-n可得

D1?

a11b1?1a21b2?1a12b1?2?a1nb1?na22b2?2?a2nb2?n

???an1bn?1an2bn?2?annbn?n

a11b1b?1?a21b2b?1

a12b1b?2?a1nb1b?n

a22b2b?2?a2nb2b?n

???an1bnb?1an2bnb?2?annbnb?n

4

行列式的计算方法 行列式的计算方法和技巧大总结

a1

11b?a2

12b??a1nb?n

?2

?(b1b2?bn)a21b?1a22b?an

2nb?

??? a?1

n1ba2n

n2b??annb?

a11a12?a1n

?(b1b2?bn)(b?1b?2?b?n)a21a22?a2n

???

an1an2?ann

a11a12?a1n

?a21a22?a2n????D an1an2?ann

12345

55533

4．已知A?32542,求

61阅读提醒您本文地址：

22211

46523

（1）A51+2A52+3A53+4A54+5A55；

（2）A31+A32+A33及A34+A35 。（www.61k.com］ 解：由行列式的性质可知

12345

55533

(1) A51+2A52+3A53+4A54+5A55=32542?0

22211

12345

(2)

12345

55533

5A31+5A32+5A33+3A34+3A35 =55533?0

22211

46523

12345

55533

2A31+2A32+A33+A34+A35 =22211?0

22211

46523

解出A31+A32+A33=0，A34+A35 =0 。

3．化为三角形行列式 5

行列式的计算方法 行列式的计算方法和技巧大总结

若能把一个行列式经过适当变换化为三角形，其结果为行列式主对角线上元素的乘积。[www.61k.com）因此化三角形是行列式计算中的一个重要方法。

化三角形法是将原行列式化为上（下）三角形行列式或对角形行列式计算的一种方法。这是计算行列式的基本方法重要方法之一。因为利用行列式的定义容易求得上（下）三角形行列式或对角形行列式的性质将行列式化为三角形行列式计算。

原则上，每个行列式都可利用行列式的性质化为三角形行列式。但对于阶数高的行列式，在一般情况下，计算往往较繁。因此，在许多情况下，总是先利用行列式的性质将其作为某种保值变形，再将其化为三角形行列式。

（2001西安电子科大）

计算n阶行列式

ycDn?

ccc

求解：

将第n行乘以(?1)分别加到第2,3,?,n?1行，得

bxaaa

baxaa

?????

baaxa

baaax

?????

y0Dn?

00c

再将第2列，?，第n?1列都加到第n列，得

bx?a0?0a

b0?0a

????

b00?a

ba?xa?x?x

x?a?

?x?aa?x

6

行列式的计算方法 行列式的计算方法和技巧大总结

按第一列展开，

2.（2004华东理工）

1

计算行列式的值1

1

求解：

方法一：化三角形 ybb?b(n?1)b0x?a0?00D00x?a?00n?????? 000?x?a0caa?ax?(n?2)ax?a0?000x?a?00Dn?y????? 00?x?a0aa?ax?(n?2)a bb?b(n?1)bx?a0?00?(?1)n?1c0x?a?00 ?????00?x?a0?y(x?a)n?2?x?(n?2)a??(?1)n?1c(n?1)b(x?a)n?2(?1)n?(x?a)n?2?y(x?(n?2)a)?(n?1)bc? 11?1a10?00a2?0，其中a1,a2,?,an都不为0。(www.61k.com] ???00?an011aa?1aD11102n?0n?1?a1a2?an101?0 ????100?1?111a?1???1?11a2aaaa?0n1102n?0n001?0??aj j?1????000?17 ?

行列式的计算方法 行列式的计算方法和技巧大总结

??aj(??

j?1

i?1

nn

1)。(www.61k.com］ ai

方法二：化三角形

??

i?1

n

1ai

1a1

1a2

?1

??aj(??

j?1

i?1

n

n

Dn?1?

1) ai

?

an

a1??

计算下面行列式的值

a2

?

anan?

a1?a1

a2?????a2

?an??

求解：

升阶化三角形。

10

Dn?0

1a1?1?1

各行减去第一行

a1a1??a1?a1

a2

?

ananan?

a2?a2????a2

?

?an??

a20?an?0

??10?2?0??????1

n

0ai

0a1

?n

a2

?an

??

i?1

?

?i

?1

?2

?

??1?2??n(1??

i?1

n

ai

?i

)。

?n

2.（2003华南师大）

a11?x

证明行列式等式

a12?x?a1n?x?

?

?

?A?x??Aij

i?1j?1n

n

a21?xa22?x?a2n?x?

an1?xan2?x?ann?x

8

行列式的计算方法 行列式的计算方法和技巧大总结

其中A?aij，Aij是aij在aij中的代数余子式。(www.61k.com)

求解：

升阶法。 1xx?x1xx

a12

a22?x 0a11?xa12?x?a1n?x?1a11左边?0a21?xa22?x?a2n?x??1a21?a1n?a2n

????????

0an1?xan2?x?ann?x?1an1an2?ann

a11a12?a1n?1a12?a1n

（按第一行展开）?a21a22?a2n?1a22?a2n

????x??????

an1an2?ann?1an2?ann

?1a11?a1,n?1

(?1)1?(n?1)x?1a12?a2,n?1

??? ?1an1?an,n?1

a11a12?a1n

（从第二项开始均按第一列展开）?a21a22?a2n

???

an1an2?ann

nnn

?x?Ai1?x

i?1?Ai2???xi?1?Ain i?1

a11a12?a1n

?a21a22?a2nnn

????x??Aij=右边

i?1j?1

an1an2?ann

1?12?31

?33?79?5

例1 计算行列式D?204?21．

3?57?146

4?410?102

解 这是一个阶数不高的数值行列式，通常将它化为上（下）三角行列式来计算． ?2??3?1??3??2?1?1?12?311?12?311?4??3?1??5??4?1?00?10?20204?1D 0204?1?2???3? ?00?10?2?4???2?0

?0

0?21?530?21?5300022?20022?20

9 -12-32040-1001-10221-1-22-2

行列式的计算方法 行列式的计算方法和技巧大总结

?4???3??5??2?3?

1?10 ?000

3000

20?100

?340

11?1

2000

20?100

?340

1

?1

?2??1?2??1???1???6??12 .

?10?5??2?4?

?0?2

00

?102?6?100?6

?a1a1

例2

计算n阶行列式D

a21?a2a2?a2

a3a3?a3

???

ananan?

．

?a1

?a1

1?a3?

?1?an

解 这个行列式每一列的元素，除了主对角线上的外，都是相同的，且各列的结构相似，因此n列之和全同．将第2，3，…，n列都加到第一列上，就可以提出公因子且使第一列的元素全是1．

61阅读提醒您本文地址：

??a1?a2???an?

?1???i?

a2a3

?

ananan?

n

1

a2a3

?

ananan?

??a1?a2???an?1?a2a3?

D ??a1?a2???an?a21?a3?i?2,?,n

????

??a1?a2???an?

10

a21

a2

a3

a3?an0?0

11?a2a3?

????1??ai?1a21?a3?

i?1??

???

1

a2

a3

?1?an?1?an

nnn ?i???1? ????

?1??ai?001?0??1??ai??1?1??ai .i?2,?,n?i?1i?1i?1???

????000?1

ab

例3 计算n阶行列式

bab

bba

???

bbb

D?b

????bbb?a

解：这个行列式的特点是每行（列）元素的和均相等，根据行列式的性质，把第2，3，…，n列都加到第1列上，行列式不变，得

a?(n?1)ba?(n?1)bD?a?(n?1)b

bab

bba

???

b

1bb?b

1ab?bb

b?[a?(n?1)b]1ba?b

?????????

1bb?aa?(n?1)bbb?a

10

行列式的计算方法 行列式的计算方法和技巧大总结

1

?[a?(n?1)b]0

bb?b00

a?b0?0a?b??0

?0

?[a?(n?1)b](a?b)n?1

???a?b

例4：浙江大学2004年攻读硕士研究生入学考试试题第一大题第2小题（重庆大学2004年攻读硕士研究生入学考试试题第三大题第1小题）的解答中需要计算如下行列式的值：

123?n?1234?

Dn?345?

n1

n12

?????n12?n?2n?1

[分析]显然若直接化为三角形行列式，计算很繁，所以我们要充分利用行列式的性质。(www.61k.com]注意到从第1列开始；每一列与它一列中有n-1个数是差1的，根据行列式的性质，先从第n-1列开始乘以－1加到第n列，第n-2列乘以－1加到第n-1列，一直到第一列乘以－1加到第2列。然后把第1行乘以－1加到各行去，再将其化为三角形行列式，计算就简单多了。

解：

12Dn?3

?

111?

1?1?????n

11?1000?0

??n?

??

11?n1?100?00

0?n0?00?

(i?2,?,n)ri?r1

112?

100?

1?0??

10?00?00

1?n0?0?n0?00

1?1?n0??n

n1?n1?

11n

2?n?2n?1

n?1?n0?

1n(n?1)??n2

?n0

00??n?0

??

(i?2,?,n)r1?

1nri

??n

??n

(n?1)(n?2)

1n(n?1)???(?n)n?1?(?1)2n2

n(n?1)

(n?1)n?1??n???1?2

2

（2000西安电子科大）

计算n阶行列式

11

行列式的计算方法 行列式的计算方法和技巧大总结

11Dn?1

21x

321

432

?n

?n?1?n?2

?1

????1xxx?

求解：

从Dn的第2列开始，每行乘以(?1)往上一行加，得

00Dn?

001

11?x0?0x1

111?x?0x

1110x111

???

111?x111

111?11111

??

????

?1?x

1

?x1

?(?1)n?101?x

?0x

?0

????0?1?x100x

???

000

000

?xx

?(?1)n?101?x

?0

?0

????0?1?x1

?(?1)n?1xn?2

4．降阶法（按行（列）展开法）

降阶法是按某一行（或一列）展开行列式，这样可以降低一阶，更一般地是用拉普拉斯定理，这样可以降低多阶，为了使运算更加简便，往往是根据行列式的特点，先利用列式的性质化简，使行列式中有较多的零出现，然后再展开。[www.61k.com）

1

2

例1、计算20阶行列式D20?3

212

321

?181920?171819?161718

?3

?2

?1

???

201918?

[分析]这个行列式中没有一个零元素，若直接应用按行（列）展开法逐次降阶直至化许许多多个2阶行列式计算，需进行20！*20－1次加减法和乘法运算，这人根本是无法完成的，更何况是n阶。但若利用行列式的性质将其化为有很多零元素，则很快就可算

12

行列式的计算方法 行列式的计算方法和技巧大总结

出结果。（www.61k.com)

注意到此行列式的相邻两列（行）的对应元素仅差1，因此，可按下述方法计算：

解：

1

D20

2?3

212

321

?1819?1718?1617

?3122?00?2122?00

2019

ci?1?ci

18?11

123?1920

1?1?

11?

??111?

111?

111?

?1?1??1?1??1?1?

???

201918?

1

(i?2,?,20)

(i?1,?19)

?1?11?1?1?1

100?00

1?2?0??

0?0?

ri?r1

34?2021

22

?21?(?1)20?1?218??21?2

18?20

a00?010a0?00

例2 计算n阶行列式Dn

?

00a?00???

??

000?a0100?0a

13

行列式的计算方法 行列式的计算方法和技巧大总结

a00?00a0?0

解 将Dn按第1行展开

0a0?000a?0Dn?a00a?0?(?1)n?1????

????

000?a

000?a100?0

?an?(?1)n?1(?1)nan?2?an?an?2.

a0D?0

0a0

00a

???

000

100

例3 计算n（n≥2）阶行列式

?????100?0a

a

?

．

a0?0

00a?0

0a?001?n

D?a??1??????解 按第一行展开，得

????

000?a

00?0a

100?0

再将上式等号右边的第二个行列式按第一列展开，则可得到

．

D?a???1?

n

1?n

??1?

00a0

?n?1??1

00ba

an?2?an?an?2?an?2?a2?1?．

a0

求n阶行列式?

ba00

0b00

????

?????

0b

求解： 利用降阶法

ab?000a?00

按第一列展开Dn

b0?00ab?00

61阅读提醒您本文地址：

?

??

?a???

??b(?1)n?1?

00?ab00?0a00?b000?ab

?an?(?1)n?1bn

一道题目可以有不同的方法来解答，另外还有一种方法就是直接用定义。(www.61k.com]由行列式的定义知此行列式除项a11a22?ann和

a12a23?an?1,nan1外其余乘积项都是零，故Dn?(?1)?(12?n)a?a?a?(?1)?(23?n1)b?b?b?an?(?1)n?1yn

14

行列式的计算方法 行列式的计算方法和技巧大总结

5．递（逆）推公式法

递推法是根据行列式的构造特点，建立起与

［注意］用此方法一定要看行列式是否具有较低阶的相同结构如果没有的话，即很难找出递推关系式，从而不能使用此方法。(www.61k.com] （2002 上海交大）

，

的递推关系，最后利用

与

，

的递推关系式，逐步推下去，从而求出

得到

的值。

的值。 有时也可以找到

xaaa

x

???

aaa

?ax

计算行列式D??a?a

??????a?a?a?x

求解：

先拆行，再用递推法。

xaaax

???

0?a0?a0?a

?axD??a?a

??????a?a?a?(x?a)?a

x

a

aax

???

aaa

a

x

a

aax

???

aaa

000?x?a

?ax??a?aa?axa??a?a

??????a?a?a??aa?????a?a?a??a

x?a0?

0?00

2ax?a0?00

2a2a?00

??

2a2a2a?

aaa?a

?(x?a)Dn?1

x?a?

?x?aa?

?a(x?a)n?1?(x?a)Dn?1

即Dn

?a(x?a)n?1?(x?a)Dn?1。同理得：Dn?(x?a)Dn?1?a(x?a)n?1。于是，

n

??(x?a)Dn??a(x?a)?(x?a)(x?a)Dn?1?n??(x?a)Dn?a(x?a)?(x?a)(x?a)Dn?1

?1?

?2?

(2)?(1)得：2aDn?a(x?a)n?a(x?a)n

当a

?0时，Dn?

1

(x?a)n?(x?a)n2

??。

15

行列式的计算方法 行列式的计算方法和技巧大总结

当a

?0时，显然Dn?xn?

1

(x?a)n?(x?a)n2

??。[www.61k.com）故

?

000?1

000?

.

1

(x?a)n?(x?a)n 2

????1???01

例1 计算行列式Dn?

??0000Dn?

??

???

????

?00

?

????

?????

解：将行列式按第n列展开,有

Dn?(???)Dn?1???Dn?2,

Dn??Dn?1??(Dn?1??Dn?2),Dn??Dn?1??(Dn?1??Dn?2),

得 Dn

??Dn?1??2(Dn?2??Dn?3)????n?2(D2??D1)??n。

?(n?1)?n,???;?n?1

nD?????n?1同理得 Dn??Dn?1??, n

,???.????

?

ay

例2 计算Dn

xay?y

xxa?y

?????

xxx?a

?yy

解

a?y0

Dn?

0?0

xay?y

x?x?a???y?

xxx?a0a?xy?x?y?x

yy?yy

xayy00a?x?y?x

xxay

?????????

xxxa000?a?x

????(a?y)Dn?1?y?(a?y)Dn?1?y(a?x)n?1

同理Dn

?(a?x)Dn?1?x(a?y)n?1

n

x(a?y）?y(a?x)n

,(x?y) 联立解得Dn?

x?y

16

行列式的计算方法 行列式的计算方法和技巧大总结

当x?y时,

Dn?(a?x)Dn?1?x(a?x)n?1?(a?x)2Dn?2?2x(a?x)n?1

??????(a?x)n?2D2?(n?2)x(a?x)n?1?(a?x)n?1?a?(n?1)x?

x0

例3 计算n阶行列式

?1x0?0

0?1x?0

???

000

000??1a1?x

．

Dn?

0?0an

???x

an?1an?2?a2

解 首先建立递推关系式．按第一列展开，得：

x0Dn?x

0?0

?1x0?0

0?0?1?0x

?0

000

n?1

?10x

0?000

n?1

n?1

?10?0

an?1an?2

???1?an0x?1?00?xDn?1???1??an???1?

????

??????

0?x?1

000?x?1

an?3?a2a1?x

?xDn?1?an ，

这里Dn?1与Dn有相同的结构，但阶数是n?1的行列式．

现在，利用递推关系式计算结果．对此，只需反复进行代换，得：

Dn?x?xDn?2?an?1??an?x2Dn?2?an?1x?an?x2?xDn?3?an?2??an?1x?an????xn?1D1?a2xn?2???an?2x2?an?1x?an ，因D1

?x?a1?x?a1，故Dn?xn?a1xn?1???an?1x?an．

?1时，显然成立．设对n?1阶的情形结果正确，往证对n阶的情形也正确．由

最后，用数学归纳法证明这样得到的结果是正确的． 当n

Dn?xDn?1?an?x?xn?1?a1xn?2???an?2x?an?1??an?xn?a1xn?1???an?1x?an ，、

可知，对n阶的行列式结果也成立．根据归纳法原理，对任意的正整数n，结论成立．

2

例4

证明n阶行列式

12

?00

01?00

?????

00?10

00?21

．

??n?112

1

Dn?00

210?000100?000

121?000121?000

证明 按第一列展开，得D?2?????????????．

n

00

00

00

??

10

21

12

00

00

00

??

10

21

12

其中，等号右边的第一个行列式是与Dn有相同结构但阶数为n?1的行列式，记作Dn?1；第二个行列式，若将它按第一列展

17

行列式的计算方法 行列式的计算方法和技巧大总结

61阅读提醒您本文地址：

开就得到一个也与Dn有相同结构但阶数为n?2的行列式，记作Dn?2．

这样，就有递推关系式：Dn?2Dn?1?Dn?2．

因为已将原行列式的结果给出，我们可根据得到的递推关系式来证明这个结果是正确的． 当n?1时，D1?2，结论正确．当n?2时，D2?21?3，结论正确． 12

设对k ≤ n?1的情形结论正确，往证k

由Dn?n时结论也正确． ?2Dn?1?Dn?2?2n??n?1??n?1 可知，对n阶行列式结果也成立． 根据归纳法原理，对任意的正整数n，结论成立．

例5.计算n阶行列式

a?xaa?aa

?yx0?00

Dn?0?yx?00

?????

000??yx

解： 将行列式按第n列展开，可得

?yx

?yx

Dn?xDn?1?a(?1)1?n??

x

?y

=xDn-1+ayn-1

∴Dn= xDn-1+ayn -1=x(xDn-2+ayn-2)+ ayn-1=…

=xn-1D1+ayn -1+ayn-2x+ …+ayxn-2

=xn-2n-1

n+a(xn-1+xn-2y+…+xy+y)

注：此题可按第一行展开即得结果。[www.61k.com］

例6.计算n阶行列式： ?a11?1

Dn?11?a2?1???

11?1?an

其中a1a2?an?0．

将Dn改写为

1?a11?1?0

D11?a2?1?0

n????

11?1?an

18

行列式的计算方法 行列式的计算方法和技巧大总结

1?a1

按cn拆开11?a2

?

1?1?1

1

?

11?0?1?a111?a2?0?1+????11?an?1 ?a1由于 ?1ri?rni?1,?,n?1a11?11?a2?1??1?a211?1?a1a2?an?1

?a11?0

11?a2?0

???

11?an

因此Dn=anDn?1按cn展开?anDn?1 ?a1a2?an?1为递推公式，而D1?1?a1，于是

?Dn?11?Dn=anDn?1?a1a2?an?1=a1a2?an???

?a1a2?an?1an?

=a1a2?an?Dn?211?????=??

?a1a2?an?2an?1an?

?D11?1?111?=aa?a????1?????n???12? aaaaaa2n?12n??1?=a1a2?an

6．利用范德蒙行列式

根据行列式的特点，适当变形（利用行列式的性质——如：提取公因式；互换两行（列）；一行乘以适当的数加到另一行（列）去； ...) 把所求行列式化成已知的或简单的形式。(www.61k.com)其中范德蒙行列式就是一种。这种变形法是计算行列式最常用的方法。

19

行列式的计算方法 行列式的计算方法和技巧大总结

1x1?1

例1 计算行列式D

1x2?1

2x2?x2

???

1xn?1

2

xn?xn

?

x12?x1

?x1n?1?x1n?2

??

n?1n?2n?1n?2

x2?x2?xn?xn

解 把第1行的－1倍加到第2行，把新的第2行的－1倍加到第3行，以此类推直到把新的第n－1行的－1倍加到第n行，便得范德蒙行列式

1x1

D?x12

?x1n?1

1x2

2

x2

???

1xn

2xn?

??

n?i?j?1

?

(xi?xj)

n?1n?1

x2?xn

a1n

n

a2

D?例2 计算n?1阶行列式

?

a1n?1b1

n?1a2b2?

a1n?2b12

n?22a2b2?

???

a1b1n?1a2b2n?1?

b1nb2n?

．其中a1a2?an?1

?0．

nn?1n?22n?1anananbnn?1?1?1bn?1?1bn?1?an?1bn?1

解 这个行列式的每一行元素的形状都是都是n，又因ai

ain?kbik，k?0，1，2，…，n．即ai按降幂排列，bi按升幂排列，且次数之和

?0，若在第i行（i?1，2，…，n）提出公因子ain，则D可化为一个转置的范德蒙行列式，即

111

b1

a1b2a2?bn?1an?1

?b1????a1?

2

?

2

?b1????a1?

n

D?aa?a

n1n2nn?1

?b2????a2??

??

2

?b2????a2??

n

??ain

i?1

n

n?1

?bibj?

????biaj?aibj? . ????aj?1≤j?i≤n?1?ai?1≤j?i≤n?1

?bn?1?

??a?n?1??b?

??n?1?

?an?1?

x

2

D?x例3 计算行列式

yz

yy2xz

zz2xy

.

解：

20

行列式的计算方法 行列式的计算方法和技巧大总结

D

(3)?(y?z)(1)

?

xx2yy2zz2

xy?xz?yzy2?yz?xzyz?z2?xy

(3)?x(1)

xyz

?x2y2z2

222

x?xy?yz?xzy?xy?yz?xzz?xy?yz?xz

?(xy?yz?xz)(y?x)(z?x)(z?y)

x1

例4 计算行列式

1x2

2x2

?????

1xn

2xn

Dn?

2x1

n?2x1nx1

?

nx2

?

n?2xnnxn

n?2x2?

解 作如下行列式,使之配成范德蒙行列式

x1

2

x1

1

2x2

????

1xn

2xn

1yy2?y

n?2

x2???x

n?22

n?1x2?nx2

P(y)?x

n?21n?1x1nx1

?x

n?2nn?1xnnxn

=

?(y?x)?(x

i

i?1

1?j?i?n

n

i

?xj)

yn?1yn

易知Dn等于P(y)中

n

y

n?1

的系数的相反数,而P(y)中y

n?1

的系数为

??xk

k?1

n

1?j?i?n

?(x

i

?xj) ,因

此,

Dn?

?x?(x

k

k??1

1?j?i?n

i

?xj)

例5、 计算n阶行列式

(a?n?1)n?1(a?n?1)n?2

Dn?

?a?n?11

(a?n?2)n?1?(a?1)n?1(a?n?2)n?2?(a?1)n?2

?a?n?21

??

?a?11

an?1an?2?a1

解：显然该题与范德蒙行列式很相似，但还是有所不同，所以先利用行列式的性质把它化为范德蒙行列式的类型。[www.61k.com]

先将的第n行依次与第n-1行，n-2行，…,2行，1行对换，再将得到到的新的行列式的第n行与第n-1行，n-2行，…,2行对换，继续仿此作法，直到最后将第n行与第n-1行对换，这样，共经过（n-1）+（n-2）+…+2+1=n（n-1）/2次行对换后，得到

61阅读提醒您本文地址：

21

行列式的计算方法 行列式的计算方法和技巧大总结

1

Dn?(?1)

n(n?1)2

1a?n?2?

??

1a?1?

1a?an?2an?1

a?n?1?(a?n?1)n?2(a?n?1)n?1

(a?n?2)n?2?(a?1)n?2(a?n?2)n?1?(a?1)n?1

n(n?1)2

上式右端的行列式已是范德蒙行列式，故利用范德蒙行列式的结果得：

Dn?(?1)

n(n?1)2

1?j?i?n

?[(a?n?i)?(a?n?j)]?(?1)

1?j?i?n

?

(i?j)

例六、设a, b, c是互异的实数, 证明:

的充要条件是a + b + c =0.

证明: 考察范德蒙行列式:

=

行列式

即为y前的系数. 于是

2

=

所以

1． 计算n阶行列式

的充要条件是a + b + c = 0.

22

行列式的计算方法 行列式的计算方法和技巧大总结

an

Dn?1??

a

1(a?1)n?a?11?(a?n)n?a?n1。[www.61k.com］ an?1(a?1)n?1?(a?n)n?1??

解： 把Dn+1的第n+1行换到第1行，第n行换到第2行，…，同时将Dn+1的第n+1列换到第1列，第n列依次换到第2列，…，再有范德蒙行列式，得

1

a?nDn?1??

(a?n)n

2． 已知方程 1?1a?n?1?a??(a?n?1)n?an1?j?i?n?1 ?n!(n?1)!?2!??(i?j)。

1

?1

1

1

111123?1415xx2x312111101111125?1415xx2x31101111248?0，求x 。 25xx2x3解：由行列式的加法性质，原方程可化为 111248?14xx2x3111248 2512xx2x3

?112439xx21111823x?2749x2x3827x3

=(2-1)(3-1)(3-2)(x-1)(x-2)(x-3)=0

得x=1或x=2或x=3。

7．加边法（升阶法）

加边法（又称升阶法）是在原行列式中增加一行一列，且保持原行列式不变的方法。

它要求：1 保持原行列式的值不变； 2 新行列式的值容易计算。根据需要和原行列式的特点选取所加的行和列。加边法适用于某一行（列）有一个相同的字母外，也可用于其第 列（行）的元素分别为 n-1 个元素的倍数的情况。

x?a1

a1

例1 计算n阶行列式Dna2a2

?

a2???ananan? x?a2??a1?a1?x?an

23

行列式的计算方法 行列式的计算方法和技巧大总结

1a1

解：Dn?

?

01??

j?1n

?Dn

an

第i行减第1行

1

?1

i?2,?,n?1?1

a1x0

a20x?0

?????

an00?x

???10

ajx

a1x00

a2?an0x0

???

00x

?000

na??jn

?x?1???

j?1x??

?a11

例2 计算n（n≥2）阶行列式Dn

11?a21?1

11?1

???

111?

，其中a1a2?an

?1?1

1?a3?

?0．

?1?an

解 先将Dn添上一行一列，变成下面的n?1阶行列式：

10

Dn?1?0

?0

11?a1

1?1

111?a2?1

????

111?

．显然，Dn?1

?Dn．

?1?an

1?1

将Dn?1的第一行乘以?1后加到其余各行，得

1a10?0

101?a2?0

1ai?1

????

倍，得：

100an

．

Dn?1??1

??1

??

因ai

?0，将上面这个行列式第一列加第i（i?2，…，n?1）列的

24

行列式的计算方法 行列式的计算方法和技巧大总结

11?1a1

Dn?Dn?1??10

?10

a10n

?1?0a2? ?1???

?i?1ai??

00

加边法的一般做法是：

1?0?a2?

100 ?

11??i?1ai

00?0

n

1a1

1?0?

10

?????

0?an??

00

0a2?0????00?an

n

?1?

? a1a2?an?1??? ????i?1ai??an

Dn?

a11?a1na21?a2n?

?

an1?ann

1

a1

?

an

1b1?bn

0?0

0a11?a1n?

?

?

a11?a1na21?a2n?

?

an1?ann

?0a21?a2n?b2

0an1?ann

特殊情况取a1?a2???an?1 或 b1?b2??

?bn?1

25

行列式的计算方法 行列式的计算方法和技巧大总结

例4、计算n 阶行列式：

x12?1Dn?

x1x2x1x2

x1x2x22?1x1x2

x1x2x1x2xn2?1

[分析] 我们先把主对角线的数都减1，这样我们就可明显地看出第一行为x1与x1,x2,…, xn相乘，第二行为x2与x1,x2,…, xn

相乘，……，第n行为xn与 x1,x2,…, xn相乘。[www.61k.com］这样就知道了该行列式每行有相同的因子x1,x2,…, xn，从而就可考虑此法。

解：

1x1x2?0x12?1x1x2?

2

Dn?0x2x1x2?1?

?

?xnx1

?xnx2

n

2i?1

xn1x1x2?x1

(i?1,?,n)x2xn?x2

61阅读提醒您本文地址：

ri?1?xir1

x1

10?0

x2?xn0?01?0?0

?

?1

?2

?xn?1x110?0

??xn

n?1

??xi

c1?xici?1(i?1,?,n)

x2?xn01?0a2?a2

00?0

???00?1?

?1??xi2

i?1

n

n?1

例五、计算n阶行列式：

a1?b1

Dn?

a1?a1

anan?

(b1b2?bn

a2?b2?

?0)

?an?bn

解 采用升阶（或加边）法．该行列式的各行含有共同的元素a1,a2,?,an，可在保持

原行列式值不变的情况下，增加一行一列，适当选择所增行（或列）的元素，使得下一步化简后出现大量的零元素．

26

行列式的计算方法 行列式的计算方法和技巧大总结

1

Dn

升阶

a1a1?a1?

a2a2?a2

??

ananan?

r2?r1r3?r1?rn?1?r1

0a1?b1?0

1a1a2?an?1b10?0?1??1

0?0

b2??0

0?

?0

a2?b2?

?

?an?bna1a2?anb10?0

0?0anan??an?x

=x

n?1

?bn

c1?

1bj?1

cj

a1a???1b1b1

00?0

j?2,?,n?1

?

?00?

b2?

=b1b2?bn(1?

aa

???) b1bn

?bn

这个题的特殊情形是

a1?xDn?

a1?a1

可作为公式记下来．

a2?a2

?

a2?x?

(x??ai)

i?1

n

8．数学归纳法

当

与

是同型的行列式时，可考虑用数学归纳法求之。［www.61k.com) 一般是利用不完全归纳法寻找出行列式的猜想值，再用数

学归纳法给出猜想的证明。因此，数学归纳法一般是用来证明行列式等式。因为给定一个行列式，要猜想其值是比较难的，所以是先给定其值，然后再去证明。（数学归纳法的步骤大家都比较熟悉，这里就不再说了）

x0

例1 计算n阶行列式D

n

?1x?0

0?1?0

???

00x

00? ?1a1?x

??0an

??

an?1an?2?a2

解：用数学归纳法. 当n = 2时，D2

?

xa2

?1x?a1

?x(x?a1)?a2?x2?a1x?a2

假设n = k时，有

Dk?xk?a1xk?1?a2xk?2???ak?1x?ak

则当n = k+1时，把Dk+1按第一列展开，得

Dk?1?xDk?ak?1?x(xk?a1xk?1???ak?1x?ak)?ak?1?xk?1?a1xk???ak?1x2?akx?ak?1

由此，对任意的正整数n，有Dn

?xn?a1xn?1???an?2x2?an?1x?an

27

行列式的计算方法 行列式的计算方法和技巧大总结

cos?10?00

12cos?1?00

例2 计算行列式D12cos??00.

n?0

??????

000?2cos?1

000?12cos?

解：D1?cos?,D2?cos2?,于是猜想 Dn?cosn?. 证明：对级数用第二数学归纳法证明.

n?1时,结论成立.假设对级数小于n时，结论成立.将n级行列式按第n行展开，有

cos?10?0

12cos?1?0

Dcos??D?1)2n?1?012cos??0n?2n?1?(?????

000?2cos?

000?1

?2cos??Dn?1?(?1)2n?1Dn?2

?2cos??cos(n?1)??(?1)2n?1cos(n?2)?

?2cos??cos(n?1)??cos(n?1)?cos??sin(n?1)?sin?

?cos[(n?1)???]?cosn?

例3 计算行列式

解：

猜测：

证明

（1）n = 1, 2, 3 时，命题成立。［www.61k.com)假设n≤k – 1 时命题成立,考察n=k的情形： 28 00001n?1. ?

行列式的计算方法 行列式的计算方法和技巧大总结

故命题对一切自然数n成立。［www.61k.com）

9．拆开法

拆项法是将给定的行列式的某一行（列）的元素写成两数和的形式，再利用行列式的性质将原行列式写成两行列式之和，把一个复杂的行列式简化成两个较为简单的。使问题简化以利计算。

例1 计算行列式

Dn?

a1??1a2a1a2???a1

anan

2

??

anan

?a2???an??n

a1a解：Dn?1?a1

a2?a2??2??a2

?1

?0?0

a2?a2??2??0

anan

a1?0?0

a2?an

?2?an

?0

?

???n

???an??n

???an??n

??1Dn?1

n

?ai?

?a1?2??n??1Dn?1=……??1?2??n?1???

?i?1?i?

．

1?x1y1

例2 计算n（n≥2）阶行列式Dn

2?x1y2

?

?n?x1yn?

?

．

?

?x2y1

??xny1

2?x2y2?n?x2yn2?xny2?n?xnyn

解 将Dn按第一列拆成两个行列式的和，即

29

行列式的计算方法 行列式的计算方法和技巧大总结

1Dn?

11

2?x1y2?n?x1yn2?x2y2?n?x2yn

?

?

?

2?xny2?n?xnyn

?

x1y1x2y1?xny1

2?x1y2?n?x1yn2?x2y2?n?x2yn

?

?

?

2?xny2?n?xnyn

．

再将上式等号右端的第一个行列式第i列（i到

?2，3，…，n）减去第一列的i倍；第二个行列式提出第一列的公因子y1，则可得

1Dn?

11

x1y2?x1ynx2y2?x2yn?

?

?

xny2?xnyn

61阅读提醒您本文地址：

?y1

x1x2xn

2?x1y2?n?x1yn2?x2y2?n?x2yn

?

?

?

2?xny2?n?xnyn

?y2?yn

111

x1?x1x2?x2xn?xn

?y1

x1x2xn

2?n2?n2?n

.

??????

当n≥3时，Dn

?0．当n?2时，D2??x2?x1??y2?2y1?．

x?a

例3 计算n阶行列式

axaax

???

aaa

，（a

Dn??a?a

?0）．

?????

?a?a?a?x

解 将第一行的元素都表成两项的和，使Dn变成两个行列式的和，即

?x?a??a

?a

Dn?

?a??a

0?a0?a?0?ax?a??a

ax??a

????

aa

x?a?a

0x

0a

??

0a

a?a

ax

aa

??

aa

? ?a

??

?ax

x?a

0x?a

0ax

?ax?a ? ?a?ax?a . ??????????a?a?

???

a

a ? ?x?a?Dn?1 ．

x?a?a?a?x

?a

将等号右端的第一个行列式按第一行展开，得：?a

??a

?????a?a?x

这里Dn?1是一个与Dn有相同结构的n?1阶行列式；将第二个行列式的第一行加到其余各行，得：

aaaax

???

aaax?a0?0

a?a

2a

n?1

2a ? a?x?a? .

?ax?a?aa0a ? 0

n?1

2a?x?a??0

??????a?a?a?x

于是有

???x?a

Dn??x?a?Dn?1?a?x?a?

（1）

另一方面，如果将Dn的第一行元素用另一方式表成两项之和：

30

行列式的计算方法 行列式的计算方法和技巧大总结

?x?a??a 0?a 0?a ? 0?a 仿上可得：D??x?a?Dnn?1?a?x?a?n?1 （2）

n

将（1）式两边乘以（2）式两边乘以?x?a?，然后相减以消去Dn?1，得：Dn?x?a?，?x?a???x?a??2n．

5.消去法求三对角线型行列式的值

例6 求n阶三对角线型行列式的值：

（1）

的构造是：主对角线元全为2，主对角线上方第一条次对角线与下方第一条次对角线的元全为1，其余的元全为0。（www.61k.com) 解 用消去法，把中主对角线下方第一条次对角线的元1全部消成0：首先从第二行减去第一行的倍，于是第二行变为

其次从第三行减去第二行（指新的第二行，以下同）的倍，则第三行变为

再从第四行减去第三行的倍，则第四行变为

类似地做下去，直到第n行减去第n – 1行的倍，则第n行变为

最后所得的行列式为

（2）

上面的行列式是三角型行列式，它的主对角线元顺次为

93）

又主对角线下方的元全为0。故

注3 一般的三对角线型行列式 的值等于（3）中各数的连乘积，即。

31

行列式的计算方法 行列式的计算方法和技巧大总结

（4）

也可以按上述消去法把次对角线元

连乘积。[www.61k.com)

9. 因式分解法

如果行列式D是某个变数x的多项式

式的乘积为g(x)，则D全部消去，得到一个三角型行列式，它的值等于该三角型行列式的主对角线元的f(x)，可对行列式施行某些变换，求出f(x)的互不相同的一次因式，设这些一次因?f(x)?cg(x)，再比较f(x)与g(x)的某一项的系数，求出c值.

例8 计算行列式Dn2x?12

?

233x?3?3?????nnn?x?1. ?解:注意x?1时，Dn?0,所以，x?1|Dn. 同理x?2,?,x?(n?1)均为Dn的因式

又x?i与x?j(i?j)各不相同 所以 (x?1)(x?2)?(x?n?1)|Dn

n?1但Dn的展开式中最高次项x的系数为1，所以Dn?(x?1)(x?2)?(x?n?1)

注：此题也可将的第行减去第一行化为三角形行列式计算.

.辅助行列式法

辅助行列式法应用条件：行列式各行（列）和相等，且除对角线外其余元素都相同。

解题程序：

1）在行列式D的各元素中加上一个相同的元素x，使新行列式D*除主对角线外，其余元素均为0；

2）计算D*的主对角线各元素的代数余子式Aii(i?1,2,?n);

3)D?D*?x?Aij

i,j?1n[1]

例8 .大连理工大学2004年硕士生入学考试《高等代数》试题，第一大题填空题第2小题需求下列n阶行列式的值。

1

1Dn??

2?n1?12?n1?2?n1???1?11

解：在Dn的各元素上加上(?1)后，则有：

32

行列式的计算方法 行列式的计算方法和技巧大总结

00

(Dn)*?

?2?n

又

0?02?n

n(n?1)

0?2?n0

?(?1)2?(1?n)n

???0?00

n(n?1)

2

A1n?A2,n?1???An1?(?1)

n

n(n?1)2

?(1?n)n?1，其余的为零。(www.61k.com)

n

n

?Dn?(Dn)*??Aij?(?1)

i,j?1

?(1?n)??Ai,n?i?1

61阅读提醒您本文地址：

i?1

?(?1)?(?1)

n(n?1)2n(n?1)2

?(1?n)?(?1)?(1?n)n?1

n

n(n?1)2

?n?(1?n)n?1

利用拉普拉斯定理

拉普拉斯定理的四种特殊情形：[1][5]

1）

AnnCmn0Bmm

0BmmAnnCmn

?Ann?Bmm

2）

Ann0

Cnm

?Ann?Bmm

Bmm

3）

?(?1)mnAnn?Bmm

4）

CnmBmm

a

Ann0

a

?(?1)mnAnn?Bmm

例9 计算n阶行列式：[1]

?a?a

b?Dn?b?

?b

解：

??

?

??????

?

?

?

?????

?

Dn

(i?2,,n?1)

a

?i?1??2

b0?0

?????0

a???

??0

a?a???0?0??0?????a

???????0?00????0???00????a

a

?

b

C2?Ci0(i?3,?n)0

?0利用拉普拉斯定理

(n?1)a??(n?2)?

00?0(n?1)ab??(n?2)?

??

?

?

2?2

0?0

n?2

0?0????0??0????

(n?2)?(n?2)

?[????(n?2)??ab(n?1)]?(???)

33

行列式的计算方法 行列式的计算方法和技巧大总结

析因法

如果行列式D中有一些元素是变数x（或某个参变数）的多项式，那么可以将行列式D当作一个多项式f(x)，然后对行列式施行某些变换，求出f(x)的互素的一次因式，使得f(x)与这些因式的乘积g(x)只相差一个常数因子C，根据多项式相等的定义，比较f(x)与g(x)的某一项的系数，求出C值，便可求得D=Cg(x) 。[www.61k.com)

那在什么情况下才能用呢？要看行列式中的两行（其中含变数x），若x等于某一数a1时，使得两行相同，根据行列式的性质，可使得D=0。那么x 法。

例7 .兰州大学2004招收攻读硕士研究生考试工试题第四大题第（1）小题。需求如下行列式的值。

?a1便是一个一次因式，再找其他的互异数使得D=0，即得到与D阶数相同的互素一次因式，那么便可用此

x

a1

Dn?1??

a1a1

[分析] 根据该行列式的特点，当x?ai.

a1x?a2a2

a2?ana2?an??a3?ana3?

x

i?1,2,?,n时，有Dn?1?0。但大家认真看一下，该行列式Dn+1是一个n+1

i?1,2,?,n,那么能否用析因法呢？我们再仔细看一下，每行的元素的和

n

次多项式，而这时我们只找出了n个一次因式x?ai.

n

数都是一样的，为：

?a?x，那么我们从第2列开始到第n+1列都加到第1列，现提出公因式?a?x，这样行列式的次数

i

i

i?1

i?1

就降了一次。从而再考虑析因法。

解：

?a?x

ii?1n

n

a1x?a2a2

a2?ana2?a3

a1

?an

xn

??(?ai?x)??

i?1

a2

?an

a2

x

a2a2?a3a3

?an?an

??an?x

?a?x

ii?1

Dn?1?

ni?1n

?

?a?x

i

?a?x

ii?1

a3?

令：

a1

Dn?1'

??

x?

a2?ana2?an??a3?ana3?

x

a2a2

显然当：x?ai.

'

i?1,2,?,n时，Dn?1'?0

。

又Dn?1为n次多项式。

?设Dn?1'?C(x?a1)(x?a2)?(x?an)

34

行列式的计算方法 行列式的计算方法和技巧大总结

又Dn?1中x的最高次项为x，系数为1，?C=1

'n

?Dn?1'?(x?a1)(x?a2)?(x?an)

因此得：

n

Dn?1?(?ai?x)Dn?1'

i?1n

?(?ai?x)(x?a1)(x?a2)?(x?an)

i?1

代数余子式

1．（2003北工大）

1

1

设n阶行列式Dn

220

303

???

n00

?1

????100?n

求第一行各元素的代数余子式之和求解：

构造行列式，将

A11?A12???A1n。（www.61k.com)

A中第一行的元素均换成1，则

A11?A12???A1n?1?A11?2?A12???1?A1n

112???3?

?

n

n

111

???

1

00ii?11213??1

n

000

?

?

n

1

?n!(1??)。

i?1i

改变aij后

Aij的值不变，构造一个行列式，使所要求的代数余子式在量行列式中相同，通过新行列式计算所要求的代数余子

式之和。充分理解代数余子式的概念，这道题目解决起来就很方便了。

2.（2005北交大）

?222?2??011?1???

01?1? 设n阶方阵A??0???????????000?1??

求

A中所有元素的代数余子式之和。

35

行列式的计算方法 行列式的计算方法和技巧大总结

求解： 易知

A?2，又

?222?2?

11?1?

(AE)??1?1

?

?1?

?1??211?1?

1???1?

??

?1?

1

?

?

??

?, ?

???

1??0??

?1?

? ??

?

??1?

1??0

1??1

?

?

?100?0??1??1?

??

?1?

?1

??2??1

即A??

????

?11

12

?11

?0??

?1?

? ??

?

??1?

1??0

?

0??

?1?

?， 1?

?

??1?

1??0

?1?2000?

??

1?1??

??1?，从而 1?故A?A?A??

??

??1??

?1???

??A

i?1j?1

nn

ij

?n?(?2)?(?1)?(n?2)?0。［www.61k.com］

由于

A计算方便，利用矩阵的初等变换可得出A?1，因此可以充分利用公式A??A?A?1来求所有代数余子式之和。

36

61阅读提醒您本文地址：

本文标题：行列式的计算方法-中学数学1.05的-3次方怎么计算？请列式。
本文地址： http://www.61k.com/1129817.html