机械手臂设计-95机械手臂设计

发布时间：2018-02-14 所属栏目：机械设备防护罩安全要求

一 : 95机械手臂设计

动伺服技术走出实验室，气动技术及气动机械手迎来了崭新的春天。目前在世界上形成了以日本、美国和欧盟气动技术、气动机械手三足鼎立的局面。我国对气动技术和气动机械手的研究与应用都比较晚，但随着投入力度和研发力度的加大，我国自主研制的许多气动机械手已经在汽车等行业为国家的发展进步发挥着重要作用。随着微电子技术的迅速发展和机械加工工艺水平的提高及现代控制理论的应用，为研究高性能的气动机械手奠定了坚实的物质技术基础。由于气动机械手有结构简单、易实现无级调速、易实现过载保护、易实现复杂的动作等诸多独特的优点。

图2-3 长度与张力的关系

2.1.3 气动肌肉的模型

在最简单的情况下，气动肌肉用作单作用驱动器，负载不变（如图2-4a）。假设气动肌肉上该负载一直存在，在没有压力的情况下，肌肉将从原始状态被拉伸一段长度，这是考虑气动肌肉的技术特性的一种理想工作状态：当加压时，气动肌肉在预拉伸状态下有最大的输出力和最佳动态性能，并且耗气量最小。在这种情况下，可用的力也最大。如果要求气动肌肉在扩张状态时无作用力（如允许附加上负载），首先就要加上用于提升负载目的的保持力，利用它的运动来移动作用力小的元件。

(a) (b)

图2-4不同外力作用下气动肌肉表现形式

当外力发生变化时（如图2-4b），气动肌肉像一根弹簧；它与力的作用方向一致。对用作“气弹簧”的气动肌肉而言，预拉伸力和弹簧刚度都是变化的。气动肌肉在常压或体积不变的情况下可用作弹簧。这些气动肌肉会产生不同的弹簧特性，这使得它可很好地适用于具体应用[26]。

在机械设计手的设计过程中，为了简化设计的模型，使设计过程简单明了，采用如图2-5的二维简化模型。在三维模拟仿真阶段，由于气动肌肉所做的是拉

图2-5 二维简化模型

图2-6 三维简化模型

伸运动，为了实现肌肉的这种运动形式，把气动肌肉中部的隔膜软管的圆柱体改为长方体,并且为了定义滑动杆运动形式的方便，把每一根气动肌肉看做是由左右两根等长的半根气动肌肉组成（如图2-6）。

2.2 气动机械手的基本结构

本课题所设计的气动机械手的结构如图2-7所示。

1. 机架 2. 气动肌肉 3. 第一肩关节 4. 第二肩关节 5. 机架臂

6. 第三肩关节 7. 大臂 8. 肘关节 9. 小臂 10. 腕关节 11. 气爪

图2-7 气动机械手的结构

气动机械手主要由起固定支撑作用的机架、机械臂和气爪三部分组成。气动机械手能够实现4个自由度（由于机构运动确定，因此机构的自由度等于机构的原动件数目，此机构有4个原动件，因此可得有4个自由度）的运动，其各自的自由度的驱动全部由气动肌肉来实现。最前端的气爪抓取物品，通过气动肌肉的驱动实现各自关节的转动，使物品在空间上运动，根据合理的控制，最终实现机械手的动作要求。驱动第一肩关节的运动有2根气动肌肉组成，机架臂有4根气动肌肉组成，大臂上安装有4根气动肌肉，小臂上安装有4根气动肌肉。

2.3 气动机械手关节结构设计

2.3.1 关节的基本方式

在气动机械手设计中，有4个自由度，相当于4个独立的关节。每个关节的驱动原理都是相同的，即由一对相当于人类拮抗的气动肌肉相互之间的对抗作用来驱动关节。其原理如图2-8所示。这种方式驱动的关节，其刚度和两个肌肉的压力之和有关，而其位置则和2个肌肉的压力差有关，因此可以实现关节位置和刚度的独立控制[27]。

图2-8 关节的基本驱动方式

2.3.2 肩关节结构设计

1) 第一肩关节的设计

第一肩关节主要是由2根气动肌肉作为驱动，实现绕Z轴（X、Y、Z轴的方向标在图2-7中，下同）转动这1个自由度，其结构简图如图2-9(a)所示。三维建模的第一肩关节结构如图2-9(b)所示。

图2-9(a) 第一肩关节结构简图

图2-9(b) 第一肩关节三维结构图

2) 第二肩关节的设计

第二肩关节和其下的4根机架臂相连接，为的是实现绕X轴旋转这1个自由度，其结构简图如图2-10a所示。三维建模的第二肩关节结构如图2-10b所示。

95机械手臂设计_机械手臂设计

图2-10(a)第二肩关节图2-10(b)第二肩关节

结构简图三维结构图

3) 第三肩关节的设计

第三肩关节是连接第二肩关节和大臂的纽带。主要零件是肩部连接腕和中部支撑杆。其中肩部连接腕固定在肩部连接轴上，在机架臂的带动下，使得大臂、小臂及气爪整体绕X轴的转动，其另一功能是连接大臂的4根气动肌肉。中部支撑杆是用来固定肘关节，是大臂的支撑杆。其三维结构图如图2-11所示。

图2-11第三肩关节三维结构图

2.3.3肘关节结构设计

1) 虎克铰简介

气动机械手的设计难点主要在于肘关节和腕关节的实现。最灵活的关节形式就是球铰，有3个自由度，但是其实现复杂，控制难度比较大。在许多气动机械手的研究中，采用的驱动器都是电机，为实现肩关节的3个自由度，结构往往比较复杂[28,29]。作为2个自由度的机构，虎克铰的结构比较简单，且2个自由度之间的运动可以独立进行控制。由于驱动方式的限制，虎克铰的应用在机器人中不是很常见。本研究采用气动肌肉，可以方便地对这种机构进行控制，实现两个自由度的运动。在本设计中，采用如图2-12所示的虎克铰形式来实现肘关节的2个自由度[27]。

图2-12 虎克铰的基本结构

2) 肘关节的结构设计

肘关节主要是由一个虎克铰的结构构成。由于虎克铰能够实现2个自由度，并且虎克铰的2根轴相互垂直，这就要求肘关节与大臂的气动肌肉的连接件必须具有两个方向单一的铰链点结构，其三维结构如图2-13所示。

图2-13 气动肌肉连接件

肘关节是连接大臂与小臂的重要关节。分别是通过中部支撑杆和前部支撑杆维系着这两个结构，其三维结构图如图2-14所示。其中一些重要的尺寸参数分别

图2-14 肘关节三维结构图

由X、Y轴方向来确定，肘关节X轴方向上的结构简图如图2-15a所示，绿色表示的是肌肉连接件，由于在X轴方向上，其与气动肌肉没有相互转动，因此表示成同一条直线，绿色只是说明这里另一个零件，Y轴方向上的结构简图如图2-15b所示。当不同相邻的两根气动肌肉组成一对时，可以实现绕不同轴的旋转。如图2-14（左图）所示，当前面的两根气动肌肉组成一对，即两根肌肉有相同的运动形式，可

知后面的是一对，在运动过程中可以实现绕Y轴的转动。同样的左、右各为一对时，可以实现绕X轴的转动。

(a) X轴方向 (b) Y轴方向

图2-15 肘关节X、Y轴方向的结构简图

2.3.4 腕关节结构设计

腕关节大体上与肘关节的结构相似，主要有一个虎克铰的结构构成。同样能够实现2个自由度，与肘关节不同的是绕着X轴、Z轴的旋转。腕关节和小臂的连接件和肘关节的连接件一样（如图2-13），是两个方向单一的铰链点。腕关节通过前部支撑杆和肘关节固定，前端安装有一个气爪。其三维结构如图2-16所示。

图2-16 腕关节三维结构图

腕关节设计过程中的一些重要尺寸参数有X轴，Z轴方向来确定。其在X轴方向上的结构简图如图2-17(a)所示，Z轴如图2-17(b)所示。

(a) X轴方向

(b) Z轴方向

图2-17 腕关节X、Z轴方向的结构简图

95机械手臂设计_机械手臂设计

第3章气动机械手关节结构参数设计

3.1 参数设计优点

一个产品的问世主要包括提出想法，初步确定方案，探讨方案进行可行性分析，最终确定方案，研制，以及最终成型。在设计的初级阶段主要是考虑方案的可行性，确定方案后，参数化设计各个结构零件，可以获得最满意的结果[30]。

结合本次所设计的气动机械手，参数化设计零件的优点是在相同的结构下，使每一个关节获得最大的运动范围，即绕各自的转动轴获得最大的转动角。

3.2 肩关节结构参数设计

3.2.1第一肩关节结构参数设计

第一肩关节的结构简图如图3-1所示。

图3-1 第一肩关节的结构简图

假定CBOEC1是第一肩关节开始的运动位置，BDD1E可绕O点旋转，逆时针旋转的极限位置是B1OE1，这时出现死点的现象，即当CB1O在同一直线上，连接BO，B1O，EO，E1O，C1O。作O点到CD的垂线交CD的延长线于F点。设OA= a，AD= d，BD= b，BC=L，BO= B1O= EO= E1O=R。

（1）确定b

b是肌肉连接件的铰链点到肩部肌肉连接件的距离，根据结构可得b=35mm。

（2）确定L

根据气动肌肉的型号，选定没有充气时长度为250mm的气动肌肉，其最大运动行程是原始长度的20%，在运动的开始位置，取其最大收缩长度的一半，即

是225mm，在加上气动肌肉本身结构（如图2-5）的其他长度，两个铰链点的长度L=225+50=275mm，L的范围是（275?25）mm。

（3）确定a

a是如图2-8b所示的肩部肌肉连接件宽度的一半，d是长度的一半。

设?为逆时针旋转时的最大角度，可知?BOB1=?，?EOE1=?，由于?BOC??EOC，所以?EOC1=?BOC=?。

?=?BOC=?FBO??FCO=arctanOFOF ?arctanFBFC

dd=arctan (3-1) ?arctana?ba?b?L

由公式（3-1）可知：

dd?dLLtan?=== 2(a?b)(a?b?L)(a?b)(a?b?L)?d1???da?ba?b?Ld

? (3-2) )

?由于tan?在??(0,)是单调增函数，b，L为已知，所以当a取得最小值时，2

tan?取得最大值，即?取得最大值。由于O点处装有一根?20mm的连接杆，因此取肩部肌肉连接件的宽度为30mm，即半宽a=15mm。

（4）确定d

由公式(2)可知，tan?

? ??47.2o

当?=47.2o代入公式(1-1)可知d无解。

计算BOE旋转到B1OE1的极限位置，其中气动肌肉CB1?250mm，C1E1?300mm。

CB1=CO?B1O=CO?

?250mm (3-3)

由公式(3-3)可得0?d?88.4mm (3-4) 已知?C1OE1=2?

C1E12?C1O2?E1O2?2C1O?E1O?cos2??3002 (3-5) 其中C1O=CO=

?= arctandd ?arctana?ba?b?L

代入公式(3-5)可得0?d?36.1mm (3-6) 根据气动肌肉的结构，在安装时，2d?24mm，

即 d?12mm (3-7)

.1有(3-4)、(3-6)、(3-7)式得 12?d?36mm

由公式(3-2)知tan?=dL，由于(a?b)(a?b?L)?d2d<<L，

d2<<(a?b)(a?b?L)，所以取最大的d时，可以得到最大的tan?，也就是最大的?,在这里取d=36mm。

（5）确定?

由公式(3-2)得 tan?=dL36?275= (a?b)(a?b?L)?d2(15?35)(15?35?275)?362 =0.564

得?=29.4o。

所以第一肩关节绕Z轴的理论最大运动范围为(?29.4o，29.4o)。

3.2.2第二肩关节结构参数设计

第二肩关节的结构简图如图3-2所示。

假定CAOEC1是第二肩关节开始的运动位置，铰链点A，E可绕O点旋转，逆时针的极限位置是A1OE1，即当CA1O在同一条直线上，连接AO，A1O，EO，E1O。作O点到CA的垂线交CA的延长线于F点。连接AE，作O点垂直AE交AE于B点。设AB= a，OB= b，AC=L,AO=A1O=EO=E1O=R。

（1）确定L

根据气动肌肉的型号，选定没有充气时长度为

230mm的气动肌肉，其最大运动行程是原始长度的

20%，在运动的开始位置，取其最大收缩长度的一半，

即是207mm，再加上气动肌肉本身结构（如图2-5）的

长度，两个铰链点的长度L=207+67=274mm，L的范

围是（274?23）mm。

（2）确定b

设?为逆时针旋转时的最大角度，可知

?AOA1=?,?EOE1=?，由于?AOC??EOC1，所以

?EOC1=?AOC=?。

?=?AOC=?FAO??FCO=arctan

arctanOF? FAOFaa=arctan?arctan (3-8) FCbb?L

有公式（3-8）可知：

aa?aLLtan?===

2aab(b?L)?a1???abb?La

? (3-9) ?由于tan?在??(0,)是单调增函数，L为已知，所以当b取得最小值时，2

tan?取得最大值，即?取得最大值。由于由于O点处装有一根?20mm的连接杆，因此取合适的最小的b=20mm。

（3）确定a

由公式(3-9)可知，tan?

得 ??60.8o

当??60.8o代入公式(3-8)可知a无解。

计算AOE旋转到A1OE1的极限位置，其中气动肌肉CA1?251mm

，=1.787

C1E1?297mm。

CA1=CO?A1O=CO?

?251mm (3-10)

由公式(3-10)可得0?a?41.3mm (3-11) 已知?C1OE1=2?

C1E12?C1O2?E1O2?2C1O?E1O?cos2??2972 (3-12) 其中C1O=CO=

?= arctanaa?arctan bb?L

代入公式(3-12)可得0?a?23.4mm (3-13) 根据气动肌肉的结构，在安装时，2a?24mm，即

a?12mm (3-14)

.4有(3-11)、(3-13)、(3-14)式得 12?a?23mm

由公式(3-9)知 tan?=aL,由于a<<L, a2<<b(b?L),所以取最大2b(b?L)?a

的a时，可以得到最大的tan?，也就是最大的?,在这里取a=23mm。

（4）确定?

由公式(3-9)得 tan?=

得?=44.5o

所以第二肩关节绕X轴的理论最大运动范围为(?44.5o，44.5o)。

3.2.3第三肩关节结构参数设计

第三肩关节通过大臂上的气动肌肉连接到肘关节上。第三肩关节的零件尺寸与肘关节的零件尺寸有关，其零件尺寸是通过肘关节的零件尺寸来确定的。因此第三肩关节的零件参数化设计详见肘关节的零件设计。

aL23?274==0.983 b(b?L)?a220(20?274)?232

95机械手臂设计_机械手臂设计

3.3 肘关节结构参数设计

肘关节的零件尺寸确定可以分为两个方向，即X轴和Y轴方向。下面分别就X轴和Y轴方向上的参数化设计进行阐述。

3.3.1 X轴方向上的结构参数设计

肘关节在X轴方向上的结构简图如图3-3所示。

假定CABC1是肘关节开始的运动位置，A，B可绕O点

旋转, 顺时针旋转的极限位置是A1OB1，这时出现死点现象，

即当CA1O在同一直线上，连接A1O，B1O。设OA= a，AD=

b，DD1=L。红色虚线框表示肘部挡板。

（1）确定b

b是肌肉连接件的长度,根据结构得b=45mm。

（2）确定L

根据气动肌肉的型号，选定没有充气时长度为230mm的

气动肌肉，其最大运动行程是原始长度的20%，在运动的开

始位置，取其最大收缩长度的一半，即是207mm，在加上气

动肌肉本身结构（如图2-5）的其他长度，两个铰链点的长度

L=207+50=257mm，L的范围是（257?23）mm。

（3）确定a

A,B表示肘部挡板上连接肌肉连接件的两个铰链点，a是两个铰链点距离的一半。

设?为顺时针旋转时的最大角度，可知?AOC1=?，?BOB1=?。

tan?=ACL?2b= (3-15) AOa

? 由公式(3-15)可知，tan?在??(0,)是单调增函数，b，L为已知，所以当a2

取得最小值时，tan?取得最大值，即?取得最大值。当a?0时，?=90o。

计算AOB旋转到A1OB1的极限位置，其中A1C?2b+Lmin=2?

45+234

=324mm。B1C1?2b+Lmax=2?45+280=370mm。

A1C= CO?A1

? A1

?a?324mm (3-16)

8 (3-17) 由公式(3-16)可得 0?a?23.mm

已知?BOB1=?，得?OBB1=???

2， ?B1BC1=?OBB1+?OBC1=???+??=?? 22

B1C12?BB12?BC12?2BB1?BC1?cos???

2?3702 (3-18)

BB12?OB12?OB2?2cos?=a2?a2?2cos?=2a2?2cos?

得BB1

BC1=AC=2b+L=347mm

?=arctanL?2b a

代入公式(3-18)得0?a?22.4mm (3-19) 根据气动肌肉的结构，在安装时，2a?24mm，

即 a?12mm (3-20)

?22mm .4由(3-17)、(3-19)、(3-20)式得 12?a

由公式(3-15)可知 tan?=ACL?2b=，且已知L=257mm，b=45mm，当取AOa

最小值a=12时，tan?取得最大值。

（4）确定?

tan?=ACL?2b257?2?45===28.9 AOa12

得 ?=88.0 o

所以肘关节绕X轴的理论最大运动范围为(?88.0o，88.0o)。

由此可以得到第三肩关节的两个铰链点之间的距离为2a=24mm。

3.3.2 Y轴方向上的结构参数设计

肘关节在Y轴方向上的结构简图如图3-4所示。

假定CAOA1C1是肘关节开始的运动位置，D，B可绕O点旋转,作以O点为圆心，OD为半径的圆。顺时针旋转的极限位置是D1OB1，这时出现死点的现

象，即当CD1O在同一直线上，连接DO，D1O，BO，B1O，C1O。设OA= a，AD= b，DC=L。

（1）确定a

设?为顺时针旋转时的最大角度，可知

?DOC=?，?BOB1=?。由于?DOC??BOC1，

所以?BOC1=?DOC =?。

?=?DOC=?AOC??AOD ACAD ?arctanAOAO

b?Lb?arctan (3-21) =arctanaa=arctan

有公式（3-21）可知：

b?Lb?aLL=tan?==?b(b?L)?a21???

aaaa

=1.10

可得 ??47.8o

计算DOB旋转到D1OB1的极限位置，其中

CD1?234mm，C1B1?280mm。

CD1=CO?D1

?234mm (3-22)

由公式(3-22)可得0?a?58.2mm (3-23) 已知?C1OB1=2?

C1B12?C1O2?B1O2?2C1O?B1O?cos2??2802 (3-24) 其中C1O=CO=

?=arctanb?Lb?arctan aa

代入公式(3-24)可得0?a?32.4mm (3-25) 根据气动肌肉的结构，在安装时，2a?24mm，

即 a?12mm (3-26)

.4有(3-23)、(3-25)、(3-26)式得 12?a?32mm

可知 tan?=aL，由于a<<L，a2<<b(b?L)，所以取最大的a时，2b(b?L)?a

可以得到最大的tan?，也就是最大的?,在这里取a=32mm。

（2）确定?

所以 tan?=aL32?257==0.563 b(b?L)?a245(45?257)?322

得?=29.4o。

所以肘关节绕Y轴的理论最大运动范围为(?29.4o，29.4o)。

由此可以得到第三肩关节长度方向的两个铰链点之间的距离为2a=64mm。

3.4 腕关节结构参数设计

腕关节加上小臂的结构等同于肘关节加上大臂的结构，因此肘关节的零件尺寸确定于腕关节的零件尺寸确定完全一样，唯一不同的是肘关节是X，Y轴方向，腕关节是X，Z轴方向。

（1）X轴方向上的结构参数设计

腕关节X轴方向上的结构简图与肘关节X轴方向的一样，因此直接得到结果：取最小值a=12mm时，tan?取得最大值，tan?=28.9，得?=88.0 o。

腕关节绕Z轴的理论最大运动范围为(?88.0o，88.0o)。

由此可以得到腕肩关节挡板上的两个铰链点之间的距离为2a=24mm。

（2）Z轴方向上的结构参数设计

腕关节Z轴方向上的结构简图与肘关节Y轴方向的一样，因此直接得到结果：取最大值a=32mm时，tan?取得最大值，tan?=0.563，得?=29.4o。

腕关节绕X轴的理论最大运动范围为(?29.4o，29.4o)。

由此可以得到腕关节两块挡板的两个铰链点之间的距离为2a=64mm。

第4章气动机械手关节的模拟仿真

4.1 仿真内容

运动仿真是结构构设计的一个重要内容,气动机械手是一个复杂的机构，确定结构后，在运行中还会发生干涉现象，因此需要进行运动学仿真分析，确保方案可行。在运动仿真过程中，对结构零件不断进行修改，最终满足设计要求[31]。

仿真的基本内容是对结构进行可行性分析，运动学分析，增大机械手的运动范围，使其更好的满足生产需要。结合本次设计的气动机械手，仿真的内容是

(1)第一肩关节的运动仿真；

(2)第二肩关节的运动仿真；

(3)肘关节X轴方向的运动仿真；

(4)肘关节Y轴方向的运动仿真；

(5)腕关节X轴方向的运动仿真；

(6)腕关节Z轴方向的运动仿真；

(7)第一、二肩关节，肘关节X轴方向，腕关节X轴方向的运动仿真；

(8)第一、二肩关节，肘关节Y轴方向，腕关节Z轴方向的运动仿真。

4.2 仿真方法

运动仿真是结构设计的一个重要内容,在Pro/E的Mechanism模块中,通过对机构添加运动副、驱动器使其运动起来,来实现机构的运动仿真。在整体设计后, 通过仿真可以模拟机构的运动,从而检查机构的运动是否达到设计要求,是否发生干涉，实现机构的设计与运动轨迹校核。同时,可直接分析各运动副与构件在某一时刻的位置、运动量以及各运动副之间的相互运动关系及关键部件的受力情况。在Pro/E环境下进行机构的运动仿真分析,不需要复杂的数学建模、也不需要复杂的计算机语言编程,而是以实体模型为基础,集设计与运动分析于一体,实现产品设计、分析的参数化和全相关,反映机构的真实运动情况[32]。

本文以PTC公司的三维建模软件Pro/E及其中的运动学仿真功能建立气动机械手关节的运动仿真模型。首先在Pro/E中建立气动机械手关节的三维模型，然后完成整个机械手的装配，设置关节的安装位置为机构运动的初始位置，添加驱动和约束，进行运动仿真。在整个过程中，需要对建立模型等前续工作进行不断

95机械手臂设计_机械手臂设计

的修改和完善，才能生成所要求的气动机械手关节的仿真模型。

4.3气动机械手关节的运动学分析

仿真时，气动肌肉作为动力源，极限位置是气动肌肉与转动轴（铰链点）在同一条直线上，即出现死点的位置。

4.3.1第一肩关节的运动仿真及分析

第一肩关节运动前后的位置如图4-1（a）和4-1（b）所示。在此运动过程中，无干涉现象，通过测量极限位置的角度，得到?=29.4o，所以第一肩关节绕Z轴的实际最大运动范围为(?29.4o，29.4o)。

（a）运动前（b）运动后

图4-1 第一肩关节仿真效果图

4.3.2第二肩关节的运动仿真及分析

第二肩关节运动前后的位置如图4-2（a）和4-2（b）所示。在此运动过程中，无干涉现象，通过测量极限位置的角度，得到?=44.5o，所以第二肩关节绕X轴的实际最大运动范围为(?44.5o，44.5o)。

（a）运动前（b）运动后

图4-2 第二肩关节仿真效果图

4.3.3肘关节X轴方向的运动仿真及分析

肘关节X轴方向运动前后的位置如图4-3所示，其中图（a）表示向上转动，图（b）表示向下转动。在此过程中，均发生干涉现象，发生图（a）现象的原因是：①肘关节有一块挡板连接板，向上转动时气动肌肉碰到挡板连接板而发生干涉；②由于挡板上的铰链点的距离太近，在运动到极限位置之前，两对气动肌肉就已发生了干涉。发生图（b）现象是由于原因②。

（a1）运动前（a2）运动后

（a）向上转动

（b1）运动前（b2）运动后

（b）向下转动

图4-3肘关节X轴方向仿真效果图

其中原因①是无法解决的，不过可以通过增加挡板的长度来增加向上转过的角度；原因②可以通过增加挡板上的铰链点的距离（如图3-3）即AB=2a的长度来改善，值得一提的是改变a的长度，A点不能运行到A1的位置，这里取a=25mm。相应的腕关节在X轴方向上的a=25mm。修改后的肘关节X轴方向运动到极限位置的效果图如图4-4所示。绕X轴的运动范围为（?60.4 o，32.6 o）。 22

（a1）运动前（a2）运动后

（a）向上转动

（b1）运动前（b2）运动后

（b）向下转动

图4-4修改后肘关节X轴方向仿真效果图

4.3.4肘关节Y轴方向的运动仿真及分析

肘关节Y轴方向运动前后的位置如图4-5（a）和4-5（b）所示。在此过程中无干涉现象，通过通过测量极限位置的角度，得到?=29.4o，所以肘关节绕Y轴的实际最大运动范围为(?29.4o，29.4o)。

（a）运动前（b）运动后

图4-5 肘关节Y轴方向仿真效果图

4.3.5腕关节X轴方向的运动仿真及分析

腕关节在X轴方向上的零件尺寸已经根据肘关节在X轴方向的零件尺寸进行修改。运动前后的位置如图4-6（a）和4-6（b）所示。在仿真过程中，无干涉现象，通过测量极限位置的角度，得到?= 70.7o，所以腕关节绕Z轴的实际最大运动范围为(?70.7o，70.7o)。

（a）运动前（b）运动后

图4-6 腕关节X轴方向仿真效果图

4.3.6腕关节Z轴方向的运动仿真及分析

腕关节Z轴方向运动前后的位置如图4-7（a）和4-7（b）所示。此过程中无干涉现象，通过通过测量极限位置的角度，得到?=29.4o，所以腕关节绕X轴的实际最大运动范围为(?29.4o，29.4o)。

（a）运动前（b）运动后

图4-7 腕关节Z轴方向仿真效果图

4.3.7第一、二肩关节，肘关节X轴方向，腕关节X轴方向的运动仿真及分析

第一、二肩关节，肘关节X轴方向，腕关节X轴方向运动前后的位置如图4-8（a）和4-8（b）所示。在此过程中无干涉现象，说明此次设计的气动机械手能在预期的范围内进行运动。

（a）运动前（b）运动后

图4-8 总运动效果图（1）

4.3.8第一、二肩关节，肘关节Y轴方向，腕关节Z轴方向的运动仿真及分析

第一、二肩关节，肘关节Y轴方向，腕关节Z轴方向运动前后的位置如图4-9（a）和4-9（b）所示。在此过程中无干涉现象，说明此次设计的气动机械手能在预期的范围内进行运动。

（a）运动前（b）运动后

图4-9 总运动效果图（2）

95机械手臂设计_机械手臂设计

第5章结论

本文设计了一个全部由气动肌肉驱动的机械手，从整体结构到各个关节、手臂零件的设计，通过理论计算和三维模拟仿真，对各个关节进行优化，最终实现气动机械手关节最大的运动范围，满足预期设计要求。

各个关节的最大运动范围如下：

（1）肩关节

第一肩关节 (?29.4o，29.4o)

第二肩关节 (?44.5o，44.5o)

（2）肘关节

肘关节X轴方向 (?60.4 o，32.6 o)

肘关节Y轴方向 (?29.4o，29.4o)

（3）腕关节

腕关节X轴方向 (?70.7o，70.7o)

腕关节Z轴方向 (?29.4o，29.4o)

该机械手能够实现4个自由度的运动，气动肌肉具有控制精确的特点，在抓取物品等进行生产实践时，能够实现高精度的动作，基本满足了实际应用需要。该气动机械手具有轻巧、安全和控制简单等特点，可以用于工厂机器人，服务机器人等和人密切接触的场合。

参考文献

[1] 徐炳辉.气动手册[M].上海科学技术出版社，2005.26~28.

[2] SMC(中国)有限公司.现代实用技术[M].北京：机械工业出版社，2005.36~37.

[3] 隋立明，张立勋.气动肌肉驱动仿生关节的理论分析[J].机床与液压，2007,

35(6):218~219.

[4] Qiu Yangzhen, Lin Yimeng. Research and Applications of High Precision Pneumatic

Manipulator.Hydraulic Pressure and Pneumatic[J]. 2006, 28(4):55~56.

[5] 王雄耀.近代气动机器人(气动机械手)的发展及应用[J].液压与气动技，1999,

12(5):13~16.

[6] 姜继海，宋锦春，高常识.液压与气压传动[M].高等教育出版社，2002.52~54.

[7] B.Tondu，P.Lopez．Modeling and control of McKibben artificial muscle robot

actuators[J]．IEEE Control System Magazine，2000, 27(6):15~38.

[8]上海工业大学流控研究室.气动技术基础[M].机械工业出版社，1982.21~22.

[9] 杜来林，等.液压与气压传动[M].北京大学出版社，2005.10~13.

[10] 郑洪生.气压传动[M].机械工业出版社，2004.108~110.

[11] [德]Wemer Deppert KunStdl.气动技术——低成本综合自动化[M].李宝仁，译.机械工

业出版社，1999.63~64.

[12] 王孝华，赵中林，等.气动元件及系统的使用与维修[M].机械工业出版社，1996.21~22.

[13] [美]Saeed B．Niku．机器人学导论——分析、系统及应用[M].孙富春，朱纪洪，刘国

栋等译．孙增圻，审校.电子工业出版社，2004.56~57.

[14] 齐进凯，陈冰冰.基于Pro/Engineer的气动机械手参数化设计[J].机械设计，2000,

22(2):257~258.

[15] 蔡自兴.机器人学[M].北京：清华大学出版社，2000.154~155.

[16]Tbndu B，Lopez.P Modeling and control of mckibben artificial muscle robot

aetuatom[J]．IEEE Control systems Magazine 2000, 5(7):15~38.

[17] 袁子荣.液气压传动与控制[M].重庆大学出版社，2002.122~124.

[18] 葛宜远.流体传动及控制技术的新成就[J].液压与气动，1998, 16(2):1~3.

[19] 路甬祥.气动技术的发展方向[J].液压与气动，1991, 5(2):2~3.

[20] 许炳辉.气动技术基础知识[J].液压与气动，1994, 5(1):39~41.

[21] J.L.Shear.Study of pneumatic process in the continuous control of motion with compressed

air-L[M].Trans of ASME,1956.233~241.

[22] Zhou Hong. Intelligent pneumatic-The latest trend in pneumatic actuators and control

systems[M].Proceeding of the 4th International Conference on Fluid Power Transmission and Control,1997.335~348.

[23] 陆鑫盛，周洪.气动自动化系统的优化设计[M].上海科学技术文献出版社，

1999.86~89.

[24] 陈新元，张安龙.装配线机械手电气混合控制[J].液压与气动，2007, 13(3):46~47.

[25] 蔡自兴．机器人学[M].北京：清华大学出版社，2000.59~60.

[26] 路甬祥. 液压气动技术手册[M]．机械工业出版社,2003.10~12.

[27] 隋立明,王祖温,包钢.气动肌肉驱动仿人臂的设计[J].液压与气动.2004, 10(9):7~8.

[28] 刘辛军，汪劲松，高峰，金振林.一种串并联结构拟人七自由度冗余手臂的设计[J].中

国机械工程，2002, 13(2):101~104.

[29] 吴伟国，邓喜君，蔡鹤皋.基于改进PYR型全方位关节的7自由度仿人手臂设计[J].中国

机械工程，1999, 10(12):1345~1346.

[30] 毛君,毕长飞.基于Pro/Engineer采煤机的三维动态仿真与优化设计[J].煤矿机械，

2006, 27(6):990~994.

[31] 路甬祥.液压气动技术手册[M].机械工业出版社，2002.65~66.

[32] 隋立明，谭世江，赵铁，张立勋.气动肌肉的结构设计与制作[J].液压与气动. 2008,

17(2):48~49.

致谢

本毕业论文是在我的导师教授的亲切关怀和悉心指导下完成的。她严肃的科学态度，严谨的治学精神，精益求精的工作作风，深深地感染和激励着我。从课题的选择到项目的最终完成，老师都始终给予我细心的指导和不懈的支持。半年来，老师不仅在学业上给我以精心指导，同时还在思想、生活上给我以无微不至的关怀，在此谨向老师致以诚挚的谢意和崇高的敬意。

在此我还要感谢研究生，正是由于她的帮助和支持，我才能克服一个一个的困难和疑惑，直至本文的顺利完成。

在论文即将完成之际，我的心情无法平静，从开始进入课题到论文的顺利完成，有多少可敬的师长、同学、朋友给了我无言的帮助，在这里请接受我诚挚的谢意!同时感谢培养我长大含辛茹苦的父母，谢谢你们！

最后感谢我的母校——大学四年来对我的栽培。

二 : 机械手臂的结构设计

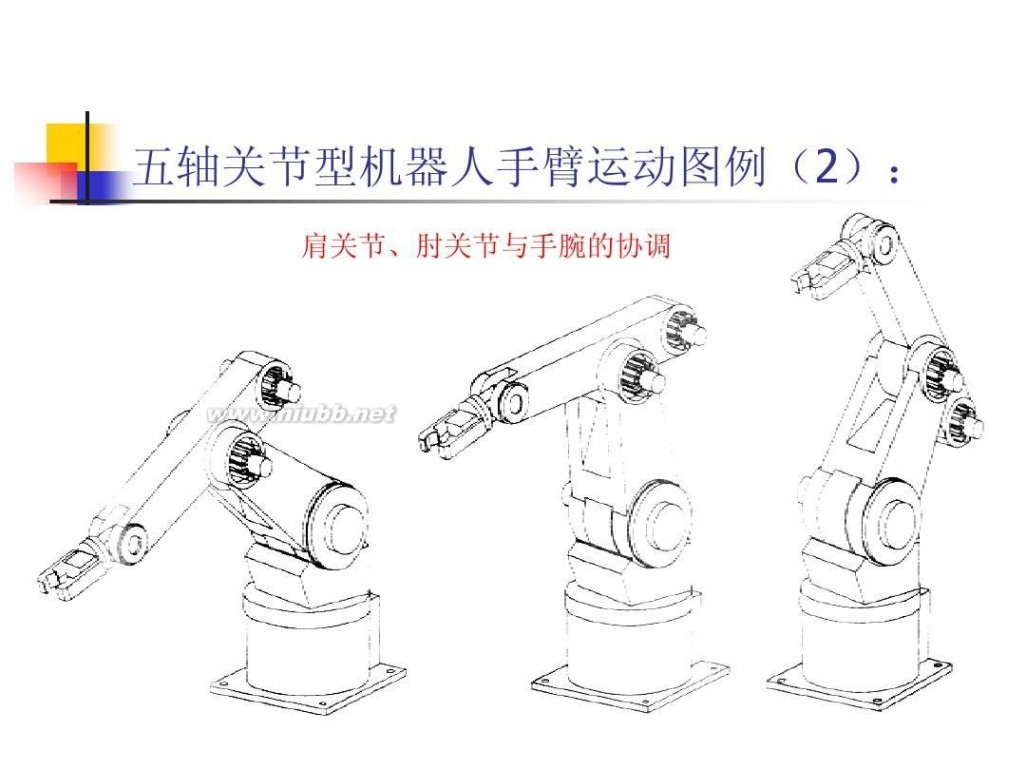
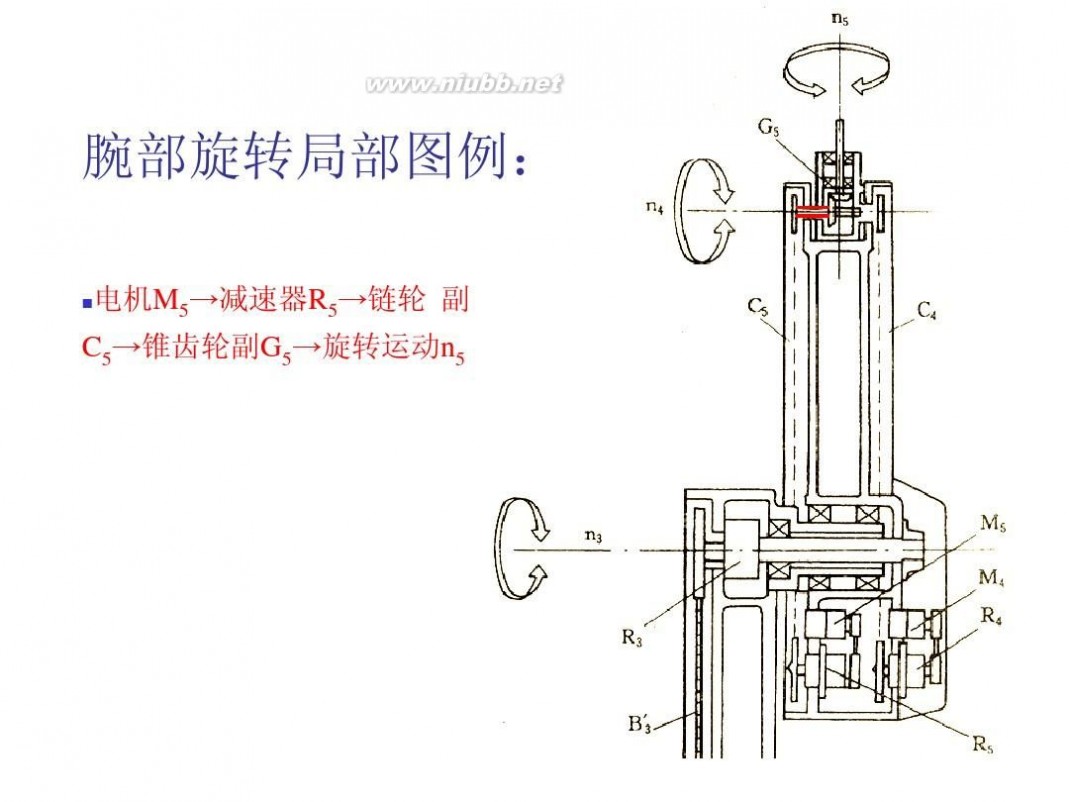
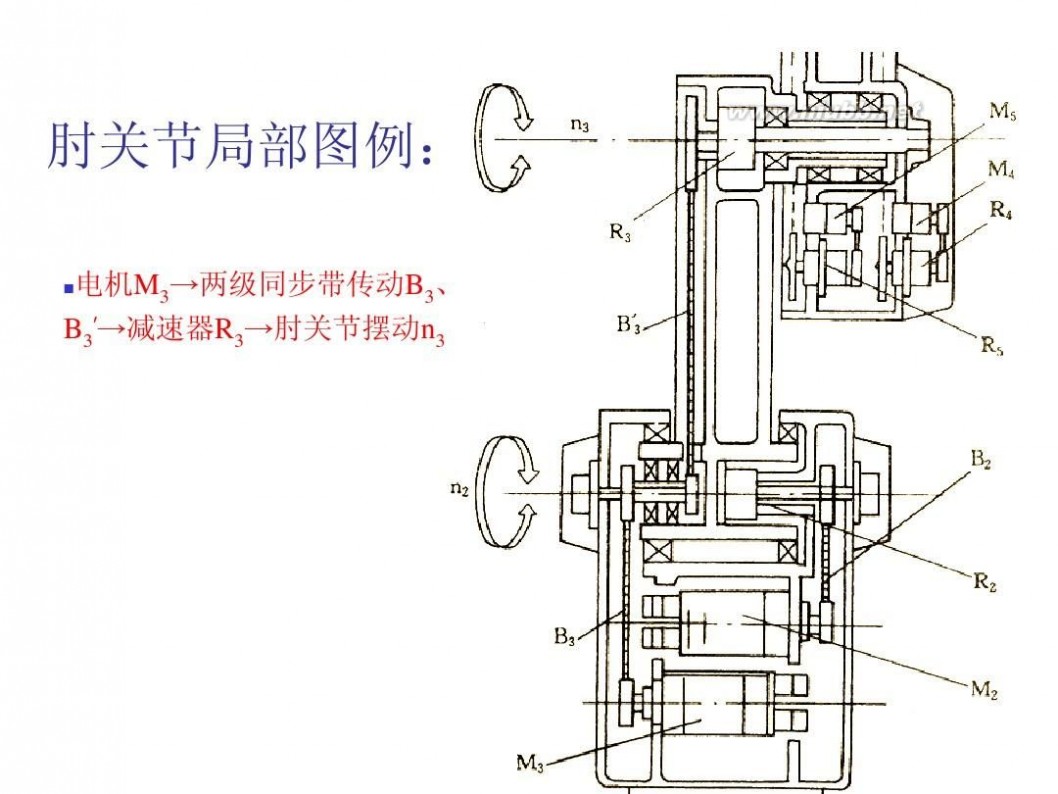
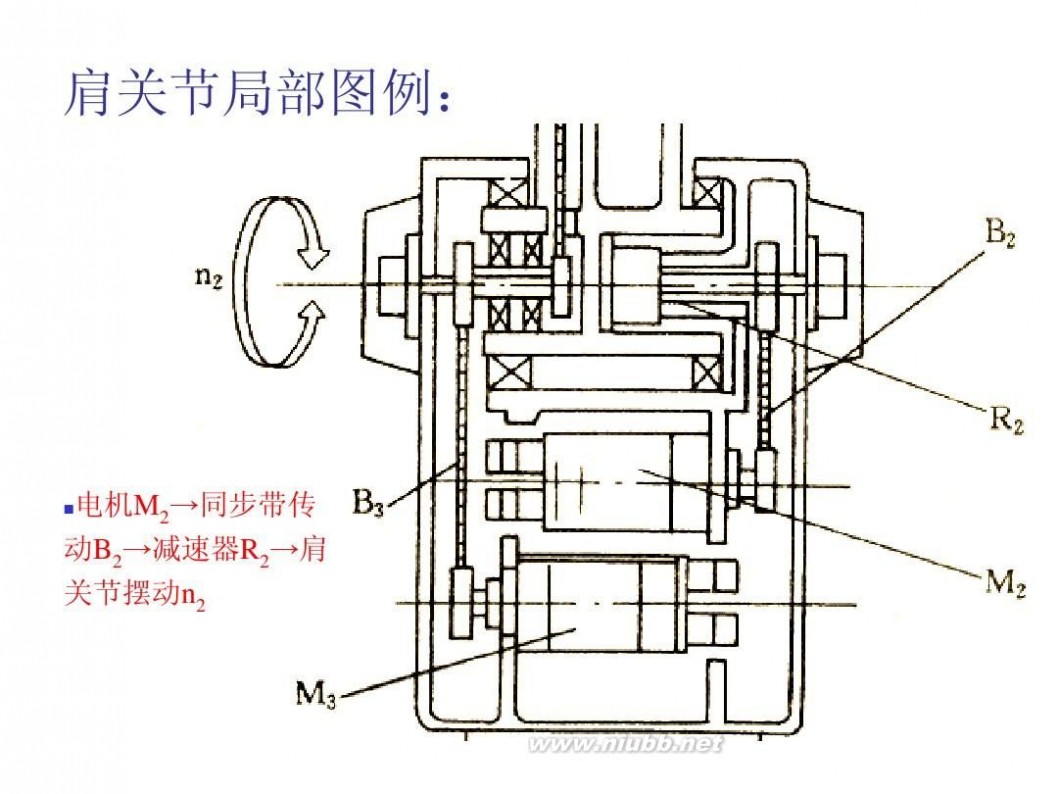
机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

机械臂机械手臂的结构设计

三 : 机械手臂结构优化设计

第$期%&&_年$月

文章编号：$&&$5W^^#!%&&_’&$5&&$W5&W

机械设计与制造

J?U1-3,@GX,C-43DJ?3>9?UA>@,

5$W5

机械手臂结构优化设计

高

微

杨中平

赵荣飞

薛娟萍!西北农林科技大学"杨凌#$%$&&’

!"#$%&%’#(&)#&(*+*’$,-./%*)01-$)121(%

()*+,-".)/(0123456-34"07)*823459,-，:;<=>?356-34

!/2@A1B,CA)DE;3-F,@C-AG".?34H-34#$%$&&"I1-3?’

4444444444444444444444444445

4444444444444444444444444444444444444444444444444444444445

4444444444444444444444444445

【摘要】机械手臂的设计是目前机器人科学研究的一个热点。这里考虑手臂的抓重、材料和运动速度，对其进行优化设计。建立了优化设计的数学模型，使用J)KL)M软件分析目标函数的性态并设计变量的可行域，求得机械手臂最优尺寸。在满足条件的情况下，使手臂质量最小，证明了该设计可以满足预设动作要求。

关键词：机械手臂；优化设计；强度条件；刚度条件；J)KL)M；软件

【!"#$%&’$】!"#$#%&’()*+#,"-(&,-.-/+&%-")01)&(0)(-20)+-0)(/#%#-/,"-01/#%#(03!"&%1-1#/+-4#)10&+&5#$$#%&’()*-/+6-%#$)(&0%’/-%1&(’7#&’"08+-0#/&-.-($%1##$)*+)9#+#(0-($%#021-+-0"#+-0&,-.+)$#.)*0"#)10&+2+%0/2,02/#$#%&’(3!"#)10&+-.%&5#%)*0"#-/+-/#)60-&(#$6:-(-.:5&(’,"-/-,0#/)**2(,0&)($&-’/-+-($$#%&’(&(’*#-%&6.#/#’&)()*9-/&-6.#6:2%&(’0"#;<!=<>%)*07-/#3?(,-%#)*+##0&(’0"#’&9#(,)($&0&)(8+-4#-/+@2-.&0:+&(&+2+80"2%1/)9#$0"-00"&%$#%&’(,)2.$%-0&%*:0"#/#@2&/#+#(0%)*0"#*)/#A%#0+)9#+#(03

()*+,%-#./)’0&12’&3&%4567$2484-)#2915:$%)19$0’,1-2$2,15:$2;;1)##’,1-2$2,15/!<=!>5:,;$+&%)

中图分类号：K7$%%文献标识码：)

机械手臂作为机器人的一个重要组成部分，一直是机器人

科学研究的热点之一。机械手臂的结构设计通常是一多解问题Y$[。目前，还未形成完备的设计方案。这里针对具体实例，运用目前较为流行的结构优化计算来调整截面尺寸和手臂长度，使其在满足强度、刚度和尺寸要求的前提下，得到最优尺寸和最小质量，实现结构优化设计。

#来稿日期：%&&]5&\5&W

耦合集：N弧面分度凸轮机构〈弧面分度凸轮

P从动盘O;%〉O;$，

端口：N轴线垂直Q弧面分度凸轮O;$R轴线

E;"分度盘O;%R轴线E;间距S中心距ITP

属性参数：

N中心距I，弧面分度凸轮R许用压力角，弧

面分度凸轮R凸轮节圆半径，从动盘R转盘节圆半径，从动盘R滚子半从动盘与凸轮在分度期的角速比，凸轮角位移P径，从动盘R滚子宽度，规则集：

N凸轮与滚子的共轭接触方程：凸轮工作轮廓在动坐标系的方程：

B$SB%U2C!U2C"51:%C-3!U2C"A5%C-3"5CU2C":$S5B%U2C!U2C"V1:%C-3!U2C"A5%CU2C"VC-3"5$S1B%C-3!U2C"V:%U2C"P

$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$

4444444444444444444444444444444444444444444444444444444445

$问题描述

机械手臂种类较多，各类型手臂结构也有相当差异。这里中手臂因其内部要按放电子线路的特殊使用要求而设计为圆环（即各截截面的直杆"考虑到经济和美观要求，采用等强度截面面所受应力相等，而尺寸不相等）设计。手臂结构可简化为图$（为简化计算手臂截面取为定值，并忽略了汽缸对手臂的支撑作用）所示。手臂是机械手支承被抓物件、手部和手腕的重要部

W结论

在虚拟制造中的弧面分度凸轮建模，不仅要求模型的数据完整一直和可靠，同时更重要是要求模型的可重用性。基于JX;元建模方法对弧面分度凸轮进行建模可以对传统模型的开发与分析产生积极重大的影响。重要表现于：

（$）增加模型数据的可交换性，减少虚拟设计中代码冗余。

（%）保证模型间的数据一致性，加强数据的互操作与模型间的无缝集成。

这里在对元建模及其建模技术的分析基础上，提出了基于JX;元建模理论的弧面分度凸轮模型虚拟设计方法，将对进一步基于JX;方法的参数约束、拓扑约束对弧面分度凸轮的参数化设计有着积极作用，也将成为弧面分度凸轮建模发展趋势。

参考文献

$张玲等R虚拟制造中的产品建模技术研究R基于产品定义单元和元建模的产品模型YZ[R机械科学与技术第六期，%&&&R$$R清华大学出版社，%&&\R%肖田元R虚拟制造YJ[R北京：

万方数据

G%/.高微等：机械手臂结构优化设计

第%期

件，其作用是带动手指去抓取物件，并按预定要求将其搬运到指定位置!"#!$#。这里设计目的是在手臂载重一定的情况下，得出一个手臂质量最小的结构设计方案。

实例：机械手的主参数为最大抓重（目前，该值通常为%&公斤左右，故设重物!%为%&’(）。影响机械手动作快慢的主要因素是手臂伸缩及回转的速度，设机械手最大移动速度为%)"*+,；最大回转速度为%"&-+,。由于结构的需要.选取手臂长度"6/&0*；

选用合金钢管作为手臂的原始材料；钢管的厚度1取为"**。查常用材料手册得出，弹性模量#2"3%&4567；许用弯曲应力!!$#2%"&567；

许用剪切应力!"#28&567；允许挠度!%#2"+%&&&；密度#29)8(+0*$。求解满足使用要求前提下手臂的最小质量。

"设计分析

手臂运动由提升重物的竖直运动与带动重物旋转的水平回转运动组成。手臂自重相对于重物来说.对手臂强度计算的影响较小，可不作考略，故设计时仅考虑重物:的作用。手臂受力如图%所示。

-.-(

-&"

图%机械手臂受力图;<()%;-=0>,-?@A>*>0A7B<07C7=*

")%抗拉强度条件

如图%所示，手臂D点处受到最大拉应力!*7E，!*7E是由弯矩5产生的拉应力!%与向心力&产生的应力!"组成。其中!%’)式中，)*为抗弯截面系数，仅与截面形状、尺寸有关。*对于外径为+内径为F的圆环截面有：

)*2

[%G()/

]

H%I(’,"H"I

!"’&-

式中，-为手臂横截面积（!"），-2!

[(+)

+./"

(

)]

2%/

!（"+/./"）H$I&’!%"$

H/I

据抗拉强度条件有：

!*7B’(0)1&-［!2

］

H4I*将式（%）（、"）（、$）（、/）及已知数据代入式（4），取32%&*+

,（"

下同）.计算整理得：

%"&+$GJ9&+"K$/+GL)/"+)&

")"抗剪强度条件

手臂D点处所受剪应力最大。因圆环截面壁厚1远小于外径M，故最大剪应力为：

"*7E’"

-据抗剪强度条件有：

万方数据

"*7B’"

7［"］

HLI

将已知数据代入式（L），计算整理得：+)&)"H0*I

")$刚度条件

如图%所示，受力分析得，(点处挠度$最大。据刚度条件$*7B’

$$#5［$］2%&&&

H9I

式中，#为材料的弹性模量（:67）；5为截面惯性矩（0*/），52!

+/.F/）H8I

将式（8）及已知数据代入式（9），计算整理得：$&+$G%8+"G&)L/"")&

")/结构尺寸限制

+6N"/")/&H0*I

$建立数学模型

优化设计追求的目标是机械手臂的质量!"最小。!"的计算表达式为：

!"H7I2(H7%.7"I’

!+"GH+."/I"#"#2&)&&4"+G&)&&%"

HJI

式中，设计变量72!7%.7"#/’!"8+#/

由第二步设计分析计算得M的值约$)40*，

故式（J）可简化为：!"H7I2&)&&/LOM

显然，"、+越小，!"值越小。据此，可写出优化设计的数学模型!/#：

*<B!"H7I2&)&&/L"+7’!"8+#

$9:9%"&+$GJ9+"K$/+.L)/"+)&+)&)"H0*I

$&+$G%8+"G&)L/"")&+66"/")/&H0*I

此数学模型是一个单目标非线性二维约束优化问题。

/优化计算

我们将用于求解优化设计数学模型的方法或寻优的方法称为优化计算方法。对于机械优化设计问题，求解常常需要经过多步迭代，最终收敛得到最优解!/#。这里运用数学规划方法的理论，根据数学模型的特点，利用5P1OPQL)4软件进行辅助优化计算与设计，以求得机械手臂的最佳设计参数!4#!L#!9#。

/)%函数的性态分析

应用5P1OPQL)4编程：

!E.R#2*>,A(=<FHC<B,S70>H&.L.$&I.C<B,S70>H&.4&.$&IIT

U根据函数的定义划分网格区域

52&)&&/L#R#ETU目标函数

*>,AHE.R.5IT

U通过三维网格模拟目标函数图形

在5P1OPQL)4下运行程序可画出目标函数的三维图形，如图"所示：

!"#$%&’#())*

机械设计与制造

+$,+

目标函数图像,/!.)#))/*10

/)I)!

()$)),)

*/)

I)/

()

)

图(函数-.)#))/*01的图像234#(56789’:;3"’<3&4=&>"8!.)#))/*01

"8#8$)?"8$8,)

同样，通过编程，-@50@A*#,可绘出各约束函数的图形。程序如下：

7BCD";EF$()#GHI+JK#GH(LI/#G+*#/#M#GF?

N)?$)?)?,)OPQ抗拉强度条件的图形，

6"D<"’M.)R)#$R,)SG.)#(SCD";EG?M?FTFPQ抗剪强度条件的图形，FTF指图形颜色为黑色

6"D<"’

7BCD";EFI)#GHI+$U#GH(+)#*/#MH(F?N)?$)?)?,)OP

Q刚度条件的图形

6"D<"’M.)R)#$R,)SG.)#/SCD";EG?M?FTFPQ截面尺寸边界条件图形

6"D<"’G.)R)#$R$)SM./)SCD";EG?M?F>FPQ长度尺寸边界条件图形，F>F指图形颜色为紫红色

6"D<"’

;3;D7EF各个约束函数图像FPQ标注图形名称;7G;E/?/,?F可行域FP

Q注明F可行域F区域

6"D<"88运行程序绘出约束函数的图形?如I所示：

各个约束函数图像

/,可行域

$./)

/)I,#.)#/

$I)#.)#(I)GI+$UG(+)#*/M(.)

(,()$()GI+JKG(LI/G+*#/MG.)

$,$),)

)$(I/

*KUJ$)#

图I设计变量的可行域

234#I27&V3WD7=743"’"8X&=3&WD7<7V34’

由图(可以看出R目标函数的图像规则?即性态好?对于多数优化方法均适用。对图I可行域分析可知，

实际起约束作用有：（$）刚度条件：

I)%I+$U%(+)#*/&())（(）结构尺寸限制条件：&+/)6)

所以?计算时只须考虑这两个条件。这样就大大简化了计

万方数据

算过程。

/#(应用-@50@A软件求解

E$P编写目标函数的>文件R"WY89’#>?返回G处的函数值8。89’:;3"’8.ZWY89’EGP

8.)#))/*#GE$P#GE(P；

E(P因设计约束含非线性约束?故需编写一个描述非线性

约束的>文件R

!"’03’["’V;=#>

89’:;3"’N:?:7\O.!"’03’["’V;=EGP

:.+I)#GE$PHIL$U#GE$PH(L)#*/#GE(PH(S:7\.NOS

EIP给定变量的初值，并调用优化函数：

G).N//)OFS@.N)+$OSW.N+/)OSDW.B7="VE$?$PSQ赋)语句

"C;3"’V."C;3>V7;EF13VCD&MF?F3;7=F?F0&=47]:&D7F?F

"88FPS

NG?8X&D?7G3;8D&4?"9;C9;O.8>3’:"’EFZWY89’F?G)?@?W?NO?NO?DW?NO?F!"’03’["’V;=F?"C;3"’VP

E/P计算结果R

I#U$*)Q最后的优化结果/)#))))Q1.I#U$*):>?0./):>8X&D.Q优化后的最小质量)#K)($

Q>(>3’.)#K)($T47G3;8D&4.

Q算法退出处条件

"9;CD";.

3;7=&;3"’VR(

Q函数调用次数89’:["9’;R$$Q函数赋值次数V;7CV3B7R$Q步长&D4"=3;6>RF>7<39>+V:&D7R]^_?^9&V3+!7‘;"’?

D3’7+V7&=:6F

Q算法

83=V;"=<7="C;R)#$U/)Q第一优化命令的长度:43;7=&;3"’VRNO

经$$次迭代计算后?求得最优方案为R1.I#U$*):>?0./):>?>(.)#K)($T4。

,结束语

这里对实例中机械手臂运动受力进行分析，求得满足强度、刚度和结构尺寸的方程，并建立了优化设计的数学模型，在此基础上编制程序求得手臂的最小质量，实现了手臂的结构优化设计。本设计的主要特点是运用-@50@A算法进行优化设计，它使得优化过程变得非常简单、容易理解和掌握?从而避免编写各

种复杂的运算程序，提高了设计效率。设计值与所求近似值很接近，说明其具有相当的可信度，并且优化结果可以明显降低加工成本?具有较高的经济价值。对目前的机械手臂结构设计方法进行了创新，为今后的设计提供了新的思路。

参考文献

$王承义#机械手及其应用N-O#北京R机械工业出版社?$JU$#(龙立新#工业机械手的设计分析N%O#焊工之友?$JJJ?I#I孙靖民#机械优化设计N-O#北京R机械工业出版社?()))#/刘惟信#机械最优化设计E第二版PN-O#北京R清华大学出版社?$JJK#

机械手臂结构优化设计

作者：

作者单位：

刊名：

英文刊名：

年，卷(期)：

被引用次数：高微，杨中平，赵荣飞，薛娟萍， GAO Wei， YANG Zhong-ping， ZHAO Rong-fei， XUEJuan-ping西北农林科技大学,杨凌,712100机械设计与制造MACHINERY DESIGN & MANUFACTURE2006(1)5次

参考文献(4条)

1.王承义机械手及其应用 1981

2.龙立新工业机械手的设计分析 1999

3.孙靖民机械优化设计 2000

4.刘惟信机械最优化设计 1997

引证文献(5条)

1.阮学云.王永生.张军.王光生基于MATLAB煤液钻空心传动轴的优化设计[期刊论文]-煤矿机械 2008(3)

2.梁喜凤.王永维.苗香雯番茄收获机械手机构尺寸优化设计[期刊论文]-机械设计与研究 2008(1)

3.方学红.李延富.张竺英供排气管对接机械手的机构研究与参数优化[期刊论文]-机械设计与制造 2008(1)

4.肖丽萍.魏文军.宋建农.靳桂萍可控变杆长空间机构在农机部件工作轨迹上的设计与应用[期刊论文]-农业工程学报2007(7)

5.梁胜龙.徐忠兰平压模切机执行机构的节能优化设计[期刊论文]-机械传动 2010(11)

本文链接：http://d.g.wanfangdata.com.cn/Periodical_jxsjyzz200601006.aspx

四 : 机械手臂结构优化设计

第$期%&&_年$月

文章编号：$&&$5W^^#!%&&_’&$5&&$W5&W

机械设计与制造

J?U1-3,@GX,C-43DJ?3>9?UA>@,

5$W5

机械手臂结构优化设计

高

微

杨中平

赵荣飞

薛娟萍!西北农林科技大学"杨凌#$%$&&’

!"#$%&%’#(&)#&(*+*’$,-./%*)01-$)121(%

()*+,-".)/(0123456-34"07)*823459,-，:;<=>?356-34

!/2@A1B,CA)DE;3-F,@C-AG".?34H-34#$%$&&"I1-3?’

4444444444444444444444444445

4444444444444444444444444444444444444444444444444444444445

4444444444444444444444444445

【摘要】机械手臂的设计是目前机器人科学研究的一个热点。［www.61k.com]这里考虑手臂的抓重、材料和运动速度，对其进行优化设计。建立了优化设计的数学模型，使用J)KL)M软件分析目标函数的性态并设计变量的可行域，求得机械手臂最优尺寸。在满足条件的情况下，使手臂质量最小，证明了该设计可以满足预设动作要求。

关键词：机械手臂；优化设计；强度条件；刚度条件；J)KL)M；软件

()*+,%-#./)’0&12’&3&%4567$2484-)#2915:$%)19$0’,1-2$2,15:$2;;1)##’,1-2$2,15/!<=!>5:,;$+&%)

中图分类号：K7$%%文献标识码：)

机械手臂作为机器人的一个重要组成部分，一直是机器人

#来稿日期：%&&]5&\5&W

耦合集：N弧面分度凸轮机构〈弧面分度凸轮

P从动盘O;%〉O;$，

端口：N轴线垂直Q弧面分度凸轮O;$R轴线

E;"分度盘O;%R轴线E;间距S中心距ITP

属性参数：

N中心距I，弧面分度凸轮R许用压力角，弧

面分度凸轮R凸轮节圆半径，从动盘R转盘节圆半径，从动盘R滚子半从动盘与凸轮在分度期的角速比，凸轮角位移P径，从动盘R滚子宽度，规则集：

N凸轮与滚子的共轭接触方程：凸轮工作轮廓在动坐标系的方程：

B$SB%U2C!U2C"51:%C-3!U2C"A5%C-3"5CU2C":$S5B%U2C!U2C"V1:%C-3!U2C"A5%CU2C"VC-3"5$S1B%C-3!U2C"V:%U2C"P

$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$

4444444444444444444444444444444444444444444444444444444445

$问题描述

W结论

（$）增加模型数据的可交换性，减少虚拟设计中代码冗余。

（%）保证模型间的数据一致性，加强数据的互操作与模型间的无缝集成。

参考文献

万方数据

机械手臂设计机械手臂结构优化设计

G%/.高微等：机械手臂结构优化设计

第%期

件，其作用是带动手指去抓取物件，并按预定要求将其搬运到指定位置!"#!$#。(www.61k.com)这里设计目的是在手臂载重一定的情况下，得出一个手臂质量最小的结构设计方案。

选用合金钢管作为手臂的原始材料；钢管的厚度1取为"**。查常用材料手册得出，弹性模量#2"3%&4567；许用弯曲应力!!$#2%"&567；

许用剪切应力!"#28&567；允许挠度!%#2"+%&&&；密度#29)8(+0*$。求解满足使用要求前提下手臂的最小质量。

"设计分析

61阅读提醒您本文地址：

-.-(

-&"

图%机械手臂受力图;<()%;-=0>,-?@A>*>0A7B<07C7=*

")%抗拉强度条件

)*2

[%G()/

]

H%I(’,"H"I

!"’&-

式中，-为手臂横截面积（!"），-2!

[(+)

+./"

(

)]

2%/

!（"+/./"）H$I&’!%"$

H/I

据抗拉强度条件有：

!*7B’(0)1&-［!2

］

H4I*将式（%）（、"）（、$）（、/）及已知数据代入式（4），取32%&*+

,（"

下同）.计算整理得：

%"&+$GJ9&+"K$/+GL)/"+)&

")"抗剪强度条件

手臂D点处所受剪应力最大。因圆环截面壁厚1远小于外径M，故最大剪应力为：

"*7E’"

-据抗剪强度条件有：

万方数据

"*7B’"

7［"］

HLI

将已知数据代入式（L），计算整理得：+)&)"H0*I

")$刚度条件

如图%所示，受力分析得，(点处挠度$最大。据刚度条件$*7B’

$$#5［$］2%&&&

H9I

式中，#为材料的弹性模量（:67）；5为截面惯性矩（0*/），52!

+/.F/）H8I

将式（8）及已知数据代入式（9），计算整理得：$&+$G%8+"G&)L/"")&

")/结构尺寸限制

+6N"/")/&H0*I

$建立数学模型

优化设计追求的目标是机械手臂的质量!"最小。!"的计算表达式为：

!"H7I2(H7%.7"I’

!+"GH+."/I"#"#2&)&&4"+G&)&&%"

HJI

式中，设计变量72!7%.7"#/’!"8+#/

由第二步设计分析计算得M的值约$)40*，

故式（J）可简化为：!"H7I2&)&&/LOM

显然，"、+越小，!"值越小。据此，可写出优化设计的数学模型!/#：

*<B!"H7I2&)&&/L"+7’!"8+#

$9:9%"&+$GJ9+"K$/+.L)/"+)&+)&)"H0*I

$&+$G%8+"G&)L/"")&+66"/")/&H0*I

此数学模型是一个单目标非线性二维约束优化问题。

/优化计算

/)%函数的性态分析

应用5P1OPQL)4编程：

!E.R#2*>,A(=<FHC<B,S70>H&.L.$&I.C<B,S70>H&.4&.$&IIT

U根据函数的定义划分网格区域

52&)&&/L#R#ETU目标函数

*>,AHE.R.5IT

U通过三维网格模拟目标函数图形

在5P1OPQL)4下运行程序可画出目标函数的三维图形，如图"所示：

机械手臂设计机械手臂结构优化设计

!"#$%&’#())*

机械设计与制造

+$,+

目标函数图像,/!.)#))/*10

/)I)!

()$)),)

*/)

I)/

()

)

图(函数-.)#))/*01的图像234#(56789’:;3"’<3&4=&>"8!.)#))/*01

"8#8$)?"8$8,)

同样，通过编程，-@50@A*#,可绘出各约束函数的图形。[www.61k.com)程序如下：

7BCD";EF$()#GHI+JK#GH(LI/#G+*#/#M#GF?

N)?$)?)?,)OPQ抗拉强度条件的图形，

6"D<"’M.)R)#$R,)SG.)#(SCD";EG?M?FTFPQ抗剪强度条件的图形，FTF指图形颜色为黑色

6"D<"’

7BCD";EFI)#GHI+$U#GH(+)#*/#MH(F?N)?$)?)?,)OP

Q刚度条件的图形

6"D<"’M.)R)#$R,)SG.)#/SCD";EG?M?FTFPQ截面尺寸边界条件图形

6"D<"’G.)R)#$R$)SM./)SCD";EG?M?F>FPQ长度尺寸边界条件图形，F>F指图形颜色为紫红色

6"D<"’

;3;D7EF各个约束函数图像FPQ标注图形名称;7G;E/?/,?F可行域FP

Q注明F可行域F区域

6"D<"88运行程序绘出约束函数的图形?如I所示：

各个约束函数图像

/,可行域

$./)

/)I,#.)#/

$I)#.)#(I)GI+$UG(+)#*/M(.)

(,()$()GI+JKG(LI/G+*#/MG.)

$,$),)

)$(I/

*KUJ$)#

图I设计变量的可行域

234#I27&V3WD7=743"’"8X&=3&WD7<7V34’

由图(可以看出R目标函数的图像规则?即性态好?对于多数优化方法均适用。对图I可行域分析可知，

实际起约束作用有：（$）刚度条件：

I)%I+$U%(+)#*/&())（(）结构尺寸限制条件：&+/)6)

所以?计算时只须考虑这两个条件。这样就大大简化了计

万方数据

算过程。

/#(应用-@50@A软件求解

E$P编写目标函数的>文件R"WY89’#>?返回G处的函数值8。89’:;3"’8.ZWY89’EGP

8.)#))/*#GE$P#GE(P；

E(P因设计约束含非线性约束?故需编写一个描述非线性

约束的>文件R

!"’03’["’V;=#>

89’:;3"’N:?:7\O.!"’03’["’V;=EGP

:.+I)#GE$PHIL$U#GE$PH(L)#*/#GE(PH(S:7\.NOS

EIP给定变量的初值，并调用优化函数：

G).N//)OFS@.N)+$OSW.N+/)OSDW.B7="VE$?$PSQ赋)语句

"C;3"’V."C;3>V7;EF13VCD&MF?F3;7=F?F0&=47]:&D7F?F

"88FPS

NG?8X&D?7G3;8D&4?"9;C9;O.8>3’:"’EFZWY89’F?G)?@?W?NO?NO?DW?NO?F!"’03’["’V;=F?"C;3"’VP

E/P计算结果R

I#U$*)Q最后的优化结果/)#))))Q1.I#U$*):>?0./):>8X&D.Q优化后的最小质量)#K)($

61阅读提醒您本文地址：

Q>(>3’.)#K)($T47G3;8D&4.

Q算法退出处条件

"9;CD";.

3;7=&;3"’VR(

Q函数调用次数89’:["9’;R$$Q函数赋值次数V;7CV3B7R$Q步长&D4"=3;6>RF>7<39>+V:&D7R]^_?^9&V3+!7‘;"’?

D3’7+V7&=:6F

Q算法

83=V;"=<7="C;R)#$U/)Q第一优化命令的长度:43;7=&;3"’VRNO

经$$次迭代计算后?求得最优方案为R1.I#U$*):>?0./):>?>(.)#K)($T4。

,结束语

参考文献

机械手臂设计机械手臂结构优化设计

参考文献(4条)

1.王承义机械手及其应用 1981

2.龙立新工业机械手的设计分析 1999

3.孙靖民机械优化设计 2000

4.刘惟信机械最优化设计 1997

引证文献(5条)

1.阮学云.王永生.张军.王光生基于MATLAB煤液钻空心传动轴的优化设计[期刊论文]-煤矿机械 2008(3)

2.梁喜凤.王永维.苗香雯番茄收获机械手机构尺寸优化设计[期刊论文]-机械设计与研究 2008(1)

3.方学红.李延富.张竺英供排气管对接机械手的机构研究与参数优化[期刊论文]-机械设计与制造 2008(1)

4.肖丽萍.魏文军.宋建农.靳桂萍可控变杆长空间机构在农机部件工作轨迹上的设计与应用[期刊论文]-农业工程学报2007(7)

5.梁胜龙.徐忠兰平压模切机执行机构的节能优化设计[期刊论文]-机械传动 2010(11)

本文链接：http://d.g.wanfangdata.com.cn/Periodical_jxsjyzz200601006.aspx

61阅读提醒您本文地址：

五 : 机械手臂的设计要求

机械手臂 -设计要求机械手臂设计机械手臂的设计要求

《异形》外骨骼机器人

1、手臂应承载能力大、刚性好、自重轻

手臂的刚性直接影响到手臂抓取工件时动作的平稳性、运动的速度和定位精度。如刚性差则会引起手臂在垂直平面内的弯曲变形和水平面内侧向扭转变形，手臂就要产生振动，或动作时工件卡死无法工作。为此，手臂一般都采用刚性较好的导向杆来加大手臂的刚度，各支承、连接件的刚性也要有一定的要求，以保证能承受所需要的驱动力。

（www.61k.com”

2、手臂的运动速度要适当，惯性要小

机械手的运动速度一般是根据产品的生产节拍要求来决定的，但不宜盲目追求高速度。

手臂由静止状态达到正常的运动速度为启动，由常速减到停止不动为制动，速度的变化过程为速度特性曲线。

手臂自重轻，其启动和停止的平稳性就好。

3、手臂动作要灵活

手臂的结构要紧凑小巧，才能做手臂运动轻快、灵活。在运动臂上加装滚动轴承或采用滚珠导轨也能使手臂运动轻快、平稳。此外，对了悬臂式的机械手，还要考虑零件在手臂上布置，就是要计算手臂移动零件时的重量对回转、升降、支撑中心的偏重力矩。偏重力矩对手臂运动很不利，偏重力矩过大，会引起手臂的振动，在升降时还会发生一种沉头现象，还会影响运动的灵活性，严重时手臂与立柱会卡死。所以在设计手臂时要尽量使手臂重心通过回转中心，或离回转中心要尽量接近，以减少偏力矩。对于双臂同时操作的机械手，则应使两臂的布置尽量对称于中心，以达到平衡。

机械臂模型

4、位置精度高

机械手要获得较高的位置精度，除采用先进的控制方法外，在结构上还注意以下几个问题：

（1）机械手的刚度、偏重力矩、惯性力及缓冲效果都直接影响手臂的位置精度。

（2）加设定位装置和行程检测机构。

（3）合理选择机械手的坐标形式。直角坐标式机械手的位置精度较高，其结构和运动都比较简单、误差也小。而回转运动产生的误差是放大时的尺寸误差，当转角位置一定时，手臂伸出越长，其误差越大；关节式机械手因其结构复杂，手端的定位由各部关节相互转角来确定，其误差是积累误差，因而精度较差，其位置精度也更难保证。

5、通用性强，能适应多种作业；工艺性好，便于维修调整

以上这几项要求，有时往往相互矛盾，刚性好、载重大，结构往往粗大、导向杆也多，增加手臂自重；转动惯量增加，冲击力就大，位置精度就低。因此，在设计手臂时，须根据机械手抓取重量、自由度数、工作范围、运动速度及机械手的整体布局和工作条件等各种因素综合考虑，以达到动作准确、可靠、灵活、结构紧凑、刚度大、自重小，从而保证一定的位置精度和适应快速动作。此外，对于热加工的机械手，还要考虑热辐射，手臂要较长，以远离热源，并须装有冷却装置。对于粉尘作业的机械手还要添装防尘设施。

本文标题：机械手臂设计-95机械手臂设计
本文地址： http://www.61k.com/1128142.html

61阅读

机械手臂设计-95机械手臂设计

可行性分析

机械仪表

计算方法