一 : 拓扑排序:拓扑排序-预备知识,拓扑排序-执行步骤
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
拓扑排序_拓扑排序 -预备知识
[www.61k.com]1个较大的工程往往被划分成许多子工程,我们把这些子工程称作活动(activity)。在整个工程中,有些子工程(活动)必须在其它有关子工程完成之后才能开始,也就是说,1个子工程的开始是以它的所有前序子工程的结束为先决条件的,但有些子工程没有先决条件,可以安排在任何时间开始。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系,可用1个有向图来表示,图中的顶点代表活动(子工程),图中的有向边代表活动的先后关系,即有向边的起点的活动是终点活动的前序活动,只有当起点活动完成之后,其终点活动才能进行。通常,我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network),简称AOV网。

例如,假定1个计算机专业的学生必须完成图3-4所列出的全部课程。在这里,课程代表活动,学习一门课程就表示进行一项活动,学习每门课程的先决条件是学完它的全部先修课程。如学习《数据结构》课程就必须安排在学完它的两门先修课程《离散数学》和《算法语言》之后。学习《高等数学》课程则可以随时安排,因为它是基础课程,没有先修课。若用AOV网来表示这种课程安排的先后关系,则如图3-5所示。图中的每个顶点代表一门课程,每条有向边代表起点对应的课程是终点对应课程的先修课。图中的每个顶点代表一从图中可以清楚地看出各课程之间的先修和后续的关系。如课程C5的先修课为C2,后续课程为C4和C6。
1个AOV网应该是1个有向无环图,即不应该带有回路,因为若带有回路,则回路上的所有活动都无法进行。如图3-6是1个具有3个顶点的回路,由边可得B活动必须在A活动之后,由
在AOV网中,若不存在回路,则所有活动可排列成1个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,我们把此序列叫做拓扑序列(Topological order),由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的,满足上述定义的任一线性序列都称作它的拓扑序列。
由AOV网构造出拓扑序列的实际意义是:如果按照拓扑序列中的顶点次序,在开始每一项活动时,能够保证它的所有前驱活动都已完成,从而使整个工程顺序进行,不会出现冲突的情况。
拓扑排序_拓扑排序 -执行步骤
由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下2步,直到不存在入度为0的顶点为止。
(1) 选择1个入度为0的顶点并输出之;
(2) 从网中删除此顶点及所有出边。
循环结束后,若输出的顶点数小于网中的顶点数,则输出“有回路”信息,否则输出的顶点序列就是1种拓扑序列。
拓扑排序_拓扑排序 -非计算机应用
拓扑排序常用来确定1个依赖关系集中,事物发生的顺序。例如,在日常工作中,可能会将项目拆分成A、B、C、D4个子部分来完成,但A依赖于B和D,C依赖于D。为了计算这个项目进行的顺序,可对这个关系集进行拓扑排序,得出1个线性的序列,则排在前面的任务就是需要先完成的任务。
注意:这里得到的排序并不是唯一的!就好像你早上穿衣服可以先穿上衣也可以先穿裤子,只要里面的衣服在外面的衣服之前穿就行。
拓扑排序_拓扑排序 -在计算机语言中的应用
拓扑序列Pascal代码(无优化)
拓扑序列C++(STL)核心代码
这里的代码可以参考这本书
,这里是我自己敲的代码,用了容器,感觉能看明白点。
拓扑序列Pascal代码(邻接表+队列优化)
这里主要是将入度为零的点加入队列stack,直接在队列内扩展就可以,效率为O(n+m)
拓扑排序_拓扑排序 -拓扑学
拓扑学是近代发展起来的1个研究连续性现象的数学分支。中文名称起源于希腊语Τοπολογ?α的音译。Topology原意为地貌,于19世纪中期由科学家引入,当时主要研究的是出于数学分析的需要而产生的一些几何问题。发展至今,拓扑学主要研究拓扑空间在拓扑变换下的不变性质和不变量。
二 : 拓扑排序
有向无环图及其应用
有向无环图 有向无环图的应用 公用表达式 AOV网-拓扑排序 AOE网-关键路径 小结和作业
有向无环图
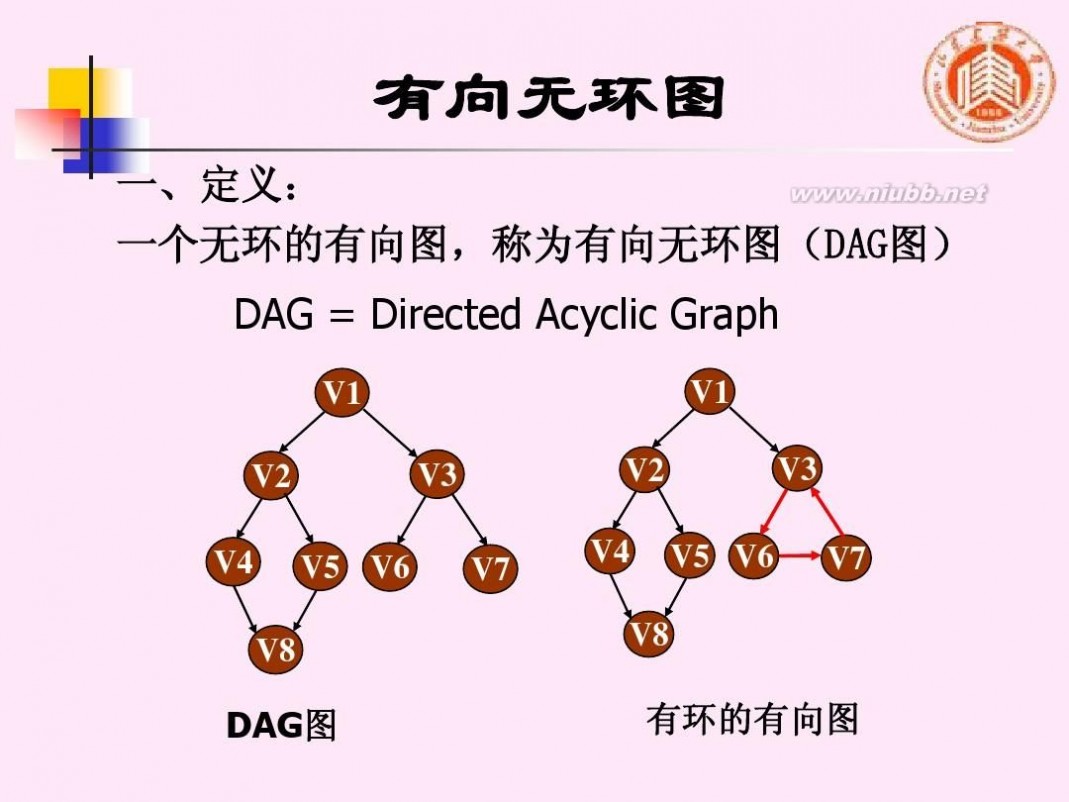
一、定义: 一个无环的有向图,称为有向无环图(DAG图)
DAG = Directed Acyclic Graph
V1 V2 V4 V8 V3 V2 V7 V4 V8 V5 V6 V1 V3 V7
V5 V6
DAG图
有环的有向图
有向无环图
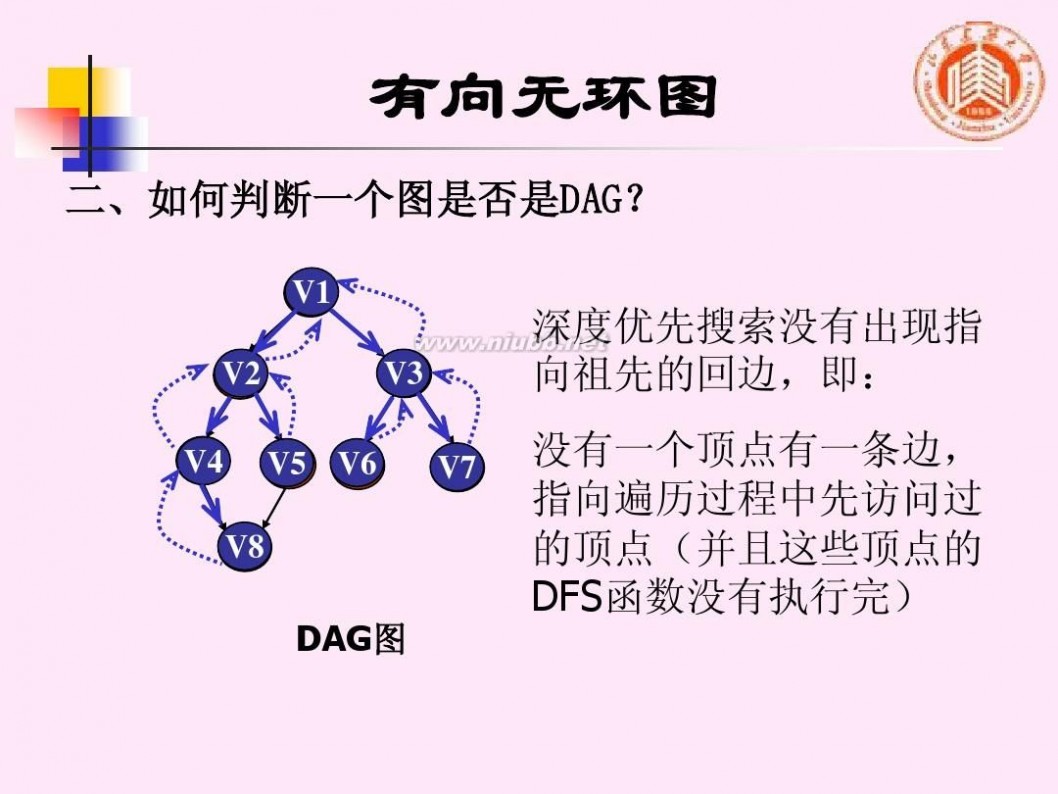
二、如何判断一个图是否是DAG?
V1 V2 V4 V5 V6 V3 V7
深度优先搜索没有出现指 向祖先的回边,即:
V8
DAG图
没有一个顶点有一条边, 指向遍历过程中先访问过 的顶点(并且这些顶点的 DFS函数没有执行完)
有向无环图
V1
V2
V3 V5 V6
V7
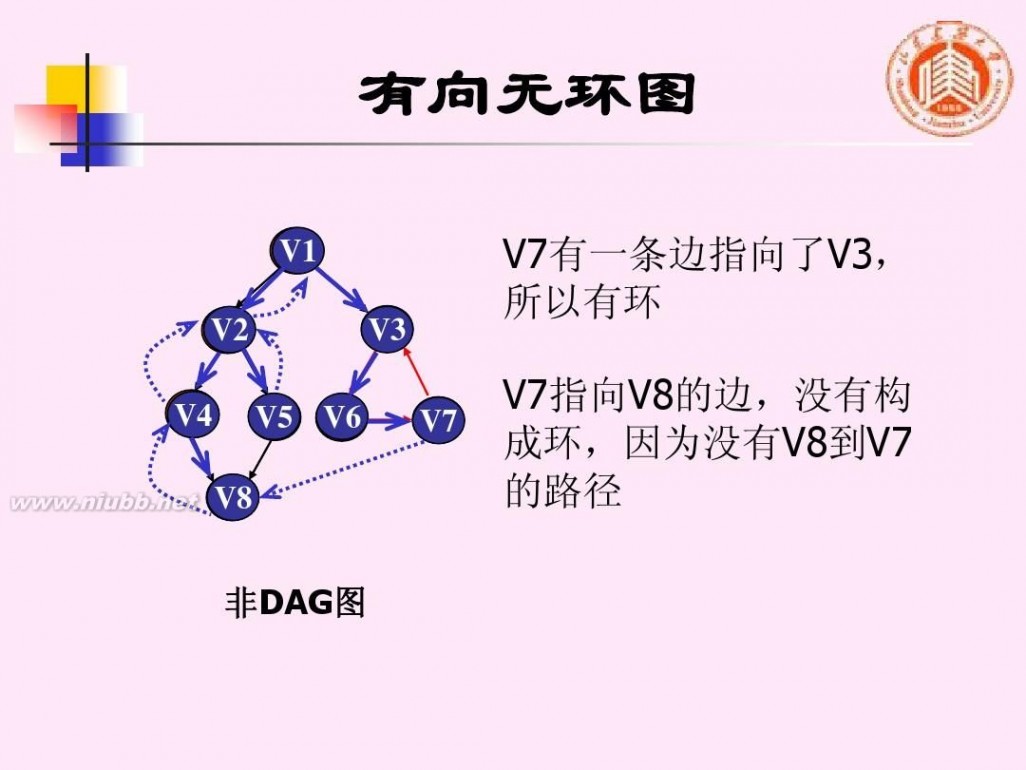
V7有一条边指向了V3, 所以有环 V7指向V8的边,没有构 成环,因为没有V8到V7 的路径
V4
V8
非DAG图
有向无环图
bool DAG(Graph G) { for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; // 访问标志数组初始化 InitStack(S);//存放顶点 for (v=0; v<G.vexnum; ++v) { if (!visited[v]) if(!DFS-DAG(G, v)) return(FALSE); // 对尚未访问的顶点调用DFS-DAG } return TRUE; }
有向无环图
Bool DFS-DAG(Graph G, int v) { // 从顶点v出发,深度优先搜索遍历连通图 G visited[v] = TRUE; Push(S,v); for(w=FirstAdjVex(G, v);w>=0; w=NextAdjVex(G,v,w)){ {if (w in S) then return(FALSE);//有回边 if(!visited[w]){ if(!DFS-DAG(G, w)) return(FALSE); } Pop(S, v);//v的所有邻接点已经遍历完 return(TRUE); } // DFS-T
公用表达式
用树表示表达式:
((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e) * + * + a b b * + c + d * e c + d * e
c
d
公用表达式
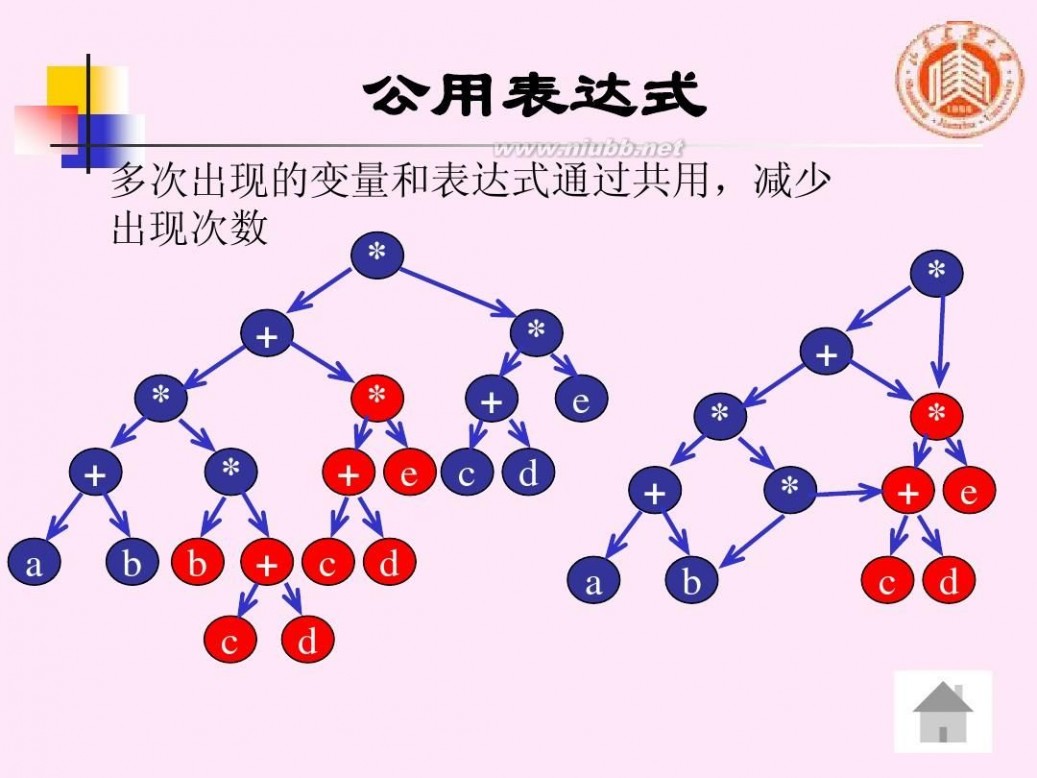
多次出现的变量和表达式通过共用,减少 出现次数 * + *
+ * + *
* *
e c
+ e *
+ a b * c + d
+
d
*
e
a
b
b
c
+
d
c
d
拓扑排序
一、定义
由集合上的一个偏序关系得到集合的全序关系的 操作 偏序:自反的、反对称的、传递的 全序:R是集合X上的偏序,对于集合X中的任何 元素x,y,如果都有xRy或者yRx,则称R是全序关 系
拓扑排序
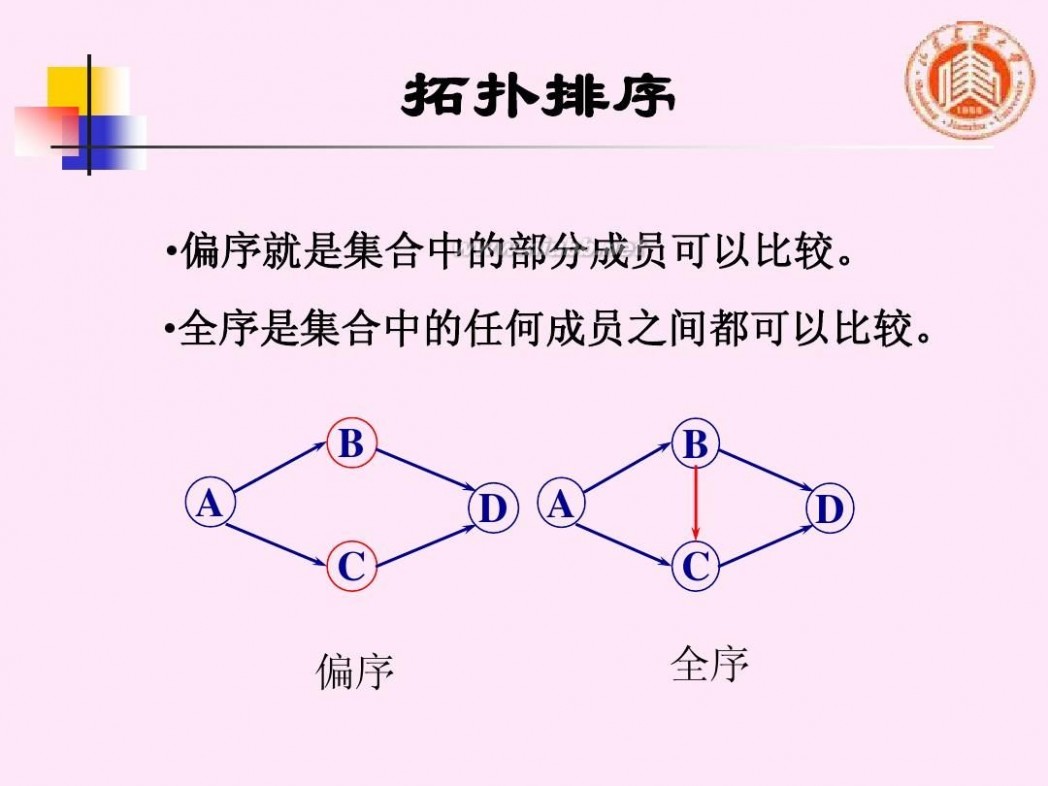
?偏序就是集合中的部分成员可以比较。 ?全序是集合中的任何成员之间都可以比较。 B A C 偏序 D A C 全序 B D
拓扑排序
按照有向图给出的次序关系,将图中顶点排成 一个线性序列,对于有向图中没有限定次序关系 的顶点,则可以人为加上任意的次序关系。
由此所得顶点的线性序列称之为拓扑有序序 列
拓扑排序
拓扑排序的用途:判断AOV网是否存在环路
AOV网(Activity On Vertex NetWork)
用顶点表示活动,弧表示活动间的优先关系的 有向图。
AOV网中不应该出现有向环:如果存在环,则某 项活动以自己为先决条件,
拓扑排序
B A C
可求得拓扑有序序列:
D
ABCD
或 ACBD
拓扑排序
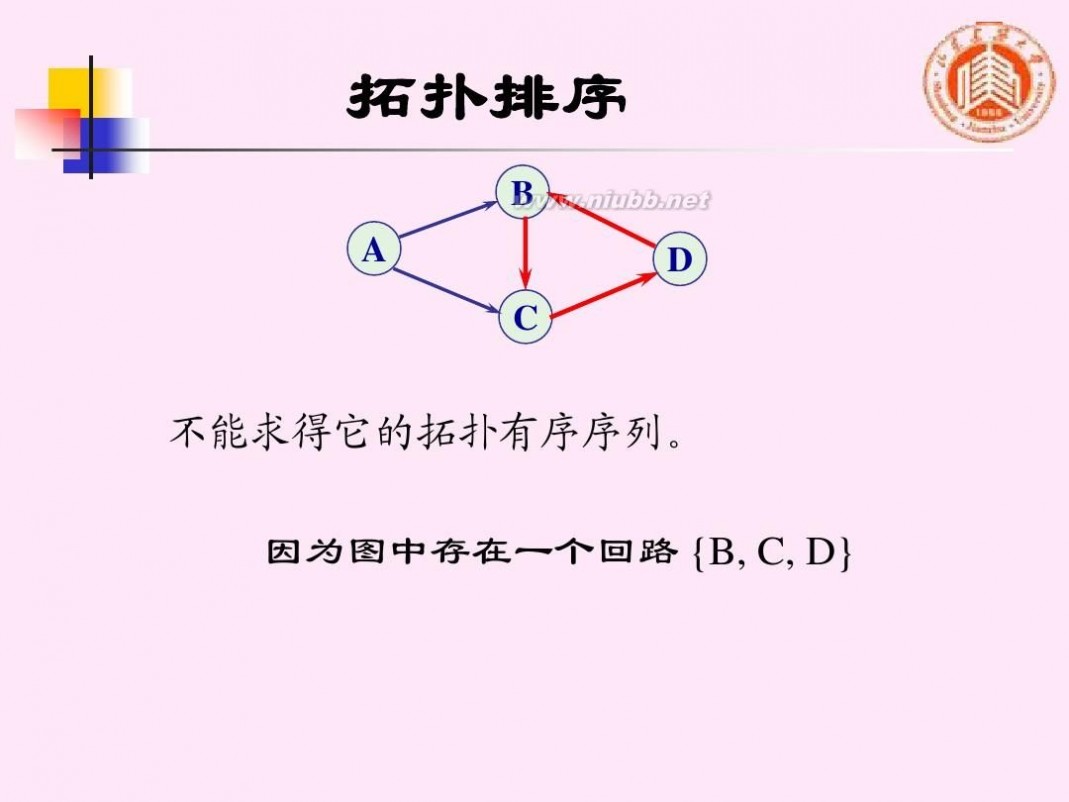
B A D
C
不能求得它的拓扑有序序列。 因为图中存在一个回路 {B, C, D}
拓扑排序---方法1
1、从有向图中选取一个没有前驱的顶点,并 输出之; 2、从有向图中删去此顶点
以及所有以它为尾 的弧; 3、重复上述两步,直至图空,或者图不空但 找不到无前驱的顶点为止。
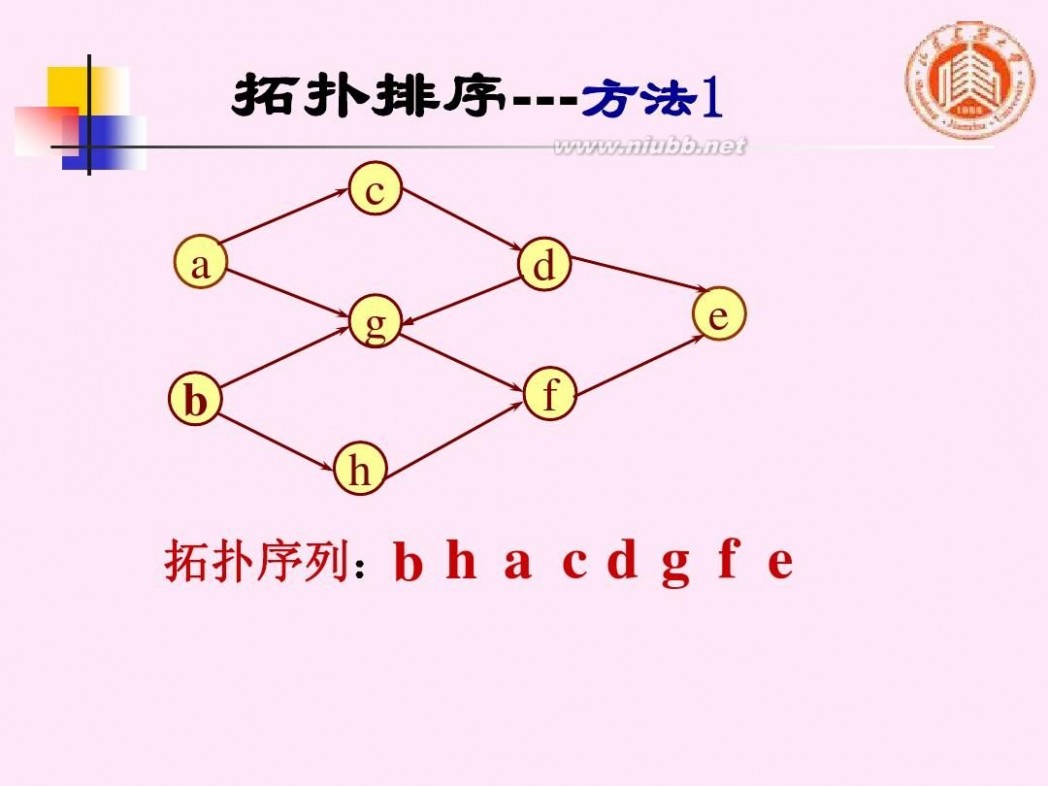
拓扑排序---方法1
c
a d e f h 拓扑序列:b
g
b
h a cdg f e
拓扑排序---方法1
在算法中需要用定量的描述替代定性的概念 没有前驱的顶点 入度为零的顶点 弧头顶点的入度减1
删除顶点及以它为尾的弧
拓扑排序---算法
Status ToplogicalSort(ALGragh G){ FindInDegree(G, indegree); InitStack(S); for(i=0;i<G.vexnum;i++){if(!indegree[i]) push(S,i);} count=0; //对输出顶点计数 while (!EmptyStack(S)) {
…………
}//while if (count<G.vexnum) return ERROR; else return OK; }
拓扑排序---算法
Status ToplogicalSort(ALGragh G){
………………
while (!EmptyStack(S)) { Pop(S, v); ++count; printf(v); for (w=FirstAdj(v); w; w=NextAdj(G,v,w)){ --indegree(w); // 弧头顶点的入度减1 if (!indegree[w]) Push(S, w); }//for }//while
………………
}
拓扑排序---算法
算法分析: 总的时间复杂度:O(n+e)
拓扑排序---方法2
c
a d e f h 拓扑序列:b
g
b
h a cdg f e
拓扑排序---方法2
对有向无环图利用深度优先搜索进行拓扑排序。
c
a
g
d e
b
f
f g d c ahb 此图的一个拓扑序列为: h a c d g f e b
h e 退出DFS函数顺序:
拓扑排序---方法2
结论:
最先退出DFS函数的顶点是出度为零的顶点,为拓 扑排序序列中最后一个顶点。 因此,按退出DFS函数的先后记录下来的顶点序列 即为逆向的拓扑排序序列。
拓扑排序---方法2
void DFS-ToplogicalSort (Graph G, int v) {//如何确定v for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; // 访问标志数组初始化 InitStack(S);//存放顶点,按照出DFS的次序 for (v=0; v<G.vexnum; ++v) { if (!visited[v]) DFS-T(G, v); // 对尚未访问的顶点调用DFS } while(!Empty(S)){//输出拓扑排序的结果 Pop(S, v); printf(“%d”, v)} }
拓扑排序---方法2
void DFS-T(Graph G, int v) {
// 从顶点v出发,深度优先搜索遍历连通图 G
visited[v] = TRUE; for(w=FirstAdjVex(G, v); w>=0; w=NextAdjVex(G,v,w)) {if (!visited[w]) DFS-T(G, w);}
// 对v的尚未访问的邻接顶点w递归调用DFS-T
Push(S, v);//顶点v的DFS函数执行完毕 } // DFS-T
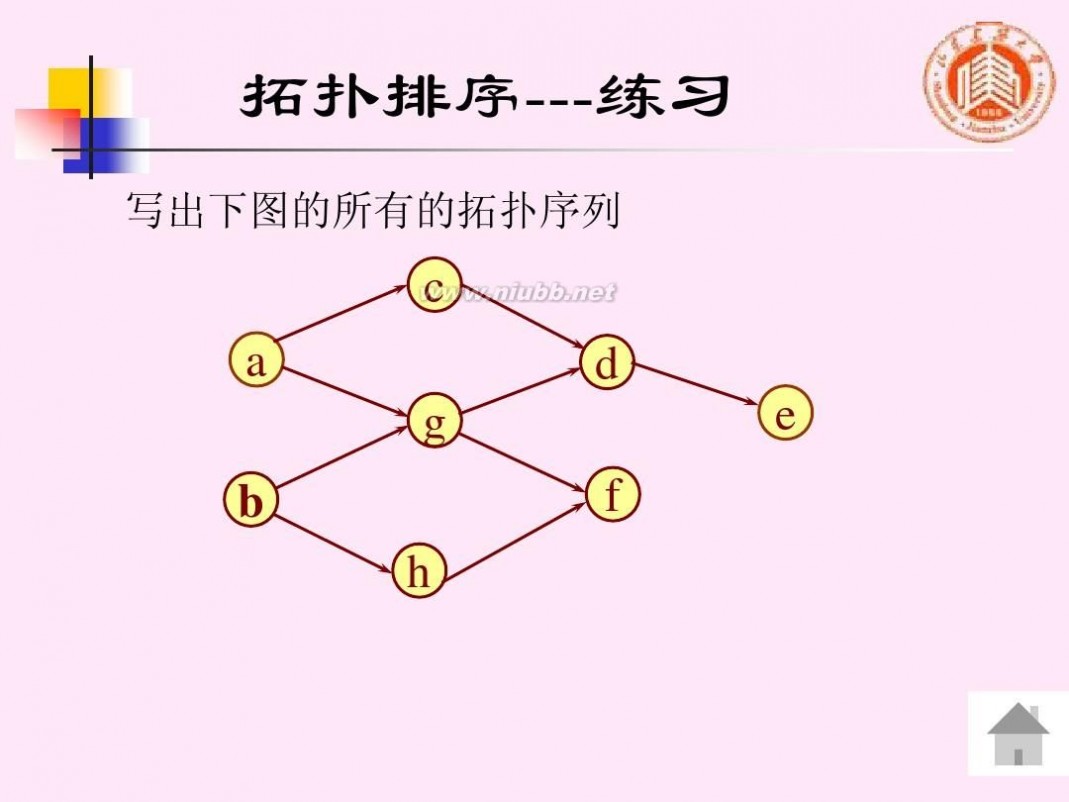
拓扑排序---练习
写出下图的所有的拓扑序列
c
a
g
d e
f h
b
关键路径
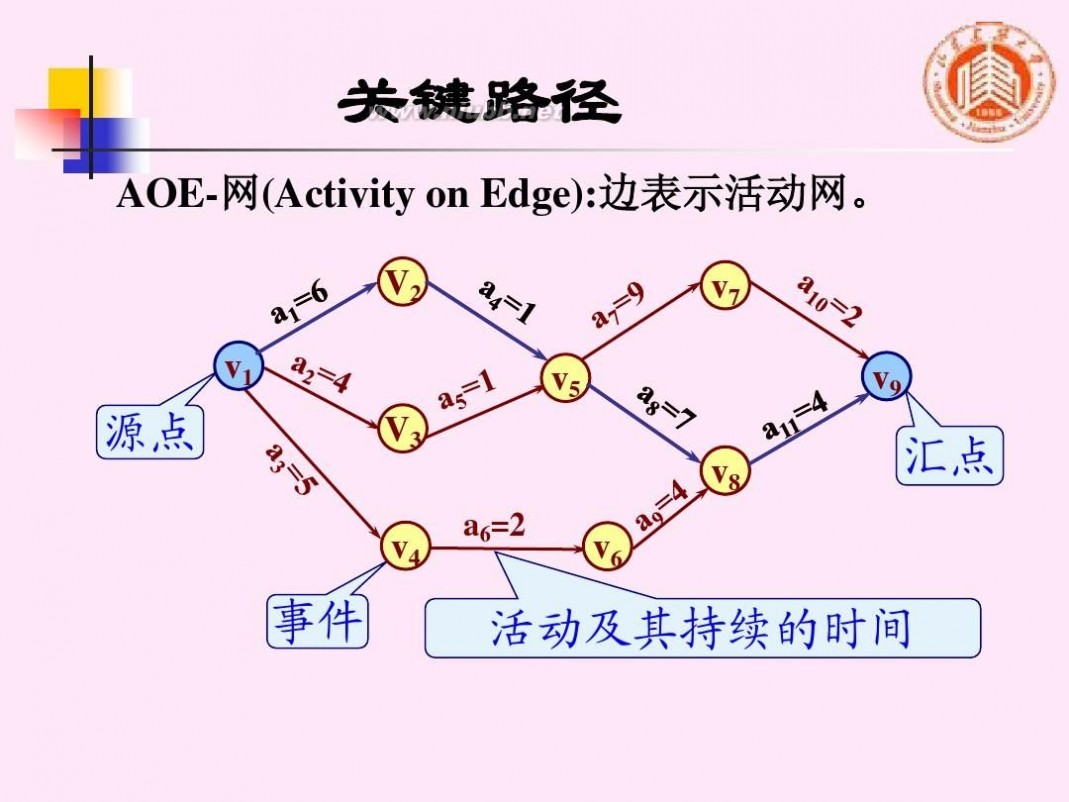
AOE-网(Activity on Edge):边表示活动网。
V2 v1 v5 V3
v7 v9 v8
源点
汇点
v4
a6=2
v6
事件
活动及其持续的时间
关键路径
AOE-网是一个带权的有向无环图,可用来估算 工程的完成时间。 假设以AOE网表示一个施工流图,弧上的权值表示
完成该项子工程所需的时间。
1、完成整个工程至少需要多少时间?
2、哪些活动是影响工程进度的关键?
关键路径
?路径最长的路径叫做关键路径
?影响工程进度的活动叫关键活动
?关键路径上的活动一定是关键活动
如何求关键路径
?用e(i)和l(i)
分别表示活动ai的最早开始时 间和最迟开始时间 ?e(i)-l(i)为活动ai 的时间余量
?e(i)=l(i)的活动是关键活动
如何求关键路径
V2 v1 V3
v7 v5
v9
v8
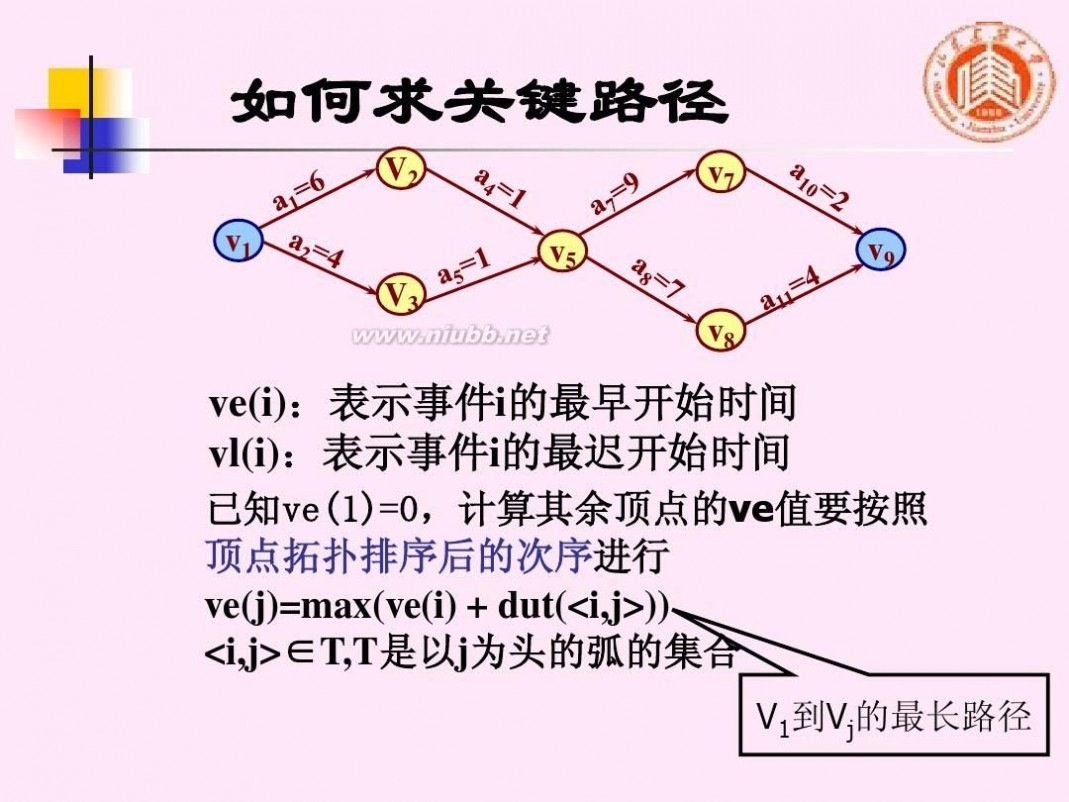
ve(i):表示事件i的最早开始时间 vl(i):表示事件i的最迟开始时间
已知ve(1)=0,计算其余顶点的ve值要按照 顶点拓扑排序后的次序进行 ve(j)=max(ve(i) + dut(<i,j>)) <i,j>∈T,T是以j为头的弧的集合
V1到Vj的最长路径
如何求关键路径
V2 v1 V3
v7 v5
v9
v8
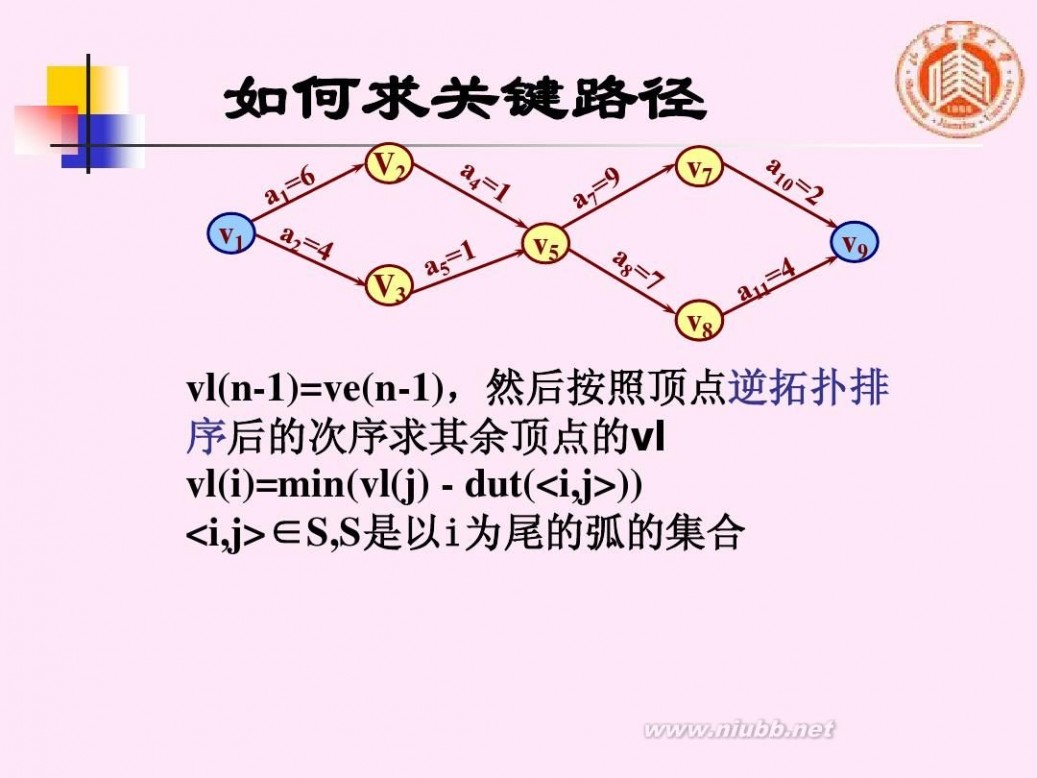
vl(n-1)=ve(n-1),然后按照顶点逆拓扑排 序后的次序求其余顶点的vl vl(i)=min(vl(j) - dut(<i,j>)) <i,j>∈S,S是以i为尾的弧的集合
如何求关键路径
用e(i)和l(i)分别表示活动ai的最早开始间 和最迟开始时间
显然有: e(i)=ve(j)
j
ai
k
l(i)=vl(k)-dut(j,k)
如何求关键路径
V2
v1 V3 v7
v5
v9
v8
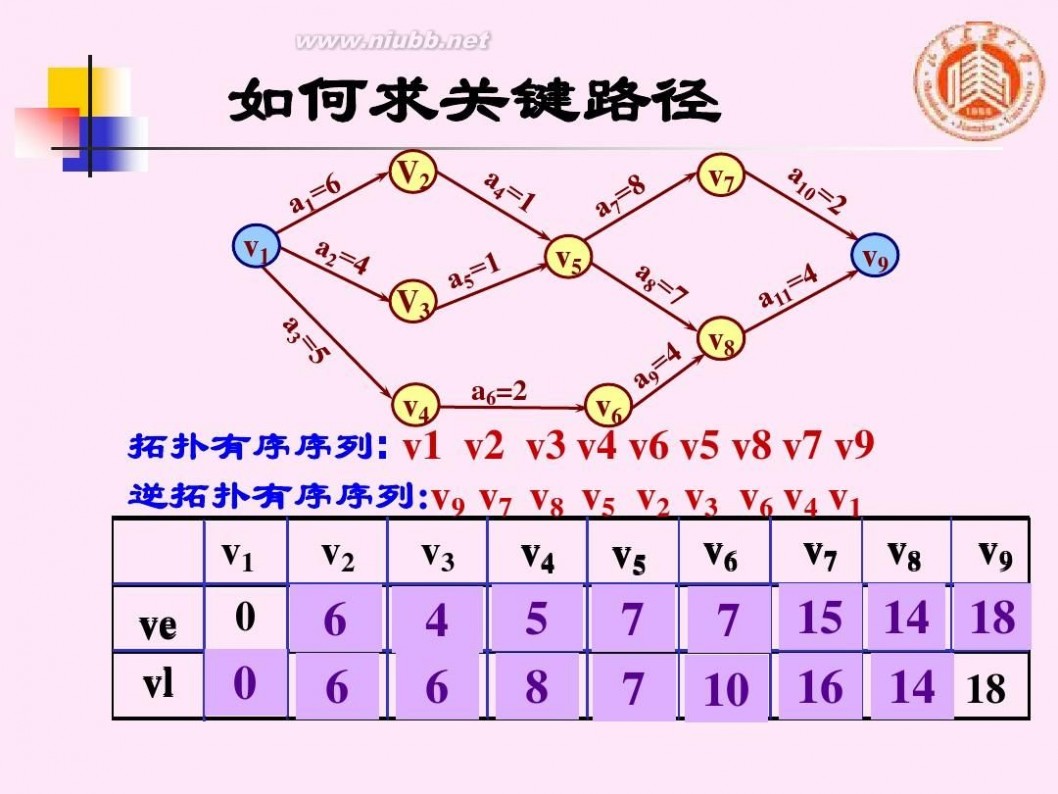
拓扑有序序列: v1 v2 v3 v4 v6 v5 v8 v7 v9 逆拓扑有序序列:v9 v7 v8 v5 v2 v3 v6 v4 v1 v7 v8 v1 v2 v3 v4 v5 v6 ve vl 0
v4
a6=2
v6
v9
0 18
0 6 18 6
0 4 18 6
0 5 18 8
0 7 18 7
0 0 0 0 7 15 14 18 18 18 18 18 10 16 14
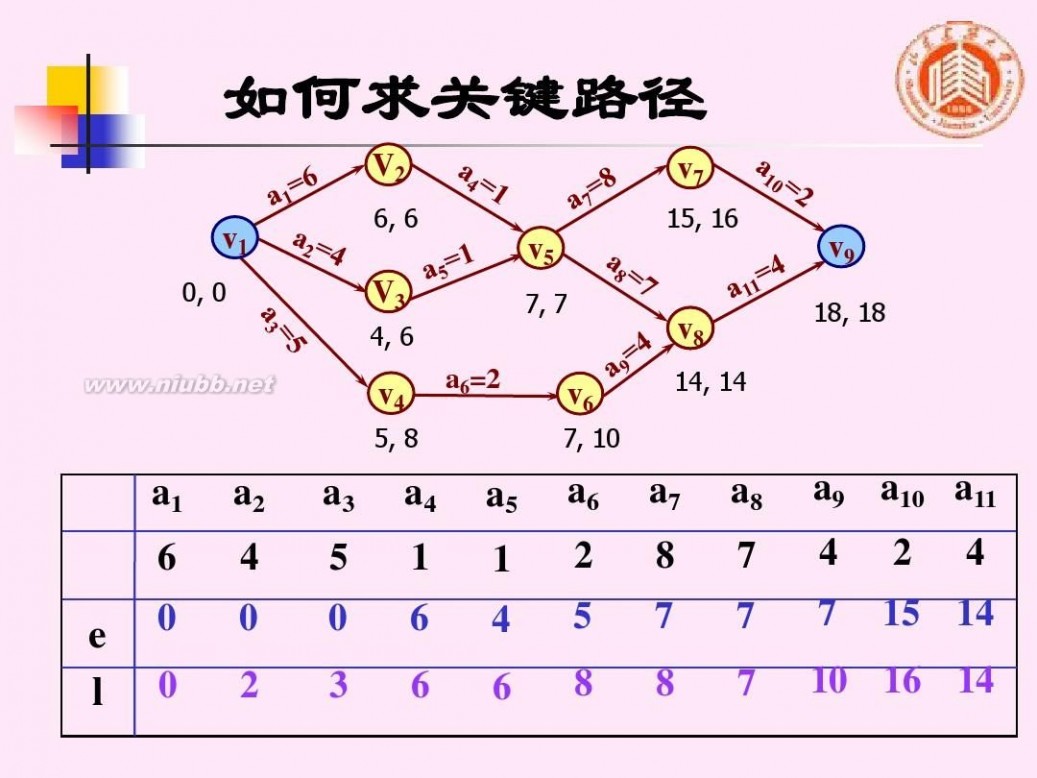
如何求关键路径
V2
v7
15, 16
v1
0, 0
6, 6
v5 V3
4, 6 7, 7
v9
v8
14, 14
18, 18
v4
5, 8
a6=2
v6
7, 10
a1 6 0 0
a2 4 0 2
a3 5 0 3
a4 1 6 6
a5 1
a6 2 5
a7 8 7
a8 7 7
a9 a10 a11
4 7 2 4 15 14
e l
4
6
8
8
7
10 16 14
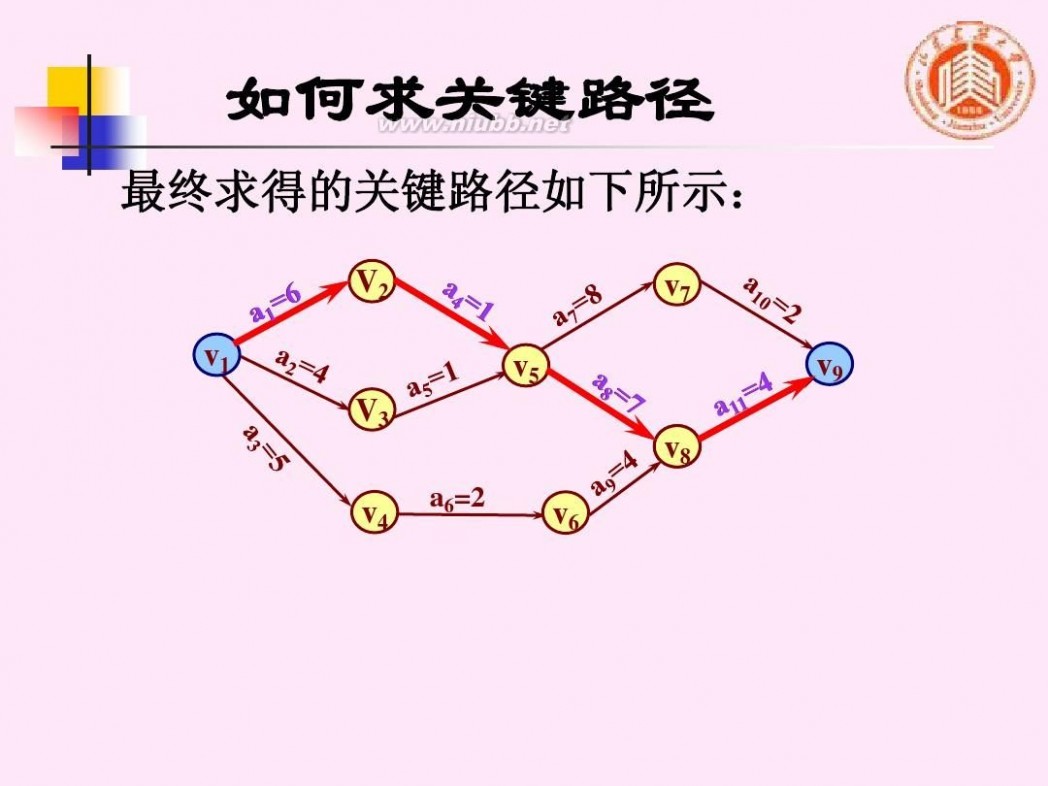
如何求关键路径
最终求得的关键路径如下所示:
V2 v1 V3 v5 v7
v9
v8
v4
a6=2
v6
关键路径算法
1)输入n个顶点和e条弧<j,k>,建立AOE网存储结构 2)求出网G的拓扑排序
若得到拓扑排序中顶点个数<n,说明G中存在 环,算法终止。
令ve[0]=0, 求其余结点的最早发生时间ve(j)=max(ve(i) + dut(<i,j>)) <i,j>∈T,T是以j为头的弧的集合
关键路径算法
3)求出G的逆向拓扑序列 从汇点出发,令vl(n-1)=ve(n-1) 求其余各顶点的最迟发生时间: vl(i)=min(vl(j) - dut(<i,j>)) <i,j>∈S,S是以i为尾的弧的集合
关键路径算法
4)根据2)和3)中所得的ve和vl,求每条弧上的 活动ai的最早发生时间e(s)和l(s) e(i)=ve(j) l(i)=vl(k)-dut(j,k) ai
j
k
5)如果某条弧上的活动ai满足e(i)=l(i),则ai为关 键活动。
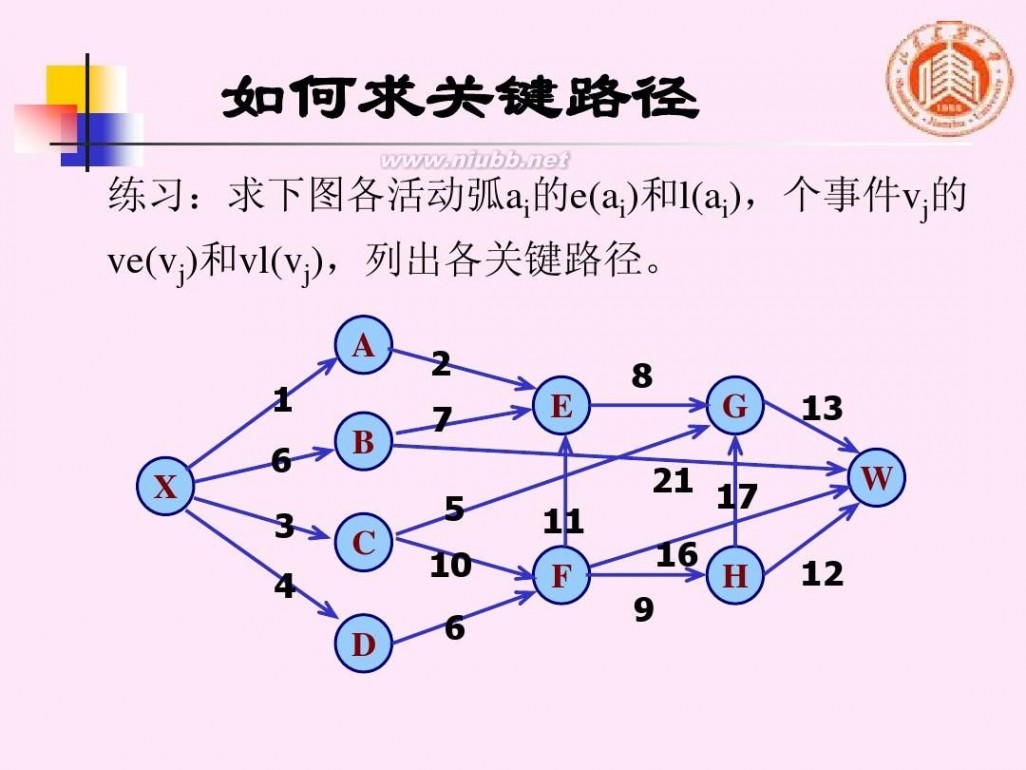
如何求关键路径
练习:求下图各活动弧ai的e(ai)和l(ai),个事件vj的 ve(vj)和vl(vj),列出各关键路径。
A
1
X 6 3 4 D B C
2 7 5 10 6 E 11
8
G
13 W 12
21 17 16
9
F
H
关键路径算法
算法描述:
1)有向网AOE采用邻接表作为存储结构
2)栈T:拓扑序列顶点栈
3)栈S:0入度顶点栈 4)返回值: ERROR:图G中有回路 OK:栈T返回图G的一个拓扑有序序列
关键路径算法
Status ToplogicalOrder( ALGragh G, Stack &T){ FindInDegree(G, indegree); InitStack(S); for(i=0;i<G.vexnum;i++){if(!indegree[i]) push(S,i);} Initstack(T); count=0; ve[0..G.vexnum-1]=0; while (!EmptyStack(S)) {
…………
}//while if (count<G.vexnum) return ERROR; else return OK; }
关键路径算法
Status ToplogicalOrder( ALGragh G,
Stack &T){
…………
while (!EmptyStack(S)) { Pop(S, v); Push(T,j);++count; //j号顶点入栈T for (p=G.vertices[j].firstarc; p; p=p->nextarc){ k=p->adjvex; if(--indegree(k)==) Push(S,k); //入度-1为0,则入栈 if((ve[j]+*(p->info))>ve[k]) ve[k]= ve[j]+*(p->info) }//for }//while if (count<G.vexnum) return ERROR; else return OK; }
关键路径算法
Status CriticalPath( ALGragh G){//输出G的关键活动 if(!) ToplogicalOrder(G,T) return ERROR; vl[0.. G.vexnum-1] =ve[0..G.vexnum-1];//用ve初始化vl while(!stackEmpty(T)){ pop(T,j); for(p=G.vertices[j].firstarc;p;p=p->nextarc){ k=p->adjvex; dut=*(p->info); if(vl[k]-dut<vl[j]) vl[j]=vl[k]-dut; }//end of for }//end of while
…………}//end of CriticalPath
关键路径算法
Status CriticalPath( ALGragh G){//输出G的关键活动
…………
for(j=0;j<G.vexnum;++j) for (p=G.vertices[j].firstarc; p; p=p->nextarc){ k=p->adjvex; dut=*(p->info);
ee=ve[j];el=vl[k]-dut; tag=(ee=el)?’*’:’’; printf(j,k,dut,ee,el,tag); }//end of for(p) }//end of status
关键路径算法
Status CriticalPath( ALGragh G){//输出G的关键活动
…………
for(j=0;j<G.vexnum;++j) for (p=G.vertices[j].firstarc; p; p=p->nextarc){ k=p->adjvex; dut=*(p->info);
ee=ve[j];el=vl[k]-dut; tag=(ee=el)?’*’:’’; printf(j,k,dut,ee,el,tag); }//end of for(p) }//end of status
关键路径算法分析
1.求关键路径的总的时间复杂度:O(n+e) 2.AOE-网求出的路径可能大于一条。
这种情况下只有同时提高所有关键路径上的 活动的速度,才能使整个工期缩短。
小结和作业
本节主要内容: 1.什么是拓扑排序 1.拓扑排序 2.如何进行拓扑排序
3. 拓扑排序算法
2.关键活动 1.什么是关键活动 2.如何求关键活动 3.关键活动算法
小结和作业
思考题:
下列关于AOE网的叙述中,不正确的是( )。 A.关键活动不按期完成就会影响整个工程的完成时间 B.任何一个关键活动提前完成,那么整个工程将会提 前完成 C.所有的关键活动提前完成,那么整个工程将会提前 完成 D.某些关键活动提前完成,那么整个工程将会提前完 成
作业:7.9,7.10
三 : 学习总结---拓扑排序
拓扑排序什么是拓扑序列
通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。离散数学中关于偏序和全序的定义:
若集合X上的关系是R,且R是自反的、反对称的和传递的,则称R是集合X上的偏序关系。
设R是集合X上的偏序(Partial Order),如果对每个x,y属于X必有xRy 或 yRx,则称R是集合X上的全序关系。
比较简单的理解:偏序是指集合中只有部分成员可以比较,全序是指集合中所有的成员之间均可以比较。
注意:
①若将图中顶点按拓扑次序排成一行,则图中所有的有向边均是从左指向右的。
②若图中存在有向环,则不可能使顶点满足拓扑次序。
③一个DAG的拓扑序列通常表示某种方案切实可行。
昨天花了一天的时间研究了下拓扑排序,觉得学到很多,所以写一下总结。
<1>有向图的表示方式可以分成邻接矩阵和邻接表两种。
邻接矩阵是指用一个n*n的数组,下标为i,j的位置记录点i和点j的关系。(适用与稀疏矩阵,对内存空间要求要比较高)
邻接表是单纯记录关系的数组,比如 i和 j 有关系, 就将 j 放在 [i][k]的位置(k为当前与i有关系的点数),这种表示法适用于关系较少的时候,但是引用进STL中的vector以后,好像数据量的大小对其就没有什么太大的影响了。
<2>拓扑排序:每次找到入度为0 的点,并将其出度清空(可以用DFS或BFS),跟据表示的方法不同,操作也会有所差别。
<3>给出有向图之后,会有存在拓扑排序和不存在拓扑排序之分,如果图中存在有向环,则不存在拓扑排序(就是在遍历的过程中直接和间接的相互指向),在处理上只要记录每个点的访问状态就可以了,是正在访问(不满足的情况),还是未访问,或是已经访问过(DFS)。
如果存在了拓扑排序,也会有拓扑排序唯不唯一的问题(如果没有要求考虑这点,用DFS会号做一些),这点其实也好处理,只要每次入度为0的点只有一个才可以(BFS)。
DFS + 邻接表
DFS + 邻接矩阵。 int vis[MAXN]; int topo[MAXN], cnt; bool DFS(int u){ vis[u] = -1; //表示当前正在访问,如果再次访问说明不存在topo排序。 for (int i = 0; i < n; i++){ if (G[u][i]){ if (vis[i] < 0) return false; //存在有向环,失败退出。 else if (!vis[i] && !DFS(i)) return false; } } vis[u] = 1; topo[--cnt] = u; return true; // 成功记录,返回true 。 } bool toposort(){ cnt = n; memset(vis, 0, sizeof(vis)); // 如果要考虑排序是否唯一,这边每次都需将所有点遍历过一遍,且每次只可有一点的入度为0。 for (int u = 0; u < n; u++) if (!DFS(u)) return false; return true; } // DFS + 邻接矩阵。int vis[MAXN];int topo[MAXN], cnt;bool DFS(int u){ vis[u] = -1; //表示当前正在访问,如果再次访问说明不存在topo排序。 for (int i = 0; i < n; i++){ if (G[u][i]){ if (vis[i] < 0) return false; //存在有向环,失败退出。 else if (!vis[i] && !DFS(i)) return false; } } vis[u] = 1; topo[--cnt] = u; return true; // 成功记录,返回true 。}bool toposort(){ cnt = n; memset(vis, 0, sizeof(vis)); // 如果要考虑排序是否唯一,这边每次都需将所有点遍历过一遍,且每次只可有一点的入度为0。 for (int u = 0; u < n; u++) if (!DFS(u)) return false; return true;}BFS(借助STL-queue) + 邻接表(借助STL-vector)// BFS + 邻接表。 vector<int> G[MAXN]; // 邻接表。 int son[MAXN]; // 入度数。 void topo(){ queue<int> que; int ok = 0; for (int i = 0; i < n; i++) if (!son[i]) que.push(i); // 入度为0时入队。 while (!que.empty()){ if (que.size() > 1) ok = 1; // 当队列中个数超多1时,表示有不唯一解。 int t = que.front(); que.pop(); cnt--; // 如果队列为空后,计数器> 0, 说明存在环结构。 for (int i = 0; i < G[t].size(); i++) if (--son[G[t][i]] == 0) // 判断减掉当前点的关系后,点的入度是否为0。 que.push(G[t][i]); } }四 : 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序
拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序
拓扑排序 拓扑排序
拓扑排序 拓扑排序

61阅读提醒您本文地址:
拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序

拓扑排序 拓扑排序
拓扑排序 拓扑排序

61阅读提醒您本文地址:
五 : 有回路的有向图能不能完成拓扑排序
有回路的有向图能不能完成拓扑排序
显然不能.首先,拓扑排序是指对于一个有向无环图G,将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若 ∈E(G),则u在线性序列中出现在v之前.那么,假设存在回路,v1,v2,v3,……,vn,v1,则边∈E(G),故v1在v2之前,类似地,v2在v3之前,……,因此,得出,v1在vn之前.又因为∈E(G),即vn在v1之前.相互矛盾,所以假设不成立.所以,一个图能够进行拓扑排序的一个必要条件就是图中不存在环.
本文标题:拓扑排序-拓扑排序:拓扑排序-预备知识,拓扑排序-执行步骤61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1