一 : 某水果店销售某中水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间
二 : 求助,管理会计题5.某公司只生产一种产品,售价每件8元,月初月末
求助,管理会计题
5.某公司只生产一种产品,售价每件8元,月初月末产成品存货成本不变,总成本与额之间的函数关系为:月总成本=180+0.625×月销售额。要求:
(1)计算贡献边际率、盈亏临界点销售量、销售100件产品时的安全边际销售量和营业利润、目标利润为150元时的销售额;
(2)如果单位变动成本提高1元,售价应定为多少,才能保持原来的贡献边际率?
1)贡献边际率=1-0.625=0.375,盈亏临界点销售量=180/(8-8*0.625)=60,
销售100件产品时的安全边际销售量=60,营业利润、目标利润为150元时的销售额=(150+180)/0.375=880;
(2)如果单位变动成本提高1元,即从8*0.625=5提高到6,贡献边际率仍保持0.375不变,那么售价=6/0.625=9.6
三 : 初一数学题1、某车间加工A型和B型两种零件,平均一个工人每小时能
初一数学题
1、某车间加工A型和B型两种零件,平均一个工人每小时能加工7个A型零件或3个B型零件。 而且3个A型与2个B型配套,就可以包装进库房,剩余不能配套的只能暂时存放起来。如果B型零件单独存放,对环境的要求远高于A型零件。已知该车间原有工人69名。(1) 怎样分配工人工作才能保证生产出的产品及时包装运进库房?(2) 后来因为工作调动,有4名工人调离了该车间。那么你认为现在应该怎样分配工人工作最合适呢?请通过计算说明你的依据。
1)设X个工人生产A零件,则(69-X)人生产B零件。
7X:(69-X)=3:2
X=27………………………………生产A零件的人数;
69-27=42(人)…………………生产B零件的人数。
2)同样的道理设m个人生活A,则(69-4-m)个人生产B。
由于B零件不易存放,故尽量让B少剩或不剩,所以令:
7m:[3(69-4-m)]≥3:2
m≥25.4
正整数m最小为26………………生产A零件的人数;
69-4-26=39(人)………………生产B零件的人数。
四 : 某企业生产1种产品,每件成本价是400元,销售价为510元,本季?
某企业生产一种产品
某生产一种产品,每件成本价是400元,销售价为510元,本季度销售了m件.为进一步扩大市场,该企业决定
在降低销售价的同时,降低生产成本.经过市场调研,预测下季度这种产品每件售价降低百分之4,销售量将提高百分之10,要是销售利润(销售利润=销售价-成本价)保持不变,该产品的成本应降低多少元?(列方程)
设该产品的成本应降低X元,则
[510(1-4%)-(400-X)](1+10%)m=(510-400)m
解这个方程得
X=10.4
所以该产品的成本应降低10.4元.
五 : 某公司以每吨10万元的价格销售某种化工产品,每年可售出该产品
| 某公司以每吨10万元的价格销售某种化工产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少mx%,其中m为正常数。 (1)当m=  时,该产品每吨的价格上涨百分之几,可使销售的总金额最大? 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大? (2)如果涨价能使销售总金额增加,求m的取值范围。 |
解:(1)由题设,当价格上涨x%时,销售总金额为: |
考点:
考点名称:二次函数的性质及应用二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于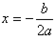 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴 ;
;
③有顶点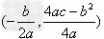 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
①当a>0时,函数f(x)的图象开口向上,在(-∞,- )上是减函数,在[-
)上是减函数,在[-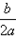 ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-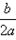 )上是增函数,在[-
)上是增函数,在[- ,+∞)是减函数。
,+∞)是减函数。
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
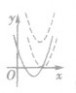 | 值域 | a>0 | a<0 |
 | 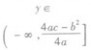 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
| a<0 | 单调性 | a>0 | a<0 |
 |  |  | |
 |  | ||
| 图像特点 |  | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为 ;
;
(3)双根式:若相应一元二次方程的两个根为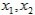 ,则其解析式为
,则其解析式为 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令 .
.
①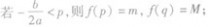
②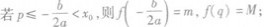
③
④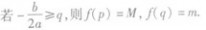
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数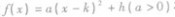 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1