一 : 正弦定理的几种证明方法

正弦定理的几种证明方法

1.利用三角形的高证明正弦定理 （1）当?ABC是锐角三角形时，设边AB上的高是CD，根据锐角三角函数的定义，

C

有CD?asinB,CD?bsinA。 由此，得

a

sina

sin?

b

sin，?

同理可得

c

sin?

b

sin，A

D

B

b 故有

?

b

sinc

sin.从而这个结论在锐角三角形中成立.

（2）当?ABC是钝角三角形时，过点C作AB边上的高，交AB的延长线于点D，根据锐角三角函数的定义，有CD?asin?CBD?asin?ABC，CD?bsinA 。由此，得

a

sinA

?

b

sin?ABC，?

同理可得

c

sinC.

c

sinC

?

b

sin?ABC

a

故有

a

sinA

b

sin?ABC

?

由(1)(2)可知，在?ABC中，

a

sinA

?

b

sinB

?

c

sinC

B D

成立.

从而得到：在一个三角形中，各边和它所对角的正弦的比值相等，即

a

sin?

b

sin?

c

sin.

1’用知识的最近生长点来证明：

实际应用问题中，我们常遇到问题：

已知点A，点B之间的距｜AB|，可测量角A与角B， 需要定位点C，即：

在如图△ABC中，已知角A，角B，｜AB｜＝c， 求边AC的长b

解：过C作CD?AB交AB于D，则

DC?

AD?ccosA

BDcsinAcsinAcosC

??sinCtanCsinCcosC

b?AC?AD?DC?ccosA?

csinAcosCc(sinCcosA?sinAcosC)csinB

??

sinCsinCsinC

推论：bc? sinBsinC

abc?? sinAsinBsinC同理可证：

2.利用三角形面积证明正弦定理?

已知△ABC,设BC＝a, CA＝b,AB＝c,作AD⊥BC,垂足为D.?则Rt△ADB

ADA 中,sinB? ,?∴AD=AB·sinB=csinB.? AB

1111∴S△ABC=a?AD?acsinB.?同理,可证 S△ABC=absinC?bcsinA.

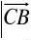
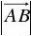
? 2222

111∴ S△ABC=absinC?bcsinA?acsinB.?∴absinc=bcsinA=acsinB,? C D 222

sinCsinAsinBabc????在等式两端同除以ABC,可得.?即. cabsinAsinBsinC

3.向量法证明正弦定理

(1)△ABC为锐角三角形,过点A作单位向量j垂直于,则j与B 的夹角为

,? 90°-A,j与的夹角为90°-C.?由向量的加法原则可得???

j的数量积运算,得到j?(?)?j?

由分配律可得?

∴|j|为了与图中有关角的三角函数建立联系,我们在上面向量等式的两边同取与向量j??j?.? Cos90°+|jCos(90°-C)=|jCos(90°-A).? j

ac?.? A C sinAsinC∴asinC=csinA.?∴

另外,过点C作与垂直的单位向量j,则j与的夹角为90°+C,j与的夹角为90°+B,可得cb?.? sinCsinB

(此处应强调学生注意两向量夹角是以同起点为前提,防止误解为j与

为90°-C,j与

的夹角的夹角为90°-B)?∴abc??.? sinAsinBsinC

(2)△ABC为钝角三角形,不妨设A＞90°,过点A作与

与垂直的单位向量j,则j的夹角为A-90°,j与的夹角为90°-C.? A 由??,得j·?+j·,?

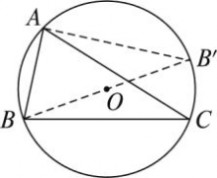
=j·ac? sinAsinC即a·Cos(90°-C)=c·Cos(A-90°),?∴asinC=csinA.?∴

另外,过点C作与垂直的单位向量j,则j与

角为?90°+B.同理,可得

4.外接圆证明正弦定理 B 的夹角为90°+C,j与夹 abcbc???.?∴ sinBsinCsimAsinBsinC

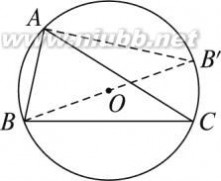
在△ABC中,已知BC=a,AC=b,AB=c,作△ABC的外接圆,O为圆心,

连结BO并延长交圆于B′,设BB′=2R.则根据直径所对的圆周角是直角以及同弧所对的圆周角相等可以得到

cc?2R.?∠BAB′=90°，∠C =∠B′，∴sinC=sinB′=sinC?sinB??.?∴ 2RsinC

ababc?2R,?2R.????2R.?同理,可得∴ sinAsinBsinAsinBsinC

这就是说,对于任意的三角形,我们得到等式?

abc??.? sinAsinBsinC

二 : 正弦定理的证明方法

《正弦定理的证明方法》证明书

正弦定理的证明方法如图1,△ABC中,AD平分乙A交BC于D,由三角形内角平分线有AB BDAC一DC由正弦定理有:由(1)(2)(3,得:韶=韶幼朋=Ac:.△ABc为等腰三角形。证明‘三角证法,:BE平分匕B二器二黯…(l)AB AC AB滋nC舀石乙二蕊丽劝元二舀丽””’‘(2)CF平分二C幼器二默…(2);EF//BC

用余弦定理：a（www.61k.com）^2+b^2-2abCOSc=c^2

COSc=(a^2+b^2-c^2)/2ab

SINc^2=1-COSc^2

SINc^2/c^2=4a^2*b^2-(a^2+b^2-c^2)^2/4a^2*b^2*c^2

=[2(a^2*b^2+b^2*c^2+c^2*a^2)-a^2-b^2-c^2]/4a^2*b^2*c^2

同理可推倒得SINa^2/a^2=SINb^2/b^2=SINc^2/c^2

得证

正弦定理：三角形ABC中 BC/sinA=AC/sinB=AB/sinC

证明如下：在三角形的外接圆里证明会比较方便

例如，用BC边和经过B的直径BD，构成的直角三角形DBC可以得到：

2RsinD=BC (R为三角形外接圆半径)

角A=角D

得到：2RsinA=BC

同理：2RsinB=AC，2RsinC=AB

这样就得到正弦定理了

2

一种是用三角证asinB=bsinA

用面积证

用几何法，画三角形的外接圆

听说能用向量证，咋么证呢?

三角形ABC为锐角三角形时，过A作单位向量j垂直于向量AB，则j 与向量AB夹角为90，j与向量BC夹角为(90-B),j与向量CA夹角为(90+A),设AB=c,BC=a,AC=b,

因为AB+BC+CA=0

即j*AB+J*BC+J*CA=0

|j||AB|cos90+|j||BC|cos(90-B)+|j||CA|cos(90+A)=0

所以asinB=bsinA

3

用余弦定理：a^2+b^2-2abCOSc=c^2

COSc=(a^2+b^2-c^2)/2ab

SINc^2=1-COSc^2

SINc^2/c^2=4a^2*b^2-(a^2+b^2-c^2)^2/4a^2*b^2*c^2

=[2(a^2*b^2+b^2*c^2+c^2*a^2)-a^2-b^2-c^2]/4a^2*b^2*c^2

同理可推倒得SINa^2/a^2=SINb^2/b^2=SINc^2/c^2

得证用余弦定理：a^2+b^2-2abCOSc=c^2 COSc=(a^2+b^2-c^2)/2ab SINc^2=1-COSc^2 SINc^2/c^2=4a^2*b^2-(a^2+b^2-c^2)^2/4a^2*b^2*c^2 =[2(a^2*b^2+b^2*c^2+c^2*a^2)-a^2-b^2-c^2]/4a^2*b^2*c^2 同理可推倒得SINa^2/a^2=SINb^2/b^2=SINc^2/c^2 得证

4

满意答案 好评率：100%

正弦定理

步骤1.

在锐角△ABC中，设BC=a,AC=b,AB=c。作CH⊥AB垂足为点H

CH=a·sinB

CH=b·sinA

∴a·sinB=b·sinA

得到 a/sinA=b/sinB

同理，在△ABC中， b/sinB=c/sinC

步骤2.

证明a/sinA=b/sinB=c/sinC=2R：

如图，任意三角形ABC,作ABC的外接圆O.

作直径BD交⊙O于D.

连接DA.

因为直径所对的圆周角是直角,所以∠DAB=90度

因为同弧所对的圆周角相等,所以∠D等于∠C.

所以c/sinC=c/sinD=BD=2R 类似可证其余两个等式。

余弦定理

平面向量证法：

∵如图，有a+b=c(平行四边形定则：两个邻边之间的对角线代表两个邻边大小)

∴c·c=(a+b)·(a+b)

∴c^2=a·a+2a·b+b·b∴c^2=a^2+b^2+2|a||b|Cos(π-θ)

(以上粗体字符表示向量)

又∵Cos(π-θ)=-CosC

∴c^2=a^2+b^2-2|a||b|Cosθ(注意：这里用到了三角函数公式)

再拆开，得c^2=a^2+b^2-2*a*b*CosC

同理可证其他，而下面的CosC=(c^2-b^2-a^2)/2ab就是将CosC移到左边表示一下。

平面几何证法：

在任意△ABC中

做AD⊥BC.

∠C所对的边为c，∠B所对的边为b，∠A所对的边为a

则有BD=cosB*c，AD=sinB*c，DC=BC-BD=a-cosB*c

根据勾股定理可得：

AC^2=AD^2+DC^2

b^2=(sinB*c)^2+(a-cosB*c)^2

b^2=sinB²·c²+a^2+cosB²·c^2-2ac*cosB

b^2=(sinB^2+cosB^2)*c^2-2ac*cosB+a^2

b^2=c^2+a^2-2ac*cosB

cosB=(c^2+a^2-b^2)/2ac

三 : 30正弦定理的几种证明方法

正弦定理的几种证明方法

1.利用三角形的高证明正弦定理 （1）当?ABC是锐角三角形时，设边AB上的高是CD，根据锐角三角函数的定义，

C

有CD?asinB,CD?bsinA。 由此，得

a

sina

sinA

?

b

sinB，?

同理可得

c

sinC

?

b

sinB

，A

D

B

b 故有

?

b

sinc

sin.从而这个结论在锐角三角形中成立.

（2）当?ABC是钝角三角形时，过点C作AB边上的高，交AB的延长线于点D，根据锐角三角函数的定义，有CD?asin?CBD?asin?ABC，CD?bsinA 。由此，得

a

sinA

?

b

sin?ABC，?

同理可得

c

sinC.

c

sinC

?

b

sin?ABC

a

故有

a

sinA

b

sin?ABC

?

由(1)(2)可知，在?ABC中，

a

sinA

?

b

sinB

?

c

sinC

B D

成立.

从而得到：在一个三角形中，各边和它所对角的正弦的比值相等，即

a

sin?

b

sin?

c

sin.

1’用知识的最近生长点来证明：

实际应用问题中，我们常遇到问题：

已知点A，点B之间的距｜AB|，可测量角A与角B， 需要定位点C，即：

在如图△ABC中，已知角A，角B，｜AB｜＝c， 求边AC的长b

解：过C作CD?AB交AB于D，则

DC?

AD?ccosA

BDcsinAcsinAcosC

??sinCtanCsinCcosC

b?AC?AD?DC?ccosA?

bc

? sinBsinC

csinAcosCc(sinCcosA?sinAcosC)csinB

??

sinCsinCsinC

推论：

同理可证：

abc

?? sinAsinBsinC

2.

利用三角形面积证明正弦定理

已知△ABC,设BC＝a, CA＝b,AB＝c,作AD⊥BC,垂足为则Rt△ADB

ADA 中,sinB? ∴ AB

111

1

∴S△ABC=a?AD?acsinB同理,可证 S△ABC=absinC?

bcsinA

2222111

∴ S△ABC=absinC?bcsinA?acsinB∴ C D

222

sinCsinAsinBabc

????在等式两端同除以ABC,可得即. cabsinAsinBsinC

3.向量法证明正弦定理

(1)△ABC为锐角三角形,过点A作单位向量j垂直于,则j与90°-A,j与的夹角为90°-C

由向量的加法原则可得

B

的夹角为

??为了与图中有关角的三角函数建立联系,我们在上面向量等式的两边同取与向量j的数量积运算,得到j?(?)?j? 由分配律可得?∴|j|∴

j??j?j

C

Cos90°+|jCos(90°-C)=|jCos(90°-A

∴

ac

?

sinAsinC

另外,过点C作与垂直的单位向量j,则j与的夹角为90°+C,j与的夹角为90°+B,可得

cb

?

sinCsinB

(此处应强调学生注意两向量夹角是以同起点为前提,防止误解为j与为90°-C,j与

的夹角

的夹角为90°-B

∴

abc

??

sinAsinBsinC

(2)△ABC为钝角三角形,不妨设A＞90°,过点A作与与

垂直的单位向量j,则j

的夹角为A-90°,j与的夹角为90°-C

,得j·=j·j·

A

由??

即a·Cos(90°-C)=c·Cos(A-∴∴

ac

? sinAsinC

A B

另外,过点C作与垂直的单位向量j,则j与角为

B.同理,可得

的夹角为90°+C,j与夹

abcbc

???.∴ sinBsinCsimAsinBsinC

4.外接圆证明正弦定理

在△ABC中,已知BC=a,AC=b,AB=c,作△ABC的外接圆,O为圆心,

连结BO并延长交圆于B′,设BB′=2R.则根据直径所对的圆周角是直角以及同弧所

对的圆周角相等可以得到

cc

?2R ∠BAB′=90°，∠C =∠B′，∴sinC=sinB′=sinC?sinB??∴

2Rsin

C

ababc

?2R,?2R∴??

?2R 同理,可得

sinAsinBsinAsinBsinC

这就是说,对于任意的三角形,

我们得到等式 abc

??

sinAsinBsinC

四 : 正弦定理的几种证明方法

正弦定理的几种证明方法

1.利用三角形的高证明正弦定理 （1）当?ABC是锐角三角形时，设边AB上的高是CD，根据锐角三角函数的定义，

C

有CD?asinB,CD?bsinA。（www.61k.com) 由此，得

a

sina

sin?

b

sin，?

同理可得

c

sin?

b

sin，A

D

B

b 故有

?

b

sinc

sin.从而这个结论在锐角三角形中成立.

（2）当?ABC是钝角三角形时，过点C作AB边上的高，交AB的延长线于点D，根据锐角三角函数的定义，有CD?asin?CBD?asin?ABC，CD?bsinA 。由此，得

a

sinA

?

b

sin?ABC，?

同理可得

c

sinC.

c

sinC

?

b

sin?ABC

a

故有

a

sinA

b

sin?ABC

?

由(1)(2)可知，在?ABC中，

a

sinA

?

b

sinB

?

c

sinC

B D

成立.

从而得到：在一个三角形中，各边和它所对角的正弦的比值相等，即

a

sin?

b

sin?

c

sin.

1’用知识的最近生长点来证明：

实际应用问题中，我们常遇到问题：

已知点A，点B之间的距｜AB|，可测量角A与角B， 需要定位点C，即：

在如图△ABC中，已知角A，角B，｜AB｜＝c， 求边AC的长b

解：过C作CD?AB交AB于D，则

DC?

AD?ccosA

BDcsinAcsinAcosC

??sinCtanCsinCcosC

b?AC?AD?DC?ccosA?

csinAcosCc(sinCcosA?sinAcosC)csinB

??

sinCsinCsinC

正弦定理的证明 正弦定理的几种证明方法

推论：bc? sinBsinC

abc?? sinAsinBsinC同理可证：

2.利用三角形面积证明正弦定理?

已知△ABC,设BC＝a, CA＝b,AB＝c,作AD⊥BC,垂足为D.?则Rt△ADB

ADA 中,sinB? ,?∴AD=AB·sinB=csinB.? AB

1111∴S△ABC=a?AD?acsinB.?同理,可证 S△ABC=absinC?bcsinA.

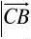
? 2222

111∴ S△ABC=absinC?bcsinA?acsinB.?∴absinc=bcsinA=acsinB,? C D 222

sinCsinAsinBabc????在等式两端同除以ABC,可得.?即. cabsinAsinBsinC

3.向量法证明正弦定理

(1)△ABC为锐角三角形,过点A作单位向量j垂直于,则j与B 的夹角为

,? 90°-A,j与的夹角为90°-C.?由向量的加法原则可得???

j的数量积运算,得到j?(?)?j?

由分配律可得?

∴|j|为了与图中有关角的三角函数建立联系,我们在上面向量等式的两边同取与向量j??j?.? Cos90°+|jCos(90°-C)=|jCos(90°-A).? j

ac?.? A C sinAsinC∴asinC=csinA.?∴

另外,过点C作与垂直的单位向量j,则j与的夹角为90°+C,j与的夹角为90°+B,可得cb?.? sinCsinB

(此处应强调学生注意两向量夹角是以同起点为前提,防止误解为j与

为90°-C,j与

的夹角的夹角为90°-B)?∴abc??.? sinAsinBsinC

正弦定理的证明 正弦定理的几种证明方法

(2)△ABC为钝角三角形,不妨设A＞90°,过点A作与

与垂直的单位向量j,则j的夹角为A-90°,j与的夹角为90°-C.? A 由??,得j·?+j·,?

=j·ac? sinAsinC即a·Cos(90°-C)=c·Cos(A-90°),?∴asinC=csinA.?∴

另外,过点C作与垂直的单位向量j,则j与

角为?90°+B.同理,可得

4.外接圆证明正弦定理 B 的夹角为90°+C,j与夹 abcbc???.?∴ sinBsinCsimAsinBsinC

在△ABC中,已知BC=a,AC=b,AB=c,作△ABC的外接圆,O为圆心,

连结BO并延长交圆于B′,设BB′=2R.则根据直径所对的圆周角是直角以及同弧所对的圆周角相等可以得到

cc?2R.?∠BAB′=90°，∠C =∠B′，∴sinC=sinB′=sinC?sinB??.?∴ 2RsinC

ababc?2R,?2R.????2R.?同理,可得∴ sinAsinBsinAsinBsinC

这就是说,对于任意的三角形,我们得到等式?

abc??.? sinAsinBsinC

本文标题：正弦定理的证明方法-正弦定理的几种证明方法
本文地址： http://www.61k.com/1200151.html