一 : 分数的基本性质和小数的基本性质有什么关系
分数的基本性质：分数的分子和分母同时扩大（或缩小）相同的倍数，分数值不变。[www.61k.com] 小数的基本性质：小数末尾添上0或者去掉0,小数的大小不变。 比的基本性质：比的前项和比的后项同时扩大（或缩小）相同的倍数,比值不变。 百分数的意义:表示一个数是另一个数的百分之几的数，叫做百分数，百分数也叫做百分率或百分比。 小数的意义：用来表示十分之几、百分之几、千分之几的数，叫做小数，是分数意义的有部分。 比的意义：表示两个数相除的式子就是比。 它和分数的关系是：比的前项相当于分数的分子，后项相当于分数的分母，比号相当于分数线； 比和除法的关系是：比的前项相当于除法中的被除数，后项相当于除法的除数，比号相当于除号。
二 : 实数的阿基米德性是什么？在哪里讲的？华师大《数学分析》里直接说。
实数的阿基米德性是什么？在哪里讲的？
华师大《分析》里直接说。高中没学过，大学也不知道在哪门课里的？
好像实变函数论有讲吧。应该是实数的性质。
三 : 数学的本质是什么？
[数学是什么]数学的本质是什么？网友蒙面大侠对[数学是什么]数学的本质是什么？给出的答复：
如果把学数学比作爬山的话，在我高中毕业的时候我以为我到了山脚下了，学完数分高代解几之后我以为我到半山腰了，学了实变复变泛函偏微点拓代拓微拓抽代交代等一大堆的东西之后我怀疑我还不到半山腰，到了大四又学了一些东西以及和很多前辈交流，现在快要毕业的我确信自己终于站在了山脚下了呢（也许过了几年又将证明我今天做这番言论是多么的无知）。。。。
未知各位答主自认自己开始上路了没有，呵呵。
唉大家洗洗睡了吧，有资格回答这问题的人在可预见的未来里应该不会上知乎的。。。
把之前的评论献给回答的各位与题主吧。
任何尝试回答这个问题的人都勇气可嘉，但任何提交了答案的人则只能认为是狂妄与无知的典型了。。。所以，先多读读书再来想这个问题吧，还没长出腿就想着跑是不对的哦。。。
网友匿名用户对[数学是什么]数学的本质是什么？给出的答复：
高中生有这样的思考，非常赞。
最简略的回答：数学是抽象。
数学研究的是抽象概念，运用的是抽像方法，数学的发展体现为抽象程度的逐渐深入。
但是深入的话，数学的本质并没有定论。我将在下面分三个部分展开，对＠涛吴 提供的维基链接中提到的各种观点做一个简短的解释。
普通数学
对应于维基上说的现实主义数学，逻辑主义数学。大多普通群众，科研工作者，和很多数学家，都采取这些观点。在这些观点下，数学与现实紧密结合，因此其应用当然也非常广泛。
这其中比较肤浅的是：
数学是生产生活生存的需要，比如几何是为了丈量土地，数学是工具。
这个观点的代表么……马克思同学（如果他真这么说过）。所以1＋1＝2，因为一个苹果，再来一个苹果，是两个苹果，这是从实践中总结的经验和规律。 比较靠谱的想法是：
数学是无实体的，永恒的客观存在，是等待被人发现的自然规律。
提问者和大多数人都有这个想法。很多数学家，包括一些大师也有这个想法。所以勾股定理不仅是丈量土地有用，还是直角三角形的普遍规律，而三角形是自然界中的对象。 另有一些数学家，和不少学计算机的认为：
数学是逻辑的一部分，是公理系统。
这个观点在实践中还是非常流行的，并且的确非常强大。但是其中很多悖论经不住下面那个文艺数学的推敲。在这个观点下，数字和运算都是公理。
文艺数学
对应于维基上的形式主义。很多数学家，很多搞哲学的，还有我个人，都持这样的观点。
形式主义认为：数学体系是一场有一定规则的思维游戏，与现实世界完全无关。
与前面那些观点不同的是，这个观点空前抽象和开放。我们从此开始发明各种变态规则，玩奇怪的非人的游戏。在这个观点认为，勾股定理在欧几里德的几何规则下才正确，但是我们可以发明其他非欧几何，让他不正确；数是代数结构中的元素，运算是游戏规则。
这个观点给数学带来了空前的发展，也导致纯数学与现实严重脱节。不管有用没用，对形式主义者来说都一样值得研究。虽然对现实不再有直接的应用，但是其他学科主动去消化的话，仍然能找到很好的归宿。
二逼数学
我想提的是直觉说。很多搞认知学的，搞神经学的，大概会持这个观点……
直觉说认为：数学是人的大脑活动，数学都是被经历过的。
说一个数学对象存在，是因为你可以在大脑中构造这个对象。所以一些激进点的人会否认“无穷”这个概念的存在。我的一个认知学老师这样对我们说：数学家们经常觉得自己来了灵感，其实他们就是学了很多之后，从经验中获得的想法，哪有什么空来的点子。
其实他们的观点我觉得有些道理，只是……类比Sheldon说自己有很牛的想法，而Amy说自己研究的就是这些想法怎么来的。
网友幻灰龙对[数学是什么]数学的本质是什么？给出的答复：
现代数学是建立在集合论基础之上。研究集合的结构和性质，特别是那些在变换下保持不变的性质，集合A经过变换T之后变成集合B，在A和B的元素之间保持不变的性质。
其中最常见的具体集合元素包括:数，量，函数，几何体，集合等；最常见的结构包括:拓扑结构，代数结构等；最常见的性质包括:代数性质，分析性质，拓扑性质等。
数学研究的基本方法有两种:一种方式是从将问题分解，每个都解决，从而解决原问题；第二种是将问题抽象泛化成更普遍的问题，在抽象层上解决，然后针对具体问题给出特定解。
做数学研究的有三种厉害:一种是在抽象上厉害。一种是在计算上厉害。一种是在构造上厉害。
如果要说和现实世界的关系。数学提供了一种对现实世界建模的框架，提供了将在一个领域上发现的规律迁移应用到所有符合假设条件的其他领域上的能力。
推荐书籍：《什么是数学》，[美] R·柯朗 H·罗宾 著/ I·斯图尔特 修订
网友言成对[数学是什么]数学的本质是什么？给出的答复：
不完全同意排名第一的答案。抽象抽象，就是将本质从现象中抽离出来，你可以说这是数学的特点，也可以说这是数学的方法，但说它就是数学的本质还不够透彻。先抛结论，数学的本质是“元界限”。
道可道也，非恒道也。名可名也，非恒名也。无名万物之始也，有名万物之母也。——《道德经》
当山还不叫山，海还不叫海，野兽没有牛羊虎狼之分，群星不分彼此，万事万物还没有被命名时，山依旧巍峨而立，海深不可测，野兽奔跑生息，群星摧残闪烁，万物自得其乐，彼时的它们和如今也并无不同。只不过或许在原始人眼中，山和海是一样的——都遥不可及，野兽都是一样的——可以食用，星星都是一样的——高不可攀。如今的我们却给他们多赋予了一些名称加以区别：那高耸于地面的叫做“山”，那广阔的水域叫做“海”。名称在事物之间强行画出了线条，线条内的就是“界限”，一个界限就是一物，一象，人类勾勒出了条条线索，由此有了森罗万象——有名万物之母也。
产生了线条，世界不再浑然一体，数量便有了意义。而数量堪称神器：一座山是“一”，一片海是“一”，一头羊是“一”，一群野兽也是“一”……“一”，这个简单的线条便可以将无限多的事物纳入它的界限，而我们还有二、三、四、五……至此，万物的界限之上又有了数字的界限，我们不妨称之为“元界限”，别急，这还不是数学本质的“元界限”。
难道“元界限”还不是终极的界限？当然，元界限也是界限，界限之上还可以有界限，比如说——代数。我可以设x=1，我也可以设x=2,3,4,5……一个x，就走到了元界限之上呢~~~哦对了，还有y，abc神马的更不在话下，嗯哼，那就叫“元元界限”好了。
不管多么高深的数学，它的工作始终是从界限中抽离出元界限。聪明的你一定会发现一个数学名词说不定都已经是元元元……元的界限了呢。反正我就用一个元字表述，就叫它“元界限”，就是这么任性。以上~
网友三胖Sir对[数学是什么]数学的本质是什么？给出的答复：
先抛结论：数学本质上是一门研究模式的科学。
——————以下内容来自以前整理的素材————————
何谓数学?如果你随机向人们提问,那你很可能得到的回答是"数学就是有关数字的一门学问".这或许是你可以得到的最多信息,然而,这种关于数学的描述,早在两千五百年前,就已经不再正确了.
到公元前五百年左右止,数学确实是有关数字的一门学问,这是古埃及和古巴比伦时期的数学.在这些古文明中,数学是以算术(arithmetic)为主的。
公元前五百年到公元前三百年，是属于古希腊的时代，这一时期，数学开始脱离数字。古希腊的数学家们更关心几何（geometry）.而正因古希腊人的努力，数学才开始逐渐进入了研究领域，而不再只是度量、计算等功利的取向。他们视数学为一种知性探索，其中包含了美学与宗教的成分。在这一时期，古希腊伟大的哲学家泰勒斯（Thales）更是引入了划时代的命题证明思想。这一思想的引入，保证了命题的正确性，揭示了各定理之间的内在联系，使数学构成了一个严密的体系。
然而，在之后的两千年中，数学的研究几乎没有任何的进展，直到17世纪中叶。从牛顿和莱布尼茨发明微积分那刻起，数学的本质就此改变。在此之前，数学大都局限于计算、度量和形状描述的静态议题上，但微积分是研究运动和变化的一门学问。有了微积分，数学家终于可以研究行星的运行、落体运动、液体流动、疾病传染etc.因此，在牛顿和莱布尼茨之后，数学变成了研究数字、形状、运动、变化以及空间的一门学问。
进入20世纪，数学迎来了爆炸的时代。1900那一年，几乎所有的数学家都相信，他们已经完成了数学的伟大版图，直到当年的巴黎国际数学家大会上，希尔伯特抛出那23个问题。
1900年，对数学人来说，是最坏的时代，也是最好的时代。
他们满心期待的完整版图出现了巨大的裂缝，但同时，在这个裂缝处，无尽的新知喷簿而出，照亮了整个时代。当时世界上所有的数学知识可以装入大约八十部书籍之中。而今日，数学将必须有十万部书籍才能容纳。1900年，数学包括了十二个主题：算术、几何、微积分等。而如今呢？代数、拓扑、复杂理论、动态系统理论…….
面对数学如此迅猛的成长，“何谓数学”这个问题也变得更难以回答。如今，一种特定的研究之所以被归类为数学，并不是基于什么被研究，相反，是基于它通过什么方法理论研究。直至最近几十年间，一个为大部分数学家所同意的有关数学的定义终于出现了：数学是研究模式的科学（science of patterns）。 数学家要做的，就是去检视抽象的模式——数值模式、形状的模式、运动的模式、行为的模式、投票模式etc.这些模式或静态，或动态，或定性，或定量。他们源自周遭的世界，源自时间和空间的深度，更源自人类心灵深处。
网友王鐏鍚对[数学是什么]数学的本质是什么？给出的答复：
数学的本质应该是就是所谓的——抽象。
一开始，数学把一切具体的量去除，只留下数字；
再后来，由物理去除一切规律下运行的物，只留下规律，再由数学把所有需要物支持的规律去除，只留下公式；
把一切外在的具象剥离出去，数学，是极致的抽象，抽象的极致。
无法再抽象的抽象，是为数学。
网友蒙面大侠对[数学是什么]数学的本质是什么？给出的答复：
看到这个问题我忍不住要回答一下。但这个问题的答案其实我是不知道的。而且我下面要说的话，你很难理解。
关于数学是什么这个问题实际上非常复杂，以至于世界上还没有人能够答出来。
尽管如此，很多人还是会认为自己能够回答上来，但他们并不知道自己在谈论是什么。比如楼上有人说数学是被发明的不是被发现的，敢这么说话，不是无知，就是狂妄。
现今世界上直接从事这方面研究的数学家是非常少的。实际上我们对数学的认识是随着时间的推移，不断变化的。直到1920年，希尔伯特依然相信可以证明全部数学的无矛盾性。然而1931年哥德尔发表了关于哥德尔不完全性定理的论文。哥德尔证明了证明一个公理系统无矛盾的唯一方法是把它传递给更大的系统，这样一来寻求全部数学的无矛盾性的希尔伯特规划其实是不通的。从现代的观点看 数学远不止由公理和做出推演的 规则构成的形式系统。但是我们对数学的理解，从哥德尔后，就基本停滞不前了。
关于数学是发明的，还是发现的？这个问题也是没有人能够回答的。现今说法是，公理系统似乎是可以被发明的，但公理系统的定理，似乎又是发现的。然而如果某某发明的公理系统可以被证明内部矛盾（公理与公理之间矛盾），那我们就不能说这个公理系统是”对“的，那我们就不能称某某的公理系统是"公理系统”。这么一来我们似乎只能发现可以被称为“公理系统“的系统，这样一来，就和我们只能发现和证明”成立的“的定理没什么区别。
我给题主的提议是，与其在英特网上问一些来历不明的人这种艰涩的问题，不如踏实的学习数学，关于数学是什么这个问题的答案，你是可以从学习数学中有所体会的。
网友蒙面大侠对[数学是什么]数学的本质是什么？给出的答复：
数字怎么定义，加减乘除怎么定义。这两个问题我可以给出目前较为靠谱的学习办法。首先，你要读公理化集合论，读完了，再去读实数理论，从无开始，如何一步步的构造出自然数，自然数的加法与乘法，再扩展到整数，有理数，无理数，实数，最后再概括的看实数系统是个什么性质的东西。可以说，集合论与数系是展开一切数学的初始，对他们理解的程度直接关系到你对整个数学大厦的整体认知。在构建集合论与数系的过程中，要时时思考他们与物理世界的联系。从而在思维中划清物理世界与数学世界的界线，数学可以从物理世界中的直观而来，但却不必一定要由物理世界而来，这种观点是柏拉图与康德比较推崇的，我个人比较偏向维特根斯坦对数学的看法，即，重言命题。
网友匿名用户对[数学是什么]数学的本质是什么？给出的答复：
一列答案看下来让人失望. 怎么会有人能回答这个问题呢? 或许可以感性的描述一下个体所感受到的数学是什么样子的, 是小说? 是诗? or something else, 但不太可能有人能明确的指出 "什么才是数学", "什么才是数学的本质", 任何尝试的作答, 都是亵渎.
大牛Terrence Tao曾经写过一篇题为what is good mathematics的文章, 被另一个大牛Alain Connes斥之为, 除了一些空洞见解外只剩狂妄自大, 我觉得这可作为以上各回答的一个remark.
网友蒙面大侠对[数学是什么]数学的本质是什么？给出的答复：
这是很朴素的数学本体论思考，我很羡慕你能自己想出这个问题。数学是被发明（像一种工具）还是被发现（像一种真理）的？数学上定义上存在的东西为什么在现实中并不总是存在（比如多维空间）？为什么数学的发展总是超出现实需求，最后却又往往能满足现实需求？数学上的美究竟是什么？
摘自维基百科数学哲学一条 [1]——
What are the sources of mathematical subject matter?
What is the ontological status of mathematical entities?
What does it mean to refer to a mathematical object?
What is the character of a mathematical proposition?
What is the relation between logic and mathematics?
What is the role of hermeneutics in mathematics?
What kinds of inquiry play a role in mathematics?
What are the objectives of mathematical inquiry?
What gives mathematics its hold on experience?
What are the human traits behind mathematics?
What is mathematical beauty?
What is the source and nature of mathematical truth?
What is the relationship between the abstract world of mathematics and the material universe?
如果你能爬完此文，相信你还是得不到答案，但至少你的思路会扩展很多。另外推荐两个牛人的两篇小文，应该也有帮助[2] [3]。
[1] http://en.wikipedia.org/wiki/Philosophy_of_mathematics
[2]
[3] http://duane.upshine.net/
网友磨牙行者对[数学是什么]数学的本质是什么？给出的答复：
我说一个几乎不可能被人同意的答案，数学压根不是什么客观规律，数学是人类思考问题解释世界的一种方法，它与客观世界没有直接联系，它完全来自人的内心，恰恰因为这个，数学看上去最为客观，最像永恒不变的规律。也最干净，最美。
首先，什么是数字?数字是用来量化事物的符号。数字是纯抽象的东东。
某些数字看起来很神秘，看起来像是上帝确定的，其实不是那么回事，为什么pi是3.14开头，它为什么是这样一个看起来永恒不变的样子?因为我们在用十进制!当你换用其他千万种进制的时候，它就有千万种形态。你可能会说无论多少种形态，它的本质不变，但仔细想想，何谓本质?pi其实就是人造出的概念，与客观世界没有直接联系。
说到这里，你可能会想到圆，难道圆形不是来自自然和宇宙吗?其实，所有几何形状都是人类为了满足自身需要制造的概念。宇宙中没有点线面，没有圆形，没有方形，我们定义出来的形状统统都不存在于宇宙中。
数学里的有理数无理数，都是人类的执念造就的，一个分数，在10进制下，它被换算成无限循环小数，无限不循环小数，你换个进制，它就可能是有限小数,一个不那么神秘的数。一块蛋糕，平均切给三个人，以三进制的视角看，这里不存在切分精度的问题，每个人可得0.1块，以十进制的视角看，切分工作要无限地循环下去才能保证公平。当然，在已有的度量体系下，无限度的追求精准度，是人类的无奈选择，我所谓用"执念"也是为了方便理解。
数学与客观世界的唯一联系是人本身。人靠光来观察世界，光走的路子是最短的，所以人类可以形成直线的概念，然后又形成折/线曲线的概念，然后再有方形圆形的概念。人有十指，所以多少种进制最后以十进制为尊。
因为数学是一种纯粹的思维工具，所以它的发展是无止境的，它不太容易受限于技术
=============14/11/26心血来潮更新一下=============
有人说我的数学水平不超过高中，其实这是高看我，我高中数学都没学好。作为一个文科生，我只能用我文科的大脑来思考这些问题，而且多年以来，我的想法并没有太多进步，但我总觉得我的思考还是有意义的，因而拿出来和大家分享一下：
关于数学与物理及其他自然科学的关系，严格来说，其他自然科学仍然也只是思维工具，因为世界没有“绝对本质”，也没有“绝对真理”。相信这一点，大部分有哲学思考能力的人会有共识。
举例来说：我们今天认为DNA是产生遗传现象的根本，也许过些年，我们就会使用新的概念来解释遗传现象，并且会有新的应用，只要有实验能够证明新理论的有效性，那么旧的概念就会被替换掉。
数学与物理学边界的模糊，我想原因无外乎物理学到达了一个境界，那就是“可理解不可想像”，到了这个境界，除了使用纯粹抽象的工具来进行研究，几乎没办法取得进步。换句话说，不制造新的、无法想像的概念，就没办法对真实世界做进一步的解析，而这些概念是否可能有价值，只能利用数学工具来论证。接下来才是对真实世界进行实验验证理论是否有真正的价值。（这个价值不是说我们的生活应用，仍然是认识世界的价值）
再举例：力的概念，由于我们对力有感知，所以它不需要想像即可接受。但是引力的概念，只有当我们看过“磁力”的表现之后，才比较容易接受。（当然，磁力和引力毕竟不同）在这个基础上，我们认同地球是有引力才使我们不会飞出去。
但是，物理学在这些“原生”概念之上加上的一些“非原生”概念，比如“功”、“力距”，就需要我们去想像，然后应用了，因为它是原生概念相互结合产生的。这里的想像指的是：在你打算应用它们的时候，你必须以一些特殊的符号、图形及一些现象去缓存它们的一部分，否则你就会感到混乱难受，时刻怀疑自己的应用过程是否正常。从某种意义上说，想像是掌握“非原生”概念的敲门砖。
对于缺乏抽象思维习惯的人来说，最容易犯的错误就是：把这些概念的一部分或者它们的一部分价值作为它们的全部去应用。
而抽象思维的本质就是适当地丢弃和接受。古人不习惯丢弃，所以很多概念无法建立。后来，人们习惯丢弃了，但仍然不习惯接受那些“非原生”概念，于是就难以在理论上做出突破。
想像总是使人们被一些不恰当的因素所干扰，难以接受应该接受的东西、丢弃应该丢弃的东西，因而无法准确把握概念本身，它既是敲门砖，也是障碍。
后来，科学家驯服了自己的想像。科学就开始进入“可理解不可想像”的境界，或者说，进入到一种“玄之又玄”的境界。时间由原来对运动的度量工具、非原生概念（个人理解）变成和空间这种原生概念平起平坐的东西，并且和空间相结合，改变了我们对世界的理解。但此时，想像仍然只是敲门砖，不能适时扔掉敲门砖，就无法理解科学。
例如：某科学家教我们把时空中的人想像成一条虫子，这是一种手段，也是一个麻烦。
很多时候，我们是用一块敲门砖去打掉另外一块敲门砖，但这只是缓兵之计，并不解决根本问题。最终只能求助于数学这种纯粹的思维工具，因为数学可以相对理性地利用想像，而不受制于想像，在数学里，想像一旦失控，逻辑就会上场，它用逻辑缓解了人们在想像上的痛苦和失误，微观上提升了思维的速度，宏观上提升研究的速度。
感觉上面说的好民科，脚踩西瓜皮，滑到哪里是哪里！而且废话好多……
网友顾智翔对[数学是什么]数学的本质是什么？给出的答复：
恩，作为一名大学本科正在读数学的学生，我对这个问题也挺有兴趣的。当然，疏浅之见，徒增笑尔。
近来我们常常听到同时也是我非常认同的一个观点是：数学是一门语言。是的，就像英语中文这样，是一种语言。那么具体的说呢，数学是人类为了研究宇宙中的规律所抽象出来的，用来进行逻辑思考的语言。
随着人类文明的发展，我们开始逐渐意识到，语言是人类思考的媒介。同样的这也适用于我们对于真理的探求。数学所研究的领域是抽象出来的，完美的理论世界，我们在研究这样一个世界的性质时，当然也可以采用我们平时说的话，比如像我国古代的《九章》，但是这样的自然语言当然是不适合用作这样的研究的，因为它太抽象了。所以我们就创造出一种语言，专门用来研究这个世界，这就是数学。
可能没有接触过高等数学的你对于这个说法无法太好的理解，但是其实你早已接触过它了。你证明问题的时候用的因为所以的符号，表示线段的字母，等号，等等等等，都是数学这门语言的字母，你接触过的定义和定理可以看成它的单词或短语，甚至固定搭配。而这门语言的语法，叫做逻辑。学习一门语言就是一种记忆单词，掌握语法，多加练习，做到理解并运用的过程——在数学中也是如此。
由于这门语言是以逻辑作为语法的，其基础也就自然是笛卡尔的二元论。笛卡尔被视为现代数学之父（之一），大概有这样的因素。后来衍生出一门学科叫做数理逻辑，也许可以视为这门语言的语法学？
当然了，这门语言和所有其他的语言都太不相同，导致很多人都觉得它并不是一门语言。当初丘成桐先生在给我们做学术报告时，说出这个观点，也让我思考了很久。关于数学的本质是什么，恐怕是一个由来已久并且也一直会有人不断讨论的题目。然而我相信，把数学视为一门语言确实是一种非常贴切的描述。
网友蒙面大侠对[数学是什么]数学的本质是什么？给出的答复：
老爸给出的答案是：找出事物之间的内在规律是数学本质。
网友郭华对[数学是什么]数学的本质是什么？给出的答复：
我觉得数学包括两个部分：（1）公理系统（2）在公理系统内的推导。公理系统的出现应该是由实际生活抽象出的思维游戏，但在这个系统内的纯思维的推导就会远远超出实际（不是不符合实际），我不想进一步蛋疼的描述自然科学和数学是相辅相成。不过数学是强大的，你看仅仅是二进制的0和1，就已经衍生了近代最大的奇迹。能定义系统的都是神，能推导延伸的也是半神。至于我这样读书读了十几年，基本不再喜欢纯科学这种思维游戏的社会主义新青年，还是站在巨人的肩膀上yy吧。
网友Godfatttther对[数学是什么]数学的本质是什么？给出的答复：
推荐《数学，确定性的丧失》
网友Gucci Koo对[数学是什么]数学的本质是什么？给出的答复：
数学的本质是一套完全抽象严谨自洽的逻辑
网友胖子邓对[数学是什么]数学的本质是什么？给出的答复：
感觉楼上都好文艺。来说点干货。
先回答楼主的问题，其实数的定义要讲清楚还是蛮复杂的。
简言之，先定义集合（公理化集合），其次在集合上定义自然数（piano公理），其次在自然数上定义有理数（四则运算其实是域的概念），在从有理数定义实数（戴德金分割），再从实数定义复数（拓域），然后证明复数域不能再延拓了，至此我们经常用到的这一套数的结构全部定义完毕。
（题主可自行谷歌括号中关键词了解每个步骤，这里轻描淡写可每个步骤都不简单啊……）
有一点需要注意的是，虽然人对数的理解来源于那种结绳记事之类的东西，但是至此，数和那种东西没什么关系，唯一的关系就是，便于理解。
另说点八卦：正是因为以上完全不是经验的而是定义的东西，因此很有可能出现的事情是，根据上面定义出来的东西根本不存在。但是希尔伯特还是那谁证明了，满足peano公理的体系不存在矛盾。
可是哥德尔给出了一个更牛逼的定理，他说满足peano公理的体系虽然不存在矛盾，但是必然存在其既不能证明为真也不能证明为假的命题。注意，是必存在，就是说假定A命题不可证真伪，就算你把A命题直接作为了公理，也就是在peano公理体系下再加入A公理，那么也必定找得到B命题不可证真伪。这个命题也就是响当当的哥德尔不完备定理。
======================================================================
来讲点我想讲的：其实初等数学的数学，是一点点皮毛而已。
数学就是发现结构，并在定义的结构上找出结构的性质。
数学的美，就美在一些天才，发现了一些极好的结构，这些结构拥有极好的性质。
数学发展到今天，主要的结构可以大致分为三类：几何（或称拓扑）结构，代数结构和分析结构。
几何研究形的结构，代数研究数的结构，这是两大基本。但是发展到近代数学，有两个问题需要解决：一个是几何和代数的关系，一个是如何研究无穷。
第一个问题，笛卡尔开了个头，解析几何——其实就是把几何问题转化为代数问题。而这个转化就有了一个桥梁，即分析结构。
这之后，几何的结构反而在数学中弱化了，因为大家发现，只要搞好了分析，就能把所有的几何问题转化成代数问题。如果学过复分析就知道，这种转化简直太美了，黎曼几何，幂级数，柯西定理最后竟然是同一件事情。也正是在这之后，分析和代数反而成为了数学中相对更重要的部分。
第二个问题，无穷的研究，起源于牛顿及莱布尼茨，柯西和魏老将其严格化，这也就是高等数学中ε-δ语言。高等数学称之为高等的原因，就在于第一次严格地定义了结构。不然回想一下，我们初中学欧式几何的时候，其实不是从五大公设出发的。
如果再深入一点，就发现其实这三大结构，其实说到底，都是在定义距离（或者称为范数）和数量。
这其实是很自然的，不然搬个凳子讲个故事好了。
有一天，dengjiaji有了一堆三角形（不要问我他怎么会有一堆三角形的……），他想做的事情很直观，就是看有几个三角形。有一天dengjiaji把三角形分出去了，那么剩多少个三角形？这就是数量的意思。
dengjiaji学会算术以后，有一天有人问他：三个图形减两个图形等于多少？dengjiaji回答说是1。然后有人问：三个三角形减两个等于多少？dengjiaji就傻了：因为他发现三角形和四边形不一样诶……他突然就开始想为什么我会觉得等腰三角形和等边三角形可以都算在三角形里，三角形和四边形就不一样呢？他想到因为三角形有三个顶点，四边形有四个顶点诶。这就有了拓扑结构了，然后dengjiaji就聪明地想到，我现在想要进一步研究这些图形，这些点之间的相对位置也是相当重要的。这就是定义距离，定义范数。
总的来说，整个人类的知识，无论是经验还是先验的，都可以看做一个集合。这个集合很乱，很杂，是个大仓库。结构就是一种法则，一个筛子，让人如何从这个很杂的仓库中筛出东西，尤其是筛出具有某些“好”的性质的东西。
我的一位老师（得狠狠感谢杨家忠老师的常微和复变课呢哈哈）说，数学呢，在一般人眼里，可以分为这么三类：
1.以上所言
2.无聊数学：比如我问你π的第7位是多少，这个问题的无聊之处在于，你回答了我第7位之后我可以再问第8位，，，，这样一直下去……
3.不可延拓数学：比如我问你，可以表示成六位质数平方和的质数是否存在？若存在，最小的是多少？这类问题是典型的初等数学的问题，也就是说，因为没有一个结构，所有的知识都是试探性的。
在数学研究者中能称为问题的问题，只有1。当然也可能有一些3，主要是由于一些大定理的小细节要抠一下所以弄。
PS：当然还有序结构等，重要但在近代数学中并没有前三者重要。这里的不重要，只是因为序结构几乎不存在什么改进，因为就是一个序嘛，所以显得不重要。但应当注意的是，序结构是最基础的运算，是一元运算（代数则是典型的二元运算），这也正是归纳法的基础结构。在用piano公理定义自然数的时候，其实就是建立了序结构的。当然选择公理相关的结构我认为也可以纳入序结构中。
（话说一直在想，人能不能想出有什么三元运算的好的结构，感觉这个一定会无比奥妙，二元运算都已经具有如此多的性质，三元不知道美到哪里去了。）
上面有人提到了公理系统，其实也并不特殊，只是结构的结构。也就是说把结构作为一个集合，研究这个集合的结构。
我也非数学专业…………，轻拍。
另：楼主提到希望给出一些书籍的建议，我觉得，不要太看科普的书。因为会给你一种“哦原来数学就是这么回事”的君临天下的优越感。
如果真的对数学感兴趣，就每一步扎实地走。数分，高代，这是大学本科的两门基础课，要入数学的门，这绝对是基础的基础。戴德金分割没学好，大谈黄金分割如何美，不是特别好的行为。古典的东西很好，很巧，但你最好先成个体系，再去谈，不然会很丢人的。
不要把自己想象成天才，比如某天一下子就顿悟了。我抱着这种心态看过图论，密码学，数论，结果看过了第零章和第一章预备和初等的部分，就趴下了。数学这种事，就要一点一点地来，装逼同理。
以及，看了诸多答案后的感想是：学数学的时候最好不要一副文艺腔一副装逼犯的样子。这样其实不会走太远，多半会成为：数学就是一种抽象思维嘛，然后巴拉巴拉扯一堆，炫，但不酷。
这种类型的话，在我看来，太七平八稳了，一点观点都没有。如果你说，数学说到底都是形，根本没有数。这个观点比抽象思维这种无趣的说法要好玩多了，如果你能把这个观点深入下去，有独到的见解，那你也可以自成一派。你也可以说，数学的本质就在于提炼美的属性，数学的本质在于建立一套语言体系。都可以的，只要你能自成一派。
数学确实是一种抽象，可是抽象的本质在于有无数本质，仅仅知道它是抽象是毫无用处的。真正重要的是，用你自己的体验理解它。无论是哪个学科，根基确实是逻辑，但观点，看问题的视角一定是最有趣的那部分。
那数学可不可以文艺？是可以的。可是我的建议是，对于大部分人来说，不要一来就文艺，这样往往会误入歧途，以自己的偏见看宇宙，却以为自己的偏见就是全部。
比如我说：数学就是一种抽象嘛，其实生活中处处都是数学直观的。欧式空间里的平行线，是那些苦恋而不得的爱人的完美隐喻。球的完美，就在于在黎曼平面上，所有直线都相交。
可不可以这么说话？可以的。可是最好在这之前搞懂黎曼几何。
在成年之前再出来得瑟一下现一下哈哈。
以上。
网友vczh对[数学是什么]数学的本质是什么？给出的答复：
题主有前途，我推荐没人翻译过的《Elements of Set Theory》。大牛写的，通俗易懂，深入浅出，而且对前置技能点的要求不多，适合高中生看的大学教材。
尽管这本书没有告诉你数学的历史，但是他至少解决了的其中一种定义的问题，你一定会喜欢的。搞定了上面这本之后，你觉得还有余力，就可以去看黄皮的有翻译的《Algebra》。长此以往，将来肯定会成为大牛的。
网友蒙面大侠对[数学是什么]数学的本质是什么？给出的答复：
近日在时间线上重新看到这个问题，引发了我的很多思考。犹豫再三，在此把我浅薄的思考写出来，只希望能稍微激发对这个问题有兴趣知友的思考。
看过其它答案之后，第一个感受是不同的答案针对的点不一样。具体来讲，一部分答案是在讲数学思想的本质，而另一部分答案试图回答的是数学这门学科的本质。题主问题的歧义就在于：这里数学到底是一种思想，还是作为一门学科？我以为，数学思想的本质并不复杂，就像很多答案已经提到的一样：用抽象的逻辑思维方法演绎归纳出事物隐藏的本质。
真正困难的如何认识数学这门学科！！似乎题主更关心的也是这个问题，针对问题的描述，我的另一个匿名回答似乎可以稍微解释一下：0.999999... = 1 吗？怎样证明？。
大致来讲，数学家研究的是：在一个无内在矛盾的公理系统（即永远不会出现逻辑上自相矛盾的两个命题都对的情况！）中抽象定义出各种有趣的对象，比如大家熟悉的自然数、实数、复数、四则运算、函数多项式等等，通过演绎归纳和逻辑运算，得出非常不显然的结论。不同的数学家信奉的公理系统不一样，但大部分数学家在意的只是公理系统的兼容性，更具体的说，我们关注的是：给定一个命题，这个命题在给定的公理系统中是否可以被证明或证伪；如果不能，在原有的公理系统上增加什么条件（如果可以，希望这个条件尽量弱）可以达到这点。有兴趣的知友可参考阅读我另一个匿名回答：数学家之间会有争论吗？。
请原谅我没有能力描述数学这门学科的本质是什么，我这里只想给出更多的例子。
首先想提到的是从欧氏几何到非欧几何。这是数学史上一个伟大的进步，当某个公设被改写之后，数学家发现，新的形式系统同样有着复杂的结构和有趣的现象。几十年后，黎曼更是提出了更一般的空间概念——黎曼几何，数学家发现研究空间曲率是理解黎曼几何的关键点。经过近百年的努力，这一系列的研究最终将庞加莱猜想变成了一个定理。
不得不提的还有康托的贡献。给无限集合分类，并最终刺激数学家关于数学基础和集合论的研究，而连续统假设更是哥德尔不完备性定理的一个绝佳例子。
数学之所以叫数学，最关键的还是“数”，所以我最主要的例子就是数。看过我前面提到的匿名帖之后，相信有些知友已经在脑海中建立起了实数的概念。可是数学家发现，实数还不够！于是数学家引入了复数i（最初的目的只是为了解三次以上的多项式方程），这个神奇的平方为-1的数（因为i想到欧拉公式的知友请留言让我为你点赞！）。又经过几十年的研究，复数域以及复数域上面的函数的很多性质都已经建立，其中尤其引人注目的是黎曼zeta函数和黎曼猜想。说到这里，会不会有人问：什么是域？关于群、环、域等代数概念的研究最早从伽罗瓦和阿贝尔开始，起因是五次或以上多项式方程的可解性问题，简单而言就是满足某种代数运算规律的集合。当数学家抽象出域的定义之后，人们发现了一类尤其重要的数域：有限域，即只有有限个元素的域。而有限域与黎曼猜想的相遇，正是最近60年来一系列数学进展的引爆点。从Weil提出Weil猜想（有限域下的黎曼猜想）开始，新的语言和工具被引入直至今日被广泛认可：scheme的语言，代数拓扑的想法被引入，Grothendieck拓扑对传统空间概念的再次颠覆，对某种universal的上同调理论的探求，在新的语言框架下不断掀起高潮的算术几何。
稍微再总结一下：布尔巴基将数学结构分为三种，比如说在实数域上，有序结构（即大小关系）、代数结构（各种代数运算及其性质）、拓扑结构（分析基础中开闭集以及极限的概念）。这三大结构一定程度上告诉我们数学研究的到底是什么。
容我多嘴一句，纯属个人观点：我一向以为数学是被发现的！！而不是被发明的！数学定理虽然经常被贯以数学家的名字，可是这些定理就像宇宙中客观存在的天体一样，不管有没有被地球人观察到并命名，它们就在那里，或明或暗，时明时暗，对有些人明却对有些人暗。
最后，如果以上讨论让你对数学产生了些许兴趣并希望进一步了解。我有以下推荐：
《思考的乐趣 (豆瓣)》：趣味数学合集，能够通过初等具体的思考让人爱上数学的一本书。
《什么是数学 (豆瓣)》：我的数学启蒙，时至今日仍是经典，虽然内容上缺少了一些关于当代数学的介绍。
想要了解更现代的数学：
《现代世界中的数学 (豆瓣)》：科普性质的文章合集，对数学的各个分支有不错的介绍。
《当代数学 (豆瓣)》：为非数学家写的数学介绍，没有《什么是数学》那么详细，但包含一部分对当代数学的概述以及重要的数学证明方法。
网友王沁宇对[数学是什么]数学的本质是什么？给出的答复：
就任何一个具体的数学体系来说，这个体系的内涵就是，给出一些基本的人为抽象出的“定义”，其次，承认一些“逻辑”，那么由定义和逻辑构建成的整个体系，就成为一个数学体系。所以，数学实际就是研究一定的游戏规则下，这个游戏的属性是如何的，具有哪些性质，是一个研究事物的存在，事物与事物互动的科学（当然事物的定义是任意的）。就这个观点来说，数学早已与“数”没有特别大的关系，因为数只是一个非常具体的数学结构而已。
四 : 债券属性「久期」的本质是什么？
[麦考利久期]债券属性「久期」的本质是什么？网友尹小二对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
楼上基本上已经把该说的都说了。我随便扯扯吧。
债券有两大风险，一是利率风险，二是信用风险。其中利率风险就是用久期来衡量的。学术点来说，久期就是用现金流作为权，计算的加权平均剩余期限。
债券还本的时间越长，面临的利率风险就越大。但是不仅仅需要考虑最后到期时的那笔本金兑付，还要综合考虑到期前的每一笔现金流。比如中国很常见的7年城投债，一般都安排在到期前的5年，平均每年20%还本，那就有很大量的现金流在第3-7年之间还掉了。与此相比，正常的7年期公司债都是在到期的那天才还本的。很明显，由于提前换本条款的存在，那个7年的城投债所面临的利率风险要远远低于7年的公司债。可是到底低多少呢？
偷懒的证券工作者就很粗暴地发明了一个粗略的估算方法，用现金流作为权重，去算一个债的所谓“加权剩余期限”，这样就能理直气壮地说，某一个债比另一个债的利率风险高还是低了。这个概念是Frederick Macaulay发明的，一般实践中会使用一个数学变换过的被称作修正久期的东西。原理相同，公式楼上应该已经贴了。
其实吧，哪怕在实践中，久期也是一个极端粗略的指标，其粗略的程度类似股票里面的市盈率了。拿最常用的修正久期来说，它所反应的是利率的边际变动将带来的债券价值变化。其坑爹之处在于，由于这个修正久期的公式是从麦考莱久期推导出来的，因此它只能反应利率曲线平移所带来的债券价值变化。而利率曲线平移出现的概率有多高呢？现实中几乎没有。
所以，与其说久期是一个定量的指标，倒不如说它是一个定性的指标，用来大致推测和比较债券的利率风险。
另外，容我吐槽一下今年以来，中国极端平坦的利率曲线。感谢周小川同志一家门。
网友陈雨桐对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
首先，久期分为麦考利久期（Macaulay Duration）和修正久期（Modified Duration），二者之间存在一个转换关系（和债券付息频率有关）；
其中麦考利久期（Macaulay Duration）用来衡量一个固定收益证券，平均几年能收回现金（比期限/Maturity多考虑了现金流在不同时间点上的权重分配，因为货币是有时间价值的；只有当现金流全部放在债券到期一笔还清时，麦考利久期才等于期限，因为只有此时现金流分布才不存在权重问题）；这个东西表明你的成本如何影响你的收益；当麦考利久期越高时，表明现金流在越远的未来才能回收，市场利率对你的收益影响就越大（因为折现期长），反之则影响越小。
而修正久期（Modified Duration）衡量的是债券的价格/收益率对于利率的敏感度（衡量利率风险），即当市场中利率变动一个微小的百分比时，你持有的债券价格/收益率如何变动？同麦考利久期，当修正久期越大时，市场利率变动对你的收益影响就越大。
当付息是连续的时候，二者相等（转换比例=1），此时久期可以同时衡量上面两个东西。只是现实中付息通常是离散的。
（具体债券市场不了解，以上只是书本式回答）
网友Hang Li对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
从数学的角度上来说，你把债券价格（Bond price）的对数看成是一个关于收益率（Yield）的函数，然后久期（Duration）是泰勒展开式的第一阶系数，凸性（Convexity）是展开式的第二阶的系数。实际上是近似了债券价格关于收益率的semi-elasticity（求中文翻译）。
比较通俗的解释自然就是楼上诸位说的“（现金流加权）平均到期时间”。
网友Liu Cao对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
来个通俗易懂版的解释：
久期是一个很好的权衡债券现金流的指标。
其实我觉得久期的英文更能反应这个指标的本质：duration。
债券有几大重要指标，面值（face value），收益率(yield rate)，到期时间(maturity)。
duration本质上其实就是加强版的maturity。
让我们看两个债券的现金流：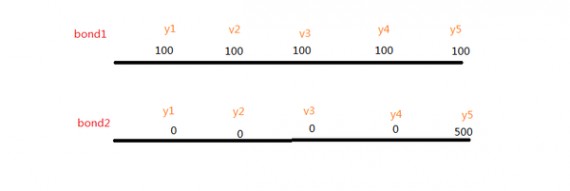
两个都是5年期的债券，maturity 都是5年，但是这一个干巴巴的到期时间数字不能表现出来现金流的变化啊。
每年都拿100，拿5年，和第5年拿500明显是不一样的。（就算我们把bond1里面每年的现金流都调低一些，调成5年后刚好终值刚好是500其实两个bond也是不一样的，因为风险不同）
于是我们就把每天的现金流按照时间加权，再除以现值：
于是我们就得到了久期这么一个好的指标，妈妈再也不用担心下图这种奇葩现金流干扰我的判断了：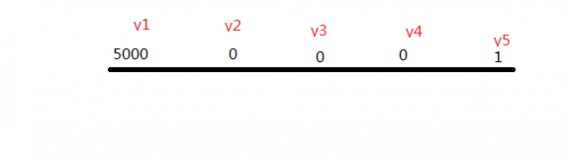
按照maturity的判断这是个5年的债券，但是我真的真的真的不关心5年后那1块钱。
于是用久期这个大神器算一下，duration=1.050186009年（折现率按5%算）
于是我们成功的揭开了这个名为5年期债券，实为1年多一点期债券的实质。
想想如果你的portfolio里面有thousands of bonds...
你想知道你大概需要承担多久的风险的时候
有duration这种东西是多么幸福吧。。
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
久期（duration）是固定收益里的一个概念。（固定收益是债的学名）
先说结论：duration越大，债的利率风险就越大。
【解释】
---逻辑分析·为啥要搞出个久期---
对于手里的债券，我们最关心的是它的价格。因为债券的价格是现金流折现的，也就是说债券价格是利率的函数。（假设不考虑信用风险，全买的是government bond好不啦）
那么手里这张债的价格就受市场利率的影响。（太好了，居然是个单变量函数）Price=f(interest rate)
但是利率每天变，每张债的面值不一样，付息方式不一样。理论上如果我想了解利率变怎么影响价格变我需要知道知道上边一堆信息，可是好麻烦…毕竟不是每天只盯一张债。就好像跟别人描述一个餐馆，可以说这个餐馆的食材新鲜、厨师火候掌握的好，餐厅环境文艺小清新巴拉巴拉，也可以说大众点评4分半。粗糙但是有效率。何况，用公式每天算一遍这活太脏太耽误事儿了，尤其是在这概念开发出来的那个没有计算机的纯真年代。
于是想出个指标大致衡量债券价格对于利率的敏感性。
学过微积分的同志们跳出来说，这很容易啊，求个导就行了呗
但是M神不会求导，他老人家1938年搞出个麦考利久期的时候，想出了一个曲线救国的解决办法。
---麦考利久期咋来的---
当你借钱给别人，最关心两件事：
1）钱什么时候回
2）每次回多少
经验来看，钱回的越快，尽早把大头还清的，这样的债风险比较小。
最简单的情况，没有利息，在说定的日子一次还清。Intuitively，5年之后还和10年之后还是不一样的。10年要经受更多未知的风雨。10年期债的duration要比5年期的duration大。太好了，恰好10就比5大，maturity可以直接拿来用！于是这个指标在这种情况下可以直接用剩余期限来衡量。
稍微复杂一点，在还清之前会零零散散收到一部分钱的情况咋办？那么我想看能不能在maturity上做个修改啥的，让它能大体上反映还钱的时间和每次还的数额，这个时候duration=weighted maturity。 然后发现，太好了，只要把权重设置成（该时点现金流的现值/债券总现值）就可以了。公式如前面知友所写。
---修正久期（modified duration）是个啥---
好了，麦考利久期完美的解决了如何简单粗暴有效地衡量一张债的利率风险。这样我就可以同时关注好多好多债辣。
数学好的同志们说这太糙了，于是用微分搞了个更准的算法。
---有的时候还有个家伙乱入：dollar duration---
神说要用微积分算久期，于是就有了修正久期。修正久期精确衡量了利率变化一个百分比，债的价格变动的比例。
但是，有了个新问题，报纸上写的利率不是按百分比变化的（按百分比变化市场做不到啊…），报纸上写的都是基点（basis point）上升多少下降多少。这个换成百分比还好说。那我不想知道债券价格变化的幅度，我想直接知道我赚了或者亏了多少钱，这还得自己重新算一遍好烦啊。
于是在modified duration的前面和后面又分别延伸出了一块，多算了一步。
现在就能输入基点变化，输出价格变化啦！
---总结---
久期是一个衡量利率变化对债券价值影响程度的指标。它让不同付息方式、不同期限的债券可以在同样的标准下进行比较。它有好多个公式以适应不同场合的需求。
久期是个好同志。
网友Deep Night对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
首先久期(Duration)是与固定债券相关的一个概念。
固定收益债券的价格由收益率(Yield)来决定的。收益率增加，债券的价格下跌，反之亦然。
我们可以把久期看作是债券价格的变化对收益率变化的斜率(一阶导数)。我们可以通过久期对债券进行一个简单的估值。这是久期的最重要的现实意义。
债券的价格变动 = -(债券的当前价格 × 久期 × 收益率的变动)
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
一句话从性质上理解：久期是债券价格对于利率变化的敏感程度，而且又恰巧是收到债券现金流的加权平均时间。
补充一句：数学帝会说那两个东西差了一个系数：1/(1+y)。。
再补充一句：其实不是“恰巧”，因为利率本身具有时间属性，而且久期大意味着风险大，正如人们所说“夜长梦多”。
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
久期就是债券现金流被收到所用的平均时间
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
本质是一个加权平均数，字面上理解就是你平均等多久会收回一定期限内的所有现金流。
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
到期时间~离到期时间越久的债券，对于利率变动越敏感。。。相对的，比方明天就到期的债券，市场利率几何几乎对持有人没有任何差别了。
网友朱梁峰对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
前两名的回答都非常之清楚。我卖弄一点点关于久期的应用方面的知识（刚学）。。
债券的利率风险是可以规避的。只要你持有的时间长度等于久期（久期的单位是年), 并将每年得到的利息收入以无风险利率投资出去，以达到利率风险免疫（immunization）的目的。
网友样小样对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
我来个超级通俗回答~
久期可以理解为债券的真实期限~(针对超级小白)
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
张三和我同时跟你借了一万块钱，我借10个月就还给你，张三要借1年。你愿意借给谁？？（假设你只能借给一个人，而且我和张三信用等级相同，不存在任何歧视和偏差）
网友邵国庆对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
課本上說的麥考利久期本質是收回資金的加權時間，就是你多少年收回資金
市場上使用的都是修正久期，可以說麥考利久期不是真久期。拿國債來說，修正久期表示單位利率變動所帶來的債券價格的變動幅度！從收益率曲線上看就是某點的切線的斜率，由於這條切線不能覆蓋所有價格變動，所以就有了凸度（二階導數）? 點擊[http://pinyin.cn/1VSvdVIOUq5] 查看這張圖片。[访问验证码是：198914请妥善保管]
网友凯石工场对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
久期是债券平均有效期的一个测度，它被定义为到每一债券距离到期的时间的加权平均值，其权重与支付的现值成比例，是一种对风险的衡量。
网友杨娟对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
不作特殊说明，一般我们提到的久期说的就是麦考莱久期
用它来衡量对利率的敏感程度，计算出久期（一般上市债券基本资料都可以看到久期），就可以知道一个利率百分点变化引起的价格变化了
网友苏小黑对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
关于duration（久期）的用途和适用范围知友们都答得很完善了，但看题目描述，但关于题主强调的这个概念的数学本质，即为什么加权剩余期限可以用来衡量利率敏感性，我认为duration和convexity数学本质上是泰勒展开的结果，令y为利率，债券价格为V=f(x)，有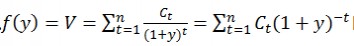
设D为duration，C为convexity，对f(y)求导，则有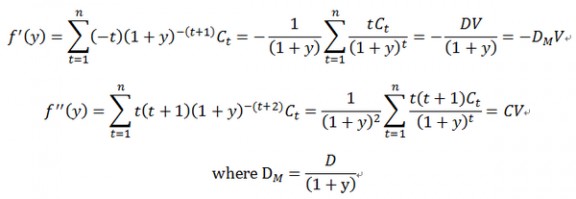
根据泰勒展开式，有根据泰勒展开式，有
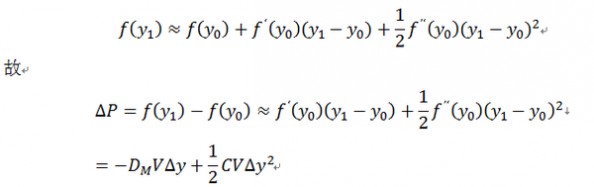因此，duration作为一个整体从泰勒展开式中剥离出来，可以因此，duration作为一个整体从泰勒展开式中剥离出来，可以近似地，线性地表达利率极小的变化所导致的债券价格变化，而convexity则可以加强这个精确性，而我们其实是再赋予它一个现金流现值加权到期期限的直观意义用来帮助理解。
网友蒙面大侠对[麦考利久期]债券属性「久期」的本质是什么？给出的答复：
Duration
Duration removes the limitation of payback as it focuses on all cash follows over the
entire life of the project. It measures how long it will be before the projet recovers the
bulk of its present value..However it can be more difficult to understand the concept
behind duration.
The main limitation of duration is that it assumes a linear relationship between
interest rates and price –that is, it assumes that for a certain percentage change in
interest rates there will be an equal percentage change in price.
五 : 两性婚姻的本质是什么
我想对王宝强说
——灵遁者
王宝强离婚事件持续这么长时间，成了大家茶余饭后的谈资。这显然已经上升为一个社会事件了，而不仅仅是个人家庭事件。所以大家很期待最终的法律判决，这也会成为大家茶余饭后的谈资。最重要的是这会影响大家对于婚姻的认识。
从事件开始说起，宝强一则离婚声明，最重要的一句是：“但我绝对无法容忍恶意背叛婚姻，破坏家庭的行为。”这则声明引来很多不同声音，有人说是为了炒作，因为宝强的新电影要上映了。也有人分析发布声明的时间和宝强公司股权变更时间，说宝强不是“傻根。”
将心比心，站在别人的立场上想问题，永远是我们应该先做的。宝强本身就是公众人物。公众人物结婚，交友，吃饭，生孩子等都是被广泛关注的。与其被爆料，偷拍，不如光明正大的说明。所以这很正常，谈不上炒作。
至于说宝强不是”傻根”，这很对。换做是你，你会怎么做。找个律师，做后续离婚安排，都是人之常情。生活中谁也不傻，你对我好，我对你好。单纯一味的付出，对婚姻往往不是好的。( 文章阅读网：www.61k.com )
王宝强无论是出生，长相以及在荧幕中塑造的形象，都是诚实，善良，勤奋的小伙。再加上马蓉是过错方，舆论一片倒向宝强，也是合理的。很多网友就说这是现实版的潘金莲与武大郎。
其实在我们的周围，类似的婚姻事件不在少数。但非公众人物，传播自然就不广。娱乐圈类似的事件更多，是因为环境使然。
不是每一个人都是圣人，这是必然的。所以婚姻关系的本质是什么很重要。婚姻关系的本质不是爱，不是性，不是孩子，不是这些具体的东西。婚姻关系的本质还是生产关系。
恩格斯先生在《家庭、私有制与国家的起源》中有详细的研究和调查说明。在文中恩格斯这样描述：“一夫一妻制度是在野蛮时代的中级阶段和高级阶段交替的时间从对偶家庭中产生的；它的最后胜利乃是文明时代开始的标志之一。它是建立在丈夫统治基础上的。”
中国是社会主义国家，社会生产资料公有，两性关系在法律上是平等的。但是恩格斯还说了：“在婚姻关系上，即使最进步的法律，只要当事人在形式上证明是自愿，也就十分满足了。至于法律幕后的现实生活是怎样的，这种自愿是怎样造成的，关于这些，法律和法学家都可以置之不问。”
所以不管出于什么原因，王宝强和马蓉走到一起了，都是自愿的。你可以说马蓉看上王宝强的钱了，你也可以说王宝强看上马蓉的容貌了。本质都是生产关系在作祟吧。
即使在社会主义国家，到今天。我们依然可以看到门户之见，父母之命对于婚姻的影响。其实婚姻选择的是一种生产关系。具体表现为生活方式，生活中的地位等等。
马蓉和宋喆在此次事件中是过错方，遭受吃瓜群众的口水压力，是必然的。这是从道德方面说的。
但社会是从道德和法律两方面制约的。那么宝强的离婚判决结果，就不难推测。在两性平等的基础上，即使作为过错方，也应该享有共同财产权利。马蓉净身出户是不可能的，就是多分和少分的区别。
那么我们吃瓜群众可能会问：“造成这样的悲剧是什么？”这是个很大的伦理问题。
我这样来说，看到一个《陕西蓝皮书》发布的新闻：“2014年全省共有对夫妻协议离婚，粗离婚率为1.86‰（不包括诉讼离婚案件数），与全国离婚率相比总体保持同步增长的态势。总体上陕西离婚率水平处于全国中等靠后位置，最突出的特点是“80后”离婚多、陕北人离婚多、高学历离婚多、“闪婚闪离”多。随着青年群体“离婚自由主义”的倾向日益突出，预计陕西省离婚率继续保持递增态势的可能性较大。”
其中80后离婚占到陕西离婚的50%。蓝皮书说明了两个原因：1、80后普遍学历高，自主性强。2、“80后”女性由于经济独立能够承担离婚带来的风险，主动提出或起诉离婚的比例明显增多。而陕北人离婚多，则是因为拆迁安置、二手房买卖、单位福利分房及商品房限购等政策原因，出现扎堆结婚、功利性离婚。
现在该我问问题了：离婚率上升是文明的进步，还是文明的落后？
我的答案是文明的进步。结婚自由，离婚也自由。放在民国之前，上哪离婚去？
从陕西蓝皮书中也可以进一步看到女性意识的崛起。两性婚姻的平等。但是对于政策性结婚和离婚，闪婚闪离我们从道德上是谴责的。这本身就构成了社会的不稳定因素。其实对结婚和离婚的个人而言，也多是痛楚。不要抱怨，你选择了这样，就得接受今天的痛楚。对于王宝强，马蓉，宋喆这句话同样适用。
说的诗意些就是，遇见是一种缘分，分手也是一种缘分。你好，我好，大家好，才是和谐的社会。更何况应该考虑到幼小的孩子，得给孩子留一片安静的成长空间，和一个好榜样。
所以综上所述，造成宝强和马蓉的悲剧原因，也是造成大多数离婚事件的原因。在婚姻关系中，王宝强是多付出的一方。马蓉是家庭财产的管理者。再者，马蓉已经通过王宝强人际关系，有独挡一面能力，自信心日益膨胀。然后再考虑到人是社会性动物，王宝强长期在外忙碌，马蓉的孤单感肯定会有。这时候禁不住诱惑或其他原因，与宋喆发生关系。直到宝强发离婚声明才东窗事发。
所以牢固的婚姻关系应该是互相喜欢，有共同的志趣和人脉圈，平等的经济分配，以及互相的包容大度。
所以我经常说两个人是因为家庭条件和互相喜欢在一起，但要长久，一定要包容。包容才能长久。但每个人都有底线，宝强是不能容忍：“绝对无法容忍恶意背叛婚姻，破坏家庭的行为。”
我相信从道德上，马蓉会对此事进行深刻的反省，并后悔。 也是对我们众多吃瓜群众一个启示和警醒。
事实上，还有一种可能的判决结果。那就是宝强或者马蓉净身出户。如果有这样的情况，那这多半不是法律的判决，而是当事人自愿。法律是容许当事人的自愿的。 但这样的觉悟，不是每个人都有。放弃自己应得的东西，是一种大悟。这种大悟已经脱离了所谓的“生产关系。“
这就是我为什么在前面说：不是每个人都是圣人，这是必然的。
但这样的圣人其实还不少，比如庄子，维特根斯坦。
在这件离婚事件中考虑到一个是孩子的爸爸，一个是孩子的妈妈，我们还是希望他们都好，孩子才好。所以都能分到财产是合理的。因为路在前面！
无论是男人出轨，还是女人出轨。除了大的社会制度，婚姻机制，我们还应该考虑到人性。但涉及人性，就往往变的不可说。比如拿孤独来说。孤独不应该是出轨的借口，但孤独的人往往会找人陪伴。还是用维特根斯坦的一句话说吧：“对于可说的，我们说。对于不可说的，我们保持沉默。”孤独的话题，属于非逻辑话题，自然是不可说的。跟大家问：“人为什么活着？”是一个概念。
但不管理论如何，众多的先贤已经告诉我们生活的哲理。那就是珍惜你现在拥有的。认真对待你眼前的东西，才是真的。
最后一个问题是问我们吃瓜群众自己的：如何做好一个吃瓜群众？
这也是个大问题，我不知道该从那说起。我只知道做好一个吃瓜群众，很重要！
摘自独立学者，诗人，作家，国学起名师灵遁者作品。
本文标题：分数的基本性质是什么-分数的基本性质和小数的基本性质有什么关系61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1