一 : 典型相关分析及其应用实例
西北第二民族学院学士学位论文
摘 要
典型相关分析是多元统计分析的一个重要研究课题.它是研究两组变量之间相关的一种统计分析方法,能够有效地揭示两组变量之间的相互线性依赖关系.它借助主成分分析降维的思想,用少数几对综合变量来反映两组变量间的线性相关性质.目前它已经在众多领域的相关分析和预测分析中得到广泛应用.
本文首先描述了典型相关分析的统计思想,定义了总体典型相关变量及典型相关系数,并简要概述了它们的求解思路,然后深入对样本典型相关分析的几种算法做了比较全面的论述.根据典型相关分析的推理,归纳总结了它的一些重要性质并给出了证明,接着推导了典型相关系数的显著性检验.最后通过理论与实例分析两个层面论证了典型相关分析的应用于实际生活中的可行性与优越性.
【关键词】 典型相关分析,样本典型相关,性质,实际应用
I
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
ABSTRACT
The Canonical Correlation Analysis is an important studying topic of the Multivariate Statistical Analysis. It is the statistical analysis method which studies the correlation between two sets of variables. It can work to reveal the mutual line dependence relation availably between two sets of variables. With the help of the thought about the Principal Components, we can use a few comprehensive variables to reflect the linear relationship between two sets of variables. Nowadays It has already been used widely in the correlation analysis and forecasted analysis.
This text describes the statistical thought of the Canonical Correlation Analysis firstly, and then defines the total canonical correlation variables and canonical correlation coefficient, and sum up their solution method briefly. After it I go deep into discuss some algorithm of the sample canonical correlation analysis thoroughly. According to the reasoning of the Canonical Correlation Analysis, sum up some of its important properties and give the identification, following it, I infer the significance testing about the canonical correlation coefficient. According to the analysis from the theories and the application, we can achieve the possibility and the superiority from canonical correlation analysis in the real life.
【Key words】Canonical Correlation Analysis,Sample canonical correlation,
Character,Practical applications
II
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
目 录
前 言............................................................... 1
第1章 典型相关分析的数学描述...................................... 2
第2章 典型变量与典型相关系数...................................... 3
2.1 总体典型相关 ................................................ 3
2.2 样本典型相关 ................................................ 4
2.2.1 第一对典型相关变量的解法............................... 4
2.2.2 典型相关变量的一般解法................................. 8
2.2.3 从相关矩阵出发计算典型相关............................. 9
第3章 典型相关变量的性质......................................... 11
第4章 典型相关系数的显著性检验................................... 15
第5章 典型相关分析的计算步骤及应用实例........................... 18
5.1 典型相关分析的计算步骤 ..................................... 18
5.2 实例分析 ................................................... 19
结 语.............................................................. 26
致 谢.............................................................. 27
参考文献........................................................... 28
附 录.............................................................. 29
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
前 言
典型相关分析(Canonical Correlation Analysis ,CCA)作为多元统计学的一个重要部分,是相关分析研究的一个主要内容.典型相关分析不仅其方法本身具有重要的理论意义,而且它还可以作为其他分析方法,如多重回归、判别分析和相应分析的工具,因此在多元分析方法中占有特殊的地位.
典型相关的概念是在两个变量相关的基础上发展起来的.我们知道,两个随机变量的相关关系可以用它们的简单相关系数来衡量;一个随机变量与一组随机变量之间的相关关系可以用复相关系数来衡量.但考虑一组随机变量与另一组随机变量的关系时,如果运用两个变量的相关关系,分别考虑第一组每个变量和第二组中每个变量的相关,或者运用复相关关系,考虑一组变量中的每个变量和另一组变量的相关,这样做比较繁琐,抓不住要领.因此,为了用比较少的变量来反映两组变量之间的相关关系,一种考虑的思路就是类似主成分分析,考虑两组变量的线性组合,从这两个线性组合中找出最相关的综合变量,通过少数几个综合变量来反映两组变量的相关性质,这样便引出了典型相关分析.
典型相关分析的基本思想是首先在每组变量中找出变量的线性组合,使其具有最大相关性,然后再在每组变量中找出第二对线性组合,使其分别与第一对线性组合不相关,而第二对本身具有最大的相关性,如此继续下去,直到两组变量之间的相关性被提取完毕为止.有了这样线性组合的最大相关,则讨论两组变量之间的相关,就转化为只研究这些线性组合的最大相关,从而减少研究变量的个数.
典型相关分析是由Hotelling于1936年提出的.就目前而言,它的理论己经比较完善,计算机的发展解决了典型相关分析在应用中计算方面的困难,成为普遍应用的进行两组变量之间相关性分析技术.如在生态环境方面,用典型相关理论对预报场与因子场进行分析,实现了短期气象预测;借助典型相关,分析了植被与环境的关系;在社会生活领域,应用典型相关分析了物价指标和影响物价因素的相关关系等等.
第 1 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
第1章 典型相关分析的数学描述
一般地,假设有一组变量X1,X2,?,Xp与另一组变量Y1,Y2,?,Yq,我们要研究这两组变量之间的相关关系,如何给两组变量之间的相关性以数量的描述.
当p?q?1时,就是我们常见的研究两个变量X与Y之间的简单相关关系,其相关系数是最常见的度量,定义为:
?xy?Cov(X,Y)
(X)(Y)
当p?1,q?1(或q?1,p?1)时,p维随机向量X?(X1,X2?Xp)',设
??11?12??X???~N(?,?),p?1????,其中,?11是第一组变量的协方差阵,?12是?Y????2122?
第一组与第二组变量的协方差阵,?22是第二组变量的协方差阵.则称R??1?21?11?12为Y与X1,X2,?,Xp的全相关系数,全相关系数用于度量一个随?22
机变量Y与另一组随机变量X1,X2,?,Xp的相关系数.
当p,q?1时,利用主成分分析的思想,可以把多个变量与多个变量之间的相关化为两个新的综合变量之间的相关.也就是做两组变量的线性组合即
U??1X1??2X2???pXp??'X
V??1Y1??2Y2???qYq??'Y
其中,??(?1,?2,?,?p)'和??(?1,?2,?,?q)'为任意非零向量,于是我们把研究两组变量之间的问题化为研究两个变量U与V之间的相关问题,希望寻求?,?使U,V之间最大可能的相关,我们称这种相关为典型相关,基于这种原则的分析方法就是典型相关分析.
第 2 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
第2章 典型变量与典型相关系数
2.1 总体典型相关
设有两组随机变量X?(X1,X2,?,Xp)',Y?(Y1,Y2,?,Yq)',分别为p维和q维随机向量,根据典型相关分析的思想,我们用X和Y的线性组合?'X和?'Y之间的相关性来研究两组随机变量X和Y之间的相关性.我们希望找到?和?,使得
最大.由相关系数的定义 ?(?‘X,?'Y)
?(?X,?Y)?
易得出对任意常数e,f,c,d,均有 ''Cov(?'X,?'Y)(?X)(?Y)''
?[e(?'X)?f,c(?'Y)?d]??(?'X,?'Y)
这说明使得相关系数最大的?'X,?'Y并不唯一.因此,为避免不必要的结果重复,我们在求综合变量时常常限定
Var(?'X)?1 , Va(r?'Y)?1
于是,我们就有了下面的定义:设有两组随机变量X?(X1,X2?,Xp)',
?X?Y?(Y1,Y2?,Yq)',p?q维随机向量?? 的均值向量为零,协方差阵??0(不?Y?
妨设p?q).如果存在?1?(?11,?,?p1)'和?1?(?11,?,?q1)',使得在约束条件Var(?'X)?1 ,Var(?'Y)?1下,
?(?1'X,?1'Y)?max?(?'X,?'Y) 则称?1'X,?1'Y是X,Y的典型相关变量,它们之间的相关系数称为典型相关系数;其他典型相关变量定义如下:定义了前k?1对典型相关变量之后,第k对典型相关变量定义为:如果存在?k?(?1k,?,?pk)'和?k?(?1k,?,?qk)',使得 ⑴ ?k'X,?k'Y和前面的k?1对典型相关变量都不相关;
第 3 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
⑵ Var(?k'X)?1 ,Var(?k'Y)?1; ⑶ ?k'X和?k'Y的相关系数最大,
则称?k'X和?k'Y是X,Y的第k对(组)典型相关变量,它们之间的相关系数称为第k个典型相关系数(k?2,?,p).
2.2 样本典型相关
以上是根据总体情况已知的情形进行,而实际研究中,总体均值向量?和协方差阵?通常是未知的,因而无法求得总体的典型相关变量和典型相关系数,首先需要根据观测到的样本数据阵对?进行估计. 2.2.1 第一对典型相关变量的解法
设总体Z?(X1,?,Xp,Y1,?,Yq)',已知总体的n次观测数据为:
Z(t)
于是样本数据阵为
?x11
?x?21?????xn1
?X(t)?
(t?1,2,?,n), ???
??Y(t)??(p?q)?1
?x1p
?
y11y21?yn1
y12y22?yn2
y1q?
?y2q??
???
?ynq??n?(p?q)?
x12?
x22?x2pxn2?xnp
若假定Z~Np?q(?,?),则由参考文献【2】中定理2.5.1知协方差阵?的最大似然估计为
??1n
???(Z(t)?Z)(Z(t)?Z)'
nt?1
?
?
1n
其中Z=?Z(t),样本协方差矩阵S??为:
nt?1
?
?S11
S??
?S21S12?
S22??
式中
第 4 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
??1n
S11??(Xj?X)(Xj?X)'
nj?1
??1n
??(Xj?X)(Yj?Y)' nj?1??1n
??(Yj?Y)(Xj?X)' nj?1??1n
??(Yj?Y)(Yj?Y)' nj?1
S12
S21
S22
?
?1n1n
X??Xj, Y??Yj
nj?1nj?1
令Uj??'Xj,Vj??'Yj,则样本的相关系数为
?(U
r(Uj,Vj)?
j?1
n
j
?U)(Vj?V)'
?
??
?(U
j?1
n
j
?U)2
?(V
j?1
n
j
?V)2
?
n?1n1n''1'
又因为:U??Uj???Xj???Xj??X
nj?1nj?1nj?1
?
n?1n1n''1'
V??Vj???Yj???Yj??Y
nj?1nj?1nj?1
?
????1n1n'''''
??(Uj?U)(Vj?V)??(?Xj??X)(?Yj??Y)'??'S12? nj?1nj?1????1n1n'''''
??(Uj?U)(Uj?U)??(?Xj??X)(?Xj??X)'??'S11?nj?1nj?1????1n1n'''''
??(Vj?V)(Vj?V)??(?Yj??Y)(?Yj??Y)'??'S22? nj?1nj?1
SUjVj
SUjUj
SVjVj
所以
r(Uj,Vj)?
?'S12?S11??S22?
'
'
由于Uj,Vj乘以任意常数并不改变他们之间的相关系数,即不妨限定取标准化的Uj与Vj,即限定Uj及Vj的样本方差为1,故有:
第 5 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
SUjUj?SVjVj?1 (2.2.1) 则 r(Uj,Vj)??'S12? (2.2.2) 于是我们要求的问题就是在(2.2.1)的约束条件下,求??Rp,??Rq,使得式(2.2.2)达到最大.这是条件极值的问题,由拉格朗日乘子法,此问题等价于求?,?,使
?(?,?)??'S12??
?
?
?
2
?
(?'S11??1)?
?
2
?
(?'S22??1) (2.2.3)
达到最大.式中,?,?为拉格朗日乘数因子.对上式分别关于?,?求偏导并令其为0,得方程组:
?
???
?S12???S11??0????
? (2.2.4)???
??S21???S22??0????
分别用?',?'左乘方程(2.2.4)得
???''
??S12????S11???
??? ''
???S21????S22???
又 (?'S12?)'??'S21? 所以 ???S21??(?S12?)??
也就是说,?正好等于线性组合U与V之间的相关系数,于是(2.2.4)式可写为:
?
????S???S11??0??S11
? ?12 或 ?
?S??S21???S22??0?21
?
?
'
'
'
?
?
S12????
(2.2.5) ?????0
??S22????
而式(2.2.5)有非零解的充要条件是:
??S11S21
?
?
S12??S22
?
?0 (2.2.6)
该方程左端是?的p?q次多项式,因此有p?q个根.求解?的高次方程
第 6 页 共 33 页
?
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
(2.2.6),把求得的最大的?代回方程组(2.2.5),再求得?和?,从而得出第一对典型相关变量.
具体计算时,因?的高次方程(2.2.6)不易解,将其代入方程组(2.2.5)后还需求解p?q阶方程组.为了计算上的方便,我们做如下变换:
?1用S12S22左乘方程组(2.2.5)的第二式,则有
??? S12S?1
22?1S22??0 S21?-?S12S22
即 S12S?1
22S21?=?S12? ?
又由(2.2.5)的第一式,得
S12???S11?
代入上式: S12S?1
22?S21???S11??0
?2?2 (S12SS21??S11)??0 (2.2.7)
?1再用S11左乘式(2.2.7),得 ?122
(S
?2?111S12S?122 S21??Ip)??0 (2.2.8)?22???rp2,对?也有p个解. 因此,对?有p个解,设为r12?r2
?1类似地,用S21S11左乘式(2.2.5)中的第一式,则有
??1S11??0 SSS12???S21S11?12111 (2.2.9)
又由(2.2.5)中的第二式,得
S21???S22?
代入到(2.2.8)式,有
(SS
?1再以S22左乘上式,得 ?12111?S12??2S22)??0 ?
(SSSS??2Iq)??0 (2.2.10)
?1?1S12S22因此对?有q个解,对?也有q个解,因此?2为S11S21的特征根,?是?122?1211112??2?
?1?1S21S11S12的特征根,?为相应特征向量.对应于?的特征向量.同时?2也是S22?2?
第 7 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
而式(2.2.8)和(2.2.10)有非零解的充分必要条件为:
?
??1?12SSSS??Ip?011122221??
(2.2.11)??
?1?1?S22S21S11S12??2Iq?0??
?1?1
对于(2.2.11)式的第一式,由于S11?0,S22?0,所以S11?0,S22?0,故
有:
??2?2?2?1?1
S11S12S22S22S21 S11S12S22S21?S11
?2?2?2?2?2?2??2
而S11有相同的特征根.如果记 S11S12S22S22S21与S11S12S22S22S21S11
?
?2?2
S12S22 T?S11
?2
11
?222
?222
?22111
则 S
S12S
SSS=TT
?'?
??'
类似的对式(2.2.11)的第二式,可得 S
??'
?'?
?222
SS
?2111
S
?211
S12S
?222
?TT
而TT与TT有相同的非零特征根,从而推出(2.2.8)和(2.2.10)的非零特征根是相同的.设已求得TT的p个特征根依次为: ???????2p?0
则T'T的q个特征根中,除了上面的p个外,其余的q?p个都为零.故p个特征根排列是?1??2????p?0,?,0???p???p?1?????2???1,因此,只要取最大的?1,代入方程组(2.2.5)即可求得相应的???1,???1.令而r(U,V)??1'S12?1'??1为第一典型U=?1X与V??1Y为第一对典型相关变量,
相关系数.可见求典型相关系数及典型相关变量的问题,就等价于求解TT的最大特征值及相应的特征向量. 2.2.2 典型相关变量的一般解法
从样本典型相关变量的解法中,我们知道求典型相关变量和典型相关系数的问题,就是求解TT的最大特征值及相应的特征向量.
??'
??'
??'
?
2
1
?
22
?
''
第 8 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
不仅如此,求解第k对典型相关变量和典型相关系数,类似的也是求TT的第k大的特征值和相应的特征向量.下面引用参考文献【2】中定理10.1.1 来得出样本典型相关的一般求法.
设总体的n次观测数据为:
??'
Z(t)
?X(t)?
(t?1,2,?,n) ???
Y??(t)??(p?q)?1
不妨设p?q,样本均值为0,协方差矩阵S为:
?S11
S??
?S21
S12?
?0 ?S22?
?2
1
?22
?
记T?S
?
?11
S12S
?222,并设p阶方阵TT的特征值依次为???????2p?0
??'
(?i?0,i?1,?,p);而l1,l2,?,lp为相应的单位正交特征向量.令 ?k?S
?
'
?'
k
?
?11k
l,?k??SS21?k
?
?
?1
k?122
?
则Uk??kX,Vk??Y为X,Y第k对典型相关变量,?k'为第k典型相关系数. 由上述分析不难看出,典型相关系数?i越大说明相应的典型变量之间的关系越密切,因此一般在实际中忽略典型相关系数很小的那些典型变量,按?i的大小只取前n个典型变量及典型相关系数进行分析. 2.2.3 从相关矩阵出发计算典型相关
以上我们从样本协方差阵S出发,导出了样本典型相关变量和样本典型相关系数.下面我们从样本相关阵R出发来求解样本典型相关变量和样本典型相关系数.
sij为样本协方差阵S的i行j设样本相关阵为R?(rij),其中rij?sij/siisjj,
?
?
列元素.把R相应剖分为
?R11 R??
?R21
R12?
?R22?
有时,X和Y的各分量的单位不全相同,我们希望在对各分量作标准化变换之后再做典型相关.
记?1?E(X),?2?E(Y)
第 9 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
?s11?D1??
?0?
?
?sp?1,p?10?
?? D?2??
?0spp???
?
?
??
sp?q,p?q??0
则 S11?D1R11D1,S22?D2R22D2 S12?D1R12D2,S21?D2R21D1, 对X和Y的各分量作标准化变换,即令
?1
X*?D1?1(X??1),Y*?D2(Y??2)
现在来求X*和Y*的典型相关变量?i*'X*,?i*'Y*,i?1,2,?,m. SX*X*?D1?1S11D1?1?R11
?1?1
S22D2?R22 SY*Y*?D2
?1
?R12 SX*Y*?D1?1S12D2
?1
S21D1?1?R21 SY*X*?D2
于是
?1?1?1?1?1?1?1
R11R12R22R21?(D1?1S11D1?1)?1D1?1S12D2(D2S22D2)D2S21D1?1
?1
11112
?122
?11
?DSSSS21D
?1?1S12S22S21?i?ri2?i 因为 S11
?1?1
S12S22S21D1?1(D1?i)?ri2(D1?i) D1S11
?1?1R12R22R21?i*?ri2?i* 所以 R11
式中?i*?D1?i,有?i*'R11?i*??i'D1R11D1?i??i'S11?i?1
?1?1R21R11R12?i*?ri2?i* 同理: R22
式中?i*?D1?i,有?i*'R22?i*??i'D2R22D2?i??i'S22?i?1,由此可见?i*,?i*为
X*,Y*的第i对典型系数,其第i个典型相关系数为ri,在标准化变换下具有不变
性.
第 10 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
第3章 典型相关变量的性质
根据典型相关分析的统计思想及推导,我们归纳总结了典型相关变量的一些重要性质并对总体与样本分别给出证明.
性质1 同一组的典型变量互不相关 ⅰ总体典型相关
设X与Y的第i对典型变量为
Ui??i'X ,Vi??i'Y,i?1,2,?,m
则有 ?(Ui,Uj)?0 ?(Vi,Vj)?0 1?i?j?m 证明详见参考文献【5】. ⅱ样本典型相关
设X与Y的第i对典型变量为
Ui??i'X ,Vi??i'Y,i?1,2,?,m
因为 SUiUi??'iS11?i?1,SViVi??i'S22?i?1,i?1,2,?,m r(Ui,Uj)?SUiUj??i'S11?j?0,1?i?j?m r(Vi,Vj)?SViVj??i'S22?j?0,1?i?j?m
表明由X组成的第一组典型变量U1,U2,?,Um互不相关,且均有相同的方差1;同样,由Y组成的第二组典型变量V1,V2,?,Vm也互不相关,且也有相同的方差1.
性质2 不同组的典型变量之间的相关性 ⅰ总体典型相关
?(Ui,Vi)??i i?1,2,?,m
?(Ui,Vj)?0 1?i?j?m 证明详见参考文献【5】. ⅱ样本典型相关
r(Ui,Vi)? ?i'S12?i? ri, i?1,2,?,m
r(Ui,Vj)?SUiVj??'iS12?j
??SS12S?j?rj?'i?j?0,1?i?j?m
第 11 页 共 33 页
1'2i11
?
1222?
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
表明不同组的任意两个典型变量,当i?j时,相关系数为ri;当i?j时是彼此不相关的.
记U?(U1,U2,?,Um)',V?(V1,V2,?,Vm)',则上述性质可用矩阵表示为 SUU?Im SUV??
?U??Im
或 S????
?V???
??? Im?
,SVV?Im
其中??diag(r1,r2,...,rm)
性质3 原始变量与典型变量之间的关系 求出典型变量后,进一步计算原始变量与典型变量之间的相关系数矩阵,也称为典型结构.下面我们分别对总体与样本进行讨论.
ⅰ总体典型相关的原始变量与典型变量的相关性详见参考文献【2】. ⅱ样本典型相关 记
A?(?1,?2,?,?m)?(?ij)p?m B?(?1,?2,?,?m)?(?ij)q?m
?s11???sp1?S11S12??? S??=?
?S21S22??sp?1,1
????s?p?q,1
??
s1p?spp??sp?q,p?sp?1,p
s1,1?p?sp,p?1sp?1,p?1
?sp?q,p?1
s1,p?q?
???
?sp,p?q?
?
?sp?1,p?q?
???
?sp?q,p?q???
则
SXU
??1n''
??(Xi?X)(AX?AX)'?S11A ni?1??1n''
??(Xi?X)(BX?BX)'?S12B ni?1??1n''
??(Yi?Y)(AX?AX)'?S21A ni?1??1n''
??(Yi?Y)(BY?BY)'?S22B ni?1
SXV
SYU
SYV
第 12 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
所以利用协方差进一步可以计算原始变量与典型变量之间的相关关系.若假定原始变量均为标准化变量,则通过以上计算所得到的原始变量与典型变量的协方差阵就是相关系数矩阵
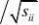
.
r(Xi,Uj)??
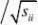
sik?kj
k?1p
r(Xi,Vj)??si,p?k?k?1
q
i?1,2,?,p , j?
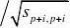
1,2,?,m
r(Yi,Uj)??si?p,k?k?1p

r(Yi,Vj)??si?p,p?k?k?1
q
i?1,2,?,q , j?1,2,?,m
性质4 设X和Y分别为p维和q维随机向量,令X*?C'X?d,Y*?G'Y?h,其中C为p?p阶非退化矩阵,h为qd为p维常数向量,G为q?q阶非退化矩阵,维常数向量.则:
ⅰ对于总体典型相关有:
bi*?G?1bi⑴ X*和Y*的典型相关变量为(ai*)'X*和(bi*)'Y*,其中ai*?C?1ai,
(i?1,2,?,p);而ai和bi是X和Y的第i对典型相关变量的系数.
⑵ ?[(ai*)'X*,(bi*)'Y*]??[ai'X,bi'Y],即线性变换不改变相关性. 证明详见参考文献【2】.
ⅱ对于样本典型相关有:
bi*?G?1bi⑴ X*和Y*的典型相关变量为(ai*)'X*和(bi*)'Y*,其中ai*?C?1ai,
(i?1,2,?,p);而ai和bi是X和Y的第i对典型相关变量的系数.
⑵ r[(ai*)'X*,(bi*)'Y*]?r[ai'X,bi'Y],即线性变换不改变相关性. 证明:⑴ 设X*和Y*的典型相关变量分别为
U?(ai*)'X*,V?(bi*)'Y*
由于 ai*?C?1ai,bi*?G?1bi
第 13 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
X*?C'X?d,Y*?G'Y?h
所以 U?(C?1ai)'(C'X?d)?ai'(C?1)'(C'X?d)?ai'X?ai'(C?1)'d
V?(G?1bi)'(G'Y?h)?bi'(G?1)'(G'Y?h)?bi'Y?bi'(G?1)'h
即有ai和bi是X和Y的第i对典型相关变量的系数. ⑵ 由⑴的证明可知
U?(ai*)'X*?ai'X?ai'(C?1)'d V?(bi*)'Y?bi'Y?bi'(G?1)'h*
由于ai'(C?1)'d与bi'(G?1)'h都是常数,所以
r[(ai*)'X*,(bi*)'Y*]?r[ai'X?ai'(C?1)'d,bi'Y?bi'(G?1)'h]?r[ai'X,bi'Y] 即有线性变换不改变相关性.
性质5 简单相关、复相关和典型相关之间的关系
当p?q?1,X与Y 之间的(惟一)典型相关就是它们之间的简单相关;当
p?1或q?1时,X与Y之间的(惟一)典型相关就是它们的复相关.复相关是典型
相关的一个特例,而简单相关又是复相关的一个特例.从第一个典型相关的定义可以看出,第一个典型相关系数至少同X(或Y)的任一分量与Y(或X)的复相关系数一样大,即使所有这些复相关系数都很小,第一个典型相关系数仍可能很大;同样,从复相关的定义也可以看出,当p?1(或q?1)时,X(或Y)与Y(或X)之间的复相关系数也不会小于X(或Y)与Y(或X)的任一分量之间的相关系数,即使所有这些相关系数都很小,复相关系数仍可能很大.
第 14 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
第4章 典型相关系数的显著性检验
设总体Z的两组变量X?(X1,X2,?,Xp)',Y?(Y1,Y2,?,Yq)',且Z?(X,Y)'~Np?q(?,?),在做两组变量X,Y的典型相关分析之前,首先应该检验两组变量是否相关,如果不相关,则讨论两组变量的典型相关就毫无意义.
1.考虑假设检验问题:
H0:?1??2????m?0
H1:?1,?2,?,?m至少有一个不为零
其中m?min?p,q?.若检验接受H0,则认为讨论两组变量之间的相关性没有意义;若检验拒绝H0,则认为第一对典型变量是显著的.上式实际上等价于假设检验问题
H0:Cov(X,Y)??12?0, H1:?12?0
用似然比方法可导出检验H0的似然比统计量
??|S| |S11||S22|
?S11S12?其中p?q阶样本离差阵S是?的最大似然估计,且S=??,S11,S22分别SS?2122?
是?11,?22的最大似然估计.
该似然比统计量?的精确分布已由霍特林(1936),Girshik(1939)和Anderson(1958)给出,但表达方式很复杂,又不易找到该分布的临界值表,下面我们采用?的近似分布.
利用矩阵行列式及其分块行列式的关系,可得出:
-1?1|S11|·|?p?S11S12S-1|S|?|S22|·|S11?S12S22S21|=|S22|·22S21|
所以
20???10??1?????1?1??|?p?S11S12S22S21|????????????01??2
p????0?(1??i?1p?2i)
第 15 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
其中?
?2
1?2i是TT??'?2?2S12S22的特征值(T?S11),按大小次序排列为?当n??1时,在H0成立下Q0??mln?近似服从?2????????0,f分布,
1这里f?pq,m?n?1?(p?q?1),因此在给定检验水平?之下,若由样本算2?22?2p
出的Q0???临界值,则否定H0,也就是说第一对典型变量U1,V1具有相关性,其相关系数为?1,即至少可以认为第一个典型相关系数?1为显著的.将它除去之后,再检验其余p?1个典型相关系数的显著性,这时用Bartlett提出的大样本?2检验计算统计量:
?1?(1??)(1??)?(1??)??(1??)
i?2?22?23?2pp?2i??2??
则统计量 1Q1??[n?2?(p?q?1)]ln?1 2
22?近似地服从(p?1)(q?1)个自由度的?分布,如果Q1???,则认为?2显著,
即第二对典型变量U2,V2相关,以下逐个进行检验,直到某一个相关系数?k检验为不显著时截止.这时我们就找出了反映两组变量相互关系的k?1对典型变量.
(k)2.检验H0: ?k?0(k?2,?,p) ?
当否定H0时,表明X,Y相关,进而可以得出至少第一个典型相关系数?1?0,相应的第一对典型相关变量U1,V1可能已经提取了两组变量相关关系的绝大部分信息.两组变量余下的部分可认为不相关,这时?k?0(k?2,?,p),故
(k)在否定H0后,有必要再检验H0(k?2,?,p),即第k个及以后的所有典型相
关系数均为0(k?2,3,?,p).
为了减少计算量,下面我们采用二分法来减少检验次数,取检验统计量为
p?1Qk??[n?k?(p?q?1)]?ln(1??i2) 2i?k
它近似服从(p?k?1)(q?k?1)个自由度的?2分布.在检验水平?下,若
第 16 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
2Qk???[(p?k?1)(q?k?1)],则拒绝H0,即认为第k对典型相关系数在显著性水平?下是显著的,否则不显著.
从第2个典型相关系数到第p个典型相关系数,共p?1个数,所以根据二
?p?1?分法的原理,将它们分为一个区间?2,p?,然后先检验第?个典型相关系数??2?
?p?1?即中位数,当??p?1??0时,即认为第?个典型相关系数不相关,否定原假?2?2?????
???p?1??p?1??设,接着检验?2,?;若当时,则检验??0??2?,?p?1???2?????2???????p?.如此?
划分区间依次检验下去,由数学分析上的区间套定理,一定存在第k个数(k?2,3,?,p),使得?k?1?0,而?k?0.
以上的一系列检验实际上是一个序贯检验,检验直到对某个k值H0未被拒绝为止.事实上,检验的总显著性水平已不是?了,且难以确定.还有,检验的结果易受样本容量大小的影响.因此,检验的结果只宜作为确定典型变量个数的重要参考依据,而不宜作为惟一的依据.
第 17 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
第5章 典型相关分析的计算步骤及应用实例
5.1 典型相关分析的计算步骤
设X(1),?,X(n)为取自正态总体的样本(实际上,相当广泛的情况下也对),每个样品测量两组指标,分别记为X?(X1,?,Xp)',Y?(Y1,?,Yq)',原始资料矩阵为:
?x11
?x?21?????xn1
x12?
?x1p
?
y11y21?yn1
y12y22?yn2
x22?x2pxn2?xnp
y1q?
?y2q??
???
?ynq??n?(p?q)?
第一步 计算相关矩阵R,并将R剖分为
?R11
R? ?R
?21
R12?
R22??
'
其中R11,R22分别为第一组变量和第二组变量之间的相关系数矩阵,R12?R21为
第一组与第二组变量之间的相关系数.
第二步 求典型相关系数及典型变量
首先求A?RR12RR21的特征根?,特征向量D1?特征根?,特征向量D2?
??
?(i)
?
?1
11
?122
?2i
?
(i)
?1?1R21R11R12的;B?R22
?
?
2i
?
(i)
.
?(i)
?D(D1??11
),?
?
(i)
?D(D2??12
?
(i)
)
写出样本的典型变量为 U1?? U2??
?
?
?
?(1)’
X,V1??
?
?
??
(1)’
Y Y
(2)’
X,V2??
(2)’
??? Up??
?
?(p)’
X,Vp??(p)Y
??
’
第三步 典型相关系数的显著性检验 首先,检验第一对典型变量的相关系数,即
第 18 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
H0:?1?0,H1:?1?0
^^
它的似然比统计量为
?1?(1??)(1??)?(1??)??(1??i2)
21
22
i?1
^
^
^2p
p
^
则统计量
1
Q1??[n?2?(p?q?1)]ln?1
2
22
给定显著性水平?,查表得??,若Q1???,则否定H0,认为第一对典型变量
相关,否则不相关.如果相关则依次逐个检验其余典型相关系数,直到某一个相
^
关系数?k(k?2,?,p)检验为不显著时截止.
5.2 实例分析
例1:某康复俱乐部对20名中年人测量了三个生理指标:体重(x1)、腰围(x2)、脉搏(x3)和三个训练指标:引体向上(y1)、起坐次数(y2)、跳跃次数(y3).数据如附录1:
解:记X?(x1,x2,x3)',Y?(y1,y2,y3)',其中样本容量n?20.
附录1中的数据用SPSS统计软件计算得六个变量之间的相关矩阵如下:
Correlations
X1
X1
X2
X3 -.366
Y1
Y2
Y3 Pearson
Correlation Sig.
(2-tailed) N Pearson
Correlation Sig.
(2-tailed) N Pearson
Correlatio
-.390 -.493(*)
.113 20
.089 20
.027 20 -.646(**
)
.002 20 .225
X2
-.353 -.552(*)
.127 20 1
.012 20 .151
X3
第 19 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
Y1
Y2
Y3
n Sig.
(2-tailed) N Pearson Correlation Sig.
(2-tailed) N Pearson
-.646(**
Correlation Sig.
(2-tailed) N Pearson Correlation Sig.
(2-tailed) N . 20 .151
.526 20
.340 20
1 .696(**)
.526 20
. 20
.001 20
.225 .696(**) 1 .340 20 .035
.001 20
. 20
.496(*) .669(**)
.884 20
.026 20
.001 20
** Correlation is significant at the 0.01 level (2-tailed).
* Correlation is significant at the 0.05 level (2-tailed).
即样本相关矩阵为:
?1?
R11=?0.870
??0.366?
??
1? ?0.3531??
?1?
??
1R22=?0.696?
?0.4960.6691?????0.390
'?
R12?R21=??0.552
?0.151?
?0.493?0.6460.225
?0.226?
?
?0.192? 0.035??
?1?1
R12R22R21??2?0 于是特征方程 R11
?1?1
R12R22R21的特征值分别为0.6630、0.0402和0.0053,于是 用Matlab求得矩阵R11
?1?0.797,?2?0.201,?3?0.073
下面我们进行典型相关系数的显著性检验,先检验第一对典型变量的相关系
第 20 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
数,欲检验:
H0:?1?0 , H1:?1?0
它的似然比统计量为
22?1?(1??2
1)(1??2)(1??3)=(1?0.6330)(1?0.0402)(1?0.0053)?0.3504
1Q1??[20?(3?3?3)]ln?1??15.5?ln0.3504?16.255 2
2?02.05(9)?16.919,Q1??0查?2分布表得,因此在??0.05的显著性水平下,.05(9),
所以拒绝原假设H0,也即认为第一对典型相关变量是显著相关的.
然后检验第二对典型变量的相关系数,即进一步检验:
H0:?2?0 , H1:?2?0
它的似然比统计量为
2?2?(1??2
2)(1??3)
?(1?0.0402)(1?0.0053)?0.9547
1?22Q2??[20?1?(3?3?3)??1]ln?2??16.08?ln0.9547?0.745?9.488??0.05(4)2
所以无法否定原假设H0,故接受H0:?2?0,即认为第二对典型相关变量不是显著相关的.由以上检验可知只需求第一对典型变量即可.
于是求?1?0.797的特征向量?,而???*
1?*11?1RR?,解得 ?122?*211
??0.775???0.350???, ?*???1.054?, ???1.5791????????0.059???0.716???*1
因此,第一对样本典型变量为
****??0.775x1?1.579x2?0.059x3 u1
****??0.350y1?1.054y2?0.716y3 v1
X与Y第一对典型变量的相关系数为?1?0.797,可见两者的相关性较为密切,即可认为生理指标与训练指标之间存在显著相关性.
例2:为了研究某企业不同部门人员工作时间的关系,随机选取25个企业进行入户调查,达到25个被访企业业务部门和技术部门经理每月工作时间和员工每月工作时间(单位为小时),具体数据如附表2
第 21 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
分析:设业务部门经理和员工每月工作时间为(X1,X2),技术部门经理和员工每月工作时间为(Y1,Y2),利用典型相关分析研究企业业务部门和技术部门人员工作时间的关系.
解:样本容量为n?25,p?2,q?2分别为随机变量X与Y的维数.
⑴ 标准化随机变量X?(X1,X2)'与Y?(Y1,Y2)'.
*根据样本均值xi与标准差Sii,依照公式xki??xki?xi
Sii?,对数据标准化.
Rxy??. Ryy???Rxx?X?⑵ 求解??Y??的相关矩阵R,并将其分块R???R???yx
将数据输入SPSS软件求得相关系数矩阵如下:
X1 Pearson
Correlatio
n
Sig.
(2-tailed)
N
X2 Pearson
Correlatio
n
Sig.
(2-tailed)
N
Y1 Pearson
Correlatio
n
Sig. Correlations X1 X2 Y1 Y2
第 22 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
(2-tailed)
N
Y2 Pearson
Correlatio
n
Sig.
(2-tailed)
N ** Correlation is significant at the 0.01 level (2-tailed). 所以样本相关矩阵
?1???1?0.735? R??? 0.7110.6931???0.7050.7050.8341???
分块后
?RxxR???R?yx
2Rxy?2?Ryy??2 2
?0.544309?1?1?1?1RxyRyyRyx??⑶ 求解M1?Rxx?0.538840?0.538840??的两个非零特征根,解得?0.534949?
2?0.6218,?2两个非零特征根为?12?0.0029.
⑷ 进行相关系数的显著性检验,取m?r个显著性检验不为0的特征根. X与Y第一对典型变量的相关系数为?1?0.7885,X与Y第二对典型变量的相关系数为?2?0.0537.
先检验第一对典型变量的相关系数,假设H01:?1?0(即第一对典型变量不相关),由典型相关系数的值可得
2?1?(1??1)(1??2
2)?0.3771
计算统计量
第 23 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
1Q1??[(n?1)?(p?q?1)]ln?1 2
?(24?2.5)ln0.3771?20.97
对于给定的显著性水平??0.05
22(p?m?1)(q?m?1)??0 Q1?20.97???.05(4)?9.488
所以否定零假设.
H01:?1?0,即第一对典型变量是显著相关的. 然后检验第二对典型变量的相关系数,假设H02:?2?0(即第二对典型变量不相关),由典型相关系数的值可得
?2?(1??2
2)?0.9971
计算统计量 1Q2??[(n?2)?(p?q?1)]ln?2 2
?(24?2.5)ln0.9971?0.05945
对于给定的显著性水平??0.05
22Q2?0.05945???(p?m?1)(q?m?1)??0.05(1)?3.841
所以无法否定假设.
H02:?2?0,即第二对典型变量不是显著相关的.由以上检验可知,只需求第一对典型变量即可.
2⑸ 求m?1个显著性检验不为0的特征根?1的特征向量l1,而
m1?1
?1?1RyyRyxl1,解得l1?(0.55216,0.521548)',m1?(0.504018,0.538134)'.
⑹ 求出r对典型相关变量uj?l'
jX,vj?m'
jY,j?1,2,?,m.
根据上面求得的特征向量l1和m1,得第一对典型相关变量为
?u1?l1'X?0.55216X1?0.521548X2 ? '?v1?m1Y?0.504018Y1?0.538134Y2
X与Y第一对典型变量的相关系数为?1?0.7885,可见其相关性较为密切. ⑺ 由于u1?l1'X?0.55216X1?0.521548X2,与业务部门经理和员工每月工作
第 24 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
时间都成正比,而且系数差不多,所以u1可以解释为业务部门人员工作时间.同理v1可以解释为技术部门人员的工作时间.可见一个企业技术部门和业务部门人员月工作时间存在显著的相关性.
第 25 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
结 语
典型相关分析是一种采用类似主成分分析的做法,在每一组变量中都选择若干个有代表性的综合指标(变量的线性组合),通过研究两组的综合指标之间的关系来反映两组变量之间的相关关系.在实际中,只须着重研究相关关系较大的那几对典型相关变量.本文首先根据典型相关分析的统计理论,初步探讨了总体典型相关变量和典型相关系数,然后重点讨论了样本典型相关分析,以及它们的一系列性质与显著性检验,并做了相应的实例分析.通过实例分析,我们进一步明确了典型相关分析是研究两组变量之间相关性的一种降维技术的统计分析方法.而复相关是典型相关的一个特例,简单相关是复相关的一个特例.第一对典型相关包含有最多的有关两组变量间相关的信息,第二对其次,其他对依次递减.各对典型相关变量所含的信息互不重复.并且经标准化的两组变量之间的典型相关系数与原始的两组变量间的相应典型相关系数是相同的.
第 26 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
致 谢
本文是在我的指导老师吴可法教授的精心指导和悉心关怀下完成的,在我的学习生涯和论文工作中无不倾注着老师的辛勤汗水和殷切关怀.吴老师宽厚的人格、敏捷的思维、严谨的治学态度、渊博的知识、积极向上的人生态度、平易近人的师长风范和两年来的谆谆教导,使我深受启迪,并永远铭记在心.从吴老师身上,我不仅学到了扎实的专业知识和技能,更学到了做人的道理,这些教诲必 将成为惠及一生的宝贵财富.在此谨向吴老师致以最衷心的感谢和美好的祝愿! 论文期间,我得到了许多老师和同学的帮助,本人在这里对他们致以衷心的感谢.
我还要感谢我的家人,是他们的理解、支持和鼓励,使我的学习能够顺利进行.
最后衷心感谢在百忙之中评审论文和参加答辩的各位专家、教授!
第 27 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
参考文献
【1】 何晓群.多元统计分析[M].北京:中国人民大学出版社,2004
【2】 高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005
【3】 方开泰.实用多元统计分析[M].上海:华东师范大学出版社,1989
【4】 王方.城镇居民消费结构影响因素的典型相关分析[J] .统计与决策,2007,(03)
【5】 施锡铨,范正绮.数据分析方法[M].上海:上海财经大学出版社,1997
【6】 王学仁.多个变量集合的典型相关分析[J] .云南大学学报(自然科学版),1983,(Z1)
【7】 王学民.应用多元统计分析(第二版)[M].上海:上海财经大学出版社,2004.1
【8】 余锦华,杨维权.多元统计分析[M]. 广州:中山大学出版社,2005.2
【9】 于秀林,任雪松.多元统计分析与应用[M]. 北京:中国统计出版社,1999
【10】张尧庭,方开泰.多元统计分析[M].北京:科学出版社,1980
【11】Kendall M. Multivariate Analysis[M]. Charles Griffin,1975
【12】Richard A. Johnson, Dean W. Wichern. Applied Multivariate Statistical Analysis (5th Ed)[M].Beijing: China Statistics Press, 2003.5
【13】刘顺忠.管理统计学和SAS软件应用[M].武汉:武汉大学出版社,2006.1
第 28 页 共 33 页
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
附 录
例1数据
某康复俱乐部的生理指标和训练指标数据
编号 x1
1 191 2 189 3 193 4 162 5 189 6 182 7 211 8 167 9 176 10 154 11 169 12 166 13 154 14 247 15 193 16 202 17 176 18 157 19 156 20
138 x2 x3 36 50 37 52 38 58 35 62 35 46 36 56 38 56 34 60 31 74 33 56 34 50 33 52 34 64 46 50 36 46 37 62 37 54 32 52 33 54 33 68 第 29 页 共 33 页y1 y2 5 162 2 110 101 105 155 4 101 8 101 6 125 200 251 120 210 215 1 50 6 70 210 4 60 230 225 2 110 y3
60 60 101 37 58 42 38 40 40 250 38 115 105 50 31 120 25 80 73 43
12 12 13 15 17 17 13 14 12 11 15
典型相关分析 典型相关分析及其应用实例
西北第二民族学院学士学位论文
例2数据
不同部门经理和员工月工作时间数据
业务部门 技术部门 经理月工作时间 员工月工作时间 经理月工作时间 员工月工作时间
企业编号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 样本均值 样本方差
191 195 181 183 176 208 189 197 188 192 179 183 174 190 188 163 195 186 181 175 192 174 176 197 190 185.72 9.7618
155 149 148 153 144 157 150 159 152 150 158 147 150 159 151 137 155 153 145 140 154 143 139 167 163 151.12 7.3729 第 30 页 共 33 页
179 201 185 188 171 192 190 189 197 187 186 174 185 195 187 161 183 173 182 165 185 178 176 200 187 183.84 145 152 149 149 142 152 149 152 159 151 148 147 152 157 158 130 158 148 146 139 152 147 143 158 150 149.24 6.7099 10.0402
二 : 浅析UMTS900M技术及应用
【摘 要】随着WCDMA用户的不断增多,用户对WCDMA网络覆盖以及室内深度覆盖提出了更高的要求。针对这种情况,就UMTS应用于900MHz频谱技术进行分析,并结合UMTS900与UMTS2100网络在单室外基站和室内覆盖两种不同场景下的比较实验,明确展现了UMTS900网络应用的优势和布设的必然性。同时结合对UMTS900网络规划中GU共存的三个关键问题的分析,提出了现网改造方案。
【关键词】UMTS 900MHz 网络覆盖 室内深度覆盖
中图分类号:TN929.5 文献标识码:A 文章编号:1006-1010(2014)-03-0070-06
1 引言
与目前3G市场中主流使用的2 100MHz相比,900MHz由于频率较低,其传输优势使基站所覆盖的范围明显增大,因此900MHz频谱的UMTS/HSDPA技术使语音与高速3G服务的传递更为经济实惠。对于运营商而言,此优点有助于大量节省成本,且得到更好的室内覆盖效果,从而能够提高其客户的整体用户体验。
由于UMTS在900MHz频段上的巨大优势,为推动3G移动通信产业的发展,3GPP在3GPP TR 25.816 V7.0.0 UMTS 900MHz Work Item Technical Report中定义了UMTS900的概念,越来越多的国家开始在900MHz频段上部署3G网络。
为了满足UMTS900快速增长的需求,终端供应商也加快了对UMTS900终端的研发和生产。据GSA调查报告,目前全球34家终端供应商已经发布了190款UMTS900-HSPA终端,这其中包括了118款UMTS900-HSPA移动终端和39款USB dongle。支持UMTS900的路由器、PC卡和内嵌模块也在市场上进行了商业发布,并且所有的UMTS900终端都支持GSM/EDGE功能。
2 UMTS900的优势
UMTS900是利用900MHz频段巨大的传输优势来提供UMTS网络服务,其上行/下行频段分别为880—915/925—960MHz。主要优势体现在以下几个方面:
(1)根据无线电波的传播特性,载波频率越低,无线信号传播得越远,相比于UMTS2100,UMTS900的传播损耗小,30%的UMTS900站点就可以达到与UMTS2100相同的覆盖范围,单站点的广覆盖意味着投资的减少。
(2)低频率的载波信号穿透性更强,在穿透建筑物墙壁时可以减少损耗,通过UMTS900网络可以提供更好的室内覆盖、深层覆盖,网络覆盖性能更好,从而提升业务服务质量,增强用户的业务体验。
(3)U900 1Mbps覆盖与G900语音覆盖相当,运营商可以以更高的性价比在更广范围提供HSPA业务。
(4)运营商在建设UMTS900网络时,还可以重用包括天线和站点等基础设施在内的原GSM网络的投资。
3 UMTS900应用分析
3.1 单站覆盖效果应用分析
就单站覆盖接收场强而言,在自由空间传输模型中,UMTS900相比UMTS2100提升6.9dB。在COST231-Hata传输模型中,UMTS900相比UMTS2100的提升,根据环境的不同[www.61k.com]分别为:
◆小型城市和郊区:11.4dB
◆大中型城市:14.4dB
UMTS2100和UMTS900单站覆盖接收场强比较如图1所示。
通过在市区、市郊和农村的实际试验比较分析可以得出:
(1)市区RSCP有90%的概率提升6dB以上;
(2)市郊RSCP有75%的概率提升9dB以上;
(3)农村RSCP有50%的概率提升11dB以上。
3.2 小区半径比较
UMTS900增益超过UMTS2100,表现在以下几方面:
(1)小区覆盖半径提升了70%;
(2)下行功率增加了40倍(16dB),从而提升了网络的功率效能;
(3)UE的发射功率降低了63倍(18dB),直接提升了手机电池的使用寿命。
UMTS2100和UMTS900小区半径测试参数比较如图2所示。
3.3 室内覆盖效果应用分析
对同室内分布进行UMTS2100和UMTS900同覆盖网络测试的情况如下:
(1)由于900MHz频段无线电波和穿透损耗小于2 100MHz,在室内场景应用中,其深度覆盖效果明显优于2 100MHz的UMTS网络。UMTS2100和UMTS900的室内覆盖RSCP比较如图3所示,由图3可知,RSCP分布比例对比情况为:
◆RSCP大于-55dBm的比例,UMTS2100网络为2.4%,而UMTS900网络为8.1%;
◆RSCP大于-65dBm的比例,UMTS2100网络为37.52%,而UMTS900网络为69.7%;
◆RSCP大于-75dBm的比例,UMTS2100网络为89.87%,而UMTS900网络为98.75%。
(2)覆盖效果的提升会直接影响到手机发射功率的下降,UMTS2100和UMTS900室内手机发射功率的比较如图4所示。
由图4可知,手机发射功率对比情况为:
◆手机发射功率小于-15dBm的比例,UMTS2100网络为21.31%,而UMTS900网络为91.71%;
◆手机发射功率小于0dBm的比例,UMTS2100网络为93.18%,而UMTS900网络为100%;
◆手机发射功率小于15dBm的比例,UMTS2100网络为99.86%,而UMTS900网络为100%。4 UMTS900网络规划
依据不同场景网络的特性,目前有2种网络规划方案:
◆在郊区或农村通过UMTS900扩展UMTS覆盖;
◆在大中型城市对热点地区利用UMTS900提供更加优质的UMTS网络。
对于室内网络,建设UMTS900来提高UMTS网络的深度覆盖。在进行UMTS900网络部署时,需要解决三个关键问题:GU共存频率分配;对GSM网络的干扰要降至最小;GU共站,以减少GU干扰并保护已有投资。
4.1 GU共存频率分配
对于GSM与UMTS的频率分配,主要有两种方式:GU频率边缘分配方式、GU频率三明治分配方式。两种分配方式如图5所示:
图5 GU频率两种分配方式
(1)GU频率边缘分配方式
该方式的优点是:GSM频率资源连续,便于进行频率规划;运营商内部只用考虑一侧的GU系统间的干扰。缺点是UMTS与异运营商的GSM系统至少要保证2.6MHz的间隔。
(2)GU频率三明治分配方式(优选)
该方式的优点是:可以将UMTS放置在内部任意位置,不用考虑与异运营商之间的干扰;如果采用U4.6/4.2/3.8M,可以为GSM节省2/4/6个频点。缺点是运营商内部要考虑双侧的干扰。
鉴于以下分析考虑,GU三明治分配方案应作为UMTS900频率规划的优选方案:
(1)GU三明治分配方案中UMTS系统到两侧GSM系统中心频率的间隔f1和f2相等,并可根据小间隔能力进行配置。当f1、f2相等且均小于2.6MHz时,UMTS两侧功率谱较低的频段可以与GSM载波共享频谱资源。此方案相对边缘分配方案可以多节省一倍的频点,提升了频谱效率,减少了对GSM系统的冲击。
(2)GU三明治分配方案可以不用单独考虑与异运营商之间的系统间干扰,而边缘分配方案必须考虑与异运营商之间的干扰问题。如果与其它运营商的GSM频率间隔小于2.6MHz,由于其它运营商基站的射频性能未知,其它运营商的GSM系统可能会对UMTS系统造成干扰,边缘分配方案为消除系统间干扰将付出更大的代价。
(3)GU频谱三明治分配,UMTS频点可以灵活调整,将UMTS频点放在恰当的位置可以兼顾扩容以及抗异系统干扰。
4.2 对GSM网络的干扰要降至最小
当UMTS和GSM两种系统同频覆盖时,一个系统的基站或终端的信号会落在另一个系统的基站或终端的接收带内,而且这种干扰不能通过接收滤波器来抑制,只能在两个同频系统间留出适当的保护区距离(见图6),进行地理上的隔离,增加干扰信号的衰减,降低G900和U900系统间的干扰,以保障两个系统都能正常的工作。
4.3 GU共站
在GU联合组网的情况下,新建UMTS网络时可以考虑共站和不共站两种场景。
由于UMTS覆盖半径大于GSM覆盖半径,所以不共站场景可减少UMTS站点数,减少设备投资。但不共站场景有如下劣势:第一,由于不共站,所以不能按照原有的蜂窝结构进行布网,不能完全利用原有的GSM站点资源,导致新建站点数量较多,增大了配套投资;第二,GU不共站时将增大GU之间的干扰。
相反,在共站场景下,可减少GU之间的干扰,同时可使运营商不必新建站点,以减少配套投资。在共站场景下通过调整UMTS功率规格可使GU的覆盖区域基本相同。对于不共天馈的场景,可通过调整天线的下倾角和方向角使每个系统达到最优覆盖性能;对于共天馈的场景,则是G900和U900的发射和接收共同连接到天线的一对端口上。
5 UMTS900网络组网方式
通过上述对UMTS900网络规划分析,针对目前现有的网络覆盖情况,结合城市和郊区两种不同场景特性,提出以下UMTS900网络部署建议。
5.1 城市组网方式
目前城市中UMTS和GSM网络建设已趋于成熟,室外2/3G网络已达到精品覆盖,但在楼宇的室内网络分布中存在UMTS网络覆盖不足、容量受限、高层导频污染、同频邻区满配、扰码规划复用等问题。
因此,城市中网络部署可以采用UMTS900网络来完善现有网络布局,针对UMTS网络需求旺盛的热点楼宇、商场、剧院等室内公共场所采用UMTS900网络覆盖方案。对此,提出以下两种城市室分UMTS网络的组网方式:
方式一:对于一般室分系统,整个室分采用UMTS900组网覆盖方式。
方式二:对于大型的室分系统,建议采用分层的建设方式,热点或中高层的区域采用UMTS900网络覆盖,低层部分采用UMTS2100网络覆盖。选用这种方式组网,室分系统与外网是同频切换,切换点优化更为便利,因此对于大型室分系统,方式二比方式一效果更好。
5.2 郊区组网方式
目前郊区农村网络以GSM网络为主,UMTS网络部署才刚刚起步,农村信息化需求逐步增强,为了扩大农村和郊区UMTS网络的覆盖,提出以下两种组网方式:
方式一:采用UMTS900+DCS1800网络覆盖方案。虽然在频谱的整体规划使用上相对完善,但改建工程量大,同时还需增加相当数量的新站点,无法达到经济、合理组网覆盖的要求。
方式二:UMTS和GSM共用带宽。鉴于郊区农村900M频谱需求相对较少,同时频率复用距离大的特点,可采用3.8M方案部署UMTS900,剩余2.2M用来部署GSM900网络,GSM900采用S211/S111组网方式。利用GU共站的方法,在原有GSM站点的基础上,更换射频模块完成GU同覆盖,UMTS900与GSM网络共机房、共机柜、共天馈、共配套,在满足网络覆盖的同时节省了网络建设和运营的成本。
6 结论
本文通过对UMTS900系统的分析和应用研究,明确了在900MHz频段上发展UMTS网络的必然性,以及对UMTS900网络规划中存在的问题进行了探讨,为今后此联通的网络建设提供了经验。
在欧洲、中东、非洲和亚太等区域市场,UMTS900正在成为终端的标准支持功能之一。随着移动宽带业务需求的快速增长、900MHz频率电信监管政策的开放,以及大量支持UMTS900终端的上市,越来越多的UMTS900频率重用网络将被部署和运营。
参考文献:
[1] 3GPP TS 25.101 V7.0.0. User Equipment(UE) radio transmission and reception(FDD)[S].
[2] 3GPP TS 25.104 V7.2.0. Base Station(BS) radio transmission and reception(FDD)[S].
[3] 3GPP TR 25.816 V7.0.0. UMTS900 MHz Work Item Technical Report[S].
[4] 陈德荣,刘永乾,蒋丽. 移动通信网络规划与工程设计[M]. 北京: 北京邮电大学出版社, 2010.
[5] Laiho J, Wacker A, Novosad T. UMTS无线网络规划与优化[M]. 郭莉,王钢,译. 2版. 北京: 电子工业出版社, 2008.
[6] 廖晓滨,赵熙. 第三代移动通信网络系统技术、应用及演进[M]. 北京: 人民邮电出版社, 2008.★
三 : 湿式电除尘新技术原理介绍及应用实例分析02
湿式电除尘新技术助燃煤电厂实现超低排放
当前,我国环境状况总体恶化的趋势尚未得到根本遏制,环境矛盾日益凸显,环保压力持续加大。部分区域和城市大气雾霾现象突出,许多地区主要污染物排放量超过环境容量。今年以来,各级政府陆续出台多项政策措施,下大力气治理PM2.5,改善空气质量。
湿式电除尘器在满足超低排放、治理PM2.5方面的效果得到业内专家一致认可,环境保护部在《环境空气细颗粒物污染防治技术政策(试行)》(征求意见稿)中明确指出:鼓励火电企业采用湿式电除尘等新技术,防止脱硫造成的“石膏雨”污染。
作为一种先进的烟气治理技术,湿式电除尘技术在欧洲、美国、日本等国家已得到广泛应用且效果良好。国内企业自主开发的湿式电除尘技术,已在燃煤电厂取得成功应用。上海长兴岛第二发电厂燃煤锅炉湿法脱硫后改造工程配套湿式电除尘器,出口粉尘排放浓度仅为
6.1mg/m3,引起业界高度关注。我国也有环保企业引进国外的湿式电除尘技术,并有多家电厂签订湿式电除尘器合同,最大配套机组为1000MW。相信随着湿式电除尘技术在我国的推广应用,其必将成为燃煤电厂满足超低排放、治理PM2.5的有力武器。
大气环境形势严峻,PM2.5控制势在必行
《火电厂大气污染物排放标准》(GB13223—2011)中规定,一般地区燃煤锅炉烟囱烟尘排放限值30mg/m3,重点地区燃煤锅炉烟囱烟尘排放限值20mg/m3,汞及其化合物污染物排放限值0.03mg/m3。
根据新修订的《环境空气质量标准》(GB3095—2012),将PM2.5
四 : 曹植生平及其作品分析
曹植是建安时代艺术成就最高的作家。他的作品数量最多,形式繁富。现存诗歌90余篇,赋45篇,还有章、表、书、论、颂、碑、赞、铭等各种文体的著述。曹植在文学上成就最高的是诗歌,他的创作以曹丕称帝为界,分为前后两个时期。前期除了一些描写华贵生活之外,有些诗描写了当时战后的残败景象,也有些诗抒发了他建功立业的抱负。他在著名的《白马篇》中写道:“弃身锋刃端,性命安可怀?”,“捐躯赴国难,视死忽为归”。后期由于理想得不到实现,内心充满悲愤和痛苦,诗歌中也流露出悲忿不满的情感。特别是《赠白马王彪》一诗以激愤的语言,控诉了曹丕对他的迫害,倾诉了极端苦闷和绝望的心情,成为文学史上一篇有名的长篇抒情诗。曹植的诗重视锤炼诗歌语言,讲究艺术形式,其作品工整对仗,辞藻华丽,钟嵘说他的诗“骨气奇高,词采华茂”。曹植一生写了很多赋,其中最著名的当为《洛神赋》。这篇赋写作者经过洛水时与洛水女神产生了爱慕之情,但终因神人相隔,不能结合,最后怅然而别。这篇赋想象丰富,描写细腻,辞采华丽,情意缠绵,具有极强的艺术感染力和很高的美学价值,是千百年来脍炙人口的名篇佳作。
曹植自幼颖慧,10岁余便诵读诗、文、辞赋数十万言,出言为论,落笔成文,深得曹操的宠爱。曹操曾经认为曹植在诸子中“最可定大事”,几次想要立他为太子。然而曹植行为放任,不拘礼法,屡犯法禁,引起曹操的震怒,而他的兄长曹丕则颇能矫情自饰,终于在立储斗争中渐占上风,并于建安二十二年(217)得立为太子。建安二十五年,曹操病逝,曹丕继魏王位,不久又称帝。曹植的生活从此发生了根本性的变化。他从一个过着优游宴乐生活的贵族王子,变成处处受限制和打击的对象。公元226年,曹丕病逝,继位,即。曹叡对他仍严加防范和限制,处境并没有根本好转。曹植在文、明二世的12年中,曾被迁封过多次,最后的封地在陈郡,232年12月27日曹植逝世,卒谥思,故后人称之为“陈王”或“”。
诗歌是曹植文学活动的主要领域。前期与后期内容上有很大的差异。前期诗歌可分为两大类:一类表现他贵族王子的优游生活,一类则反映他“生乎乱、长乎军”的时代感受。后期诗歌,主要抒发他在压制之下时而愤慨时而哀怨的心情,表现他不甘 1

被弃置,希冀用世立功的愿望。今存曹植比较完整的诗歌有80余首。曹植在诗歌艺术上有很多创新发展。特别是在五言诗的创作上贡献尤大。首先,汉乐府古辞多以叙事为主,至《古诗十九首》,抒情成分才在作品中占重要地位。曹植发展了这种趋向,把抒情和叙事有机地结合起来,使五言诗既能描写复杂的事态变化,又能表达曲折的心理感受,大大丰富了它的艺术功能。曹植还是建安文学之集大成者,对于后世的影响很大。在两晋南北朝时期,他被推尊到文章典范的地位。南朝大诗人谢灵运更是赞许有佳:“天下才共一石(dàn),子建独得八斗,我得一斗,天下共分一斗。”
曹植一生娶了两位妻子,前妻崔氏,系名门之后,其兄崔琰曾任曹魏尚书,一度得到曹操的信任。崔氏因“衣绣违制”,被曹操勒令回家并赐死。不久,崔氏之兄崔琰又因“辞色不逊”被处死。有人说,崔琰之死与其妹的死有关。曹植的后妻谢氏,曾被封为王妃,即史书中所称的“陈妃”,她是曹植后期生活的伴侣。据说,她一直活到晋代,享年80余岁。曹植有两个儿子,长子曹苗,曾被封为高阳乡公,早夭。次子曹志,被封为穆乡公,他少而好学,才行出众。曹植称赞他是曹家的“保家主也”。曹植死后,曹志继位,徙封为济北王。司马氏篡位后,曹志降为鄄城县公,后任乐平太守,迁散骑常侍兼国子博士,后转博士祭酒。太康九年(288)卒,谥曰定公。曹植还有两个女儿,在他的著作中偶有提及,但具体情况不得而知。
曹值生活在战乱频繁的时代,又深受曹操的影响,因此他前期的作品多数是吐露他自己的志向与抱负的作品。如[白马篇]、[名都篇]、
[鱼旦篇]等。[白马篇]塑造了“幽并游侠儿”的形象,[名都篇]讽刺了耽于游乐的贵族少年,[鱼旦篇]更是把热衷个人名利的庸俗小人比喻为]鱼旦与燕雀,而他自己是鸿鹄,有着“远怀柔九州”的远大抱负。
但是,曹植当时毕竟还比较年轻,生活阅历还不很丰富,活动的范围也比较狭窄。对汉末军阀混战的体验还不深,因此对人民生活方面的反映在他这时的作品中很少。只有[送应氏]一诗写出了洛阳残破的景象,表现了他对人民的同情,但与曹操的[嵩里行]和王粲的[七哀诗]比较还差许多。
2
曹操死后,曹植进入了他后期的创作,由于生活的剧变,使他在颠沛流离中增加了生活的经验。因此反映生活的深度与力度都有了很大的提高,艺术也更加成熟,产生了许多杰作。如[野田黄雀行]、[泰山梁甫行]、[ 赠白马王彪]、[杂诗七首]等。尤其是[ 赠白马王彪]在写景与抒情中控诉了曹丕残酷迫害骨肉的罪行和他渴望自由与建功立业的愿望。
曹植后期的作品虽然多数还是抒写了个人的不幸,但他同时对人民的疾苦有了深入的反映。如他在[谏伐辽东表]中曾经劝解曹叡“省徭役,薄赋敛,勤农桑”而在[泰山梁甫行]中更直接的为民生疾苦大声呼吁道:
八方各异气。千里殊风雨。剧哉边海民。寄身于草墅。
妻子象禽兽。行止依林阻。柴门何萧条。狐兔翔我宇。
曹植的诗歌主要是脱胎于汉乐府和[古诗十九首]等作品。但他在接受这些作品的影响基础上,又有了更多的发展和创造。如他的[美女篇]就是脱胎于[陌上桑],但他更讲究刻画工致与辞藻华丽,也就是说诗歌在他的手里,已经逐步趋向华美,也更加注意辞藻、对仗和警句的安排。但这也成了郭沫若先生抨击曹植的一个罪状,说他是六朝华而不实文章的始作俑者,许多人是不同意这样的看法
曹植的散文和辞赋也有非常高的成就。他的[与杨德祖书]、[与吴季重书]都很富于形象刻画,能表现他自己的性格;他在[陈审举表]中指出曹魏政权的危机不在同姓而在异姓的权臣;在[与司马仲达书]中指责了司马 3
懿拥兵自强的行为;他的杂文[籍田说]用种地作比喻,主张除去权臣。这些都说明他在政治上有一定的见地。而他最著名的作品是[洛神赋] ,在这篇赋中,他基本上抛弃了汉赋那种堆砌奇字、涩字的毛病,而用华美而清新的文字抒写了人神爱慕的感情。他的另一篇名作是[鹞雀赋],通篇用鹞与雀的对话,隐射了他自己与曹丕、曹叡的关系。唐代的[燕子赋]在文字风格上和它很相象,显然是受了它的影响。
曹操即是在剧烈阶级斗争浪潮中成长起来,从残酷的斗争现实中,吸取了不少经验和教训,利用农民革命暂时转入低潮之际,诱骗青州黄巾军百余万人归其笳制。终于倚靠这支革命武装,推行农业政策,逐渐统一黄河南北广阔地区。汉末凋敝的农村经济,农民在较为安宁的境遇里,从事于辛勤农业生产劳动,有了初步的恢复,这就给曹魏政权提供了丰厚的生活资源,客观上为建安文学繁荣奠定了物质基础。
曹操消灭了雄据四州的袁绍,在邺建立政治中心。长期转徙流离的知识分子,因曹操殷勤招邀,聚集邺城。曹植以贵公子之尊,和他们缔结深厚友情,如《文心雕龙.明诗篇》所说:
暨建安初,五言胜踊。文帝,陈思,纵辔以骋节,王,徐,应,刘,望路而争驱。并怜风月,狎池苑,述恩荣,叙酣宴,慷慨以任气,磊落以使才,不求织密之巧,驱醉逐貌,唯取昭晰之能,此其所同也。
由于他们在文酒之会中,相互奖籍,相互探索,又相互评论,曹植文学造诣具备了提高的条件。
陈寿指出,曹植十岁余诵读诗、论及辞赋十万言,显然是善属文的基本因素,这与杜工部的“读书破万卷,下笔如有神”同一旨趣。所以杨修曾惊叹地说:“若成诵在心,借书于手”,这就充分揭示了敏捷才华的生动形像。但必须指出,他在晚年,为了不让芜秽作品遗留给后世,曾付出巨大的椎炼推敲的辛勤劳动。即使犯了沉重的反胃病,也没有挫伤他删订别撰的顽强意志。曹植之所以取得卓越的成就,是以优异才能及其艰辛的创作实践密切结合的产物。
曹植文学成就,固如上述,试再进行控索,则还系于他对现实生活之深刻观察和了解。比如诗篇大部分叙述他的经历和感受。由其真挚的抒吐心灵深处的情感,而又善于从人生旅程中捕捉事物的特征,极意形容,在一定程度上客观地反映了社会现实。他在长期播迁的生活体验中,穷困遭遇折磨中,不合理的现实刺激中,观察越发深邃,表达技巧从不倦的艺术实践里,更日进于精湛之境,创作态度又严肃认真,将汉代朴质的五言诗体推向前所未有的艺术高峰。
4
文学形式是适应着作品内容而产生的。有了丰富的内容,然后才可能有完美的表现形式。离开完美的表现形式,即使有丰富的内容,也不能完满地表达出来。因为作者的思想感情,必须通过艺术形式才能传达给读者感官的。因之内容与形式之密切配合和浑然的统一,而后乃能产生优秀的作品。诗的表现形式,正如刘勰《文心雕龙。明诗篇》所指出:“四言正体,雅润为本,五言流调,清丽居宗。”曹植诗篇以四言表达的,如《应诏》、《责躬》、《元会》、《矫志》等篇,是对君上申明已意为其内容特征,因此要求体制平正,词义典雅,气息雍和渊懿,而蓄其《雅》《颂》的情韵。至于抒写感情,刻画风物,采用五言,才能达致“婉转附物,怊怅切情。”的境界。曹植因注意于形式之精确运用,使内容充分地表达出来,从而取得积极的艺术效果。宋代诗人颜延之在他撰述的《庭诰》里,作了如此的评价,他说:“五言流靡,则刘桢,张华,四言侧密,则张衡,王粲,若夫陈思王可谓兼矣!”③似非过情之誉吧!
诗人虽具丰沛的感情,恰当的艺术形式,但如果蔑视言语在诗歌里所起的巨大作用,而要求作品蕴蓄感染力量,是难以设想的。须知语言是增强作品艺术力的主要组成部分,同时又是作者传达思想感情的工具,完全不能忽视其作用。诗歌既受严密格式之制约,故必须以最洗练,最精彩的语言,表达复杂的思想感情。所以诗人选词用字,自有一定的整练阶段,章无虚语,句无冗词,叙事抒情都取得凝练和概括,表现优美的意境。曹植语言选择费过一番探索的功夫,创造了真挚动人的诗篇,如“飞观百余尺, 临牖御棂轩。 远望周千里, 朝夕见平原。 ”[《杂诗之一》]豪放雄浑的语言,反映着宏阔的意境,悲壮的情怀。
“??雠高念皇家,远怀柔九州,抚剑而雷间,猛气纵横浮??”[鰕鱼旦篇]这是豪迈激昂的心声,表现着一切的凌厉气概。
“人皆弃旧爱,君岂若平生?寄松为女萝,依水如浮萍”[《闺情》]恻怆凄婉的细语,倾吐着内心的哀怨。曹植语言由其遣词精切,语贵创造,而又俱从生活中来,形成了独特的风格。
他以锐敏深刻的观察力,猎取生活事物的形象。有如苏轼所说“作诗火急追亡述,清景一尖后难摹。”④曹植从储备的语言宝库里,选择唯一的词汇,力争把事物的形色,意趣最完整,最贴切地体现。如:
“??明月澄清景,列宿正参差。秋兰被长坂,朱华冒绿池??”[《公宴诗》]绮丽的语言,绘出西围绚烂的秋色。而“被”字与“冒”字把茂密的物象形容极致。对偶精工,置于唐人律体,也并不逊色。
“员阙出浮云,承露概太清”[《赠丁仪王粲》]这展示帝京景物壮丽的特色,而“出”、“概”二字形象地凸现器物凌云的伟观。
因此,若果只赞誉曹植“词采华茂”,而忽视其遣词精确的特质,则对他艺术成就的认只,可能不够全面吧!
诗歌语言,必须具有强烈的音乐感,咏之适口,听之忘倦,长歌恬呤,从抑扬顿挫的和谐音节里,领受诗篇孕蓄的情感。所以,诗歌皆适韵律,成为我国诗人劳精殚思毕生追求的目的,XX孜孜,务穷必蕴,不惜精力和时日。杜工部曾说:“新诗改罢自长呤”,又自诩“晚节渐于诗律细”,⑤可见诗人于此是如何寄思了。
验声之术,在汉魏以前,审声定韵,全凭耳治。而无准则作依据。要求诗歌必具“清浊齐均,既亮且和”的美感,是不容易达到的。若果轻视而不讲求,必然会使喉舌蹇凝而唇舌告劳。曹植取得精邃的音乐素养,⑥接受民歌的韵律,又可能受印度文学之影响,鸠摩罗什论印度文学时说“天竺国俗,甚重文制,其宫商体韵,以入管弦为善。凡觐国王,必有赞德,经中倡颂,皆其式也。”⑦而僧徒相传,曹植曾仿制梵呗:“陈思王尝登鱼山,临东阿。忽闻巅岫有诵经声,清犹深亮,远谷流响,俨然有灵气,不觉敛袊祗敬,便有终焉之志,即效而则之。今之梵唱,皆植依此造也。”⑧释慧皎《高僧传。十三经师论》也说:“梵呗之起,肇自陈思。”暂且不论僧徒纪录是否真确,但可以肯定曹植为了增进诗歌语言的谐和美,确曾吸取众长,丰富诗篇的韵律,如他写:“始出严霜结,今来白露晞”[《杂诗》]“孤魂翔故城,灵柩寄京师。”【《赠白马 5
王彪》】,平仄协调,音节铿锵,给诗歌声律化奠定了坚实基础。
诗之需要押韵,不仅使语言本身具有抗坠急徐的韵致,而且还有助于情感之宣泄与抑制。西晋诗人陆云对于押韵深感困难,故在他给陆机信里,不只一次地透露着急苦的心情。如《喜霁赋》:“俯顺习坎,仰炽重离,以下重得数语为佳,思不得韵,愿兄为益之。”⑼“彻与寮皆不与日韵,思惟不能得,愿赐此一字。”⑽曹植遣词叶韵,成为西晋诗人的准则,陆云给陆机信,曾经提到:“李氏云,雪与列韵,曹便复不用。人亦复云,曹不可用者,音自难得正。”⑾曹植押韵既这样谨严,而为诗人所遵守。但还需知他利用字音之高低、平仄的特质,来表达情绪的变化,而非一韵始终,无有更易。如《杂诗》“转蓬离本根”至“微藿常不充”,俱用平声字押韵,可是末句,却突然改用上声的“老”字作韵脚。我们知道,平声之字,高亢舒扬,用以体现激昂的情韵,是适当的。上声之字,则具着凄厉的音色,用它入韵,却能表达抑郁愁苦的心境。曹植以“老”字押韵,结束全章,更显出怨愤已深的决绝情绪。又如《浮萍篇》,自“浮萍寄清水”至“思君傥中还”,句中虽换韵,然都用平声字协,而“慊慊仰天叹”以下,押韵俱易仄声,也是同一思致。顾炎武《音喻》说:古之为时,主乎音者也,江左诸公之为诗,主乎文者也。文者一定而难移,音者无方而易转。”可知曹植协韵,声随情变,何曾斤斤墨守一般格律呢。
曹植诗中,往往使用双声叠韵的复音词,符合钟嵘《诗品》提示的“清浊通流,口吻调利”的调声原则,例证繁多,无须列举。
曹植赋今集中记载的,共计四十四篇,除《洛神》等三四篇外,多数是残缺不全的。可是明代文学家李献古不明乎此,竟说,“凡作赋者以巨丽为主,子建诸篇不数音则尽,读之者忘其短,但觉搦搦有余韵??”这样论点,是不符合历史实际的。今仅就遗存部分的表现观察,约略可分为三类《远游》,《明志》,《怀亲》诸赋,效物则有《芙蓉》,《鹦鹉》,《宝刀》等篇。至于《洛神赋》,兼具两类的特点。抒情情感真挚,词旨婉约。宋末逸民刘会孟评《释思赋》说“临淄笃于友于,故随所寄咏,无不贴切。”而效物刻画精工,曲尽物态。明人蒋仲舒叹赏《九华扇赋》形容的工致,不禁写出“字字圆通,中镶异彩。其缕折九华之妙,虽未经目,恍如见之”的评语。可见不论抒情,效物,达到了一定的艺术水平。但是二者不是对立而是相互渗透的。效物等赋之图绘形象,原籍以寄寓理想,抒发怀抱,绝对不是单一地就物写物为其主要目的。例如《蝉赋》,曹植赋予蝉以为类的意识和感情,宣示与物无求而含和独乐的处世态度,可是在现实的社会里,却是处处遭遇着死亡的威胁。
“苦黄雀之作害兮,患螳螂之劲斧。冀飘翔而远托兮,毒蜘蛛之网罟。欲降身而卑窜兮,惮草虫之袭予。”影射周遭密布众多的贼害者,生动地写着动与祸邻的恐怖环境,企图寻求安静地方,于是“......遥迁集乎宫宇。依名果之茂阴兮,托修干以静处......”复不自料遇着狡童。极意描绘狡童捕捉的举动、心理,暗示贼害者的卑劣意图及其阴狠手段,则更突出艰危境遇之难于回避,这就形象地把可憎恨的人与人的社会关系,具体地显现在眼前,使读者感到惊人的艺术魅力。
曹植各赋,比较汉人所作,篇幅简短,情韵不匮,和诗保持着千丝万缕的联系,自然与汉赋之铺陈堆砌,迥异其趣,而开六朝小赋的先声。
曹植各表,以其饱满的政治热情,辅之精密观察,洞悉魏王朝内部潜伏的危机。运用表这种散文形式向曹睿揭露权臣营私危国的阴谋,而力争宗室取得自由生活和政治权力的享有。在叙说里,驱使朴质平易的语言,洋洋洒洒,将隐微事理表达得十分明畅,不受任何形式的节制。亦庄亦谐,或骈或散,一任思想之自由发抒,而巧妙地运用比喻与象征的技巧,将抽象概念具体化,形象鲜明,感情充沛,因此具有巨大的说服力。例如:“......臣闻羊质虎皮,见草则悦,见豺则战,忘其皮为虎也。今置将不良,有似于此。”⑿曹植借用扬雄《法言》的话,轻轻一提,曹魏大将贪懦无能的行为,便清楚地显现出来。
“......高鸟未挂于轻缴,渊鱼未悬于钩饵者,恐钓射之术或未尽也......”⒀高鸟渊鱼象征蜀吴。委婉地 6
指摘应会蜀吴战略的错误,着墨不多,词意含蓄。
“臣伏以为犬马之诚不能动人,譬人之诚不能动天,崩城陨霜,臣初信之,以臣心况,徒需语耳。若葵藿之倾叶太阳,虽不为之回光,然终向之者诚也。臣窃自比葵藿。”⒁用葵藿之向日性,说明拥护曹睿政权的真诚与决心,同时曲折地暗示曹睿对他的冷漠态度,贴切,生动,充分表述自已的情绪。又如:
“臣窃感先帝早崩,威王弃世,臣独何人,以堪长久。常恐先朝露,填沟壑,填土未干,而声名并减......”⒂倾泄沉痛的感情和迫切要求立功的愿望。
“......臣伏自惟省,岂无锥刀之用。及观陛下之所拔援,若以臣为异姓,窃自料度,不后于朝士矣......”⒃这多么深刻尖锐的讽刺。所以刘勰对他写作的表,给了很高的评价。他说:“陈思之表,独冠华才。观其体赡而律词,辞清而志显,应物制[据《御览》改]巧,随变生趣,执辔有余,故能缓急应节矣!”⒄充分指明曹植散文的艺术性及其优越的表现技巧,不必再事辞费了。
曹植创作,影响后世最深的,莫如诗歌。这里举出几件故事,籍以说明。
“羊尝为谢[安]所爱重。安薨后,辍乐弥年,行不由西州路。尝因石头大醉,扶路唱乐,不觉至州门。左右白曰:此西州门。尝悲感不已,以马策扣扉,诵曹子建诗曰:生存华屋处,零落归山丘[《箜箎引》句]。恸哭而去。”⒅
“成帝召[桓]伊饮宴,[谢]安侍坐。帝命伊吹笛。伊神色无忤,即吹为一弄,乃放笛云......。伊便抚筝而歌。《怨诗》曰:“为君既不易,为臣良独难。忠信事不显,乃有见疑患。周公佐成王,金縢功不刊。推心辅王室,二叔反流言。”声节慷慨,俯仰可观。安泣下沾襟,乃越帝而就之,捋其须曰:“使君于此不凡!”帝期甚有愧色。⒆
“......乃与夫人妃嫔忆下决,莫不唏嘘掩涕。嫔赵国李氏诵陈思王诗云:王其爱玉体,俱享黄发期[《赠白马王彪》句]皇后以下皆哭。”⒇-南北朝士大夫和宫廷妃嫔都能背诵曹植诗句,可见流播的广泛性。明代文学家王弇州诵读《赠白马王彪》诗,回环往复数十遍,犹不能自休。⒇足证曹植诗中,蕴着丰富而真挚的情感,而这种情感在封建社会里带有普遍性,因此有人藉它来表达其所感受的悲愤,仿佛是自已从内心发泄出的。可见诗篇感人之深了。
陈寿在《魏志》本传对此作了正确的评语:“文才富艳,足以自通后世。”西晋以下的诗人,很多仿效其体制。比如左思《咏史.主父篇》用八句叙述四件史实,以收八句穷通之理,正和《豫章行》同一结构。《赠白马王彪》诗,用次章的首句蝉连上之末句,颜延之《秋胡行》便规摹而作。至于《杂诗》“仆夫早严驾”篇的组织形式,为杜甫的《潼关吏》和《新安吏》的先导。北周诗人王褒诗“斩鸡横大道,走马出长楸”显然承用《名都篇》之“斩鸡东郊道,走马长楸间”的词意。《赠白马王彪》的警语“丈夫志四海,万里犹比邻”,却为初唐诗人王勃所本,而写出了“海内存知已,天涯若比邻”的名句。
综上所述,曹植文学给予后代的影响,无疑地是深且巨的。“自通后世”的结论,陈寿早已予以肯定了。
7
从曹植的作品中,我们可以清楚地看到,曹植的人生目标非常明确,在政治上有很大抱负。他在《与杨德祖书》中说道:“吾虽薄德,位为蕃侯,犹庶几戮力上国,流惠下民,建永世之业,流金石之功,岂徒以翰墨为勋绩,辞赋为君子哉!”[1]我们认为,曹植为自己确立的人生目标并非没有依据。
从客观条件上看,时世造英雄,汉末建安时代的社会大动乱,虽然给广大人民造成了巨大的灾难,但同时也给知识分子施展抱负,实现理想提供了广阔的用武之地。曹植的后半生,虽然北方渐趋安定,但正如曹植所言:“顾西尚有违命之蜀,东有不臣之吴”,“边境未得税甲,谋士未得高枕”。[1]这样的时代环境,为曹植实现政治抱负和人生理想提供了极好的机会。
从主观条件上看,曹植也有实现其政治抱负和人生理想的良好基础。其一,他天资聪明,少年时代就才华横溢:“年十岁馀,诵读诗论及辞赋数十万言。善属文。太祖尝视其文,谓植曰:‘汝倩人邪?’植跪曰:‘言出为论,下笔成章,顾当面试,奈何倩人?’时邺铜爵台新成,太祖悉将诸子登台,使各为赋。植援笔立成,可观,太祖甚异之。”[2]其二,在生活作风方面,他崇尚简朴,不尚华丽,而且很有政治头脑,“每进见难问,应声而对”。[2]其三,他结交的朋友,也大都是如丁仪、丁廙、杨修等才异之士。正是由于这样的一些原因,曹植 “特见宠爱”[[2],建安十六年被封为平原侯,十九年又徙封为临淄侯,曹操远征孙权,又让他担负起留守邺的重任,并且“几为太子者数矣”[2],多次想让他成为接班人。
然而,曹植最终在政治上完全失败了。他不仅没能施展自己的抱负,实现自己的理想,而且致
曹植在我国中古建安时代是具有卓越成就的文学家.他继承先秦《诗》《骚》的优秀传统,又从两汉辞赋民歌中吸取营养,兼收并蓄着,从而丰富了诗赋的内容与形式,这就为六朝隋唐文学开辟了前进的道路,影响所急,无疑是较为深远的。
杨修曾惊叹地说:“若成诵在心,借书于手。”充分揭示了曹植敏捷才华的生动形象,然而曹植之所以取得卓越的成就是以优异才能及其艰辛地创作实践密切结合的产物。他的文学成就,试再进行探索,还系于他对现实生活的深刻观察与了解。如诗篇大部分叙述他的经历和感受,由其真挚地抒吐心灵深处的情感,而又善于从人生旅途中捕捉事物的特征,极意形容,在一定程度上客观地反映了社会现实,他在长期播迁的生活体验中,穷困遭遇磨难中,不合理的现实的刺激中,观察越发深邃,表达技巧从不倦的艺术实践里,更日进于精湛之境,创作态度又严肃认真,将汉代朴质的五言诗体推向前所未有的艺术高峰。
8
每每读子建的洛神赋,除了惊叹于他词采华茂外,不得不相信前人所说,建安七子中,独子建文采占七分。而洛神赋中那个瑰姿艳逸,仪静体闲且翩若惊鸿,婉若游龙的女子一直是世人所猜测的对象。我却情愿相信,这个女子就是甄后。
甄后其实在史书中并无过多的记载。三国志里倒是有一处写道曹操大败袁绍,结果曹丕先入袁府,见一妇人被发垢面垂涕,曹丕使人揽发以巾拭面,见妇人姿貌绝伦,后纳其为妃,这妇人便是袁绍之妻甄宓。就在曹丕携甄后离去时,后赶至的曹操无不悔叹:“这场战争就是为这个女人而打的啊,”心里着实后悔未早至袁府,先一步找到如此绝色美人。后来曹丕请求曹操将甄氏赐予他为妻。曹操不得已,只好同意将甄氏嫁与曹丕。而在此间,甄氏是曹植是该见过面了。
不管如何,绝美的甄氏似乎成了这场战争的理由。绝色的容颜在一场杀戮下不见苍白,反而有一丝艳光,溶入三个当世最有文采的男人眼中。蓬莱文章建安骨,有了一位才情与容貌双绝的女子映照下,方显出完美。只是,这场说不清道不明的纠葛中,却又以曹丕负美人,而曹植最是痛心疾首而告终。曹丕纳了甄氏,却又不珍惜,更是听信谗言将甄后赐死。后争嗣风波平定,曹丕顺利登上皇位,而为了让这位文采超过自己的弟弟继续沉痛于失去心爱之人的悲伤中,将甄后的枕奁金镂玉带枕赠予曹植。使其一生都沉沦于失去所爱的伤怀中。这实在是其心可诛。
曹植对甄氏心神眷念,却最终只是看着心爱之人被无情赐死,伤心之余,见着甄氏的枕奁,闻着枕上的旧香余温,遥想当时初见的美好,该是多么的伤痛。曹植睹物思人,回来时经过洛水,恍惚之间,遥见甄妃凌波御风而来。曹植伤心之余,写下《洛神赋》,把洛河中的水神当做甄后的化身,抒发对其倾慕之意。
这便是洛神赋诞生的前传,虽经不起考究,可我宁可相信这是真的。
且看洛神赋里,美丽的洛水之神宓妃,她体态轻盈柔美象受惊后翩翩飞起的鸿雁,身体婉曲轻柔象腾空嬉戏的游龙;容颜鲜明光彩象秋天盛开的菊花,青春华美繁盛如春天茂密的青松;行止若有若无象薄云轻轻掩住了明月,形象飘荡不定如流风吹起了回旋的雪花;姣如朝霞,纯洁如芙蓉,风华绝代。文章后面对于洛神离去时的描写“屏翳收风,川后静波,冯夷鸣鼓,女娲清歌。”由此我们可以感觉到他们之间的爱情之真挚、纯洁。从相遇以来一切都是如斯的美好,以致于离别后,人去心留,情思不断,浪漫而苦涩,心神为之不宁,徘徊于洛水之间不忍离去。最后,洛神的美丽形象终于消失在苍茫的暮色之中,而他却依然站在水边,惆怅的望着洛神逝去的方向,恍然若失。他驾着轻舟,溯川而上,希望能再次看到神女的倩影。然而,烟波渺渺,长夜漫漫,更使他情意悠悠、思绪绵绵。天亮后,他不得不“归乎东路”了,但仍“揽騑辔以抗策,怅盘桓而不能去”。
于是我有理由相信,甄氏被曹丕带回来时,曹植自那时起便与甄氏见过面了,而且以曹植的才情及奇骨高风,必对甄氏多有怜惜。也许,初见时并非如他们的父兄一般惊艳于甄氏的绝色姿容,想占为己有,而是怜惜甄氏乱世桃花逐水流的可怜境遇。由可怜而生情。 “美女妖且闲,采桑歧路间,柔条纷冉冉,落叶何翩翩。顾盼遗光彩,长啸气若兰,容华耀朝日,谁不希令颜。佳人慕高义,求贤良独难。盛夜处房室,中夜起长叹。”美丽的女子,性格娴静,她的一顾一盼都给人留下迷人的光彩,气息芬芳如幽兰,谁不爱慕她的美貌呢,诗意再一转,美女爱慕的是品德高尚之人,要想寻求一个贤德国的丈夫实很困难,而美女此时正当盛年,而独居闺中,忧愁怨恨,夜深不眠。因此发出长长的叹息。这是曹植的名篇美女篇。嫁与曹丕为妻的甄氏却很快色衰爱驰,遭受曹丕的抛弃,独守空闺,此情此境,曹植又如何不想起他自身呢,他这一生似乎都是怀才不遇并为他的哥哥曹丕所忌,抑郁不得志,两人相同的境遇是以拉近了两颗苦闷而寂寞的心。她们彼此神交,彼此怜惜,由此而产生的爱情超出了世俗的流声。“愿为西南风,长逝入君怀,君怀良不开,贱妾当何依”曹植的心声,何尝不是同情甄后与自己的遭遇相同所发呢。甄后的寂寞,曹丕对曹植的无情与打压, 9
让曹植愤慨却只能寄情于诗赋中。
李商隐曾诗日“宓妃留枕魏王才”,我一直感动于此。甄后的心中未必不曾对曹植动过心。人生不若初见,何事秋风悲画扇,团扇见捐,恩情不再,残红落地教人无从怜惜。美丽的甄后应是看透了曹丕的无情,更是觉得曹植有情。只是,当年由不得她选,本以为那个良人不同于别人,却仍是负了她。而反观曹植,文采斐然。品性高洁,真是谓世间的良人。只是,她已嫁,而世俗容不得她们有情。唯有藏于心间。发乎情,止乎礼。
而曹植除了婉惜,还有更深沉的悲伤。只能在甄后被赐死后,将余情化成满腔的文采,将一生的悲愤化成融入其间。因此作了这世间风华并茂的>。
白馬篇
曹植
白馬飾金羈,連翩西北馳。
借問誰家子,幽并遊俠兒。
少小去鄉邑,揚聲沙漠垂。
宿昔秉良弓,楛矢何參差。
控弦破左的,右發摧月支。
仰手接飛猱,俯身散馬蹄。
狡捷過猴猿,勇剽若豹螭。
邊城多警急,胡虜數遷移。
羽檄從北來,厲馬登高堤。
長驅蹈匈奴,左顧陵鮮卑。
棄身鋒刃端,性命安可懷?
父母且不顧,何言子與妻?
名編壯士籍,不得中顧私。
捐軀赴國難,視死忽如歸。
【賞析】:在這首詩中,曹植以濃墨重彩描繪了一位武藝高超、渴望衛國立功甚至不惜犧牲生命的遊俠少年形象,藉以抒發自己的報國激情。詩歌的風格雄放,氣氛熱烈,語言精美,稱得上是情調兼勝。
詩歌的起首即用“連翩西北馳”的畫面形象地傳達出一種勇往直前的精 10
神。接下去關於“幽井遊俠兒”的一大段文字,極盡繪聲繪色之能事,寫出他的颯爽英姿和高超的武藝,筆墨之間沸騰著一股激越高亢的情緒。這位身手不凡的白馬少年“長驅蹈匈奴,左顧陵鮮卑”,大有顧盼間強虜灰飛煙滅的豪邁氣概。
詩人不僅以激情的筆調寫出了白馬少年的英雄行為,而且以精湛的語言揭示了人物的愛國精神。詩歌的最後幾句,道出了白馬少年的思想底蘊和壯烈情懷,音哀氣壯,聲沉調遠,大有易水悲歌的遺韻。
詩歌採用了倒敘、補敘的手法。詩歌以“白馬飾金羈,連翩西北馳”突兀而起,又以“借問誰家子”十二句來補敘“西北馳”的原因。繼而又倒敘“名編壯士籍”、告別家人時的心情;最後策馬“赴國難”的一幕則與開首重合。如此章法,像電影中的“閃回”,使白馬英雄的形象漸次深化,憂國去家,捐軀濟難的主題則得到鮮明突出的表現。
【註釋】:
本篇是《雜曲歌·齊瑟行》歌辭,又作《遊俠篇》,因其所寫的是邊塞遊俠的忠勇。作者平素也有“捐疆赴難,視死如歸”的抱負和從軍出塞的經驗,寫遊俠也可能是自況。
幽并:兩州名,就是今河北省、山西省和陜西省的一部份地方,是古來出勇俠人物較多的區域。
揚聲:即“揚名”。垂:即“陲”,邊遠的地區。
楛:木名,莖可以做箭桿。
控弦:拉弓。左的:左方的射擊目標。
月支:射帖(箭靶之類)的名稱,又名素支。
猱:動物名,猿類,體矮小,尾作金色,攀緣樹木極其輕捷,上下如飛。 散:碎裂、摧毀。馬蹄:也是射帖名。
剽:輕快。
螭:傳說中的動物名,如龍而黃。
檄:用於徵召的文書,寫在一尺二寸長的木簡上。上插羽毛表示緊急就叫做“羽檄”。
鮮卑:東胡種族,東漢末成為北方強族。
懷:猶“惜”。
曹植为什么要写白马篇?
满意答案
曹植受他父亲的影响,很仰慕“重气轻命,感分遗身”“果毅轻断,虎谷生风”的侠义之风,这首《白马篇》也是他尊重游侠的一个证据。按《白马篇》亦称《游侠篇》(《太平御览》卷359);此外曹植还写过一首《结客篇》,其中写道:“结客少年场,报怨洛北荒??利 11
剑手中鸣,一击两尸僵。”在著名的《野田黄雀行》中他义说“利剑不在掌,结友何须多”。看来,他很欣赏手持利剑、恩怨分明、为朋友两肋插刀的游侠作风。
所以他创作了这首《白马篇》强烈歌颂的是一位骑着白马的青年英雄,他的身份本是“游侠”,而现在则是名单在册的卫国壮士。
《白马篇》,属乐府杂曲歌辞中的《齐瑟行》,题作《游侠篇》。因首句有“白马”二字,故
《文选》又作《白马篇》。
这首诗写在魏明帝太和间,是曹植中后期的作品。
明帝即位后,不仅“西有违命之蜀,东有不臣之吴”(《求自试表》),而且长城之内的匈奴日渐强盛,不断侵扰魏的边邑,西北部的鲜卑族群落进入了一个新的发展时期,部族力量不断增强,他们又联合西蜀,蚕食边土,给魏国安全带来巨大威胁。在此背景下诞生的《白马篇》,塑造了一个武艺超强、为国建功不惜壮烈牺牲的“游侠”形象,赞美了关键时刻能为国家利益挺身而出的“忠勇”精神,也表达了诗人“闲居非吾志,甘心赴国忧”(《杂诗》其五)的满腔
热忱。
全诗分为三个部分。
诗歌一开始,诗人便将一幅动感极强的画面陡然推到读者面前:广褒的原野上,一匠雪白的战马风驰电掣般向着西北方向飞奔,铜饰的马络头泛着金黄色的光,格外引人注目。两句中没有一字提及骑马的人,但从这马络的装饰及马奔的速度、方向上已经让人感觉到此人绝非等闲之辈。他是谁?他为何要往西北方向狂奔?诗人顺着读者的阅读期待指向,采用问答的句式,将骑马者的身份一笔带出:他是幽州、并州一带的游侠。这第一部分仅仅四句,却是用足烘托,以势见气,造成了“先气夺人”的艺术效果。清人沉德潜尝赞其“极工起调”,此例己可见诗人开篇功夫。需要注意的是,读者的两个心理期待,诗人只回答了一个,而另
一个却按下不提,这便于不动声色中,布下玄机。
按照正常的思路,当交待完诗中人物的身份后,就应该续写他“现在时”的行为过程,即撮述其典型事例,但诗人却宕开一笔,以十句诗补叙游侠的经历及他高超的武艺。这便是诗
的第二部分。
“少小去乡邑,扬声沙漠垂”,这是对游侠经历的概述。这位年轻的侠士自幼便离开了家乡,腥风血雨,斩将夺旗,大漠战尘,边塞狼烟,终于成就他游侠的英名,由少小离家到扬声边陲,这中间到底发生多少可歌可泣的故事?那只有让读者自己去回味、咀嚼了。这两句看似平常,却为读者的阅读想象提供了巨大的空间。“宿昔秉良弓,楛矢何参差”,这在追述他日常习惯的同时,对其韇丸情节进行细致描画。“宿昔”明示读者,这位游侠一直都是人不离马,手不离弓,这是生活环境形成的优良素质。韇丸中楛矢参差,这既是马上颠簸的实际写照,又显现出主人潇洒不羁的侠士性格。在作了如此铺垫之后,诗人集中笔墨,以六句诗重点描述游侠高超的箭术:只见他弓开满月,箭去流星——左射,射中了箭靶;右射,射破 12
本文标题:光谱分析技术及其应用-典型相关分析及其应用实例61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1