一 : ItBuLu:分析外部链接与域名后缀关系
最近发现一个奇怪的事情,交换链接的时候别人说域名的后缀不符合他们公司的规定,我就纳闷了。对于域名后缀是否影响网站的权重这个问题网上也有不少文章。比如有问CN域名是不是权重低,ORG,COM域名是不是权重就高。针对此,itbulu进行了如下的分析:
首先,我们随便搜索一个关键字。看到搜索结果网站的排名,较多的是COM,还有部分CN,COM.CN以及其他后缀的域名。这主要原因是COM域名是大家注册域名的首选,对于公司还是个人,首选当然是COM,如果特别看好域名组合,勉为其难就会注册NET,CN等。
其次,内容是权重高低的关键。我一个朋友手上有GOV的域名,也做了一个网站,我们很多人都默认GOV的域名权重高,PR高,但是此域名PR也就是3.为什么呢?因为我们看到的EDU,GOV都是学校,政府的网站,搜索引擎当然分配的权重就高,昨天一个朋友公司举办国际活动的官方网站,后缀是ORG的,PR达到6,从这点可以说明,权重高低,在于我们有没有维护好自己的网站,是不是用心在做。搜索引擎会判断你的网站文章的质量和原创度,当然还有可读性、可用性。
最后,我们应该如何提高自己的网站权重。提高网站权重就好比养自己孩子一样,开始时候必须原创度,中期可以进行转载,伪原创,后期维护也需要不间断的原创。专一性,针对性的主题是网站整体权重的关键。大综合性网站如果我们很难把握,itbulu建议分域名操作。
总结:域名的权重高低与网站域名后缀没有关系,只要你喜欢注册我们样的域名都可以。itbulu明年筹划做一个网站,域名已经注册好了im513.com。
本文原创文章来自: 转载注明出处,谢谢。
二 : 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析

r级小说 第四章2连续时间信号与系统的复频域分析
r级小说 第四章2连续时间信号与系统的复频域分析

三 : 时域离散信号和系统的频域分析
信号与系统的分析方法有两种:时域分析方法和频域分析方法。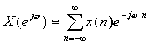 (2.2.1)
(2.2.1)
 |=
|= (2.2.2)
(2.2.2)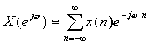 ,
, 是频率w的周期函数,周期为2p。
是频率w的周期函数,周期为2p。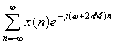 =
= 。
。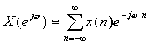 =
= =
=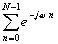
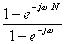 =
=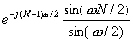

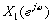 =DTFT[x1(n)],
=DTFT[x1(n)],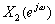 =DTFT[x2(n)],
=DTFT[x2(n)],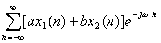 = a
= a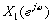 +b
+b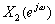
 = DTFT[x(n)],
= DTFT[x(n)],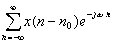
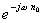

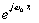 x(n)] =
x(n)] =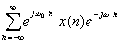
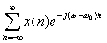 =
=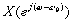
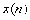 满足下式
满足下式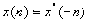
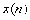 为共轭对称序列。
为共轭对称序列。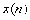 =
= +j
+j (实部加虚部)
(实部加虚部)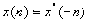
 +j
+j =
= -j
-j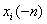
 =
= (偶函数)
(偶函数) =-
=-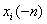 (奇函数)
(奇函数) 表示:
表示:
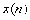 满足下式
满足下式
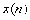 为共轭反对称序列。
为共轭反对称序列。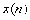 =
= +j
+j (实部加虚部)
(实部加虚部)
 +j
+j =
=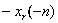 +j
+j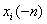
 =
=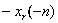 (奇函数)
(奇函数) =
=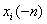 (偶函数)
(偶函数)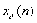 来表示
来表示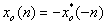
 与共轭反对称序列
与共轭反对称序列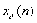 之和表示。即:
之和表示。即: +
+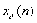 (2.2.16)
(2.2.16) =?
=? =
= +
+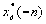
 -
-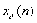
 =
= -
-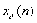 (2.2.17)
(2.2.17) =
= (
( +
+ )
)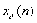 =
= (
( -
- )
) ,也可分解成共轭对称分量和共轭反对称分量之和:
,也可分解成共轭对称分量和共轭反对称分量之和: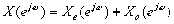
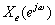 是共轭对称分量,
是共轭对称分量,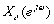 是共轭反对称分量,它们满足:
是共轭反对称分量,它们满足: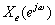 =
=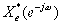 ,
,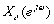 =
=


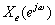 :共轭对称分量,它的实部是偶函数,虚部是奇函数;
:共轭对称分量,它的实部是偶函数,虚部是奇函数;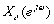 :共轭反对称分量,它的实部是奇函数,虚部是偶函数。
:共轭反对称分量,它的实部是奇函数,虚部是偶函数。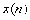 =
= +j
+j (
( 、
、 都是实数序列)
都是实数序列)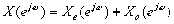
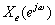 =DTFT[
=DTFT[ ]=
]=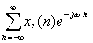 ,
,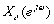 =DTFT[j
=DTFT[j ]=j
]=j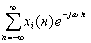 。
。 中的
中的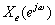 ,虚部和j一起对应于
,虚部和j一起对应于 中的
中的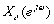 。
。 和共轭反对称部分
和共轭反对称部分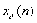 ,x(n)=
,x(n)= +
+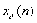
 =
= (
( +
+ )
)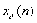 =
= (
( -
- )
) ]=
]= (
( +
+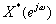 )=Re[
)=Re[ ]=
]=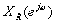
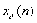 ]=
]= (
(
 )=jIm[
)=jIm[ ]=j
]=j
 =
=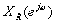 +j
+j
 +
+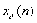
 对应于
对应于 的实部
的实部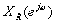 ,而序列的共轭反对称部分
,而序列的共轭反对称部分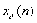 对应于
对应于 的虚部加j。
的虚部加j。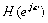 =
=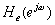 ,具有共轭对称性,
,具有共轭对称性,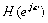 的实部偶对称,虚部奇对称。
的实部偶对称,虚部奇对称。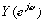 =
= ×
×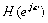 =
=
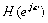 (2.2.32)
(2.2.32)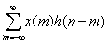
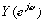 =DTFT[y(n)]
=DTFT[y(n)]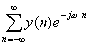 =
=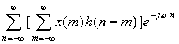
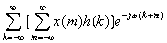

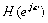

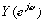 =
=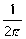
 *
*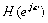 =
=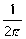
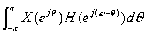
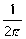
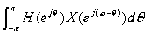
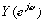 =
=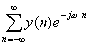 =
=

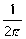
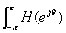
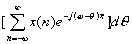
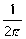
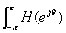
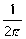
 *
*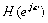
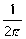 (2.2.34)
(2.2.34)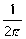
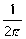
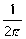
 = (2.5.4)
= (2.5.4) = ZT-1[X1(z)]+ ZT-1 [ X2(z)]+…+ ZT-1 [XK(z)]
= ZT-1[X1(z)]+ ZT-1 [ X2(z)]+…+ ZT-1 [XK(z)] 的Z变换定义为z-1的幂级数,即
的Z变换定义为z-1的幂级数,即 。
。 必为因果序列,此时应将X(z)展成z的负幂级数,为此,X(z)的分子分母应按z的降幂排列;
必为因果序列,此时应将X(z)展成z的负幂级数,为此,X(z)的分子分母应按z的降幂排列; 必为左边序列, X(z)的分子分母应按z的升幂排列;
必为左边序列, X(z)的分子分母应按z的升幂排列;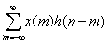
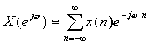 (2.2.1)
(2.2.1)四 : 主板要换,系统不变
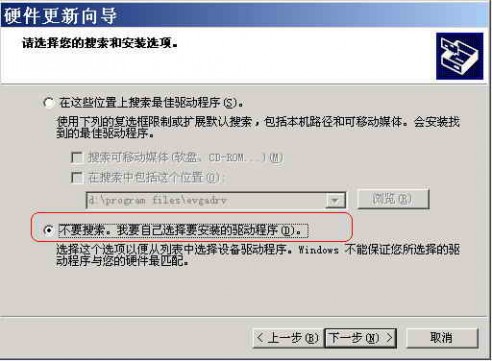
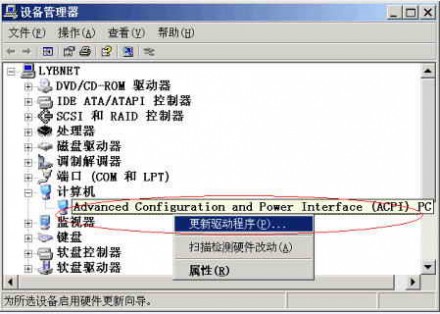
一般情况下,当我们换过新主板、RAID卡或者IDE卡之类的硬件(即系统硬件发生重大变化)后,再次进入Windows 2000/XP时,通常都不能正常进入操作系统。即使升级主板所采用的是同一厂商的芯片组也一样,例如从Intel i845芯片组主板升级为i865芯片组主板。最终结果是必须重新安装Windows系统和大部分应用软件。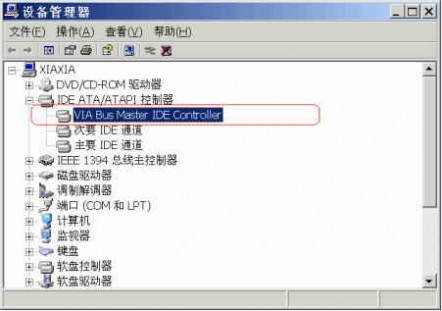



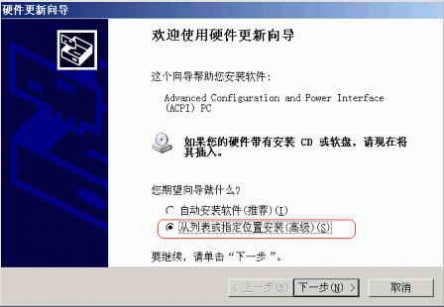

五 : 第四章2连续时间信号与系统的复频域分析
对一个n阶系统, 对一个n阶系统,若其微分方程及系统函数为
y(
n)
t ) + an 1 y ( (
n 1)
( t ) + + a1 y′ ( t ) + a0 y ( t ) = f ( t )
s n + a n 1 s n 1
s 1
an1
a1
对应的系统函数表示为
H (s ) =
1 + + a1 s + a 0
s 1
则其n阶系统的复频域模拟图如图4.40所示。 则其n阶系统的复频域模拟图如图4.40所示。 4.40所示
F ( s)
∑
Y ( s)
a0
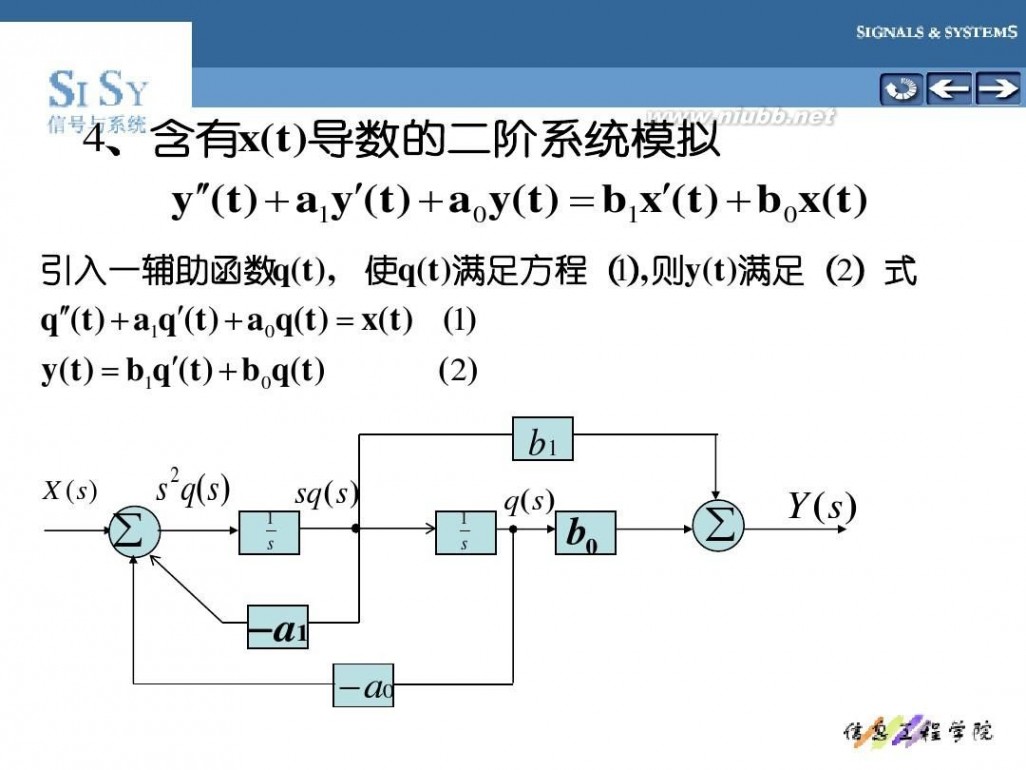
4、含有 x ( t ) 导数的二阶系统模拟 y ′′( t ) + a 1 y ′( t ) + a 0 y ( t ) = b 1 x ′( t ) + b 0 x ( t )
满足方程( , 满足( 引入一辅助函数 q(t ), 使q(t )满足方程(1)则y (t )满足(2)式 q′′(t ) + a1q′(t ) + a 0q(t ) = x(t ) (1) y (t ) = b1q′(t ) + b 0q(t ) ( 2)
b1
X (s )
∑
s2q(s)
1 s
sq(s )
1 s
q(s )
b0
∑
Y (s )
a1
a0
若系统的微分方程中含有输入函数的导数项, 若系统的微分方程中含有输入函数的导数项,如
y(n)(t)+an1y(n1)(t)+ ay′(t)+a0yt) =bmf (m)(t)+bm1 f (m1)(t)+ bf ′(t)+b f (t) +1 ( +1 0
且 m < n ,其系统函数
N ( s ) bm s m + bm 1s m 1 + + b1s + b0 H (s) = = n D (s) s + an 1s n 1 + + a1s + a0 n
bn1
b1
F (s)
∑
s 1
s 1
s 1
b0
∑
Y ( s)
an1
a1
a0
系统函数作出的, 以上讨论的框图是直接 根据系统的微分方程或 系统函数作出的, 一般称为直接模拟框图 。
5、并联模拟框图 一般n阶系统的方程为
y(n) (t) + a n1y(n1) (t) + ...+ a 1y'(t) + a 0y(t) = b mx(m) (t) + ...+ b 1x'(t) + b 0x(t) (m < n)
b m s m + b m 1s m 1 + ...b1s + b 0 Y(s ) = 则 H (s ) = n n 1 s + a n 1s + ...a1s + a 0 X(s ) (s z1 )(s z 2 )...(s z m ) = bm (s p1 )(s p 2 )...(s p n )
k1 k2 kn = + + ... + s p1 s p 2 s pn = H1 ( s ) + H 2 ( s ) + + H n ( s )
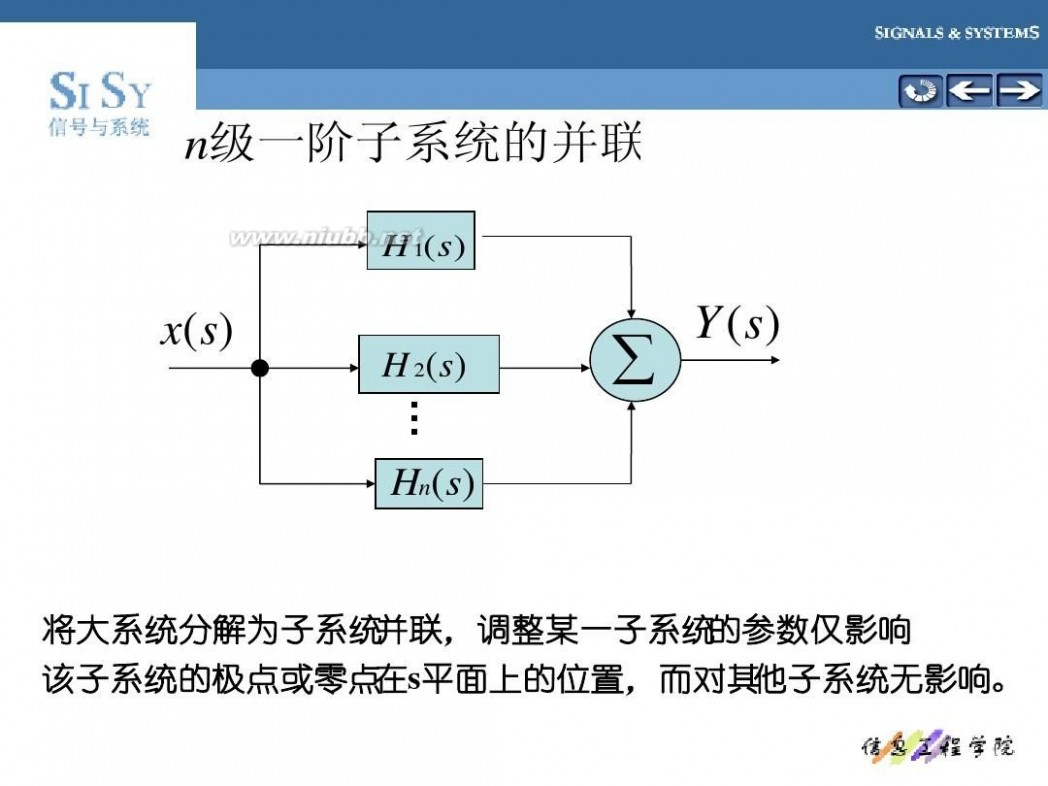
n级一阶子系统的并联
H 1( s )
x(s )
H 2( s )
∑
Y (s )
Hn (s )
并联, 将大系统分解为子系统 并联,调整某一子系统 的参数仅影响 平面上的位置, 他子系统无影响。 该子系统的极点或零点 在s平面上的位置,而对其 他子系统无影响。
…
6、级联模拟框图
H(s ) = H1(s )H 2(s)...Hr(s)
X( s)
H 1(s ) (s
H 2( s )
...
Hr (s )
Y( s)
r级一阶或二阶子系统级联
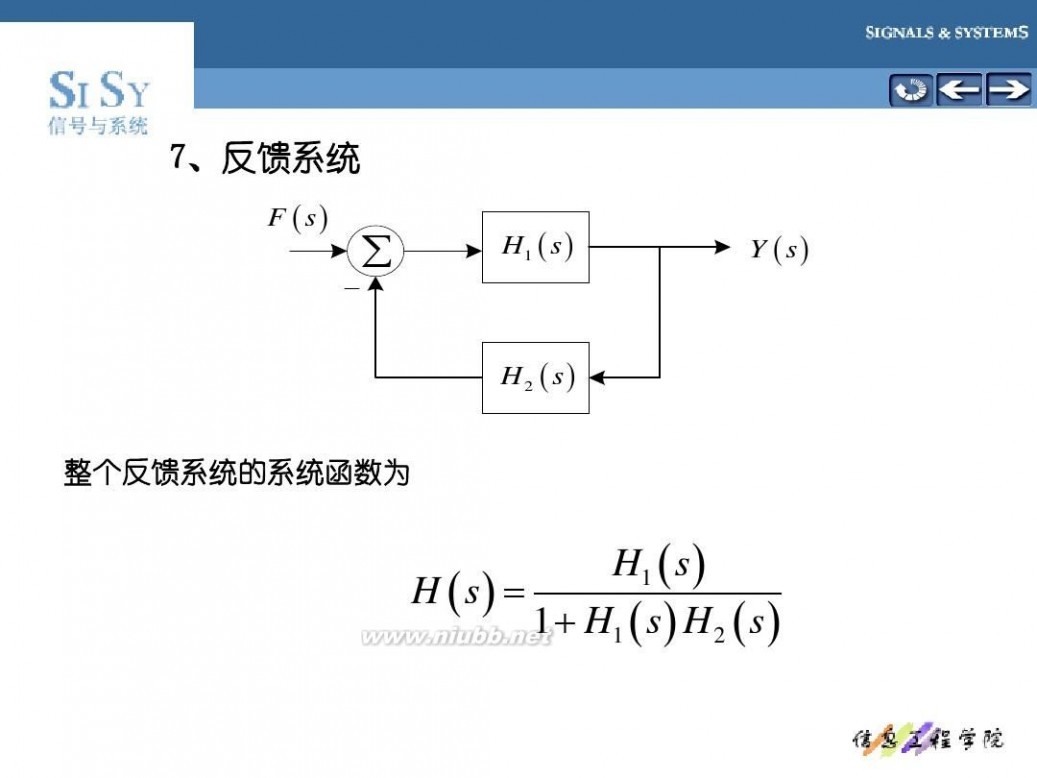
7、反馈系统
F (s)
∑
H1 ( s )
Y (s)
H2 ( s)
整个反馈系统的系统函数为
H1 ( s ) H (s) = 1 + H1 ( s ) H 2 ( s )
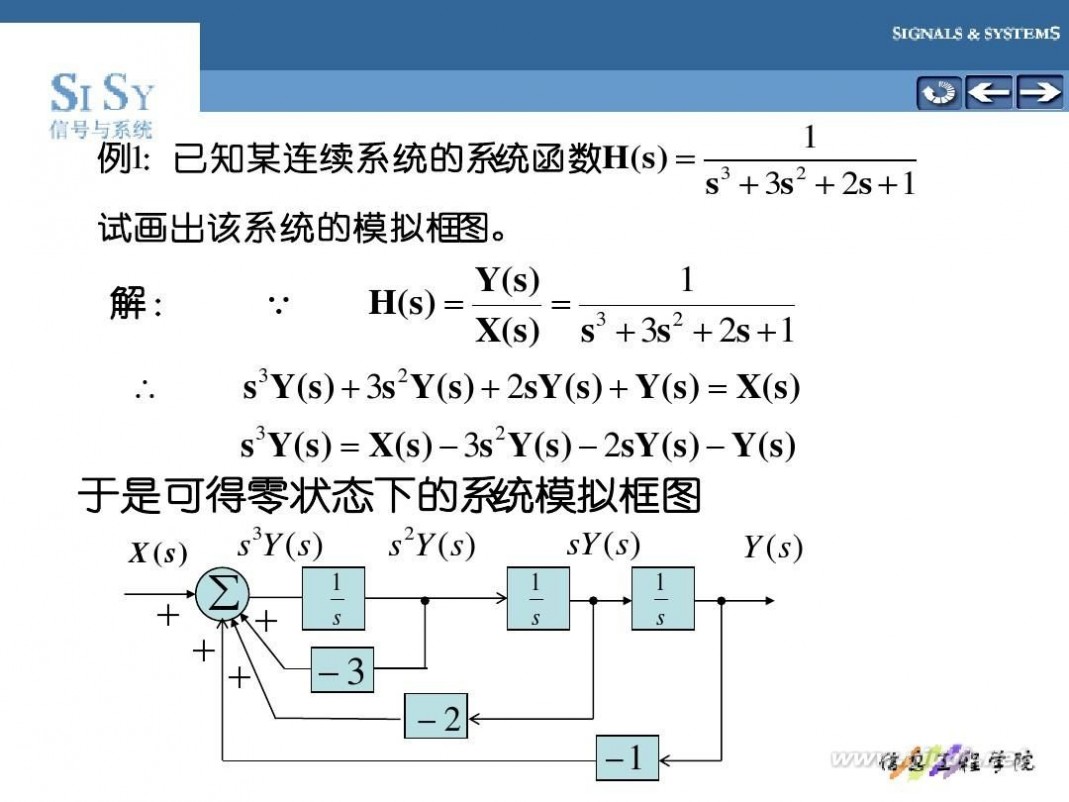
1 例1 已知某连续系统的系 统函数 H (s ) = 3 : s + 3s 2 + 2s + 1 试画出该系统的模拟框 图。
解:
∵
H (s ) =
Y (s ) 1 = 3 X(s ) s + 3s 2 + 2s + 1
∴
s 3Y(s) + 3s 2 Y(s) + 2sY(s) + Y(s) = X(s) s3Y(s) = X(s) 3s 2 Y(s) 2sY(s) Y(s)
于是可得零状态下的系 统模拟框图
X (s )
s 3Y ( s )
s 2Y ( s )
1 s 1 s
sY (s )
1 s
∑ + +
+ +
Y (s )
3
2
1
4.9
引 言
系统的稳定性
1、为什么要研究? 为什么要研究? 在系统的分析研究中,最重要的问题是系统的稳定性问题。 在系统的分析研究中,最重要的问题是系统的稳定性问题。 不稳定的系统在受到外
界或内部的一些因素扰动时, 不稳定的系统在受到外界或内部的一些因素扰动时,会使被控 制量偏离原来的平衡工作状态,并随时间的推移而发散。因此, 制量偏离原来的平衡工作状态,并随时间的推移而发散。因此, 不稳定的系统是无法正常工作的。在这一节中将讨论稳定性的 不稳定的系统是无法正常工作的。 定义,稳定的充要条件及判别稳定性的基本方法。 定义,稳定的充要条件及判别稳定性的基本方法。
引 言
例1:飞机-自动驾驶仪 飞机飞机自动驾驶仪是一种能保持或改变飞机飞行状态的自动装置。它可 飞机自动驾驶仪 以稳定飞行的姿态、高度和航迹;可以操纵飞机爬高、下滑和转弯。飞机 与自动驾驶仪组成的自动控制系统称为飞机-自动驾驶仪系统。
升 降 舵 面
稳定飞机俯仰角的原理图
2、如何研究? 如何研究?
稳定性是系统在扰动消失后,自身具有的一种恢复能力, 稳定性是系统在扰动消失后,自身具有的一种恢复能力,它是系统的一 种固有特性,这种特性只取决于系统的结构和参数,与外作用无关。 种固有特性,这种特性只取决于系统的结构和参数,与外作用无关。 由4.6 节系统函数的零、极点分布与系统的时域和频域特性的学习, 节系统函数的零、极点分布与系统的时域和频域特性的学习, 我们知道h(t)或H(S)集中表征了系统的本性,当然,它们也反映了系统是 (t)或H(S)集中表征了系统的本性,当然, 集中表征了系统的本性 否稳定。 否稳定。
由 H (s )
4 .6节 确定系统的时域和频率 4 .9节 确定系统的稳定性
特性
系统分析理论的主要内 容
3、研究步骤
给出系统稳定的定义; 1)给出系统稳定的定义; 讨论系统稳定的充要条件; 2)讨论系统稳定的充要条件; H(s)判断系统稳定的方法 判断系统稳定的方法。 3)由H(s)判断系统稳定的方法。
一、系统稳定的定义(BIBO) 系统稳定的定义( )
在线性系统中
e(t )
r (t )
h(t )
对任意的有界输入( 对任意的有界输入(Bounded input) ,即 )
e (t ) ≤ M e
也是有界输出( ),即满足 其零状态响应r(t)也是有界输出(Bounded output ),即满足
r (t ) ≤ M r
则称该系统是有界输入有界输出(BIBO)稳定的系统,简称稳定系统。 则称该系统是有界输入有界输出(BIBO)稳定的系统,简称稳定系统。式中
M e , M r 为有界正值。 为有界正值。
按此定义来判断系统稳定性将过于繁琐, 按此定义来判断系统稳定性将过于繁琐,为此导出稳定系统的充分必要条件
4.9
系统的稳定性
二、系统稳定的充要条件
一个线性系统稳定的充要条件是单位冲激响应绝对可积, 一个线性系统稳定
的充要条件是单位冲激响应绝对可积, 即
∫
∞
∞
h(t ) d t ≤ M
+∞
∞
M 为有界正值。 为有界正值。
证明 (1)充分性 要证∫ _
h ( t ) dt ≤ M
∞
则系统稳定。 则系统稳定。
系统的零状态响应为: 对任意有界输入e(t),系统的零状态响应为:
r (t ) = ∫ h(τ )e (t τ )dτ
∞
代入 e (t ) ≤ M e , 得
∞
r (t ) ≤ ∫
∞
∞
∞
h(τ ) e (t τ ) dτ
r (t ) ≤ M e ∫
∞
h(τ )dτ
充分性得证
如果满足 ∫
∞
h(t )dt ≤ M , 则
r (t ) ≤ M e M
要证系统稳定, (2)必要性 要证系统稳定,则 利用反证法来证明 假设系统稳定, h(t)不是绝对可积的 不是绝对可积的, 假设系统稳定,但它的冲激响应 h(t)不是绝对可积的,即
那么总可以找到一个有界的输入e(t)引起无界的输出r(t),例如
1 e ( t ) = sgn[h(t )] = 0 1
h(t ) < 0
h(t ) = 0 h(t ) > 0
这表明 e ( t )h(t ) = h(t ) , 则响应 r (t )
∞
r (t ) =
∞
此式表明: 此式表明:若∫
∞
∞
h(t ) d t无界,则 r (0 )也无界 无界,
r (0) = ∫ h(τ )e ( τ )dτ = ∫
因而假设不成立, 因而假设不成立,必要性得证
∫
∞
∞
h(τ )e (t τ )dτ
∞ ∞
h(τ )dτ
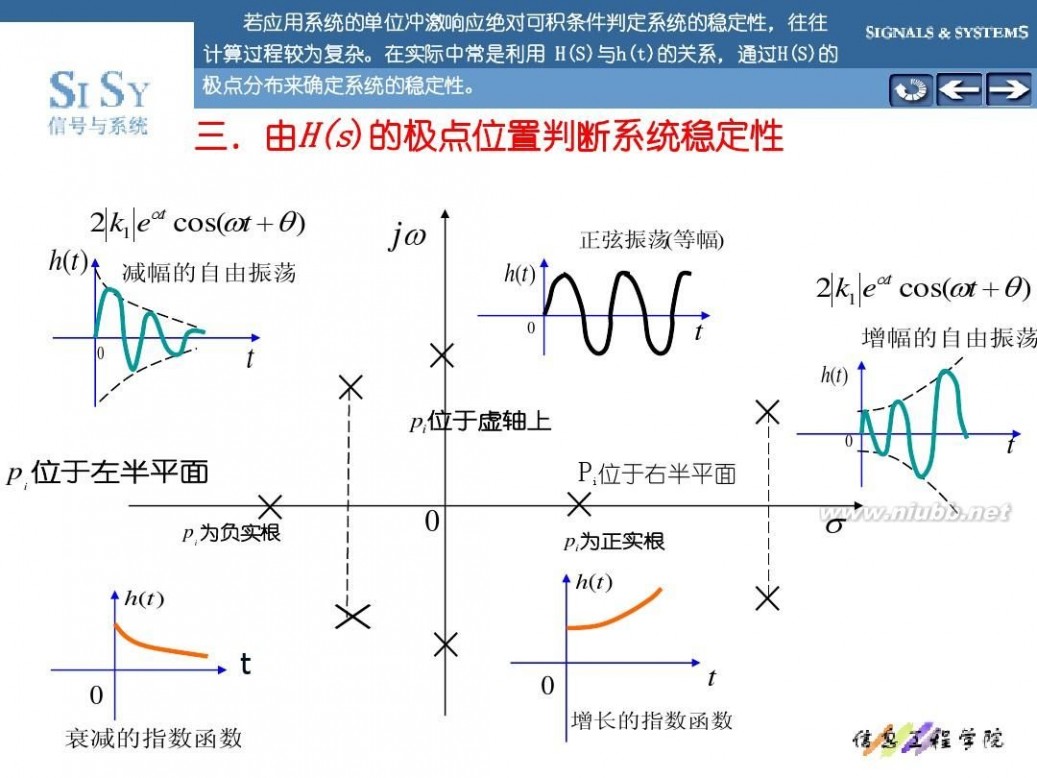
若应用系统的单位冲激响应绝对可积条件判定系统的稳定性, 若应用系统的单位冲激响应绝对可积条件判定系统的稳定性,往往 计算过程较为复杂。 H(S)与h(t)的关系 通过H(S) 的关系, H(S)的 计算过程较为复杂。在实际中常是利用 H(S)与h(t)的关系,通过H(S)的 极点分布来确定系统的稳定性。 极点分布来确定系统的稳定性。
三.由H(s)的极点位置判断系统稳定性
2 k1 e αt cos( ω t + θ )
h(t)
0
jω
h(t)
正弦振荡 (等幅 )
减幅的自由振荡
2 k1 e αt cos( ω t + θ )
t
增幅的自由振荡
t
×
×
0
0
p i 位于虚轴上
× ×
Pi位于右半平面
p i 为正实根
h(t)
0
p i 位于左半平面
t
p i 为负实根
× ×
σ
h (t )
h (t )
t
0
衰减的指数函数
×
0
×
t
增长的指数函数
因为绝对可积条件也等价于: 因为绝对可积条件也等价于:
lim h(t ) = 0
t →∞
这相当特征方程的根有负实部或位于左半平面。 这相当特征方程的根有负实部或位于左半平面。 根据H(S)极点分布,一个系统可划分为稳定,临界稳定和不稳定三种情况。 极点分布,一个系统可划分为稳定,临界稳定和不稳定三种情况。 根据 极点分布
则系统是稳定的; 1、稳定系统:若H(S)的全部极点位于s的左半平面,lim h( t ) = 0 则系统是稳定的; 稳定系统: H(S)的全部极点位于s的左半平面, 的全部极点位于
t →∞
2、临界稳定系统:若H(S)在原点处或虚轴上有单阶极点,其余极点全在s的左半面, 临界稳定系统: H(S)在原点处或虚轴上有单阶极点,其余极点全在s的左半面,
在原点处或虚轴上有单阶极点 则系统是临界稳定的; lim h( t ) = M (非零的数值或等幅振荡 ) ,则系统是临界稳定的;
t →∞
3、不稳定:若H(S)只要有一个极点位于s的右半平面,或在虚轴上和原点处有二阶 不稳定: H(S)只要有一个极点位于s的右半平面, 只要有一个极点位于 或二阶以上的重极点, 或二阶以上的重极点, lim h( t ) = ∞
t →∞
,则系统是不稳定的。 则系统是不稳定的。
然而对于三阶以上的高阶系统,求解系统的全部极点较繁琐。 然而对于三阶以上的高阶系统,求解系统的全部极点较繁琐。而实际 判断系统稳定性,并不需要知道极点的确切位置, 上,判断系统稳定性,并不需要知道极点的确切位置,而只要了解它是否 在左半s平面上。 在左半s平面上。
四、Routh — Hurwitz (罗斯 — 霍维茨 )判据
1877年 Routh提出一种判别代数方程 根的方法,不必解方程 就可知道 根的方法, 实部的根和零实部根, 1895 导出类似方法。 它包含有多少个具有正 实部的根和零实部根, 年 Hurwitz 导出类似方法。
系统稳定时, 1、系统稳定时,特征方程系数特点
无缺项; 符号相同; ①多项式的全部系数 a i 符号相同; ②无缺项;
证明
设系统的特征方程为 D ( s ) = a n s n + a n -1s n -1 + ... + a 1s
+
a0 = 0
(1)
式中 1,2,….n .n) 个根可以是实数也可以是复数, 若该方程的特征根为pi(1,2, .n),该n个根可以是实数也可以是复数,则 1)可改写成为 式(1)可改写成为
将上式展开
由此可见, 都具有负实部,则式( 由此可见,如果特征方程的根p1,p2, …pn,都具有负实部,则式(1)的 必然都大于零。 所有系数a1,a2…an必然都大于零。 必要条件是其特征方程的各项系数均为正 故系统稳定的必要条件是其特征方程的各项系数均为正, 故系统稳定的必要条件是其特征方程的各项系数均为正,即 ai>0(i=0,1,2…n) 例如特征方程
2s 3 + s 2 + s + 6 = 0
1 7 = ±j , 2 2
多项式系数全部大于零,符合上述条件,但此方程的三个根为: 多项式系数全部大于零,符合上述条件,但此方程的三个根为:
3 s1 =- , 2
s 2,3
根据必要条件,在判别系统的稳定性时,可事先检查系统特征方程的系数是否都大于零, 根据必要条件,在判别系统的稳定性时,可事先检查系统特征方程的系数是否都大于零,若 有任何系数是负数或等于零,则系统是不稳定的。但是,当特征方程满足稳定的必要条件时, 有任何系数是负数或等于零,则系统是不稳定的。但是,当特征方程满足稳定的必要条件时, 并不意味着系统一定是稳定的,为了进一步确定系统的稳定性,可以使用罗斯 罗斯- 并不意味着系统一
定是稳定的,为了进一步确定系统的稳定性,可以使用罗斯-霍维茨判据
罗斯-霍维茨判据(系统稳定的充分条件) 2、罗斯-霍维茨判据(系统稳定的充分条件)
罗斯-霍维茨判据利用特征方程的各项系数进行代数运算, 罗斯-霍维茨判据利用特征方程的各项系数进行代数运算,得出全部特征根 具有负实部的条件,以此作为判别系统是否稳定的依据, 具有负实部的条件,以此作为判别系统是否稳定的依据,
应用罗斯-霍维茨判据分析系统的稳定性时,可按下述方法进行。 应用罗斯-霍维茨判据分析系统的稳定性时,可按下述方法进行。 将系统的特征方程写成如下标准形式
D(s ) = a n s n + a n -1s n-1 + ... + a1s
将方程各项系数组成罗斯- 将方程各项系数组成罗斯-霍维茨阵列 构筑罗斯-霍维茨阵列的步骤如下: 构筑罗斯-霍维茨阵列的步骤如下: 罗斯 的步骤如下
+
a0 = 0
罗斯 — 霍维茨判别法
第一步 把 D (s ) 的所有系数按如下顺序排成两行
an an 1
an 2 an 4 an 6 an 3 an 5 an 7
Bn B n 1 Bn2 B n3 B2 0 0 Cn C n 1 C
n2
依次类推, 依次类推,排到 a 0 为止
第二步:排列R—H 阵列 第二步:排列
An
A n 1 An 2 An 3
Dn D n 1
C n3 0 0 0
An = an , An 1 = an 1 , Bn = an 2 , Bn 1 = an 3 , C n = an 4 ,
A2 A1 A0
An A n 1 An2 An3
Bn B n 1 B n2 B n3 B2 0 0
C C C C 0 0 0
n n 1 n2 n3
D D
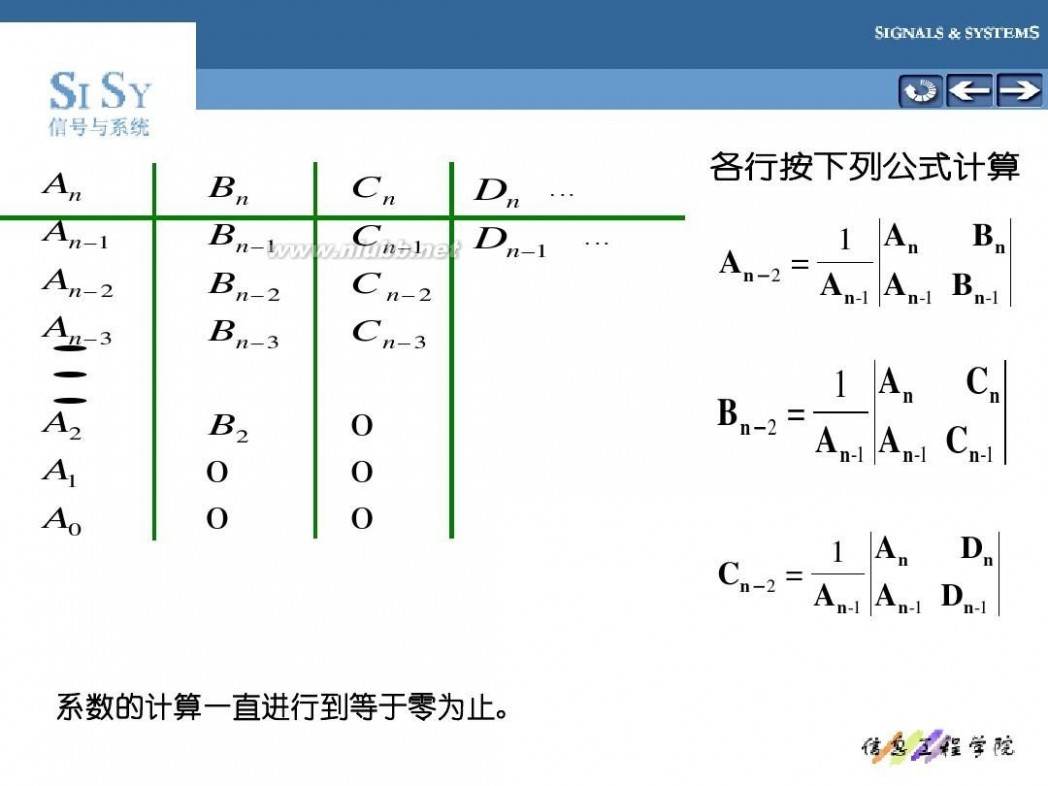
各行按下列公式计算
n n 1
A n-2
Bn 1 An = A n -1 A n -1 B n -1
A2 A1 A0
1 An Cn Bn-2 = An-1 An-1 Cn-1
Dn 1 An = A n-1 A n-1 Dn -1
Cn-2
系数的计算一直进行到等于零为止。 系数的计算一直进行到等于零为止。
用同样的前两行系数交叉相乘的方法,可以计算以下各行的系数: 用同样的前两行系数交叉相乘的方法,可以计算以下各行的系数:
A n-3
1 A n-1 B n-1 1 A n -1 Cn -1 B n-3 = = A n-2 A n-2 B n -2 A n - 2 A n - 2 Cn - 2
这个计算过程一直进行到n+1行为止。 这个计算过程一直进行到n+1行为止。 n+1行为止
罗斯- 罗斯-霍维茨判据
罗斯-霍维茨阵列中第一列数的符号相同,则系统是稳定的, 罗斯-霍维茨阵列中第一列数的符号相同,则系统是稳定的, 否则系统是不稳定的。若第一列数的符号不全相同, 否则系统是不稳定的。若第一列数的符号不全相同,则符号改变的 次数就是D(S)=0所具有的正实部根的个数。 D(S)=0所具有的正实部根的个数 次数就是D(S)=0所具有的正实部根的个数。
举
例
罗斯- (1)罗斯-霍维茨阵列第一列所有系数均不为零的情况
3 2 例1: 试判别特征方程 2 s + s + s + 6 = 0
的系统是否稳定。 的系统是否稳定。
罗斯- 解:罗斯-霍维茨阵列
A3 A2 A1 A0
2 1
1 6
2 1 11 6
1 6 0 0
∵
有符号变化
∴ 系统不
稳定
例2: S 3 + 5 S 2 + 4 S + k = 0
1 5 20 k 5 k
,K为何值时系统稳定。 为何值时系统稳定。
4 k 0 0
20 k k 5 = k 20 k 5
20 k >0 系统稳定条件为 5 k >0
故 0 < k < 20
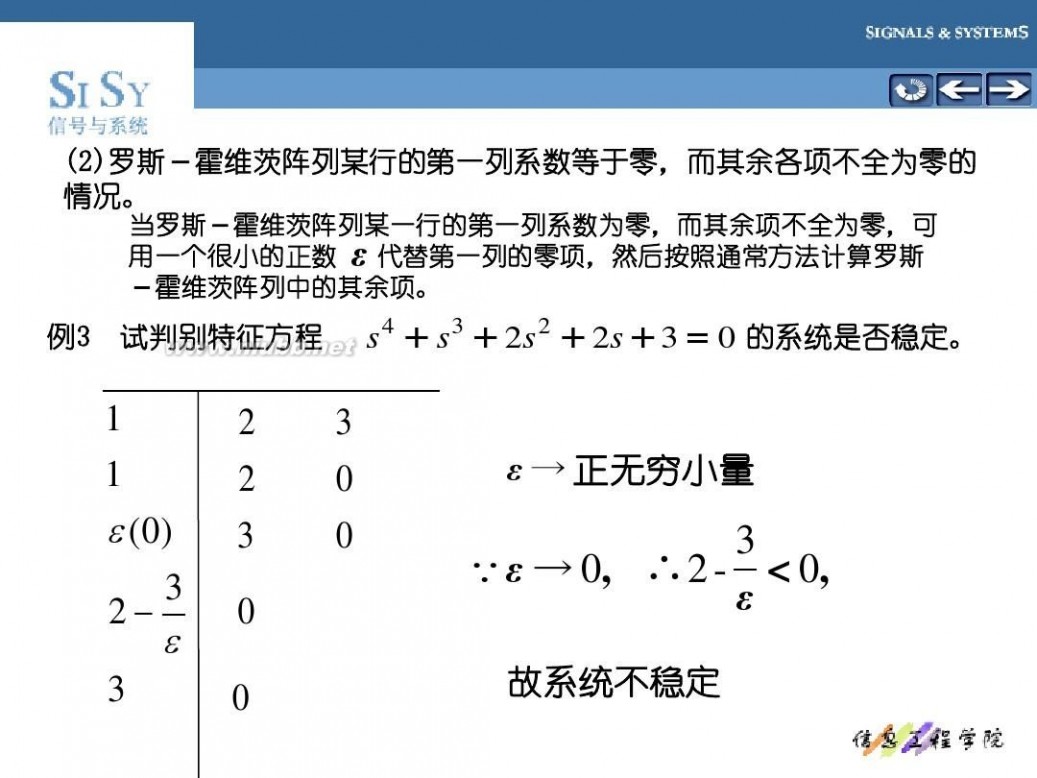
(2)罗斯-霍维茨阵列某行的第一列系数等于零, (2)罗斯-霍维茨阵列某行的第一列系数等于零,而其余各项不全为零的 罗斯 情况。 情况。
当罗斯-霍维茨阵列某一行的第一列系数为零,而其余项不全为零, 当罗斯-霍维茨阵列某一行的第一列系数为零,而其余项不全为零,可 代替第一列的零项, 用一个很小的正数 ε 代替第一列的零项,然后按照通常方法计算罗斯 霍维茨阵列中的其余项。 -霍维茨阵列中的其余项。
例3 试判别特征方程
的系统是否稳定。 s 4 + s 3 + 2 s 2 + 2 s + 3 = 0 的系统是否稳定。
1 1
2 2 3
0 0
3 0 0
ε → 正无穷小量
ε ( 0)
2 3 3
3 ∵ ε → 0, ∴ 2 - < 0, ε
故系统不稳定
ε
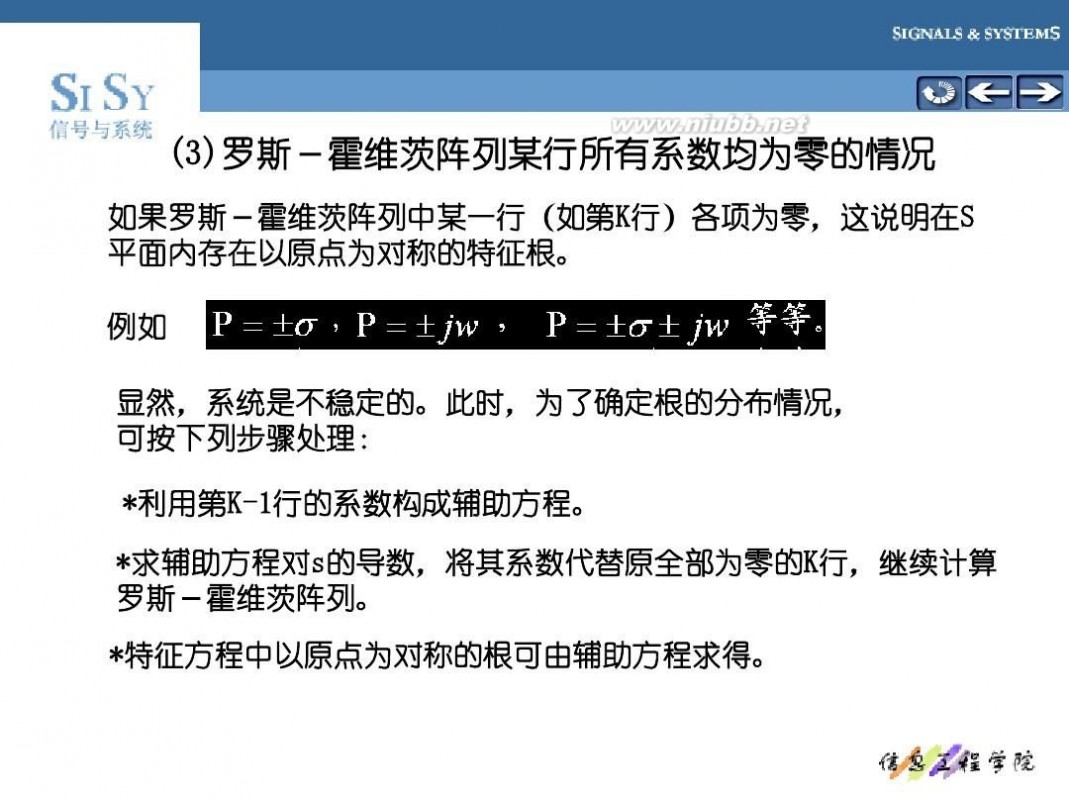
(3)罗斯-霍维茨阵列某行所有系数均为零的情况 (3)罗斯-霍维茨阵列某行所有系数均为零的情况 罗斯
如果罗斯-霍维茨阵列中某一行(如第K行)各项为零,这说明在S 如果罗斯-霍维茨阵列中某一行(如第K 各项为零,这说明在S 平面内存在以原点为对称的特征根。 平面内存在以原点为对称的特征根。 例如 显然,系统是不稳定的。此时,为了确定根的分布情况, 显然,系统是不稳定的。此时,为了确定根的分布情况, 可按下列步骤处理: 可按下列步骤处理: *利用第K-1行的系数构成辅助方程。 利用第K 行的系数构成辅助方程。 *求辅助方程对s的导数,将其系数代替原全部为零的K行,继续计算 求辅助方程对s的导数,将其系数代替原全部为零的K 罗斯-霍维茨阵列。 罗斯-霍维茨阵列。 *特征方程中以原点为对称的根可由辅助方程求得。 特征方程中以原点为对称的根可由辅助方程求得。
例4
已知系统的特征方程为
分析系统的稳定性。
解: 由特征方程列罗斯- 由特征方程列罗斯-霍维茨阵列
由上表看出, 行的各项全为零,为了求出s s 各行, 由上表看出,s3行的各项全为零,为了求出s3—s0各行,由s4行的各项 系数构成辅助方程
将辅助方程对s 将辅助方程对s求导得
用上式各项系数作为s 行的各系数继续计算罗斯- 用上式各项系数作为s3行的各系数继续计算罗斯-霍维茨阵列得
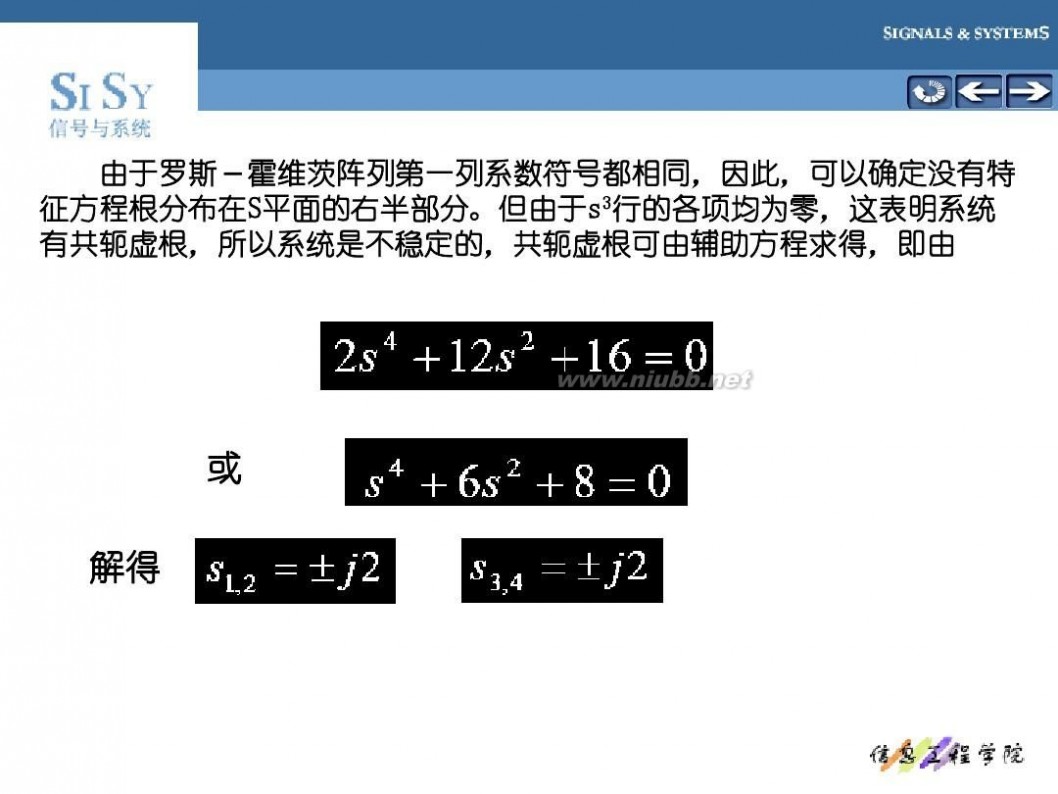
由于罗斯-霍维茨阵列第一列系数符号都相同,因此, 由于罗斯-霍维茨阵列第一列系数符号都相同,因此,可以确定没有特 征方程根分布在S平面的右半部分。但由于s 行的各项均为零, 征方程根分布在S平面的右半部分。但由于s3行的各项均为零,这表明系统 有共轭虚根,所以系统是不稳定的,共轭虚根
可由辅助方程求得, 有共轭虚根,所以系统是不稳定的,共轭虚根可由辅助方程求得,即由
或 解得
综上所述,应用罗斯-霍维茨判据分析系统的稳定性时, 综上所述,应用罗斯-霍维茨判据分析系统的稳定性时, 罗斯 判据分析系统的稳定性时 一般可以按如下顺序进行: 一般可以按如下顺序进行: 1、确定系统是否满足稳定的必要条件。当特征方程的系数 确定系统是否满足稳定的必要条件。 >0不满足(i=0,1,2,……n)时,系统是不稳定的。 不满足(i=0,1,2, n)时 系统是不稳定的。 ai>0不满足(i=0,1,2, n) 2、当特征方程的系数满足ai>0(i=0,1,2, n)时 当特征方程的系数满足a >0(i=0,1,2,……n)时,计算罗 n) 霍维茨阵列。 罗斯-霍维茨阵列的第一列系数都大于 斯-霍维茨阵列。当罗斯-霍维茨阵列的第一列系数都大于 零时,系统是稳定的。如果第一列出现小于零的系数, 零时,系统是稳定的。如果第一列出现小于零的系数,则系 统是不稳定的。 统是不稳定的。 3、若计算罗斯-霍维茨阵列时出现情况(2)和(3),此 若计算罗斯-霍维茨阵列时出现情况( 罗斯 时出现情况 ),此 时为确定系数极点的分布情况,可按情况( 时为确定系数极点的分布情况,可按情况(2)和(3)的方 法处理。 法处理。
在系统的分析中,罗斯- 在系统的分析中,罗斯-霍维茨判据可以根据系统特征方 程的系数来确定系统的稳定性, 程的系数来确定系统的稳定性,同时还能给出系统的某些参数 的取值范围。但是,它的应用也具有一定的局限性, 的取值范围。但是,它的应用也具有一定的局限性,通常它只 能提供系统绝对稳定性的结论, 能提供系统绝对稳定性的结论,而不能指出系统是否具有满意 的动态过程。此外,当系统不稳定时, 的动态过程。此外,当系统不稳定时,它不能提供改善系统稳 定性的方法和途径。 定性的方法和途径。 分析系统稳定性的其它方法如奈氏判据、根轨迹图分析法、 分析系统稳定性的其它方法如奈氏判据、根轨迹图分析法、 伯德图分析法等, 伯德图分析法等,将在以后自动控制理论的各章中分别予以介 绍。
综合举例
下图所示为一反馈网络, 例1、下图所示为一反馈网络,已知子系统 H 1 ( s ) 的单位冲激响应
h1 (t ) = ( 2e 2 t e t ) ε(t )。
为使系统稳定,实系数K应满足什么条件? (1)为使系统稳定,实系数K应满足什么条件? 在边界稳定的条件下, (2)在边界稳定的条件下,求整个系统的单位冲激响应 h (t ) 。
E (s)
∑
H 1 ( s)
R( s)
K
:(1 解:(1)
H (s) =
s s2 + (3 k ) s + 2
要使系统稳定则 k < 3
h ( t ) = co s 2 tε (t )
(2)当K=3
时,系统处于临界稳定
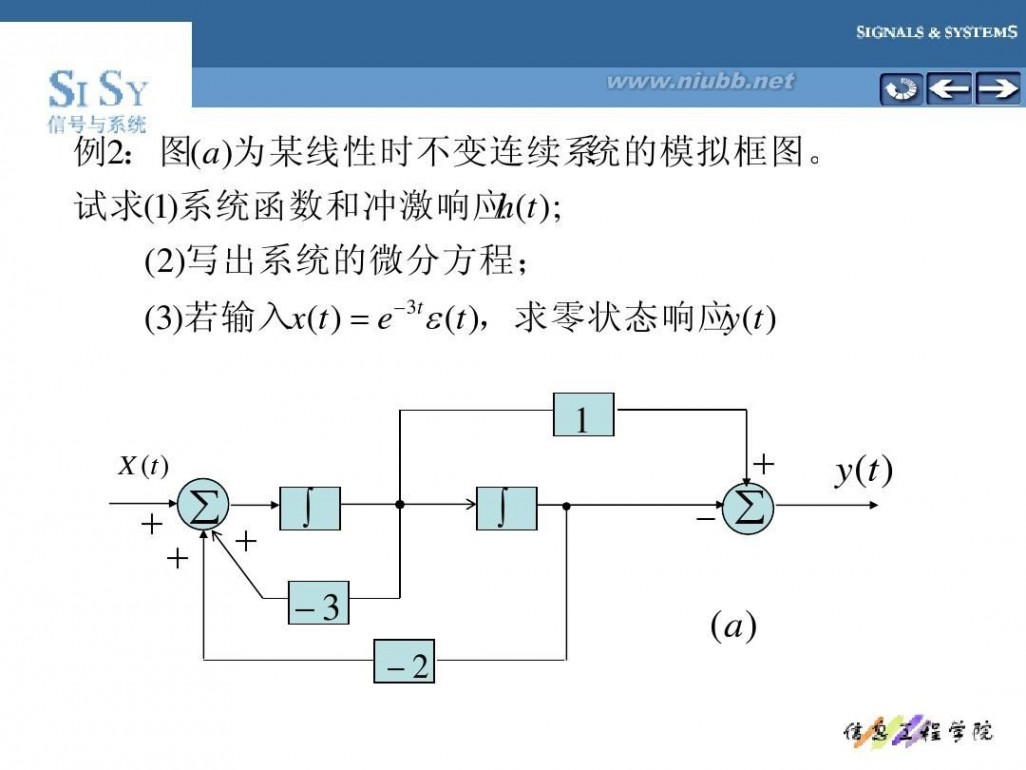
例2:图( a )为某线性时不变连续系 统的模拟框图。 试求(1)系统函数和冲激响应 h(t ); (2)写出系统的微分方程; (3)若输入x(t ) = e 3t ε (t ),求零状态响应 y (t )
1
X (t )
+ ∑+ +
∫
3
2
∫
∑
+
y (t )
(a )
(1 假设零状态, 所示。 解: )假设零状态,画 s域模拟框图如图 (b )所示。设 (b )图左边 中所标。 输入端加法器的输出为 q(s ),各积分器的输出如图 中所标。
X (s )
q (s )
1 s
s 1q ( s )
1 s
1
s 2 q ( s )
+ ∑+ +
∑
+ y (s )
3
2
(b)
由(b)可知 q ( s ) = X ( s ) 3s 1q ( s ) 2 s 2 q ( s ) 1 由上式解得q ( s ) = X ( s) 1 2 1 + 3s + 2 s (1)
输出端的加法器输出为 Y ( s ) = s 1q ( s ) s 2 q ( s ) = ( s 1 s 2 )q ( s ) s 1 s 2 X ( s) 将(1)式代入上式,得 Y ( s ) = 1 2 1 + 3s + 2 s
Y(s ) s 1 s 2 s 1 2 3 ∴ H(s ) = = = 2 = + 1 2 X(s ) 1 + 3s + 2s s + 3s + 2 s + 1 s + 2
故h(t ) = L1[H(s )] = (3e 2t 2e t )ε(t )
( 2)由H(s )得(s 2 + 3s + 2)Y(s ) = sX(s ) X(s )
∴ 系统的微分方程为 y′′(t ) + 3y′(t ) + 2y(t ) = x′(t ) x(t )
(3) X(s ) = L[x(t )] =
1 s+3
s 1 1 3 2 1 Y ( s ) = H ( s ) X( s ) = × = + + (s + 1)(s + 2) s + 3 s + 1 s + 2 s + 3
故系统的零状态响应 y(t ) = ( 2e 3t + 3e 2t e t )ε(t )
要求在微分方程中,输入信号的最高阶导数不超过输出信号的最高阶导数; 要求在微分方程中,输入信号的最高阶导数不超过输出信号的最高阶导数; 如果超过的话,冲激响应中将含有冲激的导数,就不绝对可积。 如果超过的话,冲激响应中将含有冲激的导数,就不绝对可积。
例3 试用BIBO准则判别下列因果系统是否稳定?为什么? 试用BIBO准则判别下列因果系统是否稳定?为什么? BIBO准则判别下列因果系统是否稳定
H ( s) = s+2 s+2 = s 2 2 s 3 ( s + 1)( s 3)
由于有右半平面的极点, 由于有右半平面的极点, 所以系统不稳定。 所以系统不稳定。
s +1 H ( s) = 2 s +4
s2 + 2 H (s) = 2 s + 2s + 3
由于在虚轴上有单极点,所以系统 由于在虚轴上有单极点, 是临界稳定。 是临界稳定。 系统函数分子分母的阶数相同, 系统函数分子分母的阶数相同,极点 都在左半平面。所以系统是稳定的。 都在左半平面。所以系统是稳定的。
s3 + 2 因为分子的阶数大于分母的阶数, 因为分子的阶数大于分母的阶数,冲激响 H (s) = 2 s + 2 s + 3 应中必含有其导数项,所以系统不稳定。 应中必含有其导数项,所以系统不稳定。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1