一 : (本小题满分8分)一货轮航行到M处,测得灯塔S在货轮的北偏东15°相距20里处,随后货轮按北偏西30

(本小题满分8分)一货轮航行到M处,测得灯塔S在货轮的北偏东15°相距20里处,随后货轮按北偏西30°的方向航行,半小时后,又测得灯塔在货轮的北偏东45°,求货轮的速度。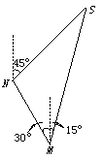 |
| 解:如图所示,∠SMN=15°+30°=45°, ∠SNM=180°-45°-30°=105°∴∠NSM=180°-45°-105°=30° 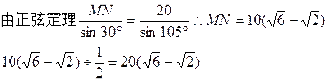 答:货轮的速度为  里/小时 里/小时 |
| 略 |
考点:
考点名称:解三角形解三角形定义:
一般地,把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。
主要方法:
正弦定理、余弦定理。
解三角形常用方法:
1.已知一边和两角解三角形:已知一边和两角(设为b、A、B),解三角形的步骤:
2.已知两边及其中一边的对角解三角形:已知三角形两边及其中一边的对角,求该三角形的其他边角时,首先必须判断是否有解,例如在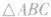 中,已知
中,已知![]()
 ,问题就无解。如果有解,是一解,还是两解。解得个数讨论见下表:
,问题就无解。如果有解,是一解,还是两解。解得个数讨论见下表:
3.已知两边及其夹角解三角形:已知两边及其夹角(设为a,b,C),解三角形的步骤:
4.已知三边解三角形:已知三边a,b,c,解三角形的步骤:
①利用余弦定理求出一个角;
②由正弦定理及A +B+C=π,求其他两角.
5.三角形形状的判定:
判断三角形的形状,应围绕三角形的边角关系进行思考,主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形、锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别,依据已知条件中的边角关系判断时,主要有如下两条途径:
①利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;
②利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数的恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B +C=π这个结论,在以上两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
6.解斜三角形应用题的一般思路:
(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如坡度、仰角、俯角、视角、象限角、方位角、方向角等;
(2)根据题意画出图形;
(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要算法简练,计算准确,最后作答,
用流程图可表示为: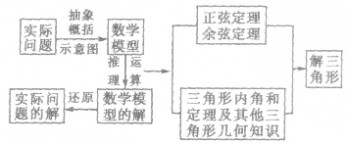
利用正弦定理、余弦定理在解决三角形的综合问题时,要注意三角形三内角的一些三角函数关系:
二 : 怕相思,已相思,轮到相思没处辞,眉间露一丝
出自明代诗人俞彦的《长相思》
折花枝,恨花枝,准拟花开人共卮,开时人去时。
怕相思,已相思,轮到相思没处辞,眉间露一丝。
赏析
这首小令从花枝写到人间的相思。上片写折花枝、恨花枝,因为花开之日,恰是人去之时,已见婉折;下片谓怕相思却已相思,且其情难言,唯露眉间,愈见缠绵。全词清新淡雅,流转自然,富有民歌风味。
三 : 如下图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30
| 如下图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟后,又测得它在货轮的东北方向,则货轮的速度为 |
 |
| [ ] |
A.20 海里/时 海里/时B.20( 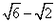 )海里/时 )海里/时C.20(  )海里/时 )海里/时D.20(  )海里/时 )海里/时 |
| B |
考点:
考点名称:正弦定理正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即 =2R。
=2R。
有以下一些变式:
(1) ;
;
(2)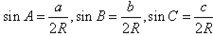 ;
;
(3) 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 
也可根据a,b的关系及 与1的大小关系来确定。
与1的大小关系来确定。
四 : 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与货轮相距20海里,随后货轮按北偏西30°的
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与货轮相距20海里,随后货轮按北偏西30°的方向航行,30分钟后又测得灯塔在货轮的东北方向,则货轮航行的速度为( )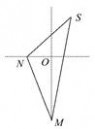
|
| B |
| 由题意知SM=20,∠SNM=105°,∠NMS=45°, ∴∠MSN=30°. 在△MNS中利用正弦定理可得,  = = , ,∴MN= 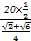 =10( =10( - -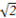 )(海里), )(海里),∴货轮航行的速度v= 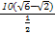 =20( =20( - -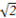 )(海里/小时). )(海里/小时). |
考点:
考点名称:正弦定理正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即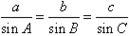 =2R。
=2R。
有以下一些变式:
(1) ;
;
(2)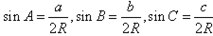 ;
;
(3) 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 
也可根据a,b的关系及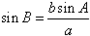 与1的大小关系来确定。
与1的大小关系来确定。
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1