一 : 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

圆锥展开图 圆锥的侧面展开图讲

二 : 圆锥展开图

圆锥的侧面展开图

教学目标

1、知识与技能：了解圆锥的侧面、底面、高、轴、母线、过轴的截面等概念，了解圆锥的侧面展开图是扇形：使学生会计算圆锥的侧面积或表面积.

教学重点：

1、圆锥的形成手段和圆锥的轴、母线、高等概念及其特征；

2、用展开图的面积公式计算圆锥的侧面积和表面积。

教学难点：对侧面积的计算和理解。

1. 圆周长：C?2?r

圆面积：S??r2

2. 圆的面积C与半径R之间存在关系C?2?R，即360°的圆心角所对的弧长，因此，1°2?R。 360

n?R n°的圆心角所对的弧长是 180

n?R ?l? 180的圆心角所对的弧长就是

*这里的180、n在弧长计算公式中表示倍分关系，没有单位。

3. 由组成圆心角的两条半径和圆心角所对的弧所围成的圆形叫做扇形。

发现：扇形面积与组成扇形的圆心角的大小有关，圆心角越大，扇形面积也就越大。

4. 在半径是R的圆中，因为360°的圆心角所对的扇形的面积就是圆面积S??R2，所以圆心角为n°的扇形面积是： n?R21?lR（n也是1°的倍数，无单位） S扇形?3602

5. 圆锥的概念

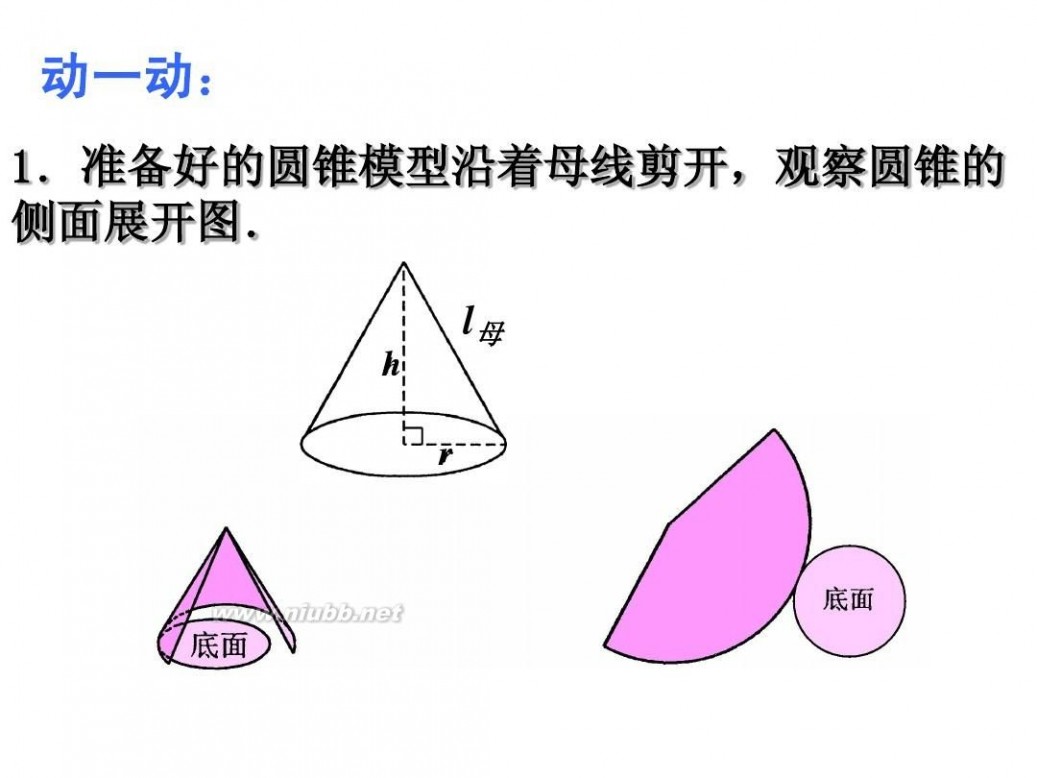
观察模型可以发现：圆锥是由一个底面和一个侧面围成的。其中底面是一个圆，侧面是一个曲面，如果把这个侧面展开在一个平面上，展开图是一个扇形。

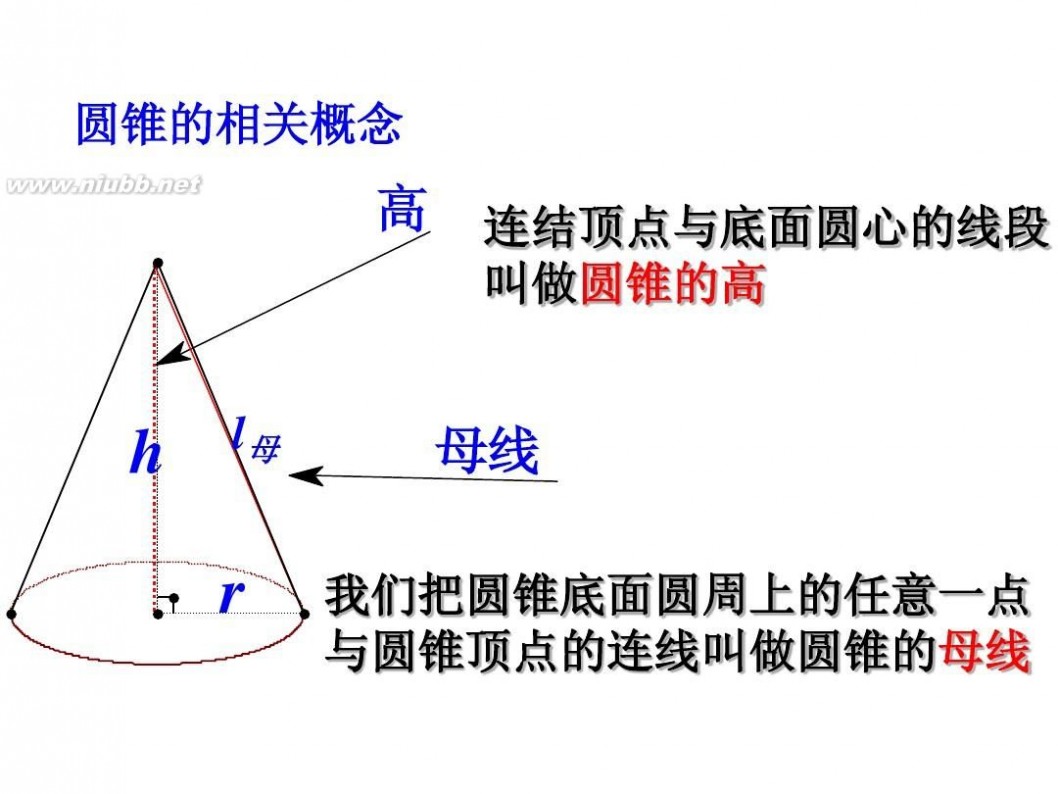
如图，从点S向底面引垂线，垂足是底面的圆心O，垂线段SO的长叫做圆锥的高，点S叫做圆锥的顶点。

锥也可以看作是由一个直角三角形旋转得到的。也就是说，把直角三角形SOA绕直线SO旋转一周得到的图形就是圆锥。其中旋转轴SO叫做圆锥的轴，圆锥的轴通过底面圆的圆心，并且垂直于底面。另外，连结圆锥的顶点和底面圆上任意一点的线段SA、SA1、SA2、

……

都叫做圆锥的母线，显然，圆锥的母线长都相等。

母线定义：连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。P122

6. 圆锥的性质

由图可得

（1）圆锥的高所在的直线是圆锥的轴，它垂直于底面，经过底面的圆心；

（2）圆锥的母线长都相等

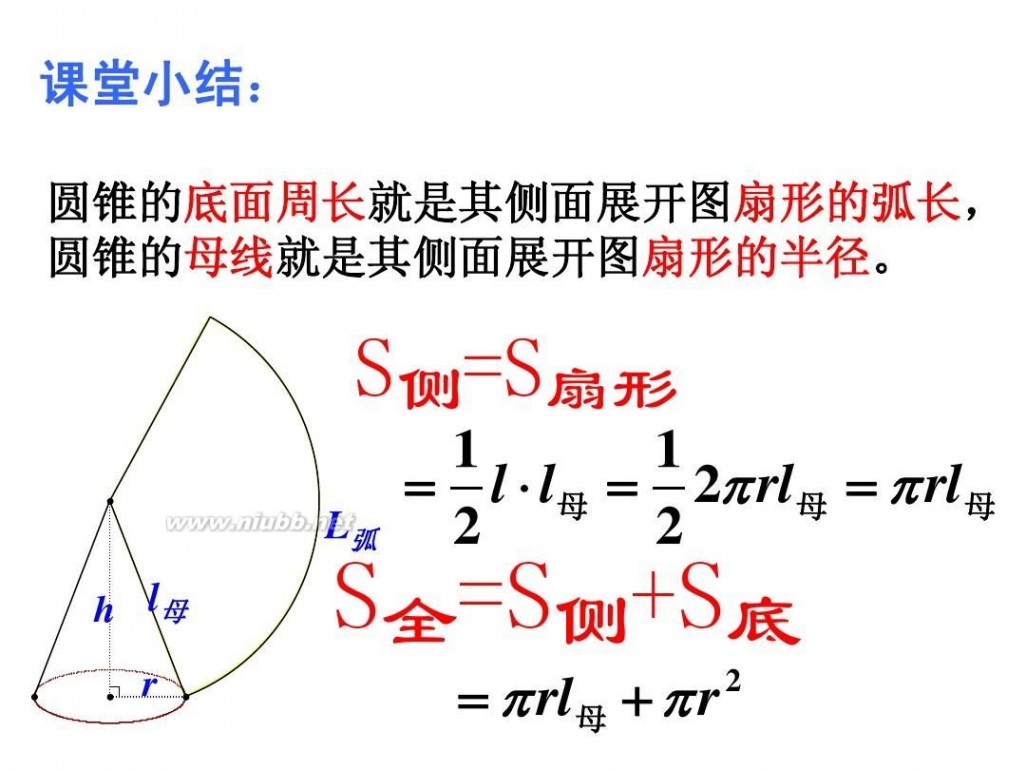
7. 圆锥的侧面展开图与侧面积计算

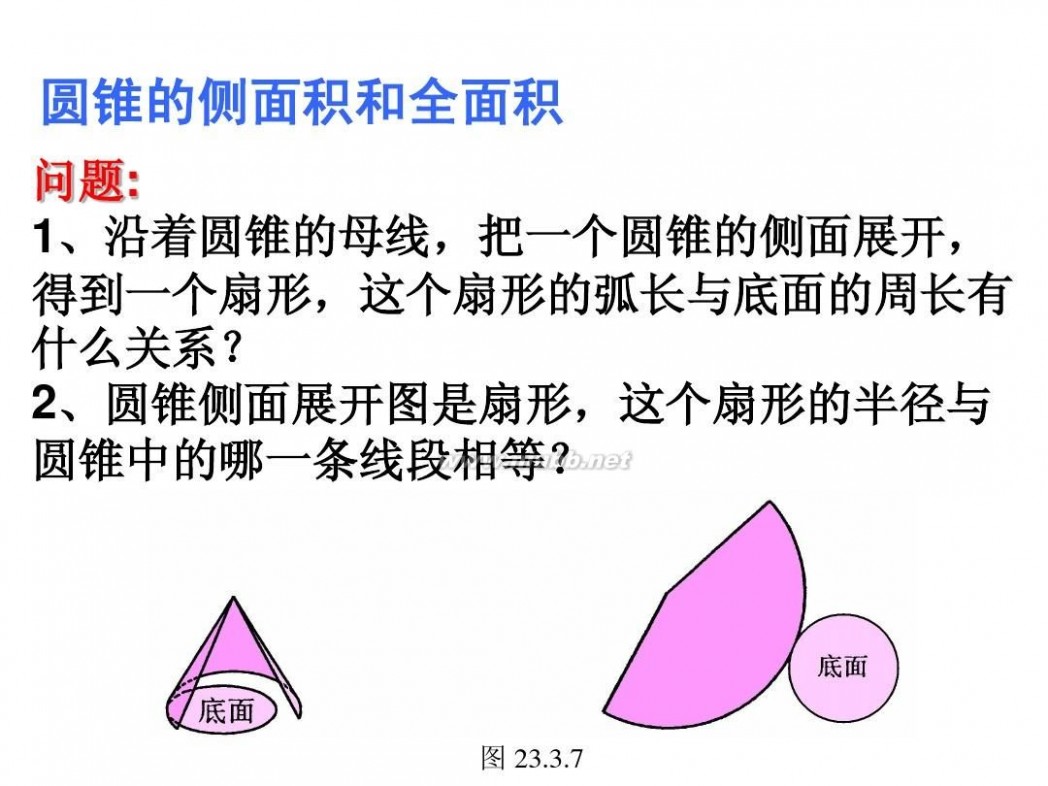
圆锥的侧面展开图是一个扇形，这个扇形的半径是圆锥侧面的母线、圆心是圆锥的顶点、弧长是圆锥底面圆的周长。

圆锥侧面积是扇形面积。

如果设扇形的半径为l，弧长为c，圆心角为n（如图），则它们之间有如下关系： c?n?l 180

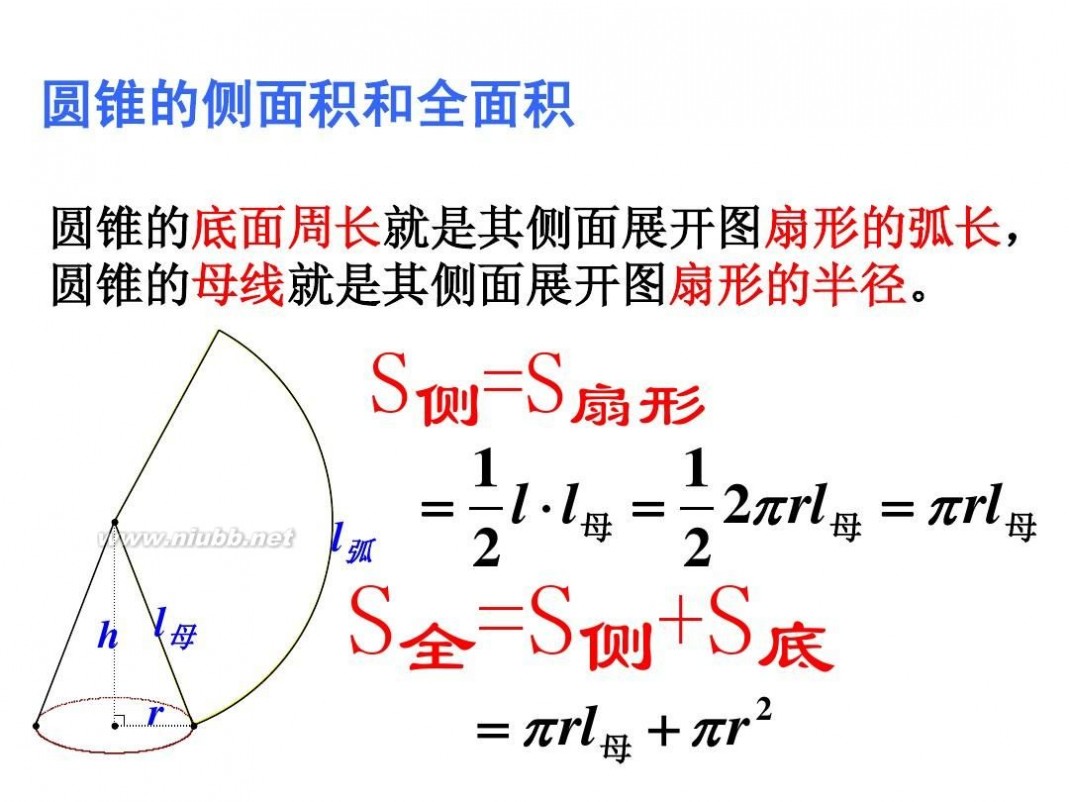
1cl??rl 2 同时，如果设圆锥底面半径为r，周长为c，侧面母线长为l，那么它的侧面积是： S圆侧面?

圆锥的全面积为：?rl??r2

圆柱侧面积：2?rh。

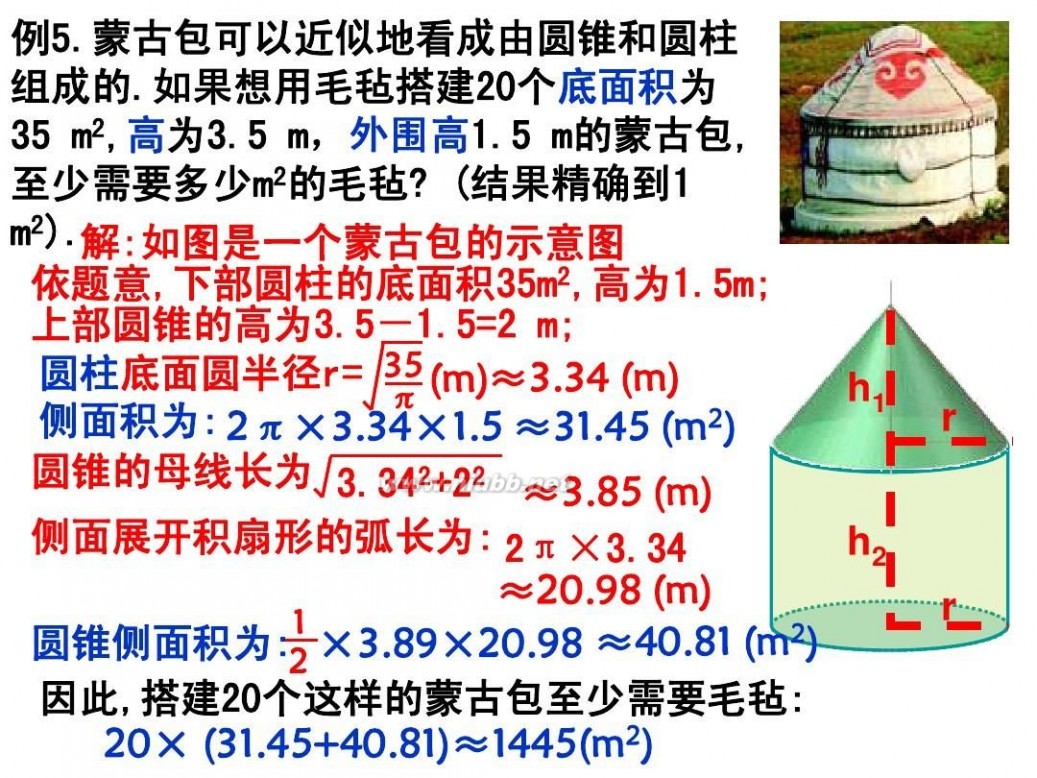
1、应用举例：

与圆锥有关的旋转体的侧面积计算

已知：Rt△ABC中，∠C=90。，AB=15cm，BC=5cm，

求： △ABC绕AC所在直线旋转一周所得到的几何体的表面积。

2、计算圆锥的侧面积

（1）.把一个用来盛爆米花的圆锥形纸杯沿母线剪开,可得一个半径为24cm,圆心角为120°的扇形.求该纸杯的底面半径和高度（结果精确到

0.1cm)

.

（2）.圆锥形的烟囱帽的底面直径是80cm, 母线长50cm. (1)画出它的展开图(2)计算这个展开图的圆心角及面积.

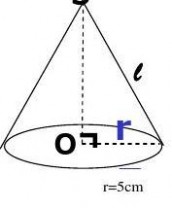
（3）.某家商店正在制作圣诞节的圆锥形纸帽.已知纸帽的母线长为15cm，底面半径为5cm,要制作10000顶这样的纸帽至少要用多少cm2的材料?

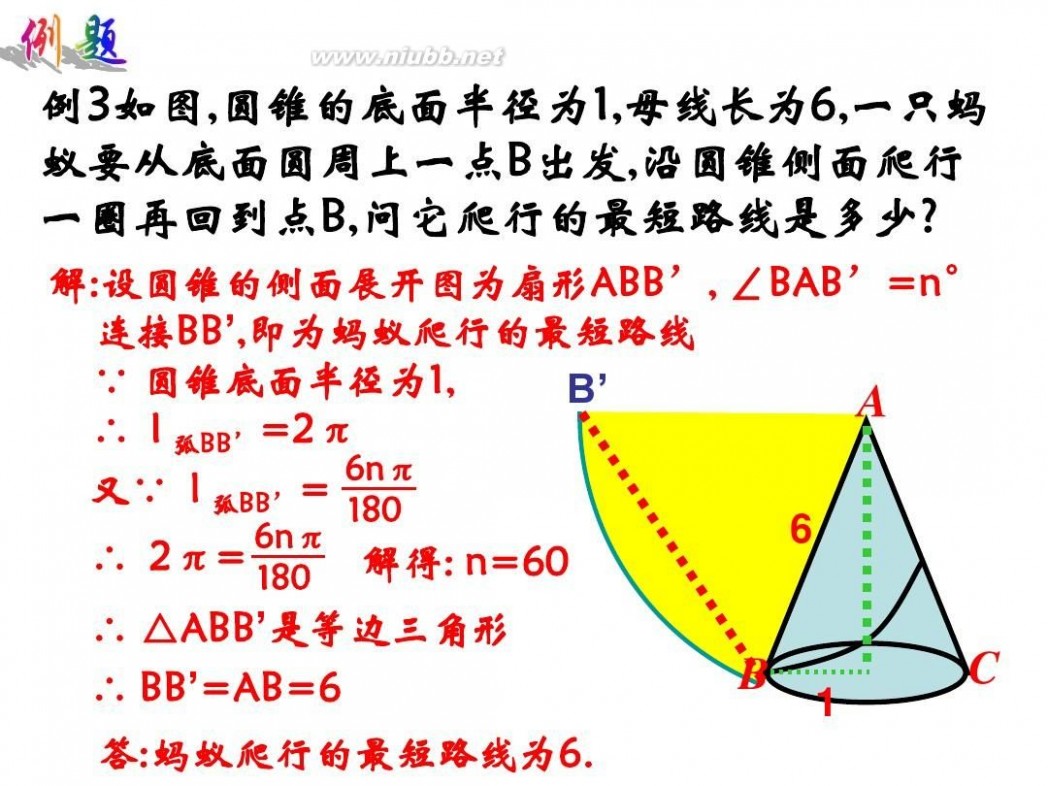
（4）、如图，圆锥的底面半径为1，母线长为6，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬行一圈再回到点B，问它爬行的最短路线是多少？

练习

一、选择题

1. 已知圆柱的底面半径为2cm，高为5cm，则圆柱的侧面积是（ ）

2222 A．20cm B．20πcm C．10πcm D．5πcm 2. 已知圆柱的底面半径为1，母线长为2，则圆柱的侧面积为（ ）

A、2 B、4 C、2π D、4π

3. 如图所示，圆柱的底面周长为6cm，AC是底面圆的直径，高BC＝ 6cm，点P是母线BC上一点且PC＝2

BC．一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距3

离是（ ）

A．（4?6

?

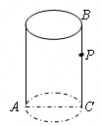
）cm B．5cm C．cm D．7cm

4. 从纸上剪下一个圆形和一个扇形的纸片（如图），用它们恰好能围成一个圆锥模型，若圆的半径为1．扇形的圆心角等于120°，则此扇形的半径为（ ）

A、

1 B、 C、3 3 D、6

5.

一个几何体的三视图如下：其中主视图和左视图都是腰长为4，

底边为

2

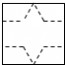
的等腰三角形，

则这个几何体侧面展开图的面积为（ ）

A、2π B、 12π C、4π D、8π

6.如图，将一张边长为3的正方形纸片按虚线裁剪后，恰好围成一个底面是正三角形的棱柱，

这个棱柱的侧面积为（ ）

A．9 B．9?3 C．9?53 D．9? 22

7. 一个圆锥的底面圆的周长是2π，母线长是3，则它的侧面展开图的圆心角等于（ ）

A、150° B、120° C、90° D、60°

8. 若一个圆锥的侧面积是10，则下列图象中表示这个圆锥母线l与底面半径r之间的函数

关系的是（ ）

A、 B、C、D、

10. 将一个圆心角是90°的扇形围成一个圆锥的侧面，则该圆锥的侧面积S侧和底面积S底的关系是（ ）

A、S侧=S底 B、S侧=2S底 C、S侧=3S底 D、S侧=4S底

11. 如图是一圆锥的主视图，则此圆锥的侧面展开图的圆心角的是（ ）

A、60° B、90° C、120° D、180°

第11题 第12题

12. 如图1，在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形，使之恰好围成图2所示的一个圆锥，则圆锥的高为（ ）

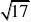
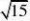
13. 一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（ ）

A．5π B．4π C．3π D．2π

14.如图，矩形ABCD中，AB=4，以点B为圆心，BA为半径画弧交BC于点E，以点O为圆心的⊙O与弧AE，边AD，DC都相切．把扇形BAE作一个圆锥的侧面，该圆锥的底面圆恰好是⊙O，则AD的长为（ ）

A.4 B.911 C. 22D.5

15. 如果圆锥的底面周长为20π，侧面展开后所得扇形的圆心角为120°，则该圆锥的全面积为（ ）

A.100π B.200π C.300π D.400π

16. 已知圆锥底面圆的半径为6厘米，高为8厘米，则圆锥的侧面积为（ ）

A．48厘米 B. 48π厘米 C. 120π厘米 D. 60π厘米

2222

A、4π B、42π C、8π D、82π

二、填空题

1. 如图，把一个半径为

12cm

的圆形硬纸片等分成三个扇形，

用其中一个扇形制作成一个圆锥形纸筒的侧面（衔接处无缝隙且不重叠），则圆锥底面半径是 cm．

2. 如图是一个几何体的三视图，这个几何体的全面积为 ．（ π取3.14）

4. 母线长为2，底面圆的半径为1的圆锥的侧面积为 ．

5.已知一个圆锥形的零件的母线长为3cm，底面半径为2cm，则这个圆锥形的零件的侧面积

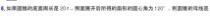
2

8.一个圆锥形的零件的母线长为4，底面半径为1，则这个圆锥形零件的全面积

是 .

9.在Rt△ABC中，∠C=90°，AC=3，BC=4，将△ABC绕边AC所在直线旋转一周得到圆锥，

则该圆锥的侧面积是 ．

10.若圆锥的侧面展开时一个弧长为l6π的扇形，则这个圆锥的底面半经是 ．

11.将一个半径为6cm，母线长为15cm的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展

开图的圆心角是 度．

212.已知一个圆锥的底面半径长为3cm、母线长为6cm，则圆锥的侧面积是 cm．

13.如图是一个圆锥形型的纸杯的侧面展开图，已知圆锥底面半径为5cm， 母线长为15cm，

2那么纸杯的侧面积为 cm．

14.若用半径为12，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆

锥底面圆的半径的长 ．

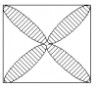
15如图，已知正方形的边长为a，求以各边为直径的半圆所围成的叶形的总面积。

三 : 圆锥的侧面展开图

圆锥的侧面展开图
────湘教版九年级数学下册3.4.2

认识圆锥

探究
应用举例 随堂练习 学以致用 拓展

课件制作: 邓成杰 授课教师: 邓成杰

小结

观察

圆锥是怎样 形成的呢？

播放

圆锥的再认识
1.圆锥是由一个底面和一个侧面围成的,它 的底面是一个圆 侧面是一个曲面. 2.把圆锥底面圆周上的任意一点与圆锥顶点 的连线叫做圆锥的母线。 3.连结顶点与底面圆心的线段叫做圆锥的高。 P 如图中a是圆锥的母线，而h就是圆锥的高 问题：圆锥的母线有几条？ a 4.圆锥的底面半径、高线、母线长 h 三者之间的关系: A O

2=r2+h2 a

r

B

练习

返回

探究

童心玩具厂欲生产一种圣诞老 人的帽子，其帽身是圆锥形(如 图)PB=15cm，底面半径r=5cm， 生产这种帽身10000个，你能帮 玩具厂算一算至少需多少平方 A 米的材料吗（不计接缝用料， 和余料,π取3.14，）？

P

a
O .

r

B

圆锥侧面展开图
1.圆锥的侧面展开图是一个扇形 2.圆锥的底面圆周长=侧面展 开后扇形的弧长，
3.圆锥的母线就是其侧面展开图扇形的半径。

圆锥的侧面积和全面积
4.圆锥的侧面积就是弧长为圆锥底面的周长、半径为 圆锥的一条母线的长的扇形面积:

S 侧 = πra
5.圆锥的全面积就是它的侧面积与它的底面积 的和: S ＝S +S =πra ＋πr2=πr(l+r)
侧 底

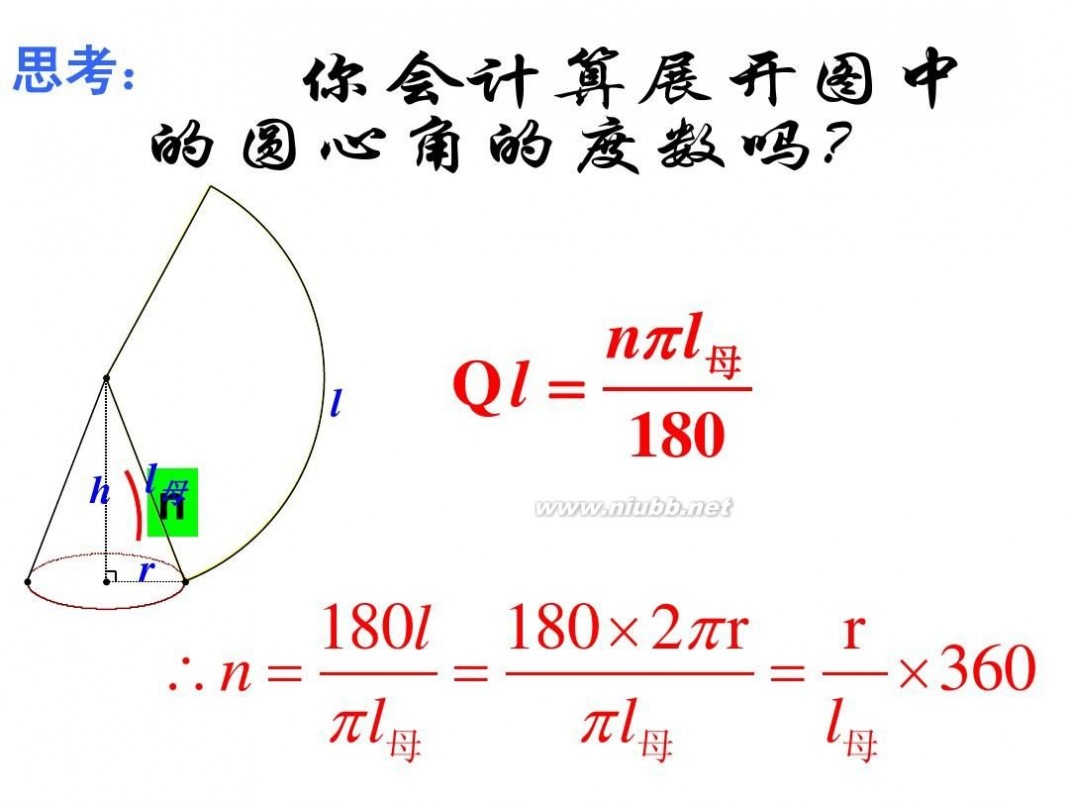
6、圆锥展开图扇形的圆心角θ与底面圆半径r、母 r 线长a的关系：θ ? ? 360 ?
a

P
?

h A O r

a B

h

a

r

返回

应用举例

例1、一个圆锥形零件的母线长为a，底面 的半径为r，求这个圆锥形零件的侧面积和 全面积． 解:圆锥的侧面展开后是一个扇形，该扇形 的半径为a，扇形的弧长为2πr，所以 1 S侧＝ 2 ×2πr×a＝πra S底＝πr2； S ＝πra ＋πr2． a 答：这个圆锥形零件的侧面积 为πra，全面积为πra＋πr2 r

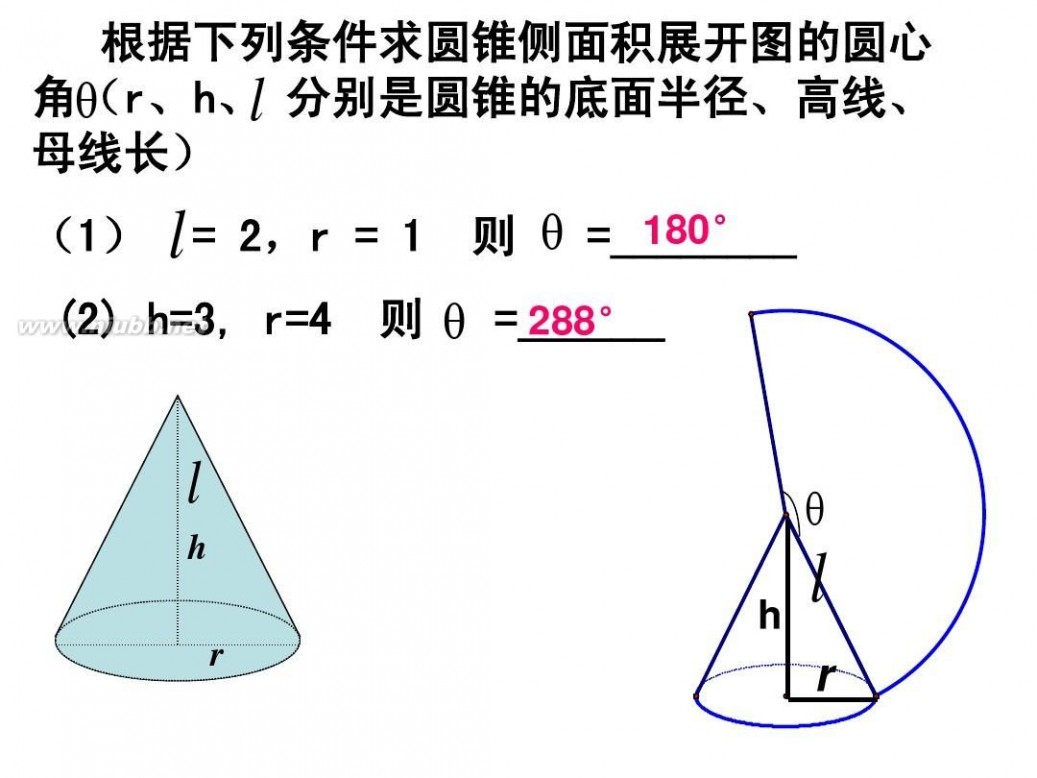
例2 填空、根据下列条件求圆锥侧面积展开图的圆? 心角（r、h、a分别是圆锥的底面半径、高线、母线 长） （1）a= 2，r = 1 (2) h=3, r=4 则 ? =________ 则 ? =__________

?

h
r

a

例3.童心玩具厂欲生产一种圣诞老人的帽子， 其圆锥形帽身的母线长为15cm，底面半径为 5cm，生产这种帽身10000个，你能帮玩具厂算 一算至少需多少平方米的材料吗（不计接缝用 料和余料，π取3.14 ）？ 解:∵ a=15cm,r =5cm,
∴S =π×15×5 ≈3.14×15×5 =235.5（cm 2 ) 235.5×10000= 2355000 （cm
圆锥侧

2

)
练习

答：至少需 235.5 平方米的材料.

随堂 练习

填空：根据下列条件求值（其中r、h、a分别 P 是圆锥的底面半径、高线、母线长）
（1）a = 2，r=1 则 h=_______ (2) h =3, r=4 则 a=_______
h A O r l B

(3) a = 10, h = 8

则r=_______

返回

随堂 练习

1、做一个圆锥烟囱帽，母线为50cm， 底面直径为80cm， （1）

画出它的展开图；(比例尺=1：10) （2）制作一个这样的烟囱帽需铁皮多少？

A

。， 2、已知：Rt△ABC中，∠C=90
AC=2 5 cm，BC= 5 cm， 求： △ABC绕AB所在直线旋转一周 C 所得到的几何体的表面积。
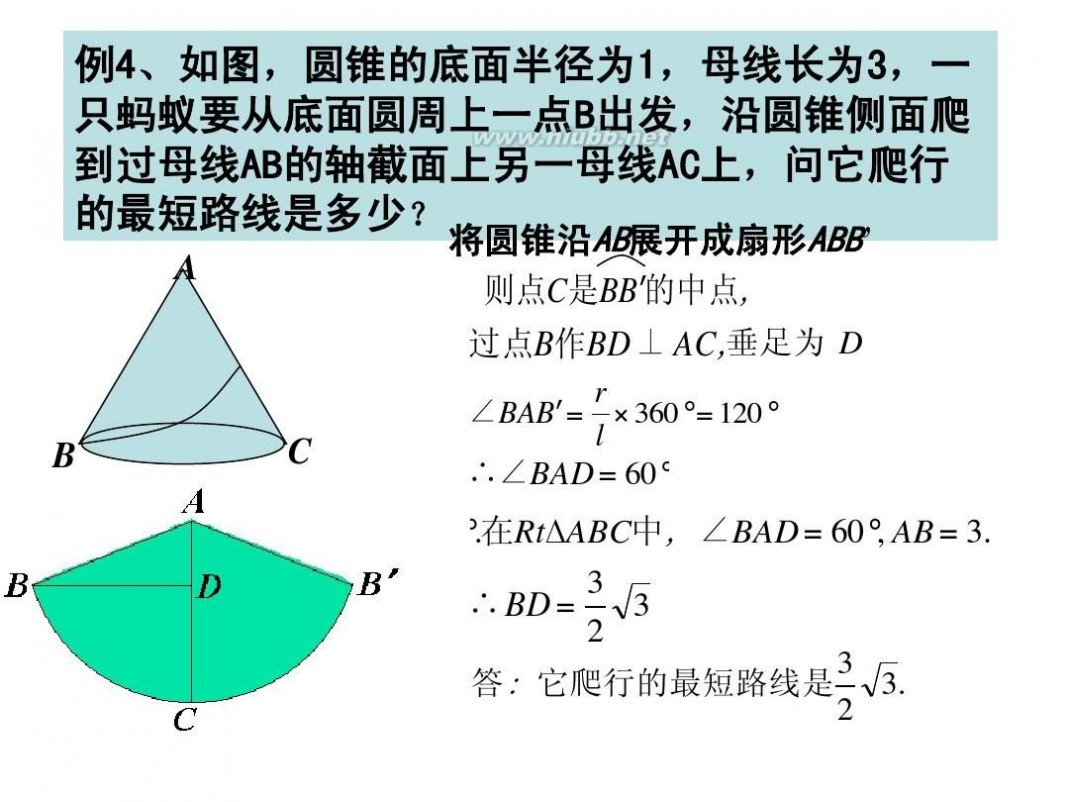
B D

A

C

D 绕AB旋转一周 B

随堂 练习

3、若圆锥的底面半径r =4cm，高线h =3cm，则它的侧面展开图中扇形的圆心 角是 288 度。 —— 4.如图，若圆锥的侧面展开 图是半圆，那么这个展开图 的圆心角是___度；圆锥底 180 半径 r与母线l的比r ：a = 1:2 ___ .
S

a
A O

r
B
返回

学以 致用

思考：如图，圆锥的底面半径为1，母线长 为6，一只蚂蚁要从底面圆周上一点B出发， 沿圆锥侧面爬行一圈再回到点B，问它爬行 的最短路线是多少？ B`
A

A

B

C

B

学以 致用

手工制作 已知一种圆锥模型的底 面半径为4cm ，高线长为3cm。你 能做出这个圆锥模型吗?
P

a h
A

O

r

B
返回

拓展

圆柱侧面展开图
1、圆柱的侧面展开图是一个矩形,它的一边长是圆柱的 母线长;它的另一边长是圆柱的底面圆周长 2、圆柱的侧面积就是一边长是圆柱的母线长,它的另一边长是 圆柱的底面圆周长的矩形面积，即

S侧=2πr×h=2πrh
3、圆柱的全面积就是它的侧面积与它的底面积的和,即

s=2πrh+πr2
r

2πr

h

h

已知：如图一几何体可看 作有一圆柱和一与其共底 的圆锥构成，圆柱的底面 半径为4cm，母线长为9cm， 圆锥母线长5cm，求它的表 面积。

返回

小结

本节课我们有什么收获? 本节课我们认识了圆锥的侧面展开图， 学会计算圆锥的侧面积和全面积，在认识 圆锥的侧面积展开图时，应知道圆锥的底 面周长就是其侧面展开图扇形的弧长。圆 锥的母线就是其侧面展开图扇形的半径， 这样在计算侧面积和全面积时才能做到熟 练、准确。

Good bye

本文标题：圆锥展开图-圆锥的侧面展开图讲
本文地址： http://www.61k.com/1108138.html