一 : 销售火爆 米家激光投影电视众筹结束
【手机中国 新闻】米家激光投影电视的有多火爆?看众筹数据就知道了。就在刚刚,米家官方微博宣布投影电视的众筹已经结束,24小时众筹金额20,537,946元,众筹进展达到了1027%!
米家激光投影电视众筹结束
米家激光投影电视的售价为9999元,可以称得上是旗下最贵的产品。该产品最大能够投射150寸的屏幕,采用超短焦设计,可以贴墙摆放,不用布线。最大5000流明的亮度能够保证即使开灯也可以看得清投射内容。
这款产品还打破了多个小米众筹记录,包括最快达到1000万,最快达到2000万,最高众筹金额,单日最高纪录等。

米家App 微博内容
第一批众筹的产品将于8月15日开始发货,如果市场反馈良好的话,相信第二批产品不久后也将登陆市场。
二 : 光电子激光投稿20090096 23
多芯光子晶体光纤同位相超模的有限元
分析*
姜源源 魏泳涛 邓国亮 胡涛 冯国英
(四川大学电子信息学院,成都 610064)
**
摘要:从Helmholtz方程出发,推导出带有移位迭代的全矢量有限元特征值方程。利用这种全矢量有限元法对多芯光子晶体光纤同位相超模场进行数值模拟分析,详细分析了19芯光子晶体光纤纤芯间距、包层空气占空比和五类空气孔直径对同位相超模场的影响,结果表明光纤结构是影响纤芯之间耦合强度的重要因素,减小空气孔直径能够增加纤芯之间的耦合强度,有利于增加模场面积,最终通过优化结构能够实现多芯光子晶体光纤同位相超模场的各纤芯等振幅输出。
关键字:大模场面积,多芯光子晶体光纤,全矢量有限元法,光纤结构,同位相超模
中图分类号:TN253 文献标识码:A
The finite element analysis of in-phase supermode of
multi-core photonic crystal fiber
Yuanyuan Jian Yongtao Wei Guoliang Deng Tao Hu Guoying Feng
(College of Electronics & Information Engineering,Sichuan University,Chengdu 610064, China)
Abstract: From the Helmholtz equation, derived the full-vectorial finite element eigenvalue equation with shift iteration.For in-phase supermode field of multi-core photonic crystal fiber by the full-vector finite element method, a detailed analysis of the 19-core photonic crystal fiber was present, the effects of core spacing and five kinds of air hole diameter on in-phase supermode field, the results show that fiber structure is an important factor,which affect on the coupling strength of cores, and reducing the air-hole diameter can increase the coupling strength between the core and mode field area, ultimately achieved equal amplitude output of different core of a fiber with in-phase supermode field through optimizing the structure of multi-core photonic crystal fiber.
Keywords: large mode area, multi-core photonic crystal fiber, finite element method, fiber structure,in-phase supermode
1.引言
光子晶体光纤(Photonic Crystal Fiber, PCF)也称为微结构光纤或多孔光纤。1996年Philip Russell等人在文献[1]报道了第一根光子晶体光纤。由于具有无截止单模传输、高
[2,3,4]
度可控的色散特性等许多传统光纤难以实现的优良特性,光子晶体光纤在光纤激光器、
[5,6,7]
非线性光学等许多领域都有着重要的应用和广阔的前景。其中,为了实现高功率激光输出,大模场面积光子晶体光纤激光器更是研究的热点之一。
大模场面积光子晶体光纤可以实现更高的激光输出功率,并且具有高转换效率、高亮度和高光束质量等优点,且由于其高度可控的结构特性成为现今研究的一个重要方向。1998 年,Knight 等首次拉制出了大模面积光子晶体光纤[8]。2003 年, N. A. Mortensen 等拉制出的具有近似三角形芯的光子晶体光纤,和普通结构的光子晶体光纤相比,在弯曲损耗等性
[9]
能基本相同的情况下, 模场面积可比普通结构增大30%左右。2006 年, J.Limpert 等制作基金项目:国家自然科学基金(批准号:60890203,10676023) 和固体激光国家级重点实验室基金资助的课题。
作者简介:姜源源(1986 - ),女,湖南省娄底市人,四川大学电子信息学院研究生,主要从事新型激光技术研究。E-mail:jiangyy124@163.com
**通讯联系人:冯国英,教授。Email: guoying_feng@yahoo.com.cn
的一种新型的掺镱大模面积双包层光子晶体光纤,通过缺失光纤中心的19 个空气孔形成,掺杂纤芯直径高达60?m2,模场面积达到了2000?m2 [10]。2007 年, Y.Tsuchida 等设计了在1.064mm处,高阶模损耗大于1dB/m, 弯曲半径可达5cm, 光束质量因子M2=1.15,模场面积可达1400 ?m2的大模面积光子晶体光纤[11]。2009年,L.Michaille等利用每个纤芯直径高达40?m
2[12]
的6芯光子晶体光纤实现了模场面积高达4240?m。然而在一些多芯光子晶体光纤中,各芯光场非均匀分布的超模(多芯光纤中每个纤芯均工作在单模状态,通过相互耦合形成的多个
[13]
模式)会导致各芯泵浦功率吸收不均匀且增加了与其他超模的模式竞争,反而降低了模场面积。因此,为了实现大模场面积,实现各芯等振幅输出是非常有意义的。
本文从Helmholtz方程出发,利用混合节点/棱边的单元基函数推导出带有移位迭代的全矢量有限元特征值方程,利用这种全矢量有限元法对多芯结构进行数值模拟。详细分析了光纤结构对19芯光子晶体光纤同位相超模模场的影响,通过分析得出:光纤结构是影响纤芯之间耦合强度的重要因素,只要合理的设计结构就能实现特殊要求的输出模场。最终可通过优化结构实现同位相超模的模式整形。
2.全矢量有限元法
在光纤中,光束的传输可以用矢量Helmholtz方程来描述:
??(
1
2
??E)?k0?rE?0 (1)
2
?r
其中?r、?r为介质的相对磁导率和介电常数;k0为真空中的光波数;E为电场矢量;?为梯度算符。
设光纤截面的求解区域为?,其边界可划分为电壁Γ1和磁壁Γ2,边界条件提法如下
n?E?0n?(??E)?0
on Γ1on Γ2
2
(2)
满足边界条件(2)的方程(1)的弱形式为
[14]
?[
Ω
1
?r
(??δE)?(??E)?k0?rδE?E]dΩ?0
(3)
其中δE为E的变分。假设电场E在光纤中没有损耗,其形式分解为如下形式
?Ez)exp(?j?z)E(x,y,z)?(Et??jz
(4) ?为光纤纵向单位矢量,j其中Et为电场的横向分量,Ez为其纵向分量,β为传播常数,z为单位虚数。将式(4)带入式(3),得:
?[
Ω
1
?r
2
(?t?δEt)?(?t?Et)?k0?rδEt?Et]dΩ
2
??
Ω
?[?
1
r
(5)
(?tδEz?δEt)?(?tEz?Et)?k0?rδEz?Ez]dΩ?0
2
其中?t是横向算符。
使用六节点直边三角形单元离散化式(5)。定义Ez的插值函数如下
Ez?Nez??L1
Et采用矢量基函数进行插值,即
L2
L3?ez (6)
其中Li(i?1,2,3)是三角形的面积坐标,ez是由单元顶点处电场纵向分量值构成的向量。对
??
Et?Wez?W12
?
?W23?
W31et (7)
?
et是由单元中节点所在边的电场横向分量值构成的向量。对连接节点i与j的单元边,矢量
?
W基函数ij定义为
?
Wij?lij(Li?tLj?Lj?tLi) (8)
其中lij为单元边长度;若节点i的总体编号小于节点j总体编号,则式(8)应乘以一负号,以保证在不同单元的相邻边上Et有相同的插值形式。
使用标准的有限元离散过程即可得如下广义特征值问题
?0??0
0??ez?Bzz
2????????
Att??et??Btz
Bzt??ez?
???Btt??et?
(9)
其中单元矩阵分别表示为:
Att?
?1?T2T
(??W)(??W)?k?WWt0r?dΩ?Ω??t
?r??1?T2T
(?N)?(?N)?k?NNt0r?dΩ?d???t
?r?
Bzz?Btt?
(10)
?
1
Ω
?r
T
WWdΩ
T
Btz?Bzt?
?
1
Ω
?r
W
T
(?tN)dΩ
为快速求解广义特征值(9),使用移位迭代法进行计算,即将公式(9)改写为如下形式
?0
(??0
0?Bzz
2?????Att??Btz
Bzt??ez?Bzz
22?
)?(???)????Btt??et??Btz
Bzt??ez?
??? (11)Btt??et?
?为介质中的最大波数。由于光纤中的可传播模式只存在于式(11)的少数低阶模式中,因此再使用逆迭代法来计算(11)式是非常有效的。关于广义特征值问题的逆迭代法,具体参考文献[15]。
3.数值模拟分析
通常多芯光子晶体光纤每个超模之间的传播常数很接近,但是只有具有最大传播常数的同位相超模(每一个纤芯的传播模式之间的相位差为零)的远场才具有较好的高斯分布,具有最好的光束质量和最高的亮度[16],因此对于大多数应用,通常希望获得同位相超模。
利用上述全矢量有限元法对如图1所示的四种多芯光子晶体光纤进行分析,其基质材料均为纯石英,折射率随波长变化曲线可由Sellmeier三项式拟合,空气占空比均为
[17]
d/Λ?40%,每个纤芯均能实现单模传输。
(a) (b) (c) (d)
图1多芯光子晶体光纤结构(a)2芯(b)3芯(c)6芯(d)7芯
Fig. 1 Multicore photonic crystal fiber (a) two cores (b) three cores (c) six cores (d) seven cores
(a) (b) (c) (d)
图2多芯光子晶体光纤同相位超模场(a)2芯(b)3芯(c)6芯(d)7芯
Fig. 2 In-phase supermode of multicore photonic crystal fiber (a) two cores (b) three cores (c) six cores (d) seven
cores
图2表示的是图1中给出的四种结构的同相位超模场模拟结果,其结果与耦合模理论计算结果相符,说明了这种方法的正确性,且有限元法可以利用多种形状的网格(三角形单元,四边形单元等等)分割计算区域,还可以根据计算精度的需要自由的设置节点个数,因此它特别适用于复杂结构光纤的数值分析。
从图中可以看出,2芯、3芯和6芯结构光纤每个芯的振幅相等,而7芯结构光纤中心芯振幅大于外圈芯。Mafi和Moloney最早提出在多芯光子晶体光纤中通过优化结构进行模式整形,实现同位相超模每个芯等振幅输出[19,20]。在这里本文主要对结构复杂的19芯光子晶体光纤结构参数进行分析。
3.1纤芯间距对同位相超模的影响
利用全矢量有限元法对如图3
所示的两种19芯光子晶体光纤结构进行数值模拟,模型(a)和模型(b)的纤芯间距分别是2Λ和3Λ,包层空气占空比相同。为了提高计算精度和适用多种结构,通常把求解区域离散成三角形单元,如图3(c)所示。图4表示的是根据图3中两种结构计算得到的x轴方向上的归一化振幅分布,从图4的模拟结果可以看出,随着纤芯与中心的距离增大,纤芯振幅减小。且发现改变纤芯间距能够改变纤芯之间的耦合强度,但值得注意的是,这两种结构纤芯之间的相对振幅差仍然保持不变。
[18]
(a) (b) (c)
图3 19芯光子晶体光纤结构(a)纤芯间距为2Λ(b)纤芯间距为3Λ(c)对应(b)所示区域计算三角
形网格图 Fig. 3 19 Cores photonic crystal fiber (a) core space is2Λ (b) core space is3Λ (c)Triangular mesh diagram
corresponding to shown area of (b) diagram
图4 对应图3中结构数值模拟的x轴方向上的归一化振幅分布
Fig. 4 The normalized amplitude distribution in the x-axis direction corresponding to model of fig3
3.2包层空气占空比对同位相超模的影响
光子晶体光纤的包层空气占空比是一个非常重要的结构参数,通过改变占空比就能够改变光纤的传播常数和色散等重要参数,因此深入了解包层空气占空比对耦合强度的影响是非常有意义的。从图5中可以看出,在空气孔间距不变的情况下减小空气孔直径虽然能够增加纤芯之间的耦合强度,但是对纤芯之间的相对振幅差影响较小。在空气孔直径保持不变的情况下改变空气孔间距对纤芯之间的耦合强度和相对振幅差影响都较小。
(a) (b)
图5 对应图3(a)模型x轴方向上的归一化振幅分布(a)孔间距不变,改变空气孔直径(b)空气孔直径
不变,改变孔间距
Fig. 5 The normalized amplitude distribution in the x-axis direction corresponding to model of fig3(a) (a) change the air hole diameter while keeping hole space unchanged(b) change the air hole space while keeping hole
diameter unchanged
3.3空气孔直径对同位相超模的影响
为了方便分析,根据空气孔排布的周期性和光纤结构的对称性,可以把纤芯划分为四类(1,2,3,4),而纤芯之间的空气孔也可分为五类(X,Y,Z,T,U)[20],如图3(a)所示,分析结果也表明这种划分是合理的。通过上述数值模拟分析发现,纤芯间距和包层空气占空比虽然能够改变纤芯之间的耦合强度,但是对于纤芯之间的相对振幅差影响很小,这是因为不管是改变纤芯间距还是占空比,在一种结构中每个纤芯之间的空气孔直径和间距都相
[18]
同,因此根据耦合模理论,其互耦合系数都相同,而通过求解由耦合模理论推导的特征值方程得到的同位相超模所对应的特征向量也应该相同,即纤芯之间的相对振幅差应该保持不变。因此为了实现每个纤芯等振幅输出,就要使一类纤芯区别于其他纤芯,即在一种结构中应该使几类纤芯之间的互耦合系数不相同,即使几类纤芯之间的空气孔直径或间距不相同。分析图3(a)所示结构,定义相对振幅差Aij为进行归一化后i类纤芯和j类纤芯处的最大振幅之差。为了进一步了解在一种结构中五类空气孔直径对耦合强度的影响,保持其它四类空气孔直径不变,通过改变一类空气孔直径计算四类纤芯之间的相对振幅差。
光电子激光投稿20090096 23_光电子激光
(a) (b)
(c) (d)
(e)
图6 对应图3(a)模型四类纤芯之间的相对振幅差(a)改变X类空气孔直径(b)改变Y类空气孔直径
(c)改变Z类空气孔直径(d)改变T类空气孔直径(e)改变U类空气孔直径
Fig. 6 The relative amplitude difference corresponding to model of fig3(a) (a) change the diameter of X air hole (b) change the diameter of Y air hole (c) change the diameter of Z air hole (d) change the diameter of T air hole (e)
change the diameter of U air hole
图6中所示的三条曲线分别表示的1类纤芯与其他三类纤芯之间的相对振幅差,从图中可以看出当四类纤芯之间的空气孔直径不相同时,五类空气孔直径对纤芯之间的相对振幅差影响很大,且不同类型的空气孔对纤芯之间的相对振幅差影响程度也不同。通过上述分析可知:减小两类纤芯之间相对应类型的空气孔直径时,纤芯之间的耦合强度增大,且当相对应类型的空气孔直径为某一特定值时,两类纤芯之间的相对振幅差为零,实现了两类纤芯等振幅输出,这有利于增大有效模场面积。由于光纤结构是影响纤芯之间耦合强度的重要因素,因此通过上述对19芯光子晶体光纤结构参数的分析,只要合理的设计结构就能实现特殊要求的输出超模场分布。
(a) (b)
图7 19芯光子晶体光纤同相位超模场(a)整形前(b)整形后
Fig. 7 In-phase supermode of 19 cores photonic crystal fiber (a) before mode shaping (b) after mode shaping
4.结论
多芯光子晶体光纤由于具有大模场面积而成为现今光纤激光器的一个研究热点,尤其关注的是具有较好光束质量的同位相超模场。本文从Helmholtz方程出发,运用变分原理推导泛函表达式,然后利用混合节点/棱边的单元基函数对泛函离散化建立了广义特征值问题,再利用移位迭代法求解特征方程。利用这种全矢量有限元法分析了四种多芯光子晶体光纤的同位相超模场,验证了方法的正确性。最后利用全矢量有限元法详细分析了19芯光子晶体光纤结构参数对输出同位相超模场的影响,通过分析发现:纤芯间距虽然能够改变纤芯之间的耦合强度,但是对于纤芯之间的相对振幅差影响很小;包层空气占空比对纤芯之间的耦合强度和相对振幅差影响都较小;减小一类空气孔直径,能够增大纤芯之间的耦合强度。最终表明只有在一类纤芯区别于其他纤芯时,即几类纤芯之间的结构参数不相同时才能实现同位相超模的各纤芯等振幅输出,为进一步增大模场面积提出一种可行的方案。
参考文献
[1] J. C. Knight, T. A. Birks, P. St J. Russell, et al. All-silica single-mode optical fiber with photonic crystal cladding[J]. Opt. Lett., 1996, 21(19): 1547-1549. 3+[2] Zhang Wei, Li Yigang, Yan Peiguang, et al. Large mode area double cladding Yb -doped photonic crystal fiber laser [J]. Journal of Optoelectronics·laser, 2005, 16(4): 418-420.
[3] J. Limpert, N. Deguil-Robin, I. Manek-Honinger, et al. High-power rod-type photonic crystal fiber laser[J]. Opt. Express, 2005, 13(4): 1055-1058.
[4] Yanming Huo, Peter Cheo, George King. Fundamental mode operation of a 19-core phase-locked Yb-doped fiber amplifier[J]. Opt. Express, 2004, 12(25): 6230-6239.
[5] Li Xibin, Chai Lu, Zhang Yuying, et al. Study on spectral gain characterization of four-wave mixing in photonic crystal fiber [J]. Journal of Optoelectronics·laser, 2009, 20(2): 260-263.
[6] Kunimasa Saitoh, Masanori Koshiba. Highly nonlinear dispersion-flattened photonic crystal fibers for supercontinuum generation in a telecommunication window[J]. Opt. Express, 2004, 12(10): 2027-2032.
[7] Jacob Riis Folkenberg, Niels Asger Mortensen, Kim P. Hansen, et al. Experimental investigation of cutoff phenomena in nonlinear photonic crystal fibers[J]. Opt. Lett., 2003, 28(20): 1882-1884.
[8] J. C. Knight, T. A. Birks, R. F. Cregan, et al. Large mode area photonic crystal fibre[J]. Electronics Letters, 1998, 34(13): 1347-1348.
[9] N. A. Mortensen, M. D. Nielsen, J. R. Folkenberg, et al. Improved large-mode-area endlessly single-mode photonic crystal fibers[J]. Opt. Lett., 2003, 28(6): 393-395.
[10] J. Limpert, O. Schmidt, J. Rothhardt, et al. Extended single-mode photonic crystal fiber lasers[J]. Opt. Express, 2006, 14(7): 2715-2720.
[11] Yukihiro Tsuchida, Kunimasa Saitoh, Masanori Koshiba. Design of single-moded holey fibers with large-mode-area and low bending losses: the significance of the ring-core region[J]. Opt. Express, 2007, 15(4): 1794-1803.
[12] L. Michaille, C. R. Bennett, D. M. Taylor, et al. Multicore Photonic Crystal Fiber Lasers for High Power/Energy Applications[J]. Selected Topics in Quantum Electronics, IEEE Journal of, 2009, 15(2): 328-336.
[13] J. A.Besley, J. D. Love. Supermode analysis of fibre transmission[J]. IEE Proc. Optoelectron, 1997, 144(6): 411-419.
[14]Li Chaoyang, Yu Li, Zhang Xiaoguang, et al. Design of Photonic Crystal Fiber Using Full Vector Finite Element Method [J]. Journal of Optoelectronics·laser, 2007, 18(1): 30-35.
[15] R. W. Clough, J. Pengjing, Wang Guangyuan. Dynamics of Structure [M]. 2nd Edition.China:Higher Education Press,1995.
[16] L. Michaille, C. R. Bennett, D. M. Taylor, et al. Phase locking and supermode selection in multicore photonic crystal fiber lasers with a large doped area[J]. Opt. Lett., 2005, 30(13): 1668-1670.
[17] T. A. Birks, J. C. Knight, P. St J. Russell Endlessly single-mode photonic crystal fiber[J]. Opt. Lett., 1997, 22(13): 961-963.
[18]Zhou Pu, Hou Jing, Chen Zilun, et al. Study on the supermode and mode selection in multicore fiber laser[J]. Acta Optica Sinica, 2007, 27(010): 1812-1816.
[19] Krishna Mohan Gundu, Miroslav Kolesik, Jerome V. Moloney Mode shaping in multicore fibers[J]. Opt. Lett., 2007, 32(7): 763-765.
[20] A. Mafi, J. V. Moloney Shaping modes in multicore photonic crystal fibers[J]. Photonics Technology Letters, IEEE, 2005, 17(2): 348-350.
三 : 光电子激光投稿20090096
多芯光子晶体光纤同位相超模的有限元
分析*
姜源源 魏泳涛 邓国亮 胡涛 冯国英
(四川大学电子信息学院,成都 610064) **
摘要:从Helmholtz方程出发,推导出带有移位迭代的全矢量有限元特征值方程。(www.61k.com)利用这种全矢量有限元法对多芯光子晶体光纤同位相超模场进行数值模拟分析,详细分析了19芯光子晶体光纤纤芯间距、包层空气占空比和五类空气孔直径对同位相超模场的影响,结果表明光纤结构是影响纤芯之间耦合强度的重要因素,减小空气孔直径能够增加纤芯之间的耦合强度,有利于增加模场面积,最终通过优化结构能够实现多芯光子晶体光纤同位相超模场的各纤芯等振幅输出。
关键字:大模场面积,多芯光子晶体光纤,全矢量有限元法,光纤结构,同位相超模 中图分类号:TN253 文献标识码:A
The finite element analysis of in-phase supermode of
multi-core photonic crystal fiber
Yuanyuan Jian Yongtao Wei Guoliang Deng Tao Hu Guoying Feng
(College of Electronics & Information Engineering,Sichuan University,Chengdu 610064, China)
Abstract: From the Helmholtz equation, derived the full-vectorial finite element eigenvalue equation with shift iteration.For in-phase supermode field of multi-core photonic crystal fiber by the full-vector finite element method, a detailed analysis of the 19-core photonic crystal fiber was present, the effects of core spacing and five kinds of air hole diameter on in-phase supermode field, the results show that fiber structure is an important factor,which affect on the coupling strength of cores, and reducing the air-hole diameter can increase the coupling strength between the core and mode field area, ultimately achieved equal amplitude output of different core of a fiber with in-phase supermode field through optimizing the structure of multi-core photonic crystal fiber.
Keywords: large mode area, multi-core photonic crystal fiber, finite element method, fiber structure,in-phase supermode
1.引言
光子晶体光纤(Photonic Crystal Fiber, PCF)也称为微结构光纤或多孔光纤。1996年Philip Russell等人在文献[1]报道了第一根光子晶体光纤。由于具有无截止单模传输、高
[2,3,4]度可控的色散特性等许多传统光纤难以实现的优良特性,光子晶体光纤在光纤激光器、
[5,6,7]非线性光学等许多领域都有着重要的应用和广阔的前景。其中,为了实现高功率激光输出,大模场面积光子晶体光纤激光器更是研究的热点之一。
大模场面积光子晶体光纤可以实现更高的激光输出功率,并且具有高转换效率、高亮度和高光束质量等优点,且由于其高度可控的结构特性成为现今研究的一个重要方向。1998 年,Knight 等首次拉制出了大模面积光子晶体光纤[8]。2003 年, N. A. Mortensen 等拉制出的具有近似三角形芯的光子晶体光纤,和普通结构的光子晶体光纤相比,在弯曲损耗等性
[9]能基本相同的情况下, 模场面积可比普通结构增大30%左右。2006 年, J.Limpert 等制作基金项目:国家自然科学基金(批准号:60890203,10676023) 和固体激光国家级重点实验室基金资助的课题。
作者简介:姜源源(1986 - ),女,湖南省娄底市人,四川大学电子信息学院研究生,主要从事新型激光技术研究。E-mail:jiangyy124@163.com
**通讯联系人:冯国英,教授。Email: guoying_feng@yahoo.com.cn
光电子激光 光电子激光投稿20090096
的一种新型的掺镱大模面积双包层光子晶体光纤,通过缺失光纤中心的19 个空气孔形成,掺杂纤芯直径高达60?m2,模场面积达到了2000?m2 [10]。(www.61k.com)2007 年, Y.Tsuchida 等设计了在1.064mm处,高阶模损耗大于1dB/m, 弯曲半径可达5cm, 光束质量因子M2=1.15,模场面积可达1400 ?m2的大模面积光子晶体光纤[11]。2009年,L.Michaille等利用每个纤芯直径高达40?m
2[12]
的6芯光子晶体光纤实现了模场面积高达4240?m。然而在一些多芯光子晶体光纤中,各芯光场非均匀分布的超模(多芯光纤中每个纤芯均工作在单模状态,通过相互耦合形成的多个
[13]
模式)会导致各芯泵浦功率吸收不均匀且增加了与其他超模的模式竞争,反而降低了模场面积。因此,为了实现大模场面积,实现各芯等振幅输出是非常有意义的。
本文从Helmholtz方程出发,利用混合节点/棱边的单元基函数推导出带有移位迭代的全矢量有限元特征值方程,利用这种全矢量有限元法对多芯结构进行数值模拟。详细分析了光纤结构对19芯光子晶体光纤同位相超模模场的影响,通过分析得出:光纤结构是影响纤芯之间耦合强度的重要因素,只要合理的设计结构就能实现特殊要求的输出模场。最终可通过优化结构实现同位相超模的模式整形。
2.全矢量有限元法
在光纤中,光束的传输可以用矢量Helmholtz方程来描述:
??(
1
2
??E)?k0?rE?0 (1)
2
?r
其中?r、?r为介质的相对磁导率和介电常数;k0为真空中的光波数;E为电场矢量;?为梯度算符。
设光纤截面的求解区域为?,其边界可划分为电壁Γ1和磁壁Γ2,边界条件提法如下
n?E?0n?(??E)?0
on Γ1on Γ2
2
(2)
满足边界条件(2)的方程(1)的弱形式为
[14]
?[
Ω
1
?r
(??δE)?(??E)?k0?rδE?E]dΩ?0
(3)
其中δE为E的变分。假设电场E在光纤中没有损耗,其形式分解为如下形式
?Ez)exp(?j?z)E(x,y,z)?(Et??jz
(4) ?为光纤纵向单位矢量,j其中Et为电场的横向分量,Ez为其纵向分量,β为传播常数,z为单位虚数。将式(4)带入式(3),得:
?[
Ω
1
?r
2
(?t?δEt)?(?t?Et)?k0?rδEt?Et]dΩ
2
??
Ω
?[?
1
r
61阅读提醒您本文地址:
(5)
(?tδEz?δEt)?(?tEz?Et)?k0?rδEz?Ez]dΩ?0
2
其中?t是横向算符。
使用六节点直边三角形单元离散化式(5)。定义Ez的插值函数如下
Ez?Nez??L1
Et采用矢量基函数进行插值,即
L2
L3?ez (6)
其中Li(i?1,2,3)是三角形的面积坐标,ez是由单元顶点处电场纵向分量值构成的向量。对
??
Et?Wez?W12
?
?W23?
W31et (7)
?
et是由单元中节点所在边的电场横向分量值构成的向量。对连接节点i与j的单元边,矢量
?
W基函数ij定义为
光电子激光 光电子激光投稿20090096
?
Wij?lij(Li?tLj?Lj?tLi) (8)
其中lij为单元边长度;若节点i的总体编号小于节点j总体编号,则式(8)应乘以一负号,以保证在不同单元的相邻边上Et有相同的插值形式。[www.61k.com]
使用标准的有限元离散过程即可得如下广义特征值问题
?0??0
0??ez?Bzz
2????????
Att??et??Btz
Bzt??ez?
???Btt??et?
(9)
其中单元矩阵分别表示为:
Att?
?1?T2T
(??W)(??W)?k?WWt0r?dΩ?Ω??t
?r??1?T2T
(?N)?(?N)?k?NNt0r?dΩ?d???t
?r?
Bzz?Btt?
(10)
?
1
Ω
?r
T
WWdΩ
T
Btz?Bzt?
?
1
Ω
?r
W
T
(?tN)dΩ
为快速求解广义特征值(9),使用移位迭代法进行计算,即将公式(9)改写为如下形式
?0
(??0
0?Bzz
2?????Att??Btz
Bzt??ez?Bzz
22?
)?(???)????Btt??et??Btz
Bzt??ez?
??? (11)Btt??et?
?为介质中的最大波数。由于光纤中的可传播模式只存在于式(11)的少数低阶模式中,因此再使用逆迭代法来计算(11)式是非常有效的。关于广义特征值问题的逆迭代法,具体参考文献[15]。
3.数值模拟分析
通常多芯光子晶体光纤每个超模之间的传播常数很接近,但是只有具有最大传播常数的同位相超模(每一个纤芯的传播模式之间的相位差为零)的远场才具有较好的高斯分布,具有最好的光束质量和最高的亮度[16],因此对于大多数应用,通常希望获得同位相超模。
利用上述全矢量有限元法对如图1所示的四种多芯光子晶体光纤进行分析,其基质材料均为纯石英,折射率随波长变化曲线可由Sellmeier三项式拟合,空气占空比均为
[17]
d/Λ?40%,每个纤芯均能实现单模传输。
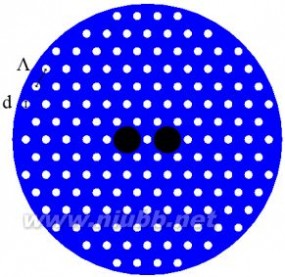



(a) (b) (c) (d)
图1多芯光子晶体光纤结构(a)2芯(b)3芯(c)6芯(d)7芯
Fig. 1 Multicore photonic crystal fiber (a) two cores (b) three cores (c) six cores (d) seven cores
光电子激光 光电子激光投稿20090096

(a) (b) (c) (d)
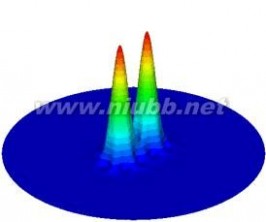
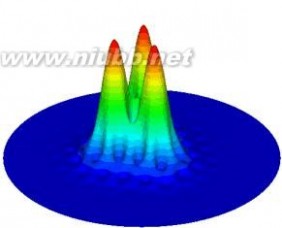
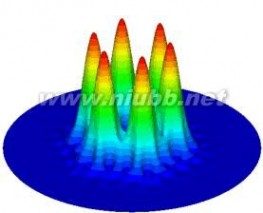
图2多芯光子晶体光纤同相位超模场(a)2芯(b)3芯(c)6芯(d)7芯
Fig. 2 In-phase supermode of multicore photonic crystal fiber (a) two cores (b) three cores (c) six cores (d) seven
cores
图2表示的是图1中给出的四种结构的同相位超模场模拟结果,其结果与耦合模理论计算结果相符,说明了这种方法的正确性,且有限元法可以利用多种形状的网格(三角形单元,四边形单元等等)分割计算区域,还可以根据计算精度的需要自由的设置节点个数,因此它特别适用于复杂结构光纤的数值分析。(www.61k.com]
从图中可以看出,2芯、3芯和6芯结构光纤每个芯的振幅相等,而7芯结构光纤中心芯振幅大于外圈芯。Mafi和Moloney最早提出在多芯光子晶体光纤中通过优化结构进行模式整形,实现同位相超模每个芯等振幅输出[19,20]。在这里本文主要对结构复杂的19芯光子晶体光纤结构参数进行分析。
3.1纤芯间距对同位相超模的影响
利用全矢量有限元法对如图3
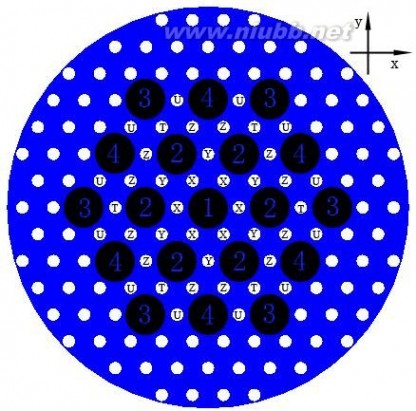
所示的两种19芯光子晶体光纤结构进行数值模拟,模型(a)和模型(b)的纤芯间距分别是2Λ和3Λ,包层空气占空比相同。为了提高计算精度和适用多种结构,通常把求解区域离散成三角形单元,如图3(c)所示。图4表示的是根据图3中两种结构计算得到的x轴方向上的归一化振幅分布,从图4的模拟结果可以看出,随着纤芯与中心的距离增大,纤芯振幅减小。且发现改变纤芯间距能够改变纤芯之间的耦合强度,但值得注意的是,这两种结构纤芯之间的相对振幅差仍然保持不变。 [18]
(a) (b) (c)
图3 19芯光子晶体光纤结构(a)纤芯间距为2Λ(b)纤芯间距为3Λ(c)对应(b)所示区域计算三角
形网格图
61阅读提醒您本文地址:
Fig. 3 19 Cores photonic crystal fiber (a) core space is2Λ (b) core space is3Λ (c)Triangular mesh diagram
corresponding to shown area of (b) diagram
光电子激光 光电子激光投稿20090096

图4 对应图3中结构数值模拟的x轴方向上的归一化振幅分布
Fig. 4 The normalized amplitude distribution in the x-axis direction corresponding to model of fig3
3.2包层空气占空比对同位相超模的影响
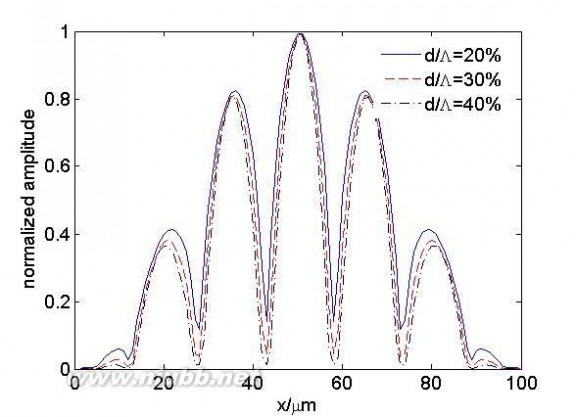
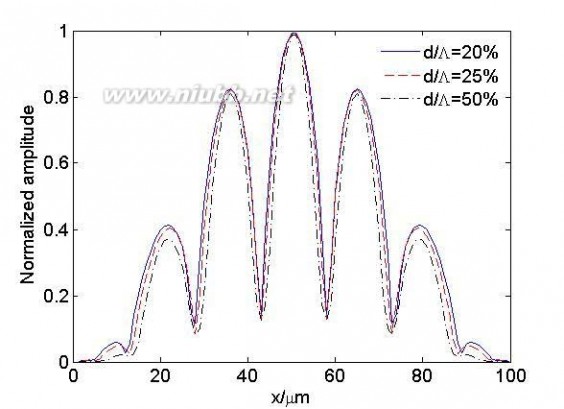
光子晶体光纤的包层空气占空比是一个非常重要的结构参数,通过改变占空比就能够改变光纤的传播常数和色散等重要参数,因此深入了解包层空气占空比对耦合强度的影响是非常有意义的。[www.61k.com)从图5中可以看出,在空气孔间距不变的情况下减小空气孔直径虽然能够增加纤芯之间的耦合强度,但是对纤芯之间的相对振幅差影响较小。在空气孔直径保持不变的情况下改变空气孔间距对纤芯之间的耦合强度和相对振幅差影响都较小。
(a) (b)
图5 对应图3(a)模型x轴方向上的归一化振幅分布(a)孔间距不变,改变空气孔直径(b)空气孔直径
不变,改变孔间距
Fig. 5 The normalized amplitude distribution in the x-axis direction corresponding to model of fig3(a) (a) change the air hole diameter while keeping hole space unchanged(b) change the air hole space while keeping hole
diameter unchanged
3.3空气孔直径对同位相超模的影响
为了方便分析,根据空气孔排布的周期性和光纤结构的对称性,可以把纤芯划分为四类(1,2,3,4),而纤芯之间的空气孔也可分为五类(X,Y,Z,T,U)[20],如图3(a)所示,分析结果也表明这种划分是合理的。通过上述数值模拟分析发现,纤芯间距和包层空气占空比虽然能够改变纤芯之间的耦合强度,但是对于纤芯之间的相对振幅差影响很小,这是因为不管是改变纤芯间距还是占空比,在一种结构中每个纤芯之间的空气孔直径和间距都相
[18] 同,因此根据耦合模理论,其互耦合系数都相同,而通过求解由耦合模理论推导的特征
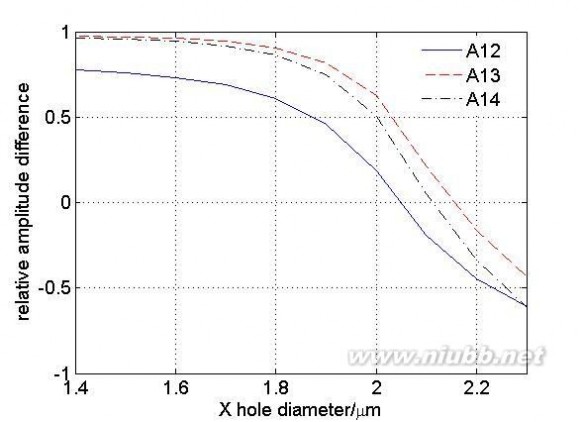
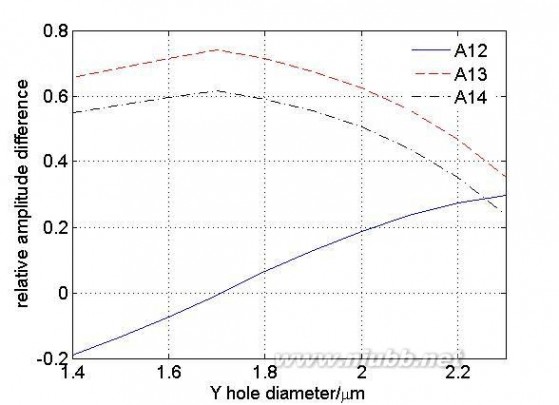
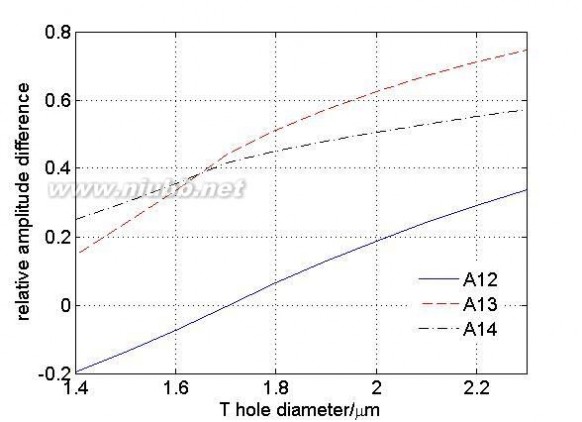
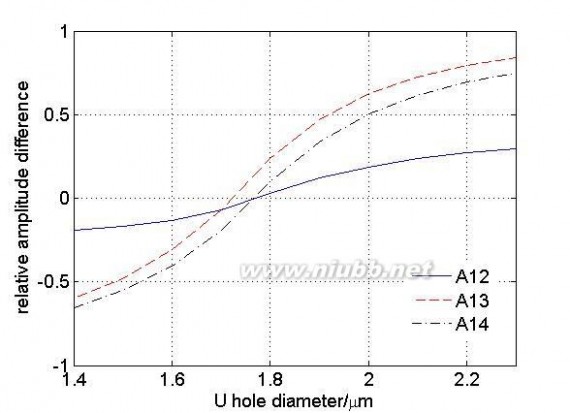
值方程得到的同位相超模所对应的特征向量也应该相同,即纤芯之间的相对振幅差应该保持不变。因此为了实现每个纤芯等振幅输出,就要使一类纤芯区别于其他纤芯,即在一种结构中应该使几类纤芯之间的互耦合系数不相同,即使几类纤芯之间的空气孔直径或间距不相同。分析图3(a)所示结构,定义相对振幅差Aij为进行归一化后i类纤芯和j类纤芯处的最大振幅之差。为了进一步了解在一种结构中五类空气孔直径对耦合强度的影响,保持其它四类空气孔直径不变,通过改变一类空气孔直径计算四类纤芯之间的相对振幅差。
光电子激光 光电子激光投稿20090096
(a) (b)

(c) (d)
(e)
图6 对应图3(a)模型四类纤芯之间的相对振幅差(a)改变X类空气孔直径(b)改变Y类空气孔直径
(c)改变Z类空气孔直径(d)改变T类空气孔直径(e)改变U类空气孔直径
Fig. 6 The relative amplitude difference corresponding to model of fig3(a) (a) change the diameter of X air hole (b) change the diameter of Y air hole (c) change the diameter of Z air hole (d) change the diameter of T air hole (e)
change the diameter of U air hole
图6中所示的三条曲线分别表示的1类纤芯与其他三类纤芯之间的相对振幅差,从图中可以看出当四类纤芯之间的空气孔直径不相同时,五类空气孔直径对纤芯之间的相对振幅差影响很大,且不同类型的空气孔对纤芯之间的相对振幅差影响程度也不同。[www.61k.com]通过上述分析可知:减小两类纤芯之间相对应类型的空气孔直径时,纤芯之间的耦合强度增大,且当相对应类型的空气孔直径为某一特定值时,两类纤芯之间的相对振幅差为零,实现了两类纤芯等振幅输出,这有利于增大有效模场面积。由于光纤结构是影响纤芯之间耦合强度的重要因素,因此通过上述对19芯光子晶体光纤结构参数的分析,只要合理的设计结构就能实现特殊要求的输出超模场分布。
光电子激光 光电子激光投稿20090096

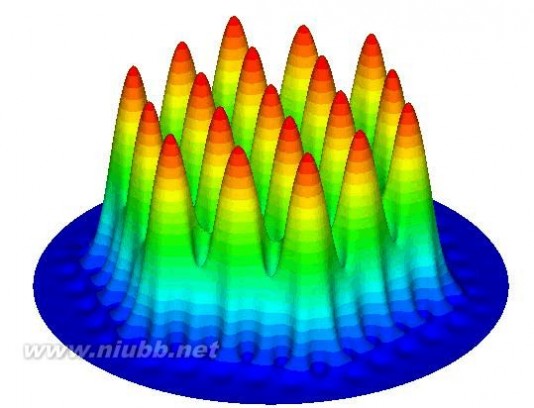
(a) (b)
图7 19芯光子晶体光纤同相位超模场(a)整形前(b)整形后
Fig. 7 In-phase supermode of 19 cores photonic crystal fiber (a) before mode shaping (b) after mode shaping
4.结论
多芯光子晶体光纤由于具有大模场面积而成为现今光纤激光器的一个研究热点,尤其关注的是具有较好光束质量的同位相超模场。(www.61k.com]本文从Helmholtz方程出发,运用变分原理推导泛函表达式,然后利用混合节点/棱边的单元基函数对泛函离散化建立了广义特征值问题,再利用移位迭代法求解特征方程。利用这种全矢量有限元法分析了四种多芯光子晶体光纤的同位相超模场,验证了方法的正确性。最后利用全矢量有限元法详细分析了19芯光子晶体光纤结构参数对输出同位相超模场的影响,通过分析发现:纤芯间距虽然能够改变纤芯之间的耦合强度,但是对于纤芯之间的相对振幅差影响很小;包层空气占空比对纤芯之间的耦合强度和相对振幅差影响都较小;减小一类空气孔直径,能够增大纤芯之间的耦合强度。最终表明只有在一类纤芯区别于其他纤芯时,即几类纤芯之间的结构参数不相同时才能实现同位相超模的各纤芯等振幅输出,为进一步增大模场面积提出一种可行的方案。
61阅读提醒您本文地址:
参考文献
[1] J. C. Knight, T. A. Birks, P. St J. Russell, et al. All-silica single-mode optical fiber with photonic crystal cladding[J]. Opt. Lett., 1996, 21(19): 1547-1549. 3+[2] Zhang Wei, Li Yigang, Yan Peiguang, et al. Large mode area double cladding Yb -doped photonic crystal fiber laser [J]. Journal of Optoelectronics·laser, 2005, 16(4): 418-420.
[3] J. Limpert, N. Deguil-Robin, I. Manek-Honinger, et al. High-power rod-type photonic crystal fiber laser[J]. Opt. Express, 2005, 13(4): 1055-1058.
[4] Yanming Huo, Peter Cheo, George King. Fundamental mode operation of a 19-core phase-locked Yb-doped fiber amplifier[J]. Opt. Express, 2004, 12(25): 6230-6239.
[5] Li Xibin, Chai Lu, Zhang Yuying, et al. Study on spectral gain characterization of four-wave mixing in photonic crystal fiber [J]. Journal of Optoelectronics·laser, 2009, 20(2): 260-263.
[6] Kunimasa Saitoh, Masanori Koshiba. Highly nonlinear dispersion-flattened photonic crystal fibers for supercontinuum generation in a telecommunication window[J]. Opt. Express, 2004, 12(10): 2027-2032.
[7] Jacob Riis Folkenberg, Niels Asger Mortensen, Kim P. Hansen, et al. Experimental investigation of cutoff phenomena in nonlinear photonic crystal fibers[J]. Opt. Lett., 2003, 28(20): 1882-1884.
[8] J. C. Knight, T. A. Birks, R. F. Cregan, et al. Large mode area photonic crystal fibre[J]. Electronics Letters, 1998, 34(13): 1347-1348.
[9] N. A. Mortensen, M. D. Nielsen, J. R. Folkenberg, et al. Improved large-mode-area endlessly single-mode photonic crystal fibers[J]. Opt. Lett., 2003, 28(6): 393-395.
[10] J. Limpert, O. Schmidt, J. Rothhardt, et al. Extended single-mode photonic crystal fiber lasers[J]. Opt. Express, 2006, 14(7): 2715-2720.
[11] Yukihiro Tsuchida, Kunimasa Saitoh, Masanori Koshiba. Design of single-moded holey fibers with large-mode-area and low bending losses: the significance of the ring-core region[J]. Opt. Express, 2007, 15(4): 1794-1803.
光电子激光 光电子激光投稿20090096
[12] L. Michaille, C. R. Bennett, D. M. Taylor, et al. Multicore Photonic Crystal Fiber Lasers for High Power/Energy Applications[J]. Selected Topics in Quantum Electronics, IEEE Journal of, 2009, 15(2): 328-336.
[13] J. A.Besley, J. D. Love. Supermode analysis of fibre transmission[J]. IEE Proc. Optoelectron, 1997, 144(6): 411-419.
[14]Li Chaoyang, Yu Li, Zhang Xiaoguang, et al. Design of Photonic Crystal Fiber Using Full Vector Finite Element Method [J]. Journal of Optoelectronics·laser, 2007, 18(1): 30-35.
[15] R. W. Clough, J. Pengjing, Wang Guangyuan. Dynamics of Structure [M]. 2nd Edition.China:Higher Education Press,1995.
[16] L. Michaille, C. R. Bennett, D. M. Taylor, et al. Phase locking and supermode selection in multicore photonic crystal fiber lasers with a large doped area[J]. Opt. Lett., 2005, 30(13): 1668-1670.
[17] T. A. Birks, J. C. Knight, P. St J. Russell Endlessly single-mode photonic crystal fiber[J]. Opt. Lett., 1997, 22(13): 961-963.
[18]Zhou Pu, Hou Jing, Chen Zilun, et al. Study on the supermode and mode selection in multicore fiber laser[J]. Acta Optica Sinica, 2007, 27(010): 1812-1816.
[19] Krishna Mohan Gundu, Miroslav Kolesik, Jerome V. Moloney Mode shaping in multicore fibers[J]. Opt. Lett., 2007, 32(7): 763-765.
[20] A. Mafi, J. V. Moloney Shaping modes in multicore photonic crystal fibers[J]. Photonics Technology Letters, IEEE, 2005, 17(2): 348-350.
61阅读提醒您本文地址:
四 : 超大电视趋向“去屏化” 海信激光影院图谋超大屏市场
9月10日,海信正式发布了全球首套100英寸激光影院,正式将第四代显示技术推向市场。海信对激光影院寄予厚望,并表示,如同10年前平板电视对CRT的换代一样,从今天起,凭借高性价比,激光影院将角逐高成本的超大屏液晶电视。

“这就是一个 “去屏化”的过程,激光显示技术的出现真正摆脱了电视机对屏的依赖,打破了‘屏’高成本的制约,实现了更大尺寸、更高画质、更自然护眼以及更震撼的音效,成为电视机历史上又一次划时代显示技术的革命”,海信电器总经理刘洪新介绍。

专家认为,激光显示技术的应用在人类视觉史上意义重大,它达到了显示领域的“至高境界”,海信激光影院的面市,为超大尺寸电视需求的消费者提供了更好的选择。

海信VIDAAMAX激光影院与超大屏电视对比
海信激光影院克服了人眼长时间观看CRT、液晶电视直射发光源造成的不适感,用户看到的是屏幕的反射光线,柔和舒适,且因配备菲涅尔无源仿生屏幕,不受环境光限制,可全天候观看;在观看距离方面,激光影院采用短焦镜头,最佳观看距离4米左右,而85英寸超大屏幕电视收视距离要6米以上。

10多年前,平板电视以其超薄、节能、色域广、寿命长等突出的优势特点迅速替代了CRT电视,而海信正是抓住了显示技术升级的大机遇,准确预言了“平板电视将取代CRT电视”,率先启动平板化产业转型,一举奠定了平板电视市场销量第一的地位。今天,海信再次拉开显示技术升级的序幕,通过激光显示技术的应用,彻底打破了“屏”对显示技术的桎梏,激光显示具有的超高清、全色域、高亮度、屏幕尺寸灵活、节能护眼等优势都是液晶大平板电视无法比拟的。
业内专家预测,激光显示作为下一代显示技术,一旦产业化会有上千亿美元的市场规模。海信在激光显示领域已经有7年的技术储备,共取得50项发明专利、10项实用新型专利,依托自主技术创新,海信已经站到了行业前沿。
本文标题:激光投影电视-销售火爆 米家激光投影电视众筹结束61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1