一 : 抛物线的简单几何性质习题一(附答案)27
抛物线的简单几何性质习题一
【同步达纲练习】
A级
一、选择题
1.若A是定直线l外的一定点,则过A且与l相切圆的圆心轨迹是( )
A.圆 B.椭圆 C.双曲线一支
2
2.抛物线y=10x的焦点到准线的距离是( ) A.2.5
B.5
C.7.5
D.抛物线 D.10
3.已知原点为顶点,x轴为对称轴的抛物线的焦点在直线2x-4y+11=0上,则此抛物线的方程是( )
A.y=11x B.y=-11x C.y=22x D.y=-22x 4.过抛物线y2=2px(p>0)的焦点且垂直于x轴的弦AB,O为抛物线顶点,则∠AOB( ) A.小于90° C.大于90°
2
2
2
2
2
B.等于90° D.不能确定
5.以抛物线y=2px(p>0)的焦半径|PF|为直径的圆与y轴位置关系为( ) A.相交 B.相离 C.相切 D.不确定
二、填空题
6.圆心在抛物线y2=2x上,且与x轴和该抛物线的准线都相切的圆的方程是 .
7.若以曲线
x
2
25
+
y
2
16
=1的中心为顶点,左准线为准线的抛物线与已知曲线右准线交于
A、B两点,则|AB|= .
8.若顶点在原点,焦点在x轴上的抛物线截直线y=2x+1所得的弦长为,则此抛物线的方程是 .
三、解答题
9.抛物线x2=4y的焦点为F,过点(0,-1)作直线l交抛物线A、B两点,再以AF、BF为邻边作平行四边形FABR,试求动点R的轨迹方程.
10.是否存在正方形ABCD,它的对角线AC在直线x+y-2=0上,顶点B、D在抛物线y2=4x上?若存在,试求出正方形的边长;若不存在,试说明理由.
AA级
一、选择题
1.经过抛物线y2=2px(p>0)的所有焦点弦中,弦长的最小值为( ) A.p B.2p C.4p D.不确定
2
2.直线y=kx-2交抛物线y=8x于A、B两点,若AB的中点横坐标为2,则|AB|为( )
A. B.4 C.2 D.42
3.曲线2x2-5xy+2y2=1( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称,但不关于y=x对称
D.关于直线y=x对称也关于直线y=-x对称
4.若抛物线y=2px(p>0)的弦PQ的中点为(x0,y0)(y≠0),则弦PQ的斜率为( ) A.-px0
2
2
B.
py0
C.px- D.-px0
5.已知抛物线y=2px(p>0)的焦点弦AB的两端点坐标分别为A(x1,y1),B(x2,y2),则y1y2x1x2
的值一定等于( )
B.-4
C.p2
D.-p2
A.4
二、填空题
2
6.抛物线y=4x的弦AB垂直于x轴,若AB的长为43,则焦点到AB的距离
为 .
7.以椭圆
x
2
5
+y2=1的右焦点F为焦点,以原点为顶点作抛物线,抛物线与椭圆的一个
公共点是A,则|AF|= .
8.若△OAB为正三角形,O为坐标原点,A、B两点在抛物线y2=2px上,则△OAB的周长为 .
三、解答题
9.抛物线y=-x
2
2
与过点M(0,-1)的直线l相交于A、B两点,O为坐标原点,若直线
OA和OB斜率之和为1,求直线l的方程.
10.已知半圆的直径为2r,AB为直径,半圆外的直线l与BA的延长线垂直,垂足为T,且|TA|=2a(2a<
r2
),半圆上有M、N两点,它们与直线l的距离|MP|、|NQ|满足条件|
MP|=|AM|,|NQ|=|AN|,求证:|AM|+|AN|=|AB|.
【素质优化训练】 一、选择题
1.过点A(0,1)且与抛物线y2=4x有唯一公共点的直线的条数为( )
A.1
2
B.2 C.3 D.4
2.设抛物线y=ax(a>0)与直线y=kx+b相交于两点,它们的横坐标为x1,x2,而x3是直线与x轴交点的横坐标,那么x1、x2、x3的关系是( )
A.x3=x1+x2
13
B.x3=
1x1
+
1x2
C.x1x2=x2x3+x3x1 D.x1x3=x2x3+x1x2
3.当0<k<时,关于x的方程
B.1个
2?x=kx的实根的个数是( )
A.0个 是( )
C.2个 D.3个
4.已知点A(1,2),过点(5,-2)的直线与抛物线y2=4x交于另外两点B、C,则△ABCA.锐角三角形
B.钝角三角形
C.直角三角形 D.不确定
5.将直线x-2y+b=0左移1个单位,再下移2个单位后,它与抛物线y2=4x仅有一个公共点,则实数b的值等于( )
A.-1 B.1
C.7
D.9
二、填空题
6.抛物线y2=-8x被点P(-1,1)所平分的弦所在直线方程为 .
7.已知抛物线y=2x的弦过定点(-2,0),则弦AB中点的轨迹方程是 . 8.已知过抛物线y2=2px的焦点F的弦AB被F分成长度为m、n的两部分,则
1m
2
+
1n
= .
三、解答题
9.已知圆C过定点A(0,p)(p>0),圆心C在抛物线x2=2py上运动,若MN为圆C在x轴上截得的弦,设|AM|=m,|AN|=n,∠MAN=θ.(1)当点C运动时,|MN|是否变化?写出并证明你的结论?(2)求
10.已知抛物线y2=4ax(0<a<1)的焦点为F,以A(a+4,0)为圆心,|AF|为半径在x轴上方作半圆交抛物线于不同的两点M和N,设P为线段MN的中点,
(Ⅰ)求|MF|+|NF|的值;
(Ⅱ)是否存在这样的a值,使|MF|、|PF|、|NF|成等差数列?如存在,求出a的值,若不存在,说明理由.
【生活实际运用】
1.已知点P(x0,y0)在抛物线含焦点的区域内,求证以点P为中点的抛物线y=2px(p>0)的中点弦方程为
yy0-p(x+x0)=y20-2px0
注:运用求中点弦的方法不难求出结论,这一结论和过抛物线y2=2px上点的切线方程有什么联系?
2
nm
+
mn
的最大值,并求取得最大值时θ的值和此时圆C的方程.
若P(x0,y0)为非对称中心,将抛物线y=2px换成椭圆
2
xa
22
+
yb
22
=1或双曲线
xa
22
-
yb
22
=1,
它们的中点弦存在的话,中点弦方程又将如何?证明你的结论. 中点弦方程在高考中多以选择题、填空题的形式出现.
2.公园要建造一个圆形的喷水池,在水池中央垂直于水面安装一个柱子OA,O恰在圆形水面中心,OA=1.25米.安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路经落下,且在过OA的任一平面上抛物线路径如图所示,为使水流形状较为漂亮,设计成水流在到OA距离1米处达到距水面最大高度2.25米.如果不计其它因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外
?
分析 根据图形的对称性,设出并求出一边的抛物线的方程,便可求出水池的半径. 以OA所在直线为y轴,过O点作oy轴的垂直线ox轴,建立直角坐标系如图
依题意A(0,1.25),设右侧抛物线顶点为则B(1,2.25),抛物线与x轴正向交点为C,OC即圆型水池的半径.
设抛物线ABC的方程为 (x-1)2=-2p(y-2.25) 将A(0,1.25)代入求得p=
2
12
∴抛物线方程为(x-1)=-(y-2.25) 令y=0,(x-1)2=1.52,x=2.5(米)
即水池的半径至少要2.5米,才能使喷出的水流不致落到池外.
【知识验证实验】
1.求函数y=
x?3x?6x?13-2
2
42
x?x?1的最大值.
2
42
解:将函数变形为y=(x?3)?(x?2)-x?(x?1),由几何意义知,y可以看成在抛物线f(x)=x2上的点P(x,x2)到两定点A(3,2)和B(0,1)的距离之差,∵|PA|-|PB|≤|AB|,∴当P、A、B三点共线,且P在B的左方时取等号,此时P点为AB与抛物线的交点,即P为(
1?
637
222
,
19?
18
37
)时,ymax=|AB|=.
2.参与设计小花园的喷水池活动. 要求水流形状美观,水流不落池外.
【知识探究学习】
1.如图,设F是抛物线的焦点,M是抛物线上任意一点,MT是抛物线在M的切线,MN
是法线,ME是平行于抛物线的轴的直线.求证:法线MN必平分∠FME,即φ1=φ2
.
解:取坐标系如图,这时抛物线方程为y=2px.(p>0),因为ME平行x轴(抛物线的轴),
2
∴φ1=φ2,只要证明φ1=φ3,也就是△FMN的两边FM和FN相等.设点M的坐标为(x0,y0),则法线MN的方程是y-y0=-p2
y0p
(x-x0),令y=0,便得到法线与x轴的交点N的坐标(x0+p,0),所
p2
p2
以|FN|=|x0+p-|=x0+,又由抛物线的定义可知,|MF|=x0+,∴|FN|=|FM|,
由此得到φ1=φ2=φ3,若M与顶点O重合,则法线为x轴,结论仍然成立. 2.课本第124页阅读材料:
圆锥曲线的光学性质及其应用
参考答案
【同步达纲练习】
A级
1.D 2.B 3.D 4.C 5.C 6.(x-12
1003
)2+(y±1)2=1 7. 8.y2=12x或y2=-4x
x2
9.解:设R(x,y),∵F(0,1),∴平行四边形FARB的中心为C(
2
,
y?12
),l:y=kx-1,代入
2
抛物线方程,得x-4kx+4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=4,且△=16k-16>0,即|k|>1 ①,
∴y1+y2=
x1?x2
4
2
2
=
(x1?x2)?2x1x2
4
2
=4k2-2,∵C为AB的中点.∴
x1?x2?x??2k??x?4k?222
??消去k得x=4(y+3),由①得,|x|>4,故动?2
?y?4k?3?y?1?y1?y2?2k2?1
?2?2
点R的轨迹方程为x2=4(y+3)(|x|>4).
10.解:设存在满足题意的正方形.则BD:y=x+b,代入抛物线方程得x2+(2b-4)x+b2=0,∴△=(2b-4)2-4b2=16-16b>0,∴b<1, ①,设B(x1,y1),D(x2,y2),BD中点M(x0,y0),则x1+x2=4-2b,∴x0=2-b,y0=x0+b=2,∵M在AC直线上,∴(2-b)+2-2=0,∴b=2与①相矛盾,故
抛物线的简单几何性质习题一(附答案)27_抛物线的几何性质
不存在满足要求的正方形.
AA级
1.B 2.C 3.D 4.B 5.B 6.2 7.95-18 8.123p
x
2
9.解:设l:y=kx-1,代入y=-
2
,得x2+2kx-2=0,设A(x1,y1),B(x2,y2),则
x1+x2=-2k,x1x2=-2,又程为y=x-1.
y1x1
+
y2x2
=
kx1?1x1
+
kx2?1x2
=2k-
x1?x2x1x2
=2k-
?2k?2
=k=1,∴直线l的方
10.证明:由|MP|=|AM|,|NQ|=|AN|知M、N在以l准,A为焦点的抛物线上,建立直角坐标系,设抛物线方程为y=2px,又|TA|=2a=p,∴抛物线方程为y=4ax,又圆的方
程为(x-a-r)2+y2=r2,将两方程相减可得:x2+2(a-r)x+a2+2ar=0,设M(x1,y1),N(x2,y2),则x1+x2=2r-2a,∴|AM|+|AN|=|PM|+|QN|=x1+x2+2a=2r,即|AM|+|AN|=|AB|
【素质优化训练】
1.C 2.C 3.D 4.C 5.C 6.4x+y+3=0 7.y2=x+2(在已知抛物线内部的部分) 8.
p2
2
2
9.解:(1)设圆心C(x0,y0),则x20=2py0,圆C的半径|CA|=x0?(y0?p),其方程
2
2
为(x-x0)2+(y-y0)2=x20+(y0-p)2,令y=0,并将x20=2py0,代入,得x2-2x0x+x20-p2=0,解得xm=x0-p,xN=x0+p,∴|MN|=|xN-xM|=2p(定值)
(2)∵m=|AM|=
2
2
2
20
(x0?p)?p
40
22
,n=|AN|=m?nmn
2
2
(x0?p)?p
2
22
,∴=
m+n=4p+2x,m2n=4p?x,∴
4
nm
+
mn
==
4p?2x04p?x
4
2
40
=
4p(p?y0)2p
p?y
2
20
2(p?y0)p?y
2
20
=2?
2py0p?y0
2
2
≤22,当且仅当y0=p时等号成立,x0=±2p,此时△MCN
12
为等腰直角三角形,且∠MCN=90°,∴∠MAN=∠MCN=45°,故当θ=45°时,圆的方程为
(x-2 p)2+(y-p)2=2p2或(x+2p)2+(y-p)2=2p2
10.解:(1)由已知得F(a,0),半圆为[x-(a+4)]2+y2=16(y≥0),设M(x1,y1),N(x2,y2),则|MF|+|NF|=x1+x2+2a=2(4-a)+2a=8
(2)若|MF|、|PF|、|NF|成等成数列,则有2|PF|=|MF|+|NF|,另一方面,设M、P、N在抛物线的准线上的射影为M′、P′、N′,则在直角梯形M′MNN′中,P′P是中位线,又有2|P′P|=|M′M|+|N′N|=|MF|+|FN|,因而|PF|=|P′P|,∴P点应在抛物线上,但P点是线段MN的中点,即P并不在抛物线上,故不存在使|MF|、|PF|、|NF|成等差数列的a值.
第 6 页 共 6 页
二 : 几度浮沉:“科技天才”李一男的抛物线人生
时代周报记者 王媛 发自广州、深圳
李一男最近一次公开亮相还要追溯到2015年的6月1日。当时,身为牛电科技创始人的李一男高调登台,发布牛电科技首款产品—小牛电动车N1,李一男声称这是他“最后一次创业”。

当时有媒体问李一男“功名显赫为何还老折腾”,李说:“做这样的选择是形势所迫。”他还补充说,“一流的人生,就是看着别人犯错误,自己不犯错误,吸取经验教训;二流的人生,是自己犯错误,自己吸取教训;三流的人生,是自己犯错误,自己还不吸取教训。我学习还不够及时,目前还只是二流的人生。”
当时的一席话,如今看来更像是一语成谶。
在这次亮相仅仅两天之后,李一男因涉嫌内幕交易罪被深圳市公安局刑事拘留,至此再未出现在公众视野。
时代周报记者发现,被抓当天,李一男的微博依旧在跟美团网的王兴互动。而他43万粉丝的微博,直到今年1月22日,仍以每日更新的频率在“虚构”着李一男的存在。
关于牛电科技目前的经营情况是否会受创始人李一男被捕影响,牛电科技方面人士在电话中向时代周报记者表示:暂时无可奉告。
3月16日,牛电科技官方微博对外表示:李一男因以往私人案件,正在配合司法部门调查与诉讼,目前仍能以适当方式参与公司重大事项的决策和运营,目前牛电科技一切运转正常。
李一男被业内称为“少年得志的技术天才”, 23岁进入华为,27岁成为华为最年轻的副总裁,曾被任正非亲切称为“红孩儿”,被李彦宏视之为“全世界能担百度CTO大任的三人之一”。
出走华为后,李相继履职百度、中移动、金沙江创投,历经港湾网络、牛电科技二次创业,不过,李一男的事业轨迹,却犹如抛物线般高开低走,一直难以复制其最初在通信领域的辉煌战绩和显赫功名,但或许谁也没想到,这条抛物线最终会因为李一男被刑拘而触底。
事发或因举报
根据检方材料,早在2015年6月3日,李一男就因涉嫌内幕交易罪被深圳市公安局刑事拘留,李一男涉嫌内幕交易发生于其在金沙江创投任职期间。
检方指控称:李一男在2014年4月,通过其妹夫和母亲的股票交易账户,满仓武汉华中数控股份有限公司(300161.SZ),成交额达到1148万余元,实际获利508万元。他还让自己的妹妹同期购买该华中数控,成交金额在499万余元,实际获利有236万余元。
“李一男之所以选股精准,是因为在华中数控并购重组的内幕信息敏感期内,与华中数控总裁李晓涛多次联络、接触。”检方指控材料如此描述。
据时代周报记者了解,李晓涛与李一男是华中科技大学校友,两人同于1993年进入华为公司共事,李晓涛历任干部部部长、研发管理部副总裁、公司高级副总裁,2012年5月,出任华中数控总裁,于2014年12月21日去职。
对于指控,李一男3月15日在深圳市中级人民法院受审时否认自己内幕操作,称与李晓涛私交一般,买卖华中数控是因为自己一贯的投资风格,也从未暗示过家人买入。
目前案件仍在审理之中。
据时代周报记者了解,李晓涛目前似乎并未因此事受牵连,有人向记者表示,因为李晓涛或并没有从中获利。
多位投资圈的人士向时代周报记者分析称,“华为2008年一位一级部门总裁年薪都按千万元计,何况是高级副总裁,按照常理来说,李一男本没有必要通过内幕交易获利。”
多位与李一男曾有过工作交集的人士向时代周报记者猜测,李一男此次出事是因为被举报。
“李一男被举报,有几点可以断定:第一,和华为没有关系,他和华为那一页早就翻篇了;第二,李一男的财富非常大,这点钱估计不是故意的,真的要做也是基金吧,那规模大多了;第三,李一男很可能没有意识到触及内幕消息交易了。”一位曾供职华为的人力部知情人士向时代周报记者分析称。
被问及所谓“内幕交易”和举报背后的内幕因由,深圳公安局一了解此案的经侦人士称敏感时期不愿多谈,仅向时代周报记者感慨道:“此人确实情商不高。”
资本投资博得10亿元身家
1970年出生于湖南长沙的李一男,15岁便考入原华中理工大学(现为华中科技大学)少年班,1993年硕士毕业后加入华为。短短两个星期后,因解决一项技术难题,李一男被破格聘为高级工程师,半年后,出任华为重要的中央研究部副总经理。
1997年,年仅27岁的李一男成为华为最年轻的副总裁。李一男在华为的火箭式上升,并不是因为靠关系,而是源于对技术的研究和判断能力。
作为一个少年得志的技术天才,凭借过人的头脑,李一男“吸睛”和“吸金”的能力自然不弱,甚至成为一股备受“热钱”追捧的强劲势能。这一点,从李一男的电动车产品仍未出世,就已经获得GGV、IDG、红杉、创新工场李开复、真格基金徐小平、明势资本、梅花天使等多家明星机构5000万美元真金白银的投票便可窥一斑。
而据时代周报记者独家调查发现,早在2013年,李一男的另外一段鲜为人道的投资经历,便让其斩获颇丰,获利近10亿。
时代周报记者查阅到杭州新世纪信息技术股份有限公司(002280)在2014年7月4日发布的《重大资产置换及发行股份购买资产并募集配套资金暨关联交易预案》,这份标的是数字天域的预案,6名自然人交易对象中惊现李一男。
根据预案,新世纪拟以重大资产置换、发行股份购买资产、发行股份募集配套资金的方式收购北京数字天域100%股权。
具体而言,就是数字天域100%股权预估值约为21.3亿元,拟置出资产净值预估值约为4.3亿元,扣除分红4280.00万元,拟置出资产作价约3.9亿元,两者差额约为17.4亿元部分,将向数字天域包括何志涛、李一男在内的11名股东发行股份购买,对应的发行数量约为13523.4万股。发行价格为12.86元每股。其中,向李一男发行股票641.685万股,占发行后总股本的2.28%。
成立于2002年的数字天域在移动互联网圈有一个不少人都曾熟知的名字:好联络。2010年,中国移动互联网真正意义上的“元年”,一些公司开始意识到智能机的爆发,积极开始尝试智能机转型,好联络就是其中的一家。
时代周报记者梳理新世纪预案公告、历年财报以及数字天域工商资料获悉,2012年9月,数字天域为引入行业优秀人才,增强公司董事会决策能力,引入李一男为公司股东。李一男合计出资284.67万,直接持有数字天域4.745%的股份,是数字天域的董事。
另外,时代周报记者查阅到2014年新世纪的一份调研报告中指出,新世纪的商户云搜索,也就是号码黄页3.0时代,将由李一男来主导。
2014年9月24日,新世纪重大资产置换及发行股份购买资产并募集配套资金暨关联交易事项获得无条件审核通过。同年12月17日,新世纪发布《重大资产置换及发行股份购买资产并募集配套资金暨关联交易实施情况暨新增股份上市公告书》,相关资产重组正式成功。
时代周报记者通过全国工商管理系统查阅的工商资料不完全统计,李一男还持有易美云(北京)信息技术有限公司47.33%的股权并担任董事长,担任GRE VENTURE的投资合伙人,持有北京无限时空网络技术有限公司4.17%的股权,持有北京悦学科技有限公司24.5%的股权。
值得注意的是,上述《预案》披露,数字天域的最大单一股东壹通讯香港,持有其37.472%股份,持有壹通讯香港100%股权的壹通讯控股背后,则隐藏着创投大鳄红杉资本,持有壹通讯控股41.41%股权,风投公司光速创投持股34.41%,英菲尼迪持股15.17%, Sure Great持股6.5%,这些资本大鳄或为数字天域借壳上市的幕后推手。
数字天域借壳“新世纪”成功上市后,李一男持股641.685万股,占比2.28%,跻身新世纪十大股东之列。
2015年3月,新世纪改名联络互动。该年4月份,联络互动实施2014年度权益分派方案,每10股派发现金股利人民币2元,以资本公积金转增股本的方式向全体股东每10股转增15股。
截至2015年三季度,李一男共持联络互动1604.21万股,持股比例2.28%。2015年12月16日,李一男于2014 年重大资产重组取得的联络互动股份12个月的禁售承诺解禁。令人吊诡的是,尽管2015年6月李一男就已处于刑事拘留状态,但截至2015年12月31日,联络互动十大股东中已无李一男身影。
时代周报记者一时无法查证李一男所持联络互动股票的处置情况,但可以明确的是,自2015年12月17日起至12月31日之间,联络互动的股价均价在60元左右。李一男掌握的1604.21万股票,当时价值高达9.6亿元。
几度沉浮
“他是少年班出身,被当成神童看,而且智商超群,才会折服任正非。”不愿具名的原华为的一技术部门人士向时代周报记者谈道。
众所周知,李一男第一次出走华为的时候位居高级副总裁。被任正非亲切称呼为“干儿子”的李一男为什么会出走?迄今仍然是一个谜。
华为前副总裁刘平曾在其回忆录《华为往事》中所写或可为参考。刘平谈到,任正非再伟大,也曾有中国传统的“父业子承”观念。他一手创建的华为帝国最理想的继承人就是他的儿子任平。
刘平在《华为往事》中写到这样一个细节:
“在李一男第一次向我透露他将离开华为的消息时,我吃惊地问他:‘你不是老板的接班人吗?怎么会想离开华为呢?’”
李一男笑了笑,说:“哪里轮得到我呀。”以他的性格,他是不可能在任平的领导下工作的,所以只有早做打算。
上述华为前技术部门人士亦向时代周报记者表示,内部流传是和任正非儿子任平不合,应该是一山不能容二虎,直到任正非站出来说不定立接班人,以轮值CEO替代。
于是,2000年底,被业内认为是任正非接班人的李一男,拿着从华为股权结算和分红的1000多万元,赴北京创办港湾网络,成为华为企业网产品的高级分销商。
在李一男离开之际,任正非的态度显然是支持的,其在五洲宾馆举办级别隆重的欢送会,要求公司高层悉数出席,期望港湾成为华为内部创业的典范。
不料,2001年,有“小华为”之称的港湾推出路由器和交换机等产品,从华为的代理商变成竞争对手,业务冲突导致关系破裂进而难逃收购厄运。
2006年华为收购港湾时,任正非甚至用了四个字来形容这场胜利:“惨胜如败。”
上述知情人士还告诉时代周报记者:“内部流传的版本是,当时华为本要裁掉所有港湾员工,但李以自身为代价,保住员工。但重回华为后,李一男仍为副总裁,但在终端公司任虚职,挂名华为首席科学家,办公室透明玻璃朝外,李感觉客户来时看他如同观动物园熊猫似的,并深感受辱,后来合同期满便旋即离开。”
2008年10月,李一男出任百度首席技术官。在百度期间,其领导了百度“阿拉丁”等计划的研发。2010年2月至2011年7月,李一男出任中国移动旗下无限讯奇12580 CEO, 2011年8月,李一男又以合伙人身份加盟金沙江创投,此后似乎一直没有开创性的成绩。
直至2015年,李一男联合创办智能电动车公司,出任牛电科技CEO,将其视之为自己的最后一次创业。李一男选择的电动车行业,无疑是一个风口:在中国保有量2亿辆,年销售量1800万的规模,养活了2000多家厂商,最大的爱玛年销量是250万辆。
然而,作为一家光环闪耀的创业公司,牛电科技享受了光芒四射的福利,就意味着必须背负着外界的高预期和低容忍度。去年至今,电动车轮彀问题备受诟病。而小牛电动在去年6月完成的7200万元的“众筹神话”,实质上也是大多基于资本和粉丝对李一男个人的信任与支持。现在,暂时失去灵魂人物李一男的牛电科技,还能不能继续吸引资本的青睐,仍是一个未知数。
三 : 抛物线的几何性质

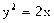 ,设A(
,设A(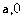 )(
)(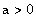 ),P是抛物线上的一点,且
),P是抛物线上的一点,且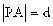 ,试求
,试求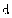 的最小值。
的最小值。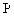 (
(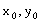 )(
)(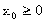 ) 则
) 则
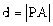
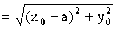
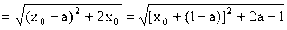
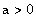 ,
,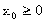
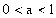 时,
时, ,此时当
,此时当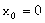 时,
时,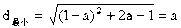
 时,
时,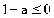 ,此时当
,此时当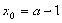 时,
时,
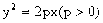 的焦点作倾斜角为
的焦点作倾斜角为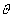 的直线
的直线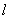 ,设
,设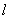 交抛物线于A、B两点,求
交抛物线于A、B两点,求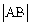 。
。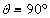 时,直线AB的方程为
时,直线AB的方程为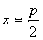
 得A(
得A(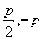 )、B(
)、B(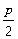 ,
,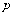 ) ∴
) ∴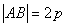
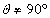 时,直线AB的方程为
时,直线AB的方程为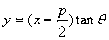
 得
得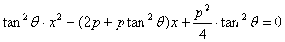
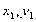 )、B(
)、B(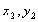 ),则
),则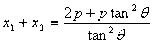

 的准线与对称轴的交点作直线,交抛物线于M、N两点,问直线的倾斜角多大时,以线段MN为直径的圆经过抛物线的焦点?
的准线与对称轴的交点作直线,交抛物线于M、N两点,问直线的倾斜角多大时,以线段MN为直径的圆经过抛物线的焦点? 的准线与对称轴的交点为(
的准线与对称轴的交点为(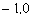 ),设直线MN的方程为
),设直线MN的方程为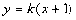
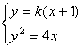 得
得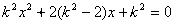
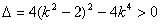
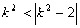 ,
,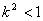 ,
,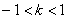
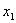 ,
,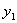 ),N(
),N(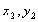 ),抛物线焦点为F(1,0)
),抛物线焦点为F(1,0)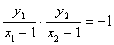 即
即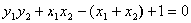
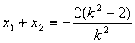 ,
,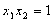 ,
,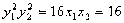 且
且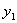 、
、 同号
同号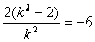 解得
解得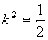 ∴
∴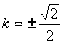
 或
或 时,以线段MN为直径的圆经过抛物线的焦点。
时,以线段MN为直径的圆经过抛物线的焦点。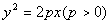 的焦点F的直线与抛物线交于A、B两点,求
的焦点F的直线与抛物线交于A、B两点,求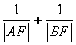 的值。
的值。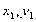 )、B(
)、B(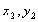 ),AB的方程为
),AB的方程为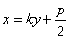
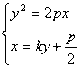 得
得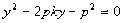 ∴
∴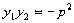
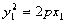 ,
,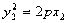 ∴
∴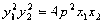
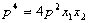 ∴
∴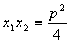 又
又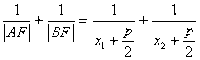


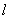 :
: 交抛物线
交抛物线 于A、B两点,试在抛物线AOB这段曲线上求一点P,使
于A、B两点,试在抛物线AOB这段曲线上求一点P,使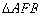 的面积最大,并求这个最大面积。
的面积最大,并求这个最大面积。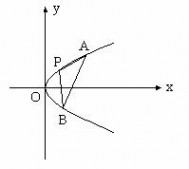
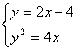 解得A(4,4)、B(1,
解得A(4,4)、B(1,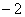 ),知
),知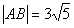 ,所以直线AB的方程为
,所以直线AB的方程为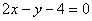
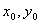 )为抛物线AOB这条曲线上一点,
)为抛物线AOB这条曲线上一点, 为P点到直线AB的距离
为P点到直线AB的距离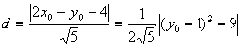 ∵
∵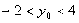
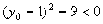 ∴
∴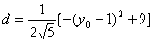
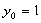 时,
时,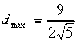
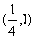 时,
时,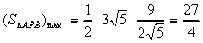
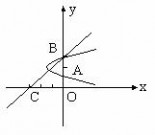
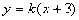 与曲线
与曲线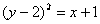 在第一象限有公共点,求
在第一象限有公共点,求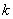 的取值范围。
的取值范围。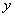 轴交于A(0,1)、B(0,3)
轴交于A(0,1)、B(0,3)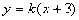 恒过C(
恒过C(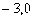 ),由图象及抛物线的延伸趋势可知
),由图象及抛物线的延伸趋势可知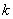 大于零且小于BC的斜率
大于零且小于BC的斜率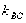 时满足题意
时满足题意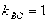 ,故
,故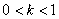 。
。
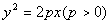 的焦点为F,经过点F的直径交抛物线于A、B两点,点C在抛物线的准线上,且BC//
的焦点为F,经过点F的直径交抛物线于A、B两点,点C在抛物线的准线上,且BC//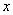 轴,证明:直线AC经过原点O。
轴,证明:直线AC经过原点O。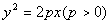 的焦点坐标为F(
的焦点坐标为F(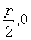 )
)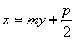
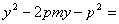 0
0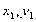 )、B(
)、B(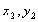 ),则
),则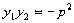
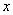 轴,且点C在准线
轴,且点C在准线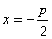 上 ∴ 点C的坐标为
上 ∴ 点C的坐标为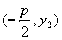
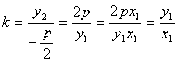
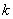 也是OA的斜率,所以直线AC经过原点O
也是OA的斜率,所以直线AC经过原点O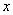 轴与抛物线准线
轴与抛物线准线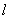 的交点为E,过点A作AD⊥
的交点为E,过点A作AD⊥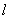 ,D为垂足
,D为垂足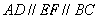 。连结AC,与EF相交于N,则
。连结AC,与EF相交于N,则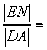
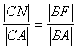
 ,根据抛物线的几何性质,得
,根据抛物线的几何性质,得 ,
,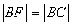
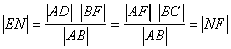

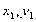 )、B(
)、B(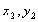 ),由已知C得
),由已知C得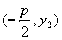
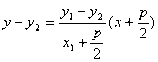 ,把原点的坐标代入,得
,把原点的坐标代入,得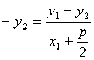
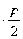 利用
利用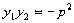 得上面等式恒成立
得上面等式恒成立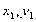 )、B(
)、B(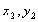 ),由已知得C(
),由已知得C(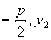 ),
),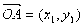
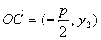

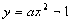 上总有关于直线
上总有关于直线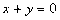 对称的相异两点,试求
对称的相异两点,试求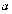 的范围。
的范围。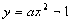 上关于
上关于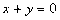 对称的相异两点坐标为A(
对称的相异两点坐标为A(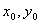 )、B(
)、B( )
)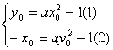
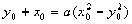 ∵
∵ ∴
∴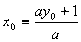 (3)
(3)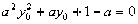
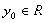 ,且
,且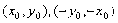 相异 ∴
相异 ∴
 ∴
∴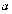 的取值范围是(
的取值范围是(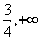 )
)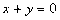 对称的两点所在直线方程为
对称的两点所在直线方程为 ,代入
,代入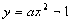 ,得
,得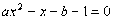
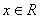 ,且两点为相异两点 ∴
,且两点为相异两点 ∴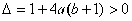
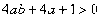 (1) 设两对称点为A(
(1) 设两对称点为A(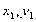 )、B(
)、B(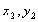 )
)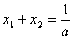 ,
,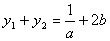 又 ∵
又 ∵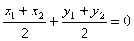
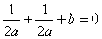 ,即
,即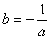 (2)
(2) ∴
∴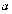 的取值范围是(
的取值范围是(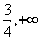 )
)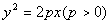 ,O为抛物线的顶点,OA⊥OB,则
,O为抛物线的顶点,OA⊥OB,则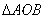 的面积是( )
的面积是( )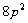 B.
B.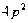 C.
C.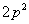 D.
D.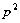
 )在抛物线
)在抛物线 上,则
上,则 的最小值是( )
的最小值是( )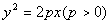 上两点,O为坐标原点,若
上两点,O为坐标原点,若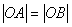 且
且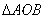 的垂心恰是此抛物线的焦点F,则直线AB的方程是( )
的垂心恰是此抛物线的焦点F,则直线AB的方程是( )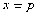 B.
B.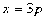 C.
C. D.
D.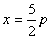
 ),
),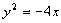 的焦点是F,P是
的焦点是F,P是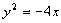 上的点,为使
上的点,为使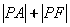 取得最小值,P点的坐标是( )
取得最小值,P点的坐标是( )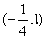 B.
B.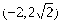 C.
C.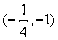 D.
D.
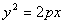 与直线
与直线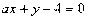 的一个交点是(1,2),则抛物线的焦点到直线的距离为( )
的一个交点是(1,2),则抛物线的焦点到直线的距离为( ) B.
B.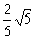 C.
C. D.
D.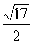
 的焦点F,点P在抛物线上,若
的焦点F,点P在抛物线上,若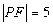 ,则P点的坐标为( )
,则P点的坐标为( )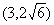 B.
B.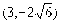 C.
C.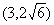 或
或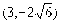 D.
D.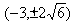
 的焦点作直线交抛物线于A(
的焦点作直线交抛物线于A(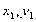 )、B(
)、B(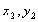 )两点,如果
)两点,如果 ,那么
,那么 ( )
( )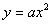 (
(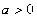 )的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是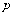 、
、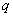 ,则
,则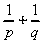 的值为( )
的值为( )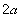 B.
B.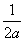 C.
C.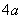 D.
D.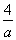
 的焦点,倾斜角为
的焦点,倾斜角为 的直线被抛物线截得的弦长为 。
的直线被抛物线截得的弦长为 。 的焦点为F,准线
的焦点为F,准线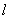 交
交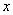 轴于点R,过抛物线上一点P(4,4)作PQ⊥
轴于点R,过抛物线上一点P(4,4)作PQ⊥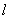 于点Q,则梯形PQRF的面积是 。
于点Q,则梯形PQRF的面积是 。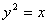 的一条焦点弦,且
的一条焦点弦,且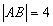 ,则线段AB的中点C到直线
,则线段AB的中点C到直线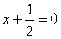 的距离是 。
的距离是 。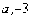 )到焦点的距离为5,则抛物线方程为 。
)到焦点的距离为5,则抛物线方程为 。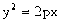 上有三点A(
上有三点A(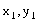 )、B(
)、B(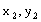 )、C(
)、C( )且
)且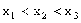 ,若线段AB、BC在
,若线段AB、BC在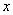 轴上射影之长相等,求证:A、B、C三点到焦点的距离顺次成等差数列。
轴上射影之长相等,求证:A、B、C三点到焦点的距离顺次成等差数列。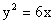 的顶点作互相垂直的两条直线,交抛物线于A、B两点,求线段AB中点的轨迹方程
的顶点作互相垂直的两条直线,交抛物线于A、B两点,求线段AB中点的轨迹方程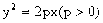 的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥
的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥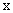 轴。证明:直线AC经过原点O。
轴。证明:直线AC经过原点O。
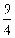 4.
4.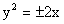 或
或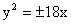 或
或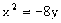
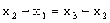 ,即
,即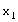 、
、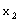 、
、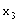 成等差数列
成等差数列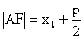 ,
,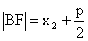 ,
,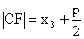
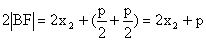
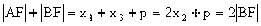
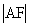 、
、 、
、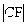 成等差数列
成等差数列 ),OA的斜率为
),OA的斜率为 ,则直线
,则直线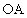 的方程为
的方程为
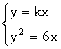 得
得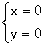 或
或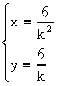 依题意得A点的坐标为A(
依题意得A点的坐标为A(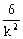 ,
,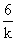 )
)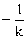 ,直线OB的方程为
,直线OB的方程为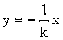
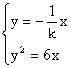 得
得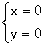 或
或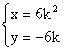 ∴ B点的坐标为
∴ B点的坐标为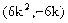
 )满足
)满足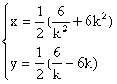 即
即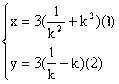
 为所求。
为所求。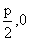 )
)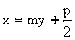
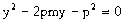
 ,则
,则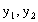 是该方程的两根 ∴
是该方程的两根 ∴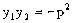
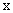 轴,且点C在准线
轴,且点C在准线 上
上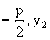 ) ∴ 直线OC的斜率为
) ∴ 直线OC的斜率为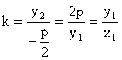
 也是直线OA的斜率 ∴ 直线AC经过原点O 本文标题:抛物线的几何性质-抛物线的简单几何性质习题一(附答案)27
也是直线OA的斜率 ∴ 直线AC经过原点O 本文标题:抛物线的几何性质-抛物线的简单几何性质习题一(附答案)27 61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1