一 : 已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象
| 已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24)。 (1)求f(x); (2)若不等式(  )x+( )x+(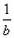 )x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围。 )x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围。 |
解:(1)把A(1,6),B(3,24)代入f(x)=b·ax,得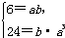 结合a>0且a≠1,解得 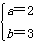 ∴f(x)=3·2x。 (2)要使 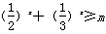 在(-∞,1]上恒成立 在(-∞,1]上恒成立只需保证函数  在(-∞,1]上的最小值不小于m即可 在(-∞,1]上的最小值不小于m即可∵函数 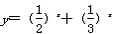 在(-∞,1]上为减函数 在(-∞,1]上为减函数∴当x=1时, 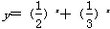 有最小值 有最小值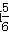 ∴只需  即可。 即可。 |
考点:
考点名称:指数函数的解析式及定义(定义域、值域)指数函数的定义:
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R,值域是(0,+∞)。
指数函数的解析式:
y=ax(a>0,且a≠1)
理解指数函数定义,需注意的几个问题:
①因为a>0,x是任意一个实数时,ax是一个确定的实数,所以函数的定义域为实数集R.
②规定底数a大于零且不等于1的理由: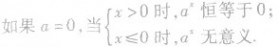
如果a<0,比如y=(-4)x,这时对于![]()
![]() 在实数范围内函数值不存在.
在实数范围内函数值不存在.
如果a=1,y=1x=1是一个常量,对它就没有研究的必要,
为了避免上述各种情况,所以规定a>0且a≠1.
③像![]() 等函数都不是指数函数,要注意区分。
等函数都不是指数函数,要注意区分。
指数函数y=ax(a>0,且a≠1)的图象和性质:
| 0<a<1 | a>1 | ||
| 图像 | 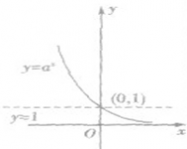 | 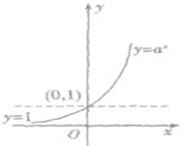 | |
| 图像 | 定义域 | R | |
| 值域 | (0,+∞) | ||
| 恒过定点 | 图像恒过定点(0,1),即当x等于0时,y=1 | ||
| 单调性 | 在(-∞,+∞)上是减函数 | 在(-∞,+∞)上是增函数 | |
| 函数值的变化规律 | 当x<0时,y>1 | 当x<0时,0<y<1 | |
| 当x=0时,y=1 | 当x=0时,y=1 | ||
| 当x>0时,0<y<1 | 当x>0时,y>1 | ||
底数对指数函数的影响:
①在同一坐标系内分别作函数的图象,易看出:当a>l时,底数越大,函数图象在第一象限越靠近y轴;同样地,当0<a<l时,底数越小,函数图象在第一象限越靠近x轴.
②底数对函数值的影响如图.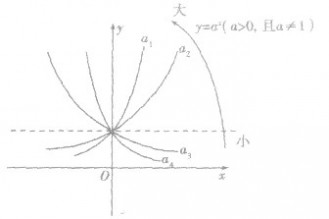
③当a>0,且a≠l时,函数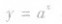 与函数y=
与函数y=![]() 的图象关于y轴对称。
的图象关于y轴对称。
利用指数函数的性质比较大小:
若底数相同而指数不同,用指数函数的单调性比较:
若底数不同而指数相同,用作商法比较;
若底数、指数均不同,借助中间量,同时要注意结合图象及特殊值,
指数函数图象的应用:
函数的图象是直观地表示函数的一种方法.函数的很多性质,可以从图象上一览无余.数形结合就是几何与代数方法紧密结合的一种数学思想.指数函数的图象通过平移、翻转等变可得出一般函数的图象.利用指数函数的图象,可解决与指数函数有关的比较大小、研究单调性、方程解的个数、求值域或最值等问题.
二 : 高一数学以知函数F(X)=log3[(mx^2+8x+n)/(x
高一数学
以知F(X)=log3[(mx^2+8x+n)/(x^2+1)],值域为[0,2],求m,n的值
值域[0,2]
所以1≤(mx^2+8x+n)/(x^2+1)≤9
所以(m-1)x^2+8x+n-1≥0.......(1)
(m-9)x^2+8x+n-9≤0 ........(2)
(1) m-1>0,△=0即15-mn+m+n=0 .......(3)
(2) m-9<0 ,△=0 即-65-mn+9m+9n=0 .......(4)
(3),(4) ===>m=5,n=5
三 : 导数问题已知函数f(x)在x=1处连续,且lim[f(x)/(x
导数问题
已知f(x)在x=1处连续,
且lim[f(x)/(x-1)]= 2
x→1
求f'(1)
由lim
由f(x)在x=1处连续,有f(1)=0
所以f'(1)=lim
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1