一 : 五魔方Megaminx( 正十二面体魔方)解法教程(图)

五魔方，原名为Megaminx。是一种十二面体魔方。它总共有50块可以移动的部分。

五魔方原来叫做“十二面体魔方”（Magic Dodecahedron），是由一些魔方爱好者和研究者同时发明的。Uwe Mefferts最终取得了五魔方的发明权和制作权，并且在他的魔方网站Mefferts商店进行销售。

五魔方是十二面体结构，总共有12个中心片，20个角片和30个边片。每个中心都有一种颜色。边片则有两种颜色，角片则有三种。每个面上都有一个中心片，角片边片各五个。

五魔方总共有两个版本，一种为6色，一种为12色。

五魔方的玩法是通过旋转将颜色打乱再进行复原。

五魔方同时也是世界魔方协会承认和指定的比赛项目之一。

尽管五魔方的外表看起来非常的复杂，并且有比三阶魔方多得多的可移动部分，其实它的解法并不比普通魔方要难多少。因为它并不是一个拥有复杂结构的魔方。它可以旋转的中间层可以类比与三阶魔方的中间层。很多五魔方的解法都是从三阶魔方总结和升华出来的。

6色的五魔方其实比12色的还要难，因为它有很多对颜色相同但是并不等价的可移动部分。作为边片的这些可移动部分都不能随意替换，所以在复原的时候要进行大量的边片替换行为。

12色五魔方的边片都不相同，所以没有这个问题。

12色的五魔方总共有1.0×1068种变化状态，六色的则有6.1×1063种。

下面，就让我们一起来学习五魔方的还原方法吧！

1. 顶层棱块

~~~~上移~~~~

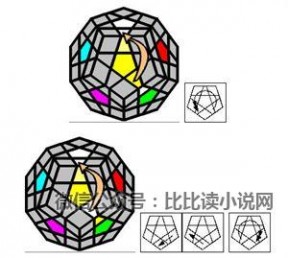
~~~~扭转:~~~~

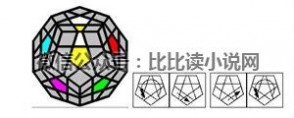
2. 顶层角块

~~~~上移:~~~

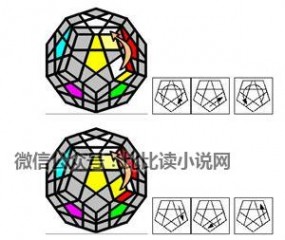
~~~~扭转:~~~~

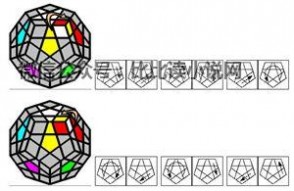
3. 第二层棱块

~~~~上移:~~~~

~

~~~~扭转:~~~~

4. 第三层角块

~~~~上移:~~~~

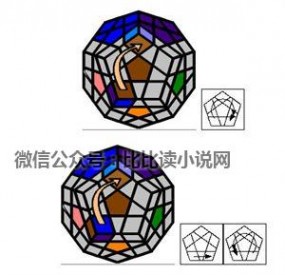
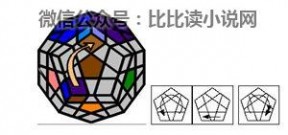
5. 第四层棱块

~~~~ 上移(到左边):~~~~

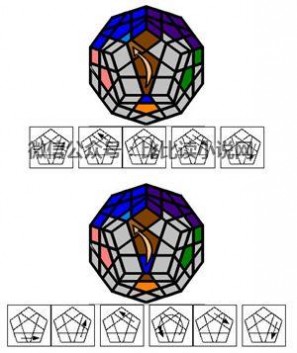
~~~~上移(到右边):~~~~

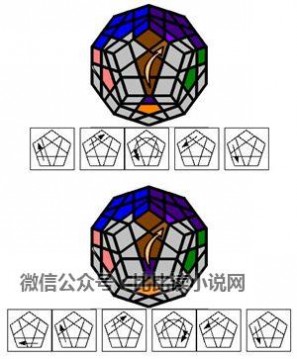
6. 第五层角块

~~~~上移:~~~~

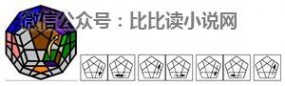
~~~~ 顺时针扭转:~~~~

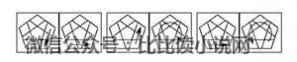
~~~~逆时针扭转:~~~~

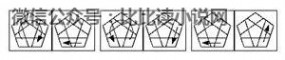
7. 第六层棱块

~~~~上移:~~~~

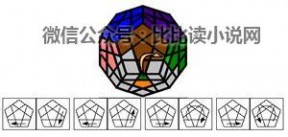
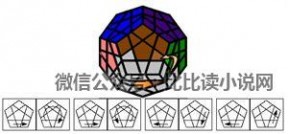
~~~~扭转:~~~~

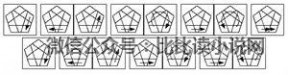
8. 底层角块

~~~~ 交换:~~~~

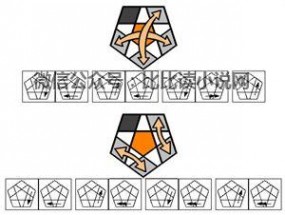
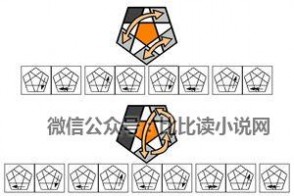
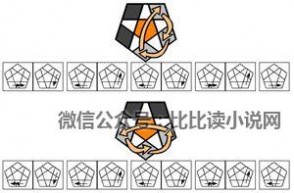
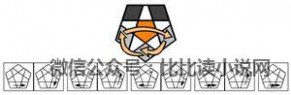
~~~~扭转:~~~~

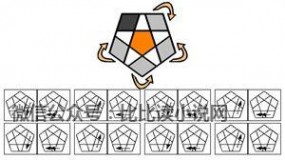
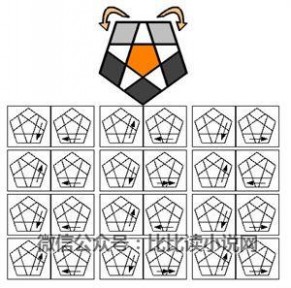
9. 底层棱块

~~~~交换:~~~~

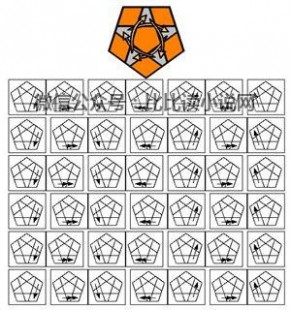
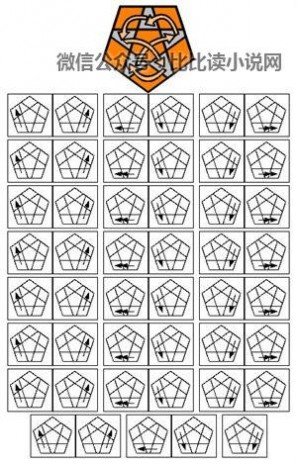
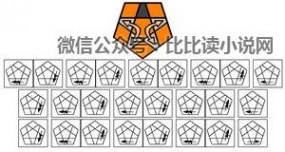
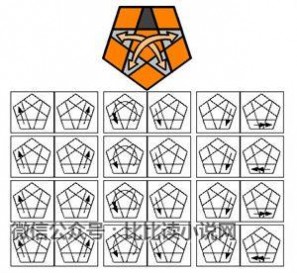
~~~~扭转:~~~~

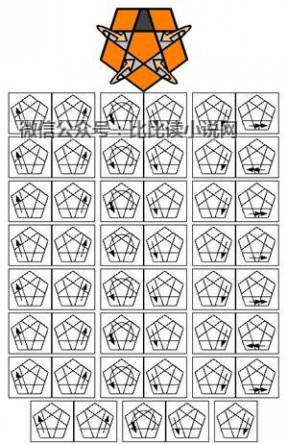
好了，就完成了，聪明的你，好好学习吧！

二 : 数学多面体问题正二十面体的面是正三角形，每一个顶点为其一端都有5

数学多面体问题

正二十面体的面是正三角形，每一个顶点为其一端都有5条棱，则其顶点数V 和棱数E的值应为( )

A.V=3,E=12 B.V=12,E=30 .V=6,E=12 D.V=12,E=6

---

每个面是正三角形有三个点

20个面共有20*3=60个点(这时各点已重复计算)

每一个顶点为其一端都有5条棱,这说明每个顶点都有5个三角形参与,即重复计算了5次)

所以正20面体的顶点个数为

20*3/5=12

每一个顶点为其一端都有5条棱

共有12个顶点

12*5=60

每一个棱都有两个端点,所以每条棱算了两次,

所以共有棱数是

60/2=30

故选答案B

本文标题：正二十面体图形-五魔方Megaminx( 正十二面体魔方)解法教程(图)
本文地址： http://www.61k.com/1173315.html