一 : 太阳的故事

　　今天，我特地起了个早，穿好衣服，急忙跑上楼顶去看太阳。

　　在楼顶上，我仰望天，几颗残星还挂在天际。显然，太阳还没起床呢！突然，我听到了村里的一声鸡啼“喔喔喔――”，公鸡在叫唤太阳起床了。呵，太阳又要出来值班，开始一天的工作了。

　　可太阳是个拖拉的孩子，无论公鸡怎样叫唤“喔喔喔，喔喔喔……”，太阳就是慢吞吞地不肯露面。人们着急了，他们等着太阳出来值班，让光明帮他们晒谷子、庄稼呢！于是，人们用力地敲起了盘子，碟子，吵得太阳再也无法睡懒觉了。太阳没办法，只好慢慢地爬上了山坡，用力一跳。噢，不行，太阳昨晚没吃饱饭，没力气往上跳。人们又着急了，纷纷为太阳搬来梯子、椅子，太阳踩着梯子和椅子一跳，终于跳上了天空。顿时，太阳发出了万道金光。

　　“太阳出来了！太阳出来了！……”刚才为太阳助跳的村民欢呼起来，纷纷跑回家搬谷子出来晒。太阳在天空中看着村们，高兴极了，他对村民们说：“你们真是我的好朋友！从明天起，我在也不睡懒觉了，我要早早的出来为大家晒谷子、庄稼！！”地里的人们一起欢呼：“太阳，你可别食言哦！！”太阳一听这话，想起自己过去的“劣史”，羞得涨红了脸，躲进了云朵里。

　　我看到这个情景，高兴得跳起来。心想：对呀！太阳，你可别食言哦！！！

 

二 : 射九个太阳的故事

1

（www.61k.com)射九个太阳的故事

传说古时候，天空曾有十个太阳，他们都是东方天帝的儿子。这十个太阳跟他们的母亲、天帝的妻子共同住在东海边上。她经常把十个孩子放在世界最东边的东海洗澡。洗完澡后，让他们像小鸟那样栖息在一棵大树上。因为每个太阳的形象中心都是只鸟，所以大树就成了他们的家，九个太阳栖息在长得较矮的树枝上，另一个太阳则栖息在树梢上。

当黎明需要晨光来临时，栖息在树梢的太阳便坐着两轮车，穿越天空，照射人间，把光和热洒遍世界的每个角落。十个太阳每天一换，轮流当值，秩序井然，天地万物一片和谐。人们在大地上生活得非常幸福和睦。人和人像邻居、朋友那样，生活在一起，日出而耕，日落而息，生活过得既美满又幸福。人和动物也能和睦相处。那时候人们感恩于太阳给他们带来了时辰、光明和欢乐，经常面向天空磕头作揖，顶礼膜拜。

可是，这样的日子过长了，这十个太阳就觉得无聊，他们想要一起周游天空，觉得肯定很有趣。于是，当黎明来临时，十个太阳一起爬上双轮车，踏上了穿越天空的征程。这一下，大地上的人和万物就受不了了。十个太阳像十个大火团，他们一起放出的热量烤焦了大地，烧死许许多多的人和动物。森林着火啦，所有的树木庄稼和房子都被烧成了灰烬。那些在大火中没有烧死的人和动物，猪突狼奔，四下流窜，发疯似地寻找可以躲避灾难的地方和能救命的水和食物。

河流干枯了，大海也面临干涸，所有的鱼类也死光了，水中的怪物便爬上岸偷窃食物。农作物和果园枯萎烧焦，供给人和家畜的食物源断绝了。人们不是被太阳的高温活活烧死就是成了野兽口中食。人们在火海灾难中苦苦挣扎，祈求上苍的恩赐!

这时，有个年轻英俊的英雄大神叫后羿，他是个神箭手，箭法超群，百发百中。他被天帝召唤去，领受了驱赶太阳的使命。他看到人们生活在火难中，心中十分不忍，便暗下决心射掉那多余的九个太阳，帮助人们脱离苦海。

于是，后羿爬过了九十九座高山，迈过了九十九条大河，穿过了九十九个峡谷，来到了东海边，登上了一座大山，山脚下就是茫茫的大海。后羿拉开了万斤力弓弩，搭上千斤重利箭，瞄准天上火辣辣的太阳，嗖地一箭射去，第一太阳被射落了。后羿又拉开弓弩，搭上利箭，嗡地一声射去，同时射落了两个太阳。这下，天上还有七个太阳瞪着红彤彤的眼睛。后羿感到这些太阳仍很焦热，又狠狠地射出了第三枝箭。这一箭射得很有力，一箭射落了四个太阳。其它的太阳吓得全身打颤，团团旋转。

就这样，后羿一枝接一枝地把箭射向太阳，无一虚发，射掉了九个太阳。中了箭的九个太阳一个接一个地死去。他们的羽毛纷纷落在地上，他们的光和热一点一点地消失了。直到最后剩下一个太阳，他怕极了，就按照后羿的吩咐，老老实实地为大地和万物继续贡献光和热。

从此，这个太阳每天从东方的海边升起，晚上从西边山上落下，温暖着人间，保持万物生存，人们安居乐业。

2

小编点评时间

天上的九个太阳都是被后裔射下来的，从此每天只有一个太阳从东方升起，温暖大地保持万物生存，使人们安居乐业。天上十个太阳确实很恐怖，后羿为人类作出重要的贡献，所以就有了后来后羿射日的传说。小朋友现在知道后羿为什么射掉九个太阳，因为我们人类只需一个太阳就够了。

三 : 太阳队队医的故事

【神医卡特】太阳队队医的故事

刀下留人

Doctor Carter

几乎每一个菲尼克斯太阳的主场比赛，托马斯·卡特都会来到美国空中走廊中心，在媒体进餐区域出入，和熟识的记者打招呼，和朋友们坐在场边看球，微笑地和太阳球迷们交流?? 但如非刻意，你很难注意到他。[www.61k.com]

看比赛的时候，他并不是和教练组以及训练人员组一样和球员们坐在一起，而是在球队板凳席后方。这个位置已经离球员们很近，可从不会被摄像机注意到。太阳官方网站上，也鲜有他的消息。球队网站的官方名单页面中，有14名球员、主教练埃尔文·金特里和4位助理教练和训练师阿隆·尼尔森的名字。但是没有“托马斯·卡特”。

“我就是球队的隐形人，”卡特说。

卡特难走入公众的视线，也有客观的原因。每支球队有很多工作职位，队医是最敏感的职位之一，他掌握着全队球员的身体状况的机密，而这些机密，很可能会影响到球队未来的交易和阵容轮转。按照NBA规定，队医一般不接受记者采访，除非得到球队官方允许。

如此种种原因，报道卡特的文章少之又少，菲尼克斯的太阳跟队记者中，只有凤凰城当地最大日报《亚利桑那共和报》的记者Paul Coro采访过卡特。向其询问上一次采访情况时，Paul很谨慎地说：“如果获得采访机会，你也一定要小心。卡特医生是一个很谦逊的人，但是，他肯定不会和你提之前做过的手术，也不会评价其他球队的医生。”

Tony Neely在太阳干了6年的保安，他以前是亚利桑那州大的橄榄球队员。在太阳工作期间，他经常能够见到卡特，“这位医生很谦和，我们都是从匹兹堡大学过来的，所以有一些共同话题。不过，他一般不会提到自己的专业。”

在得到太阳媒体官员的允许后，《爱篮球》终于得以接近这位神秘的隐形人。

托马斯医生最近一次神奇之处，体现在对同姓太阳新援的诊断上——卡特挽救了卡特。 2010年12月11日，供职于菲尼克斯620电台的记者John Gambadoro在微博上透露：“在见过太阳队医之后，文斯·卡特将确定不需要进行手术。”

“飞人卡特”刚刚在一笔三方交易中，被奥兰多魔术送至太阳。据奥兰多媒体报道，正因为考虑到卡特的伤病——他可能需要接受手术，并将因此至少休息一个月，才将他送走。就连《亚利桑那共和报》也称，“文斯·卡特已经考虑接受膝盖关节镜手术”。

卡特医生的行医哲学是：只要能够避免的手术，一定要避免。

“当时我做了仔细的检查，他并不需要手术，只需要进行一些康复治疗，就能够重新回到球场上。”卡特医生说。

仅仅缺席了4场比赛，卡特就重新回到场上。进入1月后的8场比赛，卡特场均得到19.0分，为本赛季最高的单月场均得分。卡特向《爱篮球》透露：“其实，我自己也相信我不需要手术。不过，在这里能够得到托马斯医生的确认，我真是太高兴了。”

“虽然卡特是一名医生，但不到非做不可的时候，他绝不会采取手术治疗，”训练师尼尔森说，“这次手术，可以看出他是怎样一个人：他总是把所有人的利益放在心中。”

将时间往前推，格兰特·希尔和“飞人卡特”的情况有些类似。希尔见到卡特医生时，一度以为自己将会再次进行手术。但按照卡特医生的行医哲学，希尔避免了有风险的手术，得到了一份严密的恢复治疗方案。在太阳首席训练师尼尔森的配合下，他看上去已经完全摆脱了伤病困扰。1月15日，这位38岁的老将成为现役球员中第14位冲破16000分大关的球员，

太阳队医 【神医卡特】太阳队队医的故事

“在一连串的伤病之后，我还能更继续打球。［www.61k.com]有时候，我甚至有些沮丧，不能够拿到更多的分数，但现在我拿到了16000分。我不能奢求更多了。”

还有一位重要的受益人：斯蒂夫·纳什。还在达拉斯打球时，小牛老板认为纳什年龄过大，不会发挥多大的余热了。可是到了太阳之后，他连续夺得MVP奖杯，还带领太阳打出了红极一时的“跑轰”。

“球员的自律和配合最重要，只有这样才能够保持良好的健康状态。这方面，纳什做得最好。” 托马斯向记者提起纳什时，忍不住要夸奖几句。

事实上，这两位算是惺惺惜惺惺。“托马斯的为人和行医水准都是最优秀的。我很幸运，能够碰到这样的队医和训练师，他们是最好的。”纳什说。

纵观全联盟，没有一支球队像太阳一样，靠着3个70后球员——纳什、希尔和卡特打天下。但实际上，纳什不再是库班眼中的“老人”，希尔仍有“乔丹接班人”的范儿，卡特还可以在这片沙漠之地飞翔??

“我们可以将菲尼克斯太阳队更名为本杰明·巴顿队了。”太阳执行主席隆·巴比笑着对《爱篮球》说。

1月12日，太阳主场迎战新泽西网队，第3节过后，太阳还大比分落后。上一场，太阳刚惨败于丹佛掘金，这个夜晚，他们并没有放弃比赛。比赛拖入加时，太阳齐心协力以118:109艰难取胜。卡特、纳什和钱宁·弗莱相拥而庆，球迷们的欢呼声响彻空中走廊中心。 更衣室里，记者们围住发挥出色的纳什，不断地抛给他问题。没有人注意到，在更衣室的角落，托马斯正和一位拄着拐杖的球员交谈。

加尼·拉沃尔，这个太阳本赛季刚签下的新人，在队伍内部的一次训练赛中，右膝韧带拉伤，经过卡特的检查，已经决定了要在1月19日前往圣约瑟夫医院 （St. Joseph's Hospital and Medical Center）进行膝盖手术。

圣约瑟夫医院是菲尼克斯当地著名医院，是太阳本赛季的官方合作医院。卡特将会陪同Lawal检查韧带拉伤，但这些事情，并不是他生活的全部。

“除了太阳队员，我还治疗其他的病人，我现在还是The Orthopedic Clinic Association的一员。我们在凤凰城有5个诊所，不过我只去位于亚利桑那州立大学的那个诊所。”卡特说。

卡特在宾夕法尼亚州的匹兹堡地区长大，受家庭影响，十几岁时就决心把运动医学作为毕生事业，“从小的成绩也一直都不错，所以在追求理想的路上也算顺风顺水。”

在Allegheny College拿到生物学位和化学的双学位后，卡特进入了全美排名前列的匹兹堡大学医学院，并通过医生资格考试，随后在俄亥俄大学医学院完成了骨外科实习。1991年，取得行医资格的他来到沙漠中的菲尼克斯，成为亚利桑那州立大学成为学校运动部门的专用医生。逐年的努力换来成功，他成为膝关节半月板替换和膝关节软骨损伤方面的治疗专家，还取得了关节内窥镜手术仪器的一些专利。

现在，他是美国公认的最好的骨外科医生之一，也是世界上最好的100位运动矫形外科医生之一，在业内倍受推崇。作为极具威望的河洛迪克斯协会——以运动医学之父河洛迪克斯命名的成员，他每年都会在世界各地参与研讨会，和各地的医学高人切磋技艺。

2000年8月，太阳专门聘请卡特作为球队的首席队医。

太阳这支球队，一直有一种凝聚力，很多工作人员一来到这里，就不会离开了。比如太阳的媒体主管Julie Fie女士，她在太阳已经工作了19年。近5年来，太阳的球员阵容变化很

太阳队医 【神医卡特】太阳队队医的故事

大，但是工作人员就几乎没变过。(www.61k.com）卡特表示，他感觉非常喜欢这个环境，太阳就像是一个大家庭。“只要球队不把我‘交易’走，我就会一直留在这里。”卡特说。

卡特还是一位“周末冒险家”。远足时，他甚至在驼峰山上为受伤的旅客进行临时治疗。但当自己的儿子受伤时，情况就不同了。就在今年，卡特16岁的儿子格兰迪在一场高中曲棍球比赛中膝盖骨脱臼，还拉伤了韧带。没过多久，18岁的儿子加勒特也脚部骨折。

没有“魔法般的手术”，这位医生老爸只是给出了一些普通的建议。“很多父母都希望自己的孩子能够成为下一个迈克尔?乔丹，或者是下一个科特?华尔纳，这实在让人沮丧，”卡特说。

卡特说“他不会给家人做手术”，但面对其他病人，他的心态很轻松。单说在NBA方面，他最成功的手术例子，莫过于治好了巅峰期受伤的阿马尔·斯塔德迈尔。

斯塔德迈尔当时仅仅22岁，诊断结果很糟糕：他需要进行一个独特而精确度要求极高的外科手术，这一手术有可能威胁到他的职业生涯。

对太阳球迷来说，这一手术意味着他们将在未来一年失去这名巨星。前不久，他们还刚刚签署了一份5年7300万美元的大合同。手术当天，太阳全队上下都绷紧了神经，卡特安之若素，这一天，只不过是一次再普通不过的例行上班时间。

“就像填补一个坑洞一样简单。”卡特说。

当然，球队和球迷才不会这么认为，对于斯塔达迈尔来说，这也事关数千万美元的钱途。“当我们和球队讨论这一手术有可能造成的后果时，你一定会听到类似回形针掉落地面发出的一声脆响，”卡特说，“每当得知你队中的球星将因伤报销整个赛季，你都会很震惊。” 手术成功，伤愈复出后的第1个赛季，斯塔德迈尔场均得分马上回升至20.4分和9.6个篮板。2010年，斯塔德迈尔离开卡特，离开太阳，带着“健康的身体”。看看斯塔德迈尔本赛季在纽约尼克斯的数据：26.4分和8.9个篮板。他屡次打破纽约尼克斯队史纪录，让大苹果城的球队战绩飙升。斯塔德迈尔，是卡特手下“返老还童”的典型例子。

所以，当同为大个子的姚明因脚伤赛季报销后，很多中国球迷都在网上建议“姚明在合同到期后可以加盟太阳，因为那支球队有一位‘神医’”。《爱篮球》将网友们的看法带到了菲尼克斯，带给了卡特医生。

“谢谢，谢谢你告诉我中国球迷是这样说的，这是对我最大的恭维。”卡特说。

采访时间：1月16日 地点：菲尼克斯

爱篮球：作为NBA球队队医，您每天的生活是怎样的？会随时跟随球队的步伐吗？

卡特：如果不是季后赛，我们的时间比较灵活。一般来说，我会在比赛开始前1个半小时来到球馆。其他的时候，我也可以等有事需要处理的时候再赶过来。

爱篮球：应聘NBA球队队医，需要哪些条件？是球队找你，还是你去应聘？除了首席医师外，医疗组的其他成员由谁决定？

卡特：这方面，应该说我和球队双方都有意愿。那时候，我已经在凤凰城呆了很多年，在亚利桑那州立大学当骨科首席医生，给凤凰城的其他职业球队当顾问医生，也和太阳队有过合作。其他的队医，是由我和首席训练师决定的。

太阳队医 【神医卡特】太阳队队医的故事

爱篮球：听说您会参加一些医疗大会，这会影响到在太阳的工作吗？

卡特：这是一年一届的会议，一般都在夏天赛季结束之后，所以不会影响工作。［www.61k.com]我会去参加一些专业的会议，在学术方面，我也经常发表一些专业文章。

爱篮球：NBA球队都会和当地的医院合作吗？这是一种怎样的合作方式？每一支球队都有自己的医疗医院吗？是合作医院，还是球队专属的医院？

卡特：太阳队有自己合作的医院，这个赛季，太阳队是和圣约瑟夫医院合作的。它是当地最好的医院之一，一般所需要的设备和条件，这里都能够配备。

爱篮球：所有的队医，在球队征战客场时候都要跟队前往吗？队医和体能师的分工有何不同？

卡特：在常规赛期间，我们并不需要去客场，因为如果球员在客场受伤，可以等回来之后再接受治疗。可到季后赛就不同了，我们需要跟球队一起去客场。如果在季后赛，球员受了小伤，我要马上给他治疗，让他马上能够上场。比如和洛杉矶湖人的季后赛，史蒂夫·纳什受了小伤，我4分钟就做了个小手术，让他能够马上重返赛场。

队医和体能师是互相合作的关系，手术后的恢复非常的重要，即便手术很成功，如果后续的恢复没跟上，也不能达到好的恢复效果。在这方面，我们经常和训练师沟通。

爱篮球：您是如何检查文斯·卡特的伤势的？他不需要手术吗？

卡特：不需要。我详细检查过了，不需要手术。一般的话，我只有在不可避免的情况下才会决定手术。

爱篮球：你医治好了很多著名球员。阿马尔?斯塔德迈尔，希尔，巴博萨等等。现在，您和斯塔德迈尔还有联系吗？

卡特：还有联系，有时候他会给我打电话，有时候是他的经纪人联系我。但是，如果现在他需要手术，我不可能再操刀。

爱篮球：您的儿子也受到了伤病困扰，他们现在伤情怎么样了？作为一个医生，也作为一个父亲，您在伤病面前会不会有一种“无力感”？

卡特：是的，我的儿子也伤过膝盖，他们会来找我，问我怎么办。可是，如果他需要手术，我是不会给他做的，我不会给我家人做手术。我承担不了手术任何的风险。要是我出任何问题，我太太都不会放过我。

爱篮球：面对NBA球员和面对医院的普通病人，有什么不同的感觉吗？特别是面对斯塔德迈尔这样的球员，当时斯塔德迈尔只有22岁，和太阳签下了大合同。

卡特：病人都是一样的，不管是NBA球员还是普通病人，在医生眼中没有任何区别。

爱篮球：做手术之前，您一般有时间和这些伤员交流吗？比如斯塔德迈尔，比如卡特。除了受伤的这些球员，您平时有机会和队员们交流吗？

卡特：当然会，每个决定都是双方的，如果他们不原意，即使我觉得手术是必需的，我也只能尊重他们的意愿。我们的交流很多，在训练的时候，我花很多时间和球员在一起。我们这个球队，就象一个大家庭一样。对每个队员，我都很熟悉。只有花很多时间在一起，他们才会对我很信任。

太阳队医 【神医卡特】太阳队队医的故事

爱篮球：您了解姚明的伤病吗？对他的伤病怎么看？大个子是否的确容易受伤，职业生涯结束后都要忍受伤病折磨？

卡特：姚明是个大个子，他的骨骼负担比一般人更大，确实比较容易受伤。［www.61k.com）不过好的康复手段，可以有助于他的恢复。NBA的队医之间平时都有交流，但我们不允许为别队的球员作手术。

爱篮球：一般情况下， NBA会组织这种队医交流会吗？其他球队的队医中，那个是您比较熟悉的？

卡特：前面提到了，大家都会相互交流，会打电话。大都都是比较熟悉的，因为我在NBA也11年了。

爱篮球：你发表了很多的学术文章，那你在诊所是不是还要指导一些刚出道的医生或者研究人员？

卡特：是的，我的诊所有不少的实习医生，我会指导他们。我们做的研究，除了手术，还有手术后的康复和运动的研究。

四 : 太阳的故事

太阳的故事（一）重返古希腊

本文作者：卢 昌海

说到天文学， 很多人的眼前都会浮现出深邃的天幕和宝石般闪亮的星辰。 其实， 在我们这个小小星球上所能看到的最显眼的天文现象并不在黑夜， 而是在白天。

在每一个晴朗的白天， 天空中都挂着一个极为显眼的天体： 太阳。

对于象太阳这样显眼的天体， 我们当然不必问它是什么时候被发现， 以及怎样被发现的， 因为那显然跟人类本身同样古老， 跟睁开眼睛同样直接。 但是， 除了这两个不必问的问题外， 有关太阳的其它问题可就大都不是省油的灯了， 有些甚至直到今天也没有确切答案。 不过虽然不 “省油”， 它们点亮的却是人类的智慧。 从某种意义上讲， 对这个天空中最显眼的天体的持续探索， 对那些 “不省油” 的问题的认真回答， 是人类从睁开眼睛看世界， 到逐渐理解世界的某些方面所走过的几千年漫漫长路的一个缩影。

现在就让我们从那些问题当中最简单的两个说起吧： 太阳有多大？ 它离我们有多远？

这两个问题的答案， 在今天也许已是很多小学生都知道的常识——不就是两个数字嘛。 但是， 这两个问题的答案果真只是两个数字吗？ 让我们来作这样一个设想， 假设我们用时间机器把一位知道这两个数字的小学生送回人类文明发源地之一的古希腊。 我们想知道的是： 这位来自二十一世纪的小学生能做什么？

显然， 单以某些知识——比如有关太阳有多大和离我们有多远的这两个数字——而论， 他 (她) 已经远远胜过了古希腊的任何一位先贤。 但我们会在从古希腊流传下来的史书中读到有关这位博学强记的小学生的故事吗？ 他 (她) 能凭那些博学强记的知识就成为令后世之人高山仰止的先贤中的一位吗？ 我想答案是否定的。 原因很简单， 知道两个数字和让别人理解并信服那两个数字是完全不同的事情， 后者恐怕不是一位小学生能够做到的。 如果仅仅能说出两个数字， 却无法让别人理解和信服， 那只会被当成信口开河， 而不会被载入史书。

那么， 假如不是小学生， 而是本站的读者您有幸 (或不幸) 被送回到了古希腊， 您有办法让那些喜爱思考的古希腊先贤们相信那两个数字， 相信天空中那个看上去只有贝壳大小的太阳其实是肚子里能装下一百多万个地球的庞然大物吗？ 或者换一个说法： 若是您被送回到了古希腊， 却忘记了那两个数字， 您有办法凭自己的能力， 以一种令人信服的方式重新找回它们吗？ 或者更一般地， 如果您站在了古希腊的天空下， 却忘记了所有的天文知识， 您能凭借自己的能力找回其中的多少呢？

【夕阳下的古希腊遗址】

让我们就从这个假想的问题开始重温一下人类智慧的启蒙时代， 并从那里开始讲述我们有关太阳的故事吧。

要想找回已被忘记的天文知识， 您要做的第一件事情显然就是仰望天空， 因为那里——并且只有那里——才是天文知识的直接来源。 如果您的仰望天空只是偶一为之， 您也许会觉得天上的日月星辰都是静止的， 因为它们当中没有一个会象飞鸟一样在一眼之下就让您察觉它们的移动。 但即便如此， 您也会在一天之内就发现太阳的东升西落， 因为它直接影响到周围环境的明暗和冷暖。 要发现月亮的运动也很容易， 因为在任何一个有月亮的夜晚， 您仰望天空时都很难不注意到这个独一无二的天体， 而您一旦注意到它的存在， 那么在下次仰望天空时， 就很难不注意到它的位置变化。

【星星的周日视运动】

对一般人来说， 自己所能发现的天文知识也许就到此为止了。 天上除日月之外虽然还有很多星星， 星星虽然也和日月一样东升西落， 但一个视力良好的人在一个晴朗的夜晚所能看到的星星有几千颗之多， 若非特别留意， 除了有一种繁星似尘的感觉外， 恐怕是不会对其中任何一颗星星留下具体印象的。 而如果没有对任何一颗星星留下具体印象， 那么在下一次仰望天空时就很难注意到它们的移动。

要想找回尽可能多的天文知识， 您当然不能象一般人那样过目就忘。 为了研究星星的运动， 您开始进行细致的观测， 并对不同时刻每颗星星的位置进行记录。 您很清楚， 观测越细致， 记录越详尽， 有可能找回的天文知识就越丰富。 由于在苍穹之上缺乏参照， 不易度量位置或角度， 您也许会想到在地上立一些固定的物件作为参照， 如果手下有一些可以使唤的人的话， 您也许还会想要设计建造一些更复杂的参照物， 那些东西若是建得足够牢固， 以至于能一直保留到今天的话， 就会变成重要的历史遗迹： 古观象台。

无论您的记录详尽还是粗略， 只要记录了， 哪怕只记录几天， 您也会发现所有的星星都和日月一样东升西落。 用后世的术语来说， 这是天体的周日视运动 (apparent diurnal motion)。 由此您也许还会进一步总结出一个规律， 那就是日月星辰都在围绕着地球转动， 在历史上， 这是著名的地心说 (geocentric model)， 它后来受到宗教势力的维护， 成为垄断天文界长达两千年的正统理论。 随着观测数据的积累， 以后您会发现很多理由让您放弃这一理论。 它后来也的确被放弃了， 在某些后世之人的眼里它甚至有些声名狼藉 (那其实是宗教惹的祸)。 但在一开始， 在只有粗略观测数据的年代里， 它是一种既符合观测数据， 又符合直觉的理论， 您有理由为发现这一理论而自豪。 周日视运动的发现也意味着您已经发现了 “日” 这个时间计量单位， 它是周日视运动的周期， 也可以说是昼夜交替这一粗糙周期概念的精细版[注一]。



【月相的变化】

当您的天文观测坚持到几十天时， 除了周日视运动外， 您还会注意到另一种很重要的天文周期现象， 那就是月相 (phases of the moon) 的变化。 与太阳总是圆的， 以及星星总是象一个点不同， 月亮这个夜空中最显眼的天体在不同日子里会呈现不同的形状， 有时是满月， 有时是半月， 有时则是弯月， 这种变化被称为月相的变化， 它大约每隔 29.53 天重复一次。 注意到这种有趣而美丽的周期现象， 意味着您发现了 “朔望月” (synodic month) 这一时间计量单位。 很多早期的文明都曾用过这一时间计量单位， 直到今天它仍有一定的应用， 是阴历 (lunar calendar) 这一历法的基础[注二]。

当您的天文观测坚持到十几个月时， 除了周日视运动和月相的变化外， 您还会发现一种更缓慢的天文周期现象。 您会注意到在太阳升起和落下的时候， 天空中依稀可见的那些星星的位置在一天天缓慢地改变着。 这种缓慢改变的逐渐积累， 使得在不同的季节里， 伴随太阳升起和落下的星星是不同的。 这说明什么呢？ 说明太阳在背景星空中的位置不是固定的， 除了周日视运动外， 它还参与了一种更加缓慢的运动。 仔细的观测表明， 那种运动大约每隔 365.24 天重复一次， 它既沿东西方向， 也沿南北方向， 与周日视运动所在的平面有一个 23.4° 左右的夹角， 这个夹角决定了太阳在冬天和夏天所能到达的最大纬度——即南北回归线的纬度。 注意到了那种运动， 意味着您发现了所谓的太阳周年视运动 (apparent yearly motion) 以及 “年” 这一时间度量单位， 后者是太阳周年视运动的周期， 也可以说是四季变化这一粗略周期的精细版[注三]。

您不知疲倦地坚持着自己的天文观测， 当您的头发都快花白了的时候， 您在天空中又发现了一些更微妙的运动。 您会发现在那看起来彼此相似的满天繁星之中， 有五颗星星的位置与日月一样相对于背景星空在缓慢地移动着， 其中有几颗星星的移动方式还相当复杂， 比如有时会停止， 有时还会逆行。 如果您发现了这些被后人称为行星表观视运动 (apparent motion of planets) 的现象， 那表明您已经发现了金、 木、 水、 火、 土五大经典行星。 除了这些发现以外， 在经年累月的观测中您还会偶尔发现一些流星和彗星， 并观测到一些日食和月食。



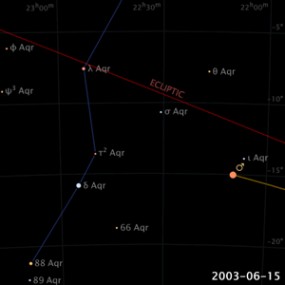
【火星的表观视运动】

在古希腊的条件下， 您自己所能从事的天文观测大致就是这些。 不过， 假如您能有幸找到一些前人留下的观测记录的话， 您也许能通过将彼此的记录相互比较， 而发现一种在您自己的有生之年里很难单独发现的东西， 即周日视运动的轴线本身的缓慢转动， 这种转动的周期约为 25800 年。 这一现象用后世的术语来说就是所谓的地球自转轴的进动 (precession of the Earth's rotation axis)， 在它的影响下， 因距离北天极 (即周日视运动的轴线北端) 很近而被称为北极星 (Polaris) 的小熊座 α 星 (α Ursa Minor) 在几千年后将会失去北极星这一光荣称号。

完成了上面这些观测发现， 您就不仅凭借自己的能力赶上了古希腊先贤们在观测天文学上曾经达到过的水准， 而且也基本上穷尽了十七世纪之前天文学上几乎所有重要的观测发现。 罗列起来似乎不难， 做起来却不无艰辛。 在不知不觉间， 您这位来自二十一世纪的人， 已几十年如一日地将古希腊人民的天文事业当成了自己的事业 (这是一种什么精神？)。

不过， 这些天文发现虽然了不起， 却还不足以让您被写入史书， 因为眼睛是人人都有的， 很多勤奋的普通人——其中既有古希腊人， 也有其它古文明国度的人——也能作出同样的发现。 真正将智者区别于普通人的除了勤奋， 还有智慧。 您虽然忘记了天文知识， 却还有几何与推理的能力， 这种能力无疑是一种智慧。 现在您要用自己的智慧来做一些单纯的天文观测无法做到的事情。 比方说， 您要寻找前面提到过的那两个数字： 太阳的大小以及它离我们的远近。

没有谷歌 (Google)， 没有百度 (Baidu)， 而且也没 “病” (Bing)， 您有办法自己找出那两个数字吗？

注释

[1]从周日视运动的周期中衍生出的 “日” 的概念其实不止一种： 由同一颗星星 (行星除外) 在两个相邻夜晚经过天空中同一个位置的时间间隔所定义的 “日” 称为恒星日 (sidereal day)； 由太阳在两个相邻白天经过天空中同一个位置的平均时间间隔所定义的 “日” 则称为平均太阳日 (mean solar day)。 由于后文即将提到的太阳周年视运动的影响， 平均太阳日比恒星日长了约 3 分 56 秒 (感兴趣的读者可以用本节给出的数据自行推算一下这两种 “日” 的差异)。 由于太阳与我们日常生活的关系远比星星密切， 我们在普通日历中所用的 “日” 是指平均太阳日。 细心的读者可能会问： 平均太阳日中的 “平均” 二字是什么意思？ 那是指将地球公转轨道等效为一个平均圆轨道， 以避免 “日” 的长短受地球公转轨道的椭圆性影响。 当然， 不作那样的平均也可以谈论 “日” 这个概念， 那样的 “日” 被称为表观太阳日 (apparent solar day)， 它的长短会随季节而变。

[2]朔望月这一中文名称中的 “朔” 指的是新月， “望” 指的是满月。 要注意的是， 朔望月只是月相变化的周期， 而不是月球绕地球公转的周期， 后者是所谓的恒星月 (sidereal month)， 只有 27.3 天 (感兴趣的读者可以用本节给出的数据自行推算一下这两种 “月” 的差异)。 另外， 朔望月不同于以太阳周年视运动为基础的阳历 (solar calendar) 中的月。 之所以不同， 是因为朔望月并不恰好等于阳历中一年的十二分之一， 如果我们用它来表示 “月”， 就无法与 “年” 合拍， 由此会导致很多不方便之处， 比方说北半球的 7 月就无法稳定地对应于夏天 (因为当 “年” 和 “月” 的不合拍累积到六个月时， 它就会变成冬天)。 不过有得就有失， 阳历中的 “月” 虽然保证了与 “年” 的合拍， 却失去了表示月相的作用， 比方说 “中秋月圆” 在阳历中就没有一个固定的日子。 由于太阳与我们日常生活的关系远比月亮密切， 我们日常所用的 “月” 是指阳历中的月。

[3]确切地说， 这个 “年” 是所谓的回归年 (tropical year)， 它比地球绕太阳的公转周期， 即所谓的恒星年 (sidereal year) 短了约 20.4 分钟， 这两者的差异是由后文即将提到的地球自转轴的进动造成的 (感兴趣的读者可以用本节给出的数据自行推算一下这两种 “年” 的差异)。 我们在阳历中所用的 “年” 是指回归年。

二零一零年一月十六日写于纽约

二零一零年一月十七日发表于本站

http://www.61k.com

太阳的故事

（本文授权转载于卢昌海老师的个人博客，欲再转载者请联系原作者

太阳的故事（二）天文自助游 推算太阳的大小和远近

本文作者：卢 昌海



虽然您要寻找的数字有两个， 但您很清楚， 实际上只要找到其中一个就行了。 因为太阳就在天上， 它看起来有多大您早就知道了， 它的真实尺寸越大， 意味着离我们越远， 反之， 真实尺寸越小， 意味着离我们就越近。 这表明， 在太阳的大小和远近这两者之间存在完全确定的关系， 只要知道任何一者， 就可以推算出另外一者。

那么， 在大小和远近这两者之间您该选择哪一者入手呢？ 从兴趣上讲， 您也许会对大小更感兴趣， 因为那才是属于太阳本身的性质， 但在实际上， 您却只能从远近入手。 对于普通物体来说， 这两种选择并无多大分别， 只要用一把尺子， 您爱测量哪一个都行。 可惜太阳却并非普通物体， 您无法直接拿一把尺子去测量它的大小。 当然， 您同样也无法直接拿一把尺子去测量它的远近。 但您知道， 测量物体的远近有一种很常用的间接方法， 那就是通过从两个不同的观测点来观测物体， 然后利用观测到的角度差异——即所谓的视角差异——来推算它的远近。 这种被称为三角视差法 (triangulation) 的方法从古至今都是测量远近的重要手段。 事实上， 远在其基本原理被理解之前， 我们的大脑和眼睛就已在本能地采用这种方法了， 我们的大脑正是利用了左右两眼之间的视角差异， 来判断物体远近的[注一]。



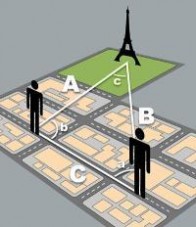
【三角视差法】

但当您试图用三角视差法来测量太阳的远近时， 却遇到了巨大的麻烦。 三角视差法需要两个观测点， 但您很快就发现， 从您能够走得到的相距无论多远的两个观测点去看太阳， 那视角差异都太小了。 地球表面的弧度， 地形的细微起伏， 乃至您的观测误差都远比您要测量的视角差异大得多。 在这种情况下进行测量， 犹如在惊涛拍岸声中去倾听远处一只水龙头的滴水之声， 您就算长一对兔耳朵也不够用。

怎么办呢？ 在哪儿才能找到第二个观测点呢？

您冥思苦想了一整夜。 当黎明的曙光照到您身上时， 您把目光投向了天空。 在那里， 您看到了一轮淡淡的上弦月 (在北半球， 上弦月是指右半边可见的 “半月”)。 看见它， 您心中忽然闪过一片灵光， 激动得几乎要象传说中的阿基米德 (Archimedes, 287BC-212BC) 那样一边裸奔， 一边大叫： “我找到了！”[注二]

是的， 您找到了， 您终于找到了第二个观测点， 那就是月亮！

别紧张， 您没喝酒， 您并不是要到月亮上去观测。 在古希腊时代人们就已知道， 月亮的月相变化并不是月亮本身在变 (在古希腊人眼里， 天上的东西是永恒不变的)， 而只是因为阳光从不同角度照射月亮所致。 在刚才看见月亮的一刹那， 您忽然想到， 既然月相是阳光从不同角度照射月亮所致， 那它实际上是在告诉您阳光照射月亮的方向， 从而也就是太阳相对于月亮的方向。 利用这一点， 您无需登上月亮就可以推算出从月亮上看太阳的角度， 这等于是为您提供了第二个观测点。

特别是， 当您看到的月亮恰好是上弦月时， 您的视线方向与阳光照射月亮的方向正好是垂直的 (如左图所示)。 这时候如果您记录下太阳的方向， 那么它与月亮方向的夹角的一边是月亮到地球的距离， 另一边则是太阳到地球的距离， 而它的一个邻角恰好是直角。 这样简单的三角关系对于即将跻身古希腊先贤行列的您来说无疑是小菜一碟， 那两个距离的比值就等于那个夹角的余弦值 (cosine)。 事实上您还知道， 那个夹角的余弦值不仅给出那两个距离的比值， 而且还给出了月亮直径与太阳直径的比值。 之所以如此， 是因为在太阳和月亮之间存在一个美妙的巧合， 那就是它们看起来几乎是一样大的[注三]。 对于两个看起来一样大的天体， 它们与我们距离的比值显然就等于它们直径的比值。



【太阳、 地球与上弦月的相对方位】

看来那个夹角很重要， 但它究竟是多少呢？ 那就得靠观测了。 不幸的是， 那是一个难度很大的观测， 因为那个夹角非常接近 90°， 接近到了让您无法分辨的程度。 而且在那个夹角如此接近 90° 的情况下， 一些在古希腊时代不为人知的因素， 比如地球大气对阳光的折射， 将足以对结果造成不可忽视的干扰 (感兴趣的读者请想一想， 那种影响会使观测到的太阳距离偏大还是偏小？)。 但不管怎么说， 您的方法是正确的， 并且即便在当时也有一定的可行性。 如果现代人用您的方法来做观测并扣除干扰的话， 将会发现那个夹角在 89°51' 到 89°52' 之间， 由此得出的结论将是太阳的直径约为月亮直径的 400 倍， 或者等价地， 太阳与我们的距离约为月亮与我们距离的 400 倍[注四]。

这个结果无疑是漂亮的， 但与您所要的答案仍有差距， 因为它只是把有关太阳的数字和有关月亮的数字联系在了一起， 除非您有办法知道有关月亮的数字， 它并不能提供您所要的答案。 那么， 您有办法知道有关月亮的数字——即月亮的大小或月亮离我们的远近 (这两个数字您也只要知道其中一个就行了)——吗？ 答案是肯定的。

在常年的天文观测中， 您和其他古希腊先贤们一样， 已经知道月食是由于地球挡住了射向月亮的太阳光所致。 您并且还注意到， 当地球的影子——确切地说是本影 (umbra)， 即完全阻隔阳光的那部分影子——“蚕食” 月亮时， 影子的边缘是圆弧状的 (这是最早使人推测地球为球形的现象之一)。 您很快就想到， 通过对比影子边缘的形状与月亮本身的形状， 您就可以估计出地球影子与月亮的相对大小。 不过， 这种方法实践起来并不容易， 因为地球的影子投射在球状的月亮上并不是一个很简单的几何问题。 您想到的一个更好的方法， 是对月亮进入地球影子与它穿过地球影子所花的时间进行比较。 在前一段时间里， 月亮移动的距离等于它自己的直径， 在后一段时间里， 它移动的距离等于地球影子的直径。 因此这两个时间的比值就等于月亮与地球影子的直径之比 (当然， 这种办法必须要在月亮恰好从地球影子正中间穿过的那种特殊的月食下才能得到可靠的结果)。



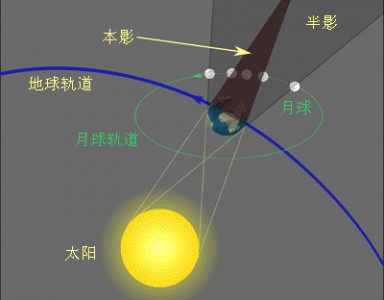
【测定月亮与地球的相对大小】

如果您进行了那样的测量， 您也许会得到一个很接近正确的结果， 即地球影子的直径约为月亮直径的 2.66 倍[注五]。 当然， 这个地球影子的直径是指地球影子在月亮轨道附近的直径， 它——如图所示——要比地球本身的直径来得小。 到底小多少呢？ 几乎恰好小了相当于一个月亮直径的大小 (这个结果不是偶然的， 感兴趣的读者可以结合太阳比地球大得多， 以及太阳和月亮看起来几乎一样大这两点来自行证明一下)。 把这个因素考虑在内， 您就得到了另一个重要结果： 地球的直径约为月亮直径的 3.66 倍。

将这个结果与前面的结果联系在一起， 您就发现了太阳的直径约为地球直径的 109 倍。 这个结果意味着太阳是一个庞然大物， 在它肚子里可以装下 130 万个地球——顺便说一下， 那是指剁碎了装， 如果要问最多能装多少个完整的地球， 那可就变成一道著名的数学难题了[注六]。

就象接力一样， 您先把有关太阳的数字与有关月亮的数字联系起来， 现在又进一步将它与地球的直径挂上了钩。 凭借几何与推理的力量， 一个天文问题已被您转变成了地理问题。 但问题是， 地球虽然就踩在您的脚底下， 它的直径却仍然不是可以拿尺去测量的。 事实上， 在古希腊时代， 多数人一生的活动都局限在几公里的范围内， 对他们来说， 地平线以外的东西就象天边一样遥远。 更不用说地球表面的大部分地区被当时还从未有人探索过的汪洋大海所覆盖。

不过您当然不是普通的古希腊人， 您总是有办法的。

在所有使人推测地球是球形的天文现象中， 除了前面提到的月食时地球影子的边缘形状为弧形外， 还有一个很重要的现象， 那就是不同纬度的人看到的星空是不一样的。 具体地说， 那些熟悉的星星或星座在不同的纬度上看时， 与天顶的夹角是不一样的 (请读者想一想， 为什么我们只提纬度而不提经度？)。 不仅星星如此， 太阳也一样。 住在北回归线附近的人大都知道， 盛夏正午的太阳是位于天顶正中央的 (证据是阳光能直射到垂直深井的底部)， 而住在北回归线以北的您却发现盛夏正午的太阳是在天顶偏南方向的， 具体偏南的角度可以用一根立在地上的垂直杆的投影来计算。 这个角度占整个圆周的比例显然就等于您与北回归线的距离 (这对您来说是可以测量的) 占整个地球周长的比例。 由此您就可以计算出地球的周长和直径。 经过这样的测量和计算， 您发现地球的直径约为 12740 公里 (当然， 这是改用后世的距离单位来表示了)[注七]。



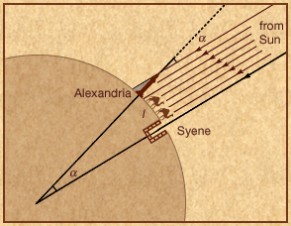
【测量地球的大小】

这样， 您就完成了一个漂亮的 “三步走战略”： 先从太阳到月亮， 再从月亮到地球， 最后归结到地面上的两个地点， 步步相连， 环环相扣。 将这些环节联系在一起， 您就得到了有关太阳的第一个数字： 太阳的直径约为 139 万公里。 由此您当然也可以推算出另一个数字： 太阳离地球约有 1.5 亿公里 (感兴趣的读者可以用 [注三] 提供的数据自行推算一下)。 如果您愿意， 您还可以写下有关月亮的两个数字： 月亮的直径约为 3500 公里， 它离地球约为 38 万公里 (更精确的数字是 384400 公里)[注八]。

站在我们这个小小星球上， 居然能推算出如此遥远天体的性质， 这是一件奇妙的事情。 在我们太阳故事的其它章节中， 在后来的科学发展史上， 这样奇妙的事情还将一再发生。 事实上， 直到今天为止， 除少数飞往过月球， 或在近地轨道上生活过的宇航员外， 几乎所有人的足迹都从未离开过我们这个小小的星球 (包括大气层)， 但我们却对越来越广阔的外部世界有了越来越精密的了解。 这种能力就是智慧。 当然， 我们在这里替您稍稍粉饰了一下， 限于当时的观测条件， 您在数值上是不可能得到象上面那样接近正确的结果的。 但对于那个时代来说， 最重要的不是数值， 而是方法， 那一系列精巧的方法足以使您当之无愧地跻身于人类最伟大的先贤之列， 永载史册。

您的古希腊虚拟人生兼自助游到这里就结束了， 但我们的太阳故事才刚刚开始。 接下来， 我们将追随历史的足印去探究另外一些重要问题： 比如那个肚子里能装下一百多万个地球的庞然大物究竟是什么？ 它真的是在围绕小小的地球转动吗？ 再往后， 我们还将一起去探究许许多多更现代、 更奇妙、 当然也更困难的问题。

注释

[1]不仅人类如此， 就连某些无法直接利用双眼视差的动物， 比如鸽子， 也会通过移动自己的脑袋来造成不同的视角， 进而判断物体的远近 (鸽子虽有两只眼睛， 但视野并不重叠， 从而不能象人类一样直接利用两只眼睛的视角差异， 而只能采用移动脑袋这样的 “下策”)。

[2]传说阿基米德受国王所托， 要鉴定一顶皇冠是否被掺了杂物。 他苦思良久， 最终在洗澡时悟出了用浮力进行鉴定的方法， 欣喜若狂的他连衣服都没穿就冲出浴室大喊： “我找到了！” 这个故事并未被记录在阿基米德著作之中， 它的真实性后来引起了一些有趣的争议。

[3]确切地讲， 由于地球绕太阳和月亮绕地球的公转轨道都是椭圆， 太阳和月亮看起来的大小都不是不变的。 其中太阳的角直径最小时为 31'27.7"， 最大时为 32'31.9"， 平均为 31'59.3"； 月亮的角直径最小时为 29'23.0"， 最大时为 33'31.8"， 平均为 31'05.3"。 我们在后文中将会看到， 月亮的角直径有时比太阳大， 有时又比太阳小这一特点对于日食的种类有着很重要的影响。

[4]在历史上， 古希腊先贤阿里斯塔克斯 (Aristarchus, 310BC-230BC) 曾经用这种方法进行过测量。 他估计出那个夹角为 87°， 与实际数值只相差不到 3°。 可惜对于这种很接近 90° 的角度来说， 哪怕只相差 1° 也足以造成很大的误差。 阿里斯塔克斯估算出的太阳直径只有月亮直径的 18-20 倍。

[5]在历史上， 这个方法也同样被阿里斯塔克斯采用过， 他估计出的地球影子直径约为月亮直径的两倍， 由此得到的太阳直径约为地球直径的 7 倍。 这个结果虽然误差极大， 但——如我们在下节中将会提到的——仍给了阿里斯塔克斯一个很重要并且很正确的启示。 阿里斯塔克斯之后的其他先贤们对地球影子的直径给出了更好的估计， 比如喜帕恰斯 (Hipparchus, 190BC-120BC) 给出的估计为月亮直径的 2.5 倍； 托勒密 (Ptolemy, 90-168) 给出的估计为月亮直径的 2.6 倍。

[6]这个数学问题被称为 “开普勒猜想” (Kepler Conjecture)， 是一个著名的数学难题。 1998 年， 美国数学家黑尔斯 (Thomas Hales, 1958 -) 发表了一个长达 250 页， 并且需要计算机辅助的证明， 但该证明迄今尚未得到数学界的公认。

[7]在历史上， 古希腊先贤埃拉托斯特尼 (Eratosthenes, 276BC-195BC) 曾经用这种方法估算过地球的周长。 插图中那两个城市 (即 Syene 和 Alexandria， 纬度分别为 24°05N 和 31°02N) 就是埃拉托斯特尼所选的观测点。 由于史学界对埃拉托斯特尼所用的距离单位尚有争议， 今天我们尚无法确切知道他的估算结果， 但一般认为是在 39690 公里到 46620 公里之间 (相应的直径在 12630 公里到 14840 公里之间)。

[8]有意思的是， 月亮的存在对于上述推理具有极大的重要性。 事实上， 如果没有月亮， 人类科学的很多早期探索都会遇到额外的困难。

二零一零年一月二十四日写于纽约

二零一零年一月二十五日发表于本站

http://www.61k.com

太阳的故事

（本文授权转载于卢昌海老师的个人博客，欲再转载者请联系原作者）

题图出处：http://tech.enorth.com.cn

太阳的故事（三）地心说vs日心说

本文作者：卢 昌海



【图片出处：http://db2.photoresearchers.com。】

我们已经知道， 天上的日月星辰并不是静止不动的， 从它们的东升西落中所能得到的最直接、 最直观的结论， 就是所有天体都在一个以地球为中心的天球上， 围绕地球转动。 这种几乎出现在所有早期文明中的猜测是地心说 (Geocentrism) 的雏形。

但世界的有趣之处就在于， 它常常给你一点希望， 似乎一个简单图像就能让你抓住点什么， 但稍稍细究一下却会发现事情并不那么妥帖。 拿日月星辰的运动来说， 星星的运动倒是的确能用一个天球的转动来描述——因为它们只有周日运动， 但太阳、 月亮及五大行星却除了周日运动外还各有各的 “私活”： 太阳有周年运动， 月亮有月相变化， 五大行星更不象话， 不仅各有各的周期， 甚至还每隔一段时间就 “倒行逆施” (逆行) 一番。 区区一个天球是无论如何摆不平那么多运动的。 怎么办呢？ 古人们想到了一招， 那就是把天球当成礼物派发， 让太阳、 月亮及五大行星各占一个， 乖乖听话的其它星星们则共享一个[注一]。

但这还不够， 因为行星的逆行还无法解释。 有人也许会说， 那有什么难的？ 让天球一会儿正转， 一会儿逆转不就行了？ 打住！ 万万不行。 要知道， 从古希腊开始直到十七世纪之前， 在差不多两千年的时间里， 人们对天体运动的描述一直遵守着两个要素： 一是天球必须为球形， 二是它的运动必须有某种类型的均匀性。 这几乎是当时对 “解释” 一词的定义， 非如此不能算是解释。 让天球象眼珠子那样乱转是万万不行的——文雅点说是不完美的。

天球必须完美， 行星却要倒行逆施， 这就让人伤脑筋了。 在被伤了脑筋的人当中就有古希腊先贤柏拉图 (Plato, 428/427BC-348/347BC)， 他给后人留了一道思考题： 如何用均匀有序的运动来描述看起来不规则的行星运动？

要说历史上的聪明人还真不少， 柏拉图的思考题一出， 很快就有人按下了抢答键。 抢答者不是外人， 而是柏拉图的学生欧多克斯 (Eudoxus, 400/408BC-355/347BC)。 他的答案很豪爽， 那就是派发更多的天球， 让每个行星都被几个同心天球共同带动， 直到满意为止。 这个答案的妙处在于可以让那些同心天球的转轴及快慢彼此不同， 但却各自保持均匀 (从而仍然是完美的)。 在欧多克斯的模型中一共用到了 27 个天球， 用这种方法， 他对包括行星逆行在内的很多天体运动现象给予了粗略描述。 为了表彰他的贡献， 我们授予他一个荣誉称号： 第一位试图对行星运动做出数学描述的先贤。

但欧多克斯的模型无法经受住哪怕只是稍微细致一点的观测考验， 而且人们早就发现行星的亮度并不是恒定的， 在当时这意味着它们与地球的距离不是恒定的， 这显然不是欧多克斯的同心天球模型所能解释的。 怎么办呢？ 另一位古希腊先贤， 以研究圆锥曲线著称的阿波罗尼斯 (Apollonius, 262BC-190BC) 支了一个妙招。 阿波罗尼斯提出太阳、 月亮及五大行星各自绕一个所谓的本轮 (epicycle) 作匀速圆周运动， 而本轮的中心则绕一个以地球为中心的所谓均轮 (deferent) 作匀速圆周运动。 用这种方式， 他不仅可以让行星与地球的距离发生变化， 而且同样可以——并且能更好地——解释行星的逆行。 不过在他的模型中出现了不以地球为中心的东西——本轮， 这对最刻板的地心说模型是一种偏离。 这种偏离是在纯粹观念与观测现实之间小心翼翼的妥协， 它看似细微， 却是一种实证精神的萌芽。



【古希腊天文学家托勒密(90-168)】

阿波罗尼斯的这种均轮加本轮的构想成为了地心说模型的新框架。 为了拟合越来越精密的观测， 地心说模型变得越来越 “轮丁兴旺”。 但不幸的是， 人们很快就发现， 轮多不一定力量大， 有一些细微现象， 比如行星的逆行幅度时大时小， 似乎无法靠简单地增添轮子来解释。 怎么办呢？ 地心说模型的集大成者， 古希腊天文学家托勒密 (Ptolemy, 90-168) 决定下猛药， 让纯粹观念再次向观测现实作出妥协——而且是重大妥协。 托勒密一举放弃了均轮的中心为地球， 以及均轮的转动为匀速这两大几乎被视为底线的观念， 引进了所谓偏心等距点 (equant point) 的概念， 对诸如行星逆行幅度时大时小之类的现象作出了一定程度的解释[注二]。

但这还不够， 因为除上述现象外， 行星运动还有一个引人注目之处， 那就是水星和金星的运动总是局限在太阳左右一个小范围之内， 而不象其它行星那样满世界乱跑。 为了解释这一现象， 这两颗行星的本轮中心被假定为永远处在地球与太阳的联线上。 把这些修正汇集到一起， 托勒密的地心说模型就基本完成了， 剩下的只是微调。



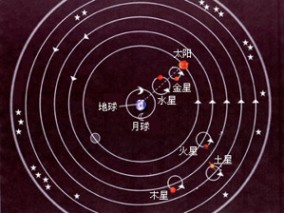
【简化版的地心说】

后人对托勒密这个与地心说联系在一起的名字往往有一种模糊的错觉， 以为那是某种保守理论的代言人。 事实上， 托勒密是一位真正伟大的天文学家， 他的伟大不仅体现在他自己的时代， 甚至还向后延伸了一千多年。 在那个重理念轻实践的时代里， 他明确提出理论必须拟合观测。 他的地心说模型就是这种努力的典范， 其精度之高， 甚至连一千四百年后的日心说模型也无法轻易超越。 当代科学史学家霍尔顿 (Gerald Holton, 1922-) 曾有过这样一句感慨： “没有什么事情比低估古希腊人的观点更容易和更错误”。 我有同感。 当我们挟两千年的历史优势来回顾某些古希腊先贤的思想时， 理所当然地会看到大量的错误， 甚至可以不夸张地说， 他们写得越多， 就错得越多 (相比之下， 象 “道可道， 非常道” 那样东方式的言简意赅实在是太有才了)。 但那些错误就象孩子学步时的摔跤， 没有它们， 人类恐怕直到今天还在爬。

在接下来一千多年的时间里， 地心说模型作为天体运动的主流模型， 成为了导航、 测绘、 及星图计算的基础。 不过， 在这一模型的发展过程中， 如上所述， 实证精神已开始萌发。 随着偏心等距点等概念的提出， 诸如天球以地球为中心以及天球必须作均匀圆周运动那样的古老信念已被显著削弱。 而且地心说虽然解释了不少现象， 带来的问题却也不少。 对那些问题的探究使一些人进行了不同的尝试， 其中最早的努力甚至在托勒密之前就出现了。

我们在 上一节 的 注四 中提到过， 古希腊先贤阿里斯塔克斯 (Aristarchus, 310BC-230BC) 曾经用我们介绍过的方法估计过太阳的直径， 结果约为地球直径的 7 倍 (相应的体积约为地球体积的 343 倍)。 虽然与现代值相差很远， 但太阳比地球更大这一定性结果还是给了阿里斯塔克斯很大的启示。 要知道， 地心说的产生在很大程度上乃是出自直觉， 而这直觉有两个来源， 一个是天体的周日运动， 另一个则是天体看上去都很小——小东西围绕大东西转似乎是天经地义的。 但如果太阳比地球更大， 这直觉就成问题了。 一个庞大的太阳有什么理由要绕一个体积不到自己 1/300 的小不点儿转呢？ 一般认为， 正是这个怀疑使阿里斯塔克斯提出了太阳才是宇宙中心的观点， 这是最早的日心说 (Heliocentrism)[注三]。

但阿里斯塔克斯的日心说并未引起什么反响， 因为它面临很多棘手的问题， 比方说如果地球在运动， 那天上的云彩为什么不会被运动的地球所抛离？ 这个问题别说阿里斯塔克斯， 就连一千八百年后哥白尼 (Nicolaus Copernicus, 1473-1543) 也难以回答。 另一个问题比较有意思， 那就是如果地球在运动， 那么星星的位置应该会象用三角测距法测距时那样显示出视差 (因为观测点随地球运动而变化)， 但实际上我们却从未发现过那样的视差， 这是为什么？ 对于这个问题， 阿里斯塔克斯作出了很正确的回答 (可惜没人相信)， 那就是星星离我们实在太远， 以至于视差小到了无法被察觉的程度。 他的这个回答本身就是一个了不起的天文发现， 因为它给当时尚无人知晓的宇宙大小设置了下限， 即宇宙起码要大到能让星星的视差不被肉眼所察觉的程度。 第三个问题来自所谓 “天贵地贱” 的观念， 当时的很多人相信天上的星星是永恒而完美的， 地上的一切则是腐朽而卑微的， 两者无论在外观还是质料上都截然不同[注四]。 而日心说却要让腐朽卑微的地球混迹于永恒完美的行星行列， 这怎么可以呢？ 这个问题在今天看来很无厘头， 但在当时却是难以抗拒的 “主流民意”。

虽然阿里斯塔克斯的日心说未能掀起波澜， 但地心说的麻烦却并未结束。 除了太阳比地球大所导致的困扰外， 地心说还有其它一些不如人意之处。 比方说行星和太阳在地心说中是有相似地位的， 但行星的本轮周期却全都是一年， 即恰好等于太阳绕地球运动的周期， 这种巧合在地心说中是很难解释的。 此外， 随着航海业的兴起及对日历与定位精度的要求日益提高， 地心说的精度也越来越成问题了。 正是在这种背景下， 1543 年， 一本全面阐述日心说的著作 ——《天体运行论》(On the Revolutions of the Heavenly Spheres) 问世了。 这是一部 “难产” 的著作， 它的作者——波兰天文学家哥白尼—— 用了长达二十三年的时间来撰写它， 完成之后又因担心触怒教会 (同时也为了进行细节完善) 而延迟了十三年， 直到去世前不久才发表。



【波兰天文学家哥白尼(1473-1543)】

哥白尼的这部著作是托勒密以来最杰出的天文学著作， 哥白尼虽然不是最早提出日心说的人， 却是最早将日心说由一个观念性学说转变为具有预言能力的定量模型的人[注五]。 在哥白尼的日心说模型中， 我们这个系列的主角——太阳——荣升为了宇宙的中心， 我们脚下的地球则变成了行星， 一边自转， 一边和其它行星一样围绕太阳公转。 地心说无法解释的行星本轮周期全都是一年的巧合在日心说中变得显而易见， 因为那不过是地球公转产生的表观现象。 天体的周日运动也有了很简单的解释， 即那不过是地球自转产生的表观现象。 不过哥白尼的日心说模型在最低阶近似上虽比同等近似的地心说模型高明得多 (因为无需引进本轮)， 但由于和地心说模型一样未能摆脱圆周运动这一束缚 (在这方面哥白尼甚至比托勒密更保守， 连偏心等距点那样的概念都不曾引进)， 从而一涉及到细微之处， 就无论以繁简程度还是精度而论， 都无法真正超越托勒密的地心说模型， 这一点直到十七世纪初德国天文学家开普勒 (Johannes Kepler, 1571-1630) 发现椭圆轨道后才得以改变。



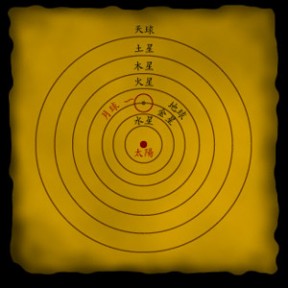
【简化版的日心说模型】

我们刚才提到， 哥白尼曾经担心自己的日心说会触怒教会。 这种担心并非杞人忧天， 因为《圣经》中有不止一处提到太阳运动而地球静止， 日心说与那些文字是有冲突的。 不过具有讽刺意味的是， 哥白尼时代的教会虽竭力维护托勒密的地心说， 仿佛后者是天经地义的真理， 但实际上， 无论托勒密的地心说， 还是资格更老的亚里斯多德 (Aristotle, 384BC-322BC) 的著作， 都并非一直就是教会的宠儿。 相反， 它们都曾经上过教会的黑名单——一度被教会所禁止。 因为那些著作的逻辑与实证色彩和教会所希望的盲从与盲信背道而驰， 而且它们在文字上虽对上帝充满了虔敬， 其所宣扬的世界体系却基本无需上帝的帮助， 把上帝这个 “活雷锋” 架空了。 不过在十三世纪中期， 教会采取了新的策略， 对一些有影响力的自然哲学著作进行 “无菌处理”， 使之与圣经接轨。 这样做既减少了对手， 又充实了自己的理论阵地， 可谓一举两得[注六]。 在哥白尼时代受教会维护的托勒密地心说就是这种经过 “无菌处理” 后具有教会特色的自然哲学。 而哥白尼要推出一种 “带菌” 的学说， 心中自然不无忐忑。

不过忐忑归忐忑， 哥白尼与教会的关系其实还是蛮 “和谐” 的， 因为他的正业其实是神职人员 (因此有人戏称哥白尼白天是神父， 晚上才是天文学家)， 他甚至把自己的《天体运行论》献给当时的教宗保罗三世 (Pope Paul III, 1468-1549)。 而《天体运行论》的出版者奥希亚德 (Andreas Osiander, 1498-1552) 更是为该书包上了一层精心制备的 “糖衣”——序言， 谦虚地宣称日心说仅仅是一个便于计算的假设， 不一定是真实的。 经过这样 “瞒天过海” 的包装， 《天体运行论》这一 “糖衣炮弹” 的发表并未受到教会的干预。 直到几十年后意大利科学巨匠伽利略 (Galileo Galilei, 1564-1642) 支持日心说的著作引起强烈反响后， 教会才意识到自己被忽悠了。



【意大利科学巨匠伽利略(1564-1642)】

伽利略的工作为日心说的胜出提供了强有力的支持。 我们前面提到过， 在地心说模型中水星和金星的本轮中心被固定在地球与太阳的联线上 (参阅 “简化版的地心说模型” 插图)， 按照那种模型， 相对于地球来说， 太阳永远只能从后方或侧后方照射水星和金星， 由此导致的结果是这两者永远只能有弯钩状的相 (感兴趣的读者请自行证明这一点)。 但伽利略却通过望远镜发现金星具有类似 “满月” 那样的相， 从而对地心说构成了判决性的打击[注七]。 另一方面， 在所有针对日心说的反对意见中， 除宗教因素外， 最棘手的问题是运动地球上的东西为什么不会被地球所抛离？ 这个问题难倒了从阿里斯塔克斯到哥白尼的所有人， 却被伽利略提出的相对性原理所回答。 甚至连 “天贵地贱” 那样的 “主流民意”， 也因伽利略发现太阳黑子而遭到了驳斥。

1632 年， 伽利略发表了名著《关于两大世界体系的对话》(Dialogue concerning the Two Chief World Systems——简称《对话》)， 对地心说和日心说这两大世界体系进行了看似不偏不倚， 实则显著青睐后者的阐述， 而且在阐述中还对已被教会认可的亚里斯多德的很多观点提出了异议。 这一切令教会很生气， 后果很严重。 其实， 伽利略倒也并非吃了熊心豹子胆， 他在 1616 年曾受到过教会的 “警告处分”， 在那之后安静过几年。 这回之所以敢 “顶风作案”， 是因为他的一位大主教朋友于 1623 年成为了教宗厄本八世 (Pope Urban VIII, 1568-1644)。 这么过硬的上层关系给了伽利略一种安全感， 使他以为 “科学的春天” 到来了。

他完全错判了形势。

Too simple, too naive！

实际情况是：《对话》发表后才不过一年， 1633 年， 罗马宗教裁判所就对伽利略进行了审判， 并裁定他有罪。 低头认罪还是顽抗到底？ 这是一个问题。 年近古稀的伽利略选择了前者， 他在认罪书中表示： “我， 伽利略， ... ... 手按圣经起誓， 我过去和现在一直相信， 在主的帮助下今后也将相信圣天主教和使徒教会所持有、 传授及教导的一切”。 对于日心说， 他表示： “我发誓今后绝不以口头或书面形式发表任何类似的东西”。

但教会的干预最终未能阻止科学在经历了中世纪黑暗后的快速复兴。 日心说先是作为一种纯粹的计算工具 (如《天体运行论》的序言所谦称的那样)， 而后作为一种具有真理性的理论还是逐渐流行了起来。 1832 年， 苏格兰天文学家亨德森 (Thomas Henderson, 1798-1844) 发现了半人马座 α 星 (α Centauri) 的视差[注八]， 从而直接证实了阿里斯塔克斯的先见之明， 同时也扫清了日心说的最后一个技术障碍。

在无可逆转的局势面前， 教会的态度也终于有了变化。 1992 年 10 月， 教宗保罗二世 (Pope John Paul II, 1920-2005) 向伽利略在引进实验方法及理解日心说方面所做的巨大贡献表示了敬意和感谢， 并承认教会对地心说的维护乃是对《圣经》作字面解读导致的错误。 2000 年 3 月， 保罗二世签署正式声明， 承认当年对伽利略的审判是错误的， 并为教会两千年来所犯的暴力、 迫害及错误道歉。 2008 年 3 月， 梵蒂冈教廷为伽利略建造了雕像——离那雕像的矗立之处不远， 便是 375 年前伽利略等待审判的地方。

无可奈何花落去， 似曾相识燕归来， 历史走过了一个漫长而沉重的轮回。

日心说与地心说的争论虽然以日心说的胜出而落幕， 但日心说将太阳视为宇宙中心的做法却很快也受到了质疑。 事实上， 太阳与星星的差别不就是前者看上去象一个圆盘而后者象一群小点吗？ 既然日心说已经把我们脚下这个看起来比太阳还大的地球与那五个看上去象小点的行星归入了同一类别， 太阳为什么就不能和星星一样呢？

思想的禁忌一旦被打破， 新的想法就会源源而生。 1584 年， 意大利哲学家布鲁诺 (Giordano Bruno, 1548-1600) 提出了太阳只是无限宇宙里的无数颗星星之一的想法[注九]。 1644 年， 法国数学家笛卡尔 (René Descartes, 1596-1650) 也提出了太阳和其它星星一样的观点 (虽然他有关太阳和星星的具体模型——漩涡模型——是完全错误的)。 今天我们知道， 太阳只是太阳系的中心， 而不是宇宙的中心。 太阳是银河系上千亿颗恒星中很普通的一员， 而银河系又只是可观测宇宙上千亿个星系中很普通的一员。

这就是太阳的真正身份——一颗非常普通的恒星， 可观测宇宙中发光星体的一百万亿亿分之一。

但无论多么普通， 太阳对于人类来说都是独一无二的。 它是光和热的源泉， 也是唯一一颗能让我们看到圆面的恒星。 它与我们的关系是如此密切， 在任何一个晴朗的白天， 它那光芒夺目的圆面哪怕只出现些许的破缺， 或几分钟的消失， 都是非同小可的事情。 在 下一节 里， 我们将一同去欣赏这种被称为日食的现象。

注释

顺便说一下， 从那时起直到中世纪， 太阳和月亮是被很多人视为行星的 (因此那时的行星实际上有七颗， 太阳和月亮都曾拥有一个名字叫行星)， 我们为了避免混淆才将它们单独列出。 托勒密的偏心等距点概念是对他所放弃的以地球为均轮中心， 以及均轮的转动必须均匀这两大观念的补偿。 在他的模型中， 地球虽不再处于均轮的中心， 但和一个被称为偏心等距点的位置对称分布在均轮中心的两侧， 均轮转动的角速度相对于球心和地球虽不再均匀， 但相对于偏心等距点却是均匀的。 这个模型可以说是天球体系中最接近椭圆轨道的构想 (偏心等距点的作用接近于椭圆的焦点)。 阿里斯塔克斯是最早提出地球绕太阳运动的人， 但在他之前就有人提出过地球运动的想法， 比如毕达哥拉斯学派的古希腊先贤菲洛劳斯 (Philolaus, 470BC-385BC) 曾提出过包括地球、 太阳在内的所有天体都围绕一个所谓的 “中央火” (central fire) 转动的观点。 细心的读者也许会问： 我们用肉眼就能看到月亮上的阴影， 这岂不是与天体的完美相矛盾？ Good question！ 古希腊人对此的解释是月亮离地球太近， 从而被 “污染” 了 (近墨者黑嘛)。 有人可能还会进一步问： 为什么要让一大批永恒完美的天体围绕一个腐朽卑微的地球转呢？ 这不是把鲜花插在牛粪上吗？ 这个大逆不道的问题就得问上帝了， 据说是它把人类造在地球上， 并让天体围绕地球转的。 在从阿里斯塔克斯到哥白尼的一千八百年间， 有一些其它人也提出过背离地心说或接近日心说的理论， 但都没有定量化， 且大都因不符合 “主流民意” 而自行或被迫放弃了。 在这一过程中为教会立下汗马功劳的是所谓的经院哲学家 (scholastic philosopher)， 其代表人物是被教会封为 “天使圣师” 的阿奎纳斯 (Thomas Aquinas, 1225-1274)。 经院哲学家以宗教教义为指导， 通过对古典哲学思想进行包装、 诠释及歪曲、 诡辩， 而构建出与圣经相协调的新体系。 在日心说模型中， 金星的 “满月” 相出现在它与地球分处于太阳两侧的情形下， 这时金星离地球的距离最大， 从而部分抵消了 “满月” 相的亮度优势， 因此金星的亮度变化远小于单纯由距离变化所预期的， 这一点曾被认为是日心说的一个困难。 不过亨德森对自己的观测缺乏信心， 直到 1839 年 1 月才发表， 在发表时间上落后于德国天文学家贝塞尔 (Friedrich Bessel, 1784-1846)， 后者于 1838 年发现了天鹅座 61 星 (61 Cygni) 的视差。 布鲁诺因为这一信念及其它若干罪名被罗马宗教裁判所起诉， 并最终判处火刑， 于 1600 年 2 月 17 日处决。

二零一零年二月九日写于纽约

二零一零年二月十日发表于本站

http://www.61k.com

太阳的故事

（本文授权转载于卢昌海老师的个人博客，欲再转载者请联系原作者）



太阳的故事（四）日食：既寻常又稀有的奇观

本文作者：卢 昌海

美国科幻作家阿西莫夫 (Isaac Asimov, 1920-1992) 曾经写过一个著名的科幻故事， 叫做 “黄昏” (Nightfall)。 在这个被许多读者推举为有史以来最优秀科幻作品之一的名篇中， 阿西莫夫虚构了一个由六个太阳组成的多星系统， 在那里的一个有 “人” 栖居的行星上， 几乎任何时候都至少有一个太阳悬在空中， 夜幕每隔 2049 年才会降临一次。 每当那一时刻来临， 地平线上硕果仅存的一个太阳会遭遇 “日全食” (total eclipse)， 传说中能夺人魂魄、 让人丧失理智， 进而毁灭整个文明世界的星星会出现在黑暗天空里。 所有人都在短时间内陷入巨大的恐慌和骚乱之中， 周而复始地亲手将星星毁灭文明世界的传说变为现实。



【日全食】

不过这只是现代。 在古代， 日食的出现可不是什么轻松的事情 (虽然有时也能导致好结果)。 古希腊历史学家希罗多德 (Herodotus, 484BC–425BC) 曾经记载过公元前六世纪米底斯 (Medians) 与利底亚 (Lydians) 两族交战时， 因遭遇日食致使双方惊恐万分、 终止干戈的事情。 那样的事情在历史上发生过多次， 甚至直到二十世纪六十年代， 柬埔寨内阁首相朗诺 (Lon Nol, 1913-1985) 的军队还在一次战斗中因遭遇日全食而惊慌失措。我们很幸运， 没有生活在那样的多星系统中[注一]。 只有一个太阳的我们早已习惯了日夜的更替， 星星在我们眼里非但不是毁灭文明世界的恐怖象征， 反而是一种魅力无穷的美景 (从这个意义上讲， 它倒也是能夺人魂魄的)。 不过， 即便对于我们来说， 如果太阳在原本应该出现的时侯突然消失， 或其圆面出现破缺， 依然是一件非同小可的事情。 在这种被称为日食 (solar eclipse) 的自然现象中， 最扣人心弦就是阿西莫夫故事中提到的日全食。 当太阳即将被全部遮盖时， 月球的巨大阴影自西向东掠过地面[注二]， 夜幕骤然降临， 星星重新闪耀， 有时还能看见美轮美奂的贝利珠 (Baily's beads) 和壮丽的日冕 (solar corona)。 这时候， 有些人将会感到颤栗——不是因为害怕， 而是由于气温的骤降。 在日全食的短暂过程中， 气温会有相当明显的降低 (比如 1878 年 7 月 29 日的日全食期间， 美国丹佛市的气温从酷热的 46°C 骤降到 28°C)。 这种笼罩整个天空和大地的大自然的华丽演出， 对亲临者来说往往是令人陶醉和毕生难忘的。

在对日食成因缺乏了解的古代， 人们对日食有过许多荒诞不经的猜测。 我们熟悉的 “天狗吃太阳” 就是其中之一。 为了吓阻天狗的 “暴行”， 民众常常敲锣打鼓、 鸣金放炮， 甚至连九五之尊的皇帝也往往要吃素斋、 避正殿， 诚惶诚恐。 类似于 “天狗吃太阳” 的传说在其它古文明也有， 只是所涉及的猛兽不尽相同， 吞吃太阳的原因五花八门而已。 最搞笑的或许是印度的一种传说， 该传说认为太阳常常向某个野蛮部落的成员借钱， 却借而不还。 对方一怒之下就会吃掉它 (但吃完后又吐出来， 看来还是惦记着还钱的事情)。 这种猛兽 (或猛人) 吃太阳的说法并不是古人对日食成因的唯一猜测。 比这种 “猛兽说” 更有情趣的是所谓的 “夫妻说”。 那种说法也是形形色色， 比如在某日耳曼传说中， 月亮和太阳是一对不和睦的夫妻， 而且太阳是妻子， 当月亮偶尔去看望太阳时就会出现日食， 但它们和睦不了几分钟就又会闹翻 (幸亏如此)， 于是太阳就会重新出现。 当然， 也有些传说不那么 “诬蔑” 太阳和月亮的夫妻关系， 比如在北美某印地安部落的传说中， 太阳和月亮是恩爱夫妻， 日食的成因——猜得到算你有本事——是太阳的手臂上抱着他们的孩子！

这些荒诞不经的传说， 以及视日食为恐怖天象的年代对于生活在现代文明社会中的人来说已经很遥远了。 对现代人来说， 有幸观赏到日食， 非但没什么恐怖， 反而是令人羡艳的经历。 有些天文爱好者甚至不惜破费， 千里迢迢地赶往日食带观赏日食。 有些天文学家更是甘当现代 “夸父”， 乘坐喷气式飞机追逐日食， 目的就是让这一天象的持续时间尽可能延长。 我们早已知道， 日食并不神秘， 它只不过是月球偶尔跑到地球与太阳之间， 挡住了阳光而已。

明白了这个浅显的道理， 我们就可以冒充天文学家来分析一下日食的的规律。 我们知道， 月球每个 “月” 都会绕地球转一圈。 既然是转一圈， 那就总会经过太阳的方向。 这么推算起来， 日食似乎每个月都应该发生一次， 每个世纪则应该有 1238 次 (请读者想一想， 为什么不是 1200 次？)。 但事实上， 在已经过去的二十世纪中， 总共只发生过 228 次日食。 在二十一世纪中， 也将只会有 224 次日食， 只占 1238 次的 18% 左右。

看来天文学家不是那么容易冒充的， 我们首先得搞明白： 那另外 82% 的日食哪里去了？

答案是： 被地球漏掉了。 要解释这一点， 我们需要对地球与月球的公转轨道特点有一个简单了解。 这其中对日食来说最重要的特点， 是地球与月球的公转轨道并不在同一平面上， 而是有一个平均为 5.14° 的夹角。 由于这个夹角的存在， 即使月球位于地球和太阳之间， 它相对于地球公转轨道平面来说， 也往往不是偏上， 就是偏下， 它的影子多数时候只能投射在清冷的虚空之中， 而无法触及地球， 从而无法形成日食 (上图中左、 右两侧的情形就是如此)[注三]。



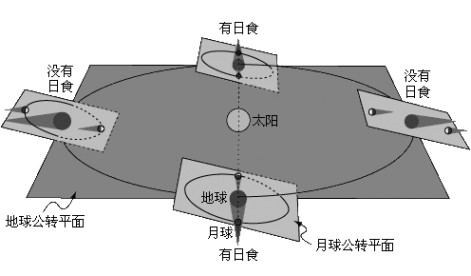
【地球、月球的公转轨道与日食】

那么什么时候才会有日食呢？ 显然只有当月球不仅位于地球和太阳之间， 而且还恰好离地球公转轨道平面不远时。 由于整个月球公转轨道 (作为一个椭圆) 与地球公转轨道平面的交点只有两个， 因此月球只有运动到地球和太阳之间， 并且又恰好在这两个交点之一的附近时， 才能形成日食。 在天文学上， 这两个交点有自己的名字， 视月球自南向北还是自北向南穿越地球公转平面而定， 分别被称为升交点 (ascending node) 和降交点 (descending node)， 两者的联线则被称为交点线 (line of nodes)。 用这种术语， 形成日食的条件也可以表述为： 月球运动到地球和太阳之间， 并且交点线与太阳方向几乎重合 (这保证了月球在两个交点之一的附近)。 从上图中不难看到， 交点线与太阳方向几乎重合的情形在整个地球公转周期上只会出现在两个时段里 (即上图中两个 “有日食” 的位置附近) ， 因此日食的发生并非每月一次， 而似乎是每年只有两次。

如果每年有两次日食的话， 一个世纪就是 200 次。 这与前面提到的次数接近了不少， 但仍有偏差， 可见在日食的频率中还隐藏了别的玄机。 这玄机之一就在于月球的公转轨道并不是固定不变的。 受主要来自太阳的引力摄动影响， 月球的公转轨道平面在不断改变着方位， 由此导致的结果是交点线会缓慢转动， 这种转动的方向与地球公转的方向相反， 周期约为 18.61 年， 被称为交点的退行 (regression of nodes)。 如果不存在交点的退行， 交点线将每隔半年与太阳方向重合一次， 日食将会有规律地出现在每年年历的固定时段中， 它在历史上的神秘感也将褪去不少。 但由于存在交点的退行， 日食的出现时间就变得有些扑朔迷离了。 因为交点线离开太阳方向后， 无需经过半年， 就会由于自己的转动而提前与太阳方向再次重合。 简单的计算表明， 这之间的间隔只有 173.3 天 (读者可以利用交点线的转动周期为 18.61 年这一信息自行计算一下)。 两次这样的间隔则是 346.6 天， 这被称为交点年或食年 (eclipse year)， 这个时间单位在分析日食时有着重要作用。

由于每个食年都包含了交点线与太阳方向的两次重合， 而 “食年” 的长度 (346.6 天) 只有 “年” (365.24 天) 的 95% 左右。 这么推算起来， 每个世纪包含的食年数目约有 105 个， 而日食的次数则应该有 210 次左右。 这比前面的 200 次又进了一步， 但仍比实际次数来得少， 这又是怎么回事呢？ 这次的答案更加微妙， 但关键之处其实已蕴涵在了前文的措辞之中。 我们在前面提到， 日食发生的条件是月球运动到地球和太阳之间， 并且又恰好在两个交点之一的附近。 这里的 “附近” 二字十分关键。 为什么是 “附近” 而不必正好在交点上呢？ 一个主要的原因是地球是一个庞然大物。 这就好比用一只很大的箩筐去兜别人扔过来的东西， 东西哪怕扔歪一点， 也照样能兜到。 日食的形成也一样， 由于地球很大， 月球即使偏离交点， 只要偏得不太过分， 影子就仍能投射到地球上， 从而仍能形成日食。 那么， 多大的偏离才不过分呢？ 计算表明， 只要偏离在 15.35° 以内， 就能确保日食； 如果偏离在 9.92° 之内， 则不仅能确保日食， 而且还能确保日全食； 甚至当偏离在 15.35° 以外， 但在 18.52° 之内时， 仍有一定的可能性会发生日食 (这时是否发生日食将取决于月球及太阳离地球的远近等其它因素)， 这个允许偏离的最大范围所对应的时段被称为食季 (elipse season)。

由于偏离可以发生在交点的任何一侧， 因此食季的角度范围是 18.52° 的两倍， 即 37° 左右。 在地球绕太阳的公转中， 走过这样一个角度范围所需的的时间约为 37 天， 这就是食季的长度。 由于这个长度比一个 “月” 来得长， 因此在一个食季中， 至少会发生一次日食。 运气好的话， 月球有可能会两次经过能形成日食的位置， 这样我们就能在一个食季中看到两次日食。 比如即将到来的 2011 年的 6 月 1 日和 7 月 1 日这两个同属一个食季的日子就都将出现日偏食 (可惜中国不在那两次日偏食的日食带上)。 由于在一个食季中有一定的可能性出现两次日食， 因此每个世纪的日食次数要比食季本身的数量略多， 而且各个世纪的日食次数不尽相同。

现在让我们来介绍一些更精确的日食规律。 我们已经知道， 日食的发生是因为月球遮挡了太阳。 很明显， 这时的月相必定是新月 (因为太阳在月球的正后方)。 因此， 日食发生的粗略条件虽然取决于食年和食季， 确切日期却是由新月决定的 (读者如果想要推算日食的时间， 这一点是很重要的[注四])。 在太阳、 地球和月球这一系统中， 非常巧合的是： 19 个食年几乎恰好等于 223 个朔望月——两者都很接近 6585 天。 这说明与任何一次日食相隔 6585 天， 就几乎铁定会有另外一次日食。 更巧合的是， 月球每两次经过近地点 (或远地点) 的时间间隔——即所谓的近点月 (anomalistic month)——为 27.55455 天[注五]， 239 个近点月也几乎恰好就是 6585 天。 由于近点月描述的是月地距离——从而也是月球的角直径——的变化周期， 而月球的角直径是影响日食种类及持续时间的重要因素 (因为月球的角直径越大， 就越容易形成日全食， 而且能遮挡太阳的时间也就越长)。 因此 6585 天是食年、 朔望月和近点月的共同倍数这一巧合， 意味着每隔 6585 天， 与日食有关的太阳、 地球和月球的各种位置参数都几乎恰好彼此相同， 由此导致的结果是出现两次几乎一模一样的日食！ 6585 天这个周期由于这一特点而变得很奇妙， 它有一个专门的名称， 叫做沙罗周期 (Saros)， 这个名称来自古巴比伦， 它的希腊文含义是 “重复”。 古巴比伦人早在两千五百多年前就知道了这一周期。 由于日食的确切日期取决于新月， 而新月之间的间隔是朔望月， 因此沙罗周期的确切长度由 223 个朔望月所确定， 比较精确的数值是 6585.32 天， 或 18 年零 11 天又 8 小时[注六]。

作为应用沙罗周期的例子， 我们可以看一看 2009 年 7 月 22 日经过中国长江流域的， 被称为 “最壮观日食” 的日全食， 那次日食的全食时间长达 6 分 39 秒， 属于超长日全食。 与它以沙罗周期相间隔的前三次日食分别发生在 1955 年 6 月 20 日， 1973 年 6 月 30 日和 1991 年 7 月 11 日， 也都是日全食， 全食时间分别为 7 分 8 秒， 7 分 4 秒和 6 分 53 秒， 与当前天文条件下日全食持续时间的理论上限 7 分 31 秒 (请读者想一想， 这一理论上限在什么条件下可以实现) 相差不多， 也都是超长日全食， 彼此间非常相似。 不仅如此， 我们还可以很放心地预言， 与那次日食往未来方向间隔一个沙罗周期的 2027 年 8 月 2 日， 也一定会发生一次持续时间很长的日全食 (瞧瞧， 现在咱们也能预言日食了)。

利用沙罗周期的特点， 人们对日食进行了归类， 将被沙罗周期所分隔的各次两两相似的日食归为同一序列， 称为沙罗序列 (Saros cycle)。 每个沙罗序列有一个序列号， 比如 2009 年 7 月 22 日那次日食所属的序列号是 136， 即沙罗序列 136 (Saros cycle 136)。 那是一个著名的沙罗序列， 它之所以著名， 除了当前的全食时间特别长以外， 还有一个更重要的原因， 我们将在本节的末尾予以揭晓。

有关沙罗序列， 还有几个重要特点值得一提。 细心的读者也许注意到了， 在沙罗周期中， 除了 18 年零 11 天这个大头外， 还有一个 8 小时的零头。 这个零头虽然不大， 却不容忽视。 由于地球每 24 小时自转一周， 因此这 8 小时的零头意味着同一个沙罗序列中， 相邻的两次日食在经度上大致相差 1/3 个地球， 即 120°， 比如前面提到的经过中国长江流域的沙罗序列 136 日食， 它的上一次日食发生在中美洲和太平洋上， 下一次则将移师非洲北部。 同一地点的观察者是无法观察到沙罗序列中的相邻日食的 (从这点上讲， 古巴比伦人能够发现沙罗周期实在是一件很奇怪的事情， 感兴趣的读者可以查查资料， 探究一下他们是如何发现沙罗周期的)。 有关沙罗周期的另一个重要特点是它具有一定的寿命， 而不能千秋万载。 这是因为虽然 19 个食年的长度非常接近 223 个朔望月， 但毕竟不是完全相等。 仔细的计算表明， 前者比后者长了 0.46 天。 由此导致的后果， 是经过一个沙罗周期后， 月球相对于升交点或降交点的位置将会偏离 0.48°。 我们在前面说过， 日食食季的角度范围约为 37°， 因此经过不到 80 个沙罗周期， 月球位置的总偏移就会超过食季的角度范围， 这意味着沙罗序列的终结， 这个过程的总时间约为 1300 多年。 因此沙罗周期是不能千秋万载的——确切地说是只能千秋， 不能万载。



【日食的图示】

在接下来的篇幅中， 我们简单介绍一下日食的种类。 在日食中， 如果月球的本影扫过地球， 相应的日食就称为日全食， 被本影扫过的区域称为全食带； 如果本影无法触及地球， 但其延长区——即所谓的束后本影 (antumbra)——扫过地球， 相应的日食就称为日环食 (annular eclipse)， 被束后本影扫过的区域称为环食带； 如果本影和束后本影都无法触及地球， 而只有半影扫过地球， 相应的日食就称为日偏食 (partial eclipse)， 被半影扫过的区域称为偏食带。 显然， 在日全食发生时， 月球的角直径必须大于太阳， 而在日环食发生时， 月球的角直径必须小于太阳。 这两种情形都能发生， 是因为我们在第二节中提到过的一个事实： 即 “在太阳和月球之间存在一个美妙的巧合， 那就是它们看起来几乎是一样大的”。 这一巧合， 加上月球和地球的公转轨道都是椭圆， 从而月地和日地距离都会随时间改变这一特点， 使得月球的角直径有时候比太阳大， 有时候比太阳小。 这是我们有时候能看到日全食， 有时候能看到日环食的根本原因。日食的发生还有其它一些规律， 限于篇幅， 我们就不介绍了。 对日食规律的研究不仅能让天文学家们预言未来日食出现的时间、 地点及持续时间， 而且还能帮助历史学家们还原某些曾经提及过日食的历史事件的准确时间 (比如希罗多德所记载的那次因日食而终止的战争就被历史学家们确定为最有可能发生在公元前 585 年)， 并且校正古代的历法。 对日食规律的推算——如我们在上面所做的——从原理上讲虽然是直接了当的， 但要想做得精确却很不容易， 需要考虑各种细微引力摄动的影响。 以对日食带的推算为例， 由于月球阴影在地球表面大部分区域的运动速度高达每秒几百米， 几分钟的时间误差就足以造成上百公里的空间误差。 依据这样的预言去追逐日食， 就会象革命大片中那些智力低下的敌军一样， 完全扑错地方。

由于无论月球的角直径比太阳大还是小， 两者终究都很接近， 而地球表面又是弧形的， 因此偶尔会出现一种更罕见的日食， 那就是地球表面的某个区域离月球较近， 使得月球看上去比太阳略大， 从而形成日全食。 而该区域之外的某个其它区域离月球较远， 使得月球看上去比太阳略小， 从而形成日环食。 这种同时具有全食和环食的特殊日食被称为全环食 (hybrid eclipse)。 在本世纪的 224 次日食中， 日全食、 日环食、 日偏食和全环食的次数将分别为 68、 72、 77 和 7 次。 如此种类繁多的日食出现在同一颗行星上， 这不仅在太阳系中是绝无仅有的， 甚至在任何其它恒星的周围， 其形成概率也是微乎其微的。 从这个意义上讲， 我们在地球上所能看到的日食是一种极为稀有的天象奇观。 事实上， 即便对地球来说， 这种奇观也不是任何时候都存在的。 日食带的狭窄 (全食和环食带的最大宽度都只有两三百公里) 说明月球与地球的距离只要再大一点， 日全食就将不复存在， 只要再小一点， 日环食就会烟消云散。 而天文学家们早就知道， 月球与地球的距离一直都在增加 (目前的增加速度为每年 38 毫米)， 因此早年的地球上不存在日环食， 未来的地球上则不会有日全食。 从地质学时标上讲， 目前这么丰富多彩的日食格局即使在地球上也是我们这个时代独有的。

在结束本节前， 我们还要补充一点， 算是对本节标题的注释。 我们在本节中虽然只讨论了日食， 但前面提到某些概念， 比如食季， 是同时适用于日食和月食的。 食季既是日食的摇篮， 也是月食的温床， 在一个食季中， 月球挡在太阳和地球中间就是日食， 地球挡在太阳和月球中间则是月食。 那么这两种情形哪一种更容易发生呢？ 仔细的分析表明， 是日食， 日食的食季长度要明显大于月食。 因此， 在地球上所能看到的日食次数要明显多于月食[注七]。 从这个意义上讲， 日食在大范围上虽然很稀有， 在如今我们这个小小星球上却很寻常， 因此是一种 “既寻常又稀有的奇观”。

读到这里， 有些读者也许会感到困惑， 因为在多数人的印象里， 日食远比月食稀罕。 之所以会有这种印象， 是因为月食发生时， 只要天气许可， 半个地球上的人都可以看到， 而日食发生时， 即便老天开眼， 也只有一个狭长日食带上的人才有眼福， 而且这日食带还常常落入海洋、 沙漠、 雪山、 极地等人烟稀少的地区。 因此虽然从总次数上讲日食比月食更多， 但除非你不惜跋山涉水去追逐日食， 否则你所能看到的日食会明显少于月食。 尤其是， 假如你特别眷恋家乡， 一步都不愿离开的话， 也许一辈子都未必能看到一次日食 (但依然可以看到几十次月食)。 以日全食为例， 在地球表面随机选定的地点上， 平均每隔 410 年才能看到一次[注八]。

日食——尤其是日全食——不仅是一种美丽的天象奇观， 在天文学家们的眼里， 更是研究太阳的绝佳机会。 对于天文学上的多数研究来说， 研究对象的过于暗淡是天文学家们面对的主要困难之一， 但对于太阳研究来说， 情况恰恰相反， 过于明亮才是最大的 “麻烦制造者”。 太阳的明亮甚至使得天文学家们不敢用精密的哈勃望远镜观察离太阳最近的水星。 在这种情况下， 日食的存在对于太阳研究有着极大的重要性。 这种重要性早在两百多年前就得到了令人瞩目的确立。 在 1780 年 10 月 27 日的日全食期间， 美国独立战争的交战双方 (英、 美) 为了让哈佛大学的天文学家们能在全食带上进行科学研究， 破天荒地作出了停战一天的决定 (可惜天文学家们不争气， 竟然算错了日食带， 以至于功败垂成)。

最后， 我们要兑现诺言， 来揭晓前面提到过的使 2009 年 7 月 22 日经过中国长江流域的日全食所属的沙罗序列 136 著名的 “更重要的原因”。 这个原因很简单： 如果我们将 2009 年 7 月 22 日往前推 5 个沙罗周期， 即 32927 天， 我们将得到一个日子： 1919 年 5 月 29 日。 在那个日子里也发生了一次属于沙罗序列 136 的日全食， 它的持续时间也很长： 6 分 51 秒。 熟悉物理学史的读者看到这个日期也许已经想起来了， 是的， 在那一天英国天文学家爱丁顿 (Arthur Eddington, 1882–1944) 对广义相对论中光线的引力偏折效应进行了检验。 那次检验也许是日全食期间所有科学研究中最著名的一次， 正是它使得沙罗序列 136 更加出名。

注释

在阿西莫夫所设想的这种多星系统中， 由于存在极为复杂而且巨大的引力摄动， 行星实际上是几乎不可能维持周期或准周期轨道， 从而几乎不可能为生物进化提供足够稳定的环境。 在人们探讨什么样的行星上有可能演化出高等生物时， 双星、 三星或多星系统中的行星基本上是可以被直接排除在外的。 因此阿西莫夫在那篇小说中设想的环境只是一种科幻的虚构。 这指的仅仅是普通情形， 在某些特殊情形下， 月球的阴影不是自西向东掠过地面， 而是从空中直接压向地面的。 感兴趣的读者可以想一想， 在什么情况下月球的阴影会从空中压向地面？ 另外也请想一想， 月球的阴影自西向东掠过地面， 与月球的东升西落是否矛盾？ 如果地球的直径不是 12700 公里， 而是 90000 公里以上， 月球的影子 (包括本影和半影) 就总能投射到地球上。 那样的话， 日食就真的会大约每个月都出现一次。 作为用新月推算日食确切日期的例子， 让我们推算一下 2010 年 1 月 15 日经过中国四川、 湖北等地的日环食之后的下一次日食的时间。 由于两个食季之间的平均间隔 (即食年的一半) 是 173.3 天， 很接近 6 个朔望月 (约 177 天)， 考虑到食季的长度有 37 天， 而日环食和日全食通常位于食季的中部， 因此我们可以预期， 2010 年 1 月 15 日的日环食之后相隔 6 个朔望月的那一天， 即 2010 年 7 月 11 日， 会有一次日食。 事实上也的确如此， 那一天有一次日全食， 只可惜它的日食带主要在南太平洋上， 只有一小段经过南美洲南端。 感兴趣的读者请将 2010 年 1 月 15 日这个日子往回推 6 个朔望月， 您将得到我们在本节中介绍过的另一次日食。 “近点月” 与 “恒星月” 的差别来自于月球近地点 (或远地点) 的进动， 这种进动与月球公转方向相同， 周期为 8.85 年 (读者可以据此定量验证一下两者的关系)。 想要验证沙罗周期的读者可以采用以下数据： 1 食年 = 346.620077 天， 1 朔望月 = 29.53059 天 (近点月的数据在正文中已经给出了)。 这里要顺便提醒读者的是， 如果一个沙罗周期中的 18 年间恰好有 5 个而不是 4 个闰年， 则沙罗周期的历法表示将是 18 年零 10 天又 8 小时。 为了行文简洁， 后文将不再提醒这一点。 另外还有一点要提一下， 那就是日食的种类及持续时间与地球到太阳的距离也有关系 (不过这个关系比较次要， 因为地球公转轨道的椭率远小于月球)。 沙罗周期只比 18 年多 10 或 11 天 (即 0.03 年) 这一特点， 意味着相隔一个沙罗周期后， 地球与太阳的相对位置也几乎不变。 早在 1887 年， 奥地利天文学家奥普泽 (Theodor von Oppolzer, 1841-1886) 就对从公元前 1208 年到公元 2161 年这 3368 年间的所有日食和月食进行了计算， 结果是日食约有 8000 次， 月食只有约 5200 次。 更具体地说， 北半球的日全食多于南半球。 在一个随机选定的北半球地点上平均每隔 330 年就会有一次日全食， 而南半球的这一间隔长达 540 年。 产生这种差异的原因， 是因为地球在北半球的夏季里离太阳较远 (位于远日点附近)， 这时太阳的表观直径较小， 容易形成日全食。 而恰恰是在这段时间里， 北半球被太阳照到的范围大于南半球 (因为是北半球的夏季)， 从而在日全食最容易形成的时段里有机会看到更多的日全食。 不过北半球并不能永远保有这一优势， 由于地球自转轴和地球公转轨道的进动， 这一优势将在几千年之后逆转。

二零一零年四月十四日写于纽约

二零一零年四月十五日发表于本站

太阳的故事（五）爱丁顿在1919

本文作者：卢 昌海

我们在上节末尾提到， 英国天文学家爱丁顿利用 1919 年 5 月 29 日的日全食， 对广义相对论中光线的引力偏折效应进行了检验。 在本节中， 我们就来聊聊这段或许是日全食期间所有科学研究中最著名的往事， 作为太阳故事的插曲。

这段往事既然与验证广义相对论有关， 当然得从广义相对论的 “始作俑者” 爱因斯坦 (Albert Einstein, 1879-1955) 说起。 1907 年 11 月， 爱因斯坦正在赶写一篇有关狭义相对论的综述[注一]。 他一边写， 一边思考着一个棘手的问题， 那就是如何将狭义相对论推广到非惯性系中。 结果有一天， 他产生了一个灵感。 他在后来访问日本期间所做的一次演讲中回忆了当时的情形， 他说当时他正坐在伯尔尼专利局的办公室里， 忽然一个念头闪了出来， “如果一个人自由下落， 他将不会感觉到自己的体重”。 这个念头就是著名的等效原理 (equivalence principle) 的雏形。 按照等效原理， 引力场和加速场在小范围内是不可分辨的[注二]， 由此导致的一个必然结果， 是光线会在引力作用下偏折 (因为做加速运动的观测者可以让光线看起来是弯曲的)。 1911 年， 爱因斯坦对这种光线的引力偏折效应进行了定量计算， 结果发现掠过太阳表面的光线会偏折 0.83 角秒 (arc second)[注三]。

爱因斯坦的这一计算虽然在很多环节上都打着相对论的旗号， 其实与相对论并无必然关系， 把光当成在牛顿引力场中运动的普通物质也能得到同样的结果。 事实上， 后来有人从对历史文献的 “考古” 中发现， 早在 1808 年， 德国科学家索德纳 (Georg von Soldner, 1776-1833) 就得到过同样的结果。 甚至比那更早， 1784 年， 著名的英国科学家卡文迪许 (Henry Cavendish, 1731-1810) 就在一篇未发表的手稿中指出过星光在牛顿引力场中会弯曲。 当然， 爱因斯坦并不知道那些陈年旧帐， 对他来说， 那是等效原理的推论， 是一个新的结果。

显然， 如果光线在引力场中会偏折， 那么当一颗星星出现在太阳近旁时， 它的实际方位与表观方位之间就会出现偏差。 这个偏差原则上是可以通过比较太阳不在视线附近时星星的方位与太阳在视线附近时星星的表观方位之间的差异来进行测量的。 但这里有一个问题， 那就是太阳实在太抢眼了， 一出场就会使得 “六宫粉黛无颜色”——整个天空基本上就看不到星星了， 更别说是在它的 “卧榻之侧” 了。 怎么办呢？ 只有等待机会。 等待什么机会呢？ 等待日全食的机会。 因此， 爱因斯坦在 1911 年论文的末尾写道： “由于日全食期间位于太阳附近那部分天空中的星星会变成可见的， 理论的这一推论是有可能被观测到的。” 他并且呼吁： “非常希望天文学家们能过问此处所提的问题， 即使上述考察看起来显得根据不足或冒险行事。”



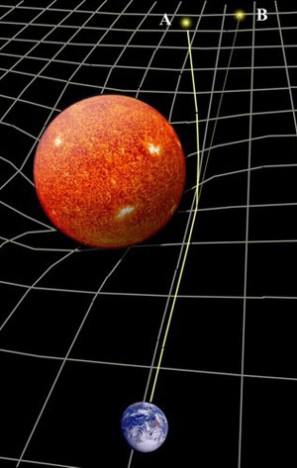
【太阳近旁的星光偏折（A 和 B分别为星星的实际方位与表现方位）】

最早被爱因斯坦的呼吁打动并愿意付诸行动的， 是在柏林天文台 “打杂” 的一位名叫弗洛恩德里希 (Erwin Freundlich, 1885-1964) 的德国天文学家。 这位曾跟随著名数学家克莱因 (Felix Klein, 1849-1925) 学习数学的年轻人当时正干着一些绘制星表之类 “嘴里都快淡出鸟来了” 的乏味工作。 1911 年 8 月的某一天， 事情有了一点转机， 他接待了一位来自布拉格 (Prague) 的物理学家。 这种接待工作原本倒也不是什么美差， 因为轮得到他去接待的人一般是不重要的。 但此次接待的物理学家稍有些不同， 他本身虽然不重要， 却恰好认得一位有点重要——并且正在变得越来越重要——的人物： 爱因斯坦。 闲聊中， 那位物理学家向弗洛恩德里希传达了爱因斯坦 1911 年的论文精神。 弗洛恩德里希立刻就对爱因斯坦的预言产生了兴趣， 因为那比他当时正在做的任何事情都更有意思。 于是他与爱因斯坦建立了通信联系， 讨论如何验证光线的引力偏折。

当然， 验证的方法爱因斯坦已经说了， 是利用日全食。 但问题是， 日全食的机会不是经常有的， 即便有也往往得跋山涉水前往日食带才能观测， 这就涉及到了钱的问题。 那么， 有没有不花钱的办法呢？ 爱因斯坦出了一个点子， 他建议弗洛恩德里希找一些以前日全食期间拍摄的旧相片， 看能否有所发现。 弗洛恩德里希采纳了这个点子， 向世界各地的天文学家索要了一些日全食期间拍摄的旧相片。 可惜结果很令人失望， 那些相片无一具备验证光线偏折所需的清晰度。

没办法， 只能花钱了。

弗洛恩德里希把目光瞄准在了 1914 年 8 月 21 日的日全食上。 那是一次属于沙罗序列 124 的日全食， 全食时间约为 2 分 14 秒， 全食带从西亚延伸到北欧， 其中离德国较近的观测点在俄国。 弗洛恩德里希决定多管齐下： 一方面与其它天文学家联系， 希望届时能分享他们的相片， 另一方面自己也筹集了经费， 前往俄国亲自进行观测。 事情的筹划虽不无困难， 但总算是办下来了。 但他没有料到的是， 随着第一次世界大战的爆发和蔓延， 1914 年 8 月 1 日， 德国对俄国宣战了。 这一来， 已经抵达俄国的弗洛恩德里希等人的身份立刻发生了戏剧性的变化， 由国际友人变成了敌国奸细。 俄国人民的眼睛是雪亮的， 很快就把他们这一小撮带着可疑仪器的德国人扣留了起来。 所幸的是， 他们后来被作为战俘交换回了德国， 但试图验证广义相对论的光线引力偏折效应的努力就此付诸了东流[注四]， 这是爱丁顿故事之前的主要序曲。

这段序曲中比较微妙的是， 在 1914 年的时候， 爱因斯坦虽然正在他的大学同学格罗斯曼 (Marcel Grossmann, 1878-1936) 的帮助下快速推进着广义相对论的研究， 他对太阳近旁光线引力偏折角度的预言却仍停留在 0.83 角秒上， 只有正确值的一半。 一些注意到这一历史细节的传记或科普作品喜欢就这一点进行发挥， 认为假如弗洛恩德里希能如愿以偿地拍摄 1914 年的日全食， 爱因斯坦的理论很可能会遭到一次观测的否决。 其实就当时的情形来说， 这个可能性是很小的。 因为一方面， 当时的观测误差很大， 要在 0.83 角秒和两倍于此的正确值之间作出无争议的区分是不容易的。 另一方面， 人们从弗洛恩德里希先前对日全食旧相片的处理中发现， 他的分析手段存在缺陷， 与后来人们普遍使用的手段相比， 具有更大的误差。 除这两点外， 还有一个因素也不容忽视， 那就是在光线偏折的正确值尚未出炉的时候， 人们并未对如今称为 “牛顿值” 的这个错误结果与广义相对论的结果进行区分， 他们更关心的是光线偏折到底是有还是无。 因此只要观测证实偏折存在， 哪怕具体数值有一定出入， 考虑到误差很大， 也依然会被视为是对爱因斯坦理论的重大支持。 因此， 那次观测的流产并不象一些作者所渲染的那样富有戏剧性。

现在回到爱因斯坦这边来。 1915 年底， 爱因斯坦完成了广义相对论， 并将太阳近旁光线的引力偏折角度修正为了 1.7 角秒， 即原先结果的两倍。 此时的爱因斯坦虽远没有后来那样的公众知名度， 在学术界却已是重量级人物了。 1913 年， 柏林大学为了把他从苏黎世挖到柏林， 不惜派出了象普朗克 (Max Planck, 1858-1947) 和能斯特 (Walther Nernst, 1864-1941) 那样史上最牛的猎头阵容， 动用了包括普鲁士科学院院士在内的超级诱饵， 才告得手。

虽然战争还在继续， 爱因斯坦所在的柏林几乎成了与世隔绝的孤城， 但爱因斯坦在广义相对论上所取得的重大进展， 还是很快就通过中立国荷兰的物理学家洛仑兹 (Hendrik Lorentz, 1853-1928) 和艾伦菲斯特 (Paul Ehrenfest, 1880-1933) 传到了一些感兴趣的人那里， 其中包括莱顿天文台 (Leiden Observatory) 的台长德西特 (Willem de Sitter, 1872–1934)。 德西特一直对爱因斯坦的工作怀有浓厚兴趣， 是除爱因斯坦本人以外最早研究广义相对论的人之一。 为了让英国同行们也能分享爱因斯坦的工作， 他将一份爱因斯坦的论文寄给了英国皇家天文学会。 而当时任皇家天文学会秘书的不是别人， 正是爱丁顿。 德西特寄来的论文第一时间就落到了他的手里。



【英国天文学家爱丁顿(1882–1944)】

就象把大陆和台湾隔开的不仅仅是台湾海峡， 把英国科学界和德国科学界隔开的也并不仅仅是英吉利海峡。 两百多年来， 这两个国家的科学界之间一直存在着嫌隙 (牛顿-莱布尼茨之争留下的恶果)， 而且当时英国和德国正处于交战状态， 情况更是雪上加霜。 但爱丁顿却是一个例外， 他是一位坚定的和平主义者， 丝毫不受英、 德两国之间任何争斗的影响， 对德国科学家及其工作没有任何成见。 爱因斯坦在一篇阐述广义相对论场方程的通讯中曾经表示： “任何人只要对这一理论有着充分理解， 就很少能从它那不可思议的魔法中逃脱出来”。 巧得很， 爱丁顿恰好就具有使自己 “对这一理论有着充分理解” 所必需的数学功底， 他的命运也就可想而知了。 在此后两年多的时间里， 爱丁顿被广义相对论那 “不可思议的魔法” 所彻底吸引， 成为了当时为数不多通晓并积极传播广义相对论的物理学家之一[注五]。 而广义相对论对光线引力偏折的预言自然也引起了他的极大兴趣。

1918 年， 爱丁顿开始与皇家天文学家、 格林威治天文台 (Royal Greenwich Observatory) 台长戴森 (Frank Dyson, 1868-1939) 商量组织日食远征队， 检验广义相对论的光线引力偏折效应的计划。 这个计划当时对爱丁顿来说有着双重意义， 一方面当然是可以检验让他如此着迷的广义相对论； 另一方面， 则可以使他摆脱一个现实困境。 我们在前面提到， 爱丁顿是一位和平主义者， 事实上， 他的和平主义立场还相当激进， 激进到了因拒服兵役而将自己推到牢狱之灾边缘的程度。 在这个节骨眼上， 检验广义相对论成为了戴森帮他在英国海军部面前开脱的最好理由[注六]。

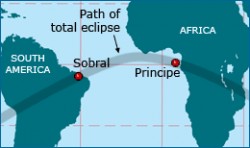
方略既已确定， 接下来就是寻找合适的日全食了。 我们在上节中曾经说过， 对单一地点来说， 日全食的出现是相当稀有的。 拿英国来说， 当爱丁顿想要检验广义相对论时， 英国本土已有近两百年没有发生日全食了 (英国本土的上一次日全食发生在 1724 年)， 而且未来的短时间内也不会有。 爱丁顿如果想在英国本土进行观测， 起码得再等上九年， 因为英国本土只有到 1927 年才会有新的日全食， 而且持续时间只有 24 秒， 实在是 “匆匆， 太匆匆”。 因此爱丁顿选了一个更近、 并且更好的时机， 这个时机就是我们在上节末尾提到的发生于 1919 年 5 月 29 日， 属于沙罗序列 136， 持续时间长达 6 分 51 秒的超长日全食。 那样的日全食对观测来说无疑是极为有利的。 而更有利的则是， 那时的太阳将位于包含许多亮星的金牛座 (Taurus) 毕星团 (Hyades)。 这样的机会哪怕在全世界范围内也不是常有的。 那次日全食唯一不利的条件， 是全食带远在赤道附近， 横贯非洲、 大西洋及南美洲， 却远离欧洲。 在对几个候选地点进行气候分析之后， 爱丁顿在非洲和南美洲各选了一个观测点， 其中非洲的观测点选在非洲西海岸附近的小岛普林西比 (Principe)， 南美洲的观测点则选在了巴西亚马逊丛林中的小镇索布拉 (Sobral)。

【1919年日食的全食带】

不过， 由于这两个地点远离英国本土， 爱丁顿的计划能否实现， 还得看战争能否及时结束。 只有战争结束了， 远征队才能平安穿越大西洋 (否则会受到德国潜艇的威胁)。 幸运的是， 第一次世界大战的战火在燃烧了四年， 付出了 1500 万条人命的代价后， 终于在 1918 年 11 月熄灭了。 1919 年 3 月， 两支英国远征队如期出发， 其中爱丁顿亲自率领的一支前往非洲的普林西比， 另一支前往南美洲的索布拉。 观测的过程想必大家早已在其它科普作品中读到过， 本文就不赘述了， 基本上就是环境是如何如何的闷热不堪， 蚊虫是如何如何的毁人不倦， 天气是如何如何的忽好忽坏， 心情是如何如何的 “此起彼伏” (宋丹丹语)。 最终的结果是两支考察队都拍到了相片， 满载而归。

接下来就是数据分析。 爱丁顿后来很喜欢讲述的一个故事， 是说远征队出发前他的助手曾经问戴森， 假如观测到的结果是爱因斯坦预言值的两倍， 会怎么样？ 戴森回答说， 如果那样的话， 爱丁顿就会发疯， 而你只好一个人回来了。 其实， 主要的数据分析是在回英国之后才做的， 爱丁顿即使要发疯也得回英国来发。 由于数据比较微妙， 分析过程持续了较长时间。 具体地说， 索布拉远征队使用了两类不同的观测方法， 一类用的是一架四英寸折射望远镜， 拍摄的相片共有八张 (其中一张因云层干扰而没能拍到星星， 因此有效相片为七张)， 这些相片显示的偏折角度为 1.98 角秒， 与爱因斯坦的预言比较接近， 误差也相对较小。 另一类用的是天体照相仪 (astrograph)， 拍摄的相片共有十九张， 这些相片显示的偏折角度约为 0.9 角秒， 与 “牛顿值” 比较接近， 但这些相片的图像比较模糊， 据怀疑是因为仪器中的定天镜 (coelostat mirror) 受热变形所致。 爱丁顿自己那组用的也是天体照相仪， 共拍摄了十六张相片， 但其中只有两张质量较好， 经分析得到的偏转角度为 1.61 角秒， 也比较接近爱因斯坦的预言。

那么结论是什么呢？ 爱丁顿作出了自己的选择， 他以仪器有问题为由丢弃了 0.9 角秒那组比较接近 “牛顿值” 的结果， 而保留了索布拉远征队的 1.98 角秒的结果， 以及他自己那组其实也不怎么靠得住的 1.61 角秒的结果。 这两组结果的平均非常接近爱因斯坦的预言。 因此爱丁顿的结论是广义相对论对光线偏折的预言得到了证实。

1919 年 11 月 6 日， 英国皇家学会和皇家天文学会举行联合会议， 正式宣布了爱丁顿的观测结果及结论。 会议由电子的发现者， 皇家学会主席， 著名实验物理学家汤姆生 (J. J. Thomson, 1856-1940) 主持。 在巨幅的牛顿画像前， 戴森报告了观测结果， 他表示， 在仔细研究了相片之后， 他认为它们毫无疑问地证实了爱因斯坦的预言。 汤姆生主席基本接受了这个乐观结论， 表示这是自牛顿以来有关引力理论最重要的结果[注七]。 特意从剑桥赶来参加会议的著名哲学家怀特海 (Alfred Whitehead, 1861-1947) 后来在自己的著作《科学与当代世界》(Science and the Modern World) 中回忆了当时的情形， 他写道：

“那种洋溢着浓厚兴趣的气氛完全是希腊戏剧式的。 我们都齐声称颂着这一卓越事件在发展过程中所显示出的命运的律令。 舞台本身就充满了戏剧性： 传统的仪式和后面悬挂着的牛顿画像都在提醒我们， 最伟大的科学成就在两个多世纪后的今天第一次得到了修正。”

这无疑是科学史上的一个著名时刻， 不过在那之前， 爱丁顿的观测结果就在一个小范围内传开了。 早在 9 月 22 日， 洛仑兹就已经发电报将消息告诉给了爱因斯坦。 稍后， 10 月 4 日， 普朗克向爱因斯坦表示了祝贺。 10 月 22 日， 普鲁士科学院院士， 德国哲学及心理学家斯顿夫 (Carl Stumpf, 1848-1936) 也向爱因斯坦表示了 “最诚挚的祝贺”， 并表示， 在经历了军事和政治的失败后， 德国科学能够取得这样的胜利令人感到自豪。 而爱因斯坦在接到洛仑兹的电报后随即将消息转告给了已罹患重病的母亲 (他母亲在几个月后就病逝了)[注八]。

很多科普或传记作品在描述爱因斯坦得知爱丁顿观测结果后的反应时， 喜欢渲染他的自信与超脱。 毫无疑问， 爱因斯坦对广义相对论有着极强的信心， 但再好的理论也必须经过观测的检验。 因此任何物理学家只要还在关心作为研究对象的大自然， 就无法在一个重大的观测检验面前保持超脱， 爱因斯坦也不例外。 事实上， 爱因斯坦一直非常在乎天文学家们对广义相对论的验证。 拿光线的引力偏折来说， 他不仅反复呼吁天文学家们对此进行检验， 而且还在弗洛恩德里希为 1914 年的远征筹集经费时， 一方面动用自己的影响力给予帮助， 另一方面表示若有必要， 将亲自出资支持弗洛恩德里希的观测。 而在爱丁顿的结果出炉前， 爱因斯坦也不止一次在给亲友的信中询问观测结果， 或流露出等待结果的急切。

爱丁顿在 1919 年的故事大致就是这些。 他后来把获得观测结果的那一刻称为自己一生最伟大的时刻。 那一刻不仅是他个人的伟大时刻， 而且也使爱因斯坦几乎在一夜之间获得了世界性的公众影响。 但这些耀眼的光环并未让学术界失去应有的沉稳， 对于爱丁顿处理观测数据的方法， 很快就有人提出了质疑。 由于篇幅关系， 本文就不展开讨论那些质疑了。 不过要指出的是， 爱丁顿的论文如实列出了所有的观测数据， 其中包括被他以仪器有问题为由丢弃的数据。 他是在公布了全部数据的基础上进行自己的分析与取舍的。 因此人们对他数据取舍的合理性虽然可以有各种看法， 但如果把那种取舍渲染成类似于舞弊的行为则是很不恰当的。 另外要指出的一点是， 1978 年， 当爱因斯坦诞辰一百周年的日子即将到来时， 当时任格林威治天文台台长的默里 (Andrew Murray) 与同事哈维 (Geoffrey Harvey) 等人用包括计算机处理在内的现代手段重新分析了被爱丁顿丢弃的那些相片， 结果发现它们所记录的星光偏折其实不是当年以为的 0.9 角秒， 而是 1.55±0.34 角秒。 因此即使是那些相片， 也与爱因斯坦的结果更为接近。

当然， 更重要的是， 无论是广义相对论， 还是其它科学理论， 也无论已经出现了多么具有轰动效应的检验， 新的检验都永远不会停息。 在爱丁顿之后， 更多的人对广义相对论产生了兴趣， 在后来的日全食期间， 更多的天文学家加入了检验的行列。 再往后， 随着技术的发展， 日全食已不再是检验星光偏折的唯一机会， 检验的精度也由原先的百分之几十提高到了万分之一量级。 直到今天， 人们依然在用各种手段检验着广义相对论的各种预言， 科学就是这样一种不断自省、 永不停息的努力。

注释

他的这篇题为 “关于相对性原理和由此得出的结论” 的综述是应德国《放射性与电子学年鉴》的编辑斯塔克 (Johannes Stark, 1874-1957) 的约稿而写的。 斯塔克是德国实验物理学家， 斯塔克效应 (Stark effect) 的发现者， 1919 年的诺贝尔物理学奖得主。 他后来成为 “德意志物理学” 的狂热鼓吹者， 对爱因斯坦展开了激烈攻击。 但在 1907 年， 两人的通信是完全彬彬有礼的， 斯塔克对当时还在专利局的爱因斯坦的称呼是 “非常尊敬的同事”， 爱因斯坦对斯塔克的称呼则是 “非常尊敬的教授先生”。 对等效原理的确切含义感兴趣的读者可参阅本人的短文 从等效原理到 Einstein-Cartan 理论。 这是爱因斯坦 1911 年原始论文所给出的数值， 利用现代天文数据， 爱因斯坦当年结果所对应的数值应为 0.87 角秒， 完整的广义相对论预言则是 1.75 角秒。 下文在引述各种当年所采用的数值时， 将不再一一注释。 不过即便没有战争的干扰， 他们的观测也不可能成功， 因为那天的全食期间太阳恰好被厚厚的灰云所遮盖。 打算与弗洛恩德里希合作的美国里克天文台 (Lick Observatory) 台长坎贝尔 (William Campbell, 1862-1938) 带领的美国远征队当时也在那里， 他们虽然未被扣留， 却也因为天气原因而无功折返 (返回时因战争原因， 将仪器暂时留在了俄国)。 坎贝尔后来在 1918 年 6 月 8 日的属于沙罗序列 126 的日全食期间再次进行了观测 (那次的全食带经过美国)。 但可惜他留在俄国的仪器因战争原因尚未运回， 只能用一些临时拼凑的仪器， 而当时的天气状况也不佳， 拍到的相片质量很差。 此外， 在弗洛恩德里希之前， 1912 年 10 月 10 日的属于沙罗序列 142 的日全食期间， 曾有一支阿根廷远征队前往巴西进行观测， 结果因遭遇雨天而失败。 有一个流传很广的故事说波兰人西尔维斯坦 (Ludwik Silberstein, 1872–1948) 曾对爱丁顿说世界上只有三个人懂得广义相对论， 而爱丁顿是其中之一。 爱丁顿不置可否， 当西尔维斯坦让他不要太谦虚时， 他说： “不， 我只是在想那第三个人是谁。” 这个故事印度裔美国物理学家钱德拉塞卡 (Subrahmanyan Chandrasekhar, 1910-1995) 曾听爱丁顿亲口说过， 因此应该是真的， 只不过这个故事对广义相对论的难度显然有所夸大， 事实上， 即便在那时， 除爱因斯坦和爱丁顿外， 懂广义相对论的起码还应该算上希尔伯特 (David Hilbert, 1862-1943)、 魏尔 (Hermann Weyl, 1885-1955)、 德西特等人。 另外一个也流传很广的传闻是美国《纽约时报》散布的， 说爱因斯坦将自己的某部文稿交给出版商时警告对方说世界上理解他的人不超过十二个。 这个故事的真实性不得而知。 钱德拉塞卡在他撰写的爱丁顿传记中认为， 如果不是当年人们夸大了广义相对论的难度， 很多二十世纪六七十年代的工作在二三十年代就应该能很容易地实现。 对于这个看法， 当然是见仁见智， 不过广义相对论的难度曾受到很大夸张是不争的事实。 爱丁顿的拒服兵役能被英国当局容忍， 还有一个原因是因为不久前的 1915 年， 优秀的英国年轻物理学家莫塞莱 (Henry Moseley, 1887-1915) 在战斗中阵亡。 英国科学界在震惊之余， 许多著名科学家出面为爱丁顿请愿， 表示让象爱丁顿那样的杰出科学家参军不符合英国的长远利益。 有很多作者在引述汤姆逊的话时， 将之改为了 “这是人类思想史上最伟大的成就之一——也许是最伟大的成就”， 这是加油添醋。 当日的会议记录显示， 汤姆逊并未说过那样的话。 洛仑兹电报所传达的含义其实相当模糊， 它的内容是这样的： “爱丁顿发现了太阳边缘的星光偏折， 初步数值在 9/10 角秒及其两倍之间”。 从这个电文中很难判断爱丁顿所证实的究竟是爱因斯坦还是牛顿。 而爱因斯坦给他妈妈的信中也只是笼统地写道： “今天有个好消息， 洛仑兹来电报告诉我英国远征队证实了太阳使光线偏折。”

二零一零年四月三十日写于纽约

二零一零年五月一日发表于本站

http://www.61k.com

太阳的故事（六）阳光里的奥秘

本文作者：卢 昌海

在前面几节中， 我们介绍了太阳的大小和远近，地心说 vs 日心说，日食的规律等。 那些介绍所涉及的分析手段大都是几何手段。 从本节开始， 我们将介绍一类全新的手段： 物理手段。 我们将会看到， 那是一类远比几何手段更有效的手段， 在它的帮助下， 科学家们很快就将太阳研究推向了纵深。 这种从几何手段向物理手段的过渡， 是与天文学自身的发展脉络基本一致的。 因为在历史上， 人们对天文学的研究首先是从研究天体运动的几何规律入手的[注一]， 用物理手段研究天文的所谓 “天体物理” (astrophysics) 这一重要分支则是在晚得多的时候才出现的 (而且它的出现与本节所要介绍的内容有着密切关系)。

天文学沿这样的历史轨迹发展不是偶然的， 拿太阳来说， 想对它进行深入研究， 首先必须克服一个显而易见的困难， 那就是它离我们实在太远了 (1.5 亿公里)， 而且也实在太热了 (表面温度就足以使任何已知的物质气化)， 我们几乎永远也不可能象研究地球一样到太阳上去钻个孔、 挖个洞、 采集一些样本。 这一现实的困境曾使一些人深感悲观。 1835 年， 实证主义哲学的创始人， 法国哲学家孔德 (Auguste Comte, 1798–1857) 曾经预言， 人类永远也不可能了解太阳和星星的化学组成。

幸运的是， 与很多其他哲学家曾经发表过的有关科学的高论一样， 孔德的预言很快就破灭了。 因为太阳虽然很遥远， 而且很热， 但它却很慷慨的把一样东西送到了地球上， 那就是阳光。 这个初看起来很寻常的事实有着极不寻常的推论。 有了它， 我们这个星球才有生命。 但阳光带给我们的不仅仅是生命， 还有信息， 比如有关太阳化学组成的信息， 这是孔德所不知道的。 事实上， 比孔德的预言早了二十年， 1814 年， 德国物理学家夫琅禾费 (Joseph von Fraunhofer, 1787-1826) 就发明了一种新的仪器， 叫做光谱仪 (spectroscope)， 为人们解读阳光里的信息提供了工具。

不过在介绍夫琅禾费之前， 我们先要 “论资排辈” 一下， 向大家引见两位前辈。

这两位前辈中的第一位对所有人大概都是 “久闻大名， 如雷贯耳” 的， 他就是牛顿 (Isaac Newton, 1643-1727)。 在十七世纪六十年代中期， 牛顿做过很多光学实验， 在其中一组实验中， 他让阳光从一个小孔射入屋内， 然后经过一个三棱镜， 最后投射到一块屏上。 他惊讶地发现， 出现在屏上的居然是一个色彩缤纷的长椭圆形影像。 虽然在牛顿那个时代， 人们对光的本性还一无所知， 但牛顿毕竟是牛顿， 他敏锐地意识到——并且通过进一步的实验证实了——这一现象所揭示的有关阳光的重要性质： 那就是阳光是由不同颜色的单色光组合而成的。 出现在屏上的彩色影像， 则是由于不同颜色的单色光在三棱镜中的偏折角度不同， 而被投射到屏上的不同位置所产生的。 如今我们知道， 牛顿发现的这一现象就是所谓光的色散 (dispersion)， 即不同波长 (从而颜色各异) 的光在色散介质中的折射率不同， 从而偏折角度不同。 而他在屏上看到的彩色影像则是最粗糙的阳光光谱——确切地说是阳光光谱中的可见光部分 (这部分约占阳光总能量的 40%)。 牛顿的这一重大发现可以算是一种很原始的光谱分析 (spectrum analysis)， 它是人类在探索光的本性道路上迈出的重要一步[注二]。



【光的色散】

但是从了解太阳的角度上讲， 牛顿所看到的光谱却有一个问题， 那就是它不仅可以从阳光中得到， 而且也能从其它白色或接近白色的光源中得到， 因此它带给我们的信息似乎并不是太阳所特有的。 那么， 在阳光里是否还隐藏着更微妙的信息， 甚至是太阳所特有的信息呢？ 由于牛顿不能长生不老， 对这些问题的探索就要依靠牛顿之后的科学家了。 可惜的是， 牛顿实在超前得太多了， 在接下来一百多年的时间里， 无论科学家们怎么重复和改进他的实验， 都只能看见与他看见过的相同的彩色影像。 这影像会不会就是大自然给我们的终极答案呢？ 没有人知道， 但科学家们没有气馁， 他们持续不断地进行着新的尝试。 正是因为科学界有这样的恒心和毅力， 象牛顿那样的高人也终有被超越的一天。

功夫不负有心人， 在十九世纪到来后的第二年， 1802 年， 一位英国化学家终于窥视到了黎明前的曙光。 所不同的是， 这缕曙光不是彩色， 而是黑色的！ 发现这缕曙光的英国化学家就是我们要介绍的第二位前辈， 他曾经是一位医生， 后来转向了科学， 他的名字叫做沃拉斯顿 (William Wollaston, 1766-1828)。

1802 年， 沃拉斯顿对牛顿的实验进行了重复和改进。 他采用了质量很好的三棱镜， 并用狭缝取代了牛顿的小孔 (以便让更多的阳光进入)， 结果他发现了一个前人不曾发现过的细节： 在那熟悉的彩色光谱中， 存在几条很细的暗线。 那些暗线是什么呢？ 沃拉斯顿作了一个猜测， 认为它们大都是不同颜色之间的分界线。 他的这个猜测在当时听起来是有一定道理的， 因为他所发现的暗线只有寥寥数条， 而人们描述光谱所用的颜色也只有寥寥数种 (红、 橙、 黄、 绿、 蓝、 青、 紫)， 两者之间的确存在粗略的匹配性。 但他没有想到的是， 那些看似不起眼的暗线， 已经让他站在了一座巨大冰山的尖顶上。 十一年后， 当那座冰山的更多部分显露在人们面前时， 他的猜测就不攻自破了。

那位让人们窥知冰山更多部分的人， 就是夫琅禾费。



【纪念夫琅禾费诞辰两百周年的邮票】

有了光谱仪的帮助， 隐藏在阳光里的真正奥秘终于比较清晰地显露在了人们面前。 与沃拉斯顿一样， 夫琅禾费也看到了暗线。 但他的光谱仪远比沃拉斯顿的三棱镜精密， 因此他看到的暗线不是寥寥数条， 而是有几百条之多， 他对它们进行了仔细的编号。 为了纪念夫琅禾费的贡献， 人们把那些暗线称为了夫琅禾费线 (Fraunhofer lines)。 后来随着光谱仪技术的进一步改良 (比如使用更好的三棱镜， 更精密的透镜， 使用光栅等)， 以及照相技术的加盟， 人们在阳光光谱中观测到的暗线数目也越来越多。夫琅禾费出生于一个光学仪器世家， 父亲和爷爷都是玻璃工匠， 母亲那一方与玻璃工艺的渊源更是可以回溯到十七世纪早期。 但很不幸的是， 在夫琅禾费 10 岁和 11 岁时， 他的母亲和父亲先后去世， 慕尼黑的贫民窟里从此多了一位年幼的孤儿。 在随后的几年时间里， 夫琅禾费靠替一位镜片制造商做学徒维持着艰难的生计。 1801 年， 厄运再次降临到他的身上， 他所住的贫民窟里的 “脆脆楼” 垮塌了。 好在 14 岁的他被人从瓦砾堆下救了出来， 算是不幸中的万幸。 夫琅禾费的悲惨遭遇引起了恰巧途经垮塌现场， 后来成为巴伐利亚国王的马克西米利安一世 (Maximilian I, 1756-1825) 的同情， 在他的资助下， 夫琅禾费进了学校， 并在十年后成为了光学研究的高手。 1814 年， 夫琅禾费发明了光谱仪。 这种仪器的核心部分虽仍是三棱镜， 但在三棱镜的前后分别用透镜或透镜组对光线进行了汇聚， 从而大大提高了分辨率。

但那些暗线到底是什么呢？ 这个曾经困扰沃拉斯顿的问题也困扰着夫琅禾费。 他首先怀疑的是自己的仪器： 那些暗线会不会是自己仪器的缺陷造成的呢？ 他对这种可能性进行了排查， 排查的方法很简单， 那就是观察其它光源。 如果暗线是仪器的缺陷造成的， 那就应该与光源无关， 从而应该同样地出现在其它光源的光谱中。 观察的结果很快排除了那种可能性——其它光源的光谱中并没有出现同样的暗线分布。 这样， 夫琅禾费就得到了一个结论： 太阳光谱中的暗线是阳光本身的特征。 由于那些暗线看上去虽然繁杂， 却每一条都有固定的位置 (这也是夫琅禾费能对它们进行编号的基础)， 它们显然隐藏着某种奥秘， 而且这奥秘必定与太阳有关。

那么， 这奥秘究竟是什么呢？ 夫琅禾费不知道， 其他人也不知道。 这局面多少有点尴尬， 就好比已经发现了通往阳光奥秘的大门， 却找不到开门的钥匙。 这种尴尬局面持续了四十多年， 在此期间， “功臣” 夫琅禾费和沃拉斯顿， “反面陪衬” 孔德等都先后离开了人世。

解密的日子终于还是到来了。

1859 年， 两位德国人在光谱研究上取得了突破性的成果。 这两位德国人一位是化学家， 名叫本生 (Robert Bunsen, 1811-1899)， 以他名字命名的 “本生灯” (Bunsen burner) 直到今天仍被许多化学实验室所使用； 另一位是物理学家， 名叫基尔霍夫 (Gustav Kirchhoff, 1824-1887)， 以他名字命名的 “基尔霍夫电路定律” (Kirchhoff's circuit laws) 直到今天仍是求解电路问题的重要工具。 这两人当时都在海德堡大学 (University of Heidelberg)， 本生当时正在研究化学元素被加热后所发射的光谱， 那些光谱中有一些亮线， 而且不同元素的亮线位置是不同的。 本生打算利用这一特点作为证认化学元素的新手段。 这在当时是一个很高明的想法。 不过想法虽然高明， 他用来观测光谱的设备却是滤色片一类老掉牙的东西， 精度很低。 这时候， 他的朋友基尔霍夫给他支了一招， 建议他使用光谱仪。 本生采纳了这一建议。 在接下来的一段时间里， 本生和基尔霍夫进行了合作， 他们不仅证实了每种化学元素都有自己独特的光谱， 就象每个人都有自己独特的指纹一样， 而且还通过光谱研究发现了两种新元素： 铯 (Cesium) 和铷 (Rubidium)， 显示了这种手段的巨大威力。



【德国物理学家基尔霍夫(1824-1887)】

在研究中， 基尔霍夫自己也作出了一生中又一项重要发现。 他注意到， 如果某种元素在加热后所发射的光谱中有某些亮线， 那么当光穿越由该元素制成的稀薄冷蒸汽时， 在光谱中原先的亮线位置上就会出现暗线。 由于亮线源于光的发射 (相应的光谱被称为发射光谱)， 暗线源于光的吸收 (相应的光谱被称为吸收光谱)， 因此基尔霍夫的发现也可以表述为：一种元素能发射什么样的光， 它也就能吸收什么样的光， 两者相互对应。 这个重要规律后来被称为基尔霍夫热辐射定律 (Kirchhoff's law of thermal radiation)[注三]。 现在我们知道， 光谱线是电子在不同能级之间跃迁产生的： 电子从高能级跃向低能级时会发射能量， 由此产生的是发射光谱， 从低能级跃向高能级时会吸收能量， 由此产生的就是吸收光谱。 由于这两者是由同一组电子能级决定的， 它们之间相互对应也就不足为奇了。 不过这一切直到二十世纪初才随着量子理论的发展而被人们所了解。 在基尔霍夫的时代， 人们对光谱线的了解还停留在 “知其然， 却不知其所以然” 的水平上， 基尔霍夫热辐射定律也只是一个经验规律。

但把这一经验规律与他和本生所做的事情联系起来， 基尔霍夫立刻意识到了这一整套方法的重要价值。 很明显， 太阳光谱中的夫琅禾费线——那成百上千条的暗线——正是太阳上的吸收光谱[注四]， 既然吸收光谱与发射光谱是相互对应的， 那么我们只要将夫琅禾费线与已知元素的发射光谱相比较， 就可以证认出太阳上的元素。 这样， 基尔霍夫就找到了开启大门， 破解阳光奥秘的钥匙。 对于基尔霍夫的这一重要发现， 本生曾经作过这样的记述：

“基尔霍夫和我现在正忙于一种让我们夜不能寐的研究之中。 基尔霍夫做出了一个有关太阳光谱中暗线起因的奇妙的、 完全出人意料的发现。 他能在太阳或火焰的连续光谱中， 在与夫琅禾费线严格对应的位置上， 以人工加强的方式产生出那些暗线。 这就找到了一种方法， 能让我们象确定化学试剂中的氯化锶那样精确地确定太阳和星星的组成。”

利用基尔霍夫的发现， 科学家们很快就在太阳光谱中证认出了大量和地球上相同的元素 (孔德同学的悲观预言正式入住历史博物馆)。 有些读者或许还记得， 我们在第三节中曾经提到过一种叫做 “天贵地贱” 的古代观念， 按照那种观念， 完美的天体和卑微的地球是由完全不同的质料组成的。 那种观念后来因伽利略发现太阳黑子而遭到了驳斥。 不过， 伽利略所驳斥的只是天体的完美性， 对那种观念的真正毁灭性的打击， 则是来自人们对天体化学成分 (即所谓质料) 的了解， 因为是它直接证实了天体与地球由相同质料所组成， 而这正是光谱学手段的功劳。

随着研究的深入， 科学家们不再满足于象牛顿那样利用普通的日光来做研究， 他们开始寻找新的机会， 其中最重要的机会就是日全食。 在 1868 年 8 月 18 日的日全食 (属于沙罗序列 133) 期间， 法国天文学家詹森 (Pierre Janssen, 1824-1907) 远赴印度观测了太阳光谱， 结果在太阳大气层中的色球层 (chromosphere) 的光谱中发现了一条波长为 5875? 的黄色亮线[注五]。 不同寻常的是， 这条亮线在地球上任何已知元素的发射光谱中都找不到对应。 这是怎么回事呢？ 是詹森搞错了吗？ 有可能， 但这种可能性很快就被排除了， 因为两个月后， 英国天文学家洛克耶 (Norman Lockyer, 1836-1920) 也在对同一次日全食的光谱记录中发现了同样的亮线。 两组独立的观测同时搞错， 而且错得一模一样的可能性无疑是很小的。

看来那条亮线并不是错误， 既然不是错误， 那它是什么呢？ 联想到本生和基尔霍夫通过光谱学手段发现新元素的故事， 这一问题的答案显然已呼之欲出。 是的， 答案就是新元素——一种在地球上尚未被发现过的新元素。 由于这一元素是在太阳上发现的， 洛克耶将之命名为了 “氦” (Helium)， 这个名称来自表示太阳的希腊语 helios (?λιο?)。 不过， 氦虽然是在太阳光谱中被发现的， 它作为 “太阳元素” 的身份却并未维持很久。 1895 年， 人们在地球上也发现了这种元素。 光谱学方法不仅让我们了解了太阳的化学组成， 而且还帮助我们发现了新元素。 追根溯源， 这一切当然都离不开夫琅禾费所发明的光谱仪， 它是如此地卓有成效， 以至于英国天文学家德拉鲁 (Warren De la Rue, 1815-1889) 曾经表示， 即便我们能跑到太阳上去， 把一些太阳上的物质拿到实验室来研究， 也不会比用光谱仪得到的结果更精确。 为了纪念夫琅禾费的重大贡献， 人们在他的墓碑上刻下了这样一句墓志铭： 他使星星变得更近。 事实上， 他不仅使星星变得更近， 还为一个新领域的开创奠定了基础， 因为整个天体物理学都是随着光谱学方法的应用而产生的。

氦元素的发现引起了人们对日全食太阳光谱的更大兴趣。 第二年， 1869 年 8 月 7 日的日全食 (属于沙罗序列 143) 期间， 天文学家们又对太阳光谱进行了仔细观测， 结果居然又有新的斩获： 他们在比色球层更外部的所谓日冕 (corona) 的光谱中发现了一条波长为 5303? 的绿色亮线。 这条亮线在所有已知元素的发射光谱中也找不到对应。 在随后的若干年里， 这样的新发现一而再， 再而三地出现， 人们在日冕光谱中发现的新谱线居然增加到了 24 条之多。 看来除了氦以外， 太阳上还有其它新元素。 至于那 24 条新谱线是来自一种还是多种新元素， 暂时还没法知道， 人们姑且先取了一个名字， 叫做 “氪” (coronium)[注六]， 它来自日冕的英文名 corona。 但与后来在地球上找到了的氦不同的是， 那神秘的 “氪” 元素从未在地球上露过面。 难道 “天贵地贱” 的古老观念毕竟还是有那么一丁点儿的正确， 太阳上毕竟还是有一些地球上不存在的元素吗？ 这个疑问直到二十世纪三十年代后才真相大白， 原来并不存在什么 “氪” 元素， 那些日冕光谱中的新谱线乃是来自一些被剥去了外层电子后的金属离子 (比如铁离子、 钙离子和镍离子)。 以那条 5303? 的绿色亮线为例， 它是来自被剥去了 13 个电子 (占总数的一半) 的 “无上装” 铁离子 (Fe13+) 的发射光谱。

现在我们知道了太阳上有哪些元素。 但科学家们的胃口比这更大， 他们不仅关心太阳上有哪些元素， 而且还想知道它们各自所占的比例——用天文学家们的术语来说， 叫做元素的丰度 (abundance)。 这对于进一步探索发生在太阳上的物理过程具有极大的重要性。 幸运的是， 物理学的威力完全能满足科学家们这一得寸进尺的要求。

推算元素的丰度从技术上讲并不容易， 但基本原理却并不复杂。 我们已经知道， 谱线的位置可以用来确定元素的存在， 但谱线带给我们的信息并不只是位置。 当我们观测到一条谱线时， 还会得到另一条信息， 那就是谱线的强度。 这条额外信息所携带的正是有关元素丰度的知识。 为什么呢？ 因为无论吸收光谱还是发射光谱， 它的强度都与产生谱线的元素的丰度有关， 丰度越大， 谱线就越强， 反之， 丰度越小， 谱线则越弱。 知道了这一关系， 我们就可以用谱线的强度来反推元素的丰度。 当然， 这是典型的 “站着说话不腰疼”， 实际计算起来有许多技术性的困难需要克服， 因此这种计算直到 1925 年才有人去做。



【英国天文学家佩恩(1900-1979)】

最早进行这种计算的是一位年仅 25 岁的 “灭绝师太” (女博士)。 这位名叫佩恩 (Cecilia Payne, 1900-1979) 的 “师太” 出生于英国。 1919 年， 当爱丁顿验证广义相对论的故事风靡世界的时候， 她有幸聆听了爱丁顿的讲座， 从此爱上了天文学。 不过在英国这样一个社会习俗比较保守的国家里， 女性从事天文研究是很困难的 (其实别说从事天文研究， 她所就读的剑桥大学当时甚至不给女性颁发学位)， 于是她远渡重洋到美国去读博士。 在读博士期间， 佩恩对太阳上的元素丰度进行了研究。 1925 年， 她的研究得出了一个惊人的结果： 这个太阳系里最重的天体竟然主要是由元素周期表上最轻的元素——氢和氦——组成的！ 虽然当时人们对太阳上的元素丰度还一无所知， 但自从 “天贵地贱” 的观念破灭之后， 很多人已经想当然地走到了另一个极端， 认为太阳和地球有着相似的组成。 在这种情形下， 佩恩也知道自己的结果有点骇人听闻， 为保险起见， 她在发表前特意征求了一下当时恒星光谱研究的权威， 著名美国天文学家罗素 (Henry Russell, 1877-1957) 的意见[注七]。

没想到这一征求征出了苦恼， 因为罗素给了她一个很负面的回答， 他表示佩恩的结果是 “显然不可能的”。 受罗素的威名所慑， 佩恩修改了论文的措辞， 表示自己所发现的氢和氦的丰度 “被认为是有问题的”， “几乎可以肯定是不符合实际的”。 这样的措辞很快就被证实为是谦虚得过火了。 因为在接下来的几年间， 其他天文学家们也陆续独立地得到了与佩恩一样的结果。 四年之后， 就连罗素本人也得到了同样的结果。 在铁的事实面前， 罗素终于意识到自己错了， 在他的论文中， 他宣布自己的结果与四年前佩恩的结果有着 “很令人满意的一致”。 权威毕竟是权威， 四年前， 因为罗素的影响， 佩恩修改了措辞， 弱化了结论， 而四年后， 同样也是因为罗素的影响， 佩恩的结果加速成为了主流， 她的博士论文更是被誉为了天文学领域中最重要的博士论文。 在那之后， 佩恩继续从事着天文学研究。 1934 年， 她与一位俄国天文学家结了婚 (从此告别 “师太” 生涯)。 1956 年， 她成为了哈佛大学有史以来第一位女性正教授及系主任。

如今我们知道， 太阳是一个巨大的 “氢气球”， 在它的总质量中， 氢占了 71% (在原子数目中则占了 91.2%)， 氦占了 27.1% (在原子数目中则占了 8.7%)， 其余所有元素加起来也只占不到 2% (在原子数目中则只占不到 0.2%)。 事实上， 不仅太阳如此， 绝大多数 “青壮年” 时期的恒星都是如此， 甚至在目前整个宇宙的可见物质中， 氢和氦也是绝对的 “主流”。

在本节的最后， 我们要对元素丰度的计算再作两点补充。 细心的读者也许注意到了一个问题， 那就是太阳光谱——无论吸收光谱还是发射光谱——主要来自太阳大气层， 因此通过光谱学研究得到的元素丰度应该是针对太阳大气层而非整个太阳的。 事实的确如此。 不过另一方面， 太阳是一个高温气态的星球， 托这种恶劣环境的福， 在太阳内部很大的体积范围内都存在强烈的对流， 使得太阳大气层的元素丰度与内部基本一致。 不仅如此， 对太阳模型及太阳起源的研究都显示， 即便在不存在显著对流的区域， 元素丰度仍与外部接近 (唯一的例外是核心区)。 因此， 我们通过光谱学手段得到的元素丰度是对太阳整体元素丰度的一个不错的近似 (确切地说是重元素丰度略微偏低)。

另一点需要补充的是， 有关太阳元素丰度的计算需要用到统计物理、 量子力学等领域的知识， 且计算量相当巨大， 很容易出错。 这其中有一个著名的例子， 那就是人们在铁元素丰度计算的量子力学部分中曾经犯过一个错误， 导致铁元素的丰度被低估了十倍， 那个错误直到 1968 年才被纠正。 除计算量巨大外， 元素丰度计算所面临的另一类困难， 是有些元素——比如氦——的谱线产生于色球和日冕中的一些远离平衡态的区域， 从而很难建立理论模型。 不过， 我们今天所知的太阳元素丰度已经不单纯是光谱分析的结果， 而是得到了一些其它手段， 比如日震学 (helioseismology) 手段的印证， 因此具有比单一手段更大的可靠性。

注释

当然， 在几何规律的背后有着动力学的规律， 比如牛顿运动定律和万有引力定律。 不过在太阳系中， 太阳是一个例外， 它的质量远大于行星质量， 具备 “稳坐钓鱼台” 的资格， 因此在研究太阳时较少涉及动力学。 牛顿的三棱镜实验是从 1664 年开始的， 比较完整的实验则是在 1666 年初做的。 在牛顿之前， 也有学者注意到过类似的现象， 并提出过类似的想法 (但都不如牛顿的细致和系统)。 比如出生于爱尔兰的英国科学家玻意尔 (Robert Boyle, 1627-1691) 曾用三棱镜观察到过阳光里的彩色； 牛顿的老冤家英国科学家胡克 (Robert Hooke, 1635-1703) 则曾经提出过颜色由蓝色与红色两种基色组成的想法 (后来被牛顿推翻)。 我们在前面曾经提到过， 为了判定太阳光谱中的暗线是否来自仪器缺陷， 夫琅禾费曾检验过其它光源， 他当时也注意到了太阳光谱中的某些暗线对应于普通光源中的亮线， 可惜他没有对之作进一步的考察， 从而错过了作出同样发现的机会。 细心的读者也许会提出两个问题。 一个是： 基尔霍夫热辐射定律中的吸收光谱是由冷蒸汽产生的， 太阳上的温度那么高， 为什么也有吸收光谱？ 答案是： 所谓 “冷蒸汽” 是相对于光源温度而言的。 太阳吸收光谱主要来自太阳大气层中的光球层 (photosphere)， 那里的温度用日常标准来衡量虽然极高， 相对于太阳内层而言， 却是一个 “凉风习习” 的地方， 它的吸收作用大于发射作用， 因而仍是 “冷蒸汽”。 第二个是： 阳光从太阳来到地球， 除穿越太阳大气层外， 还必须穿越地球大气层， 那么， 夫琅禾费线会不会是来自地球大气层呢？ 答案是： 的确有少数夫琅禾费线是来自地球大气层的， 比如被夫琅禾费标记为 A 和 B 的两条暗线实际上是来自地球大气层中的氧分子。 在地球大气层之外观测太阳光谱时就不会看到那两条暗线 。 读者也许会觉得奇怪， 太阳的光谱是吸收光谱， 光谱线不都是暗线吗？ 怎么忽然冒出一条亮线来了？ 这是有原因的， 原因就是色球层中存在比内层温度更高的区域， 使光谱由吸收光谱变成了发射光谱 (由此可见， 光谱不仅能帮我们辨认太阳上的元素， 还能带给我们有关太阳温度的信息)。 除色球层外， 下文即将提到的日冕中的亮线也是如此。 至于色球层与日冕这两个太阳大气层的外围区域为什么反而会有高温， 我们将在后文 第十三节 中加以介绍。 本文对 coronium 的中文译名 “氪” (见诸于一些在线英汉网站) 加了引号， 因为这个汉字通常是用来表示一种惰性气体元素： 氪 (krypton)。 张昌明、 肖耐园的《天文学教程》对 coronium 的译名是 “气” 字下面一个 “免” 字， 字形与含义颇为相合。 可惜这个字我在手头的 PDF 版本的《辞海》里都没能找到， 更遑论计算机输入， 只好拿 “氪” 字滥竽充数了。 读者请勿将这位罗素与哲学家罗素 (Bertrand Russell, 1872-1970) 混淆起来。 此罗素非彼罗素。 此罗素是一位天文学家， 他一生最著名的工作是与丹麦天文学家赫茨普龙 (Ejnar Hertzsprung, 1873-1967) 各自独立地发现了恒星的光谱类型与光度之间的关系， 即著名的赫罗图 (Hertzsprung–Russell diagram)。

二零一零年四月三十日写于纽约

二零一零年五月二十九日发表于本站

http://www.61k.com

太阳的故事

（本文授权转载于卢昌海老师的个人博客，欲再转载者请联系原作者）



太阳的故事（七）物理自助游

本文作者：卢 昌海

自上一节开始， 我们的太阳故事已延伸到了物理领域。 由于我们有关太阳的现代知识几乎全都来自物理手段， 因此在本节及以后的多数章节中， 我们将继续与物理 “亲密接触”。 说到物理， 很多读者的脑海里也许会浮现出中学物理课上学过的一些基本概念， 这其中很重要的一个就是被牛顿称为 “物质的量” (quantity of matter)， 并在其名著《自然哲学的数学原理》的第一页上就试图定义的概念： 质量。

这样一个重要概念当然也适用于太阳。 本节的第一个任务， 就是要查一查太阳的 “资产”——它的 “物质的量”。 对于我们日常生活中接触到的普通物体来说， 测定质量是一件毫不困难的事情。 天平、 杆秤、 磅秤等都可以帮我们达到这一目的。 这些测量手段有一个共同特点， 那就是借助于所谓的静力学平衡手段。 在历史上， 早在质量的含义还仅仅停留在字面意义上那个 “物质的量”， 而不涉及象惯性和引力那样的动力学性质的年代里， 人们就是用这类手段来测定质量的。

但是， 就象大小和远近这样的简单测量一涉及到太阳就变得不再轻而易举一样， 质量的测定一涉及到太阳， 也就立刻变得棘手了。 无论天平、 杆秤还是磅秤， 想用来测定太阳的质量， 都无异于是白日做梦。 怎么办呢？ 我们想起了上一节的思路。 在上一节中我们介绍过， 为了探索太阳的化学组成， 科学家们研究了阳光， 它给我们带来了远在 1.5 亿公里以外的太阳的信息。 那么， 除阳光外还有没有别的什么东西也能够不受遥远距离的阻隔， 为我们带来有关太阳的信息呢？ 有， 那就是引力， 它不仅能向我们申报太阳的 “资产”， 而且还采取了一种我们自己就能实践的方式， 为我们再次开展 “自助游” 活动提供了便利。

我们这次自助游所采用的将是物理手段， 其中首先要利用的就是引力。

与上次自助游所采用的几何手段不同， 人们对引力的了解要晚得多。 如果我们想再玩一次重返古希腊之类的游戏的话， 我们要重返的将不是古希腊， 而是十七世纪。 另外， 与阳光能够直接产生视觉不同， 引力本身是看不见摸不着的。 了解引力的主要途径， 是研究它所导致的物体——尤其是天体——的运动， 这正是十七世纪科学家们曾经做过的事情。 不过十七世纪毕竟不同于古希腊。 古希腊的很多推理在今天已是一些中小学生都能理解或反驳的， 但十七世纪的某些科学成就即便在今天， 也足以难倒不少理工科的大学生。 因此本节虽也号称 “自助游”， 却不能象上一次那样 “徒步” 进行， 而需要先介绍一些十七世纪的东西， 作为代步工具。 当然， 这样做的另一个目的是让整个系列的内容更加完整。

我们刚才提到， 了解引力的主要途径， 是研究它所导致的物体——尤其是天体——的运动。 这种研究曾经导致了象日心说那样的重大天文进展。 但对于了解引力本身而言， 真正的进展却是出现在十七世纪初期的 1609 年。 那一年， 一位德国天文学家发表了几项重大成果。 此人的大名我们在第三节中已经提到过， 他就是开普勒。 是他， 发现了行星运动的椭圆轨道， 将沿用两千年的超级教条——天球——送进了历史博物馆； 同样也是他 (而不是哥白尼)， 使日心说在精度上超越了地心说。

但在作出这些辉煌成就的同时， 他也亲手葬送了一个十三年前 (1596 年) 由他自己提出， 且受他钟爱的模型。 那个模型将当时已知的太阳系六大行星 (水星、 金星、 地球、 火星、 木星、 土星) 的天球用三维空间中仅有的五种正多面体 (正八面体、 正二十面体、 正十二面体、 正四面体、 正六面体) 以内切和外接的方式相分隔。 那个模型不仅让开普勒一度以为发现了上帝创世计划中最宏伟的几何设计， 而且还引起了当时已富盛名的丹麦天文学家第谷 (Tycho Brahe， 1546-1601) 的注意[注一]。 1600 年， 开普勒应邀成为了后者的助手。 一年后， 第谷去世， 他的职位及观测数据都被开普勒所继承。 在望远镜时代来临之前， 第谷的观测数据堪称举世无双。 正是有那样精密的数据做后盾， 加上自己的常年努力， 开普勒才发现了他的行星运动定律， 追根溯源起来， 很多缘分都来自他当年那个模型。 可惜再珍贵的模型如果与观测不符， 也只能被放弃。 假如科学研究本身也有定律的话， 这或许就是第一定律， 而开普勒很了解这一定律。



【开普勒的名著《世界的和谐》】

开普勒第三定律是一条非常漂亮的定律， 任何人只要看一眼那些数据之间近乎完美的关联， 就不难欣赏到它的美。 开普勒本人对之也非常满意， 称它为 “和谐定律” (Harmonic Law)。 开普勒的这些定律是牛顿之前人们在研究天体运动方面所达到的最高成就， 为最终发现万有引力定律做出了重要铺垫。 不过对于我们想要做的事情， 即推算太阳的质量来说， 它们还不够， 因为其中还缺少一样东西， 那就是质量这个主角。 事实上， 开普勒三大定律全都是运动学定律， 只涉及时间和空间这样的运动学概念， 而没有质量和引力那样的动力学概念[注二]。开普勒在 1609 年所发表的不仅有被称为开普勒第一定律的行星椭圆轨道， 而且还有所谓的开普勒第二定律， 即行星与太阳的连线在单位时间内扫过恒定的面积。 但这两条定律加在一起， 似乎也赶不上当年那个模型所具有的和谐与秩序。 那个模型虽然被迫放弃了， 开普勒却深信它所体现的和谐与秩序必定还有其它体现方式， 为此他继续进行着不懈的探索。 十年之后 (1619 年)， 他终于找到了一条新的规律。 他为这一新规律撰写了一部新著作， 书名就叫《世界的和谐》(Harmony of the Worlds)。 在那部著作中， 他提出了自己的第三定律： 行星轨道半长径 (即椭圆轨道长轴长度的一半) 的三次方与轨道周期的平方之比是一个常数。

为了推算太阳的质量， 我们还得等一个人， 一个将质量概念全面引进物理的人， 一个能对引力作出数学描述的人， 这个人就是牛顿。 公元 1687 年， 牛顿发表了巨著《自然哲学的数学原理》。 在这部著作中， 他完整地阐述了自己的三大运动定律及万有引力定律， 为物理学的发展开辟了崭新的道路。 用另一位科学巨匠爱因斯坦的话说， 牛顿所发现的道路在他那个时代 “是一位具有最高思维能力及创造力的人所能发现的唯一道路”。

沿着这条 “唯一道路”， 人们对开普勒三大定律有了更深入的了解， 那三大定律不仅适用于行星绕太阳的运动， 而且也适用于卫星绕行星的运动。 那么， 我们所关心的东西——质量——在哪里呢？ 就在开普勒第三定律中的那个常数——即轨道半长径的三次方与轨道周期的平方之比 (以下简称 “开普勒常数”)——里。 利用牛顿的运动定律和万有引力定律可以很容易地证明， 那个常数正比于中心天体的质量[注三]。

主角终于露面了！

既然质量就出现在开普勒常数中， 那我们是不是就可以用开普勒第三定律来计算太阳质量了呢？ 很遗憾， 答案暂时还是否定的。 因为质量在开普勒常数中的出现还捆绑了一个陌生的、 来自牛顿万有引力定律的东西： 万有引力常数。 开普勒常数正比于中心天体的质量是不假， 但在比例系数中却包含了万有引力常数。 因此只有知道了万有引力常数的数值， 才能真正推算天体的质量。 但万有引力常数的数值是多少呢？ 很可惜， 那在牛顿时代还是一个谜。

搞了半天， 原来是空欢喜一场。 质量虽然出现了， 却 “犹抱琵琶半遮面”。 但即便如此， 我们依然有一件事情可以做， 那就是推算太阳质量与地球质量的比值。 推算的方法很简单： 既然开普勒常数正比于中心天体的质量， 那就说明地球轨道 (它的中心天体是太阳) 的开普勒常数正比于太阳质量， 而月球轨道 (它的中心天体是地球) 的开普勒常数正比于地球质量， 它们的比值则等于太阳质量与地球质量之比。 这个计算是我们现在就可以做的， 那个暂时让人摸不清路数的万有引力常数在计算比值时会自动消去。 这个计算所需的全部数据都已在第一、二两节中介绍过了， 即：

地球的轨道半长径 (很接近太阳离我们的平均距离)： 150,000,000 公里 地球的轨道周期 (恒星年)： 365.24 天 月球的轨道半长径 (很接近月球离我们的平均距离)： 384,400 公里 月球的轨道周期 (恒星月)： 27.3 天

由此可以得到：

地球轨道的开普勒常数： 2.5×1019 月球轨道的开普勒常数： 7.6×1013

当然， 这两者都是有量纲的 (请读者想一想， 它们的量纲是什么？)， 不过这量纲跟万有引力常数一样， 会在求比值时自动消去， 因此不必理会。 这两个常数的比值约为 330,000。 这样我们就得到了一个重要结果：太阳的质量约为地球质量的 33 万倍。 将之与我们在第二节中已经得到的 “太阳的直径约为地球直径的 109 倍” 联系起来， 我们立刻可以得出另一个重要结论，太阳的平均密度约为地球平均密度的 1/4， 这跟我们在上节末尾介绍过的太阳上轻元素占很大比例的结果在定性上是一致的[注四]。

现在我们的处境与第二节中曾经遇到过的相差无几了， 即有关太阳的数字已经与有关地球的数字连在了一起。 如果我们有办法知道地球的质量， 就可以顺藤摸瓜地得到太阳的质量。 但问题是， 地球的质量虽然只有太阳质量的 33 万分之一， 却同样是不能拿天平、 杆秤、 磅秤之类的工具来测量的。 为了测定地球的质量， 我们同样必须借助引力。 而一旦涉及引力， 万有引力常数就是一道绕不过去的坎。

既然绕不过去， 就只好放手一搏了。 那么， 怎样才能知道万有引力常数的数值呢？ 很简单， 那就是测定一对质量已知的物体之间的引力。 这个答案对谁都不是秘密， 但万有引力常数却对谁都是秘密， 因为这个答案所提议的测定在当时是连牛顿也没法办到的； 因为引力这个貌似强大、 能把硕大无朋的天体玩得团团转的力量， 其实却是自然界中最微弱的相互作用。 它的强大纯粹来自 “集体的力量”， 因而只有在天文尺度上才是显著的。 可是天文尺度上的物体——即天体——的质量却全都指着万有引力定律来测定， 这就变成了一个先有鸡还是先有蛋的问题： 要想知道天体的质量， 首先得知道万有引力常数的数值； 而要想知道万有引力常数的数值， 又首先得知道某些天体的质量。



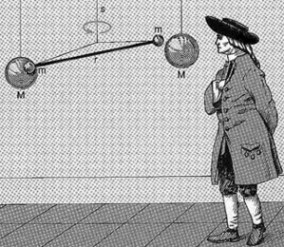
【卡文迪许的扭秤实验】

知道了万有引力常数， 我们就可以计算太阳和地球的质量了。 计算的方法很多， 既可以用开普勒第三定律， 也可以通过其它方法， 其中最简单的或许是将我们熟悉的地球表面重力加速度 (9.8 米/秒2) 与万有引力定律给出的加速度相对比[注五]。 既然是自助游， 这点小小计算就留给读者们自己享用了， 计算的结果将会表明：地球的质量约为 60 万亿亿吨(6×1024千克)[注六]。 将这一结果与前面已经推算出的太阳质量与地球质量的比值联系起来， 就立刻可以得到太阳的质量约为 2 千亿亿亿吨(2×1030千克)。这个近乎死循环的局面直到一百多年后的 1798 年才被打开。 那一年， 英国科学家卡文迪许 (Henry Cavendish, 1731-1810) 通过一个极精巧的扭秤实验， 破天荒地直接测定了两个普通物体 (它们的质量当然是已知的) 之间极为微弱的引力。 虽然卡文迪许的目的是测定地球的平均密度 (由此也可以直接得到地球质量)， 但从他的数据中不难算出万有引力常数的数值为 6.75×10-11(这是国际单位制下的数值， 量纲留给读者自行推算)。 自那以后很多其他人也对万有引力常数进行了测定。 引力在日常尺度上的微弱性给所有这类测定设置了公平的障碍， 从中反衬出的则是卡文迪许的高超技艺， 因为他所达到的精度直到一个多世纪后才有人超越。 对万有引力常数的测定直到今天依然是一件很困难的事情。 截至 2006 年， 国际科技数据委员会 (CODATA) 对这一常数的最佳推荐数值为 6.67428×10-11， 相对误差约为万分之一。 在所有基本物理常数中， 这样的精度就算不是最低， 也是接近垫底的。 不过太阳和地球这样的庞然大物毕竟不是每盎司都得斤斤计较的黄金珠宝， 这样的精度对于测定它们的质量来说已是绰绰有余了。

这样我们就完成了本次自助游的第一站： 查明太阳的 “资产”。 “资产” 既已查明， 接下来我们就要去关心一下太阳的 “开销” 了， 即它以电磁辐射 (以下将笼统地称为 “光”) 的形式每秒种挥霍掉的能量。 天文学家们把这种挥霍速度称为太阳的光度 (luminosity)。

推算太阳光度的思路很简单， 那就是测定地球公转轨道附近单位时间内垂直入射到单位面积上的阳光能量， 即所谓的太阳常数 (solar constant)。 由于太阳很均匀地把光明洒向人间， 因此一旦知道了太阳常数， 将它乘上半径 1.5 亿公里 (即地球公转轨道半径) 的虚拟球面的面积， 就可以得到太阳的光度。

那么怎样才能测定太阳常数呢？ 最简单的办法就是在阳光直射地面的时候， 在地上放一盆 “单位面积” 的凉水， 然后观察它在 “单位时间” 内的温度升高。 将这一温度升高乘上水的比热和质量， 就可以得到水从阳光中吸收的能量。 在理想条件下， 这个能量就等于太阳常数。 当然， 在实际实验中， 阳光未必直射地面， 水面面积未必是 “单位面积”， 观测时间也未必是 “单位时间”， 不过这些小小变通相信是难不倒读者的。



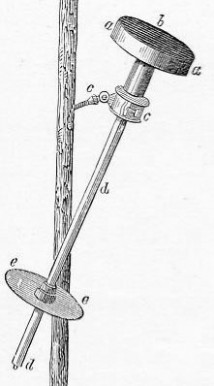
【普耶特测量太阳常数的仪器，顺便请读者们思考一个“正大综艺” 式的问题:仪器下方的圆盘 e是做什么用的？】

为了减少大气干扰， 天文学家们想了很多其它办法， 比如将观测地点移到高山之巅。 但要想真正摆脱地球大气的干扰， 只有到外层空间去测量才行， 这种 “奢侈” 的设想随着航天时代的来临成为了可能。 从 1978 年到 1998 年的二十年间， 天文学家们利用人造卫星对太阳常数进行了持续测定， 结果发现太阳常数约为 1366 瓦/米2， 由此我们可以推算出太阳的光度约为 384 亿亿亿瓦(3.84×1026瓦)。 384 亿亿亿瓦是个什么概念呢？ 它相当于每秒钟爆炸 920 亿个百万吨级的氢弹！ 这样一个结果， 居然可以从观察自家后院的一盆水得到粗略的估计， 这不禁让人想起一个有关美国物理学家费米 (Enrico Fermi, 1901-1954) 的故事来。 1945 年， 在美国进行第一次核试验时， 这位卓越的物理学家只用几张从空中飘落的纸片， 就估算出了爆炸的当量 (估算结果约为实际值的一半)。 这种堪与福尔摩斯相媲美的奇妙推算无疑正是物理学的诸多魅力之一。真正困难的是那 “理想条件” 四个字。 要想切实做到这四个字， 必须保证在那个 “单位时间” 里入射到 “单位面积” 上的阳光完全被水吸收， 一点都不损失， 而且还要保证那是水与外界唯一的能量交换。 这两点要想切实做好显然都是很困难的。 在历史上， 最早测定太阳常数的是法国物理学家普耶特 (Claude Pouillet, 1791-1868) 和英国天文学家赫歇耳 (John Herschel, 1792–1871)[注七]。 1837 年， 他们两人彼此独立地进行了实验。 “太阳常数” 这一名称就是普耶特所取的。 为了尽可能接近 “理想条件”， 普耶特和赫歇耳都做了一些努力， 但效果并不理想， 因为有一个因素在当时的条件下是无论如何也没法消除的， 那就是地球大气对阳光的吸收和反射。 这一因素不仅没法消除， 甚至还会随时间、 地点、 阳光倾角、 天气条件等因素的不同而不同， 连校正都很困难。 由于这种因素的干扰， 普耶特测得的太阳常数只有正确值的一半左右， 赫歇耳的稍大些， 但也强不了太多。

不过在这里， 我们要提醒读者一点， 那就是早在对太阳常数作出精确测定之前， 人们就已意识到， 所谓太阳常数其实不是一个真正的常数。 即便扣除地球大气的干扰及地球离太阳的距离变化等因素， 也没有任何物理理由表明太阳常数会是一个真正的常数。 太阳常数的大小完全取决于发生在太阳上的物理过程。 而再显而易见不过的事情就是， 发生在象太阳那样的巨大星球上的物理过程是千变万化的， 绝不可能给出一个简单的常数。 事实上， 对太阳常数的跟踪观测表明， 它的数值随时都在变化， 既有接近周期性的变化， 也有非周期性的变化， 不过变化的幅度倒是很小。

好了， 现在让我们进入本次自助游的最后一站： 推算太阳的表面温度 (以下简称温度)。 太阳很热是凡地球人都知道的事实， “赤日炎炎似火烧” 嘛。 但到底有多 “热” 呢， 仅仅靠形容词是不够的， 温度才是硬道理。 因此很多天文学家都想知道太阳的温度。 事实上， 测定太阳常数的一个早期动机就是想推算太阳的温度。 可惜的是， 人们早期测定的太阳常数及由此推算出的太阳光度虽与现代值相距不远 (起码在同一数量级上)， 但将它们与温度联系起来的理论基础却一直空缺着， 这种理论 “真空” 导致了一片混乱的局面。 拿推算温度的手法来说， 可谓是五花八门， 从子虚乌有的 “热力线” (heat-rays) 到并不适用的牛顿冷却定律 (Newton's Law of Cooling)， 不一而足。 拿推算结果来讲， 从一千多度到几百万度， 天差地别、 应有尽有。 为了鼓励可靠的研究， 1876年， 法国巴黎科学院 (Paris Academy of Sciences) 特意为推算太阳温度设了一个奖， 可惜还是无济于事， 那奖被法国物理学家瓦耳勒 (Jules Violle, 1841-1923) 以一个很不靠谱的 1,500-2,500°C 的推算所获得。



【奥地利物理学家斯忒藩(1835-1893)】

除上面这种方法外， 我们再介绍一种虽然比较粗糙， 但却别有趣味的方法。 在上面的推算中， 除用到斯忒藩－玻耳兹曼定律外， 还需要知道斯忒藩－玻耳兹曼常数的数值， 以及太阳的光度。 但事实上， 只要有斯忒藩－玻耳兹曼定律所给出的四次方关系， 即便不知道斯忒藩－玻耳兹曼常数的大小， 甚至不知道太阳的光度， 我们依然能推算出太阳的表面温度。 方法很简单： 我们知道， 地球表面的平均温度约为 290K (即 17°C——这是对地域和时间的双重平均)， 虽然很容易被忽略， 但这样温度的星球也会向外辐射能量， 而且这个能量也可以近似地用斯忒藩－玻耳兹曼定律来描述。 由于不能象太阳那样亲自发光， 地球表面的能量主要来自阳光[注八]。 因此地球能维持目前的表面温度， 说明它向外辐射的能量与它所接收的阳光能量基本相等。 利用这一关系， 我们就可以推算出太阳的表面温度。 推算的过程很简单， 读者不妨自己试试， 您将会发现， 斯忒藩－玻耳兹曼常数在推算过程中会自动消去， 推算的结果约为 6,000K， 虽不如前面的方法精确， 却也相差不远。对太阳温度进行推算的理论基础直到 1879 和 1884 年， 才先由奥地利物理学家斯忒藩 (Joseph Stefan, 1835-1893) 从实验数据中得到， 后由其同胞玻尔兹曼 (Ludwig Boltzmann, 1844-1906) 从热力学上推出。 他们发现， 一个黑体在单位面积上的辐射功率 (即每秒钟辐射出的能量) 正比于绝对温度的四次方。 这一定律如今被称为斯忒藩－玻耳兹曼定律 (Stefan–Boltzmann law)， 其中的比例系数则被称为斯忒藩－玻耳兹曼常数 (Stefan–Boltzmann constant)。 在国际单位制下， 斯忒藩－玻耳兹曼常数的数值为 5.67×10-8(量纲仍留给读者自己去推导)。 斯忒藩－玻耳兹曼定律虽然针对的是黑体， 但恒星辐射大都比较接近黑体辐射， 因此该定律对恒星辐射也近似适用。 有了这一定律， 推算太阳的表面温度就有了理论基础。 推算的方法很简单： (绝对温标下) 表面温度的四次方乘上斯忒藩－玻耳兹曼常数就是太阳表面每平方米的辐射功率， 再乘上太阳的表面积， 就是太阳的总辐射功率 (即每秒钟辐射出的总能量)， 也就是我们前面刚刚推算过的太阳的光度。 由此不难得到——请读者们 “自助” 完成——太阳的表面温度 (确切地说是光球层的有效温度) 约为 5,800K(K 为绝对温标， 摄氏温标的 0°C 约为 273K， 本系列今后若提到温度而不注明温标， 指的都是 K)。

这个方法的趣味之处就在于它是利用行星的温度来反推恒星的温度。 但更有趣的是， 将它反过来用， 我们也可以由恒星的温度来推算出一定距离外的行星温度。 这一特点常被天文学家们用来估计恒星周围有可能抚育生命的所谓可栖息带 (habitable zone) 的位置和宽度。 当然， 这种推算的局限性是很大的， 比如它既要求行星上存在水和大气那样能使温度均匀的东西， 又要求那大气不能象金星大气那样富含温室效应气体。

自此我们就圆满完成了本次自助游的全部目标， 即本节标题所宣称的推算太阳的质量、 光度和表面温度。 在 “游戏结束” 之前， 我们再派发一个小红包——介绍一下太阳的光谱类型。 在斯忒藩－玻耳兹曼定律问世之后不久， 德国物理学家维恩 (Wilhelm Wien, 1864-1928) 用热力学方法证明了一个定律， 叫做维恩位移定律 (Wien's displacement law)。 这一定律表明， 表面温度越高的物体， 其光谱分布就越往短波方向偏移， 表现在颜色上则是往蓝色方向偏移。 利用这一特点， 天文学家们将恒星依照光谱特征分为了七个大类， 分别标记为 O, B, A, F, G, K, M。 其中 O 型天体为蓝色， 表面温度最高， 在 33,000K 以上， M 型天体为红色， 表面温度最低， 在 3,700K 以下。 象太阳这样的黄色天体为 G 型， 表面温度在 5,200-6,000K 之间。 在每个类型之中， 依照温度从高到低的顺序又分出十个亚型， 分别用阿拉伯数字 0-9 来表示， 0 表示温度最高， 9 表示温度最低。 太阳的光谱类型为 G2， 在 G 型之中算是温度较高的[注九]。

注释

按照今天的称呼惯例， 第谷·布拉赫应被称为 “布拉赫”， 就象艾萨克·牛顿被称为 “牛顿”， 阿尔伯特·爱因斯坦被称为 “爱因斯坦” 一样。 不过在第谷所生活的年代， 当地的习惯是用名而非姓作为称呼， 因此第谷·布拉赫就被称为了 “第谷”， 并延用至今。 在开普勒时代， 引力的概念尚未形成。 不过开普勒本人倒是很早就猜测过太阳是行星运动的原因。 开普勒第三定律的发现使他更坚定了自己的猜测。 因为这一定律表明， 离太阳越近的行星运动得越快， 这种相关性强烈地暗示着行星运动的原因来自太阳。 据说开普勒是作出这种猜测的第一人 (不过他所猜测的太阳对行星的影响类似于磁力， 而不是引力)。 感兴趣的读者可以针对圆周运动这一特例自行证明这一点。 当然， 就象很多其它经验规律一样， 开普勒定律的成立是有条件的， 比如要忽略来自其它天体的影响。 而且， 开普勒第三定律中的那个常数实际上是正比于中心天体及绕其运动的天体的总质量， 只有在中心天体的质量远大于绕其运动的天体的质量时， 才可以近似为中心天体的质量。 对太阳系的全部行星和卫星而言， 这一近似都基本成立。 我们在后文中将会看到， 太阳物质的密度分布是极不均匀的， 从核心到外层有着天壤之别。 不过这个号称简单的方法需要用到万有引力定律的一个不太简单的推论： 那就是质量呈球对称分布的物体在其外部产生的引力相当于全部质量都集中在球心。 这个推论在牛顿那个时代是只有牛顿才能证明的独门绝活， 直到今天也足以难倒一部分理工科大学生。 将这一结果与地球的直径联系起来， 就可以得到地球的平均密度约为 5.5 克/厘米3。 若进一步与前面得到的太阳平均密度约为地球平均密度的 1/4 联系起来， 则可以得到太阳的平均密度约为 1.4 克/厘米3。 这位赫歇耳通常称为小赫歇耳， 他是天王星的发现者、 有时称为老赫歇耳的 威廉·赫歇耳 (William Herschel, 1738–1822) 的儿子。 说到老赫歇耳， 顺便提一下， 他也在某种程度上测定过太阳的辐射能量。 在 1800 年所进行的一组观测中， 他曾将一个温度计放在太阳光谱的红端以外 (他的本意是让那个温度计不被阳光照到， 从而可以用来记录环境温度)， 结果发现记录下来的温度存在反常升高， 由此他推断出阳光中存在着波长比红光更长的肉眼无法看见的部分， 即红外线。 除阳光外， 在地球表面所接受的能量中也有来自地球内部的贡献。 不过后者的平均功率只有 0.06 瓦/米2， 不到阳光能量的万分之一， 在我们的计算中可以忽略。 在有些文献中， 太阳的光谱类型被标记为 G2V， 这里的 V 所表示的不是英文字母 “V”， 而是罗马数字的 “5”， 它来自另一种分类细则， 所表示的含义是主序星 (即壮年的恒星)。

二零一零年六月二十五日写于纽约

二零一零年六月二十六日发表于本站

http://www.61k.com

太阳的故事

（本文授权转载于卢昌海老师的个人博客，欲再转载者请联系原作者）



太阳的故事 (八) 光明的源泉　恐怖的核心

本文作者：卢 昌海

爱因斯坦和他的年轻合作者英费尔德 (Leopold Infeld, 1898-1968) 曾经写过一本非常出色的科普著作， 叫做《物理学的进化》(The Evolution of Physics)。 在那部著作中， 他们作过一个令人印象深刻的比喻， 那就是把科学的发展比喻成一个侦探故事。 他们这样写道：

自从柯南·道尔写出绝妙的故事以来， 在几乎所有侦探小说中都有这样一个时刻， 侦探收集到了为解决问题的某个阶段所需的全部事实。 那些事实往往看起来很奇特、 不连贯， 并且彼此毫不相干。 可是大侦探知道这时不必继续调查了， 现在只有纯粹的思维能把搜集到的事实联系起来。 于是他拉拉小提琴， 或躺在安乐椅上抽抽烟。 突然间， 老天爷， 他找到了联系！ 他不仅对手头所有的线索都有了解释， 而且知道某些其它事情也一定发生了。 因为现在他已经确切地知道在哪里可以找到它， 如果愿意的话， 他可以出去收集他理论的进一步证实。

我们的太阳故事进行到这里， 也差不多到了那样一个时刻， 可以——甚至必须——象大侦探一样解决一些谜团了。 不过与大侦探的单枪匹马及 “老天爷， 他找到了联系！” 那样的戏剧性不同， 科学家们收集事实的过程更象是现代侦探连续剧中那些跨省市的联合行动。 因为除了大侦探自己收集的事实外， 来自同事、 同行乃至其它部门的协助往往也对案情的侦破起着关键作用。 而科学家们解决谜团的过程， 与其说是 “拉拉小提琴， 或躺在安乐椅上抽抽烟”， 不如说更象是现代侦探连续剧中的大型案情分析会。 在那样的分析会上， 很多人 (尤其是新手) 会提出很多设想。 当那些设想被一一排除后， 某位幸运儿 (多半是男主人公) 会提出一个真正的好想法。 当然， 一个精彩的侦探故事往往是曲折的， 一个曾经的好想法也许后来又遇到新问题， 然后不得不召开新的案情分析会。 我们将会看到， 科学的发展常常也是如此。

现在就让我们来观摩一场有关太阳的案情分析会， 会议的主题是太阳为什么会发光？ 或者用更学术一点的话说， 是恒星的能量产生机制是什么？

太阳为什么会发光？ 这是一个很古老的问题。 既然是很古老的问题， 当然曾经有过很古老的回答， 比方说 “上帝安排的”。 但那样的回答就好比是说凶案是上帝做的， 不必查了。 那样的人做神父远比做侦探合适， 我们就不邀请了[注一]。

那么， 我们所邀请的第一位侦探是谁呢？ 是英国天文学家赫歇耳(William Herschel, 1738-1822)。 此人是太阳系第六大行星——天王星——的发现者， 在天文史上是一位赫赫有名的前辈。 不过我们这场案情分析会虽然打算开成一个 “团结的大会”、 “奋进的大会”， 却不是一个论资排辈的地方。 在这个分析会上， 赫歇耳的资格虽老， 却必须被列入 “菜鸟” 行列 (这也比较符合侦探片中新手总是先发言的惯例)， 因为他的提议确实是太 “菜” 了一点。 那提议是这样的： 太阳之所以发光， 是因为它有一个因炽热而发光的大气层， 那大气层的下面则有可能是一个凉爽、 甚至可能有生命居住的固态表面！

今天的读者也许很难理解， 象赫歇耳那样著名的天文学家怎么会想出如此不靠谱的提议？ 难道是超前学习了韩乔生同学的 “意识流”？ 在这里， 我们要为赫歇耳说几句公道话， 因为他的提议在如今看来虽然极度离奇， 在当时却并非单纯的臆想。 事实上， 赫歇耳之所以作出那样的提议， 是因为他注意到了太阳上的黑子， 他认为那是透过太阳大气层中的空隙所看到的太阳表面， 那表面既然呈现黑色， 想必是凉的， 这就是他那提议的依据。 那依据虽然是错误的， 在当时却不失为是一种可能性。 在科学史上， 错误的假说可以说是层出不穷， 一些反科学人士往往以此为由来抨击科学。 其实， 科学之所以有今天的声望， 从来就不是因为她不会出错， 而是因为她不断地寻求实证， 并且在这过程之中不断地纠正错误， 去芜存菁。 我们在后文中将会看到， 黑子的 “黑” 是一种相对的颜色， 它并不等于日常意义上的 “凉”。 我们在第六节中介绍过的太阳光谱的类型也间接证实了太阳 “表面” 非但不凉， 而且要比大气层 (确切地说是光球层) 更热， 因为否则的话， 太阳大气层的光谱将会是发射光谱而非吸收光谱 (参阅第六节的注四)。 除上述误判外， 赫歇耳的提议还有一个很大的问题， 那就是无论多热的大气层如果得不到能量的补充， 都会很快冷却下来， 这与太阳长时间稳定地发光是完全矛盾的[注二]。

有这么多严重问题， 赫歇耳的资格再老， 也只能到一旁凉快去了。 接下来有两人几乎同时发了言， 这两人一位是德国医生兼物理学家迈耶 (Julius von Mayer, 1814－1878)， 另一位是苏格兰物理学家沃特斯顿 (John Waterston, 1811-1883)。 说来也巧， 这两人不仅发言时间相近， 学术经历也相似： 他们都在热力学领域中做过一些先驱性的工作， 前者研究了热功当量和能量守恒， 后者研究了气体分子运动论， 但两人的工作都在很大程度上被同时代人所忽略。 到了十九世纪四十年代后期， 这对 “难兄难弟” 又几乎同时对太阳为什么会发光产生了兴趣。 与赫歇耳时代不同， 当这两人开始研究这一问题时， 能量守恒的观念已初步形成 (如前所述， 迈耶本人就是研究这一观念的先驱之一)， 因此他们不能象赫歇耳那样随意假设一种近乎静态的发光机制， 而必须寻求能让太阳持续发光的能量来源。

作为起点， 他们两人都分析了一种土得掉渣的假说， 即把太阳当成一个燃烧的大煤球。 这种 “煤球说” 的提出是不需要想象力的， 凡用过煤炉的人都有可能想到， 但推翻它却需要一些专业知识。 经过计算， 迈耶发现太阳虽然大得惊人， 但与它那更惊人的光度相比却还不够大， 假如太阳果真是个大煤球的话， 即便维持燃烧所需的氧气不是问题， 它也只能燃烧几千年。 沃特斯顿的研究则表明， 不仅大煤球烧不了多久， 其它化学反应也强不到哪里去， 至多能撑 20000 年 (感兴趣的读者可以利用化学过程所涉及的能量与原子外层电子的能量同一量级这一特点核实一下他们的结果)。 如果时光能倒转两百年， 他们这些结果将不仅不是问题， 反而是天大的优点， 因为那跟神学家们 “推算” 出的世界历史的长度大致相当。 但在十九世纪中叶， 学术界已基本断定地球的年龄远不止那个量级。 而依照当时流行的康德-拉普拉斯星云假说 (Kant-Laplace nebular hypothesis)， 太阳和地球是由同一片星云收缩而成的， 彼此年龄相近。 既然太阳和地球的年龄相近， 而地球的年龄远不止几千年， 那么只能燃烧几千年的 “大煤球” 显然不可能是太阳持续发光的能量来源。 因此 “煤球说” 也被排除掉了。

排除了 “煤球说” 之后， 迈耶和沃特斯顿各自提出了自己的假说。 迈耶提出太阳之所以持续发光， 是因为不断有陨星坠落到太阳上。 沃特斯顿则认为是太阳自身引力收缩产生的热量使它持续发光。 两者之中， 沃特斯顿的 “引力说” 由于与康德-拉普拉斯星云假说存在共性——即都与引力收缩有关——而占有一定优势。 不过优势归优势， 两人的论文投寄出去后的命运却是相同的： 那就是都被拒掉了——迈耶的论文被巴黎科学院 (Paris Academy) 所拒， 沃特斯顿的则被伦敦皇家学会 (Royal Society of London) 所拒。 但即便如此， 沃特斯顿还是找到机会于 1853 年向英国科学进步协会 (British Association for the Advancement of Science) 报告了自己的理论， 他的报告打动了两位著名人物： 德国物理学家亥姆霍斯 (Hermann von Helmholtz, 1821-1894) 和英国物理学家汤姆生 (William Thomson, 1824-1907)， 即后来的开尔文勋爵 (Lord Kelvin)。 他们成为了我们这个案情分析会的下两位发言者。

这两人之中， 亥姆霍斯的发言很简短， 中心思想就是坚决拥护沃特斯顿的 “引力说”。 汤姆生则比较健谈， 他虽然也表态支持 “引力说”， 却详细回顾了自己的 “心路历程”。 他坦承， 自己曾经喜欢过迈耶的 “陨星说”， 但在接触过程中逐渐认清了后者存在的问题， 那就是假如太阳系中仍有那么多陨星， 我们地球也应该会分到一瓢羹， 这与地球目前的 “冷清” 状态显然不符 (事实上， 考虑到我们这些地球生物的脆弱性， 地球若果真分到那 “一瓢羹” 的话， 我们早就挂掉了)。 不仅如此， 假如太阳的巨大能量真的来自陨星， 那陨星的数量必须极为庞大， 它们的坠落将使太阳的质量增加， 进而影响行星的轨道。 由此导致的后果之一， 是过去几千年中地球的公转周期应该缩短几个星期。 这与天文观测显然也是矛盾的。 “吾爱 '陨星说’， 但吾更爱真理”， 面对如此严重的问题， 汤姆生毅然决然地抛弃了 “陨星说”， 转而投入 “引力说” 的怀抱。

与 “陨星说” 相比， “引力说” 的确显得高出一筹。 亥姆霍斯和汤姆生的研究表明， 太阳的半径只要每年收缩几十米， 就足以维持目前的光度 (感兴趣的读者不妨自己估算一下， 看能否证实他们的结果)。 相对于 139 万公里的太阳直径而言， 那样小幅的收缩在当时是任何人都无法察觉的， 因而不与观测相矛盾。 而且， 那样的收缩可以持续几千万年， 与汤姆生本人所估算的地球年龄具有相同的量级。 这一点给了他很大的信心， 使他在有生之年里保持了对 “引力说” 的从一而终。 若干年后， 当人们利用新发现的放射性现象对地球年龄作了重新估算， 发现它远比几千万年更古老时， 汤姆生依然固执己见， 凭借自己的巨大威望将 “引力说” 全面推向了二十世纪。

但在有关地球年龄越来越铁的证据面前， 汤姆生的威望虽高， 终究只是螳臂挡车。 在这一点上， 亥姆霍斯醒悟得比较早， 他曾表示， 如果能发现新能源， 我们就可以把太阳的年龄延长。 这虽然是一句没什么技术含量的大白话， 却也道出了一个努力方向， 那就是寻找新能源。 只不过 “煤球说” 所用的化学能 (本质上是电磁能) 和 “引力说” 所用的引力能都被排除了， 新能源在哪里呢？ 这个问题自然而然就成为了下一位发言者的主题。

这位发言者是我们的老朋友了， 他就是英国天文学家爱丁顿， 他的准备工作比前几位发言者都更充分， 因为他从兄弟单位那里拉来了以下几项 “友情赞助” (赞助者全都是诺贝尔奖得主)：

1905 年， 爱因斯坦提出了著名的质能关系式： E=mc2。 它表明在貌似寻常的物质之中蕴藏着惊人的能量。 1919 年， 新西兰物理学家卢瑟福 (Ernest Rutherford, 1871-1937) 在卡文迪许实验室里实现了所谓的人工原子核嬗变 (nuclear transmutation)， 即用人工手段将一种原子核变成另一种[注三]。 1920 年， 英国化学家阿斯顿 (Francis William Aston, 1877-1945) 发现了氢原子核 (即质子) 的质量要比重元素单个核子的平均质量略大。

这几项 “赞助” 落到爱丁顿那训练有素的大脑里， 很快就变成了一个有关新能源的大胆构想： 既然原子核可以彼此转变， 而质子的质量要比重元素单个核子的平均质量略大， 那么只要能把质子聚合成重原子核——比如氦核。 前者所包含的多余质量就应该会按照爱因斯坦质能关系式所确定的 “汇率” 转变为巨大的能量[注四]。 简单的估算表明， 这种被称为核聚变 (nuclear fusion) 的能量产生机制足以支撑太阳 100 亿年以上， 与有关地球年龄的所有测定都完全相容[注五]。

当然， 这只是理论可能性， 它能否成为现实， 关键得看太阳上的质子是否真能聚合成重原子核。 在爱丁顿时代， 那还是一个谜， 因为核子世界的一个重要成员——中子——尚未被发现， 有关核子相互作用的理论也尚未建立起来。 不过爱丁顿很乐观， 他表示 “在卡文迪许实验室里能够做到的事情对于太阳来说应该不会困难”。 但他乐观不等于别人也乐观， 他的观点一经提出， 就遭到了一位重量级英国物理学家金斯 (James Jeans, 1877-1946) 的强力反对。 两人互不相让， 展开了公开而激烈的争论， 他们的争论一度成为皇家学会的一道风景， 吸引了很多听不懂他们争论的科学家来看热闹 (科学家也是人， 他们的好奇心也并不总是集中在大自然上的)。

那么， 金斯反对爱丁顿的理由是什么呢？ 最核心的一条理由是这样的： 质子之间存在很强的静电斥力， 为了让它们彼此接近到能够发生核聚变的程度， 它们的热运动能量必须大到能克服静电斥力的程度， 这要求极高的温度， 而太阳内部是不可能有那样高的温度的。 对此， 爱丁顿的回答是： 象氦核那样的重原子核的存在是一个既有事实， 如果连恒星内部的温度都不够高， 那么宇宙中的重原子核从何而来呢？ “我们不跟宣称恒星不够热的人争论， 我们请他去找一个更热的地方”——他用这样一句掷地有声的名言把球扔回给了金斯。

这球金斯没能接住， 因为当时没有人知道更热的地方 (不过富有戏剧性的是， 后来人们发现， 还真的存在一个比恒星内部更热的地方， 而且包括氦核在内的某几种重原子核确有相当一部分是在那里被产生出来的。 那个地方就是大爆炸初期的宇宙)。 爱丁顿虽然把球扔回给了金斯， 但要想让别人真正信服， 光靠扔皮球是不行的， 他必须正面论述自己理论的可行性。 为此， 爱丁顿对恒星结构模型进行了研究。 在那些具有开创意义的研究中， 他估算出太阳核心的温度约为 4000 万度， 核心物质的密度则为 80 克/厘米3(相当于黄金密度的四倍)。 由于缺乏核相互作用理论的引导， 他无法对核聚变的细节做出可靠描述， 但他的估算结果在数量级上是大致成立的[注六]。

几千万度的高温， 比黄金还高得多的密度， 那样的数据看上去有些离奇。 但福尔摩斯说得好： 当你排除了所有的不可能， 剩下的无论看起来多么不可能， 一定就是真相。 爱丁顿的理论就颇有那样的意味。 如果我们对已被排除掉的 “煤球说”、 “陨星说” 和 “引力说” 分一下类的话， 那么从尺度上讲， 它们中既有宏观的， 也有原子尺度的； 从相互作用上讲， 则既有电磁的， 也有引力的。 既然那些都被排除掉了， 剩下的尺度就该轮到原子核尺度， 而剩下的相互作用则该是弱相互作用和强相互作用了， 这正是爱丁顿假说的基本特点[注七]。 但福尔摩斯的话虽然精彩， 毕竟不是金科玉律。 爱丁顿的假说真的代表真相吗？ 这个悬念我们要请下一位发言者来揭晓。 那位发言者也做了充分准备， 而且拉 “赞助” 的功夫也不含糊， 总计拉到四项之多 (赞助者除伽莫夫外， 也全都是诺贝尔奖得主)：

1928 年， 俄国物理学家伽莫夫 (George Gamow, 1904-1968) 发现了量子力学的隧道效应， 即微观粒子有一定概率穿越经典意义上不可穿越的 “障碍”。 这一发现在很大程度上破解了金斯的诘难， 因为即便太阳核心不够热， 依然有一部分质子可以通过隧道效应来克服静电斥力造成的 “障碍”。 1932 年， 英国物理学家查德维克 (James Chadwick, 1891-1974) 发现了中子， 为理解原子核结构铺平了道路[注八]。 1934 年， 意大利物理学家费密 (Enrico Fermi, 1901-1954) 提出弱相互作用的四费密子理论 (four-fermion theory)， 为近似描述核子反应中的弱相互作用部分提供了理论基础。 1935 年， 日本物理学家汤川秀树 (Hideki Yukawa, 1907-1981) 提出了强相互作用的介子理论， 为近似描述核子反应中的强相互作用部分提供了理论基础。

有了上述 “赞助”， 我们的发言者很快就拟定了一份出色的发言稿， 为爱丁顿的假说提供了决定性的支持。 这位发言者是二十世纪三十年代从纳粹德国逃往美国的许许多多物理学家中的一员， 他的名字叫做贝特 (Hans Bethe, 1906-2005)。 在贝特开始研究恒星能量产生机制时， 对这一问题感兴趣的物理学家已经不少， 其中包括后来的美国原子弹之父奥本海默 (Robert Oppenheimer, 1904-1967)、 美国氢弹之父泰勒 (Edward Tellar, 1908-2003)， 以及著名的苏联物理学家朗道 (Lev Landau, 1908-1968)。 不过贝特并不是一个人在战斗， 他有合作者， 此人名叫克里奇菲尔德 (Charles Critchfield, 1910-1994)， 是一位研究生， 在与贝特合作前曾跟随伽莫夫学习。

1938 年， 在伽莫夫的建议下， 克里奇菲尔德研究了质子与质子之间的核反应。 在得知贝特也在从事类似的研究后， 伽莫夫让克里奇菲尔德把论文寄给贝特， 由此促成了两人的合作。 贝特和克里奇菲尔德的合作揭示了发生在太阳内部最重要的核聚变反应， 即所谓 “质子-质子链” (proton-proton chain， 简称 pp 链) 的具体实现方式。 这种实现方式中最主要的一类被称为第一类质子-质子链 (简称 ppI 链)， 它是这样进行的：



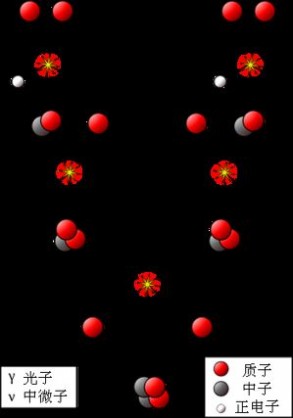
【第一类质子-质子链】

两个质子 p 聚合成氢的同位素氘核2H (左上角数字表示核子数， 下同)。 一个氘核2H 与一个质子 p 聚合成氦的同位素3He。 两个3He 通过扔掉两个多余质子 p 而聚合成一个标准氦核4He。

这整个过程释放出的能量约为 26.7 MeV (MeV 为百万电子伏特， 是描述核反应能量的常用单位， 约合 1.6×10-13焦耳)， 其效率是普通化学反应的几百万倍以上。 在太阳核心所产生的能量中， 这类质子-质子链的贡献占了约 85%， 是当之无愧的产能大户[注九]。

除质子-质子链外， 贝特还研究提出了另一种恒星核反应机制， 称为碳氮氧循环 (CNO cycle)， 也称为碳氮循环 (CN cycle)， 因为参与该反应的氧核是15O， 而不是最常见的16O。 这种反应所需的温度比质子-质子链更高， 在象太阳这样的小质量恒星的能量产出中只占了 1% 左右。 但它在质量比太阳大 30% 以上的恒星中却占据着主导作用， 因而在恒星核物理中的总体重要性不亚于质子-质子链。 与贝特几乎同时， 德国物理学家魏茨泽克 (Carl von Weizs?cker, 1912-2007) 也独立地完成了同样的工作。 魏茨泽克也是当时这一领域的主要研究者之一， 并且正是受到他的影响， 贝特才将自己的研究方向由单纯的核物理转到恒星核物理上。 1939 年， 贝特写了一篇综述性的论文， 对恒星能量产生机制作了比较完整的阐述。 也许是由于对质子-质子链和碳氮循环这两类反应同时作出重要贡献的缘故， 贝特成为了 1967 年度诺贝尔物理学奖的唯一得奖人， 得奖理由中很重要的一条就是发现恒星能量产生机制。

在研究恒星能量产生机制的同时， 人们对爱丁顿的太阳模型也进行了修正。 其中最重要的修正是关于核心温度的， 那温度虽仍是一个很难用日常指标来衡量的恐怖数字， 但因为有隧道效应的帮助， 比爱丁顿所估计的 4000 万度要低得多， 约为 1570 万度。 这个温度的重估是十分必要的， 因为核聚变反应的剧烈程度与温度有着极为敏感的依赖性， 温度越高， 核聚变反应越剧烈。 如果太阳的核心温度果真有 4000 万度， 整个太阳将会象一个超级氢弹一样， 在惊天大爆炸中化为灰烬 (我们的命运自然也可想而知)。 与核心温度的调低相反， 重新估计后的太阳核心密度则比爱丁顿的估计更高， 约为 160 克/厘米3， 而太阳的核心压强也极为惊人， 达到 2500 亿个大气压。 这些数字的可怕之处一般人可能难以体会， 我们可以举两个例子： 维持在太阳核心温度上的物质， 哪怕只有玻璃弹珠那样一小块， 也足以熔化几百公里以外的钢铁[注十]； 而太阳的核心压强， 则相当于在手指甲那样的面积上压上几亿吨的重物。 可以毫不夸张地说， 太阳核心这个太阳系的光明源泉， 是一个不折不扣的恐怖核心。

好了， 现在我们终于有了一个理论， 象大侦探的理论一样， 能对手头的线索 (比如太阳的光度及维持这一光度的漫长时间) 作出解释。 从某种意义上讲， 爱丁顿和贝特是幸运的， 因为当爱丁顿开始思考恒星能量产生机制时， 人们对物理世界的了解已经深入到了理解这一问题所必需的原子核尺度上， 爱因斯坦也已经提出了质能关系式； 而当贝特开始研究恒星能量产生机制的细节时， 人们已经有了关于核子相互作用的初步理论。 那些理论若是不存在， 爱丁顿和贝特就是再高明十倍， 恐怕也将会 “巧妇难为无米之炊”。 我有时会想， 如果某个遥远星球上存在着其它智慧生物， 他们会如何理解这个世界， 我们称之为科学的东西在他们那里会以一种什么样的顺序发展？ 那是我心中有关他们的最大好奇。 至于他们长什么样？ 能活多少岁？ 对我来说倒是细枝末节的。

最后让我们再回到本节开头所引的爱因斯坦和英费尔德的文字中来。 有读者可能会问： 爱丁顿和贝特等人的理论虽然给出了太阳的能量产生机制， 但那恐怖核心却是一个我们永远也不可能到达的地方， 我们有什么办法来检验他们的理论呢？ 答案是： 通过检验理论的推论。 事实上， 我们很快将会看到， 由爱丁顿和贝特等人提出的这个恒星能量产生机制的确很象爱因斯坦和英费尔德所说的大侦探的理论， 它不仅解释了我们手头的线索， 而且也预言了某些其它事情一定已经发生。 我们下一步要做的， 就是去验证那些事情， 收集有关我们理论的进一步证据。

但出乎意料的是， 我们信心满满的收集行动却遇到了非常棘手的困难。 大自然似乎嫌我们这个侦探故事还不够离奇曲折， 而决心要为我们增添一些新的情节。 在下一节中， 我们将一同去面对那些困难， 同时欣赏一下大自然为我们增添的新情节。

注释

值得一提的是， 在很古老的回答中也有相对不错的。 比如公元前五世纪的古希腊先贤阿那克萨哥拉 (Anaxagoras, 500BC-428BC) 曾经设想太阳是一个烧红的大铁球。 理由是他亲眼目睹过如火球般从天而降的陨铁， 他认为那是太阳的碎片。 他这个提议当然也很 “菜”， 但起码与赫歇耳的提议有一拼。 不过这一点也不能用来苛求赫歇耳， 因为能量守恒定律的确立是赫歇耳去世之后的事情 (在那之前只有一些关于机械能的粗糙概念)。 如今连小学生都会追问的热能从何而来的问题， 在赫歇耳时代并不是显而易见的。 卢瑟福最早实现的人工原子核嬗变是用 α 粒子 (即氦核4He) 轰击氮核14N， 从中产生出氧的同位素17O (同时发射出一个质子)。 在那之前的 1901 年， 卢瑟福与他的同事索迪 (Frederick Soddy, 1877-1956) 还共同发现了原子核的自然嬗变。 除这一构想外， 爱丁顿还提出过一个更大胆的想法， 那就是让电子和质子彼此湮灭， 使它们的质量完全转变为能量。 那种过程如果可能的话， 将比核聚变更强大。 可惜 (更恰当地说是幸运) 的是， 那种过程是不可能发生的， 因为否则的话， 整个物质世界都将因电子和质子的湮灭而崩溃。 而且如果恒星的能量果真来源于湮灭过程的话， 将不会留下任何残骸， 这与当时已经发现的作为恒星残骸而存在的白矮星相矛盾。 因此爱丁顿的那个想法很快就被放弃了。 不过有意思的是， 几年之后， 英国物理学家狄拉克 (Paul Dirac, 1902-1984) 出于不同的理由又重蹈了一次覆辙。 需要指出的是， 核聚变能够释放巨大能量的想法早在阿斯顿发现氢原子核的质量要比重元素单个核子的平均质量略大的同一年， 就由法国物理学家佩林 (Jean Perrin, 1870-1942) 提出过。 另外要指出的是， 由于中子尚未被发现， 在爱丁顿等人的早期设想中需要把一些电子塞进原子核里， 以中和一部分质子电荷。 除估计太阳核心的温度、 密度等参数外， 爱丁顿还分析了恒星质量与光度之间的关系， 并对著名的赫罗图作出了定性解释。 那些工作对于人们接受他的观点起了很大的促进作用。 严格讲， 爱丁顿的假说并不是具有这些特点的唯一假说。 在 1896 年法国物理学家贝克勒尔 (Henri Becquerel, 1852-1908) 发现放射性现象之后， 曾有人猜测太阳的能量来自重核裂变成轻核的核裂变反应。 不过人们很快就意识到太阳上没有足够多的重元素来长期提供裂变能量， 因此那个猜测很快就被推翻了。 值得一提的是， 卢瑟福早在 1921 就猜测过中子的存在, 用以解释原子核的稳定性 (在原先的理论中， 原子核是由质子和电子构成的， 它面临的一个很棘手的困难， 就是禁锢在原子核中的电子的能级远高于实验观测到的核能级)。 质子-质子链中的其它几类实现方式与第一类的区别在于3He 生成4He 的方式各不相同。 对太阳来说， 那另外几类实现方式对总能量的贡献约为 14%。 这是假定那一小块物质的温度始终维持在太阳的核心温度上。 只有那样， 它才能熔化几百公里外的钢铁。 如果我们仅仅是从太阳核心挖出一小块物质， 它的温度会因辐射能量而急剧降低， 情形将很不相同。

二零一零年七月十九日写于纽约

二零一零年七月二十日发表于本站

http://www.61k.com

太阳的故事

（本文授权转载于卢昌海老师的个人博客，欲再转载者请联系原作者）

图片出处：维基百科

太阳的故事 (九) 细小的粒子，巨大的谜团

本文作者：卢 昌海

在上节中， 我们介绍了作为太阳能量产生机制的爱丁顿和贝特的理论 (以下简称恒星核聚变理论)， 它能很好地说明太阳为什么可以长时间发射如此惊人的能量， 而且它是能够说明这一现象的唯一理论， 从这个意义上讲， 它已经经受住了初步的观测检验。 但这种检验毕竟是很间接的， 如果打个比方的话， 有点象是通过测量一个黑箱的输出功能来检验有关它内部结构的猜测， 哪怕检验合格， 也未必能让所有人都信服， 因为它终究不如打开黑箱直接窥视里面的结构来得确切。

科学家们想要的正是象打开黑箱直接窥视那样的确切性。

粗看起来， 这胃口似乎有点贪婪， 谁能打开一只被 2500 亿个大气压所包围着的， 具有 1570 万度高温的黑箱呢？ 但幸运的是， 在这貌似不可能的任务上， 大自然却很慷慨地为我们准备了一扇窗户——一扇能让我们直接窥视太阳核心奥秘的窗户。

只不过窥视的结果却让科学家们足足困惑了三十年。

我们先来说说那扇 “窗户”。 我们知道， 普通的窗户之所以能让我们窥视东西， 是因为它能让光子通过， 而我们的眼睛或仪器则通过接收那些光子来获取信息。 太阳核心既然是太阳系的光明源泉， 发射光子自然是份内之事， 而我们在地球上能见到阳光， 说明我们能接收来自太阳的光子。 既然一个能发射， 一个能接收， 粗看起来， 那扇能让我们窥视太阳核心奥秘的窗户就是普通的窗户。 可惜那只是错觉。 我们在后文中将会看到， 由太阳核心所发射的光子要经历十几万年的漫长时间才能到达太阳表面， 这个过程比唐僧取经还要艰难无数倍， 而且到达太阳表面， 继而抵达我们眼睛或仪器的早已不是由核聚变反应所产生的那些光子， 而是不知多少代之后的 “子孙” 了。 那样的光子虽仍能如第六节所说的那样带给了我们大量的信息， 但此光子非彼光子， 有关太阳核心的信息早就丧失殆尽了。

因此能让我们窥视太阳核心奥秘的窗户并不是普通的窗户， 尤其光子并不是能让我们窥视太阳核心奥秘的东西。 那么能使我们透过那扇窗户窥视太阳核心奥秘的究竟是什么东西呢？ 这还得从那些核聚变反应说起。

我们介绍过， 那些核聚变反应中被称为 “第一类质子-质子链” 的反应提供了约 85% 的太阳能量， 而那个核反应的第一步是 “两个质子聚合成氢的同位素氘核2H”。 细心的读者也许早已注意到了， 那样的反应其实是不可能发生的， 因为反应前后的电荷数目不同： 两个质子带两个单位的正电荷， 而一个氘核却只带一个单位的正电荷。 那样的反应如果发生的话， 现代物理学中最可靠的守恒定律之一——电荷守恒定律——就泡汤了。 很明显， “两个质子聚合成氢的同位素氘核2H” 那样的简略提法只关注了反应过程中的原子核部分， 而忽略了反应产物中必须包含的另一个带正电的粒子。 那个粒子叫做正电子， 它是电子的反粒子， 它的出现保证了电荷守恒。

但这还不够， 因为有一样重要性不在电荷之下的东西还不守恒， 那就是能量。 只不过这一点不是仅凭细心就可以发现的， 而必须通过实验。 但早在那样的实验成为现实之前的二十世纪二十年代末， 物理学家们就已经注意到了在与之类似——即反应产物中有一个电子或正电子——的核反应过程中能量似乎是不守恒的[注一]。 由于当时刚刚经历了量子力学革命， 物理学家们心中的 “革命意识” 还比较高涨， 遇到那样的异常现象， 有些人就开始往物理学革命的路数上去想， 其中包括著名的丹麦物理学家玻尔 (Niels Bohr, 1885-1962)， 他一度猜测能量守恒定律在原子核尺度上将不再适用。 他的这种 “冒进” 想法遭到了奥地利物理学家泡利 (Wolfgang Pauli, 1900-1958) 的批评。 1930 年， 泡利提出了一个不同的想法。 他认为貌似不守恒的那部分能量其实是被一种尚未被观测到的细小的中性粒子带走了。 那种中性粒子起初被称为 “中子”， 后因该名称被一种大质量的中性粒子——即我们如今所说的中子——所霸占而改称为了中微子 (neutrino)。 在 “两个质子聚合成氢的同位素氘核2H” 这一反应中， 如果把中微子和正电子一起加入到反应产物中去， 电荷与能量就都守恒了。

这个由泡利提出的中微子就是使我们能透过那扇窗户窥视太阳核心奥秘的家伙。

中微子这个细小的家伙为什么有那样的神通呢？ 原因很简单： 因为它与物质的相互作用极其微弱。 事实上， 在主宰微观世界的三大相互作用中， 它只参与其中最弱的一种， 即所谓的弱相互作用。 相互作用微弱所导致的一个直接后果， 就是穿透能力超强。 在物理实验室里， 人们常常用铅来屏蔽辐射， 但中微子却可以不太困难地穿越整整一光年厚的铅。 正因为有如此超强的穿透能力， 它才能在早年的实验中携带能量轻松逃离， 给物理学家们留下一个能量不守恒的犯罪现场， 甚至让玻尔那样的 “神探” 都栽了跟斗[注二]。 也正因为有如此超强的穿透能力， 它才可以取代光子成为我们窥视太阳核心奥秘的工具， 因为厚达七十万公里， 让光子举步为艰的太阳物质对它来说几乎是完全透明的。

窗户既然开启了， 那么接下来的问题就是： 透过这扇窗户， 我们想窥视什么样的奥秘？ 在这方面， 科学家们的胃口倒并不贪婪——起码到目前为止还并不贪婪， 他们只想确认太阳的核心是不是真的如恒星核聚变理论所预言的那样发生着大规模的核聚变反应。 确认的方法就是探测核聚变反应中必然会产生的那些中微子， 即所谓的太阳中微子 (solar neutrino)， 因为那是唯一一种能几乎不受阻碍地逃离太阳核心的粒子。

在介绍那些探测之前， 让我们首先估计一下， 假如恒星核聚变理论成立， 太阳每秒钟会产生多少个中微子？ 这个估计并不困难， 因为太阳上的核聚变反应虽然有很多类型， 最终结果却都是将四个质子和两个电子结合成一个氦原子核[注三]， 每个这样的结合过程都将发射两个中微子 (感兴趣的读者不妨以第一类质子-质子链为例自己清点一下数目)。 简单的比较表明， 四个质子和两个电子的总质量比一个氦原子核大了 26.7 MeV (约合 4.27×10-12焦耳)。 这表明太阳核心每产生 26.7 MeV 的能量， 就会发射两个中微子。 由于我们在第七节中已经知道太阳的光度约为 384 亿亿亿瓦， 即每秒种产生 384 亿亿亿焦耳的能量。 由此不难算出太阳每秒种发射的中微子数量约为 180 万亿亿亿亿个 (1.8×1038)[注四]。 这是一个什么概念呢？ 它相当于每秒种——不分白天黑夜——都会有几百亿个中微子穿过你身上每平方厘米的面积！ 这就是爱丁顿和贝特等人的这个恒星核聚变理论所预言， 而我们将要去收集证据加以验证的 “某些其它事情”。 不过大家不必为这个巨大的数字而担心， 虽然你一生都会 “沐浴” 在汹涌的中微子洪流中， 却很可能一生都不会有一个中微子与你发生任何相互作用——当然， 微不足道的万有引力除外。

数量如此巨大的中微子在地球附近除了来自太阳核心的核聚变反应外， 再没有第二种可能了， 因此只要能从实验上证实它们的存在及数量， 就将是对恒星核聚变理论的判决性支持。 但问题是， 要想从实验上证实中微子的存在， 必须让它们在我们的探测器里留下踪迹。 可中微子既然能穿透整个太阳， 穿透整整一光年的铅， 当然也能不留丝毫踪迹地穿透我们的探测器。 它的这种超强的穿透力既是为我们提供信息的前提， 同时却也是对实验技术的最大挑战。

但物理学家们还是有办法的。 办法很简单， 那就是 “人海战术”， 这其实是对付小概率事件的通用办法。 我们知道， 让一个人掷 30 次硬币要想全都掷出正面几乎是不可能的 (概率只有十亿分之一)， 但如果让全中国十几亿人每人都掷 30 次硬币， 那么一轮下来就会有很大的概率出现一个掷出 30 次正面的人， 这就是 “人海战术” 的威力。 科学家们对付中微子的办法也是如此， 只不过是把 “人” 换成物质。 中微子与物质的相互作用虽然微弱， 但只要有合适的探测物质， 并且数量足够多， 当大量的中微子与它们擦身而过时， 还是会有个别中微子留下踪迹的。

那么什么样的物质适合做探测物质呢？ 1946 年， 出生于意大利的核物理学家庞蒂科夫 (Bruno Pontecorvo, 1913-1993) 研究了这个问题。 他提出了探测物质所应具备的一系列条件， 其中包括：

不太昂贵——因为所需数量很大， 太昂贵了负担不起。 与中微子反应后必须生成放射性元素， 以便我们能通过放射性来判定它们的存在， 进而推断反应的发生。 所生成的放射性元素必须有合适的半衰期， 以便我们既有时间分离它们， 又不必等太久来判定它们的存在。 除中微子外， 其它因素造成同样反应的可能性必须很小， 以免干扰结果。

在这样一些条件下， 庞蒂科夫推荐了几种探测物质， 其中最重要的一种是氯 (Chlorine) 的同位素37Cl。 它与中微子反应后会生成氩 (Argon) 的同位素37Ar (同时放出一个电子以平衡电荷)。37Ar 是一种放射性元素， 半衰期约为 35 天。

二十世纪五十年代， 美国物理学家戴维斯 (Raymond Davis, Jr., 1914-2006) 率先展开了这方面的实验研究。 考虑到氯在常温常压下是气体， 体积过于庞大， 戴维斯采用了常温常压下呈液态的四氯化碳 (Carbon Tetrachloride——CCl4)。 他的实验室位于地下五米左右， 使用的四氯化碳约为 3800 升。 在这样简陋的条件下， 他只能得到一个有关太阳中微子数量的很宽松的上限， 比理论值高出了好几个数量级[注五]。

结果虽然寒碜， 毕竟算是开山之作， 戴维斯还是写成一篇论文发了出去。 可惜的是， 论文在审稿人那里遭到了 “温柔一刀”。 审稿人在审稿意见中很幽默地指出： 象这种缺乏精度的研究， 就好比是站在山顶上， 用自己的手去碰月亮， 然后得出结论说月亮要比自己的手能碰得到的地方更高。 审稿人的结论是： 这样的研究是不应该写成论文的。

太伤自尊了。

看来必须把实验做大。 从二十世纪六十年代中期开始， 戴维斯与美国天体物理学家巴克尔 (John Bahcall, 1934-2005) 合作， 开始在美国南达科他州 (South Dakota) 一座名为 Homestake 的金矿的矿井里建造一个巨大的中微子探测器。 巴克尔是研究太阳模型的专家， 他对太阳中微子流量的理论计算， 在几乎所有太阳中微子探测实验中都是最重要的参照之一[注六]。 戴维斯的这个新实验被称为 Homestake 实验， 它的探测器位于地下 1500 米深处。 这种 “深挖洞” 的做法是太阳中微子实验中的标准做法， 目的是减少其它因素——比如宇宙线——的干扰。 为了便于相互比较， 人们往往用等效水深来表示中微子探测器的深度。 Homestake 实验中的这个 1500 米的深度用等效水深来表示大约为 4200 米。 在 Homestake 实验中， 探测物质是近 40 万升 (约 600 吨) 的四氯乙烯 (Tetrachloroethylene——C2Cl4)。



【Homestake 探测器】

1967 年， 戴维斯的实验装置基本建成。 1968 年， 他得到了第一批观测结果， 但误差很大。 直到 1970 年， 经过各种改进， 他才得到了具有统计价值 (即不至于被误差淹没) 的结果。 这结果是一个好消息和一个坏消息的混合。 好消息是他的确探测到了太阳中微子， 坏消息则是他探测到的中微子流量明显小于理论预言。 这个结果催生了一个新名词： 太阳中微子问题 (solar neutrino problem)。

Homestake 实验持续进行了 25 年 (1984 年之后改由宾西法尼亚大学主持)， 检测到的平均中微子流量约为理论预言的 1/3。 这是一个令人尴尬的结果， 因为尽管检测到的流量只有理论预言的 1/3， 却依然是一个除恒星核聚变理论外， 绝无任何其它机制可以在地球附近产生的巨大流量， 从这个意义上讲， 它足以作为恒星核聚变理论的铁证。 但另一方面， 1/3 毕竟不是 1， 连四舍五入都入不到 1。 它作为定性证实虽然马马虎虎， 从定量上讲， 却是一个很糟糕的结果。 这一点令戴维斯和巴克尔深感不安。 自第一批论文发表之后， 他们对实验和理论的各个方面都进行了仔细复核， 试图缩小观测与理论的差距， 却始终无法如愿。 1989 年， 他们在一篇文章中写道： “对我们来说很惊讶， 也许还相当失望的， 是意识到自那些论文发表以来， 尽管对细节进行了十几年的复核及持续改进， 却无论在观测还是标准理论上都没什么定性的改变。”

既然自己的努力遇到了挫折， 那就看看别人是怎么做的吧。 物理学上的任何实验都必须能够重复， 而且要尽可能由不同的实验小组、 不同的实验设备、 不同的实验方法、 在不同的地点来重复， 这样可以最有效地减少单一小组、 单一设备、 单一方法所可能存在的从心理因素到系统误差在内的各种不足。 这种研究规范是物理学能够令人信赖的一个重要原因。

探测太阳中微子的不同方法其实早在 Homestake 实验开始运作之前就已经有人在研究了。 1966 年， 俄国物理学家库兹明 (Vadim Kuzmin, 1937-) 提出了一种新的探测方法， 利用镓 (Gallium) 的同位素71Ga 作为探测物质。71Ga 与中微子反应后会生成锗 (Germanium) 的同位素71Ge (同时放出一个电子以平衡电荷)。71Ge 是一种放射性元素， 半衰期约为 11 天。

利用71Ga 来探测太阳中微子有一个 Homestake 实验无法比拟的优势， 那就是能够探测到的中微子能量范围要宽广得多。 我们在上节中介绍过， 在太阳核心所产生的能量中， 第一类质子-质子链的贡献占了 85% 左右。 毫无疑问， 这是太阳核心最重要的核聚变反应， 也是太阳中微子的最大来源。 但这类反应所产生的中微子的最大能量只有 0.423 MeV (平均能量为 0.267 MeV)， 而 Homestake 实验所能探测到的中微子的最低能量——即所谓的阈能 (threshold)——却是 0.814 MeV， 大大高于第一类质子-质子链所产生的中微子的能量。 这就意味着 Homestake 实验对太阳中微子中数量最庞大的那部分是 “视而不见” 的 (当然， 那部分中微子在实验与理论对比时是被除去的)。 考虑到检测中微子的极端困难性， 这种 “视而不见” 无疑是极大的 “浪费”。 而利用71Ga 来探测太阳中微子的最大好处就是能弥补这一缺陷， 因为它所能探测到的中微子的最低能量为 0.233 MeV， 从而涵盖了很大一部分来自第一类质子-质子链的中微子[注七]。 除这一点外， 利用71Ga 来探测太阳中微子还有一个很大的好处， 那就是在理论上， 人们对第一类质子-质子链的研究要比对那些所占比例小得多的其它反应彻底得多， 因而能提供更可靠的理论数据。

设想是有了， 将它变为现实却是一件费时费力费钱的事情， 利用71Ga 作为探测物质的太阳中微子实验直到二十世纪九十年代初才开始出结果。 从事此类实验的有两个研究小组， 一个是由苏联和美国的科学家联合进行的， 称为 SAGE (Soviet-American Gallium Experiment 的缩写) 实验， 地点位于苏联高加索山区 (Caucasus mountains) 一条四公里深的隧道内， 等效水深约为 4700 米； 另一个是由美、 德、 法、 波兰、 意大利、 以色列等国的科学家联合进行的， 称为 GALLEX (Gallium Experiment 的缩写) 实验， 地点位于意大利阿布鲁佐大区 (Abruzzo) 一个等效水深约 3200 米的地下实验室内。 在实验手段上， SAGE 采用的实验物质是 30 吨液态镓 (1991 年增加到 57 吨)， GALLEX 采用的则是 101 吨三氯化镓 (gallium trichloride) 溶液。



【左：SAGE 和；右：GALLEX 实验所在的山区】

那么这两组新实验的结果如何呢？ 它们是 “A. 找到了全部的太阳中微子” 呢？ 还是 “B. 证实了 Homestake 实验那缺斤短两的结果”？ 答案是： “C. 以上都不对”。 这两组新实验探测到的太阳中微子流量既不是 1/3， 也不是 1， 而大约是理论流量的 60%[注八]。

有点盲人摸象的意味了， 你摸到一个脑袋， 我摸到一条大腿。 真相到底如何呢？ 还得再摸摸看。

另一组 “摸象” 的 “盲人” 是日本人， 他们的实验结果其实比 SAGE 和 GALLEX 出得更早， 他们的实验地点在日本神岡町 (Kamioka) 的一座等效水深约 2700 米的地下矿井内， 称为神岡观测站 (Kamioka Observatory)， 原先从事的是一度很热门的质子衰变研究。 自 1985 年开始， 该观测站经过扩建后改称为神岡核子衰变实验 II 期 (KamiokaNDE-II)。 自 1987 年起， 该实验室的探测器——神岡探测器——开始进行太阳中微子探测。

神岡探测器探测太阳中微子的方式与 Homestake、 SAGE、 GALLEX 等实验都不相同， 它核心部位的探测物质是 2142 吨高度纯净的水， 所利用的反应过程则是中微子与电子的碰撞。 这种碰撞当然是小概率事件 (因此要用几千吨水)， 但如果发生了， 就有可能使电子获得能量， 如果入射中微子的能量很高， 电子所获得的能量也会很多， 运动速度甚至可以超过光速——别紧张， 只是超过水中的光速， 没有破坏相对论。 人们在电磁学研究中早就知道， 当电子在水中的运动速度超过水中的光速时， 会发射一种特殊的辐射， 叫做切伦科夫辐射 (Cherenkov radiation)。 通过观测这种辐射， 物理学家们就可以确定反应的发生。



【超级神岡探测器】

神岡探测器的这种与众不同的探测原理使它具有一种 Homestake、 SAGE、 GALLEX 等实验都不具有的优势， 那就是可以确定中微子与电子发生反应的时间、 位置、 入射方向、 入射能量等细节。 这些细节对于统计太阳中微子的数量来说虽不是必须的， 但对于深入探索太阳核心的其它奥秘却有很大价值[注九]。 不过有得就有失， 神岡探测器也有一个很大的问题， 那就是阈能特别高。 为了使碰撞后的电子能够 “超光速”， 并且发射足够强劲的切伦科夫辐射， 入射中微子的最低能量要达到 7.2 MeV， 只有 “极少数极少数” 的太阳中微子能具有如此高的能量。

从 1987 年到 1990 年， 神岡探测器在积累了 1040 天的数据后得到了一个结果： 它探测到的太阳中微子流量约为理论流量的 46%。 1995 年， 在积累了 2079 天的数据基础上， 上述结果被修正为 55%。 1996 年， 神岡观测台耗资一亿美元建造了更大的探测器， 称为超级神岡 (Super-KamiokaNDE) 探测器， 它的探测物质增加到了 50000 吨高度纯净的水， 它对切伦科夫辐射的探测灵敏度达到了可以探测到月亮上一支烛光的惊人程度， 而它的阈能则降低到了 5.5 MeV。 一句话， 它在各方面都有了长足的改进。 自 1998 年起， 超级神岡探测器开始发布探测结果， 它所探测到的太阳中微子流量约为理论流量的 47%， 与其它各组实验都不相同。

杯具了！

二十世纪就在这样忙忙碌碌的太阳中微子研究中走到了尾声。 虽然在这类研究中， 无论实验还是理论都存在不小的误差， 但有一点已经可以确定， 那就是探测到的太阳中微子流量明显小于理论预言， 而且两者在不同的能量范围内有不同的差距。 中微子这个细小的粒子， 给即将到来的新世纪留下了一个巨大的谜团。 究竟是太阳原本就没有发射那么多中微子呢？ 还是有些太阳中微子失踪了？ 如果是失踪， 那它们究竟跑到哪里去了呢？

注释

这里所说的 “反应产物中有一个电子或正电子” 的核反应过程是指当时人们正在积极研究的重原子核的 β 衰变， 那种反应过程中的能量异常现象其实更早些时候就被注意到过， 但直到二十世纪二十年代末， 随着其它可能性被陆续排除掉， 才真正威胁到了能量守恒定律。 另外要说明的是， 那些实验所导致的只是中微子的提出， 包括正电子在内的反粒子概念的提出则是出于其它原因， 时间上也更晚一些 (感兴趣的读者可参阅拙作反物质浅谈)。 中微子直到 1956 年才由美国物理学家考恩 (Clyde Cowan, 1919-1974)、 莱因斯 (Frederick Reines, 1918-1998) 等人所发现。 莱因斯因此而获得了 1995 年的诺贝尔物理学奖 (考恩不幸已经去世)。 确切地讲， 这只是现阶段的主要反应模式。 在后文中我们将会看到， 当太阳步入 “晚年” 后情况将会有所变化。 另外要说明的是， 参与反应的两个电子的参与方式有不止一种： 主要的方式是与反应产物中的正电子湮灭； 稀有的方式是直接参与反应， 那样在反应产物中就不会有正电子 (因为电荷已经平衡了)。 这个估算也请读者自己去做。 不过要提醒的是， 这个估算是有系统误差的， 感兴趣的读者请思考一下， 什么因素会造成系统误差？ 它会使估计出的中微子数量偏大还是偏小？ 他所得到的这一上限为 40000 SNU。 SNU 是所谓的太阳中微子单位 (Solar Neutrino Unit)， 它描述的是中微子探测器探测太阳中微子的能力。 一个 SNU 表示每秒种每一万亿亿亿亿 (1036) 个探测器原子可以俘获一个太阳中微子。 有读者也许会问： 我们前面不是已经很轻松地计算出了太阳中微子流量吗？ 何必还要什么专家呢？ 答案是： 我们计算的只是太阳中微子的总量， 对实验探测来说重要的不是总量， 而是中微子数目随能量的分布， 因为各个探测器所能探测到的中微子能量范围各不相同， 在不同能量上的探测灵敏度也各不相同。 中微子数目随能量的分布与太阳内部各种核聚变反应的相对比重等各种复杂因素有着密切关系， 是非常困难的理论问题。 这一点从两者所能俘获的太阳中微子流量的大小可以看出。 Homestake 实验所能俘获的理论流量约为 8 SNU， 而以71Ga 为探测物质的探测器所能俘获的理论流量高达 130 SNU 左右。 由于对太阳中微子流量的理论计算存在几种彼此接近， 但互不相同的结果， 因此视所用理论结果的不同， 不同文献给出的实验与理论的比值存在一定差异。 其它几种探测器之所以做不到这一点， 是因为它们反应产物的半衰期长达十几或几十天， 等到人们能通过反应产物的衰变来确定反应的发生时， 有关反应的细节信息早已不复存在了。

二零一零年九月三日写于纽约

二零一零年九月四日发表于本站

http://www.61k.com

太阳的故事

太阳的故事 (十) 标准太阳模型 vs 粒子物理标准模型

本文作者：卢 昌海

由太阳中微子带来的这些问题被称为太阳中微子问题 (solar neutrino problem)， 有时也被称为太阳中微子之谜， 或太阳中微子失踪之谜。 不过严格来说， 这最后一个名称是需要论证的， 这就好比在现实世界中要把一个案件定性为失踪案， 是需要经过排查的。 在本节中， 我们就从那些排查说起。

我们要排查的第一种可能性是观测出问题的可能性。 这种排查之所以必要， 是因为中微子是一种相互作用极其微弱， 从而在观测上极易 “漏网” 的粒子。 这 “漏网” 达到一定程度， 就有可能无中生有地产生出太阳中微子问题来， 就象早年的核物理实验因为无法探测到中微子， 而无中生有地闹出了能量不守恒的伪问题来一样。

那么， 太阳中微子问题是否也有可能是那样的伪问题呢？ 答案是否定的。 理由有两条： 一是太阳中微子问题乃是几组独立实验的共同结果， 这种结果的可靠性要比单一实验大得多。 二是 GALLEX 和 SAGE 这两组实验都用流量已知的人工中微子源对探测器进行过校正， 从而进一步确保了它们的可靠性。 因此我们有充分的理由相信， 太阳中微子问题并不是观测错误导致的伪问题。

既然不是伪问题， 那就是真问题了； 而既然不是观测问题， 那就是理论问题了。 因此接下来要排查的就是哪部分理论出了问题。 我们知道， 对太阳中微子流量的理论预言来自所谓的太阳模型， 这是一种在学术界有着广泛共识的模型， 也称为标准太阳模型 (standard solar model)。 这一模型以太阳的大小、 光度、 表面温度等可观测数据为约束， 对太阳内部物态的分布、 压强的平衡、 能量的产生与传输、 辐射的吸收与发射等主要因素及相互关系给出了定量描述。 它决定着太阳核心产生中微子的机制及数量。 但标准太阳模型并不是故事的全部， 因为太阳中微子被产生之后还必须经历一个传播环节： 它必须穿越几十万公里的太阳物质以及日地之间将近一亿五千万公里的距离， 才能进入我们的探测器。 而描述这一传播环节的是一个有关粒子物理的模型， 那也是一种在学术界有着广泛共识的模型， 叫做粒子物理标准模型 (standard model of particle physics)。 这一模型对目前已知的所有基本粒子及其相互作用作了相当精密的描述。 因此， 与太阳中微子问题有关的理论其实有两个部分， 它们拥有一个共同的名字叫做 “标准模型”。 而所谓 “哪部分理论出了问题”， 归根到底是两个标准模型之争， 即标准太阳模型 vs 粒子物理标准模型。

这两个标准模型哪个更可靠呢？ 在谜底揭晓之前如果让物理学家们押宝的话， 我想绝大多数物理学家会把宝压在粒子物理标准模型上[注一]。 因为这个模型自二十世纪六十年代后期建立以来， 已经得到了无数的检验， 其中包括所预言的新粒子及其参数得到证实那样堪称经典的检验。 粒子物理标准模型所描述的虽然是肉眼无法看见的微观世界， 但对物理学家们来说， 实验室里数不胜数的粒子反应图片无时无刻不在述说它的实在性。 与之相比， 标准太阳模型所受到的检验却少得可怜， 其中被寄予厚望的太阳中微子实验偏偏又得出了令人尴尬的结果。 而且与粒子物理标准模型所描述的相对纯粹的微观世界不同， 标准太阳模型涉及的是一个巨型天体的内部世界， 只要想想我们脚底下的地球尚且如此复杂， 我们对标准太阳模型的信心就很难不打上几分折扣。 因此直到二十世纪九十年代， 曾因研究大统一理论而闻名的美国物理学家乔治 (Howard Georgi, 1947-) 还在一篇论文中宣称太阳中微子问题与粒子物理无关， 他并且很体贴地表示： 天体物理学家们能够把太阳中微子的数目计算到只差两到三倍的程度， 就已经很了不起了。 言下之意， 实验与理论的这点出入是不足为奇的， 可以由标准太阳模型负全责， 别来烦粒子物理。 另一位知名的美国物理学家德雷尔 (Sidney Drell, 1926-) 也表示， 粒子物理标准模型已经辉煌到了难以被放弃的程度。

既然 “民意” 如此， 那我们就先考虑标准太阳模型出问题的可能性吧。 我们在第八节中提到过， 太阳核心核聚变反应的剧烈程度与太阳的核心温度有着极为敏感的依赖性。 由于太阳中微子来自于核聚变反应， 它的流量当然也与后者的剧烈程度， 从而与太阳的核心温度有着极为敏感的依赖性。 因此， 标准太阳模型出问题的最大可能性， 就是它所预言的太阳核心温度出了错。 如果太阳核心的实际温度比标准太阳模型所预言的低， 那么太阳核心核聚变反应的剧烈程度， 以及它所产生的太阳中微子的流量就会大幅降低。 计算表明， 托太阳核心温度与核聚变反应之间的敏感依赖性的福， 太阳的核心温度只要调低几个百分点， 就足以使太阳中微子的流量减少几十个百分点， 从而与观测结果定性相符。

初看起来， 这是一种很大的可能性， 因为在描述象太阳核心那样远离经验的环境时， 出现几个百分点的温度误差不仅是完全可能的， 甚至可以说是无可避免的。 但细想一下却又不然， 理由很简单： 将太阳的核心温度调低几个百分点虽然能定性地调和中微子流量的理论与观测之间的差距， 同时却也会导致太阳光度的大幅降低——因为核聚变反应的剧烈程度大幅降低了， 而这是与观测完全相悖的。

不过仅凭这一点还难不倒物理学家们， 因为有一些方案可以在调低太阳核心温度的同时维持太阳的光度不变。 这其中比较拙劣的方案是利用我们在上节中提到， 并将在后文中进一步介绍的 “由太阳核心所发射的光子要经历十几万年的漫长时间才能到达太阳表面” 这一特点。 利用这一特点， 有人提出了一个很离奇的假设， 那就是太阳的核心温度是在不久之前才突然变低的， 由此导致的效果尚未传到太阳表面， 从而尚未影响太阳光度。 这个假设的拙劣之处是显而易见的， 因为它是为解决太阳中微子问题而特意炮制的， 而且它甚至比太阳中微子问题更难理解。 这种用一个比原始问题更难理解的假设来解决问题的做法几乎是与科学的宗旨背道而驰的。 连这样的 “天方夜谭” 都被提出来了， 可见人们是多么希望把问题归咎于标准太阳模型。

不过， 修改标准太阳模型的方案也并不都是拙劣的。 相对高明的方案是在调低太阳核心温度的同时扩大核反应区域的范围， 以抵消核反应剧烈程度降低造成的影响， 从而达到维持光度不变的目的。 但不幸的是， 我们在上节中已经介绍过， 太阳中微子的总流量是与太阳光度直接对应的。 一旦维持太阳光度不变， 也就维持了太阳中微子的总流量不变。 因此这种方案至多能解释某些特定能量范围——比如高能区——内的太阳中微子问题 (因为核心温度的调低会影响各种核聚变反应的相对比例， 从而影响不同能量中微子的相对比例——尤其是减少高能中微子的数量)。 但随着实验结果所涵盖的能量范围越来越宽， 太阳中微子问题早已不仅仅是特定能量范围内的问题， 而变成了总流量上的问题， 这就超出了维持太阳光度不变的那些方案的解释范围[注二]。

但对修改标准太阳模型的方案构成更沉重打击的， 则是我们在后文中将要介绍的所谓日震学研究， 那种研究证实了标准太阳模型的许多细节， 从而为修改标准太阳模型的努力设置了相当苛刻的限制。 事实上， 标准太阳模型看似 “五大三粗”， 只用寥寥几个方程式来描述整个太阳的基本特征， 但它对物理原理的运用却是相当缜密的， 甚至达到了 “牵一发动全身” 的精密性。 比如要想调低太阳的核心温度， 就必须同时调节太阳内部重元素比例之类的参数， 那些参数有不少是可以用日震学手段进行检验的， 而检验的结果几乎无一例外地支持了标准太阳模型。

除日震学研究外， 对标准太阳模型的支持还来自另外一个领域， 那个领域不是别的， 正是把怀疑目光引向标准太阳模型的太阳中微子研究本身。 我们说过， 标准太阳模型出问题的最大可能性， 就是它所预言的太阳核心温度出了错。 之所以这么说， 首要原因当然是太阳核心温度与中微子流量有着极为敏感的依赖性， 从而在表观上具备解决太阳中微子问题的潜力， 但另一方面也是因为我们无法直接测定太阳核心温度， 从而无法进行实验裁决。

实验鞭长莫及的地方， 往往就是理论遍地开花的地方。

但细心的读者也许还记得， 我们在上节中曾经把中微子表彰为 “取代光子成为我们窥视太阳核心奥秘的工具”。 既然给予了这么高的荣誉， 我们就要问： 在它让我们窥视到的 “太阳核心奥秘” 中， 是否包括了太阳的核心温度呢？ 很幸运， 答案是肯定的， 就像光谱可以告诉我们发光体的温度一样， 太阳中微子的能谱也可以带给我们有关太阳核心温度的信息。 这一答案， 加上象神岡探测器那样能够测定中微子能量的探测器的问世， 使我们可以通过太阳中微子的能谱来推算太阳的核心温度。 而推算的结果与标准太阳模型的符合程度远高于修改方案。

自此， 修改太阳模型的努力算是撞上了南墙， 虽不能说从此无人问津， 但希望已变得很渺茫了。 而太阳中微子问题也确实可以定性为失踪案了， 因为标准太阳模型既然没有问题， 就说明太阳中微子的流量确实要比实验探测到的大， 一部分太阳中微子确实失踪了。

现在留给我们的就只剩一条路了： 修改粒子物理标准模型。 粒子物理标准模型再是 “辉煌到了难以被放弃的程度”， 到了这个地步， 我们也只得在它头上动土了。 不过在动土之前， 我们先要对失踪者——中微子——的家世做一个彻查。 据我们目前掌握的情况， 中微子家族共有三兄弟， 个个都是偷运能量的好手。 我们前面所说的中微子只是最早落网的那个， 它的全名叫做电子中微子 (electron neutrino)。 除电子中微子外， 人们在 1962 年和 2000 年又先后发现了另外两种中微子， 分别叫做 μ 子中微子 (muon neutrino) 和 τ 子中微子 (tau neutrino)[注三]。 这种三兄弟结构为从修改粒子物理标准模型角度解决太阳中微子问题提供了一条重要思路， 叫做中微子振荡 (neutrino oscillation)。

什么是中微子振荡呢？ 简单地讲就是中微子三兄弟之间的相互转变——比如电子中微子变为 μ 子中微子， μ 子中微子变为 τ 子中微子等。 这种转变可以循环往复， 因而称之为振荡。 中微子振荡之所以有可能解决太阳中微子问题， 是因为太阳核心所产生的全都是电子中微子， 而我们在上节中介绍过的那些中微子探测器所探测的也主要是电子中微子[注四]。 因此假如来自太阳核心的电子中微子在飞往地球的途中有一部分转变成了 μ 子中微子或 τ 子中微子， 就会逃过探测器的检验， 而造成中微子失踪的假象。 这就好比一位用几个马甲 (笔名) 轮流发贴的网民， 从 IP 地址上显示他一共发了一百个贴子， 但你若只搜索其中一个马甲， 就只能搜到一部分贴子。

有关中微子振荡的想法有着不短的历史。 事实上， 早在中微子的兄弟被发现之前， 也早在太阳中微子问题出现之前， 就有人提出了中微子振荡的想法， 此人就是我们在上节中提到过的那位出生于意大利的核物理学家庞蒂科夫。 1958 年， 庞蒂科夫提出了中微子和反中微子相互振荡的可能性[注五]。 在 μ 子中微子被发现之后， 1967 年， 他与时俱进地修改了自己的猜测， 提出电子中微子与 μ 子中微子也有可能发生振荡。 从某种意义上讲， 他的这些猜测可以说是预言了太阳中微子问题的出现， 因为中微子振荡必然会导致只对电子中微子敏感的中微子探测器无法探测到全部中微子。 当戴维斯的 Homestake 实验让太阳中微子问题粉墨登场后， 庞蒂科夫又与俄国物理学家格里波夫 (Vladimir Gribov, 1930-1997) 一起， 在第一时间重申了自己的猜测。

当然， 通过修改粒子物理标准模型来解决太阳中微子问题的方案并非只有中微子振荡这一种， 只不过其它方案都很短命， 比如有一种方案叫做中微子衰变。 它认为中微子之所以失踪， 不是因为披上了其它马甲， 而是半路夭折了。 在粒子物理中， 粒子的夭折有一个很文雅的名字叫衰变[注六]。 可惜的是， 这种方案在 1987 年遭到了判决性的否证。 那一年， 包括神岡探测器在内的几组中微子探测器观测到了一批来自大麦哲伦星云 (Large Magellanic Cloud) 中的一次超新星爆发——即著名的超新星 1987A——的反中微子。 那些反中微子经过了近 17 万年的长途跋涉才抵达地球。 由于粒子与反粒子有着相同的寿命， 如果中微子在从太阳到地球的区区 8 分 20 秒时间里就会夭折掉一部分， 那我们是绝不可能观测到那么多来自超新星 1987A 的反中微子的。 因此， 中微子即便会夭折， 也绝不可能那么快地夭折。 既然中微子不能那么快地夭折， 那就只好让方案本身夭折了。

真正有希望的还是中微子振荡。

那么， 中微子振荡需要从哪里入手修改粒子物理标准模型呢？ 是从添加中微子的质量入手[注七]。 在粒子物理标准模型中， 所有中微子都是无质量的。 在理论上可以证明， 如果所有中微子都是无质量的， 中微子振荡就不可能发生[注八]。 因此， 要想有中微子振荡， 就必须从添加中微子质量入手， 修改粒子物理标准模型。

接下来我们想知道的是： 在中微子振荡中， 中微子相互转变的概率满足什么样的规律？ 因为只有知道了这一点， 才能与观测相比较。 简单的理论分析表明， 中微子相互转变的概率与中微子的质量、 能量、 相互间的混合， 以及飞行距离等诸多因素都有关联[注九]。 这些关联不仅为拟合观测数据提供了许多可调节的参数， 而且也定性地解释了不同能量的中微子有不同的失踪比例这一现象。 就凭这两点， 它已经比我们前面提到过的那些方案更有希望。

可惜那只是表面现象。

后来当人们更细致地研究了中微子振荡之后， 却发现了一些问题。 比如计算表明， 要想用中微子振荡来解释观测结果， 需要假定中微子的某些参数与象日地距离那样与中微子风马牛不相及的参数之间满足一定的巧合关系。 这种有赖于巧合的解释是物理学家们素来不喜欢的， 因此是一个不好的兆头。 如果说这还只是口味问题， 那另外几个问题可就都是 “你死我活” 的级别了。 比如计算表明， 由中微子振荡所导致的中微子失踪率应该呈现明显的季节变化 (这是因为中微子相互转变的概率与飞行距离有关， 而在不同季节里， 日地距离是不同的)， 但观测却并未发现与理论预期相一致的变化。 此外， 中微子相互转变的概率与能量有关这一特点虽然定性地符合不同能量的中微子有不同失踪比例这一特点， 但在定量上， 观测所显示的失踪率与能量的相关性——尤其在高能区——却明显小于理论的预期。

这样一来， 情况就又有些不妙了。 如果连中微子振荡也行不通， 那岂不是连最后一条路也要变成绝路？ 幸运的是， 在中微子振荡中还有一个重要因素起到了 “挽狂澜于既倒” 的作用， 那就是物质对中微子振荡的影响。 虽然没有明说， 我们前面提到的中微子振荡其实都是指真空中的振荡， 但事实上， 太阳中微子一出世就得穿越厚达几十万公里的太阳物质， 这会对它们产生一定的影响。 有读者也许会问： 我们在上节中不是说过， 太阳物质对中微子来说几乎是透明的吗？ 是的， 我们曾经说过。 但透明不等于完全没有影响， 玻璃对光来说也是透明的， 却可以导致各种光学效应。 太阳物质对于中微子来说也是如此， 虽然透明， 但会有一定的影响——尤其是对高能中微子会有一定的影响。 而且更重要的是， 太阳物质对不同类型的中微子有着不同的影响， 对电子中微子的影响要比对 μ 子中微子和 τ 子中微子大， 由此导致的后果是对中微子振荡——尤其是对高能中微子的振荡——产生影响。 这种影响早在 1978 年， 就由美国物理学家沃芬斯坦 (Lincoln Wolfenstein, 1923-) 研究过。 1985 年， 俄国物理学家米克耶夫 (Stanislav Mikheyev) 和斯米诺夫 (Alexei Smirnov, 1951-) 推进了这一研究， 并得到了一些重要结果。 这种物质对中微子振荡的影响因此而被冠以他们三人的姓氏首字母， 称为 MSW 效应 (MSW effect)。 后来的定量计算表明， 考虑了 MSW 效应后的中微子振荡与所有的太阳中微子观测都相容， 并且是唯一一种与所有观测都相容的解释。

不过， 中微子振荡作为太阳中微子问题的正解， 它的真正确立则是建立在更直接的实验裁决之上的。 这种裁决首先来自日本的超级神岡探测器。 1998 年， 超级神岡探测器通过检测宇宙线在地球大气层中产生的 μ 子中微子与电子中微子的相对数目， 首次直接证实了中微子振荡的存在[注十]。 在太阳中微子研究中， 神岡系列探测器可谓居功至伟， 占据了不止一项第一。 除首次直接证实中微子振荡外， 我们在上节中提到的它能测定中微子入射方向这一特点 (它对中微子振荡的证实也有赖于这一特点)， 还使它成为了第一个直接证实太阳中微子来自太阳方向的探测器 (此前的其它探测器都只能从数量上间接推断中微子来自太阳， 因为其它来源都不可能如此巨大)。 而在前面提到的对来自超新星 1987A 的反中微子的探测中， 它立的也是头功。

超级神岡探测器虽然证实了中微子振荡的存在， 但对于解决太阳中微子问题来说却还不够一锤定音， 因为它在证实中微子振荡时所观测的并不是太阳中微子， 而是能量远高于太阳中微子的由宇宙线产生的中微子。

那么， 对太阳中微子问题最一锤定音的裁决来自哪里呢？ 来自加拿大的萨德伯利中微子观测台 (Sudbury Neutrino Observatory - 简称 SNO)。 这座位于等效水深 6000 米处的观测台所用的观测物质是 1000 吨重水。 这 “重水” 与超级神岡探测器所用的 “水” 虽只有一字之差， 对于太阳中微子探测来说却有天壤之别。 我们知道， 水分子是由一个氧原子与两个氢原子组成的， 而重水 “重” 在哪里呢？ 就 “重” 在那两个氢原子被换成了氘原子上。 氘原子的原子核是由一个质子和一个中子组成的。 当中微子与那样的原子核相遇时， 有一定的概率会发生所谓的中性流反应 (neutral current reaction)， 其结果是 “棒打鸳鸯”——将氘核拆散成单独的质子和中子。 与其它探测器所依赖的反应不同， 这种中性流反应对三种中微子是完全一视同仁的。 因此无论中微子披的是什么马甲， 都能被检测到。 更妙的是， 除中性流反应外， 中微子与重水还可以发生其它类型的反应， 那些反应则与其它探测器一样， 只对电子中微子敏感[注十一]。 因此， 萨德伯利中微子观测台可以在测定中微子总流量的同时确定电子中微子的比例， 从而既验证标准太阳模型的预言， 又检验中微子振荡。



【SNO 探测器】

2001 年， 萨德伯利中微子观测台发布了观测结果， 非常漂亮地显示出中微子的总流量在实验精度范围内与标准太阳模型相符， 而电子中微子所占的比例， 则与中微子振荡所预期的一致。

这样， 太阳中微子之谜就被解开了， 谜底就是中微子振荡。 在标准太阳模型与粒子物理标准模型的对决中， 居然是标准太阳模型取得了胜利， 这让很多人跌破了眼睛。 此后， 人们又通过大量的其它实验 (包括使用来自加速器及核反应堆的中微子) 进一步证实了中微子振荡。 经过如此曲折的努力， 我们终于完成了第八节末尾所说的为恒星核聚变理论收集进一步证据的工作， 使这一理论得到了牢不可破的确立。

2002 年， 那位半个世纪前被审稿人揶揄过的 “站在山顶上， 用自己的手去碰月亮” 的太阳中微子探测先驱戴维斯以 88 岁的高龄， 与超级神岡探测器的 “头领”， 日本物理学家小柴昌俊 (Masatoshi Koshiba, 1926-) 一同荣获了诺贝尔物理学奖。

2004 年， 戴维斯当年的合作者、 太阳模型专家巴克尔撰写了一篇评述太阳中微子问题的文章。 在文章的末尾， 他这样写道：

当我回顾过去四十年在太阳中微子研究领域所取得的成就时， 我感到了惊讶。 由数以千计的物理学家、 化学家、 天文学家和工程师组成的国际团队用他们的合作， 展示了通过统计地下矿井里一个盛满纯净液体的游泳池里的放射性原子的数目， 就能告诉我们有关太阳核心的重要事实， 以及被称为中微子的奇异基本粒子的性质。 若非亲身经历了太阳中微子的传奇， 这对我来说将会是难以置信的。

一段传奇虽已落幕， 但围绕它的谜底却有许多新的问题有待探索， 比如中微子的质量从何而来？ 中微子的质量与电子等粒子的质量是否是同一类型的？ 等等。 一个小小的中微子尚且有如此多的奥秘， 更何况太阳呢？ 因此大家不要离开， 我们的太阳故事还将继续。

注释

研究太阳中微子问题涉及理论、 实验及观测等诸多方面， 参与者来自许许多多不同领域， 但为行文简洁起见， 本节将把参与者统称为 “物理学家”， 这里预先向其它各 “家” 致以歉意。 在这里顺便提一下， 在调低太阳核心温度的同时除了要维持太阳的光度外， 还必须维持它的核心压强， 因为那是抵抗引力坍缩的资本。 为了维持太阳的核心压强， 物理学家们也引进了一些假设， 比如假设太阳核心具有速度惊人的自转， 从而能用离心力来抵御一部分引力； 或假设太阳核心存在强度惊人的磁场， 从而能用磁场压来抵御一部分引力。 这些假设各有各的问题， 比如核心的高速旋转会使太阳的整体形状及引力四极矩发生变化， 与观测矛盾； 而太阳核心的强磁场即便存在， 也会很快衰减。 这三种中微子分别用电子、 μ 子及 τ 子这三种带电轻子来命名不是偶然的， 它们之间的一一对应是粒子物理标准模型的基本特征之一。 确切地讲， 在太阳中微子的能量范围内， Homestake、 SAGE 及 GALLEX 探测器都只能探测电子中微子， 神岡及超级神岡探测器则有一定的能力探测 μ 子中微子和 τ 子中微子， 但敏感度只有探测电子中微子的 15% 左右。 读者也许会觉得奇怪， 在太阳中微子问题尚未出现， 实验上又还没发现第二种中微子的年代， 庞蒂科夫同学为什么要提出中微子振荡呢？ 那是因为不久之前， 人们刚刚发现了中性 K 介子系统中的粒子振荡现象。 由于中微子也是中性的， 因而庞特考沃猜测它也具有类似性质。 有读者也许会问： 中微子已经很 “微” 了， 它还能衰变成什么呢？ 一般认为， 那可能会是标准模型中不存在的所谓右旋中微子或左旋反中微子。 那种粒子比中微子更不像话， 连弱相互作用都不参与， 因而被称为惰性中微子 (sterile neutrino)。 不过， 惰性中微子若是存在， 其质量有可能相当大， 在有些模型中甚至可以达到大统一能标 (1015GeV) 的量级， 比质子还重一千万亿倍。 因此， 以它为衰变产物的中微子衰变其实在理论上就不太可能。 若无特殊说明， 当我们提到微观粒子的质量时， 指的都是静质量。 这是因为， 我们通常所说的电子中微子、 μ 子中微子和 τ 子中微子都是依据它们参与弱相互作用的方式来区分的， 用物理学家们的术语来说， 是所谓的弱本征态。 在中微子全都无质量的情形下， 那就是区分中微子的唯一方式。 但假如中微子有质量， 我们就可以引进另一种区分方法， 即按照质量来区分。 那样区分出来的中微子状态被称为质量本征态。 一般来说， 弱本征态与质量本征态是彼此混合但互不相同的， 通俗地讲就是 “你中有我， 我中有你”， 这正是中微子振荡的温床。 因此中微子振荡只有在中微子有质量 (并且质量彼此不同) 时才会发生。 确切地说， 是与中微子质量本征值的平方差、 中微子的能量、 中微子弱本征态与质量本征态之间的混合矩阵 (mixing matrix)， 以及中微子的飞行距离等因素有关。 超级神岡探测器所检测的是宇宙线在地球大气层中产生的 μ 子中微子与电子中微子的相对数目随中微子入射方向的变化。 由于入射方向不同的中微子从产生到被检测之间的飞行距离各不相同 (两个极端情形是： 自上而下入射的中微子的飞行距离约为大气层的厚度， 即十几公里； 自下而上的中微子的飞行距离则为整个地球的直径， 即约 13000 公里)， 如果存在中微子振荡， 它们应该有不同的转变概率。 通过研究这种转变概率与飞行距离的关联， 物理学家们不仅证实了中微子的振荡， 而且对某些中微子参数进行了估计。 具体地讲， 除中性流反应外， 中微子与重水之间还可以发生另外两类反应： 一类是所谓的带电流反应 (charged current reaction)， 它使氘核分裂为两个质子 (同时放出一个电子以平衡电荷)， 在太阳中微子的能量范围内， 这种反应只能由电子中微子诱发， 从而只能检测电子中微子。 另一类则是与神岡及超级神岡探测器所用相同的反应， 即中微子与电子的碰撞， 它对电子中微子最敏感， 但同时也有 15% 左右的相对敏感度检测到 μ 子中微子和 τ 子中微子。

二零一零年十月一日写于纽约

二零一零年十月一日发表于本站

http://www.61k.com

太阳的故事 (十一) 光子大逃亡

本文作者：卢 昌海

在前面几节中， 我们介绍了发生在太阳核心区里的太阳能量产生机制。 这一机制不仅在理论上可行， 而且经过对太阳中微子的细心探测， 以及对太阳中微子问题的艰辛求解， 在观测上也得到了很漂亮的确立。 从某种意义上讲， 隐藏在太阳最深处的那个最远离经验的 “恐怖核心”， 反而可以说是成为了整个太阳结构中被我们了解得最可靠的部分。

如果说迄今为止我们的太阳故事所展现的大都是太阳研究中的坚实大地——那些被观测或实验牢牢确立了的事实或理论——的话， 那么从本节开始， 我们将会更多地去欣赏太阳研究中的绚烂天空——那些尚在云端里的谜团。 我们将会看到， 那样的谜团简直是层出不穷， 而且在绝大多数谜团面前， 我们再也没有象解决太阳能量产生机制或太阳中微子问题那样的好运气了， 因为那些谜团中的绝大多数直到今天依然是未解之谜。 当然， 这本身未尝就不是一种好运气， 尤其是对于正在从事或有志于从事太阳研究的人来说更是如此， 因为生在一个有许多未解之谜可以探索的时代里， 要远比生活在一个只能在 “小数点后第六位数字” 上做文章的时代幸运得多。

好了， 现在继续我们的太阳故事。

读者们想必还记得， 在我们的注意力被喧宾夺主的中微子吸引走之前， 我们是在谈论与阳光有关的话题， 比如太阳的光谱、太阳的光度、太阳为什么会发光等。 现在我们要把注意力转回到阳光上来——毕竟， 那是太阳之所以成为太阳的最重要特征， 也是它对我们最至关重要的东西。 我们已经知道， 阳光的巨大能量来源于发生在太阳核心区的核聚变反应。 那个核心区有多大呢？ 细致的研究表明， 它从 “ground zero” 算起， 向外延伸到大约四分之一个太阳半径——即 17 万公里——处。 从体积上讲， 这一区域在整个太阳中所占比例不到 2%， 但由于密度超高， 占太阳质量的比例却达到一半左右。 在这一区域的边缘， 太阳物质的密度从最中心的 160 克/厘米3左右降到了约 20 克/厘米3(略高于黄金的密度)， 温度则降到了 800 万度左右。 那样的环境虽然仍很恐怖， 对于氢核聚变成氦核的核聚变反应来说却已低得有些勉强了， 在那以外， 核聚变反应就基本绝迹了[注一]。

但这个边缘对于太阳能量的主要载体——诞生于恐怖核心的无数光子来说， 却是一段新的征程——一条逃亡之路——的开始， 它们将用十几万年的漫长时间， 穿越厚达几十万公里的太阳物质， 把巨大的能量带出去， 让 “红星” 照耀四方。

与中微子的 “挥一挥衣袖， 不带走一片云彩” 相比， 光子的逃亡之路可就艰辛多了。 原因很简单， 因为光子会参与电磁相互作用——即与带电粒子发生相互作用。 而更糟糕的是， 在太阳的恶劣环境下， 物质粒子间存在着极为猛烈的相互碰撞， 其结果是 “鸡飞蛋打”——几乎每个原子都会被碰掉一些电子。 那些被碰掉的电子当然全都是带电粒子， 而那些丢了电子的原子——其中大多数已经变成了一丝不挂的原子核——也都是带电粒子。 因此太阳物质几乎是清一色由带电粒子组成的， 是所谓的等离子体 (plasma)。 光子穿越这种到处都是带电粒子的物质时， 就象女人穿越到处都是化妆品专柜的购物城， 将会无可避免地受到巨大干扰。

但不管怎么干扰， 光子终究是要逃出去的， 否则我们就看不到太阳了。 我们首先要问的是： 在带电粒子的重重包围之下， 那些光子究竟是以何种方式完成胜利大逃亡的庄严任务的？

解决这个问题的思路并不深奥， 甚至在中学物理中就已经有了， 因为所谓的光子大逃亡， 归根到底是一个能量传输问题， 即把太阳核心所产生的能量传输出去。 而能量的传输有三种众所周知的方式： 传导 (conduction)、 对流 (convection) 和辐射 (radiation)。 从微观上讲， 这三种传输方式的差别在于： 传导主要是通过物质粒子间的相互碰撞来传输能量， 但那些物质粒子本身却并不参与大范围的运动， 我们做饭时热量通过锅底传到锅内所用的就是这种传输方式； 对流主要是通过物质粒子本身的大范围运动来传输能量； 我们做饭时， 沸腾的水就是用这种方式在传输能量； 而辐射则主要是通过光子本身来传输能量， 我们围坐在一个火炉旁所感受到的 “温暖” 就是用这种方式传输过来的能量。

在这三种能量传输方式中， 传导在气态物质中通常起不到主要作用 (请读者想一想这是为什么？)， 象太阳那样的巨型 “气球” 也不例外， 因此这一选项可以被排除掉。 这样一来， 我们就只剩下了两个选项： 对流和辐射。 一道选择题只有两个选项， 这运气看来很不错， 因为就算瞎蒙也该有一半的可能性答对。

但有关太阳的这道选择题却是一个例外。

对于这道选择题， 早年的天文学家们曾经作出过自己的选择， 那就是对流， 理由是我们所熟悉的唯一一种大范围气态物质——地球大气——就是用这种方式来传输能量的。

可惜那是一个错误选择。

这一选择在 1906 年遭到了德国物理学家史瓦西 (Karl Schwarzschild, 1873-1916) 的反对。 史瓦西认为对于象太阳内部那样与地球大气截然不同的物理环境， 很可能存在一种具有太阳特色的能量传输方式， 而不能简单地套用地球大气的经验。 作为对这一观点的论述， 他提出了一种判断太阳内部是否会出现对流的巧妙方法， 那就是从理论上分析一小团太阳物质的运动， 看它能否演变成对流。

具体地说， 史瓦西从理论上考察了一小团由于偶然原因而变得比周围环境稍热的太阳物质。 由于热胀冷缩的缘故， 那一小团物质的体积会稍稍膨胀， 密度则会稍稍降低， 由此产生的后果是在周围物质的浮力作用下上升。 但在上升的过程中， 由于周围太阳物质的压强在变小 (因为太阳物质的压强是越往上就越小——请读者想一想这是为什么？)， 它会发生进一步的膨胀， 这种膨胀会使它的温度降低[注二]。 另一方面， 随着这一小团物质的上升， 它周围环境的温度也在降低， 因为太阳内部物质的平均温度也是越往上 (即越远离核心区) 就越低。 既然那一小团物质与它周围环境的温度都在降低， 显然就出现了哪个温度降低得更快的问题。 如果是周围环境的温度降低得更快， 那么该小团物质将会在上升过程中维持比周围环境更热的特点， 从而持续上升， 那样就会产生对流。 反之则它的上升势头会因温度降低得比周围环境更快而终止， 并在重力的作用下转为下降， 那样就不会产生对流。

这样， 史瓦西就提出了一个分析太阳内部能否产生对流的判据， 即通过比较太阳内部物质的平均温度变化与一小团特定物质在上升过程中的温度变化， 来判断能否产生对流。 这一判据被称为史瓦西判据 (Schwarzschild criterion)。 利用这一判据， 史瓦西推翻了前人的选择， 代之以自己的选择， 那就是辐射。

可惜那也是一个错误选择。

读者可能会纳闷： 一道只有两个选项的选择题， 怎么会两个选项都错误呢？ 原因很简单： 因为两个选项都不完全， 都只在一定区域内才适用， 把无论哪个选项当作完整答案都是错误的。 那么， 怎样才能得到完整答案呢？ 只有一个办法， 那就是计算。 既然史瓦西给出了分析太阳内部能否产生对流的判据， 那我们就可以——而且必须——通过计算来作出判断。 这种计算所依据的就是我们在前几节中已经多次提到过的标准太阳模型。 那个模型是建立在一系列很基本的物理原理——比如能量的守恒、 压强的平衡等——的基础之上的， 虽然算不上精细， 但以粗线条而论却有很大的可靠性。 史瓦西本人虽然由于他那个时代的知识所限而没能得到正确结论， 但我们这些 “站在巨人肩上” 的幸运儿却毫无疑问可以做得比他更好一些。

那么利用标准太阳模型所做的计算给出了怎样的答案呢？ 那答案就是： 太阳内部的能量传输方式既不是单纯的对流也不是单纯的辐射， 而是在不同区域内有不同的主导方式。 具体地说， 在从太阳核心区的边缘 (即太阳半径的四分之一处) 到太阳半径的 70% 处 (即距离太阳中心约 49 万公里处) 的厚度约 32 万公里的物质层内， 史瓦西判据得不到满足， 能量的传输以辐射为主。 这一层因此而被称为辐射区 (radiative zone)， 它占太阳总体积和总质量的比例分别约为 32% 和 48%。 在辐射区的外部边缘， 太阳物质的温度降到了 “只有” 200 万度， 密度则降到了 0.2 克/厘米3(相当于水的密度的五分之一)。 在那以外直到太阳表面的厚度约 20 万公里的物质层内[注三]， 史瓦西判据得到满足， 能量的传输方式转为以对流为主， 这一层因此而被称为对流区 (convective zone)， 它约占太阳总体积的 66%， 但由于物质密度很低， 在太阳总质量中却只占了 2% 左右 (仍相当于 6600 个地球的质量)。



【太阳的内部结构】

有了这样的大致图像， 现在我们可以来谈谈光子大逃亡的具体过程了。 由太阳核心核聚变反应所产生的光子大都 “膘肥体壮” (满载着能量)， 比如第一类质子-质子链所产生的光子的能量在百万电子伏特 (MeV) 量级上， 属于伽马射线 (gamma ray) 的范围[注四]。 如果它们在逃往时有象中微子那样的能耐， 接下来的故事将只需两秒钟就能完成， 不过那样的话， 我们也就不可能在这里读这篇文章了， 因为那样的话， 地球将会沐浴在致命的伽马射线之中， 生命的产生几乎是不可能的。 幸运的是， 如前所述， 光子由于会参与电磁相互作用， 从而在本质上是等离子体的太阳物质中无可避免地会受到巨大阻挠。 计算表明， 在太阳辐射区中， 可怜的光子平均飞行不到一毫米就会遭遇 “灭顶之灾”——被带电粒子所吸收。 不过带电粒子的胃口也很有限， 并无能力把一个高能光子单独 “消化” 掉。 事实上， 它们 “吞下” 光子后一方面会通过碰撞把一部分能量分给其它带电粒子， 另一方面会几乎立刻就重新吐出一个或多个光子。 那些浴火重生的新光子在能量和运动方向上都有很大的随机性， 有些甚至 “天堂有路它不走， 地狱无门自来投”——重新向着 “地狱” (核反应区) 的方向飞去。 如果我们追踪一个高能光子和它那些被吸收后重新发射出来的 “子孙后代” 的去向， 我们将会发现， 它们就像一群醉汉一样随处游荡。

不过， 如果我们更仔细地观察这群 “醉汉”， 我们又会发现一些微妙的特点。 比如当它们往太阳表面方向运动时， 平均来说会比往相反方向运动时多走一小段距离， 那是因为太阳物质的分布是越往表面方向密度越低， 因此往表面方向运动的光子在被带电粒子吸收之前就有可能运动较长的距离。 由于这个微妙的差别， 那些 “醉汉” 虽然混混噩噩， 总体上却是在缓慢地向着太阳表面方向运动着。 另一个微妙的特点是， 被带电粒子发射出来的新光子的 “诞生地” 越靠近太阳表面， 其平均能量就越低。 这是太阳物质的温度越靠近表面就越低这一特点所产生的平均意义上的影响。 因为这两个微妙特点的共同存在， 光子在辐射区中的逃往路线虽然极度曲折， 但最终的效果却是慢慢地向外逃逸， 而且在逃逸过程中逐渐 “减肥” (能量逐渐降低)。 那么， 这种逃亡生涯啥时候才是个尽头呢？ 计算表明， 一个高能光子穿越太阳辐射区平均需要 17 万年的时间[注五]， 这并不是因为光子的运动速度变慢了， 而纯粹是因为运动路线过于曲折。

在辐射区中， 由于史瓦西判据得不到满足， 太阳物质不会发生显著的对流， 因此这个区域内的太阳物质相对来说是比较宁静的。 如果我们能乘坐一艘假想的飞船缓缓穿越这一区域的话， 相对来说将不会太颠簸。 不过这种宁静在我们抵达辐射区的顶部时就开始消失了。 在那里， 由于史瓦西判据开始得到满足， 太阳物质无法继续维持大体上静态的平衡， 无时不在的温度涨落将会使得热气团上升、 “冷” 气团下降， 从而形成对流。 如果我们继续乘坐飞船的话， 滋味可就不太好受了。

细心的读者在这里可能会提出一个问题： 那就是史瓦西判据得到满足只是说明在太阳物质中会产生对流， 却并不表明对流一定会成为能量传输的主导方式， 那么在对流区里究竟是以哪一种能量传输方式为主导呢？ 答案是对流 (否则就不叫对流区了)， 因为在对流区里， 太阳物质由于温度降低而变得不那么透明了， 从而对辐射产生了抑制作用[注六]。 在对流区里， 光子携带的能量变成了热气团的内能， 随着它们的对流运动而传向太阳表面。 要说团体的力量还就是大， 气团的运动速度虽然远不能与光子相比， 但它们却不会象光子那样处处受到阻挠， 其结果是， 光子要用 17 万年的时间才能走完厚度为 32 万公里的辐射区， 对流却只需十来天的时间就能走完厚度为 20 万公里的对流区。

那么， 对流区中对流的具体形式， 即那些气团的具体运动又是怎样的呢？ 这却是一个极难回答的问题， 因为用流体力学理论所做的简单评估表明， 太阳对流区中的对流是所谓的湍流型对流 (turbulent convection)， 它作为能量传输方式是非常有效的[注七]， 但从机理上讲却复杂得令人望而生畏， 因为它涉及到一种迄今仍未被完全理解的现象——湍流 (turbulence)。 科学家们研究湍流已有上百年的历史， 却始终未能参透它的奥秘。 美国物理学家费曼 (Richard Feynman, 1918-1988) 曾把湍流称为是 “尚未解决的经典物理学问题中最重要的一个”。 而据说著名物理学家海森堡 (Werner Heisenberg, 1901-1976) 在去世前不久也曾表示， 当他见到上帝时将会问上帝两个问题： 一个是为什么会有相对论， 另一个是为什么会有湍流。 他认为上帝有可能可以回答第一个问题[注八]。

但研究太阳结构的科学家们却想要回答第二个问题。

这个愿望迄今仍未实现。 不过在长期的研究中， 科学家们发展出了一些近似理论， 其中很重要的一个近似理论是德国空气动力学家普朗特 (Ludwig Prandtl, 1875-1953) 在二十世纪二十年代提出的， 它把湍流中的流体元与分子运动论中的分子相类比， 尤其是将湍流运动中一个流体元在与其它流体元相混合之前所走过的平均距离与分子运动论中的分子平均自由程 (即分子在两次相邻碰撞之间所运动的平均距离) 相类比。 这种近似理论被称为混合程理论 (mixing length theory)。 自二十世纪三十年代开始， 德国天体物理学家比尔曼 (Ludwig Biermann, 1907-1986) 等人将这一理论运用到了研究太阳对流区的能量传输上。 二十世纪五十年代， 人们又进一步将这一理论与恒星结构模型结合起来， 使之变得更为系统。 再往后， 随着计算机技术的飞速发展， 人们开始对太阳对流区中的运动进行计算机模拟， 混合程理论在那里也得到了重要应用。 这类理论虽然明显只具有近似意义， 但迄今为止的模拟计算显示， 它可以给出定性上还算不错的结果。 这种类型的结果是目前人们对太阳对流区研究的最佳成果之一。

与深藏在太阳内部的核反应区及辐射区不同， 对流区由于一直延伸到太阳表面， 因此对这一区域的研究结果是可以与直接观测相对比的。 这就好比当我们研究一锅沸水的时候， 哪怕这水是不透明的， 我们也可以通过观察因水流翻腾而形成的表面波纹来推断水的沸腾程度及其它一些相关特征。 太阳的表面也是如此。 早在 1801 年， 英国天文学家赫歇耳(William Herschel, 1738-1822) 就在太阳表面——确切地说是在太阳大气层底部的光球层中——发现了无数形如米粒的斑点， 这种斑点被称为了米粒 (granule)——科学家们在取名字方面的想象力看来是很贫乏的。



【太阳表面的 “米粒”】

这些 “米粒” 当然只是远远看起来才象是米粒， 如果跑近了看的话， 每个的线度都有 1500 公里左右， 是面积比新疆还大的巨型结构， 只不过是放在太阳的庞大表面上， 才显得微乎其微而已。 简单的估算表明， 太阳表面足可容纳几百万个 “米粒”。 左图是一幅典型的 “米粒” 图片， 细致的观测表明， 在那些 “米粒” 中， 炽热的气体以每秒几百米的速度从明亮处升起， 并向外迸射出大量光子——它们此刻的能量已降到了可见光区附近。 由于那儿已是太阳的表面， 再没有什么东西可以有效地阻碍重获自由的光子， 它们随即以天下第一的逃命速度飞离太阳， 为历时十几万年的长征划上句号。 由于光子的逃离带走了能量， “米粒” 中的气体温度迅速下降， 并在颜色较暗的边缘部位收缩下沉。 一个 “米粒” 的典型寿命只有几分钟。

太阳表面的 “米粒” 是发生在对流区中的对流运动的体现， 这一点是毫无疑问的。 但与这种对流有关的一个插曲值得在这里介绍一下。 曾经有一段时间， 天体物理学家们普遍认为 “米粒” 以及太阳表层的对流运动是人们在流体力学中所发现的一种称为贝纳胞 (Bénard cells) 的结构在太阳上的翻版。 贝纳胞是 1900 年法国物理学家贝纳 (Henri Bénard, 1874–1939) 在自下而上加热一个液体薄层时所发现的对流形式， 它与太阳表面的 “米粒” 不仅具有外观上的相似性， 而且在生成条件上也一度被认为是相同的， 因为两者都被认为是在重力和浮力的共同作用下由对流运动产生的。



【普通流体中贝纳胞】

粗看起来， 这是一个展示不同尺度物理现象之间相似性的漂亮结果。 但这种相似性却在 1958 年遭到了严重质疑， 因为人们发现在贝纳胞的形成过程中， 一个曾经被忽略的因素——液体的表面张力——起了不可忽视的作用。 为了证实这一点， 科学家们甚至在 “阿波罗 14 号” (Apollo 14) 登月飞船的无重力环境下进行了贝纳胞实验， 结果发现在重力和浮力都不存在的环境下依然可以出现贝纳胞， 它的幕后推手是表面张力。 这一结果不仅打破了对贝纳胞的传统理解， 而且直接削弱了它与太阳 “米粒” 之间的可比性， 因为在太阳表面极端稀薄的气体环境里并不存在表面张力， 因此 “米粒” 的形成机制与贝纳胞起码是不可能完全相同的。 这段插曲是一个很好的例子， 说明在太阳物理学的研究中存在很多微妙的地方， 只有很仔细地考虑到太阳环境的特殊性， 才能避免似是而非的理解。

太阳表面的 “米粒” 除了那无数个线度约为 1500 公里的 “小” 米粒外， 二十世纪五十年代， 人们在观测太阳表面物质的速度分布时， 还发现了一种线度为 2-3 万公里的大尺度结构， 它的面积比整个地球的表面积还大， 它名字则跟 “米粒” 一样贫乏， 叫做超米粒 (supergranule)。 这种 “超米粒” 的寿命比普通 “米粒” 长得多， 可以有 1-2 天。 在太阳圆面上， 几乎每一时刻都分布着两三千个 “超米粒”。 与 “米粒” 不同的是， “超米粒” 的速度分布基本上是水平的， 无法找到象热气团上升、 “冷” 气团下沉那样简单的物理结构， 从而无法把它们与对流运动简单地联系起来。 “超米粒” 的结构和成因也因此而成为了太阳物理中的一个不解之谜。

更热闹的是， 除了 “米粒” 和 “超米粒” 外， 1981 年， 人们还发现了一种线度约几千公里， 介于 “米粒” 和 “超米粒” 之间的新型 “米粒”， 它的名字读者们一定猜到了， 就叫中米粒 (mesogranule)。 “中米粒” 的发现受到了一部分天体物理学家的欢迎， 因为早在 1961 年就有人提出过， 太阳对流区中的对流有可能具有不同的层次， “米粒” 和 “超米粒” 分别对应于其中较小和较大的层次， 但介于两者之间的层次却一直未能得到观测上的支持。 “中米粒” 的发现可以说是填补了这一空白。 但不幸的是， 这一观测与理论之间看上去很美的契合后来也遭到了质疑。 有些科学家在仔细研究了观测数据后， 认为 “中米粒” 有可能只是对太阳表面物质的速度分布进行分析时采用了不恰当的统计方法所导致的 “幽灵结构”， 它其实根本就不存在。 这方面的争议迄今仍未得到解决。

因此， 不仅 “超米粒” 是一个谜， “中米粒” 也是一个谜， 只不过前者之谜在于结构和成因， 而后者则干脆连存在性本身都是一个谜。 那么普通 “米粒” 又如何呢？ 它是唯一一种与对流运动存在明显对应的 “米粒”， 从这个意义上讲， 它是三种 “米粒” 当中被理解得最充分的一种。 但即便对于它， 也仍有很多微妙的地方有待理解， 否则人们也就不会轻易犯下将它视为贝纳胞那样的错误了。 事实上， 如果把太阳上各种主要的复杂因素——比如太阳的自转或磁场等——的影响全都考虑在内的话， 即便对于普通 “米粒” 的结构和成因， 也还有很多需要探索的地方。

现在让我们把迄今介绍过的太阳内部结构列成一个简单的表格：

区域名称范围主要现象检验方法

核心区0-17 万公里核聚变反应探测各个能区的太阳中微子

辐射区17-49 万公里以辐射为主的能量传输？

对流区49-69.5 万公里以对流为主的能量传输观测太阳表面的各种 “米粒”

这个表格最引人注目的地方想必读者们都看出来了， 那就是在辐射区的检验方法一栏中有一个问号。 其实不仅在辐射区的检验方法一栏中有一个问号， 在对流区的检验方法一栏中也起码有半个问号， 因为观测太阳表面的各种 “米粒” 虽然能告诉我们一些有关对流区的信息， 但那些信息大都局限在最靠近太阳表面的那部分对流区里， 相对于厚度达 20 万公里的整个对流区来说充其量只能算是 “皮毛”。

那么， 有没有什么手段， 能象太阳中微子带给我们核心区的信息那样， 带给我们有关对流区深处及辐射区的信息呢？

注释

当然， 太阳核心区的边界并不是一个鲜明的几何边界， 而是一个有一定厚度的渐变区域， 而且即便在这一渐变区域之外， 核聚变反应也只是少到可以忽略而并非绝对不可能。 这一点不仅适用于核心区的边界， 而且也适用于后面将要提到的任何其它区域之间的边界。 在史瓦西的分析中， 这一小团物质的上升过程被假定为是绝热的， 即与周围太阳物质之间几乎不交换热量。 这是一种近似。 在这种近似下， 膨胀会使这一小团物质的内能减少 (因为一部分内能会消耗在膨胀导致的对外做功上)， 从而使得温度降低。 另外顺便提一下， 这位史瓦西就是那位给出了广义相对论的第一个非平凡严格解——史瓦西解——的史瓦西。 需要提醒读者注意的是， 这里所说的太阳表面并不是我们肉眼所见的太阳表面， 后者——如我们将在后文中加以介绍的——其实是隶属于太阳大气层的。 人们通常把能量在 0.1 MeV 以上的光子称为伽马射线。 作为对比， 可见光光子的能量只有 2-3 eV。 熟悉布朗运动 (Brownian motion) 或随机游走 (random walk) 问题的读者可以利用本文提供的信息自己估算一下这一时间， 看能否得出数量级相近的结果。 温度降低之所以能使太阳物质变得不那么透明， 一个重要的原因是随着温度降低， 重原子核开始有机会俘获一部分电子， 这些俘获了一部分电子的重原子核吸收光子的能力比裸核大得多 (因为它们有密集的电子能级， 可以通过电子跃迁吸收光子)。 太阳物质在对流区里变得不那么透明不是偶然的， 事实上， 正是因为太阳物质变得不那么透明了， 才使得温度分布发生了新的变化， 进而使史瓦西判据得到了满足。 湍流性对流不仅是一种极为有效的能量传输方式， 而且对太阳来说还有许多其它影响， 比如能使太阳的物质均匀化， 以及能把太阳深处的重元素带到太阳表面等。 人们能够在太阳光谱中发现重元素的谱线， 在很大程度上就得益于湍流性对流的存在。 这个故事流传甚广， 但可信度不高， 八卦价值大于历史价值。

二零一零年十一月二日写于纽约

二零一零年十一月四日发表于本站

http://www.61k.com

太阳的故事 (十三) 谜团锦簇的太阳大气层

本文作者：卢 昌海

我们的太阳故事到这里已接近尾声了。 在本节中， 我们将探索太阳的最后一个组成部分： 大气层。 那是一个肉眼通常难以窥视的地方， 但利用各种仪器的帮助及日全食的机会， 天文学家们已经对它进行了颇为细致的观测。 观测的结果如何呢？ 概括地说是四个字： 谜团锦簇。 事实上， 在这个谜团锦簇的太阳大气层中， 我们将要面对的谜团可能要比在前面各节中遇到的加起来还多。 这是因为太阳大气层比太阳内部更复杂吗？ 未必。 更有可能的原因是我们对太阳大气层的观测远比对太阳内部来得细致。 有一句西方俗语说得好： 魔鬼存在于细节之中 (the devil is in the details)， 太阳大气层无疑就是一个例子。

我们在上节中已经提到过太阳大气层的某些部分。 比如厚度约 500 公里的温度最低层， 厚度约 2000 公里的色球层等。 本节的探索将从色球层开始， 因为它将带给我们第一个谜团——色球层反常高温之谜。

色球层这一名称来自希腊文词根 “chromos”， 含义是颜色 (color)。 我们在第六节中介绍过的太阳元素 “氦” 就是在色球层的光谱中被发现的。 色球层的一个很引人注目的特点， 就是一反太阳内部温度自核心向外逐层递减的趋势， 出现了外层温度比内层更高的奇怪现象， 即所谓的色球层反常高温。 这种反常高温的原因是什么呢？ 或者更具体地说， 它所需的能量从何而来呢？ 科学家们进行了长期研究， 并提出了一些可能的机制。 目前看来比较靠谱的机制主要有两种： 一种是声波加热， 另一种是阿尔文波 (Alfvén wave) 加热。

声波加热顾名思义， 就是认为色球层反常高温所需的能量来自于声波。 太阳上的声波我们在上节中曾经介绍过， 它们以太阳的肚子为谐振腔， 形成很多模式， 并且如上节的[注七]所说， 在被对流区顶部反射时会有一部分 “漏网”， 形成诸如 “五分钟振荡” 那样的大气层振荡现象。 那么， 那部分 “漏网之鱼” 的最终命运会如何呢？ 答案是： 很悲惨。 一般认为， 色球层就是它们的葬身之地， 而它们葬身之时留下的唯一 “遗产” 就是能量——维持色球层反常高温所需的能量。 这就是所谓的声波加热机制。 不过这种机制有一个显著的缺点， 那就是只在能量需求不大的色球层下部才比较有效， 在真正急需能量的色球层上部却不够 “给力”。 计算表明， 大部分声波根本没到色球层上部就 “出师未捷身先卒” 了。

那么色球层上部高温所需的能量又来自何方呢？ 一般认为， 也是来自一种波， 叫做 “阿尔文波”。 那是一种沿着下文将要介绍的太阳磁场中的所谓磁通量管 (magnetic flux tube) 传播的波， 是瑞典物理学家 提出的。 研究表明， 这种阿尔文波可以远比声波传得更高， 从而可以为色球层的上部送去 “温暖”， 这就是所谓的阿尔文波加热机制。 不过， 声波加热与阿尔文波加热这两种机制的 “高低搭配” 是否算是解决了色球层反常高温之谜呢？ 目前还没人能打保票， 因为很多细节仍有待完善。



【色球层中的 “小火舌” —— 针状物】

反常高温并不是色球层带给我们的唯一谜团， 色球层中的另一种现象也对天文学家们提出了挑战， 那就是所谓的针状物 (spicule)。 早在 1877 年， 意大利天文学家塞奇 (Angelo Secchi, 1818-1878) 就在色球层的边缘上发现了这种形如尖针的东西。 后来的观测证实， 那是一些底面积与四川省差不多大， 高度相当于几百个珠穆朗玛峰的 “小火舌”。 这样的 “小火舌” 在整个色球层中通常有六、 七万个之多， 它们的温度在一万度左右， 底部物质以每秒几十公里的速度向上升腾。 这些 “小火舌” 的成因也是一个谜团， 一般认为， 它们与 “五分钟振荡” 有着密切关系， 但很多细节同样有待完善。

不过， 我们对色球层的理解虽然是 “缺点错误在所难免”， 总体来说还算差强人意 (这个词常被误用为 “不能使人满意”， 这次是按正确的含义来用， 表示 “勉强使人满意”)。 与之相比， 色球层以上部分的麻烦可就大多了。 经过一个厚度 200 公里左右的 “薄如蝉翼” 的过渡区 (transition region)， 太阳大气层的温度剧增到了 100 万度以上。 那里便是日全食相片中最吸引眼球的东西——日冕 (corona)。 日冕这一名称的希腊文词根表示的是王冠 (crown)。 我们小时候画太阳时， 通常会画上一些象征阳光的锯齿状轮廓， 日冕就有点象那轮廓， 只是形状要复杂得多。 日冕不仅形状复杂， 其它方面也很复杂， 比如它的密度分布极不均匀， 有些地方甚至有巨大的空洞， 称为 “冕洞” (coronal hole)； 它的温度分布也同样极不均匀， 平均为 100-300 万度， 局部的低温和高温则比比皆是[注一]。

日冕给天文学家们带来的谜团是显而易见的， 那就是它为什么会有如此高的温度？ 这个谜团与色球层的反常高温之谜如出一辙， “难度系数” 却高得多。 因为声波与阿尔文波这两种为色球层送去 “温暖” 的加热机制， 对于 “高高在上” 的日冕来说， 都显得有些 “力不从心”。 这其中声波加热机制连色球层上部都难以到达， 自然就甭提了。 阿尔文波的情况要强一些， 它能为日冕提供一部分能量， 但数量却不够。 因此， 解决日冕高温之谜还需要有其它机制的加盟， 这其中比较有希望的一种机制， 是美国天体物理学家帕克 (Eugene Parker, 1927-) 在 1988 年提出的所谓 “纤耀斑” (nanoflare) 加热机制。 按照这种机制， 日冕中常常会发生微型爆炸， 即所谓的 “纤耀斑”， 这是我们将在下文中介绍的耀斑 (flare) 的 “迷你版”， 威力 “仅” 相当于几百个氢弹， 数量却很频繁， 足以为日冕送去大量 “温暖”， 甚至有可能是日冕能量的主要来源。 当然， 这后一点目前谁也说不准。 一般认为， 太阳上不同规模耀斑的数量分布与自然界的很多其它随机现象一样， 近似地满足所谓的幂律分布 (即数量与规模之间满足近似的幂函数关系)。 按照这种分布， “纤耀斑” 的存在是不成问题的， 数量也应该是比较大的， 但是否大到能为日冕提供足够能量的程度， 则与幂律的幂值有关， 人们对之尚有争议。 纤耀斑加热机制如此， 其它机制的情况也大致相若， 各有各的争议之处。 那些争议不解决， 日冕的高温之谜当然也就无法解决。

日冕不仅温度极高， 体积也极为庞大。 看过日冕相片的读者想必都对日冕的体积留有深刻印象。 从相片上看， 日冕有时能延伸到几个太阳半径处， 其体积之大甚至超过了太阳本身。 与地球大气层 (厚度约 100 公里) 的体积仅为地球体积的百分之几相比， 日冕的体积无论绝对值还是相对值都是极为巨大的。 但这是否就是太阳大气层的边缘呢？ 答案是否定的。 事实上， 早在二十世纪五十年代中期， 英国天文学家查普曼 (Sydney Chapman, 1888-1970) 就曾提出， 日冕虽然看上去只延伸到几个太阳半径处， 但如此高温的气体是不可能被禁锢在那样 “小” 的范围之内的。 据他估计， 日冕应该能一直延伸到地球轨道以外 (感兴趣的读者请思考一下， 这与地球没有被 “烤焦” 这一显而易见的经验事实是否矛盾？)。

与查普曼这一看法的提出几乎同时， 德国天文学家比尔曼 (Ludwig Biermann, 1907-1986) 也提出了一个与太阳外围有关的想法， 那就是我们如今称之为太阳风 (solar wind) 的想法。 比尔曼的想法源于一个众所周知的现象， 即彗星的尾巴——彗尾 (comet tail)——总是沿背离太阳的方向伸展的， 哪怕当彗星本身背离太阳运动时也是如此， 仿佛是被一股来自太阳的 “风” 吹起来的[注二]。

查普曼与比尔曼的想法看起来很不相同， 在空间范围上却存在巨大的重叠， 它们彼此间是否有关联呢？ 上文提到过的美国天体物理学家帕克作出了肯定的回答。 他的研究表明日冕不可能是一团宏观上静止的弥散气体， 而应该是一种向外运动的 “气流”——即 “太阳风”。 这样他就把查普曼的巨型日冕与比尔曼的太阳风联系了起来， 他并且为太阳风构筑了一个具体的模型。 有意思的是， 帕克这项如今被视为太阳风研究的开山之作的重要研究， 在当年却遭到了审稿人的拒绝， 后来亏得著名美籍印度裔天体物理学家钱德拉塞卡 (Subrahmanyan Chandrasekhar, 1910-1995) 的慧眼相识， 才得以发表。

有关太阳风的猜测很快就得到了观测证实。 自二十世纪五十年代末起， 苏联的 “月球” (Lunar) 系列航天器、 “金星一号” (Venera 1) 行星探测器， 以及美国的 “水手二号” (Mariner 2) 行星探测器都先后观测到了太阳风[注三]。 如今我们知道， 太阳风是太阳大气层外围的一种相当显著的现象， 每秒钟从太阳上带走将近 200 万吨的物质。 当然， 这一乍看起来很惊人的数量相对于太阳的巨大质量来说只是 “毛毛雨” (感兴趣的读者可以利用本系列提供的数据， 估算一下这种 “毛毛雨” 可以 “下” 多少年)。 太阳风除了造成彗尾的 “轻舞飞扬” 外， 更显著的结果是在太阳周围的星际介质中 “吹泡泡”， 被它吹出的泡泡称为 “日球层” (heliosphere)， 其边缘通常被广义地视为是太阳大气层的边缘。 那么这个边缘究竟在哪里呢？ 一般认为， 是在离太阳 100-200 天文单位 (即 150-300 亿公里) 处。 这个距离远远超过了所有太阳系已知行星的轨道半径， 因此从某种意义上讲， 我们一直都生活在太阳的大气层中——不仅我们如此， 所有已知的太阳系行星都是如此， 真所谓 “普天之下， 莫非王土”[注四]。

作为谜团锦簇的太阳大气层的成员， 色球层和日冕都给天文学家们出了难题， 太阳风也不例外。 迄今为止， 人们尚未找到一个能全面描述太阳风特征的模型。 观测表明， 太阳风的 “风速” 约在每秒 200-800 公里之间。 其中 “风速” 在每秒 400 公里以下的被称为慢太阳风 (slow solar wind)， “风速” 在每秒 400 公里以上的则被称为快太阳风 (fast solar wind)。 太阳风模型必须解释， 却迄今尚不能给出满意解释的一个老大难问题， 就是这两者——尤其是快太阳风——的起源。 一般认为， 快太阳风粒子的起源需要一个合适的加速机制， 这种机制与日冕的加热机制很可能存在密切关系， 甚至有可能是同源的 (比如阿尔文波有可能对两者都起着重要作用)， 但具体如何， 还有待进一步研究。

以上就是对太阳大气层各主要成员的大致罗列。 如果小结一下的话， 那么太阳大气层底部有一个很 “凉快” 薄层叫做温度最低层， 自那以上温度不降反升， 在温度不算太高的色球层中， 有几万个底面积 “只有” 四川省那么大， 高度 “只有” 珠穆朗玛峰的几百倍那么高的 “小火舌”。 在那以上， 经过一个 “薄如蝉翼” 的过渡区， 是体积大得惊人的日冕， 那里的物质极度稀薄， 温度却高得邪乎， 还时不时地有几百个氢弹炸来炸去。 再往外， 则是以比火箭还快几十倍的速度劲吹到几百亿公里外的太阳风。 这就是太阳大气层的日常景观， 这种景观有一个很文雅的名称， 叫做 “宁静太阳” (quiet sun) ——别揉眼睛， 您没看错， 是叫做 “宁静太阳”。

“宁静” 的意思就是没什么 “活动”。 “宁静” 时尚且如此， 那么有 “活动” 时又会怎样呢？

太阳大气层中的各种 “活动” 有一个很没创意的共同名字， 就叫 “太阳活动” (我们在上节末尾已经提到过这一名称)。 在太阳活动中， 资格最老的是黑子。 早在两千多年前， 中国古籍中就出现了有关黑子的记载， 西方人记载黑子也有一千多年的历史。 不过黑子的发现虽早， 长期以来却很少有人认清它的真面目， 而常常把它当成所谓的行星凌日 (planetary transit)， 即行星从太阳前面经过。 直到十七世纪初， 才由伽利略明确提出黑子是太阳自身的 “污点”。 这个看似稀松平常的结论， 对当时的 “天贵地贱” 观念给予了当头一击 (参阅第三节)[注五]。 不仅如此， 这一结论还给另外一些人造成了困扰， 比如我们在第八节中提到过的英国天文学家赫歇耳， 就曾被黑子的 “黑色” 所误导， 而以为太阳表面很凉快， 甚至有可能存在生物。

那么这个蒙蔽了大伙儿几百年， 甚至把赫歇耳那样的著名前辈都给误导了的黑子到底是什么东西？ 它为什么会出现在光芒万丈的太阳上呢？ 这些谜团直到二十世纪初才逐渐揭开面纱。 首先被搞清楚的是， 黑子展现的绝不是赫歇耳所幻想的有可能有生物栖息的凉快表面， 它的温度实际上高达 4,000 度左右 (请读者想一想， 我们介绍过的哪一种手段可以使我们得到这一信息？)， 足以熔化素以耐高温著称的金属元素 “钨”。 黑子之所以呈现黑色， 完全是因为它不幸生在了一个比它更 “白” 的环境里 (黑子周围太阳物质的温度比它高了一千多度)， 从而被衬黑了。 如果我们能将黑子周围的阳光全部滤掉的话， 黑子非但不黑， 反而会呈现出耀眼的光芒。 另外， 黑子看上去很小 (黑子的英文名字中的 “spot” 和中文名字中的 “子” 都有 “小” 的意思)， 那也只是相对于太阳的庞大而言的， 它的实际块头可不小， 即便小黑子的面积也有新疆那么大， 大黑子更是可以吞下整个地球。



【太阳黑子 (右下角的对照物为地球)】

黑子的 “黑” 和 “小” 这两个品性算是被搞清楚了， 但它为什么能 “出高温而不染”， 维持这么 “低” 的温度呢？ 这可就不是一个简单问题了。 它所牵扯到的是太阳大气层中最重要的幕后推手： 太阳磁场。

1908 年， 美国天文学家黑尔 (George Hale, 1868-1938) 通过光谱学手段发现， 黑子中存在强度约为 0.3 特斯拉 (0.3T) 的磁场[注六]。 这是很强的磁场， 比地球磁场强一万倍左右， 也比太阳表面的平均磁场强得多。 这一强磁场的存在为揭开黑子的 “维稳” 之谜提供了线索。 这线索就是： “维稳” 离不开 “警力”， 而磁场恰恰可以充当这种 “警力”， 因为它会产生一种特殊的压强， 叫做磁场压。 正是在磁场压的帮助下， 温度较低 (从而内部压强也较低) 的黑子才能抗衡住外部物质的高压而维持稳定 (黑子一般能维持几天至几星期， 在太阳大气层中算是比较稳定的结构)。 进一步的计算还表明， 强磁场对太阳物质的对流会产生抑制作用， 使得能量无法经由对流有效地传至黑子内部， 这就解释了黑子温度偏低的原因。 更令人欣慰的是， 在理论上还可以证明， 太阳物质的运动会通过一种所谓的 “对流坍塌” (convective collapse) 现象， 而自发地造成某些区域的磁场强度增加。 这种磁场强度增加的区域通常呈管状分布， 被称为 “磁通量管”。 磁通量管伸出或插回太阳表面的地方通常就会形成黑子。 由此可见， 磁场的存在除了能解释黑子的主要特征及 “维稳” 机制外， 还可以解释它成因。 不仅如此， 由于磁通量管的伸出与插回总是 “成双成对”， 且极性相反的， 它还可以解释有关黑子整体分布的一个重要特征， 那就是黑子常常成对出现， 且每对黑子的磁场极性彼此相反。

但是， 磁场的存在虽然解释了黑子的成因、 主要特征及 “维稳” 机制， 却不等于说黑子就没有带给我们其它谜团了， 那样的谜团其实还不少。 细致的观测表明， 黑子有着复杂的结构， 除了被称为 “本影” (umbra) 的黑色中央区域外， 半径在 5000 公里以上的大黑子四周通常还有所谓的 “半影” (penumbra)， 它们的颜色较浅， 包含了很多纤维状结构。 更仔细的观测还表明， 本影中有时会出现亮点， 半影内则有时会出现漩涡状结构， 在黑子消亡前， 本影内有时还会出现明亮的桥状结构。 这些细致结构的成因及演化目前都还是有待探索的谜团。



【太阳耀斑】

太阳活动的另一个重要成员叫做耀斑。 如果说黑子是一种很低调的太阳活动， 那么耀斑就恰好相反， 它极为张扬， 是 “爆炸式” 的活动——这可不是比喻， 因为它实际上就是爆炸。 一个大耀斑通常可以释放出几十亿亿亿焦耳的能量， 相当于一百亿个百万吨级氢弹同时爆炸！ 在大耀斑爆发时， 太阳大气层的局部温度可以在短时间内升高到 2,000-3,000 万度， 比太阳核心的温度还高。 耀斑的威力极为惊人， 虽然发生在一亿五千万公里之外的太阳上， 却足以对地球产生显著影响。 事实上， 1859 年 9 月， 人类记录下的第一个大耀斑就是以它对地球的显著影响引起人们的注意的， 它所发射的带电粒子流猛烈撞击地球磁场， 产生的极光 (aurora) 一直延伸到赤道附近， 使无数没有机会前往极地的人领略了一次天象奇观。 随着技术的发展， 耀斑对地球的影响得到了越来越多的显现机会。 1984 年 4 月， 一个普通耀斑中断了美国总统里根 (Ronald Reagan, 1911-2004) 的 “空军一号” 专机与地面的通讯， 使美国情报部门大为紧张， 以为是苏联人在做手脚。 2006 年 12 月， 一个小耀斑将正在进行舱外作业的国际空间站的宇航员逼入 “发现者” 号航天飞机仓惶躲避 (他们实际上还是慢了一步， 所幸那只是小耀斑， 他们所受的辐射剂量不大)。

耀斑给我们提出的问题是显而易见的： 那就是它为什么会发生？ 它的能量来自何方？ 科学家们对这些问题进行了长期研究。 与黑子一样， 一般认为耀斑的发生也跟太阳磁场有着密切关系。 一种目前比较流行的观点认为， 耀斑的发生很可能是磁通量管的重组造成的。 太阳上的磁通量管就象橡皮筋一样， 可以通过应力等形式储存能量 (上文提到的阿尔文波之所以能沿磁通量管传播， 也正是因为这一特性)。 随着太阳物质永不停息的运动， 磁通量管会被拉伸、 扭曲、 缠绕， 这些过程会大大增加储存在磁通量管中的能量。 但这种过程是不可能永远持续下去的， 因为能量越高的状态就越不稳定， 最终将会有一个时刻， 如同橡皮筋突然断裂一样， 磁通量管发生重组， 由拉伸、 扭曲、 缠绕后的复杂状态一举重组回相对简单的状态， 并将因拉伸、 扭曲、 缠绕而储存起来的能量在很短的时间内释放出来， 由此形成的就是耀斑。 这个过程有点象小孩搭积木， 随着积木越搭越高， 势能越积越多， 它会变得越来越不稳定， 最终会有一个时刻， 积木突然垮塌， 原先储存在积木中的势能被突然释放出来 (释放的形式之一就是撞击桌面或地面发出的轰然之声)。

这种机制得到了一定程度的观测支持。 人们发现， 耀斑通常发生在极性变化较为复杂的黑子区域附近， 那里不仅有强磁场， 而且磁通量管的分布较为复杂， 容易发生上述机制所要求的拉伸、 扭曲、 缠绕等过程。 但这种机制也并非没有问题。 比如前面提到的帕克在二十世纪六十年代曾对磁通量管的重组进行过估算， 结果发现那需要几小时甚至几天的时间才能完成， 而耀斑的能量释放过程往往持续不到一分钟， 两者大相径庭。 为了解决这一问题， 科学家们提出了许多修正方案， 比如有人提出磁通量管的重组只需发生在一小段而不是整段上， 从而能在短得多的时间内完成。 也有人提出磁通量管在重组前会破碎成许多小圈， 从而大大增加接触面积， 使重组得以 “提速”， 等等。 总之， 方案人人会提， 各有巧妙不同， 但越是巧妙的方案所需的观测证实通常也越精密， 其中很多都超出了目前的观测能力， 因此耀斑的发生机制到目前为止还是一个谜， 探索的道路还很漫长。

除耀斑外， 太阳大气层中的另一种爆发现象近来也受到了越来越多的关注， 那就是所谓的日冕物质抛射 (coronal mass ejection)。 一定规模的日冕物质抛射的发生频率从几天一次到一天几次不等， 它们与耀斑的主要差别——顾名思义——是会抛射出大量的 “物质”， 主要是带电粒子， 数量约有几十亿至上百亿吨， 飞行速度约为每秒几百公里， 所携带的动能与大耀斑的总能量相近[注七]。 这些质量相当于几万艘万吨巨轮的带电物质若不幸与地球相遇， 将会造成大型的地磁暴， 其威力往往要比耀斑造成的地磁暴更厉害——这也正是人们越来越关注日冕物质抛射的主要原因。

1989 年 3 月， 一次小规模日冕物质抛射引发的地磁暴， 造成了加拿大魁北克省电力系统的崩溃， 并使得极光范围一直延伸到美国南部的德克萨斯州， 很多人甚至担心美苏双方的军事通信系统会因地磁暴的干扰而触发核大战。 小规模日冕物质抛射尚且如此厉害， 大规模日冕物质抛射倘若击中地球， 结果更是不堪设想。 2009 年 5 月， 美国国家海洋与大气管理局 (NOAA) 发布了一份太阳风暴 (solar storm) 警报， 认为 2013 年有可能会是太阳活动较频繁的年份， 其中某些太阳活动的规模有可能不在 1859 年那次大耀斑之下。 这其中最令人担忧的就是大规模日冕物质抛射击中地球的可能性。 有人也许会说： 1859 年的大耀斑不就是一次天象奇观吗？ 并没有造成严重后果啊？ 是的， 1859 年的大耀斑确实没有造成严重后果， 但今天的人类社会早已不是 1859 年那样子了。 我们今天引以为傲的现代文明已经极大地依赖于各种各样的电子及电力设备。 在这种情况下若被大规模日冕物质抛射所击中， 后果将远不是天象奇观那么浪漫， 而很可能是灾难性的， 比如很可能出现全球性的电力中断。 现代社会是如此彻底地依赖电力， 就连象加油站那样以提供其它能源为目的的系统， 也已经离不开电力。 一旦发生全球性的电力中断， 后果将不堪设想， 那时想要修复哪怕一座爆炸了的变压器都会极度困难。 科学家们估计， 那样的灾难倘若发生， 人类恐怕要用几年的时间才能逐渐恢复， 在此期间， 连食物和水的供应都会出现困难， 其结果将是比任何大型战争或重大瘟疫还要可怕得多的生命损失， 就连发达国家也难以幸免 (事实上， 在那样的灾难面前， 发达国家反而有可能更脆弱， 因为它们比其它国家更依赖于电子及电力设备)。



【太阳风暴假想图】

当然， 这只是最坏情形， 即便真的发生大规模日冕物质抛射， 它直接击中地球的概率也并不大， 但想到人类只能仰仗大自然的概率恩赐来侥幸度日， 毕竟是一种很无奈的感觉。 太阳对于我们实在太重要了， 为今后有可能发生的来自于太阳的灾难预作准备， 是除好奇心之外， 人类研究太阳的一个最重要的动机。 事实上， 最近几年来， 人们已经开始建立所谓的 “太空气象” (space weather) 系统， 试图对主要由太阳活动引起的地球附近的空间环境变化进行研究及预测， 以服务于我们这个脆弱星球上的脆弱系统。 但到目前为止此类系统尚不能作出真正意义上的预测 (比如前面提到的美国国家海洋与大气管理局有关 2013 年太阳风暴的警报就完全有可能是错误的)。 它所能做的真正可靠的事情， 只是利用带电粒子从太阳运动到地球所需的几天时间， 通过已经发生的太阳活动， 来为我们提供几天的预警时间而已。

那么， 日冕物质抛射是如何发生的呢？ 很不幸， 这也是一个未解之谜。 人们提出了很多理论， 但各有各的问题。 比如很多人曾经认为， 日冕物质抛射与耀斑有着直接关联， 甚至完全就是由耀斑造成的。 但后来的研究发现， 很多大耀斑并不导致日冕物质抛射， 而某些小规模的日冕物质抛射则似乎没有与之相伴的耀斑。 因此日冕物质抛射与耀斑之间看来并不存在可靠的因果关联。 但一般认为， 两者之间虽没有因果关联， 却也绝非毫不相干。 佐证这一点的最好证据， 就是几乎所有大规模的日冕物质抛射都有与之相伴的耀斑。 另外， 日冕物质抛射与耀斑一样， 都几乎铁定是与太阳磁场存在极密切的关系， 而且极有可能都是磁通量管的重组造成的 (事实上， 日冕物质抛射很可能是整段磁通量管遭到 “抛弃” 所致)。 只不过究竟什么样的磁通量管分布会造成耀斑， 什么样的磁通量管分布会造成日冕物质抛射， 目前还不得而知。

从黑子到耀斑， 再到日冕物质抛射， 太阳活动的形式是丰富多彩的。 那么， 在这些活动中有没有什么共同特征呢？ 有， 那就是太阳周期 (solar cycle)， 那也是我们在结束走马观花般的本节前， 最后要介绍的话题。



【太阳周期 (顶端为极小年， 底部为极大年)】

太阳周期是德国天文学家施瓦布 (Heinrich Schwabe, 1789-1875) 通过对太阳黑子数目长达 17 年的持续观测， 并借鉴历史数据所发现的。 它最初的含义是黑子数目的变化周期。 但后来的研究发现它同时也影响着耀斑、 日冕物质抛射等其它太阳活动， 甚至对太阳的光度及太阳风的强弱也有一定影响， 可以说是所有太阳活动的共同特征。 另一方面， 在揭示出太阳周期所具有的广泛影响力的同时， 它作为周期现象的品质却在下降。 现代观测表明， 太阳周期并不是严格意义下的周期现象， 它的平均值约为 11 年[注八]， 但有时可以短至 9 年， 有时又可以长达 16 年， 甚至还出现过长达几十年没有显著活动的所谓 “蒙德极小期” (Maunder Minimum)。 不过， 尽管有这样的起伏， 太阳活动的规律性仍是足够显著的， 起码存在着近似意义上的周期性， 而绝不是随机现象。 在一个太阳周期中， 太阳活动最少的年份称为太阳活动极小年 (solar minimum)， 太阳活动最多的年份则称为太阳活动极大年 (solar maximum)。 前面提到的美国国家海洋与大气管理局有关太阳风暴的警告， 其实就是对太阳活动极大年的预测， 即认为 2013 年很可能是即将来临的一个太阳活动极大年。

尽管太阳周期不是严格意义下的周期， 但作为一种显著的近似现象， 它的存在依然是需要解释的。 为了寻找这种解释， 科学家们付出几十年的艰辛努力， 可惜的是——读者们一定猜到我要说什么了——迄今为止这也仍是一个未解之谜。

当然， 这并不是说几十年的努力毫无成果。 相反， 成果不仅有， 而且还不小。 在这里我们介绍其中较受青睐的一个， 即所谓的 “发电机机制” (dynamo mechanism)。 在介绍之前， 首先让我们一同分析一下， 解释太阳周期的切入点应该在哪里？ 大家请不要拍砖， 这并不是拿一个研究性的问题来卖弄知识或为难读者。 事实上， 对太阳周期的具体解释虽然是极困难的研究课题， 切入点的选择却是相当显而易见的。 通过本节的介绍， 我们已经知道太阳活动有一个共同的幕后推手， 那就是太阳磁场。 而我们前面刚刚介绍过， 太阳周期是所有太阳活动的共同特征。 既然一组现象有一个共同的幕后推手， 那么它们的共同特征最有可能归因于什么呢？ 当然就是那个共同推手， 即太阳磁场。 因此， 解释太阳周期的切入点应该是太阳磁场， 这也正是发电机机制的切入点。 发电机机制的精髓之处， 就是将太阳磁场本身的演化也纳入了解释范围之内， 从而在很大程度上具有统领整个领域的潜力。

发电机机制出现于二十世纪六十年代， 此后经历了几次起落。 它的早期设想是这样的： 在太阳活动的极小年中， 太阳内部存在着弱磁场 (象太阳这样的巨型等离子气团中存在弱磁场并不是难以想象的事情， 不存在反倒是难以想象的)。 这种场在太阳内部主要由南极指向北极， 被称为极向场 (poloidal field)。 极向场在太阳内部自转不均匀性的带动下， 将会发生扭曲， 使磁通量管沿赤道方向遭到拉伸， 形成所谓的环形场 (toroidal field)。 随着扭曲的加剧， 环形场的强度会持续增强。 计算表明， 当环形场的强度增加到一定程度时， 磁通量管将会出现上浮的现象。 不仅如此， 磁通量管在上浮过程中还会产生新的极向场[注九]， 从而构成极向场与环形场之间的相互支撑。 当磁通量管浮出太阳表面时， 将如上文说过的那样， 在伸出和插回太阳表面的地方形成一对磁场极性相反的黑子。 粗略的分析表明， 这种机制有一个很漂亮的地方， 那就是可以解释有关黑子分布的所谓斯波勒定律 (Sp?rer's law)， 即在每个太阳周期中， 自极小年到极大年， 太阳黑子几乎总是首先出现在高纬度区域， 然后向低纬度区域扩张， 而且南北半球上的黑子对有着相反的极性。 那么太阳周期又是如何出现的呢？ 是因为磁通量管的相互湮灭。 当南北半球那些极性相反的黑子对扩张到赤道附近时， 磁场方向相反的磁通量管会相互湮灭， 从而使磁场分布逐渐回到最初时的弱磁场状态——这就是一个新周期的开始。

这些结果初看起来很令人振奋， 不仅对太阳周期作出了说明， 还附送了对斯波勒定律的解释， 简直是 “买一送一”。 可惜好景不长， 问题很快就出现了， 而且恰恰就出在那附送的部分上。 原来， 发电机机制的早期研究有一个先天不足， 那就是对太阳内部的自转状况一无所知。 当然， 在那种早期研究中， 无知有无知的快乐， 那就是便于作假设， 因此当时人们对太阳内部的自转状况作了相当任意的假设， 目的之一就是解释斯波勒定律。 但不久之后， 我们上节所介绍的日震学手段就粉墨登场了， 它无情地粉碎了那些无知年代的快乐假设， 因为它所探测到的太阳内部的实际自转状态与早期所假设的并不一致。 那么， 利用太阳内部的实际自转状态是不是仍能解释斯波勒定律呢？ 很遗憾， 不能。 事实上， 它很不幸地会导致黑子分布规律的逆转， 即变成了从低纬度向高纬度扩张， 与斯波勒定律恰好相反。 这样一来， 原先 “买一送一” 的友情馈赠反倒变成了躲都躲不开的 “硬性搭售”。 更麻烦的是， 早期发电机机制被认为是在对流区中起作用的， 新的研究却发现， 太阳对流区的环境过于恶劣， 到处是强劲的湍流。 在那样的环境下， 磁通量管很快就会被撕碎， 从而根本就不可能有时间来孕育足够强的磁场。 这样一来， 发电机机制连对流区这一 “老巢” 都失守了。

这些问题给发电机机制蒙上了巨大的阴影。 但天文学家们没有放弃， 而是积极寻找着解决之道。 到了二十世纪九十年代中期， 一种新设想为发电机机制注入了新活力。 这种新设想就是 “迁居”——将发电机机制的作用地点由对流区迁移到差旋层中。 差旋层我们在上节末尾曾经提到过， 它是对流区底部以下的一个薄层， 是太阳刚性自转与非刚性自转的交界层。 这样的交界层自然也会造成极向场的扭曲， 从而也可以启动发电机机制[注十]。 但与对流区不同的是， 差旋层由于地处对流区底部以下， 因而是一个相对稳定的地方， 发电机机制可以在那里从容不迫地积累强磁场。 不仅如此， 计算表明， 这种新设想所导致的黑子分布规律与斯波勒定律又重新一致了， 从而排除了一个重大硬伤， 使局势进一步明朗起来。 不过硬伤虽已被排除， 软伤的有无却是谁也无法打包票。 发电机机制作为一个非线性模型， 存在着诸如混沌之类的复杂性， 而太阳周期本身也是一种复杂现象， 这两者的拟合在细节上几乎无可避免地存在很大的不确定性， 使得谁也无法保证目前这明朗局势是否是昙花一现， 甚至只是回光返照。 我们只能说发电机机制是迄今为止有关太阳磁场及太阳周期的比较有希望的机制。

我们对太阳各部分的介绍到这里就全部结束了， 这些介绍归根到底是从空间角度加以介绍。 也许让读者不无失望的是， 我们居然是在一堆谜团的重重包围之下结束了漫长的旅程。 但换个角度想想， 这岂非恰恰是这一领域充满生机的明证吗？ 在下一节， 同时也是全系列的最后一节中， 我们将由空间转往时间， 去进行一次时间之旅， 探索太阳的过去和未来。

注释

日冕的温度是用光谱学手段测定的。 我们在第六节中提到过， 十九世纪下半叶， 人们曾在日冕中发现过许多新谱线， 甚至一度以为发现了新元素， 后来才意识到它们来自于高度电离的金属离子。 这一点虽然打碎了发现新元素的美梦， 却给了人们一个估算日冕温度的机会， 因为电离需要高温， 要想产生那些日冕谱线所对应的高度电离的金属离子， 必须有 100-300 万度的高温， 这就是日冕温度的观测由来。 看过彗发相片的读者可能会觉得奇怪， 彗发 “仿佛是被一股来自太阳的 ‘风’ 吹起来的” 是一种很容易萌发的感觉， 为何直到二十世纪五十年代才由比尔曼提出太阳风的想法呢？ 这是因为对这种感觉有一种更简单的解释， 那就是彗发是被阳光本身的光压 “吹” 起来的。 比尔曼是在排除了这种可能性之后才提出 “太阳风” 的想法的， 而非单纯猜测。 另外还要提到的是， 比比尔曼早一个世纪的十九世纪中叶就有人提出过类似于太阳风的想法， 起因是太阳耀斑与地磁暴之间存在时间关联， 仿佛后者是由前者所发射的粒子流引起的 (请读者想一想， 这种 “太阳风” 与比尔曼的有何区别？)。 太阳风的存在首先由航天器而非地面观测站所证实不是偶然的， 因为太阳风是一种以电子和质子为主的带电粒子流， 它们会被地磁场所排斥， 从而很难被地面观测站所直接探测。 另外要提到的是， 太阳风早已不再被视为是日冕的一部分了， 甚至连它是否属于太阳大气层， 有些文献也有不同的选择。 日球层的边缘不是一个单一概念， 它自内向外包含了三个层面： 太阳风的风速由超声速变为亚声速的地方被称为 “终端激波” (termination shock)； 太阳风的压强减弱到无法再推动星际尘埃 (即两者压强相等) 的地方被称为 “日球层顶” (heliopause)； 星际介质的运动首度因遭遇太阳风而减速的地方被称为 “弓形激波” (bow shock)。 另外要提到的是， 有些人将日球层的边缘或其中某一个层面——比如 “日球层顶”——视为太阳系的边界， 那是不合适的， 因为它无法涵盖被认为是太阳系最外围的所谓奥尔特云(Oort cloud)。 令人感慨的是， 太阳黑子不仅在相对蒙昧的伽利略时代对某些观念造成了冲击， 甚至在三百多年后的中国文革期间， 还因为太阳所承载的政治象征而成为了禁忌， 有些教师甚至因为讲授太阳黑子而被打倒， 乃至打死。 黑尔的这一研究利用了荷兰物理学家塞曼 (Pieter Zeeman, 1865-1943) 在 1897 年所发现的所谓塞曼效应 (Zeeman effect)， 它表明光谱线在磁场作用下会分裂， 且裂距与磁场强度成正比， 这一效应开启了用光谱学手段测算磁场强度的大门。 耀斑也能抛射物质， 但数量要少得多。 另外顺便说一下， 无论耀斑还是日冕物质抛射， 它们释放的能量虽然都极其可观 (瞬间释放的能量能占到整个太阳能量的一个很可观的比例)， 但由于频谱分布极为宽广， 在可见光范围内的相对比例很小， 因此不是肉眼所能感知的。 有一个细节在这里要提一下， 那就是两个相邻的太阳周期在太阳活动的规模、 分布等方面虽然相似， 太阳磁场的极性却是相反的。 如果把这个差别也考虑进去， 那么太阳周期更确切地说是约为 22 年。 这一点是上文提到的美国天文学家黑尔所提议的。 这一点是美国天体物理学家帕克的贡献。 他提出， 在磁通量管的上浮过程中， 因太阳自转而产生的科氏力 (Coriolis force， 地球上台风中心附近的气流旋转方向主要就是受其影响而形成的) 将会使它形成新的扭曲， 那些新扭曲在湍流的帮助下将会合并成携带极向场的新磁通量管。 将发电机机制的作用地点移到对流区底部以下的想法， 实际上早在差旋层被发现之前的二十世纪八十年代初就有人提出过， 不过细节性的研究直到二十世纪九十年代中期才出现。

二零一一年六月十一日写于纽约

二零一一年十一月一日发表于本站

太阳的故事 (大结局) 太阳的过去和未来

本文作者：卢 昌海

按我们目前对物理学定律的了解， 在四维的物理时空中， 我们可以在三个空间维度中自由运动， 却只能在时间中 “随波逐流”， 既不能回到过去， 也无法随意前往未来[注一]。 可人类的好奇心却偏偏对许多事物的过去和未来颇怀有浓厚兴趣， 大至宏伟的宇宙， 小至普通的生命， 人类都想知道它的过去和未来。 就连懵懵懂懂的小孩有时也会问： 我是从哪里来的？ 我们太阳之旅的最后一站就要来回应这种好奇心， 去探索太阳的过去 (起源) 是怎样的？ 它的未来 (归宿) 又将如何？ 这些问题不仅是我们的好奇心所系， 而且与人类的命运不无关系——假如人类能在地球上存在得足够久的话。

但过去和未来既然是去不了的地方， 我们又如何能探索呢？ 这个看似严重的问题并没有难倒科学家。 事实上， 我们这整个太阳故事， 都是在探索去不了的地方： 从太阳的核心到它的大气层， 哪儿都不是我们能去的， 但通过科学方法， 我们依然得到了许多能与观测相印证， 从而有很高可信度的结果。 探索太阳的过去和未来也是如此。 从某种意义上讲， 它甚至比前面几节的探索还略微容易些， 因为有大量的参照物可供借鉴。 那参照物就是其它天体， 它们各有各的年龄， 有的尚处于 “襁褓” 阶段， 有的是 “小伙子”， 有的已 “人到中年”， 有的则已步入 “古稀”。 通过对它们的观测， 我们就能知道太阳的过去和未来大致会是什么样子的， 并印证有关太阳演化的理论或假说。 这就好比对不同年龄的人进行观察， 我们就能知道自己的过去和未来大致会是什么样子的。

当然， 我们也不能低估这种探索的难度。 毕竟， 判断天体的年龄是需要知识的， 那种知识的获取则是有一定难度的。 事实上， 单是破除天体永恒完美的宗教式观念， 从而使天体的年龄概念有意义， 就经历了一个漫长的过程 (参阅第三节)。 对天体年龄的具体判断则更复杂， 在理论和观测上都是很有难度的。 直到今天， 科学家们仍在为观测及判定某些特定年龄段的天体而努力着。 这种难度导致的一个结果， 就是有关太阳演化的早期理论大都带有较大的猜测性， 而且主要局限于关注太阳的起源。 至于太阳的归宿， 在连太阳为什么会发光那样的问题都尚未得到解决的年代， 是很难进行有价值的探索的， 因此直到二十世纪三十年代之后， 才有值得一提的发展。 今天， 随着太阳模型的逐步完善以及观测、 计算技术的快速发展， 我们对太阳演化的研究已变得越来越定量， 也越来越有可信度了。 当然， 这一切距离 “结题” 无疑还差得很远， 这么大的课题几乎注定是要长期探索的。

现代太阳演化理论的奠基者一般被认为是德国哲学家康德 (Immanuel Kant, 1724-1804)。 1755 年， 这位对自然科学怀有浓厚兴趣的哲学家在《自然通史和天体论》(General History of Nature and Theory of the Heavens) 一书中提出了太阳系起源的所谓星云假说 (nebula hypothesis)。 康德这一假说的灵感由来是比较特别的， 因为在他那个年代， 人们对其它天体的年龄还缺乏认识， 从而无法以它们为参照物。 康德是从一个完全不同的角度， 即太阳系与当时正被陆续发现中的星云之间的相似性， 而得到的灵感[注二]。 不过， 康德毕竟是哲学家而不是科学家， 他的著作虽然提出了星云假说的雏形， 却也充斥着纯粹的臆想， 比如他认为绝大多数行星上都存在居民， 而且在这纯属臆想的东西之上， 还言辞凿凿地提出了离太阳越远的行星上的居民越优秀那样的荒唐结论[注三]。 对此， 英国哲学家罗素 (Bertrand Russell, 1872-1970) 作过一句很幽默的评价： “这种见解作为地球人的谦虚值得赞许， 但并无任何科学依据”。

继康德之后对星云假说作出重大贡献的是法国数学家拉普拉斯 (Pierre-Simon Laplace, 1749-1827)。 1796 年， 他在科普著作《宇宙体系论》(The System of the World) 的附录中独立地提出了星云假说。 拉普拉斯对星云假说的论述作为一部科普读物的附录， 明显不如康德的论述来得详细， 但却比康德的论述更紧凑、 更物理、 更注重于为假说寻找观测依据， 并且也更注重于一些后来被证实为重要的因素， 比如星云的自转。 由于拉普拉斯在科学界的声望要明显高于康德， 他对星云假说的 “插足” 在很大程度上促成了这一假说在即将到来的十九世纪的流行。 为了纪念拉普拉斯的贡献， 后人将他的名字与康德并列， 将星云假说称为康德-拉普拉斯星云假说， 简称星云说。

虽然有拉普拉斯作后盾， 星云说的 “星运” 依然不是一帆风顺的， 在经历了十九世纪的风光后， 星云说开始面临越来越多的细节性困难， 甚至一度走向了衰落。 与这种衰落遥相呼应的， 则是一些其它假说——比如灾变说 (认为行星源于外来天体与太阳的碰撞)、 爆发说 (认为行星源于太阳的爆发)、 俘获说 (认为行星是太阳的 “俘虏”) 等——的 “揭竿而起”。 当然， 即便在所谓的衰落期， 星云说仍有一定的发展， 只是不再象十九世纪那样唯我独尊而已。 二十世纪八十年代之后， 随着新恒星周围的行星盘被观测天文学家所发现， 星云说的命运迎来了新的转机。 时至今日， 星云说虽依然面临一些困难 (太阳系作为一个比太阳更复杂的系统， 它的起源理论存在困难是意料中的事)， 其主流地位却已基本无可撼动。 而且星云说的困难大都集中在解释行星和卫星的某些特征上， 对于太阳的起源， 则几乎已达到了铁板钉钉的确切度。 事实上， 即便在所谓的衰落期， 星云说的对手们也很少挑战它对太阳起源的描述， 而将注意力集中在行星和卫星上。

有着两百多年历史的星云说奠定了研究太阳过去 (起源) 的理论框架， 那么对太阳未来 (归宿) 的研究又如何呢？ 这方面的研究历史要短得多。 这是因为决定太阳未来的最重要因素： 太阳的能量来源， 以及那来源可以支撑多久， 直到二十世纪三十年代末才得到初步解决 (参阅第八节)。

下面我们就来介绍一下目前学术界有关太阳过去和未来的主流看法。

按照星云说， 太阳 (以及太阳系的其它主要天体) 都是由所谓的星际云 (interstellar cloud) 坍缩而成的。 但星际云有好几种类型， 究竟什么样的星际云最有可能成为太阳或其它恒星的 “摇篮” 呢？ 要想回答这一问题， 我们首先要对星际云的分类作一个简单介绍。 星际云的分类是以宇宙中含量最丰富的元素——氢——的形态为依据的。 具体地说， 星际云通常分为三类， 也称为三个区 (之所以称为 “区”， 是因为不同类型的星际云所占据的往往是同一片大星际云的不同区域)：

氢以离子状态存在的被称为 HII 区， 它的温度最高 (往往能达到 10,000K)。 氢以原子形态存在的被称为 HI 区， 它的温度适中 (通常在 100K 左右)。 氢以分子形态存在的被称为分子云 (molecular cloud)， 它的温度最低 (往往只有 10K 左右， 几乎是整个星系中最冷的物质)， 平均密度则较高 (每立方厘米约有几百个粒子)， 相当于太阳附近星际介质密度的 100 倍以上， 因而也被称为稠密云 (dense cloud)[注四]。



【离我们较近的分子云： 猎户星云 (Orion Nebula)】

在这三类星际云中， 最有可能成为太阳或其它恒星 “摇篮” 的是分子云。 为什么呢？ 因为一片星际云要想坍缩， 必须满足一个显而易见的条件， 那就是不能无限期地 “维持现状” (否则坍缩就无从谈起了)。 这一条件有一个学术名称， 叫做不稳定性 (instability)。 那么， 一片星际云怎样才会有不稳定性呢？ 答案是它的总质量必须足够大。 而且星际云的温度越高、 密度越低， 出现不稳定性所需要的总质量就越大。 这一结果是不难理解的， 因为使星际云坍缩的动力是引力， 负隅顽抗的则是它作为弥散气体所具有的压强。 如果在两者的竞争中引力占到上风， 并且在坍缩过程中能持续占到上风， 坍缩就会很自然地发生， 这样的星际云就有不稳定性。 明白了这一点， 也就不难理解 “温度越高、 密度越低， 所需要的总质量就越大” 了。 因为温度高意味着压强大， 密度低则意味着引力弱， 两者都不利于引力。 为了克服这些不利因素， 引力必须倚仗它的 “独门武功”， 那就是总质量。 因为总质量越大， 引力就越强， 这是压强所不具有的特点。 因此在 “温度越高、 密度越低” 那样的不利条件下， “所需要的总质量就越大”。

具体的计算表明， 星际云产生不稳定性所需的最小质量正比于温度的 3/2 次方， 反比于密度的 1/2 次方。 这一结果是英国物理学家金斯 (James Jeans, 1877-1946) 在 1902 年给出的。 为了纪念这一早期研究， 人们把这种不稳定性称为金斯不稳定性 (Jeans instability)， 相应的最小质量则称为金斯质量 (Jeans mass)。

那么， 分子云的金斯质量有多大呢？ 计算表明， 约为太阳质量的几千倍 (相应的线度约为几十至上百光年)。 而 HI 区和 HII 区的星际云由于温度更高、 密度更低， 从而金斯质量更大， 大到了实际上很少能达到的程度， 因此不容易成为太阳或其它恒星的 “摇篮”[注五]。

有了不稳定性， 坍缩就将是不可避免的， 因为很多偶然因素——比如附近超新星爆发产生的激波， 星际云的相互碰撞， 星际云穿越星系旋臂所遇到的干扰等——都能触发坍缩的发生。 那么， 坍缩的具体过程会是怎样的呢？ 质量约为太阳质量几千倍的分子云， 会不会坍缩成一个质量达几千个太阳质量的超级恒星呢？ 答案是否定的。 事实上， 质量达几千个太阳质量的超级恒星不仅在观测上从未被发现过， 在理论上也被认为是不可能的。 这其中一个很重要的原因， 就是在坍缩过程中， 随着密度的增加， 金斯质量将会减小 (因为金斯质量反比于密度的 1/2 次方)， 从而导致分子云中一些较小的部分发生独立的坍缩， 使整片分子云分裂成小块。 而且那样的小块随着密度的增加还会进一步分裂， 使得最终形成的恒星质量远小于星际云的总质量。

但这种分裂也不会无限制地持续下去 (否则就只有粉末而不会有恒星了)。 当分子云的密度大到一定程度后， 坍缩过程中释放出来的引力势能将被裹在其中而无法及时散去， 这将造成分子云温度的上升， 从而遏制金斯质量的进一步减小 (因为金斯质量正比于温度的 3/2 次方)。 计算表明， 这时候的金斯质量大约在太阳质量的几分之一至几倍之间， 相应的分子云线度则在几千至几万天文单位之间。 这种分子云被称为原恒星云 (protostellar cloud)， 太阳系的前身就是那样一片原恒星云。

原恒星云通常是扁盘状的， 这是因为星际云通常存在缓慢的自转， 在坍缩过程中， 这种看似不起眼的自转会使得平行于转轴方向的坍缩比垂直于转轴方向的坍缩更容易进行 (因为后者会因角动量的守恒而旋转得越来越快， 从而产生越来越显著的离心效应， 阻碍坍缩的持续进行)， 由此导致的结果就是使分子云的形状逐渐变成一个与转轴相垂直的扁盘。 这一形状对于解释太阳系行星大致处于同一平面是很重要的。

原恒星云经过一二十万年的进一步坍缩后， 其中心区域因引力势能无法及时散去而造成的升温效应变得越来越显著， 最终使得热运动产生的压强大到了能抗衡引力的程度。 这时的原恒星云中心部分被称为原恒星 (protostar)， 它处于一种近似的流体静力平衡状态 (hydrostatic equilibrium)。 不过， 这种近似的平衡状态虽能对原恒星本身的坍缩造成显著阻碍， 却并不能阻止外侧物质继续向中心凝聚。 这种凝聚过程被称为吸积过程 (accretion)， 为这种过程 “添砖加瓦” 的外侧物质则被称为吸积盘 (accretion disk)。 吸积过程对于恒星的成长是极其重要的， 太阳刚刚成为原恒星时， 它的质量仅为目前质量的 1% 左右， 其余 99% 的物质全靠吸积过程来 “侵吞”。



【原恒星与吸积盘想象图】

吸积过程从物理上讲是非常显而易见的， 但由于被浓密的吸积盘所包围， 起码在最初阶段是很难被观测到的， 从而是星云说观测验证中为数不多的盲区之一。 原恒星的吸积过程大约持续几十万年， 当这一过程接近完成时， 吸积盘上的物质已大都被原恒星所侵吞， 使后者的质量大为壮大， 并获得了一个新头衔： 主序前星 (pre-main sequence star)。

由于阻碍观测的吸积盘上的物质大都被侵吞， 使得主序前星成为了一种能被直接观测到的天体。 事实上， 早在 1852 年， 英国天文学家辛德 (John Russell Hind, 1823-1895) 就在金牛座 (Tauri) 中发现了主序前星这种特殊阶段的天体， 并将其编号为金牛座 T 星。 当然， 那时人们还并不知道此类天体在恒星演化过程中的地位， 只是将其作为一颗亮度变化着的天体记录在册。 如今， 金牛座 T 星已成为了一大类天体的 “代言人”， 这类天体被统称为金牛座 T 型星 (Tauri T star)， 它们是象太阳那样的小质量恒星的主序前星[注六]。

主序前星由于刚刚由星际云吸积而成， 其 “身材” 在一定程度上还保持了星际云的 “飘逸”， 而远不如成熟恒星那样结实， 它的表面温度比成熟恒星低得多， 体积却极为庞大。 除此之外， 主序前星的另一个显著特点是有强劲的恒星风 (对太阳来说就是太阳风)。 事实上， 原恒星的吸积过程之所以终止， 除了吸积盘上的物质基本用罄外， 强劲的恒星风将残余物质吹离也是一个重要原因。 有意思的是， 主序前星所具有的表面温度低、 体积庞大、 恒星风强劲等特点都类似于后文将要介绍的红巨星 (red giant star)， 只不过前者是恒星演化的早期阶段， 后者则是晚期阶段[注七]， 但这 “一老一少” 的遥相呼应， 颇象人世间孩童与老人的相似之处。

主序前星的日常活动主要就是 “瘦身”——在引力作用下进一步缓慢收缩， 这种瘦身活动除了能优化 “身材” 外， 一项最重要的功劳， 就是为主序前星提供能量。 我们在第八节中曾经提到过迈耶、 亥姆霍斯、 汤姆生等人所主张的 “引力说”。 在那里， 它是被当作失败假说来介绍的， 但此刻我们却要为它恢复一点名誉， 因为对于今天的太阳来说， 它虽然是一个失败假说， 但在主序前星那一 “特定历史时期” 它却是完全适用的。 因为那时的太阳核心温度还没有高到能引发核聚变反应的程度， 引力收缩确实是一种很重要的 “替代能源”。

当主序前星的演化进行到后期时， 随着核心温度的持续升高， 一些 “点火温度” 较低的轻核将被相继点燃。 比如当核心温度达到 100 万度时， 最 “易燃” 的氘核将被点燃， 核心温度达到 300 万、 500 万、 600 万度时锂核 (3Li)、 铍核 (4Be)、 硼核 (5B) 也将被相继点燃。 这些轻核的聚变与引力收缩一起， 为后期的主序前星提供能量。 太阳作为主序前星的 “瘦身” 过程总共约持续几千万年至一亿年。 最终， 当核心温度达到 800 万度时， 太阳一生的一个重要时刻来临了： 它肚子里储备最丰富的氢元素终于被点燃了。 这是太阳的 “成人礼”， 这时的太阳就正式步入了一生最稳定、 并且持续时间很长的阶段——主序星 (main sequence star) 阶段。 今天的太阳已经在这一阶段度过了 46 亿年的漫长时光， 相对于预期寿命来说还只是 “中年” 而已。

主序星虽然是太阳一生最稳定的阶段， 但在如此漫长的时间长河中， 它的性质仍会发生缓慢变化。 发生这种变化的主要原因， 是氢核的含量经长期消耗后逐渐降低， 导致核反应数量有所下降， 从而使辐射压在与引力的抗衡中屈居下风。 辐射压一旦屈居下风， 太阳核心就会被引力所压缩。 但这种压缩是暂时的， 因为太阳核心一经压缩就会升温， 而升温将使核聚变反应加速， 重新产生出足够强的辐射压来抗衡引力。 这种微妙的平衡机制在太阳内部持续起着作用， 使太阳保持着总体的稳定。 但这种核心温度的逐渐升高会传到外层， 使太阳的表面温度也逐渐升高， 并因此而逐渐膨胀。 当然， 这都是极缓慢的过程。 研究表明， 从主序星伊始到今天， 太阳的表面温度大约升高了 5%， 半径大约膨胀了 6%， 光度则大约增加了 40%。

很明显， 这种升温和膨胀的趋势不仅存在于过去， 也将持续存在于未来。 计算表明， 再过 10 亿年， 太阳的光度将在今天的基础上再增加 10% 左右。 这一变化将在地球上导致一系列连锁反应。 首先是地表温度上升， 接着是海洋蒸发加剧， 然后是大气层中水蒸气的含量增加。 再接下来则是最糟糕的一步， 那就是温室效应。 我们今天谈论温室效应时关注得最多的是二氧化碳， 但实际上看似很无害的水蒸气才是最重要的温室效应气体 (只不过它受人类活动的影响不如二氧化碳那样显著而已)。 全球范围内水蒸气含量的增加将导致严重的温室效应。 在比较悲观的估计中， 整个海洋将因此而蒸发殆尽。 当然， 一定数量的地下水将得以留存， 并在某些地方渗出地表， 成为弥足珍贵的新水源。 大气层中的水蒸汽有时也会以暴雨的形式倾泻而下， 形成昙花一现的湖泊。 但地表的大部分地区将变成闷热的荒漠， 多数生物将会绝种， 幸存的物种将大都转入穴居生活。 如果那时人类仍存在于地球上的话， 或许将借助技术手段加入穴居的行列。

但那样的 “好景” 也是有期限的， 随着太阳光度的继续增加， 地球上的环境将继续恶化。 在 30 亿年后的未来， 地球的温室效应将彻底失控， 那时的地球将会变得类似于今天的金星——那里的温度常年高达 460°C， 别说生物无法忍受， 连熔点较低的金属都将被熔化。 那时的地球有生物幸存的可能性将是微乎其微的。 而如此凄惨的景象比起即将到来的更可怕的浩劫来说， 仍然算不上什么。

在距今约 40 亿年之后， 太阳一生的另一个重要时刻来临了——它核心区的氢燃料在经过了将近九十亿年不间断的燃烧后终于到了 “油尽灯枯” 的一天。 太阳从此告别了主序星阶段， 步入老年恒星的行列。 那时候， 太阳的形态将再次发生重大变化， 而离太阳最近两颗行星——水星和金星——则将迎来自己的末日。

由于氢燃料的耗尽， 太阳核心区的下场只有一个， 那就是坍缩。 但这种坍缩导致的升温很快就会点燃核心区以外的一个壳层中的氢。 因此， 这时的太阳内部将发生两件事情： 一件是氢燃料耗尽后的核心区在引力作用下发生坍缩， 另一件则是核心区以外的一个壳层内的氢发生燃烧， 成为新的核反应区。 后者产生的高温高压将使整个太阳外层发生远比主序星阶段剧烈得多的膨胀， 那时的太阳将变成一颗体积和光度都极为巨大， 表面温度却因膨胀过于剧烈而下降到 2,600K 左右的天体， 那样的天体叫做红巨星。 太阳在红巨星阶段将逗留几亿年。 那么， 变成红巨星后的太阳究竟有多大呢？ 一般认为， 它的体积将达到目前体积的一千万倍， 足以膨胀到目前的地球轨道之外。 这一阶段的太阳虽然表面温度有所降低， 但因表面积的巨大增加， 总光度依然极为惊人， 约为目前光度的两千倍以上。 这是闪耀了近九十亿年的太阳在谢幕前的最后演出。 在这场演出中， 离太阳最近的 “群众演员” 水星和金星将相继 “殉职”， 从太阳系行星行列中除名。

但我们脚下这颗地球的命运却比较微妙。

太阳的肚子虽然将膨胀到目前的地球轨道之外， 但在这缓慢的膨胀过程中， 比目前强劲得多的太阳风将带走大量的太阳物质 (整个红巨星阶段被太阳风带走的质量有可能达到太阳总质量的 1/3)。 太阳物质的损失将减弱太阳对地球的引力束缚， 从而使地球公转轨道缓缓远离太阳。 不过， 这种远离是否足以使地球躲过烈火焚身的浩劫， 学术界尚无定论。 大家比较有共识的是： 地球似乎恰好踩在自己的生死线上， 靠近一点就是死， 离远一点则是生。 至于究竟是死还是生， 不同的理论模型给出的结论不尽相同。



【太阳变成红巨星后的地球想象图】

另外一点比较有共识的是， 即便地球能侥幸躲过烈火焚身的浩劫， 地球上的景象也将是不折不扣的地狱景象： 殷红似血的太阳几乎占据整个天幕， 两千多度的高温从近在咫尺的天空中疯狂地倾泻着热量， 地表的很多物质将被熔化， 岩浆般的洪流四处流淌， 使这个曾经如此多姿多彩的生命乐园变得面目全非。 但即便那样的浩劫也很可能只是将最终的毁灭稍稍延后一些而已， 因为地球与比邻而居的太阳外层之间的潮汐作用将逐渐消耗地球轨道运动的能量， 使地球的轨道逐渐向内缩减， 重新投向死神的怀抱[注八]。

此时， 太阳系外围天体的环境也将发生剧烈的变化， 某些外行星卫星上的亘古寒冰将会融化， 成为太阳系中新的海洋——当然， 它们的成分与今天的地球海洋是截然不同的。

那么坍缩中的太阳核心又将如何呢？ 它会一直坍缩下去吗？ 答案是否定的。 由于氢的耗尽， 太阳核心的主要成分将变成氦， 随着氢壳层的不断燃烧， 越来越多新生成的氦将加入到坍缩中的氦核心上。 而它的温度则随着坍缩的进行而不断升高。 最终， 当氦核心的质量达到太阳总质量的 45% 以上时， 它的坍缩将使温度升高到一亿度以上。 这时候， 很 “耐热” 的氦核终于也被点燃了， 开始发生氦核聚变成碳核12C， 以及氦核与碳核聚变成氧核16O 的核聚变反应。 这个点火过程几乎瞬息之间就能传遍整个氦核心， 称为 “氦闪” (Helium flash)。 此后的太阳核心将进入最后一个燃烧阶段——氦燃烧阶段。

氦燃烧的一个很突出的特点， 是它对温度的依赖性比氢燃烧还要敏感得多， 哪怕核心温度只有 2% 的升高或降低， 也会导致光度的加倍或减半。 由于这种敏感依赖性， 太阳的光度和体积将会发生频繁的脉动， 尚未被太阳风带走的太阳外层物质将会在这种脉动中惨遭抛弃。 与氢燃烧相似， 氦燃烧也将经历一个核心区的氦先耗尽， 然后延烧至核心区以外的一个壳层上的过程， 只不过整个历时比氢燃烧短得多， 总共只有几千万年。

在太阳这整个晚年阶段中被太阳风及脉动抛射出去的太阳外层的物质， 将在行将就木的太阳周围形成一片美丽的小星云， 称为行星状星云 (planetary nebula)。 这种星云早在十八世纪时就已被发现， 因其在小型望远镜中形象与行星相类似而得名。 但它们的真正身份则是在晚得多的时候才被 “揭发” 出来的。 “揭发” 的证据主要有两条： 一是它们普遍在向外膨胀， 说明它们是某种抛射过程的产物； 二是在它们的中心发现了致密的核心， 那样的核心与耗尽了核燃料后的恒星残骸完全相符。 行星状星云中除了包含恒星外层那些未经燃烧的轻元素外， 还包含一些被对流带到外层的碳、 氧等恒星核聚变反应所生成的重元素。 在遥远将来的某一天， 它们也许将与宇宙中的其它物质汇集成新的大型星际云， 并成为新一代恒星， 行星， 乃至生命的原材料。



【较著名的行星状星云： 环状星云 (Ring Nebula)】

对于太阳来说， 那时的它已用尽了所有可资利用的核燃料， 抛掉了所有可以抛掉的外层物质， 成为了一个富含氦燃烧产物——碳和氧——的光秃秃的内核。 当然， 其中还有大量的电子， 因为太阳核心是电中性的， 不可能只有原子核。 这个内核的质量略多于目前太阳质量的一半， 它初始时的温度极高， 但却没高到足以点燃碳核与氧核的程度， 燃烧了近百亿年的太阳核心烘炉就此永久性地熄了火。 那么， 此时的太阳用什么来抗衡引力呢？ 答案是： 依靠一种新的压强——电子简并压强 (electron degeneracy pressure)。 这种压强源于物理学上的一条著名原理， 叫做 “泡利不相容原理”， 它表明象电子那样的粒子是一群极有 “个性” 的家伙， 每个都想拥有一个独一无二的状态， 这种 “个性” 导致的后果之一就是它们倾向于占据较大的空间。 这就好比一群人如果个个都想拥有单独的房子， 而不愿与人合租， 他们所占据的空间就会较大。 这种占据较大空间的倾向在宏观上的表现就是压强， 这就是所谓的电子简并压强。

在太阳的核心永久熄火后， 正是这种电子简并压强抗衡住了引力， 使太阳处于一个稳定状态。 这一状态极为致密， 虽然拥有太阳的全部残留物质 (约为地球质量的 20 万倍)， 体积却与地球相当。 如果我们能从那时的太阳上舀下一汤匙物质的话， 它将重达几吨！ 处于这一阶段的晚年恒星将在很长时间内维持很高的温度， 发出炽热的白光， 因此被称为白矮星 (white dwarf star)。 这种白矮星自二十世纪初以来已被大量地发现， 成为印证星云说最后一个环节的可靠证据[注九]。 白矮星虽然炽热， 但由于不再产生新的能量， 最终将在冰冷的星际空间中逐渐冷却， 由白变黑， 成为一颗不再发光的冰冷天体——黑矮星， 它的巨大引力场将是曾经生机勃勃的太阳系的最后墓碑。 如果那时有什么智慧生物路过太阳的话， 将只能从那巨大的引力场中发现它的存在， 而它曾经抚育过的无数生灵， 则早已成为过往烟云。

这就是太阳的归宿， 也是我们太阳故事的尾声[注十]。 当我们在本系列的开头遥望那光芒夺目的太阳时， 哪怕有最高明的想象力， 我们能想象出科学为我们勾勒出的如此宏大的图景吗？ 这种图景与最高明的想象相比也毫不逊色， 但与单纯的想象截然不同的是， 它的每一个结论都有直接间接的证据， 它的每一步推理都有严密可靠的逻辑， 它用观测去印证， 用逻辑来衔接， 它所展现的是科学最动人心魄的力量和美感。

注释

回到过去或前往未来的 “旅行” 被称为时间旅行。 按我们目前对物理学定律的了解， 这两者在可行性上是有很大差别的， 前者很可能原则上就不可行， 而后者只是目前的技术无法办到而已 (因此我对后者加了 “随意” 二字， 以示其并非不可能， 只是并非轻而易举)， 感兴趣的读者可参阅拙作时间旅行: 科学还是幻想？。 很难能可贵的是， 在那个很多人视银河系为整个宇宙的年代， 康德将星云视为了与银河系具有相似地位的所谓 “岛宇宙” (island universe)， 与二十世纪之后才确立起来的河外星系的概念不谋而合。 康德的《自然通史和天体论》有不止一种中译本， 较新的译本收录于《康德著作全集》第一卷 (李秋零主编， 中国人民大学出版社 2003 年版)。 不过有必要提醒有兴趣参阅该译本的读者注意的是： 该书第 334 页将康德的这一臆想错译成了含义截然相反的 “他们的居处离太阳越近， 他们就越优秀、 越完善”。 与之相对应地， HI 区和 HII 区星际云通常被合称为漫射云 (diffuse cloud)。 不过 “漫射云” 这个译名 (参阅中国天文学会天文学名词审定委员会的 “天文学名词” 网站) 我个人认为不是很妥帖， 因为 “漫射” 一词给人一种较明显的动态感觉， 与此处的实际含义有一定出入， 不如译成 “弥散云” 更为合适。 另外要指出的是， 此处所谓的 “稠密” 和 “弥散” 是相对的， 与我们日常所接触的气体相比， 哪怕稠密云也是 “弥散” 得一塌糊涂的东西， 密度不到海平面空气的一亿亿分之一， 甚至比一般实验室里的高真空还要 “弥散” 得多。 比如 HI 区星际云的金斯质量往往高达 100,000 个太阳质量以上， 数量要比分子云稀少得多。 不过稀少归稀少， 那样的星际云毕竟还是有的， 因此确实有一部分恒星的形成被认为是始于 HI 区星际云的坍缩。 除金牛座 T 型星外， 主序前星还有另外两个主要类别： 猎户座 FU 型星 (FU Orionis star) 和赫比格 Ae/Be 型星 (Herbig Ae/Be star)， 其中前者一般被认为是金牛座 T 型星的早期演化阶段， 而后者则是大质量恒星的主序前星。 这一点也正是对主序前星与红巨星进行观测区分的关键所在， 因为恒星演化的早期阶段与经历了核聚变反应后的晚期阶段在元素丰度上存在很大差异， 这种差异可以用光谱学手段予以分辨。 红巨星作为恒星晚年演化阶段的想法是二十世纪三十年代之后确立起来的。 但有意思的是， 英国小说家威尔斯 (H. G. Wells, 1866-1946) 在 1895 年发表的著名科幻小说《时间机器》(The Time Machine) 中有一段关于太阳未来的描述非常类似于红巨星： “我被地球的命运之谜所吸引， 停停走走， 一步千年地迈进着， 怀着奇异的兴趣注视着西边天幕上的太阳变得越来越大， 越来越暗淡 ... ... 最终， 在三千多万年之后， 太阳的巨大红色圆面遮蔽了将近十分之一的暗淡天空。” 不过， 撇开字面上的相似性不论， 威尔斯对红巨星的真正威力显然没什么认识， 在他的小说中， 那时的地球上仍存在着地衣、 苔藓及很多穴居的生物。 白矮星只是象太阳这样的小质量恒星的归宿， 而非恒星的唯一归宿。 质量远大于太阳的恒星将会坍缩成更致密的中子星， 甚至成为黑洞。 相应的， 它们的核聚变反应也不会终止于氦燃烧， 而将经历若干重核的燃烧， 并且它们在 “临死之前” 还将发生威力惊人的大爆炸——超新星爆发 (supernova)。 当然， 这还不是太阳最终、 最遥远的命运， 后者是与整个宇宙的命运息息相关的， 所涉及的因素包括宇宙学常数的大小、 宇宙的开放与封闭等。 那些话题由于远远超出了本系列的范围， 就不在此处介绍了。

二零一一年七月三日写于纽约

二零一一年十一月二十四日发表于本站

http://www.61k.com

太阳的故事

***寻找太阳系的疆界（一）***

记得念小学的时候， 读过一篇课文， 叫做 “数星星的孩子”， 讲述汉朝天文学家张衡的童年故事。 时隔这么多年， 小学的很多课文我已经忘记了， 但那篇数星星的课文却依然历历在目。 那时候， 我住在杭州的郊外， 家门口有一个池塘， 在许多个晴朗的夏夜里， 我和小伙伴们也常常坐在池塘边仰望星空。 那时候， 郊外的天空还没有被都市的灯光所污染， 在广袤的天幕下， 那一颗颗璀璨夺目的星星显得格外的晶莹和美丽。 自远古以来， 这种无与伦比的美丽就吸引了一代又一代的追随者， 他们中的一些人甚至将自己的一生都献给了探索星空奥秘的科学事业。 人类寻找太阳系疆界的故事只是科学史上的几朵小小浪花， 但在那些故事中， 有浪漫， 也有艰辛， 有情理之中， 也有意料之外， 有功成名就的兴奋， 也有错失良机的遗憾， 它们就像天上的星星一样美丽动人。

一. 远古苍穹

很多故事都会用 “很久很久以前” 作为开始， 仿佛久远的年代是成就一个好故事的要素。 现在让我们也从 “很久很久以前” 开始， 来讲述人类寻找太阳系疆界的故事吧。

在很久很久以前， 一群古希腊的牧羊人孤单单地生活在辽阔的原野上。 他们白天与羊群为伍， 在原野上漫游， 夜晚则与星空为伴， 期待黎明的到来。 渐渐地， 他们注意到在黎明之前， 在晨光渐露、 太阳即将跃出地平线的时候， 天边有时会出现一颗闪烁的星星。 与多数星星不同的是， 那颗星星的位置会一天天地变化， 有时甚至会连续一段时间不出现。 他们把这颗出现在黎明时分的星星叫做 “晨星” (morning star)。 细心的牧羊人还注意到， 在黄昏时分， 在日沉大地、 暮色四合的时候， 天边有时也会出现一颗闪烁的星星， 它的位置也会一天天地变化， 有时也会连续一段时间不出现。 他们把那颗出现在黄昏时分的星星叫做 “晚星” (evening star)。 后来人们用希腊及罗马神话中的太阳神阿波罗 (Apollo) 表示晨星， 用希腊或罗马神话中的信使赫耳墨斯 (Hermes) 或墨丘利 (Mercury) 表示晚星。 很多年之后， 人们意识到晨星和晚星实际上是出现在不同时刻的同一颗星星， 据说毕达哥拉斯 (Pythagoras) 是最早意识到这一点的人[注一]。 在群星之中， 这颗星星的位置变化最为显著， 往来如梭， 仿佛天空中的信使， 信使墨丘利便成了它的名字。

【开普勒的行星几何模型】

象这样的小故事在人类文明的几乎每一个早期发源地都曾有过。 那时的人们就已经知道， 在浩瀚的夜空中， 多数星星的位置看上去是固定的， 象晨星 (晚星) 这样会移动的星星是十分少见的。 这样的星星被称为行星， 它的英文名 planet 来自希腊文 πλαν?τη? (planētēs)， 其含义是漫游者。 被远古人类所发现的行星共有五颗， 这个数目在长达几千年的时间里从未改变过， 甚至一度被认为是永恒不变的真理。 在东方的中国及深受中华文化影响的其它东方国家如日本、 韩国及越南， 人们将五颗行星与阴阳五行联系在一起， 并以此将它们分别命名为水星 [即上面提到的墨丘利 (Mercury)]、 金星 [在西方世界中被称为维纳斯 (Venus)， 她是罗马神话中掌管爱情与美丽的女神]、 火星 [在西方世界中被称为玛尔斯 (Mars)， 他是罗马神话中的战神]、 木星 [在西方世界中被称为朱比特 (Jupiter)， 他是罗马神话中的众神之王] 和土星 [在西方世界中被称为萨坦 (Saturn)， 他是朱比特的父亲， 是罗马神话中掌管农业与收获的神]。 很明显， 这种命名方式除了起到命名作用外， 还代表了古代东方文化对行星数目 “五” 的一种神秘主义的解读。 类似的解读方式不仅存在于东方， 也存在于西方； 不仅存在于古代， 也存在于近代。 哥白尼 (Nicolaus Copernicus) 的日心说提出之后， 地球本身也被贬为了行星， 行星的数目由 “五” 变成了 “六”， 对此， 著名的德国天文学家开普勒 (Johannes Kepler) 提出了一个几何模型， 试图将天空中存在六颗行星与三维空间中存在五种正多面体这一几何规律联系在一起[注二]。

诸如此类的对行星数目的神秘主义解读虽然并没有什么生命力， 但除了因日心说导致的地球地位变更外， 行星数目的长期不变却是不争的事实。 一百年、 两百年， ...， 一千年、 两千年， ...， 这个数目是如此地根深蒂固， 天文学家们大都在事实上将之视为了不言而喻， 他们做梦也没想到， 这个数目有一天竟然也会被改变。 这一天是 1781 年 3 月 13 日， 改变这个数目的是生活在一座英国小镇的一位业余天文学家， 他的名字叫做赫歇耳 (William Herschel)， 他发现了太阳系的第七颗行星， 从而成为几千年来发现新行星的第一人。 赫歇耳的发现出乎了包括他自己在内的所有人的意料， 这一发现不仅为他本人赢得了永久的荣誉， 也将观测天文学带入了一个崭新的时代， 一个由赫歇耳 “无心插柳” 而开启的天文学家们 “有心栽花” 的时代， 人类从此开始了寻找太阳系疆界的漫漫征途。

二. 乐师星匠

【英国天文学家赫歇耳(1738 – 1822)】

赫歇耳的一生非常出色地实践了两种截然不同的职业， 其中最出色的职业 - 天文学家 - 不仅出现在对常人来说很难有开创性成就的后半生里， 而且 - 从某种意义上讲 - 就象他对新行星的发现一样， 是一个无心插柳的故事。

赫歇耳于 1738 年 11 月 15 日出生在当时属于英王领地的德国中北部城市汉诺威 (Hanover) 的一个音乐之家[注三]。 赫歇耳具有很高的音乐天赋， 他十四岁就参加乐队， 不仅擅长多种乐器， 而且还能独立作曲， 他亲自创作的交响曲和协奏曲就有几十首之多。 1757 年秋天， 十九岁的赫歇耳移居到了英国[注四]， 以演奏及讲授音乐为生。

赫歇耳的音乐成就以常人的标准来衡量应该说是颇为可观的， 但放在他的简历中， 却无可避免地要被他巨大的天文成就所淹没。 不过他在英国的音乐生涯中有一件事情值得一提。 那是在十八世纪六十年代中期， 当时英国的教会刚刚开始引进风琴， 需要招募一批风琴演奏者， 年轻的赫歇耳也参加了一个风琴演奏职位的竞逐。 当时的竞争颇为激烈， 而赫歇耳在风琴演奏上并无经验。 但他敏锐地发现当时英国教会引进的风琴与欧洲大陆的风琴相比有一个缺陷， 那就是缺少控制低音部的踏板。 为了弥补这一缺陷， 聪明的赫歇耳对两个低音琴键进行了改动， 从而演奏出了通常需要低音踏板的配合才能演奏出的低音部。 他的表演不仅赢得了评审的一致赞赏， 而且让他们深感神秘 (当然， 他顺理成章地成为了优胜者)。 赫歇耳在这一竞争中显示出的过人的动手及设计能力， 将为他日后的天文生涯立下汗马功劳。

【赫歇耳位于巴斯的住所(已辟为博物馆)】

1766 年， 赫歇耳迁居到了英国西南部的一座名叫巴斯 (Bath) 的小镇， 在一所教堂担任风琴演奏师， 开始了他在那里长达十六年的生活。 这座当时人口仅有两千的观光小镇因而有幸见证了赫歇耳一生最辉煌的工作。 在巴斯期间， 赫歇耳的音乐生涯达到了巅峰， 他不仅是风琴演奏师， 而且还担任了当地音乐会的总监， 并开班讲授音乐课程。 1772 年， 收入已颇为殷实的赫歇耳给他母亲寄去了足够雇一位佣人的钱， 从而把他妹妹卡洛琳 (Caroline Herschel) 从母亲为她安排的枯燥繁重的家务劳动中解救了出来， 并接到巴斯。

与赫歇耳一样， 卡洛琳也是一位颇有音乐天赋的人， 但她一生注定要跟随哥哥去走一条未曾规划过的道路。 在接卡洛琳到巴斯之前， 已成为镇上知名音乐家的赫歇耳潜心学起了数学。 赫歇耳学数学的本意是想多了解一些和声的数学机理， 从而加强自己的音乐素养。 但结果却因学数学而接触了光学， 又因接触光学而对天文学产生了浓厚的兴趣， 最终走上了一条业余天文学家之路。 而卡洛琳则成为了他在天文观测上不可或缺的助手[注五]。

赫歇耳所走的这条业余天文学家之路， 不仅为他自己走出了一片绚烂的天地， 也成就了业余天文学的一段 - 也许是最后一段 - 黄金岁月。 十八世纪的许多职业天文学家过分沉醉于由牛顿 (Isaac Newton) 所奠定， 并经欧拉 (Leonhard Euler)、 拉格朗日 (Joseph Louis Lagrange)、 拉普拉斯 (Pierre Simon Laplace) 等人所改进的辉煌的力学体系之中。 他们热衷于计算各种已知天体的轨道， 以此检验牛顿力学， 同时也为经纬及时间的确定提供精密参照。 在一定程度上， 当时的许多职业天文学家变得精于验证性的计算， 却疏于探索性的观测。 在这种情况下， 自赫歇耳之后半个多世纪的时间里， 业余天文学家们对天文学的发展起了重要的补充作用， 这一时期天文学上的许多重大的观测发现就出自他们之手。

【赫歇耳的 “七英尺望远镜”】

常言道： “工欲善其事， 必先利其器”。 对天文观测来说， 必备的工具是望远镜。 由于当时高质量的望远镜极其昂贵， 赫歇耳决定自己动手制作望远镜 (也顺便可以实践因学数学而接触的光学知识)。 望远镜的问世是在十七世纪初， 其确切的发明者现已不易追溯， 但德国裔荷兰人利普歇 (Hans Lippershey) 于 1608 年最早为自己制作的望远镜申请了专利， 从而留下了文字记录， 因此人们一般将他视为望远镜的发明者。 1609 年， 科学巨匠伽利略 (Galileo Galilei) 在得知了有关望远镜的消息后， 很快制作出了自己的望远镜。 伽利略制作的望远镜在结构及放大率上都大大优于包括利普歇在内的同时代人制作的望远镜。 他并且也是最早将望远镜用于天文观测的人[注六]。 通过望远镜， 伽利略获得了一系列前所未有的天文发现， 其中包括发现月球上的环形山、 太阳黑子及木星的四颗卫星 (现在被称为伽利略卫星) 等。 不过伽利略所用的是折射望远镜， 这种望远镜由于透镜 (主要是物镜) 所具有的色差等当时技术难以消除的效应而无法达到很高的放大率。 十七世纪后期， 另一位科学巨匠牛顿发明了反射望远镜[注七]， 用反射面替代了折射望远镜中的物镜， 从而避免了透镜色差带来的困扰。 赫歇耳所制作的就是反射望远镜， 这种望远镜的反射面可以用金属制作而无需使用玻璃。

为了制作望远镜， 赫歇耳将自己在巴斯的住所改造成了望远镜 “梦工厂”： 客厅被用来制作镜架与镜筒， 卧室变成了研磨目镜的场所， 厨房里则架起了熊熊的熔炉。 赫歇耳细心试验了许多不同成分的合金， 最后选择了用 71% 的铜与 29% 的锡组成的合金， 作为制作反射面的材料。 在制作望远镜期间， 除妹妹卡洛琳外， 赫歇耳还得到了弟弟亚历山大 (Alexander Herschel) 的帮助。 赫歇耳一生制作的望远镜有几百架之多， 不仅满足了自己的需要， 而且还通过出售望远镜使家庭获得了数目不菲的额外收入。 在长期的制作中， 他的作坊也一度发生过严重的事故， 导致熔融的金属四处飞溅， 幸好大家闪避及时， 奇迹般地未造成人员伤亡。

1778 年， 赫歇耳的家庭作坊制作出了一架直径 6.2 英寸、 焦距 7 英尺的反射望远镜。 这架望远镜在天文史上有着重要的意义， 被后世称为 “七英尺望远镜”。 后来的检验表明， 赫歇耳这架 “七英尺望远镜” 的性能全面超越了当时英国格林威治 (Greenwich) 皇家天文台的望远镜。 赫歇耳用自己的双手制造出了当时全世界最顶尖的观测设备， 为自己的天文观测之路迈出了无比坚实的第一步。 终其一生， 赫歇耳孜孜不倦地建造着更大的望远镜， 一次再次地刷新着自己 - 从而也是整个天文学界 - 的纪录， 他在这一领域的优势不仅在其有生之年从未被反超过， 甚至在去世之后仍保持了很长时间。

三年后的一个春季的夜晚， 一颗略带圆面的星星出现在了赫歇耳那架 “七英尺望远镜” 的视野里， 他一生最伟大的发现来临了。

注释

除墨丘利 (即水星) 外， 另一颗内行星 - 金星 - 也只有在清晨和黄昏才容易被肉眼所看见 (请读者想一想， 为什么水星和金星只有在清晨和黄昏才容易被肉眼所看见？)， 因而也曾被远古的观测者误分成晨星和晚星。 后来也是古希腊人首先意识到它们其实是出现在不同时刻的同一颗行星。 具体地讲， 开普勒提出的几何模型是这样的： 将六颗行星与三维空间中仅有的五种正多面体按以下顺序自内向外排列： 水星、 正八面体、 金星、 正二十面体、 地球、 正十二面体、 火星、 正四面体、 木星、 正六面体、 土星。 排列的方式是： 每个行星轨道所在的球面都与其外侧的正多面体相内切 (最外侧的土星轨道除外)， 同时与其内侧的正多面体相外接 (最内侧的水星轨道除外)。 开普勒的这一模型虽然精巧， 但与精密的观测以及他自己后来发现的行星运动定律不相符合， 不久之后就被放弃了。 喜欢几何的读者不妨计算一下这一模型所给出的相邻行星的轨道半径之比， 并与观测数值作一个比较。 赫歇耳出生时的名字是 Friedrich Wilhelm Herschel， 后来所用的名字 Frederick William Herschel 是他移居英国后入乡随俗而改的。 确切地讲， 为了与后文用卡洛琳 (Caroline) 称呼他妹妹 Caroline Herschel， 以及用亚历山大 (Alexander) 称呼他弟弟 Alexander Herschel 相平行， 我们应该称他为威廉 (William) 。 不过由于他是科学史上的著名人物， 对这样的人物， 人们习惯于用姓而不是名来称呼， 就象我们一般不用艾萨克 (Isaac) 和阿尔伯特 (Albert) 来称呼牛顿 (Isaac Newton) 和爱因斯坦 (Albert Einstein) 一样。 在此之前， 赫歇耳曾在英国逗留过大约九个月， 较好地掌握了英语。 卡洛琳自己后来也成为了一位天文学家， 她在寻找彗星方面有不俗的成就， 总共发现了八颗彗星。 值得注意的是， 伽利略在其早期著作《星际使者》(The Starry Messenger) 的开篇曾以第三人称的口吻将望远镜说成是自己的发明 (不过他在正文中提到自己在制作望远镜之前听说过他人制作望远镜的消息)。 由于这段文字的影响， 伽利略曾被一些人视为是望远镜的发明者， 这一说法如今已被否定。 不过平心而论， 伽利略在改进望远镜方面所做的贡献是巨大的， 不仅大大提高了放大率， 而且据说是他首先解决了望远镜成像的上下倒置问题。 另外他在制作自己的望远镜之前只是听说过有关望远镜的消息， 而未见过实物。 因此将伽利略视为望远镜的发明者之一也并不过分。 反射望远镜的设计在牛顿之前就已存在， 但牛顿最早制作出了具有实用价值的反射望远镜。 牛顿的制作水平之高， 使伦敦的工匠们在几年之后都没有能力加以效仿。

二零零七年三月二十七日写于纽约

二零零七年五月十一日发表于本站

二零零九年七月十三日最新修订

http://www.61k.com

寻找太阳系的疆界 (二)

三.巡天偶得

天文观测在外人看来也许是一项很浪漫的事业，但实际上虽不乏浪漫，却也充满了艰辛。即便拥有高质量的望远镜，一项天文发现的背后也往往凝聚着天文学家常年累月的心血。赫歇耳不仅在制作望远镜上走在了同时代人的前面，在天文观测上也有着常人难以企及的细心和热忱。他一生仅巡天观测就进行了四次之多，每一次都对观测到的天体进行了系统而全面的记录。其中最早的一次是通过一架口径4.5英寸的反射望远镜进行的，涵盖的是所有视星等亮于4的天体[注一]。由于视星等亮于4的天体用肉眼都清晰可见，这样的观测对于他精心制作的望远镜来说无疑只是牛刀小试。而且，这类天体既然用肉眼就能看见，从中做出任何重大发现的可能性显然都是微乎其微的。用功利的眼光来看，这样的巡天观测几乎是在浪费时间，但对赫歇耳来说，天文观测的乐趣远远超越了任何功利的目的。从这样一次注定不可能有重大发现的巡天观测开始自己的观测生涯，极好地体现了赫歇耳在天文观测上扎实、沉稳、严谨、系统的风格。除了这种极具专业色彩的风格外，赫歇耳对天文观测的酷爱程度也是非常罕见的。他对观测的沉醉，实已达到了废寝忘食的境界。在他从事观测时，食物常常是卡洛琳用勺子一小口一小口地喂进他的嘴里，而睡觉则往往要托坏天气的福。正是这样的专业风格与忘我热诚的完美结合，最终成就了天文观测史上的一次伟大发现。

几年下来，赫歇耳以及他所制造的望远镜在英国学术圈里渐渐有了一些知名度。“七英尺望远镜”建成后，赫歇耳开始用这架举世无双的望远镜进行自己的第二次巡天观测，这次巡天观测的目的之一是寻找双星(赫歇耳一生共找到过800多对双星，是研究双星的先驱者之一)，所涵盖的最暗天体的表观亮度约为8等，相当于上次巡天观测所涉及的最暗天体表观亮度的四十分之一，或肉眼所能看到的最暗天体表观亮度的六分之一。显然，这次巡天观测所涉及的天体数量比上一次大得多，工作量也大得多。

1781年3月13日夜晚10点到11点之间，赫歇耳的望远镜指向了位于金牛座(Taurus)一“角”(ζ星)与双子座(Gemini)一“脚”(η星)之间的一小片天区。在望远镜的视野里，一个视星等在6左右，略带圆面的新天体引起了赫歇耳的注意。那会是一个什么天体呢？由于恒星是不会在望远镜里留下圆面的，因此这一天体不象是恒星。为了证实这一点，赫歇耳更换了望远镜的镜片，将放大倍率由巡天观测所用的227倍增加到460倍，尔后又进一步增加到932倍，结果发现这个天体的线度按比例地放大了(请读者思考一下，赫歇耳既然有放大率更高的镜片，在巡天观测时为什么不用？)。毫无疑问，这样的天体绝不可能是恒星，恒星哪怕在更大的放大倍率下也只会是一个亮点，而不会呈现出圆面。那么，它究竟是一个什么天体呢？赫歇耳认为答案有可能是星云状物体，也有可能是彗星。但就在他试图一探究竟的时候，巴斯的天公却不作美，一连几天都不适合天文观测，赫歇耳苦等了四天才等来了再次观测这一天体的机会，这时他发现该天体的位置与四天前的纪录相比，有了细微的移动。由于星云状物体和恒星一样是不运动的，因此这一发现排除了该天体为星云状物体的可能性。于是赫歇耳的选项只剩下了一个，那就是彗星，他正式宣布自己发现了一颗新的“彗星”。



【旅行者号拍摄的天王星】

发现新彗星虽然算不上是很重大的天文发现，但每颗新彗星的发现都能为天文学家们新增一个研究轨道的对象，而这在当时正是很多人感兴趣的事情。因此天文学家们一得知赫歇耳发现新“彗星”的消息，便立即对新“彗星”展开了观测。令人奇怪的是，这颗新“彗星”并没有象其它彗星那样拖着长长的尾巴。用后人的眼光来看，或许很难理解如此显著的疑点为何没有让赫歇耳意识到自己所发现的其实不是彗星，而是一颗新的行星。但在当时，“新行星”这一概念对很多人来说几乎是一个思维上的盲点。不过科学家毕竟是科学家，他们是不会始终沉陷在盲点里漠视证据的。赫歇耳的发现公布之后，英国皇家学会的天文学家马斯克林(NevilMaskelyne)在对该“彗星”进行了几个夜晚的跟踪观测之后，率先猜测它有可能是一颗新的行星，因为它不仅没有彗星的尾巴，连轨道也迥异于彗星。当然，凭借短短几个夜晚的观测，马斯克林只能对新天体的轨道进行很粗略的推断。几个月之后，随着观测数据的积累，瑞典天文学家莱克塞尔(AndersJohanLexell)、法国科学家萨隆(BochartdeSaron)，以及法国天体力学大师拉普拉斯彼此独立地从数学上论证了新天体的轨道接近于圆形，从而与接近抛物线的彗星轨道截然不同。与此同时，赫歇耳本人也借助自己无与伦比的望远镜优势对新天体的大小进行了估计，结果发现其直径约为54700公里，是地球直径的四倍多[注二]。显然，在近圆形轨道上运动的如此巨大的天体只能是行星，而绝不可能是彗星。因此到了1781年的秋天，天文学界已普遍认为赫歇耳发现的是太阳系的第七大行星。这颗行星比水星、金星、地球和火星都大得多，甚至比它们加在一起还要大得多，它绕太阳公转的轨道半径约为30亿公里，相当于土星轨道半径的两倍，或地球轨道半径的二十倍。

几千年来，人类所认识的太阳系的疆界终于第一次得到了扩展[注三]。

赫歇耳的伟大发现立即被英国天文学界引为骄傲，赫歇耳本人也因此而获得了巨大的荣誉。1781年11月，英国皇家学会将自己的最高奖——考普雷奖(CopleyMedal)授予了赫歇耳，并接纳他为皇家天文学会的成员。赫歇耳从此成为了职业天文学家。为了让赫歇耳有充裕的财力从事研究，皇家学会免除了他的会费。不仅如此，英王乔治三世还特意为他提供了津贴，并亲自接见了他。后来乔治三世干脆请赫歇耳迁居到温莎堡(WindsorCastle)附近，以便能时常向皇室成员讲解星空知识。作为回报，赫歇耳在皇家学会的提示下写了一封感谢信，盛赞乔治三世对他的慷慨资助，并提议将新行星命名为“乔治星”(GeorgianPlanet)。虽然在新天体的命名中发现者通常享有优先权，但象“乔治星”这样一个富有政治意味的名字还是立即遭到了英国以外几乎所有天文学家的一致反对。赫歇耳本人也私下承认，这个名字是不可能被普遍接受的。在新行星的命名竞赛中最终胜出的，是德国天文学家波德(JohannElertBode)，他提议的名称是乌拉诺斯(Uranus)，这是希腊神话中的天空之神，也是萨坦(土星)的父亲。这一名称之所以胜出，是由于它与太阳系其它行星的命名方式具有明显的传承关系：在其它行星的命名中，朱比特(木星)是玛尔斯(火星)的父亲，萨坦(土星)是朱比特(木星)的父亲，有这样一连串“父子关系”为后盾，在土星之外的行星以萨坦(土星)的父亲乌拉诺斯来命名无疑是顺理成章的[注四]。在中文中，这一行星被称为天王星。

发现天王星的那年赫歇耳已经四十二岁，一生的旅途已经走过了一半。在后半生里，他放弃了音乐生涯，将全部的精力都投注在了星空里，孜孜不倦地继续自己的天文事业，并且作出了卓越的贡献。除发现天王星外，他还分别发现了土星及天王星的两颗卫星[注五]。他在恒星天文学、双星系统及银河系结构等领域的研究都具有奠基意义。他所绘制的星图远比以往的任何同类星图都更全面，同时他还是最早发现红外辐射的科学家。

1822年8月25日，赫歇耳在自己工作了几十年的观星楼里离开了人世。他的一生只差3个月就满84岁，只差4个月就是他所发现的天王星绕太阳公转一圈的时间。

四.命运弄人

听完了发现天王星的故事，有读者也许会提出这样一个问题，那就是天王星为什么没有更早被人们发现？我们前面提到过，天王星的视星等在6左右，事实上，在最亮时它的视星等甚至可以达到5.5(请读者想一想，什么情况下天王星看起来会最亮？)。这样的亮度连肉眼都有可能勉强看到，却为何没有更早就被人们发现呢？赫歇耳之前的天文学家们虽然没有象“七英尺望远镜”那样出色的望远镜，但他们的望远镜用来观测象天王星这样一个原则上连肉眼都有可能看到的天体却是绰绰有余的。自伽利略之后的那么多年里，那么多的天文学家在那么多个晴朗的夜晚仰望苍穹，却为何会将发现新行星的伟大荣誉留到1781年呢？

我们在前面的叙述中已经知道，赫歇耳发现天王星的过程并不是一个有意寻找新行星的过程，甚至在发现天王星之后他还一度将之视为彗星。这一切都表明天王星的发现带有一定的偶然性，是一个“无心插柳”的过程。与赫歇耳同时代的一些天文学家曾因此而将赫歇耳对天王星的发现视为是好运气之下的偶然发现。赫歇耳的一生在荣誉上大体是看得比较淡的，但他对这种将他发现天王星的过程视为偶然的说法还是明确表示了反对。他写下了这样的文字：

我对天空中的每颗星星都进行了有规律的排查，不仅包括[象天王星]那样亮度的，还包括许多暗淡得多的，它[天王星]只不过是恰好在那个夜晚被发现。我一直就在逐渐品读大自然所写的伟大著作，如今恰好读到了包含第七颗行星的那一页。假如有什么事情妨碍了那个夜晚，我必定会在下个夜晚发现它。我望远镜的高品质使得我一看到它便能感觉出它那可以分辨的行星圆面。

赫歇耳的这段文字不仅为自己发现天王星的必然性做了注解，而且也很好地说明了为什么在他之前那么多的天文学家都一直没有发现天王星。要知道，看到一颗暗淡的新行星虽然困难，但比这困难得多的则是要判断出它是行星而不是恒星。天王星被发现之后，人们对历史上的天文纪录进行了重新排查，结果发现天王星在赫歇耳之前起码已被记录了二十二次之多，其中最早的一次可以追溯到1690年，比赫歇耳早了将近一个世纪。可惜留下这二十二次纪录的天文学家们无一例外地与发现天王星的伟大荣誉擦肩而过。之所以会如此，是因为其中没有一位意识到自己观测到的不是恒星，而是行星。我们知道，在气象条件良好的夜晚，单凭肉眼就可以看到数以千计的星星，借助小型望远镜的帮助所能看到的天体数量更是多达数十万，这其中绝大多数都是恒星，任何人都不可能、也绝无必要对它们一一进行跟踪观测。因此除非意识到或怀疑到自己所观测的有可能不是恒星，天文学家们通常是不会随意对一个天体进行跟踪观测的，而如果不进行跟踪观测，就无法发现行星的运动，从而也就失去了从运动方式上辨别行星的机会。

那么赫歇耳为什么会想到要对天王星进行跟踪观测呢？正是因为他意识到了自己所观测的有可能不是恒星。如我们在上一节中所介绍，赫歇耳在发现天王星的过程中换用了几种不同的镜片，放大率从227倍增加到932倍[注六]，从而不仅发现了天王星的圆面，而且还发现其线度随放大率的增加而增加。因此他在静态条件下就发现了天王星与恒星的区别。这是历史上所有与天王星擦肩而过的天文学家们从未有过的优势。以英国的天文学家为例，当时英国皇家天文台最好的望远镜的放大率也只有270倍。赫歇耳拥有如此巨大的设备优势，他成为发现天王星的第一人也就绝非偶然了。而最终使这一伟大发现成为必然的，是赫歇耳所进行巡天观测。这样的巡天观测正是赫歇耳所说的“品读大自然所写的伟大著作”，在这样周密而系统的“品读”中，一颗象天王星那样的6等星的落网是必然的。



【行星的表观逆行】

不过，命运有时会跟人开残酷的玩笑。在赫歇耳之前曾经记录过天王星的所有天文学家中，最令人惋惜的是一位法国天文学家，他叫拉莫尼亚(PierreCharlesLeMonnier)。自1750年之后，他先后十二次纪录了天王星的位置。其中从1768年12月28日到1769年1月23日的短短二十几天里，他不知出于何种考虑，竟然八次纪录了天王星的位置。照理说，这样密集的纪录是足以显示天王星的行星运动的。但是命运女神却向可怜的拉莫尼亚开了一个最最残酷的玩笑。我们知道，由于地球本身在绕太阳运动，我们在地球上观测到的行星在背景星空中的运动实际上是它们相对于地球的表观运动。对于象天王星这样轨道位于地球公转轨道之外，从而轨道运动速度低于地球轨道运动速度的行星来说，它的表观运动方向有时会与实际的公转方向相反。这就好比当我们坐在一辆正在行驶的车子里观测其它车辆时，如果我们自己的车速比较快，就会看到一些与我们同向行驶的车辆相对于我们在倒退。在天文学上，这样的表观运动被称为表观逆行。表观逆行在行星的表观运动中只占一小部分。在行星从表观逆行转入正向运动的过程中，会有一小段时间看上去是几乎不动的。这就好比一辆倒行的汽车在转为正向行车的过程中，会有一小段时间看上去速度为零。拉莫尼亚万万没有想到的是，他那八次密集纪录竟然恰好是在天王星从表观逆行运动转为正向运动的那一小段时间附近，那时候的天王星相对于背景星空几乎恰好是看起来不动的[注七]！

如果说赫歇耳成为天王星的发现者有什么偶然性的话，这也许就是最大的偶然性。

注释

视星等是描述天体表观亮度的参数，视星等越低，天体的表观亮度就越高。具体地讲，一等星的表观亮度是六等星的100倍(请读者从中推算一下，视星等每降低1等，表观亮度会增加多少？)。正常的肉眼在最佳观测条件下所能看到的最暗天体的视星等约为6等。 赫歇耳得到的这一数值略大于现代观测值，后者为赤道直径51118公里，两极直径49946公里。 这里我们没有把质量微不足道的彗星计算在内。 在新行星的命名基本得到公认之后，一些英国天文学家仍固执地延用着“乔治星”这一名称，直至十九世纪中叶。 赫歇耳晚年曾认为自己还发现了天王星的另外四颗卫星，但那些“发现”后来要么被证实为是错误的，要么因存在明显的疑点而未得到公认。 这还不是赫歇耳当时拥有的最高放大率，后者高达2010倍，比英国皇家天文台最好的望远镜高出将近一个数量级，一度让他的同时代人觉得匪夷所思，有人甚至怀疑那是胡吹。为了平息怀疑，赫歇耳应邀将自己的望远镜带到皇家天文台与那里的望远镜进行了比较。比较的结果是赫歇耳当之无愧地坐上了当时望远镜制作的头把交椅。在比较的过程中最有戏剧性的是马斯克林(即那位最早猜测天王星是行星的天文学家)的反应。他在刚看到“七英尺望远镜”时对它的镜架很感兴趣，打算为自己的望远镜也配备一个，但在比较了两架望远镜的性能后，却沮丧地承认自己的望远镜也许根本就不配拥有一个好的镜架。 拉莫尼亚的性格比较暴躁，人缘也不好，被普遍视为是一位不细心的观测者，这一点曾被认为是他未能发现天王星的原因。不过有关他“不细心”的某些具体传闻，比如说他将有关天王星的数据随手写在一个纸袋上，实际上是讹传。

二零零七年三月二十九日写于纽约

二零零七年八月二日发表于本站

二零零九年七月十四日最新修订

关于本文

寻找太阳系的疆界（三）

五.虚席以待

一颗自十七世纪末以来就被反复观测过的六等星竟会是太阳系的第七大行星，赫歇耳的这一发现不仅一举击碎了太阳系行星数目亘古不变的神话，而且激起了人们对寻找太阳系疆界的极大兴趣。“新行星”这一概念几乎在一夜间就从被人遗忘的垃圾股变成了万众瞩目的积优股，引发了天文学家们极大的热情。在太阳系中，象天王星这样“大隐隐朝市”的行星究竟还有多少？人们恨不能立刻就揭开谜底。

可星海茫茫，到哪里去寻找新行星呢？难道要再象赫歇耳一样来一次巡天偶得？幸运的是，太阳系行星的分布就象地球上居民的分布，有一定的规律可循。其中最显著的规律就是行星轨道大都分布在黄道面(即地球的公转轨道平面)附近。这表明，寻找新行星不必漫天撒网，而只需在黄道面附近寻找-这就好比在地球上寻找一位居民时，无需掘地三尺，也不必潜入深海。更幸运的是，行星的分布似乎还有着进一步的规律，这规律帮了天文学家们的大忙。

水星对应于n=-∞，rn=0.4(观测值为0.4)；这个规律的发现可以回溯到天王星发现之前的1766年。那一年，德国天文学家提丢斯(JohannDanielTitius)注意到：如果以地球公转轨道的半径为单位(这被称为天文单位)，那么各大行星的轨道半径近似地满足一个非常简单的数学关系式：rn=0.4+0.3×2n，其中

金星对应于n=0，rn=0.7(观测值为0.7)； 地球对应于n=1，rn=1.0(观测值为1.0)； 火星对应于n=2，rn=1.6(观测值为1.5)； 木星对应于n=4，rn=5.2(观测值为5.2)； 土星对应于n=5，rn=10.0(观测值为9.5)。

这个经验法则除了对火星和土星有5?7%的偏差外，对其它几个行星都很准确[注一]。提丢斯将这一结果加注在了自己1766年翻译的瑞士博物学家波涅特(CharlesBonnet)的著作《自然的沉思》中，但在加注时未曾标明自己的名字[注二]。



【德国天文学家提丢斯(1729 – 1796)】

提丢斯匿名加注的这些结果起初并未引起什么注意。但六年后的1772年，德国天文学家波德-即我们在第三节中提到的那位后来在天王星的命名竞赛中胜出的波德-在为自己的热门著作《星空知识指南》准备新版时，注意到了提丢斯加注在《自然的沉思》中的经验法则。他立刻被这一法则所吸引，将之添加到了自己的著作中。但很不应该的是，波德在添加这些内容时完全没有提及波涅特或提丢斯的名字。不提提丢斯倒也罢了，因为提丢斯在加注那些内容时是匿名的，可是连波涅特的名字也不提，波德在这件事情上是有显著的剽窃之嫌的。



【德国天文学家波德(1747 – 1826)】

波德的《星空知识指南》在当时所受的热烈欢迎，加上波德本人此后几年的积极宣传，在客观上大力传播了提丢斯的经验法则。而波德这位不太光彩的“热心人”则成了这一传播的最大受益者，这个经验法则很快就被张冠李戴成了“波德定则”。九年之后，天王星的发现给了波德定则一个极大的支持，天王星的轨道半径与波德定则有着极好的吻合，误差只有2%(请读者自行查验)，这一点使得许多原本认为波德定则纯系巧合的天文学家深受震动，也使波德定则成为后来几十年间天文学家们寻找新行星的重要向导。随着波德定则重要性的提升，历史的真相也开始得到了显现。1784年，在“借用”提丢斯的结果整整十二年之后，波德终于承认了提丢斯的贡献。但那时生米早已煮成熟饭，波德的名字与提丢斯的定则已变得难舍难分，后世的天文学家们往往折衷地将这一定则称为提丢斯-波德定则。

现在让我们回到寻找新行星的宏伟大业上来。细心的读者或许已经从前面列举的行星轨道数据中看出了一个问题，那就是火星和木星这两个相邻行星的轨道在提丢斯-波德定则中分别对应于n=2和n=4，中间在距太阳2.8天文单位的地方缺了一个n=3。大自然怎么会在火星和木星之间留下如此显著的一个空缺呢？这个问题提丢斯在提出他的定则时就注意到了。这个奇怪的空缺似乎是在虚席以待一颗尚未露面的新行星，但当时天王星尚未被发现，太阳系六大行星的观念还根深蒂固，提丢斯未敢在太岁头上动土，于是他猜测那里可能存在一颗火星或木星的卫星[注三]。这个猜测很大胆，但也很荒唐，且不说如此远离行星的“卫星”能否稳定地存在，即便真有那样的卫星，又如何能用来填补属于行星轨道的空缺呢？这不成了“指鹿为马”吗？更何况卫星的轨道是以行星为中心的，它与太阳的平均距离与相应的行星与太阳的平均距离相差无几，从数值上讲也根本不可能对应于n=3的空缺。波德对这个空缺也很着迷，不过他在这点上比提丢斯略胜一筹，在“借用”提丢斯的结果时，他果断地将提丢斯那破绽百出的卫星猜测改成了行星猜测。

显然，如果提丢斯-波德定则可以信赖，那么寻找新行星的首选战场就应该是火星与木星之间距太阳2.8天文单位的这一神秘空缺。相对于遥远的外行星，这一空缺距离地球可算是近在咫尺，观测起来相对也该容易许多。于是天王学家们纷纷将目光汇聚到了那里。

在那里，他们将会发现什么呢？

六.失而复得

星空的浩淼对于没有真正体验过它的人来说是不容易想象的。即便知道了距离，以及大致的轨道平面，即便离地球如此之近，寻找一颗新行星依然不是一件容易的事情，因为行星出现在轨道的哪一段上仍然是未知的。这就好比警察抓捕逃犯，即便知道逃犯一定就在某座城市里，要想抓住依然不是一件容易的事情，因为逃犯躲在城市的哪个角落仍然是未知的。

当时有意在夜空中抓捕“逃犯”的“警察”还真不少，其中有位叫做扎克(FranzXavervonZach)的匈牙利人尤为热心，他曾经拜访过赫歇耳，并从此对寻找新行星产生了浓厚兴趣。自1787以来，扎克花了整整十三年的时间试图寻找位于火星与木星之间的新行星，却一无所获。眼看着“逃犯”将要安然度过十八世纪，扎克意识到单枪匹马抓捕逃犯的效率实在太低，便决定改变策略。他找了几位运气跟他差不多坏的伙伴商议了一下，决定将新行星的轨道区域分为24块，分别交由24位“天空警察”进行分片搜索。布下这样的天罗地网，无论狡猾的“逃犯”躲在哪个角落都将会难以遁形。老实说，这个分片包干的金点子并非扎克的首创，而是以前就有人提议过，只不过从未付诸实施。

出人意料的是，正当扎克广发英雄帖给欧洲各地的天文学家，抓捕计划已如箭在弦的时侯，从意大利的西西里岛(Sicily)忽然传来了“逃犯”落网的消息！勇擒“逃犯”的是一位单枪匹马的明星警察，名叫皮亚奇(GiuseppePiazzi)，他当时从事的工作并不是“抓逃犯”，而是“查户口”——为六千七百多颗星星确定坐标。这是一项枯燥而繁重的工作，为了完成这项工作，皮亚奇一片一片有规律地巡视着星空，在这点上他很象当年的赫歇耳。他这苦力活一干就是十一年。1801年1月1日，新世纪来临后的第一天，皮亚奇的望远镜指向了金牛座。这个星座真是天文学家们的幸运星座，二十年前赫歇耳就是在这附近发现了天王星，而此刻“户籍警”皮亚奇也在这里迎来了自己一生的一个重要时刻。他对这一小片天区中的50颗星星的坐标进行了纪录，第二天，当他对这些星星进行复核时，发现其中有一颗暗淡星体的位置发生了移动！为了确定这种移动不是观测误差，皮亚奇立即对这一天体进行了跟踪观测，结果证实了这种移动的确是天体本身的移动。



【意大利天文学家皮亚奇(1746 - 1826)】

1月24日，皮亚奇写信向同事波德、拉兰德(JosephLalande)，及挚友奥里安尼(BarnabaOriani)宣布了自己的发现。为了谨慎起见，他在给波德和拉兰德的信中将自己发现的天体称为彗星。毫无疑问，这是一个与赫歇耳将天王星称为彗星同样的错误，不过在经历了天王星的发现后，皮亚奇比赫歇耳要稍稍大胆一点，他在给挚友奥里安尼的信中指出这个天体有可能是一个“比彗星更好”的东西，因为它的运动缓慢而均匀，并且不象彗星那样朦胧。为了最终确定这个天体的性质，皮亚奇决定进行更多的观测，并计算它的轨道。可惜他的观测只进行到2月11日就因病中止了。而这时波德、拉兰德及奥里安尼尚未收到他的信件。等那三位收到姗姗来迟的信件，想要确认皮亚奇的观测结果时，新天体已经运动到了太阳附近，消失在了光天化日之中。

虽然失去了当场验证的机会，但波德(他直到3月20日才收到皮亚奇的信)坚信那就是自己期待已久的新行星。当然，相信归相信，最终的判断只能留给观测。好在新天体是不可能一辈子躲在太阳背后的，至多几个月，它必将重返夜空。可问题是：那时候到哪里去找回这颗暗淡的新天体呢？事实证明，这个问题并非杞人忧天，这颗“越狱逃亡”的新天体并没有因为留下过案底就变得容易寻找。日子一天天流淌着，无论天文学家们如何努力，皮亚奇的新天体却再也没有露面。

有读者可能会问：皮亚奇不是对新天体进行了跟踪观测吗？从他的观测数据中把新天体的轨道计算出来不就行了？这个想法是一点都不错的，可实际做起来却绝非易事。在新天体失踪的那些日子里，扎克(他也深信皮亚奇的新天体就是自己想要寻找的新行星)的学生伯克哈特(JohannKarlBurckhardt)就曾对新天体的轨道进行了计算。按照他的计算，天文学家们采取了突击搜查，可惜却扑了个空。皮亚奇自己也进行过计算，结果也劳而无功。计算新天体的轨道之所以困难，是因为皮亚奇的观测只持续了一个多月，所涵盖的只是新天体公转周期的2%左右，而且其中还很不凑巧地包含了表观逆行部分，使结果变得更为复杂。要从这样的观测片断中推算出整个轨道来，无疑是很困难的。更何况观测总是有误差的，从这么少的观测数据来推断轨道极易造成误差的放大。最后，我们也不能忘记当时还没有计算机，所有的计算都要依靠纸和笔来完成，这样的计算动辄就要花费很长的时间，有时甚至还不如拿起望远镜直接碰运气来得快捷。因此，推断新天体的轨道，从而预测新天体的位置虽然不是不可能，但却需要福尔摩斯般的技巧，只有第一流的数学高手才能将这种可能性变为现实。

幸运的是，当时就有一位这样的数学高手前来助人为乐。此人还不是一般的高手，他就是人类有史以来最伟大的数学天才之一，被后人尊称为“数学王子”的德国数学家高斯(CarlFriedrichGauss)。

当天文学家们为寻找皮亚奇的新天体而忙碌时，这位当时才二十四岁的数学天才决定助他们一臂之力。在这个节骨眼上，由高斯这样的数学巨匠(虽然当时的高斯还不象后来那么有名)来帮天文学家们计算一个小小的天体轨道，简直就象是摇滚巨星跑来替一家小酒馆义演。高斯仅用两个月的时间，就不仅计算出了新天体的轨道，而且提出了比旧方法高明得多的一整套计算轨道的新方法[注四]。高斯把他的计算结果寄给了扎克，后者欣喜若狂，立即公诸于世。借助高斯的计算结果，扎克于1801年12月7日重新找到了皮亚奇的新天体。经过持续观测，他终于在1802年的新年钟声即将敲响的那个夜晚确认了新天体的二度落网，它的位置与高斯的预测只差半度。几个小时之后，德国业余天文学家奥伯斯(HeinrichWilhelmOlbers)也独立地确认了同样的发现。这颗在1801年的第一个夜晚被“抓获”，又在同一年的最后一个夜晚被重新“捉拿归案”的新天体被称为色列斯(Ceres)。这是皮亚奇所取的名字，它是罗马神话中的谷物女神，同时也是皮亚奇所在的西西里岛的保护神。在中文中这一天体被称为谷神星[注五]。

高斯的计算相当精确地给出了谷神星的轨道，它的半径被确定为2.77天文单位，与提丢斯-波德定则吻合得很好(误差只有1%)。看来人们终于找到了位于火星与木星之间的新行星。事实上，早在谷神星被找回之前，对提丢斯-波德定则深信不疑的波德就已急不可耐地将之称为行星了。不过在欣喜之余，天文学家们也感到了一丝困惑：谷神星被皮亚奇发现时的视星等只有8，不仅无法与金、木、水、火、土五大行星相比，甚至比遥远的天王星还暗淡得多，一颗距地球如此之近的行星，为什么会如此暗淡呢？

注释

当然，这里采用是现代的表述方式，提丢斯本人的表述是这样的：“将太阳到土星的距离分成100份，那么水星与太阳被4个这样的部分所分隔；金星被4+3=7个这样的部分所分隔；地球被4+6=10；火星被4+12=16；......所分隔”。 直到1772年再版后，提丢斯才用一个字母“T”(他的姓氏首字母)标明自己所注的内容。而到了1783年，不知是否是出于对波德“借用”其成果的不满，他又过分慷慨地将自己发现的这一经验规律归功给了德国哲学家沃夫(ChristianvonWolff)，其实沃夫只是曾经列出过行星轨道半径的相对大小，并未提出或暗示过任何经验规律。 提丢斯虽然未敢在太岁头上动土，不过比提丢斯更大胆的人也是有的。事实上，早在十六世纪末，开普勒就曾猜测过火星与木星之间存在着行星(他还猜测水星与金星之间也存在行星)。在提丢斯之前大约五年，德国哲学家兰伯特(JohannHeinrichLambert)也曾猜测过火星与木星之间的行星。 高斯在计算中采用了他自己1794-1795年间发展起来的，后来被称为“最小平方法”的方法。不过他直到1809才发表这一方法，从发表时间上讲晚于法国数学家勒让德(勒让德于1806发表了最小平方法)。 确切地讲，Ceres只是皮亚奇为谷神星所取名字的前半部分，他提议的全名是CeresFerdinandea，其中Ferdinandea是当时那不勒斯和西西里的统治者。与赫歇耳当年提议的“乔治星”一样，Ferdinandea这个带有政治意味的名称也立刻就被天文学家们丢弃了。

二零零七年八月十四日写于纽约

二零零七年八月二十日发表于本站

二零零九年七月十五日最新修订

寻找太阳系的疆界 （四）

七. 名份之争

正当人们为谷神星感到困惑的时候， 更大的麻烦出现了： 1802 年 3 月 28 日 - 距离谷神星被重新发现仅仅过了三个多月 - 与扎克几乎同时找回谷神星的奥伯斯在试图观测谷神星的时候， 意外地发现了另外一颗移动的星星。 这个天体后来被他称为派勒斯 (Pallas)， 这是希腊神话中的智慧女神 - 也叫雅典娜 (Athena)。 在中文中， 这一天体被称为智神星。

智神星被发现之后， 高斯立刻用自己的新方法计算了它的轨道， 结果发现它的轨道虽然不太圆， 但平均半径与谷神星几乎完全一样， 也是 2.77 天文单位。 这下麻烦大了， 一个轨道区域居然挤进了两颗行星， 这真是前所未闻的怪事， 简直比缺了一颗行星还让人觉得不可思议。 如果说发现谷神星带给大家的是喜悦， 那么智神星的出现就多少有点令人尴尬了。 谷神星的卧榻之侧居然有智神星酣然沉睡， 这可能吗？ 这可以吗？ 急性子的波德率先对智神星投下了不信任票， 他猜测奥伯斯发现的只是一颗彗星(彗星真可怜， 总是被人拿来当替代品)。 要说波德的这一怀疑还真是有点厚此薄彼， 想当初谷神星尚在越狱潜逃期间， 他就热情万丈地以行星头衔相赠， 而现在智神星只不过晚来了几个月， 就怀疑人家是彗星世界的奸细。



【地球 (右)、月球 (左上)、谷神星 (左下) 大小对比】

这时候行星观测的元老级人物赫歇耳出来放话了， 他说依我看这两个天体谁也没资格当行星， 因为它们都太小了， 只能称为小行星 (asteroid)[注一]。 在人们大都期盼新行星的时候， 赫歇耳说出这样的话来多少有些扫大家的兴， 但以他的身份， 说话自然不会是信口开河。 那么他的依据何在呢？ 原来他老人家已经悄悄为这两个暗淡的小家伙度量了 “身材”， 结果发现它们的直径只有两百多公里。 这样的直径还不到月球的十分之一， 又岂能有资格坐在行星的宝座上？ 今天我们知道， 谷神星的直径实际有将近一千公里， 智神星也有五百多公里， 远远大于赫歇耳的估计 (但仍比月球小得多)。 不过这倒也不能怪赫歇耳， 这两个天体实在太小， 小到了就连他的望远镜也无法通过观测其圆面来判断大小， 而只能通过间接手段进行估计， 从而误差很大。 不过一开始人们所不知道的是， 谷神星的小其实让赫歇耳吃了一个不大不小的哑吧亏： 在谷神星 “潜逃” 的那些日子里， 嗜观测如命的赫歇耳也当仁不让地加入到了追捕者的行列， 却也象其他人一样铩羽而归。 他之所以失败， 部分原因就是因为他以为凭借自己天下无双的望远镜， 应该能像发现天王星那样直接从圆面上发现谷神星， 结果却阴沟里翻了船。 谷神星即便在他的望远镜里， 也依然保持了苗条的身材， 丝毫不显山露水。 究其原因， 都是太小惹的祸。

现在该是它为自己的 “小” 付出代价的时候了。

但赫歇耳的这一提议却遭到了很多人的反对。 客气的将之视为文字游戏， 不客气的则干脆认为赫歇耳之所以这样提议， 目的乃是要让自己发现天王星的贡献盖过皮亚奇和奥伯斯发现谷神星和智神星的贡献 (看来荣誉有时还真是一种包袱)。 也许归根到底， 是人们期待新行星已经期待得太辛苦， 实在不想失去已经被发现的新 “行星”。 不过皮亚奇和奥伯斯这两位发现者本人反倒是没有介意， 他们同意了赫歇耳的观点 (皮亚奇提议用 planetoid 取代 asteroid， 但在谷神星和智神星不具有行星资格这点上他并无异议)。

这场早期的行星名份之争并未持续太久。 两年之后， 1804 年 9 月 1 日， 德国天文学家哈丁 (Karl Harding) 在火星与木星之间又发现了一颗新天体， 这颗新天体很快被命名为婚神星 (Juno)， 它的轨道也基本满足提丢斯-波德定则的预期。 这下算是热闹了， 在火星和木星之间抢夺行星宝座的天体由两个变成了三个。 不过热闹是热闹了， 同时却也成为了最终葬送所有候选者荣登行星宝座机会的导火索。 正所谓 “三个和尚没水喝”， 没有新行星虽然令人失望， 可新行星太多了却更让人受不了， 于是大家逐渐同意了赫歇耳的提议， 将这几个小家伙通通贬为了 “小行星”[注二]。 后来的观测表明， 在火星和木星之间存在着成千上万的小行星， 它们环绕太阳组成了一个美丽的小行星带。

不过当时谁也不会想到， 某些小行星的名份会在时隔两个世纪之后又起了微妙的变化， 这是后话。

八. 轨道拉锯

小行星带的发现对提丢斯-波德定则无疑又是一个很大的支持， 同时也填补了行星轨道分布中唯一的空缺。 如果太阳系还存在其它行星， 那么寻找的范围应该是在天王星的轨道之外， 对应于 n=7 的地方。 这一轨道的半径为 38.8 天文单位。 不过， 无论天文学家们对提丢斯-波德定则的信心如何爆棚， 一个再明显不过的事实是： 即便提丢斯-波德定则真的是一个普遍规律 (事实上它并不是)， 它也绝不可能告诉我们太阳系到底会有几颗行星。 提丢斯-波德定则中的 n 可以无限地增加， 太阳系却不可能是漫无边际的。 小行星带由于出现在火星和木星之间的空缺上， 因此很多人有理由相信在那里能有所发现。 但天王星之外是否存在新的行星， 则完全是一个未知数， 这使得天文学家们寻找新行星的兴趣在经历了天王星和小行星带的发现之后有所降温。

可惜树欲静而风不止， 老天爷看来并不想让天文学家们的日子过得太平静。

天王星被发现之后， 摆在天文学家们面前的一个显而易见的任务就是计算它的轨道。 这在当时是很受青睐的工作， 这项工作几乎立刻就展开了。 如我们在第三节中所说， 在短短几个月内， 萨隆、 莱克塞尔， 和拉普拉斯就各自计算出了天王星的近似圆轨道， 这对于确定天王星的行星地位起了重要作用。 两年后， 拉普拉斯和他的法国同事梅尚 (Pierre Méchain) 又率先计算出了天王星的椭圆轨道。

计算出了轨道， 人们就可以预言天王星在每个夜晚的位置。 一颗遥远行星在天空中的舞步居然可以用科学家手中的纸和笔来导演， 这是牛顿力学最令人心醉的地方， 也一直是天文学家们在艰苦计算之余最大的欣慰和享受 - 那种惬意的感觉， 宛如是在劳作之后品尝一坛醇香四溢的美酒。 不幸的是， 这美酒在天王星这里却变了味。 当天文学家们放下手中的纸和笔， 将望远镜指向理论预言过的位置， 打算像往常一样欣赏一次理论与观测的完美契合时， 这位太阳系的新成员却出人意料地缺席了。

天王星的缺席让天文学家们感到了一丝意外。 但他们没有想到的是， 这小小的意外竟是他们与天王星之间一场长达数十年的拉锯战的开始。

天文学家们起先并未对天王星的缺席太过担忧， 因为天王星的轨道周期长达 84 年， 而当时积累的观测数据只有区区两年， 还不到轨道周期的 3%， 凭借这么少的数据是很难进行精确计算的。 那么怎样才能改善计算的精度呢？ 显然需要更多的数据。 可积累数据需要时间， 这却是半点也着急不得的。 怎么办呢？ 波德想出了一个好主意， 那就是翻旧账， 看看天王星是否在赫歇耳之前就曾经被天文学家们记录过。 如果记录过， 那么将那些历史记录与自赫歇耳以来的现代数据合并在一起， 就可以既提高计算的精度， 又避免漫长的等待。 这个一举两得的好主意没有让波德失望， 如我们在第四节中所说， 天王星的确在赫歇耳之前就曾被反复记录过， 其中最早的记录是英国天文学家弗拉姆斯蒂德 (John Flamsteed) 留下的， 时间是 1690 年， 比赫歇耳早了 91 年。



【英国天文学家弗拉姆斯蒂德(1646 – 1719)】

在历史记录与现代数据的共同帮助下， 奥地利天文学家菲克斯米尔纳 (Alexander Fixlmillner) 率先对天王星轨道作了重新计算， 他的计算包含了 1690 年弗拉姆斯蒂德的记录、 1756 年梅耶 (Tobias Mayer， 德国天文学家) 的记录， 以及 1781 年至 1783 年间赫歇耳和他自己的观测数据。 他计算与观测数据之间的误差只有几角秒[注三]， 这在当时是很不错的结果。 1786 年， 菲克斯米尔纳发表了他的结果。 在天文学家们与天王星的轨道拉锯战中， 菲克斯米尔纳为天文学家们拔得了头筹。

可惜好景不长， 菲克斯米尔纳的计算发表后才过了两年， 天王星就扳回了一城 - 它偏离了菲克斯米尔纳的轨道。 心有不甘的菲克斯米尔纳尽了最大的努力试图挽救自己的计算， 却沮丧地发现历史记录与最新的观测数据仿佛变成了一付跷跷板的两个端点， 一端压下去， 另一端就会跷起来。 看来鱼和熊掌已无法兼得， 菲克斯米尔纳决定舍鱼而取熊掌， 他做了一个在他看来最合理的选择， 那就是抛弃年代最为久远的弗拉姆斯蒂德的观测记录。 做出了这种 “壮士断腕” 的行动后， 菲克斯米尔纳再次计算了天王星的轨道， 总算重新将误差控制在了十角秒以内。

但人们对菲克斯米尔纳的选择并不满意， 因为被他抛弃的弗拉姆斯蒂德的记录虽然年代久远， 观测手段相对简陋， 但信誉却丝毫不容低估。 弗拉姆斯蒂德是格林威治天文台的奠基者， 也是英国第一位皇家天文学家， 不仅拥有显赫的头衔， 而且素以观测细心著称。 他当年曾为牛顿的巨著《自然哲学的数学原理》提供过大量的观测数据[注四]， 他所绘制的星图不仅在当时无与伦比， 甚至在一个世纪之后仍被奉为经典。 在赫歇耳进行天文观测时， 放在他桌上作为参考的正是弗拉姆斯蒂德的星图。 因此抛弃弗拉姆斯蒂德的记录于情于理都很不妥当， 菲克斯米尔纳的新计算能否算是胜利， 实在很难论断。



【法国天文学家达兰伯利(1749 - 1822)】

可要是不抛弃弗拉姆斯蒂德的记录， 跷跷板却又摆不平， 这该如何是好呢？ 简单的逻辑告诉我们， 在观测与理论出现矛盾时， 如果观测没有问题， 那问题就应该出在理论上。 当时的理论确实有一个致命的弱点， 那就是只考虑了太阳的引力， 而没有考虑其它行星的影响， 这其中尤以木星和土星的影响最不容忽视。 1791 年， 法国天文学家达兰伯利 (Jean Baptiste Joseph Delambre) 率先考虑了这两颗巨行星对天王星轨道的影响。 他的计算很好地拟合了当时已知的所有观测数据， 其中包括被菲克斯米尔纳抛弃过的弗拉姆斯蒂德的数据， 以及不久前才被发现的拉莫尼亚的早期观测数据。

在木星和土星这两位老大哥的坐镇之下， 天王星的气焰终于被打压了下去， 天文学家们重新夺回了阵地， 太阳系也重新恢复了往日的循规蹈矩[注五]。 这一 “和谐太阳系” 维持了较长的时间， 直到 1798 年英国天文学家霍恩斯比 (Thomas Hornsby) 视察战场时， 胜利的果实还在枝头挂着。 可就在人们以为战争已然落幕， 刀枪可以入库的时候， 天王星这个注定不肯让天文学家们平静过完十八世纪的家伙， 却将枪口重新探出了大幕！

自 1800 年 (十八世纪的最后一年) 起， 天王星的轨道开始系统性地偏离达兰伯利的计算。

沉默了八年的天王星不鸣则已， 一鸣惊人， 而天文学家们的手中却已无牌可打， 只得仓惶退避。



【法国天文学家波瓦德(1767 – 1843)】

这一退堪称惨败， 整整二十年没缓过劲来。 直到 1820 年， 才有一位叫做波瓦德 (Alexis Bouvard) 的法国天文学家站出来绝地反击。 这二十年里天文学家们倒也没闲着， 现在数据增加了二十年自不用说， 手头的历史记录也增添了两项： 一项是新发现的弗拉姆斯蒂德在 1712-1715 年间的观测记录， 这项记录很好地填补了弗拉姆斯蒂德 1690 年的记录与拉莫尼亚 1750 年的记录之间原本长达 60 年的数据空白； 另一项则是英国天文学家布莱德利 (James Bradley) 1753 年的观测记录。 这时天文学家手中的数据早已不再匮乏， 不仅不匮乏， 反而多到了能噎死人的程度。 波瓦德稍加检视， 就发现自己面临的局面与 30 年前菲克斯米尔纳曾经面临过的有着惊人的相似： 那就是历史记录与现代数据无论如何也不能匹配。 30 年前的局面还有木星和土星来解围， 30 年后的今天还能依靠什么呢？ 无奈之下， 波瓦德只得效仿菲克斯米尔纳的 “壮士断腕”， 可如今的局面比 30 年前还要糟糕， 连断腕都不够， 得断臂 - 将赫歇耳之前的所有历史记录一笔勾销才行。 就这样， 波瓦德靠着 “壮士断臂” 的悲壮， 于 1821 年计算出了一个新轨道， 这个轨道与自赫歇耳以来的新数据勉强吻合。

可这样的反击能算是成功吗？ 恐怕连惨胜都算不上吧？ 人们还从未在一颗行星的轨道计算上栽过如此多、 如此大的跟斗。 而且这次付出的代价也实在太大了一点， 居然把凝聚了那么多天文学家心血的所有历史记录都丢弃了。 更何况即便如此， 波瓦德的轨道与某些现代数据的偏差也仍然高达 10 角秒左右， 这虽不致命， 却也令人疑惑。 不过对于自赫歇耳以来的新数据而言， 这一轨道毕竟是当时最好的， 并且事实上也是唯一一个尚堪使用的轨道， 聊胜于无， 因此一些天文学家还是勉强接受了它。

可光有天文学家的接受是没有用的， 关键还得看天王星这位 “敌人” 是否赏脸。

那么 “敌人” 的回答是什么呢？

注释

赫歇耳提出的名称是 “star-like”， 意思是 “象星星一样”， 形容其小。 “asteroid” 是这一名称在希腊文中的对应。 这一名份之争的完全落幕其实经历了一个较长的时间。 直到 1852 年， 还有天文学教材将当时已发现的小行星与行星合在一起 (共计 23 颗)， 统称为行星。 不过这一趋势在那之后便嘎然而止。 角秒 (也叫做弧秒) 是非常小的角度， 等于一度的三千六百分之一， 或者圆周 (三百六十度) 的一百二十九万六千分之一。 弗拉姆斯蒂德后来与牛顿闹翻了， 此后牛顿利用其至高无上的地位， 以种种不甚光彩的手段对弗拉姆斯蒂德进行了打击。 在这几年中， 天文学家们在人间的日子却过得很不平静， 在法国大革命最血腥狂热的 1794 年， 最早计算出天王星圆轨道的萨隆死于断头台。

二零零七年八月十五日写于纽约

二零零七年九月二十六日发表于本站

二零零九年七月十六日最新修订

关于本文

寻找太阳系的疆界 （五）

九.众说纷纭

在这个节骨眼上“敌人”倒是很沉得住气，没有立刻表态。但仗打到这个份上，“敌人”的不置可否反倒让天文学家们无所适从，几乎陷入了“窝里斗”。事实上，很多天文学家对波瓦德付出的“断臂”代价耿耿于怀，因为按照波瓦德的轨道，那些被丢弃的历史记录与计算之间的偏差高达几十角秒[注一]。这么大的偏差居然同时出现在这么多彼此独立的观测结果中，难不成留下历史记录的那些天文学家全都在观测天王星的时候喝了酒？这实在是令人难以置信的事情。就连波瓦德本人也不得不承认，造成历史记录与现代数据无法匹配的真正原因有待于后人去发现。

但耿耿于怀也好，难以置信也罢，“敌人”既然没有反对，天文学家们也不便自己拆自己的台，于是有人开始为波瓦德抛弃历史记录的做法寻找可能的解释。其中有一种解释认为天王星曾经被某颗彗星“撞了一下腰”，从而偏离了正常的轨道[注二]。如果是这样，那么历史记录与现代数据无法匹配就不再是问题了，因为它们描述的分别是碰撞前和碰撞后的轨道，本来就应该彼此不同。由于历史记录一直覆盖到1771年(那是拉莫尼亚的最后一次记录)，而现代数据则开始于1781年(那是赫歇耳的第一次观测)，因此人们猜测该撞击发生在1771-1781年间。

但是像彗星撞击这样为了特定目的而提出的建立在偶然事件基础上的假设，是科学家们素来不喜欢的。因为人们若是时常用这类假设来解释问题的话，科学就会变成一堆零散假设的杂乱集合，而丧失其系统性。更何况彗星撞击天王星不仅概率实在太小，而且由于彗星的质量与天王星相比简直就是九牛一毛(事实上比九牛一毛还远远不如)，即便真的撞上天王星，也万万不可能对后者的轨道产生任何可以察觉的变化。反过来说，倘若真有一个天体可以通过撞击天王星而显著改变其轨道，那么该天体的质量必定极其可观，那样的撞击若果真发生在1771-1781年间，绝对会是一个令人瞩目的天象奇观，又怎可能不留下任何直接的观测记录呢？因此，彗星撞击说从各方面讲都是一个很糟糕的假设。连这样糟糕的假设都被提了出来，天文学家们在天王星问题上的处境之绝望可见一斑。

更糟糕的是，即便在那样的处境下，天王星还是毫不手软地往天文学家们的伤口上撒了一把盐。自1825年起，天王星故伎重演，开始越来越明显地偏离波瓦德的轨道。几年之后，两者的偏差已经达到了令人绝对无法忍受的30角秒。

“敌人”那姗姗来迟的回答终于被等到了，可惜却是一个那么残酷的回答。

这时候天文学家们实已一败涂地，而且还败得极其难看，因为天王星早不出手晚不出手，偏偏是在天文学家们“臂”也断了，“血”也流了，还煞费苦心地为自己的断臂找了借口之后才出手。那情形，怎一个“惨”字得了？当然，到了这时候，人们也已经习惯了，失败早已不是新闻，天王星若是乖乖听话了反倒会成为新闻。

屡战屡败之下，天文学家们开始改换思路。

仔细想想，彗星撞击说虽然很失败，却也并非一无是处，起码在思路上，它尝试了用外力的介入来解释天王星的出轨之谜。沿着这样的思路，天文学家们又提出了另外一些假设，比如认为天王星的出轨是由某种星际介质的阻尼作用造成的。这种假设以前曾被用来解释某些彗星的轨道变化，但用它来解释天王星的出轨却面临一个致命的困难，那就是介质的阻尼作用只能阻碍天王星的运动，而绝不可能起到相反的作用。说白了，就是只能让天王星运动得更慢，而绝不可能相反。但不幸的是，天王星的运动却有时比理论计算的慢，有时却比理论计算的快，这样的偏差显然是不可能用介质的阻尼作用来解释的。

还有一种假设则认为天王星出轨是由一颗未知卫星的引力干扰造成的。这种假设也有一个致命的弱点，那就是如果真的存在那样的卫星，它的质量应该远比当时已知的两颗天王星卫星大得多，那么大的卫星为何一直未被发现呢？这是很难说得通的。更何况卫星绕行星运动的周期相对于行星的公转周期来说一般都很短(比如月球绕地球运动的周期只有地球公转周期的十二分之一，对外行星来说这一比例通常更小)，由此造成的行星轨道变化应该是短周期的，可是天王星出轨的方式却呈现长期的变化，这是卫星假设无法解释的，因此卫星假设也很快就脸朝下地躺倒了。

除这些假设外，有些天文学家还提出了另外一种可能性，那就是万有引力定律也许并不是严格的平方反比律，甚至有可能与物质的组成有关。这种可能性虽然很难被排除，但万有引力定律是一个“牵一发动全身”的东西，一旦被修正，所有天体的运动都将受到影响，其中也包括那些一直以来被解释得非常漂亮的其它行星及卫星的运动。要想对万有引力定律动手脚，让它解释天王星的出轨，同时却又不破坏其它行星的运动，无疑是极其困难的-如果不是完全不可能的话。而且单凭天王星的出轨就在天体力学祖师爷牛顿的万有引力定律头上动土，也似乎太小题大做了一点，因此这种假设的支持者寥寥无几。

就这样，从拉普拉斯、梅尚、菲克斯米尔纳、达兰伯利，到波瓦德，一次次的计算全都归于了失败；从彗星撞击说、介质阻尼说、未知卫星说，到引力修正说，一个个的假设全都陷入了困境。天王星出轨之谜的正解究竟在哪里呢？到了十九世纪三十年代末，天文学家们在盘点自己的“假设仓库”时发现那里只剩下了一张牌。这张牌是唯一一个没有倒下的假设，这个假设已是最后的希望，可这个希望的背后却是一道令人望而生畏的数学难题。

天王星出轨之谜的正解期待数学高手的横空出世！

十.数学难题

这个硕果仅存的假设读者们想必已猜出来了，那就是在天王星轨道的外面还存在另一颗大行星，正是它的引力作用干扰了天王星的轨道，使它与天文学家们捉了将近半个世纪的迷藏(请读者们定性地想一想，天王星之外存在新行星的假设为何能避免前面提到的介质阻尼说和未知卫星说所遭遇的困难？)。在天王星之外存在新行星的猜测本身其实并不出奇。事实上，自天王星被发现之后，稍有想象力的人都可以很容易地想到这一点。不过，泛泛猜测一颗新行星的存在是一回事，将这种猜测与已知天体的运动联系起来，从而形成一种具有推理价值的假设，乃至于用这一假设来解决一个定量问题，则是另一回事。后者无疑要高明得多，困难得多，它的出现也因此要晚得多-直到1835年才正式出现。

1835年的11月，著名的哈雷彗星经过了将近76年的长途跋涉，重新回到了近日点。天文爱好者和天文学家们共同迎来了一次盛况空前的天文观测热潮。就在万众争睹这个多数人一生只有一次机会能用肉眼看到的美丽彗星时，天文学家们却注意到了一个小小的细节：那就是哈雷彗星回到近日点的时间比预期的晚了一天。一个长达76年的漫长约会只晚了区区一天，算得上是极度守时了，但天文学家们的敏锐目光并未放过这个细小的偏差。法国天文学家瓦尔兹(BenjaminValz)和德国天文学家尼古拉(FriedrichBernhardNicolai)几乎同时提出了一个假设，那就是哈雷彗星的晚点有可能是受一颗位于天王星轨道之外的新行星的引力干扰所致[注三]。由于当时天王星出轨之谜早已传得沸沸扬扬，瓦尔兹进一步猜测这颗未知行星有可能也是致使天王星出轨的肇事者，这便是天王星出轨之谜的新行星假设。

与那些一出道就遭遇致命困难的其它假设相比，新行星假设没有显著的缺陷，这个难能可贵的特点使它很快就脱颖而出。到了1837年，就连波瓦德也开始接受这一假设了。波瓦德的外甥在给英国皇家天文学家艾里(GeorgeBiddellAiry)的一封信中提到，他舅舅(即波瓦德)已开始相信天王星出轨的真正原因在于天王星之外的未知行星的干扰[注四]。艾里当时是英国格林威治天文台的台长，他在我们后面的故事中将是一位重要人物。艾里对天王星出轨之谜也非常关注，他手头掌握着大量的观测数据，并且还撰写过有关这一问题的详尽报告。通过对天王星轨道数据的细致分析，艾里发现了一个当时鲜为人知的问题，那就是计算所得的天王星位置不仅在角度上与观测数据存在着众所周知的偏差，而且在径向-即天王星与太阳的距离-上也与观测数据存在偏差。艾里认为这种偏差的存在表明理论计算本身还有缺陷，他把这看成是解决天王星出轨之谜的关键。至于新行星假设，艾里则很不以为然。

艾里对新行星假设的不以为然，以及他对天王星出轨症结的判断后来被证实为是不正确的。他个人所持的这些观点虽不足以阻挡新行星假设快速流行的步伐，但由于他在英国天文学界举足轻重的地位，他的这种日益孤立的见解为后来英国在寻找新行星的竞争中落败埋下了种子。

新行星假设虽然受到了广泛关注，但要想证实这一假设却绝非易事。证实它的最直接的方法显然就是找到这颗未知的新行星，通过观测确定其轨道，然后再根据其轨道计算它对天王星的影响。如果这种影响恰好能够解释天王星的出轨，那么新行星假设就算得到了证实。

可问题是，究竟该到哪里去寻找这颗未知的新行星呢？它离太阳的距离比天王星还要遥远(如果提丢斯-波德定则有效的话，它离太阳的距离应该比天王星远一倍左右)，因此一般预期其亮度要比天王星暗淡得多。另一方面，它的移动速度则要比天王星慢得多，因此不仅搜寻的难度大得多，而且判断其为行星也要困难得多。这样的搜寻听起来意义非凡，实际上却是一项风险很大的工作，很可能投入了巨大的人力、物力及时间，结果却换得竹篮子打水一场空。另一方面，当时各大天文台都有相当繁重的观测任务(其中有些虽号称是天文观测，其实却是“为国民经济保驾护航”一类的测绘及定位任务)，既没有意愿也没有条件进行这种额外并且高风险的搜寻工作。

既然依靠观测这条路走不通了，那么对新行星假设的判定就只能通过纯粹的数学计算来实现了。毫无疑问，这种执果求因的计算要比计算一颗已知行星对天王星的影响困难得多，因为新行星既然是未知的，它的质量、轨道半径、轨道形状、与天王星的相对角度等所有参数也就都是未知的。因此在计算时既要通过天王星出轨的方式来反推那些参数的数值(这是相当困难的数学问题)，也需要对无法有效反推的参数数值进行尽可能合理的猜测，然后还得依据这些反推或猜测所得到的参数来计算新行星对天王星的影响，并通过计算结果与观测数据的对比来修正参数(这是相当繁重的数值计算-别忘了那时可还没有计算机)。这种反推、猜测、计算、对比及修正的过程往往要反复进行很多次，才有可能得到比较可靠的结果。因此要求计算者既有丰富的天体力学知识，又有高超的计算能力，而且还要有过人的毅力、耐心和细致。

幸运的是，历史不仅给了天文学界这样的人物，而且很慷慨地一给就是两位。

注释

多数读者可能对天文观测的精度没有概念。几十角秒的误差是个什么概念呢？那相当于丹麦天文学家第谷(TychoBrahe)的观测误差。第谷是十六世纪的天文学家，比最早观测天王星的弗拉姆斯蒂德还早了一个世纪，他的全部观测都是依靠肉眼进行的(望远镜的发明是他去世之后的事)。因此几十角秒的误差所对应的精度是肉眼观测的精度(虽然对于肉眼来说这应该算是最高的精度-因为第谷是他那个时代最杰出的天文观测者)。望远镜发明之后，天文观测的精度有了数量级的提高。据分析，伽利略的观测精度就已达到了两角秒。 有的读者可能会觉得奇怪，天文学家们怎么每次碰到问题时，都会拿彗星说事？发现新行星时先说是彗星，不想让某个天体(比如智神星)成为行星时也说是彗星，现在又说天王星被彗星撞了腰。原因其实很简单，因为在那时侯，天空中最常被观测到的不速之客就是彗星。 早在1758年，即天王星尚未被发现的时候，就有天文学家猜测象哈雷彗星这样有机会远离太阳的彗星，有可能受到遥远的未知行星的影响。不过那种猜测在当时并未得到任何具体数据的支持。 据艾里后来回忆，他甚至在1834年就曾收到过一位名叫赫西(ThomasHussey)的英国业余天文学家的类似提议，不过那个提议没有明说未知天体是一颗行星。

二零零七年十一月一日写于纽约

二零零七年十一月三日发表于本站

二零零九年七月十七日最新修订

关于本文

寻找太阳系的疆界 （六）

十一. 星探出击

就在波瓦德向天王星轨道问题发起唐吉诃德式冲击的前一年，即1819年，一个小男孩降生在了英国康沃尔郡(Conwall)的一个农夫家庭，他被取名为约翰?亚当斯(JohnCouchAdams)。这个孩子很早就显露出超乎常人的数学计算能力。还在孩提时期，他就自学掌握了大量数学技巧。在十六岁那年，他通过复杂的计算相当准确地预言了发生在当地的一次日食，震动了乡邻，也预示着他一生的追求。



英国天文学家亚当斯 (1819 – 1892)

1839年，亚当斯进入剑桥大学的圣约翰学院深造。两年后的一个夏日，他在一家书店里看到了艾里有关天王星问题的报告。那时候，观测数据与波瓦德轨道的偏差已达到了创纪录的70角秒，天王星出轨之谜比以往任何时候都更尖锐。已有十八年历史的波瓦德轨道虽已千疮百孔，却仍象幽灵一般浮现在天文学家们的眼前，刺痛着他们。但这一切对于年轻的亚当斯却是一个巨大的机会。对一位十六岁就能预言日食的年轻数学高手来说，有什么能比与天王星出轨之谜这样的绝世难题同处一个时代更令人兴奋呢？亚当斯立即就被这一问题深深地吸引住了。

不过，吸引归吸引，年轻的亚当斯还不能马上就投入到这个问题中去。为了替自己今后从事真正的学术研究创造尽可能有利的条件，他必须首先完成剑桥大学的学业，为两年后将要到来的毕业考试做好准备。这些虽不是他的终极兴趣，却对他最长远的学术前途有着至关重要的影响。现实人生往往就是如此，你想做一件事，但生活却用这样那样的其它事情来牵制你的兴趣。不过处置得宜的话，这种牵制未必会成为羁绊。亚当斯的努力没有白费，1843年，他以最优异的成绩通过了毕业考试，据说他的数学成绩竟比第二名高出一倍以上。几星期后，他又获得了剑桥大学的最高数学奖-史密斯奖，并如愿以偿地成为了圣约翰学院的研究员(fellow)。

1843年的最后几个月，亚当斯的生活甚至比考试前还要繁忙。放在他面前的是三重任务：一是对天王星轨道进行研究，这是他的梦想和兴趣，他终于可以追逐自己的梦想了，但在时间上却必须与其它任务共享；二是要完成圣约翰学院的教学任务，这是生存的需要；三是替剑桥天文台的台长查利斯(JamesChallis)计算一颗彗星的轨道，这是他与剑桥学术界的正式交流，同时也是一次很好的热身，因为这一计算要求考虑木星对彗星的引力干扰，而天王星出轨之谜的关键也正在于其它行星的引力干扰，两者不无相似之处(当然后者要困难得多)。亚当斯有关彗星的计算发表于1844年初，他的结果与一位法国天文学家的计算吻合得很好，这一点很让他高兴。但他也许做梦也不会想到，自己与那位法国天文学家的命运在未来几年里竟会交织出那么多的故事和风波。

那位法国天文学家的名字叫做勒维耶(UrbainLeVerrier)，他出生在法国的诺曼底，比亚当斯大八岁。他正是历史带给天文学界的另一位数学高手！

与完成彗星轨道的计算几乎同时，亚当斯也完成了对天王星轨道的初步分析。他首先仔细检查了波瓦德的计算，发现并纠正了一些错误，但这些小打小闹并不足以挽救波瓦德的轨道。在确信波瓦德轨道已经无可救药之后，亚当斯正式采纳了新行星假设。那颗神秘的新行星究竟在哪里呢？亚当斯开始了用纸和笔寻找答案的艰难历程。作为计算的起点，他假定新行星在提丢斯-波德定则所预言的距太阳38.8天文单位的椭圆轨道上运动。他的初步评估得到了令人振奋的结果：新行星对天王星的影响看来的确可以解释天王星的出轨之谜。但为了得到可靠的结果，亚当斯需要更多的数据，于是他向自己刚刚帮助计算过彗星轨道的查利斯求援。

查利斯此人在我们后面的故事中也是一位重要人物，他当时很够意思，立即就写信向艾里索要数据。艾里这人我们已在上节中提到过，他是当时格林威治天文台的台长，在英国天文学界算得上是重量级的人物。在那之前，他也曾但任过剑桥天文台的台长，因而是查利斯的前任。如我们在上节中所说，艾里很关心天王星出轨之谜，手头也有最新的观测数据，但他对新行星假设并不看好。艾里工作一丝不苟，但为人古板，缺乏想象力。在他管束下的格林威治天文台台规森严、条框众多。这一切对后来故事的发展有着不可忽视的影响。亚当斯通过查利斯向艾里索要数据，也许是他与艾里之间第一次打交道。这次交道虽然间接，但却非常顺利，艾里立刻就寄来了数据。

可惜这也是接下来两年半的关键时间里亚当斯与艾里之间唯一一次顺利的交道。

拿到了数据，亚当斯立刻就投入到了更精密的计算之中。不过，学院的教学任务与彗星计算还是从他那里夺走了一部分时间。1844年秋天，查利斯又让亚当斯帮他计算一颗彗星的轨道-那是一颗新发现的彗星。那时亚当斯对此类计算早已轻车熟路，秋叶尚未落尽，他的计算结果就出来了。但出人意料的是，亚当斯如此麻利的计算竟然还是慢了一步，一个已不再陌生的法国名字抢在了他的前面：勒维耶。

但亚当斯此刻已无暇品味自己与这位法国同行在研究课题上二度撞车的深刻寓意了，他的精力越来越多地投入到了推测未知行星轨道的计算之中。如我们在上节所说，这是一项极其复杂的计算。如果说扎克和他那些试图围捕小行星的朋友是天空警察，那么亚当斯就应该算是星探-当然不是寻找演艺明星的星探，而是星空侦探，他要做的是通过“罪犯”在“犯罪现场”-即天王星轨道-留下的蛛丝马迹，来推断其行踪。

亚当斯从1780年到1840这60年的现代观测数据(其中很多是艾里提供的)中以每三年为一个间隔整理出了21组数据。他分别计算了这21组数据与波瓦德轨道的偏差，并与新行星产生的影响进行比较及拟合。由于新行星的轨道参数中除用提丢斯-波德定则确定的半长径外，其余全都是未知的，他需要通过不断调整参数来寻求最佳的拟合效果。在计算中他还采用了高斯计算谷神星轨道时所用的误差控制方法。考虑到当时的计算主要依靠手算[注一]，这实在是一件令人望而生畏的工作。亚当斯以惊人的专注和毅力进行着计算-这也是他一贯的风格。他的兄弟乔治(GeorgeAdams)曾有一段时间陪伴他熬夜，帮他验证一些计算结果。在乔治撰写的回忆中，他提到有很多次当他实在熬不下去时，他想让亚当斯去睡觉(那样他自己也可以休息)，亚当斯总是说：再等一会儿。而那“一会儿”却总是无穷无尽般的漫长。在亚当斯沉醉于计算的那些日子里，他几乎神游物外，甚至在与乔治一起散步时都需要后者提醒他避开障碍物。经过这样没日没夜的努力，当下一个秋天来临时，1845年9月，亚当斯的计算终于有了结果。

十二.三访艾里

按照亚当斯的推算，新行星的质量约为天王星的三倍，运动轨道则是一个半长径为38.4天文单位(比一开始假定的38.8天文单位略小)的椭圆轨道。在这样一颗新行星的影响下，亚当斯将天王星的出轨幅度由原先的几十角秒压缩到了1-2角秒，并预言了新行星1845年10月1将在天空中出现的位置。由于亚当斯在计算中只用到了现代数据，因此一个很自然、并且也很重要的问题是：他的计算是否也可以解释历史记录？为此，亚当斯进行了验证，结果发现答案是肯定的。历史纪录与现代数据的跷跷板第一次被摆平了，这在很大程度上印证了计算结果的可靠性，也间接印证了新行星假设的合理性。

亚当斯这些繁复计算的完成，在时间上与他为预测新行星位置所选的1845年10月1日这一日子已相距不远。如果他能象当年的赫歇耳那样拥有一流的望远镜，且精于观测的话，完全有可能通过几周甚至-如果运气好的话-几个夜晚的观测，就亲自发现那颗新行星，因为他所预测的位置距离新行星当时在天空中的实际位置只相差了不到两度[注二]。可惜亚当斯并没有那样的条件，于是他将自己的计算结果告诉查利斯，再次寻求后者的帮助。

查利斯也再次表现出了够意思的特点，只不过他的“意思”似乎总也离不开书信，他接到亚当斯的请求后，于9月22日替亚当斯写了一封推荐信，让他面呈给艾里。查利斯在信中称亚当斯的计算是可以信赖的。但令人困惑的是，查利斯身为剑桥天文台的台长，自己就拥有搜索新行星所需的一切技术条件，却为何要舍近求远地把亚当斯推荐给艾里呢？而且他作为年长者，居然没有建议亚当斯正式发表那些“可以信赖的”的计算结果，这又是为什么呢？对此，一个可能的解释是查利斯其实并未真正相信亚当斯的结果。亚当斯的能力虽然已经通过替他计算彗星轨道而不止一次地得到了显现，但那些计算的难度与通过天王星轨道来反推一颗未知行星的行踪相比，无疑还相差很远。不管是出于什么原因，查利斯这位堪称当时全英国最了解亚当斯的天文学家，在这个至关重要的历史节骨眼上没有选择直接的帮助和参与，这是他与发现新行星的机会第一次擦肩而过。

九月底，亚当斯带着查利斯的推荐信来到格林威治天文台拜访艾里。这是他第一次拜访艾里，可惜艾里当时正在在法国开会，让他扑了一个空。出师不利的亚当斯只得留下查利斯的推荐信无功而返。艾里回到天文台后看到了查利斯的推荐信，他很快就给查利斯回了信，对错过与亚当斯的会面感到遗憾，并礼貌地表示对亚当斯的工作很感兴趣，欢迎后者与他建立通信联络。亚当斯得知这一消息后决定再次访问艾里。

1845年10月21日下午3点左右，亚当斯再次来到了格林威治天文台[注三]。不巧的是，艾里居然又不在。不过这次他只是暂时外出，于是亚当斯向艾里的管家表示自己过一会儿会再来，并留下了一张一页纸的计算结果。亚当斯在附近溜达了大约一个小时后重新来到了艾里家。不幸的是，不知是由于管家的疏失还是其它什么原因，艾里似乎并未收到亚当斯的“拜山帖”，也不知道他会返回。因此当亚当斯第三次登门拜访时，被告知艾里正在吃午饭，不见客人[注四]。因为吃午饭就不见客人，这听起来似乎有些无理，其实在英国这样一个礼仪森严的国家里却不足为奇，尤其是艾里乃是天文界的资深前辈，而亚当斯只是一位初出茅庐的年轻人，艾里在吃饭时不见亚当斯丝毫不算出格。但尽管礼仪如此，连吃三次闭门羹还是让亚当斯失去了耐心，他没等艾里吃完午饭就返回了剑桥。



【格林威治天文台】

回到剑桥后，亚当斯把寻求观测支持的事搁到了一旁，他决定进一步改进自己的计算。在他第一轮的计算中，曾将未知行星的轨道半长径假设为38.8天文单位，这是提丢斯-波德定则的预言。但提丢斯-波德定则虽已接连被天王星和小行星带的发现所支持，却终究没什么理论基础，因此亚当斯对建立在提丢斯-波德定则基础上的轨道半长径假设并不满意。在新一轮的计算中，他决定放弃这一假设，而尝试一个稍小一点的轨道半径：37.3天文单位。

另一方面，艾里最终还是看到了亚当斯留下的那一页计算结果。两个星期之后，即11月5日，他给亚当斯回了一封信。在回信中，艾里与亚当斯自己一样，也质疑了提丢斯-波德定则的有效性，但他同时还提出了另外一个问题：那就是如何解释天王星出轨之谜中的径向偏差。我们在第十节中曾经介绍过，天王星轨道的径向偏差在艾里眼中是很重要的问题，他甚至认为这很可能就是解决天王星出轨问题的关键。由于他的这一看法并未得到其他天文学家的重视，因此艾里一有机会就要重提这一问题，对亚当斯自然也不例外。

但这回却轮到艾里吃闭门羹了，因为亚当斯并未对艾里姗姗来迟的信件作出回复。亚当斯的沉默落在艾里眼中无疑变成了一个信号，让他以为自己的问题已击中对方的要害，两人的联系就此中断。

那么，亚当斯为什么不回复艾里的信件呢？据他后来在一封为此事而向艾里表示歉意的信中所说，那是因为他并未意识到艾里对这一问题如此看重。很多年后，他在给一位朋友的信中则表示，他当时觉得艾里的问题太过简单，因此没有及时回复。不过亚当斯的这些解释颇有避重就轻之嫌，其可信度是值得怀疑的。艾里怎么说也是前辈，哪怕他真的提了一个太简单或不重要的问题，甚至我们把亚当斯对前不久的闭门羹一事还耿耿于怀的可能性也考虑在内，作为后辈的他似乎也都没有理由用不回信这样失礼的方式来处理。这样的事情别说在英国，即便在礼仪相对宽松的其它国家，恐怕也是不合情理的。

如果亚当斯自己所说的原因不合情理，那么真正的原因会是什么呢？从逻辑上讲，最有可能的答案恐怕就是：他是因为无法及时对艾里的问题作出明确回答，才没有回复的。这一点后来得到了一些史料的佐证，因为人们在亚当斯残存的笔记中发现他曾试图解决艾里的问题。这与他在上述信件中所说的并未意识到艾里对这一问题的看重，以及认为艾里的问题太过简单显然是有些自相矛盾的。

但无论出于什么原因，忽视也好、为难也罢，甚或只是纯粹的偶然，亚当斯与艾里三番四次无法建立有效的联系，无论对他们两人，还是对整个英国天文学界都是一个极大的遗憾。就在机遇从亚当斯、查利斯和艾里的指缝间一次次遗落的时候，一位法国天文学家把自己的目光投向了天王星的出轨问题。

这已是此人第三次与亚当斯在相同的问题上相遇。

注释

当然，对数表等数学表格对部分计算可以起到辅助作用。 需要提醒读者的是，这一偏差是指计算位置与实际位置的偏差，而非计算误差(请读者想一想，这两者的差别是什么？)。后来有人对这一数据，乃至英国方面的整个故事都提出了质疑，对此我们将在后文中加以介绍。 据说人们并未在当时遗留的日记、信件等文字记录中找到亚当斯第二次访问艾里的确切日期，因此10月21日这个日期是后人的推断。 关于这一点，艾里夫人曾留下过两个不同版本的书面说法，后人据此认为有关艾里一家当时正在吃午饭的传言未必确凿。由于艾里一家当时正在做什么对整个事件的发展并无特殊重要性，因此本文不予细究，这里提一下只是为了告诉读者史学界对这一细节存有不同看法。

二零零七年十二月四日写于纽约

二零零七年十二月十七日发表于本站

二零零九年七月十八日最新修订

寻找太阳系的疆界 （七）

十三. 殊途同归

这位法国天文学家的名字大家一定猜出来了。是的，他就是两次在彗星轨道计算中与亚当斯不期而遇的勒维耶。勒维耶有着与亚当斯同样杰出的数学技能，不过他的天文之路却略显曲折。1830年，初出茅庐的勒维耶在报考法国第一流的理工学校巴黎综合理工学院(?colePolytechnique)的竞争中不幸落败。由于勒维耶在当地学校的成绩一向十分优异，他父亲将失败的原因归咎于当地整体教育水平的低下。望子成龙的他毅然变卖了房产，将勒维耶送到巴黎复习备考。第二年，脱离了山沟沟的勒维耶终于变成了金凤凰，不负重望地进入了巴黎综合理工学院。

与亚当斯一样，勒维耶以最优异的成绩通过了学校的毕业考试。不过毕业后的勒维耶却一度进入了与天文学风马牛不相及的政府烟草部门，并跟随化学家盖-吕萨克(JosephLouisGay-Lussac)从事过一些化学方面的研究[注一]。1837年，当巴黎综合理工学院的一个天文学教职出现空缺时，盖-吕萨克建议并推荐勒维耶获得了这一教职。虽然对导师建议的转行感到意外，但勒维耶很快就发现天文学是一个可以充分展现自己数学才华的迷人领域。转行天文后的勒维耶主要从事天体轨道的计算与分析。短短几年间，他便在该领域树立起了自己的名声。

勒维耶的理论研究有着鲜明的系统性，这一点与当年赫歇耳的观测工作颇有异曲同工之处。自1840年以来，勒维耶对太阳系天体的运动做了近乎地毯式的研究，先后考察了水星、金星、地球、火星、木星、土星及若干彗星的运动。1845年秋天，在巴黎天文台台长阿拉果(Fran?oisArago)的提议下，他将注意力转向了当时已知的最后一个行星：天王星。

与亚当斯一样，初涉天王星问题的勒维耶也对波瓦德轨道进行了细致分析，也发现并纠正了一些错误，他的结论也和亚当斯一样，那就是波瓦德轨道已经无可救药了-仅凭木星和土星的影响是无论如何也摆不平天王星轨道的。接下来，勒维耶又近乎地毯式地逐一分析了我们在第九节中介绍过的几种试图解决天王星出轨之谜的假设，并将它们一一排除。这样，他顺理成章地将注意力转向了当时已知的最后一个假设：新行星假设，并且与亚当斯一样，走上了用纸和笔寻找新行星的艰难之旅。

作为计算的出发点，勒维耶也采用了提丢斯-波德定则，把新行星的轨道半径假定为38.8天文单位(在计算过程中微调为了38.4天文单位，与亚当斯第一次计算的结果相同)。不过与亚当斯所用的椭圆轨道不同的是，他假定新行星的轨道为圆形。为了确定新行星在轨道上的位置，他将轨道按角度均匀地分割成了40个区段，每段9°(因为整个圆周有360°)。显然，在任何一个选定的时刻-勒维耶将之选为1800年1月1日-新行星必定位于这40个区段中的某一个区段内。那么它究竟位于哪一个区段呢？勒维耶再次发挥了自己的系统风格，他逐一考察了新行星在选定时刻位于40个区段中的任何一个区段内所能对天王星轨道产生的影响。通过极其繁复的计算、对比和排除，到了1846年5月底，勒维耶终于找到了能够使天王星轨道最接近观测结果的那个区段。在此基础上，他预言了1847年1月1日新行星所处的位置。

勒维耶的计算结果与亚当斯的相当接近。英吉利海峡两边的这两位数学高手的智慧之剑指向了同一个天区，只不过当时勒维耶和亚当斯谁也不知道对方的工作。

与亚当斯不同的是，勒维耶公开发表了自己的计算，从而引起了一定程度的关注，因为那时天王星出轨之谜已经困扰天文学家们达半个世纪之久，新行星假设成为解决这一谜团的主流假设也已有差不多十个年头，这还是第一次有人计算出新行星的确切位置(亚当斯的结果因为没有发表，除查利斯和艾里外，尚处于无人知晓的状态)。1846年6月下旬，勒维耶的论文抵达了艾里所在的格林威治天文台。

如果说其他天文学家对勒维耶结果的关注在很大程度上是出于新奇，那么对艾里来说，勒维耶的结果则带来了一定的震动，因为这一结果与他大半年前曾经见过的亚当斯的结果相当接近[注二]。亚当斯在当时还是一个籍籍无名的年轻人，但勒维耶已有一定的知名度，艾里也许可以忽略亚当斯，但对勒维耶的结果却不能等闲视之。而且更重要的是，在这么困难的问题上，两个人同时算错并非不可能，但错得如此接近却令人难以置信。因此，这时的艾里对亚当斯和勒维耶的结果已不得不刮目相看，他甚至向包括小赫歇耳(JohnHerschel-发现天王星的老赫歇耳的儿子)在内的几位朋友及同事提及了这两人的计算彼此接近，以及在近期内借助计算结果发现新行星的可能性。

不过，要让艾里信服勒维耶的计算还必须解决他心头的一个老大难问题，那就是他当年曾问过亚当斯，却未得到回答的那个天王星轨道的径向偏差问题。这一问题依然盘亘在艾里的脑海里，于是他写信给勒维耶，询问他的计算能否解决这一问题。1846年7月1日，艾里从勒维耶的回信中得到了非常肯定的答复。这下艾里终于信服了。但即便如此，他却并未采取立即的行动。从我们这个史话的角度看，艾里此时的迟钝是一件非常奇怪的事情，但我们不能忘记，在这位皇家天文学家的日程中本就有太多的东西需要他去关注-虽然那些东西的重要性在事后看来与他错过的东西相比根本就不值一提。幸运的是，艾里早年的一位数学老师在关键时候击碎了他的迟钝。7月6日，艾里与这位名叫皮考克(GeorgePeacock)的数学教授谈及了天王星出轨问题及亚当斯和勒维耶的计算。老教授对艾里同学的迟钝大为惊讶，敦促他立即采取行动。

三天后，艾里终于采取了行动。

而这时候，勒维耶在做什么呢？他和亚当斯一样，投入到了新一轮的精密计算之中。在这一轮的计算中，他决定放弃前一轮计算所采用的两个不太令人满意的假设：其中一个是提丢斯-波德定则，勒维耶和亚当斯一样，认为这是一个没有足够理论基础的假设；另一个则是圆轨道假设，这无疑是一个过于特殊的假设。放弃这两个假设后，勒维耶将新行星的轨道调整为了半长径为36.2天文单位的椭圆轨道。

勒维耶对新计算的沉醉，在无意间为艾里及英国天文学界创造了一个难得的机会。因为一方面，沉醉于计算的勒维耶把寻求观测支持的事情搁到了一边；另一方面，勒维耶进行新计算这一消息本身在一定程度上降低了欧洲大陆的天文学家们对他前一轮计算的重视程度。这样的局面对于艾里以及他的少数英国同事来说无疑是非常有利，因为只有他们知道亚当斯的结果，从而也只有他们才知道勒维耶的计算并非孤立结果。一个复杂的计算，它是孤立结果还是得到过独立来源的佐证，其可信度是截然不同的。英国人曾将亚当斯提供的先机轻轻葬送，但此刻的他们趁着欧洲大陆的天文学家们对勒维耶的计算将信将疑，心存观望之际，提前洞悉了这一结果的可信度，并决定展开行动，这无疑是再次将先机揽到了自己身旁[注三]。

那么，英国绅士们能够把握住这稍纵即逝的先机吗？

十四.剑桥梦碎

如果要在格林威治天文台的历任台长中评选几位从事天文观测最少的台长，艾里无疑会名列前茅。自从1835年出任台长以来，八年的时间里，艾里参与过的观测仅占同期天文台观测总数的千分之二。即便在发现新行星的荣誉有可能唾手而得的时候，艾里仍没有打算亲自参与观测。他更感兴趣的问题倒是让谁来摘取这一荣誉。结果他选择了剑桥天文台，那是他就任格林威治天文台台长之前任职过的地方，那里有他亲自督建的高品质的诺森伯兰望远镜(Northumberlandtelescope)[注四]。而且，亚当斯、艾里自己，以及剑桥天文台的现任台长查利斯都是剑桥的毕业生，让剑桥天文台成为新行星的发现地，无疑可以演绎一出最完美的“剑桥天文故事”。



【诺森伯兰望远镜落成之初 图片出处：www.61k.comuk】

不过平心而论，要说艾里选择剑桥天文台而非自己所在的格林威治天文台是纯粹的心血来潮或浪漫胸怀，却也并非实情。事实上，格林威治天文台的名头虽大，可是由于承担了太多时间及经纬方面的测定任务，它所拥有的望远镜已经按这些特殊任务的需要进行了改动，比方说它的方向已被固定在了特定的子午线(即经线)上，以便能精确测定日月星辰穿越子午线的时间，而且它的放大倍率也比不上剑桥天文台的望远镜(格林威治天文台的望远镜口径只有6.7英寸，而剑桥的诺森伯兰望远镜的口径达11.75英寸)。这些都使得格林威治天文台已变得不再适合行星搜索工作了。因此艾里的选择也可以说是形势使然。

主意既定，艾里便于1846年7月9日写信给查利斯，叙述了剑桥天文台搜索新行星的有利条件，然后请他展开搜索。艾里并且表示，如果查利斯本人没有时间的话，他可以从格林威治天文台抽调一位助理予以协助。但艾里的信发出之后却变成了泥牛入海，查利斯并未及时回复。等了四天没有回信，艾里终于着急了，他再次写信给查利斯，提醒他寻找新行星的重要性应当凌驾于任何不会因推延而失效的其它工作之上。

查利斯居然还是没回信。

原来艾里的这位继任者当时并不在剑桥，而是在度假。当年的天文学家既没有电话也没有电子邮件，更没有个人博客可以随时向外界展示自己的行踪。艾里对查利斯度假的消息一无所知，白白着了一场急。7月18日，查利斯终于回到了剑桥天文台，他立刻给艾里回了信，表示将尽快展开观测。艾里随即给查利斯提供了一个以勒维耶和亚当斯的计算结果为中心，东西范围30°，南北范围10°的区域作为搜索范围。

但查利斯在动作迟缓方面并不比他的前任艾里先前的拖拉来得逊色，他的“尽快”足足经过了十天的时间才付诸实施。在那期间，他向亚当斯提及了自己将要搜索新行星的消息。此时亚当斯的新一轮计算已接近完成，他向查利斯提供了一些新的数据[注五]。这时距离艾里收到勒维耶的回信已相隔近一个月，所幸欧洲大陆的情势并无实质变化，勒维耶的新一轮计算仍未结束，欧洲大陆的各主要天文台也仍无动于衷。

7月29日晚，查利斯的搜索行动正式展开。英国天文界的成败在此一举。

按照后来查利斯向艾里及英国报刊提供的叙述，在搜索中，他首先以亚当斯提供的位置为中心，观测了宽度为9弧分(弧分也叫做角分，一弧分等于1/60度)的区域中所有视星等在11以上的天体。几天之后他的观测因天气而受阻。8月12日天气转好，查利斯对7月30日曾经观测过的天区进行了复测。然后他开始对比7月30日的观测结果与8月12日的复测结果。这种对比是搜索行星的标准手段，如果在对比中发现任何一个天体的位置发生了变化，那么这个天体就有可能是查利斯所要寻找的新行星。一组、两组、三组......查利斯一连对比了三十九组数据，全都匹配得完美无缺，这表明那些都不是他要寻找的新行星。虽然还剩下一些数据尚未对比，但查利斯觉得这一天的对比不会有什么收获了。他想起自己手头还有一些彗星数据需要处理，于是便提前终止了对比工作。

这一决定酿成了查利斯一生最大的遗憾，也彻底葬送了艾里梦想的“剑桥天文故事”。

查利斯完全没有想到，在这场无形的竞争中，就在他迎来长久阴霾之后的第一个好天气时，幸运女神又一次-也是最后一次-将垂青的目光投到了英国人的头上。新行星的数据此刻就静静地躺在他8月12日的复测记录中。那一天，查利斯只要再多对比十组数据，就会发现8月12日所纪录的第四十九个天体-一颗蓝色的8等星-在7月30日的纪录中是不存在的。这说明那个天体7月30日还不在他所观测的天区中，8月12日却进入了该区域，那是一个移动的天体，那个移动的天体正是艾里要他寻找的新行星！

一招失误，满盘皆输。

在八月份余下的日子里，查利斯继续对附近的天区进行搜索，结果一无所获。九月初，他放弃了搜索。

注释

盖-吕萨克在化学方面有不少贡献，比如我们在中学化学课上接触过的气体化合体积定律，即盖-吕萨克定律，就是以他的名字命名的。 如果将他们的计算统一折算成平均日面经度(meanheliolongitude)的话，那么亚当斯的结果是1845年10月1日新行星位于经度323.5°；勒维耶的结果则是1847年1月1日新行星位于经度325°。 严格讲，欧洲天文学界并非铁板一块，在欧洲的某些地方曾有过一些零星的观测。 该望远镜是一位诺森伯兰公爵(DukeofNorthumberland)于1833年捐助的，故而得名。 关于亚当斯向查利斯提供的究竟是什么数据，后来有人提出了质疑。质疑者认为亚当斯当时提供的其实是勒维耶第一轮计算的结果。如果那样的话，那些数据与亚当斯当时即将完成的计算应该没什么关系。

二零零八年一月一日写于纽约

二零零八年一月一日发表于本站

二零零九年七月十九日最新修订

寻找太阳系的疆界 （八）

十五.欲迎还拒

查利斯的失败，宣告了英国人在这场几度领先的无形竞争中丧尽先机、黯然出局。虽然此刻他们还不清楚自己究竟失去了什么，但历史的风标已无可阻挡地偏向了后来居上的欧洲大陆。

就在查利斯终止新行星搜索之前不久，1846年8月底，勒维耶完成了他的新一轮计算。那时候，他在整个计算中用去的稿纸数量已经超过了10000页。勒维耶的新结果与原先的结果相当接近(偏差只有1.5°)，这是一个好兆头，它表明勒维耶的计算方法很可能具有良好的稳定性。按照勒维耶的计算，虽然新行星的轨道半径比天王星大了将近一倍，但由于其质量也比天王星大得多，因此亮度依然可观。勒维耶很清楚，再好的计算若是离开了观测的验证，也只能是空中楼阁。他已经用了一年的时间来构建这座宏伟的楼阁，现在是该让一切落地生根的时候了。于是他开始尽其所能地劝说天文学家们对新行星展开搜索。

而此时的英国几乎只剩下了一个人还在为新行星的命运做最后的奔走，他就是亚当斯。比勒维耶晚了几天，亚当斯也完成了自己的新计算。只不过，勒维耶循正常而公开的学术渠道发表了自己的所有计算，而亚当斯却仍在继续那种曾让自己一再碰壁的私下交流。9月2日，他给艾里写了一封信，一来通报自己的第二轮计算结果，二来则答复一年前艾里在信中问起过的天王星轨道径向偏差问题(这封信从一个侧面说明亚当斯当年对径向偏差问题的沉默，并非是因为没有意识到艾里对这一问题的看重，或觉得该问题太简单)。可惜的是，亚当斯和艾里的每一次重要交往似乎都注定要以失败告终。亚当斯的信件抵达格林威治天文台时，艾里又出了远门。不过这回亚当斯多少也学了一点乖，不再把宝完全押在艾里一个人身上了，他决定赶往英国科学进步协会(BritishAssociationfortheAdvancementofScience)在南安普敦(Southampton)的一次会议，以便报告自己的结果。

可人要是背了运，喝凉水都会塞牙。

当亚当斯赶到南安普敦时，天文方面的会议早已结束。错过了会期的亚当斯只能郁闷地再次将自己埋首于计算之中，他将新行星的轨道半径进一步缩小为34.4天文单位，开始了自己的第三轮轨道计算。

另一方面，勒维耶的命运虽然比亚当斯顺利，除了艾里等少数人外，不仅整个欧洲都将他视为新行星位置的唯一预言者，他的工作甚至还远隔重洋传到了美国。自八月份以来，勒维耶预言新行星位置的消息更是越出了学术界的范围，得到了媒体的宣传。可当他试图说服各大天文台将那些溢美之词，以及对新行星的期盼之意转变为货真价实的搜索行动时，却遭遇了意想不到的困难。各天文学台的“老总”们虽毫不掩饰对他结果的极大兴趣，以及对他水平的高度赞许，可一涉及到动用自己手下的人力和设备进行新行星搜索时，却一个个支支吾吾、推三推四起来。甚至连他的本国同行也不例外，一年前亲自敦促他研究天王星出轨问题的巴黎天文台台长阿拉果只进行了极短时间的搜索就放弃了。

读者也许觉得奇怪，发现新行星是何等的美事？各大天文台应该争先恐后、抢破脑袋才是啊，怎么反倒你推我让、欲迎还拒呢？难不成是“老总”们突击学习了“孔融让梨”的先进事迹？各大天文台之所以会有这样奇怪的反应，主要有两大原因：第一是信心不足。谁都知道发现新行星意味着巨大的荣誉，但同时也都知道寻找新行星是一件很困难的事情。虽说此次的情况有所不同，勒维耶已经计算出了新行星的位置，而且轰传天下。可这计算新行星位置的壮举，乃是前所未闻的故事，天文学家们心里究竟信了几成，恐怕只有他们自己才清楚。溢美之词是廉价的，观测时间却是无价的，该不该用无价的时间去验证廉价的评语，这是让“老总”们不无踌躇的事情。

第二个原因则是制度死板。当时各大天文台都有繁重的观测任务，也都有比较死板的规章制度，对观测日程作哪怕细微的变更都不太容易，要想凭空插入一个耗时未知、结果莫测的行星搜索计划更是难上加难。格林威治天文台甚至还有过观测助理因擅自寻找新行星而受到艾里惩罚的事情。因此即便象查利斯那样既得到艾里的嘱托，又有台长的权力，并且因知晓亚当斯与勒维耶的双重结果而具备信心优势的人，也只愿花费很有限的时间和精力进行观测，且还心猿意马、草率从事，以至于功败垂成。而艾里本人把观测任务交给剑桥天文台，虽有演绎剑桥故事的美好心愿及其它客观原因，但心底里-据后人分析-也是不想打乱格林威治天文台的正常工作。

十六.生日之夜

一次次客气的回绝让勒维耶很是沮丧，他搜肠刮肚地寻找关系，试图找到一个突破口。这时他忽然想起了自己曾经认得过的一位柏林天文台的天文学家，此人名叫伽勒(JohannGottfriedGalle)，是柏林天文台台长恩克(JohannFranzEncke)的助理。说起来，勒维耶与伽勒的关系其实疏远得很，唯一值得一提的联系是一年前伽勒曾给勒维耶寄过一份自己的博士论文。而忙于计算的勒维耶甚至连封感谢信都没有回。真所谓此一时彼一时也，若非如今这档子事，勒维耶这辈子能否想得起伽勒来都是个问题，而此刻勒维耶一想到伽勒登时觉得亲切无比，犹如看到了救命稻草。1846年9月18日，勒维耶给伽勒写了一封信，将伽勒的一年前的博士论文狠狠地夸奖了一通，然后笔锋一转，谈到了自己预言的新行星位置，他希望伽勒能帮助寻找这颗行星。

9月23日，勒维耶的信送到了伽勒手中。



【德国天文学家伽勒 (1812 – 1910, 左)与达雷斯特 (1822 – 1875, 右)】

虽然被冷落了一年，能够收到当时已颇有名气的勒维耶的来信(而且还是满含赞许的来信)伽勒还是感到非常兴奋，并且他也被勒维耶的预言深深吸引了。勒维耶的信终于落到了能被它打动的人手里，不过更妙的则是这封信的抵达时间：9月23日，这一天正好是伽勒的老板恩克台长的55岁生日。伽勒虽是柏林天文台的资深成员，但按规矩却仍没有擅自使用天文台的望远镜进行计划外观测的权力，他想要观测新行星，必须得到台长恩克的允许。

恩克作为台长，消息自然是灵通的，他早就知道勒维耶预言新行星的事，但和其他天文台的台长一样，他对此事也一直采取了旁观的态度。换作是在平时，伽勒的要求可不是那么容易过关的。不过人在生日的时候心情通常比较愉快，而且那天晚上同事们早已约定在恩克家中庆祝他的生日，并无使用望远镜的计划，因此在伽勒的软磨硬泡之下，恩克终于答应给对方一个晚上的时间进行观测。

拿到了尚方宝剑，伽勒拔腿就往观测台走。这时一位年轻人叫住了他。此人名叫达雷斯特(HeinrichLouisd'Arrest)，当时还是柏林天文台的一位学生，他碰巧旁听到了伽勒与恩克的谈话。达雷斯特请求伽勒允许自己也参加观测。由于天文观测不仅是观测，而且还需要进行数据的纪录与比对，有助手参与显然是非常有利的，于是伽勒答应了达雷斯特的请求，两人一同前往观测台。

我们在第四节中曾经介绍过，发现行星的主要途径有两种：一种是通过行星的运动(比如小行星的发现)，另一种则是通过行星的圆面(比如赫歇耳发现天王星)。由于通过运动发现行星通常需要对不同夜晚的观测数据进行对比，而恩克只给了他们一个夜晚的时间，因此伽勒和达雷斯特将希望寄托在了观测新行星的圆面上。他们将望远镜指向了勒维耶预言的位置，以那里为中心展开了观测。

那个夜晚秋高气爽，万里无云，是进行天文观测的绝佳天气。但天气虽然帮忙，运气却似乎并不垂青于他们。时间一分一秒地过去，他们并未发现任何显示出圆面的天体。夜色越来越浓，希望却越来越淡，难道勒维耶的预言错了？又或是预言没错，但误差太大，从而新行星离预言的位置太远？如果是这样，他们就必须扩大搜索范围，而这显然不是短短一个夜晚就能搞定的。



【柏林天文台】

百般无奈之下，达雷斯特提议了一个方法：他们虽然只有一个夜晚的观测时间，从而不可能通过对自己的数据进行对比来发现新行星的运动，但他们搜索的这片天区以前当然也有人观测过(虽然目的各不相同)。如果他们刚才观测过的天体中有一颗是行星，那么在人们以前绘制的星图上，它显然不会处在同样的位置，甚至应该完全不在同一片天区里，因为以前绘制的星图与他们自己的观测在时间上相距较远。

由此看来，只要他们能在自己的观测中发现一颗不在星图上的天体，那个天体极有可能就是他们想要寻找的新行星。这是一个绝妙的新思路。当然，他们的运气好坏还取决于星图的详尽程度。

仿佛与他们的机智遥相呼应，柏林天文台最近恰好编过一份详尽的星图，那份星图此刻就放在恩克的抽屉里。伽勒和达雷斯特赶紧找来了那份星图，然后由伽勒将望远镜中看到的天体的位置一个个报出来，达雷斯特则在星图上一一寻找-找到一个就排除一个。半个小时过去了，兴奋的时刻终于来临，当伽勒报到一颗视星等为8等，与勒维耶预言的位置相差不到1°的暗淡天体时，达雷斯特喊了起来：那颗星星不在星图上！

此刻的时钟已悄然划过零点，崭新的一天已经来临[注一]。在这个不眠之夜里，一个天体力学的神话已被缔造，天文学的历史翻开了辉煌的一页。此时恩克的生日派对仍在进行，激动不已的伽勒和达雷斯特赶到恩克的住所，向他报告了这一消息。恩克立即中断了生日派对，与他们一同赶往观测台，三人一直观测到黎明。第二天，在同样完美的天气条件下，他们又仔细复核了一次，发现那个天体的位置移动了，并且移动的幅度与勒维耶的计算完全吻合。毫无疑问，他们已经发现了勒维耶预言的新行星[注二]。

9月25日早晨，走下观测台的伽勒写信向勒维耶报告了发现新行星的消息。

这个消息很快就席卷了整个天文学界，并将在不久之后掀起一场风暴。

注释

尽管如此，人们通常仍将1846年9月23日作为新行星的发现日。 经过仔细的观测，他们也确定了新行星的圆面大小，比勒维耶预言的小了百分之二十左右。

二零零八年一月三十日写于纽约

二零零八年一月三十一日发表于本站

二零零九年七月十九日最新修订

寻找太阳系的疆界 （九）

十七.名动天下

虽然近代天体力学史上从来就不乏精密的计算和预言，比如我们在第六节中曾经提到，高斯预言的谷神星位置与实际观测只差半度。至于有关日食、月食及彗星周期等的预言，则更比比皆是。但那些计算所涉及的天体，其存在性及部分轨道数据都是已知的，所有的计算和预言都只是从有关该天体的已知数据出发，来推测未知数据。而象勒维耶这样通过已知行星的运动，来间接推算一颗远在几十亿公里之外，没有任何观测数据的未知行星的轨道，并将其位置确定到如此精密的程度，这不仅是前所未有的壮举，而且充满了引人遐想的空间。一时间，所有人都被这令人眩目的伟大成就所震撼，这一成就的“总设计师”勒维耶几乎在一夜之间就达到了自己一生荣耀的顶点。来自欧洲各地的赞美与祝贺如雪片般飞来，很多人激动地将勒维耶的成就称为天文史上最伟大的成就。

在伽勒给勒维耶报讯的同时，他的老板恩克也亲自给勒维耶写了信，在信中，除了向勒维耶表示“最诚挚的祝贺”外，恩克还写道：“您的名字将永远与对万有引力定律有效性的能够想象得到的最惊人验证联系在一起”。德国天文学家舒马赫(HeinrichSchumacher)的评论则是：“这是我所知道的最高贵的理论成就”，这位舒马赫曾试图帮助勒维耶联络德国及英国的天文学家进行新行星搜索，可惜那些被他联络到的天文学家无一例外地丧失了机会。除天文学界外，欧洲的媒体也迅速报道了这一消息，并在公众中激起了极大的兴趣。10月5日-新行星发现后的第十天-法国科学院每周一次的例行会议几乎成了勒维耶的明星秀，闻讯而来的民众把科学院的入口挤得水泄不通，人人争睹勒维耶的巨星风采，每张嘴巴都在念叨着勒维耶的名字。甚至连法国国王也被勒维耶的盛名惊动，亲自聆听了勒维耶对自己发现的介绍。

在这涌动的热潮中，许多法国民众开始将新行星称为“勒维耶星”。提议以发现者的名字命名行星，这在行星发现史上并非头一遭，在法国尤其如此。当年赫歇耳发现的天王星在法国就一度被称为“赫歇耳星”，更何况此次发现新行星的首要功臣就是法国人。这时候，倒是勒维耶本人很谦虚地提议了一个不同的名字：奈普顿(Neptune)，这是罗马神话中的海洋之神。这个名字既符合行星命名的神话惯例，又与新行星在望远镜里呈现的美丽蓝色珠联璧合，是一个很漂亮的提议[注一]。不过这一名字尚未得到公认，连续几天的“群众运动”及“勒维耶星”的“黄袍加身”就使勒维耶的想法产生了变化。他觉得新行星若果真被命名为“勒维耶星”，倒也是一件很幸福的事情。这样的命名虽有违惯例，但考虑到此次的情形是如此地独一无二，勒维耶觉得自己享受一个独一无二的命名也并不为过。在他的示意下，巴黎天文台的台长阿拉果公开提议将新行星命名为“勒维耶星”。但这一提议终究没能与已成主流的神话命名体系相抗衡，更何况此时此刻，一场巨大的风暴已然来临，小小的命名之争很快就淹没在了惊涛骇浪之中。等到风浪平息之后，最终还是海洋之神成为了新行星的名字，在中文中，这一行星被称为海王星[注二]。



【旅行者号拍摄的海王星】

海王星被发现时的视星等为8，虽然超出了肉眼所能辨别的极限，但在望远镜所能观测的天体中却是比较亮的。因此与天王星的情形一样，天文学家们很快就发现海王星其实也早在其被伽勒和达雷斯特发现之前，就已被反复记录过。这其中最该痛哭流涕的无疑是查利斯，在与新行星擦肩而过的所有人中，他是唯一一位以搜寻新行星为目的，并且观测到了目标，却仍失之交臂的人。悔恨排行榜上的亚军则属于法国天文学家莱兰德(MichelLalande)，此人的“冤情”堪比其同胞拉莫尼亚(参阅第四节)。1795年5月8日及5月10日，莱兰德两次观测到了海王星。次数虽不算多，但与拉莫尼亚不同的是，莱兰德明确注意到了该天体在两天之中的位置变化。此时此刻，新行星的发现实已呼之欲出。但令人难以置信的是，莱兰德竟鬼使神差般地认定自己5月8日的观测是不准确的，而且连进一步的确认及后续观测都没做，就将这千载难逢的机会拱手送还给了命运女神，从而创下了行星观测史上最离奇的失误。

在曾经记录过新行星的人之中，最让人意想不到的则是伽利略。1979年，人们发现这位科学启蒙时代的宗匠竟然早在1612-1613年间-即不仅比海王星的发现早了两百三十多年，甚至比天王星的发现还早一百七十多年-就至少两次观测到了海王星。另外值得一提的是，小赫歇耳曾在1830年的一次天文观测中搜索过距离海王星当时的位置只差半度的天区。小赫歇耳很好地继承了父亲的事业，当时已成为英国最有声望的天文学家之一。以他的观测设备及观测水平，若当时他的观测区域稍稍扩大一点，就极有可能缔造一段父子双双发现新行星的佳话。但这样的佳话假如出现，勒维耶用笔尖发现海王星的更伟大的奇迹将不复存在。小赫歇耳在给朋友的信中表示，如果那样的话，连他自己都将感到遗憾。这句话也许是心里话，也许只是一种风度，但对于对于行星发现史来说，这句话倒是千真万确的。海王星以如今这种方式被发现，实在是行星发现史上最动人的故事。

不过这故事虽然动人，却也没有后人渲染的那样完美，这是后话。

十八.轩然大波

海王星的发现在知道亚当斯工作的一小部分英国天文学家中引起了极大的震动。发现海王星的消息传到英国时，艾里正在欧洲大陆度假，当时在英国的知情人除亚当斯本人外，主要有两个：一个是查利斯，另一个则是小赫歇耳。



英国天文学家小赫歇耳 (1792 – 1871)

小赫歇耳成为知情人的具体时间史学界尚有争议，传统的说法是他曾在6月29日皇家天文台的一次会议期间听艾里提到过亚当斯与勒维耶的计算[注三]。那是艾里极罕见的一次向他人提及亚当斯的名字，那个消息给小赫歇耳留下了深刻印象。9月10日，他在英国科学进步协会的一次演讲中，将预言海王星的位置比喻为哥伦布从西班牙海岸直接看到美洲[注四]。当时海王星尚未被发现，小赫歇耳并未在这番泛泛之语中提及预言者的名字，不过由于勒维耶的工作早已广为人知，几乎所有的听众都以为小赫歇耳指的就是勒维耶的预言。现在海王星已被发现，勒维耶也已名动天下，作为英国天文界的领军人物之一，小赫歇耳不愿坐视英国在这场无形竞争中一败涂地。10月3日，他在伦敦的一份周报上发表文章，公布了亚当斯在整个事件中的角色。这是这一事件的英国版首次被公开。小赫歇耳在文章中除了提及亚当斯的结果外，还表示正是因为知道亚当斯与勒维耶的结果几乎相同，才使他有足够的信心将预言海王星的位置比喻为哥伦布从西班牙海岸直接看到美洲[注五]。

在除亚当斯本人之外的三位英国知情人中，小赫歇耳无疑是最没有心理包袱的，因为他在这一事件中纯粹是旁观者。与他不同的是，艾里与查利斯很早就知道了亚当斯的结果，因此这两人对英国在这一竞争中的落败很难脱得了干系。尤其是查利斯，他的疏失对于一位职业天文学家来说堪称是丑闻。查利斯是9月30日得知海王星被发现的消息的，当时他还不知道自己早在一个多月前的8月12日就曾观测到过海王星，因此心中尚无愧意。不仅没有愧意，他还有苦水要倒。因为他在9月29日看到了勒维耶发表的最新计算结果，那篇文章重新引起了他对新行星的兴趣，当天晚上，他恢复了已中断近一个月的搜索，并且成功地发现了一个有圆面的天体-那正是海王星。可惜没等他有机会复核，就传来了海王星已被发现的消息。查利斯觉得自己实在有点冤，运气也实在有点背，因此他立即给剑桥的一份刊物写了信，除提及亚当斯的工作外，还着重提到自己过去两个月以来一直在从事着早晚会成功的搜索工作，并在9月29日事实上独立地发现了海王星。查利斯的信也发表于10月3日。

若干天之后，当查利斯发现自己一个多月前的重大疏失时，他的自我惋惜才转变为悔恨与惭愧。

10月11日，艾里回到了英国，他在9月29日就得知了海王星被发现的消息。无论以学术地位还是实际作用而论，艾里在整个英国版的故事中都处于中枢地位，他很快也对事件作出了反应。不过，他没有诉诸媒体，而是直接给勒维耶写了信。在信中艾里告诉勒维耶，英国方面在他之前就有过完全相同的预言。虽然艾里表示自己这封信的目的绝不是要抹煞勒维耶的贡献，并且他也承认英国方面的工作不如勒维耶的工作来得广泛，但他对“时间上更早”及“结果相同”这两点的强调，还是让勒维耶很受伤。

在英国方面的主要当事人中，唯一未发表声明的是亚当斯本人，他虽然很沮丧，但没有参与优先权之争。相反，他将精力投入到了利用已经公布的观测数据计算海王星的真实轨道上来，并于10月份完成了计算，成为最早在直接观测数据之上完成海王星轨道计算的天文学家。

勒维耶收到艾里的来信时，小赫歇耳和查利斯的文章也几乎同时传到了法国。这突如其来的三柄利刃让勒维耶既感震惊又觉震怒。勒维耶的震惊和震怒是有道理的，艾里在海王星发现之前与他有过多次信件往来，如果英国方面早就有过与他平行的工作，艾里为什么早不提晚不提，偏偏要等到海王星被发现之后才提？查利斯的举止更是可疑，他在刊物上的声明发表之后，又于10月5日给不止一位欧洲大陆的天文学家去信，讲述自己9月29日发现却没来得及确认海王星的“祥林嫂”故事。而在那些故事中他却只字未提亚当斯的名字，这不是前后矛盾又是什么？至于小赫歇耳，他竟然声称对勒维耶结果的信心乃是因为其与名不见经传的亚当斯的结果相吻合，这对勒维耶来说简直太伤自尊了。



法国天文学家阿拉果 (1786 – 1853)

来自英国方面的消息不仅激怒了勒维耶，也激怒了整个法国天文界。在他们看来，这分明是英国方面蓄意捏造事实，企图抢夺荣誉的卑劣行径。人不可以无耻到这种地步，法国天文学家们的心里那是相当的愤怒，他们立即展开了犀利的反击。10月19日，巴黎天文台台长阿拉果在巴黎科学院的会议上发表了声援勒维耶，讨伐艾里、小赫歇耳及查利斯的檄文。在这篇檄文中，阿拉果大量援引了艾里等人写给法国天文学家的信件，指出其相互矛盾之处，并痛斥英国人的卑劣企图。阿拉果在檄文的最后情绪激昂地指出：在每一双公正的眼睛里，这一发现都仍将是法国科学院的辉煌成就，也将是让子孙后代景仰的最高贵的法国荣誉。

阿拉果的檄文发表后，法国乃至欧洲其他国家的媒体都迅速跟进，展开了对艾里等人的围剿。法国的有些报道干脆将这三人称为“窃星大盗”(考虑到海王星的大小，这罪名在理论上可比地球上的“窃国大盗”大得多)。更糟糕的是，阿拉果所引的艾里等人与法国同行的通信一经曝光，在英国天文学界也引起了轩然大波。因为艾里与查利斯不仅从未向法国同行们提及过亚当斯的工作，也向绝大多数英国同行隐瞒了消息。这一点让许多英国天文学家也感到了愤怒，这其中有位天文学家叫作辛德(JohnRussellHind)，他曾在格林威治天文台当过助理。伽勒发现海王星的消息传到英国后，他是第一位重复这一发现的英国人。但在那之前，他就曾与查利斯讨论过搜索新行星的问题。倘若查利斯未曾向他隐瞒亚当斯的工作，他也许早就展开了认真的搜索。而如果艾里与查利斯及早向英国天文界全面报告亚当斯的工作，说不定会有更多的英国天文学家投入搜索行动。不仅如此，更有人指出，倘若艾里与查利斯在1845年秋天亚当斯的第一轮结果出来之后就认真对待，则历史说不定早已被改写，根本就没法国人什么事。从这个意义上讲，艾里与查利斯是导致英国天文学界整体失利的罪魁祸首。某些激进的英国批评者甚至认为艾里有可能与勒维耶串通一气，出卖了亚当斯的计算。这种指控当然是无稽之谈，但艾里与查利斯一度在欧洲大陆及英国本土同时遭到抨击，“猪八戒照镜子，里外不是人”，则是不争的事实。

艾里等人掀起的这场轩然大波不仅极大地伤害了法国人民的感情，而且还严重破坏了英国天文学界自身的和谐，这场风波该如何落幕呢？

注释

有关这一提议的由来，赫歇耳在给伽勒的一封信中声称是法国经度局(TheBureauofLongitude)的决定，但法国经度局却否认了这一说法。人们一般认为，这一命名是赫歇耳自己的提议，至多曾与经度局的人有过非正式的交流。 海王星这一名称直到1847年才基本得到公认，但为了方便起见，我们在下文讲述1847年以前的事件时也将用这一名称来称呼新行星。 这一细节是艾里于11月13日在皇家天文学会就海王星事件召开的质询会上回顾这一事件时提供的，但史学界对此有一定的争议，因为人们未能查到支持这一说法的文字记录。 小赫歇耳是否在那次会议上说过那样的话，也同样因为没有找到可以作证的文字记录，而有一定的争议。 我个人觉得奇怪的是：史料中没有任何有关那段时间小赫歇耳本人从事新行星搜索的记载，以他的家世背景(父亲是天王星的发现者)，如果他真的对亚当斯和勒维耶的共同预言有那么大的信心，为何没有亲自搜索新行星呢？

二零零八年二月十一日写于纽约

二零零八年二月十一日发表于本站

二零零九年七月十九日最新修订

关于本文

寻找太阳系的疆界 （十）

十九.握手言和

在所有针对艾里和查利斯的抨击中，有一点无疑击中了要害，那就是在海王星发现之前，他们在一定程度上隐瞒了亚当斯的工作。事先隐瞒，有荣誉时却突然提出，这使得他们的声明在外人-尤其是在法国天文学界-眼里有一种为抢夺荣誉而临时炮制的感觉，成为他们取信于别人的最大障碍。

如果说一开始艾里对亚当斯的工作还只是忽略而非隐瞒，那么在他得知了勒维耶的工作(详见第十三节)之后，这样的理由就不大说得通了。很多人认为，艾里和查利斯存了将发现海王星的荣誉留给剑桥的私心，从而有意向同行们隐瞒了亚当斯的工作。这一看法虽从未得到艾里和查利斯的承认，但应该说有一定的合理性[注一]。艾里本人的说法，则是坚称他自始至终就不曾对亚当斯的工作有足够的重视，即便后来因了解了勒维耶的工作而意识到其结果很可能是正确的，也由于该结果并未正式发表而鲜有提及。但无论出于何种原因，法国方面以此为由全面否认英国方面的声明，甚至认为亚当斯的工作是子虚乌有的骗局，显然是有欠冷静的。

如果要盘点一下在发现海王星的过程中英国方面几位当事人的个人过失，那么查利斯显然有着极大的过失。作为一位职业天文学家兼天文台台长，在比对观测数据时如此草率，无论如何是说不过去的。这一点，连他的英国同行们也嗤之以鼻，后来有评论者尖刻地嘲讽道：查利斯是不朽的——他因失败而不朽。

另一方面，艾里虽也饱受抨击，但平心而论，他前前后后的行为倒是都有说得通的理由。比方说亚当斯1845年秋天吃到的几次闭门羹就不能怪艾里，因为亚当斯并未预约。有人也许会对亚当斯第三次登门时艾里正在吃午饭一事感到奇怪，因为当时已是下午四点，但这个古怪的午饭时间却是艾里医生的要求。而艾里看到亚当斯留下的计算结果后隔了两个星期才回复，则是两个因素的共同结果：一是他的妻子即将生第九个小孩(姜昆和李文华的相声说得好：多子女的坏处，就是个人受罪、国家受累)；二是他手下有位职员正好卷入了一桩谋杀丑闻的调查之中。任何人同时碰到这样的家事和公事，恐怕都难免会受到影响。至于他在自己信中所提的天王星轨道径向偏差问题被亚当斯搁置后，不再关注对方，则更是合理的反应。

最后，亚当斯作为这一事件中唯一保持低调的当事人[注二]，虽然得到了英国同行的普遍嘉许，但他没有循正式途径发表自己的计算，无论是因为信心不足，还是为了精益求精，对后来的风波都有直接的负面影响-虽然人们很难拿这一点来批评他。

令人欣慰的是，有关海王星发现的这场轩然大波，在短短几个月之后就在学术界平息了下来。这其中小赫歇耳在遭受法国方面猛烈攻击的情况下坚持斡旋，并用华丽的文字对勒维耶进行安抚，以及艾里在度过了对法国方面公布其私人信件的短暂愤怒期之后采取的克制态度，都起了不小的作用。而英国皇家学会也在这场风波中显示出了非比寻常的气度，将1846年的考普雷奖授予了勒维耶。六十五年前，发现天王星的赫歇耳所获得的第一个崇高荣誉就是考普雷奖，而此时亚当斯尚未获奖，皇家学会就把奖项授予了勒维耶，而且还在获奖理由中称勒维耶的工作是“现代分析应用于牛顿引力理论的最令人自豪的成就之一”，这对勒维耶无疑是极大的安抚[注三]。英国人向来珍视自己的荣誉，这回却将最高荣誉授予了法国方面的竞争者，但英国皇家学会通过这一行为表现出的泱泱气度又何尝不是一种荣誉呢？



【考普雷奖章】

当然，争论的最终平息还要部分归功于亚当斯的论文。他的论文发表后赢得了一片赞许，很多人(不光是英国人)甚至认为他的方法在数学上比勒维耶的更为优美。法国学术界也最终承认了亚当斯的才华[注四]。1847年6月，亚当斯和勒维耶在英国科学进步协会的一次会议上首度相遇。两人用亲切的交谈开始了他们终生的友谊，也打消了人们对他们会面的担忧。这正是：度尽劫波兄弟在，相逢一笑泯恩仇。

优先权之争的落幕，也终结了勒维耶用自己名字命名海王星的短暂打算。因为这一打算不仅有违行星命名的传统，也与天文学界好不容易达成的亚当斯与勒维耶共享荣誉的共识相违背。

亚当斯与勒维耶这两位当年曾为了请人观测新行星而四处奔走的天体力学高手，后来都亲自担任了天文台的台长：勒维耶于1854年接替去世的阿拉果担任了巴黎天文台的台长，亚当斯则于1861年接替离职的查利斯成为了剑桥天文台的台长。不过他们两位在天文台台长的位置上干得并不出色，亚当斯基本上是把观测事务全都推给了资深助理，勒维耶则不仅同样疏于观测(有人认为他甚至从未在望远镜里看过一眼让他名垂青史的海王星)，而且还因与下属关系恶劣而一度下岗。亚当斯后来两度担任皇家天文学会的主席，在那期间，他亲自向达雷斯特(即与伽勒一起发现海王星的那位学生，他的贡献曾被很多人忽视)和勒维耶颁发过奖项。不过他颁给勒维耶的奖项-如我们在后文中将会提到-却是一个乌龙奖项。

海王星事件落幕后，艾里将他手中有关这一事件的信件及其它资料存入了格林威治天文台的档案之中。这些档案被后人称为“海王星档案”(NeptuneFiles)。出人意料的是，这些档案在一个半世纪之后又重新掀起了一场风波。

二十.秘密档案

海王星的发现在科学界引起了极大的轰动。自那以来，这一发现一直被视为天体力学最辉煌的成就，就象亚当斯与勒维耶的同时代人曾经赞许过的那样。但是，过于夺目的历史光环却也掩盖了这一成就背后的不完美性，以至于后世的很多文章过分渲染了海王星位置与勒维耶的预言相差不到1°这一辉煌之处，却忽略了计算结果中那些与观测不那么相符的地方。

我们在第十八节中曾经提到，在海王星被发现之后，亚当斯是第一个利用实际观测数据对其轨道进行计算的天文学家。亚当斯的计算表明，海王星轨道的半长径只有30.05天文单位(现代观测值为30.06天文单位)。稍后，海王星的质量也得到了较为准确的测定，结果表明其质量与天王星几乎相同。将这些结果与亚当斯及勒维耶的计算相比较，不难看到彼此间存在不小的差距。亚当斯的两次计算所采用的天王星轨道半长径分别为38.4和37.3天文单位；勒维耶的两次计算所采用的轨道半长径则分别为38.4和36.2天文单位，均显著大于实际值。而且，除勒维耶的第一次计算采用了圆轨道外，亚当斯和勒维耶所采用的轨道椭率均在0.1以上，比实际值(约为0.011)大了一个数量级。此外，亚当斯和勒维耶所采用的海王星质量为天王星质量的2到3倍，远远高于实际值。因此，亚当斯和勒维耶的计算无论在天体质量，还是轨道参数上都存在较大的误差。不过幸运的是，对海王星质量的高估，与对其轨道半长径的高估造成的影响在一定程度上得到了抵消，从而大大增加了亚当斯和勒维耶的计算与真实情形的接近程度。但即便如此，后来的分析表明，在海王星长达165年的漫长公转周期中，亚当斯和勒维耶的计算只在其中十余年的时间里才是真实轨道的良好近似，而1840-1850年恰好就是这幸运的十年。从这个意义上讲，海王星的发现虽然是一个伟大的天体力学成就，但它在离计算值如此之近的地方被发现却有一定的偶然性[注五]。

海王星的发现过程是动人心魄的，就连对这一发现过程所做的历史研究也充满了奇峰突起的意外篇章。海王星事件的落幕虽快，却落得并不彻底。一个多世纪以来，一直有人对事件的真相存有疑虑，尤其是对英国方面的说法感到怀疑。终于，这段暗流涌动的历史在相隔一个半世纪后的二十世纪九十年代末又掀起了一阵新的波澜。

我们在上一节的末尾曾经提到，海王星事件落幕之后，艾里将后来被称为“海王星档案”的一批资料存入了格林威治天文台的档案之中。这些海王星档案在此后一个多世纪的时间里一直处于秘密保存状态，直到二战后的1956年，才随着格林威治天文台的搬迁而重现天日。但颇为离奇的是，这些档案露面后不久就重新失去了踪影。1969年，海王星研究者罗林斯(DennisRawlins)在试图查阅海王星档案时，被告知这些档案已不知去向。海王星档案的下落从此成为了一个谜，有人甚至认为这些档案的失踪，乃是英国方面刻意掩盖历史真相的手段。

几十年的时光悄然流逝，海王星档案依旧杳无踪影。1998年，这些档案的昔日藏身之地，有着323年辉煌历史的格林威治天文台因为经费方面的原因而走到了关闭的边缘。世事的变迁似已让这悬案变得越来越没希望了，但就在这“山重水复疑无路”的时候，事情出现了意想不到的转机。1998年10月8日，作为关闭工程的一部分，工人们正准备拆除格林威治天文台的电话线，这时候资深档案管理员珀金斯(AdamPerkins)接到了一个来自遥远的南半球国家智利的电话。电话是从位于智利拉塞里纳(LaSerena)的塞罗托洛洛天文台(CerroTololoObservatory)打来的。在电话中，珀金斯听到了一个让人几乎不敢相信的消息：失踪了几十年的海王星档案在刚刚去世的恒星天文学家艾根(OlinEggen)的遗物中被发现了！

原来，有藏书癖好的艾根在二十世纪六十年代中期利用其在格林威治天文台工作的机会，窃取了包括海王星档案在内的重达百余公斤的档案[注六]。



【海王星档案】

海王星档案的失而复得很快就在史学界掀起了一场新的波澜。有些人在对那些档案进行研究后，提出了一个惊人的观点，即艾里、查利斯、小赫歇耳、亚当斯等人当年讲述的英国版故事是不真实的，亚当斯在对海王星的预言上不应该享有与勒维耶同等的荣誉。这其中最主要的一位，是一度有过伦敦大学学院荣誉研究员头衔的英国人科勒斯特姆(NickKollerstrom)。2001年，科勒斯特姆通过互联网披露了海王星档案的部分内容，并对艾里等人当年的说法提出了全方位的质疑。2003年7月及2004年12月，美国的两份颇具影响力的主流科普杂志《天空和望远镜》(Sky&Telescope)及《科学美国人》(ScientificAmerican)先后刊文介绍了科勒斯特姆的质疑，并且所取标题颇为惊人。《天空和望远镜》的标题为：“秘密档案改写海王星的发现”；《科学美国人》的标题则是：“被盗行星之案”。很多其它媒体也引述或转述了科勒斯特姆的观点，他的正式论文则发表在了2006年3月出版的英国学术季刊《科学史》(HistoryofScience)上。

一时间海王星的发现史似乎重新陷入了重重迷雾之中，英国人真的“盗窃”了海王星，历史真的要被改写吗？

注释

如我们在第十五节中所说，仅凭勒维耶的计算，多数天文学家采取的只是观望态度。因此知道亚当斯的结果在很大程度上可以算是“剑桥帮”的秘密武器。不过这一看法无法解释艾里为何曾向小赫歇耳等少数同事提及过亚当斯与勒维耶的计算(小赫歇耳虽也曾就读于剑桥，但他并不在剑桥天文台从事观测，应该与艾里设想的剑桥故事没有关系)，并明确提出了存在近期内依据这些计算发现海王星的可能性(参阅第十三节)。 后来有人对亚当斯是否真的是一位"timid"(害羞)或"modest"(谦虚)的人提出了异议。但无可否认的是，亚当斯即便在成名之后仍相当低调。他一生谢绝过两次巨大的荣誉：一次是1847年，在小赫歇耳等人的推荐下，维多利亚女王决定授予他爵士头衔，那是牛顿曾经获得过的头衔；另一次则是1881年艾里退休时，他受到推选接替艾里的位置-那是英国天文学界最尊崇的位置。找遍全英国，恐怕也找不出第二位谢绝这两项荣誉的人。 两年后，即1848年，亚当斯也获得了考普雷奖。 与勒维耶不同的是，亚当斯的计算细节从未被全部发表，并且他的计算草稿也从未被全部找到。这使得一直有人对亚当斯的工作存有疑虑。不过依据曾经公布过的资料，后人已基本复现了亚当斯的计算方法。 在后文讲述完冥王星的发现后，我们还会再次谈及这一问题。 按格林威治天文台后来的说法，档案不是被盗，而是被艾根“借”走了。在艾根去世前，有人曾怀疑是他带走了海王星档案，但他一直予以否认。

二零零八年二月二十八日写于纽约

二零零八年三月一日发表于本站

二零零九年七月二十日最新修订

寻找太阳系的疆界（十一）

二一.先入之见

科勒斯特姆对传统海王星发现史的质疑包含了很多方面。从小的方面说，他质疑了传统故事的许多细节，比如亚当斯对艾里的第二和第三次访问(中间相隔一小时)是否真的是在1845年10月21日下午？艾里在他第三次来访时是否真的是在吃午饭？艾里当时到底有没有收到亚当斯的“拜山帖”？艾里是否真的在1846年6月29日的会议期间提及过亚当斯和勒维耶的计算？小赫歇耳是否真的说过发现海王星如同哥伦布从西班牙海岸直接看到美洲这样的话？等等。这些细节从历史研究的严谨性上讲无疑是可以探究的，甚至也可以影响对若干当事人个人过失的大小认定，但很难对事件的整体真实性起到扭转乾坤的作用。

但是从大的方面说，科勒斯特姆的质疑也涉及到了一些比较重要的问题。比如我们都知道，亚当斯早在1845年秋天就完成了第一轮计算，并且在访问艾里时留下过一页纸的计算结果。那么，他当时的计算结果究竟是什么呢？传统文献沿用的一直是艾里在海王星发现之后提供的说法，即亚当斯的计算结果与海王星的真实位置只差了1°44'(我们在第十二节中所说的“不到两度”指的就是这一说法)。但科勒斯特姆在查阅了一页据称很可能是亚当斯给查利斯的文件，并对比了亚当斯本人的若干笔记后提出，亚当斯当时的计算结果并没有艾里所说的那样精确，而很可能是一个误差达3°的结果。科勒斯特姆认为，这样的结果虽然仍是引人注目的，但却不足以引导人们进行有效的搜索。

应该说，科勒斯特姆对这一点的考证是值得重视的，但他的结论却相当突兀，甚至可以说是莫名其妙。3°的偏差虽然比1°44'大了将近一倍，但仍是一个相当小的偏差。若真的有人依据这一结果进行搜索，是完全有可能发现新行星的，因为人们搜索新行星的范围通常都不会定得很小(比如我们在第十四节中提到的艾里向查利斯建议的搜索范围就达30°×10°)。而且更重要的是，我们在前面曾经提到，无论亚当斯还是勒维耶，他们的计算结果与海王星的真实轨道都存在不小的差异。在这种情况下，亚当斯的第一轮计算哪怕真的偏差了3°，也不是什么大不了的问题。甚至哪怕与亚当斯当时计算有关的具体文件已不可考，也不足以改写历史。因为艾里在得知勒维耶的第一轮计算结果后，曾于1846年6月25日在给一位英国同事的信中，提到过亚当斯的结果与勒维耶的很接近。当时海王星尚未被发现，我们没有任何理由怀疑艾里在私人信件中所说的那些话。仅此一点，就足以证实亚当斯确实得到过与勒维耶相接近的结果，从而具备与勒维耶分享荣誉的工作基础。

除了对亚当斯第一轮计算的偏差提出质疑外，科勒斯特姆还提到，亚当斯第二轮计算与真实位置的偏差比第一轮的更大[注一]，并且他在1846年9月2日给艾里的信中曾对自己的预测作过幅度高达23°的错误变动。科勒斯特姆据此认为，亚当斯既没有稳定的计算结果，也不具备对自己计算的基本自信。应该说，与勒维耶相比，亚当斯在自信心上的确显得比较欠缺。不过我们对他们工作的评价，首要的依据是他们的计算方法是否正确，以及他们的计算结果能否对实际观测起到引导作用。受当时的计算能力(尤其是数值计算能力)所限，他们两人的计算误差都是比较大的，勒维耶的计算误差达10°左右，亚当斯的有可能更高。在这样的误差下，第二轮计算的实际偏差是变大还是变小，并不能有效地衡量他们计算方法的优劣，甚至也不能作为判断他们计算误差的充分依据。至于亚当斯对自己预言所作的巨幅变更，据分析很可能是因为将瑞士天文学家瓦特曼1836年公布的一组错误数据视为了新行星的观测位置(因为瓦特曼在公布数据时曾宣称那是他观测到的新行星)，与他计算方法的正确与否无关。而且那次巨幅变更只是一次孤立的预言，与他的两轮系统计算并无实质关联。退一步说，即便勒维耶的计算的确比亚当斯更为精确，甚至精确很多，但从上文提到的艾里给同事的信件，以及艾里因两人的预测相近而催促查利斯进行观测来看，亚当斯的结果也仍足以对实际观测起到引导作用。因此，这方面的质疑同样不足以改写历史。

如果说上面那些质疑还只是单纯的技术性质疑，所涉及的只是亚当斯计算的技术水准，那么科勒斯特姆的另一类质疑，则把锋芒指向了艾里等人的诚信。在这类质疑中，他通过对艾里、查利斯等人的文章及信件(尤其是信件)中各种细节乃至语气的辨析，指出他们有可能在有关这一事件的若干叙述中撒了谎。这种辨析在当年优先权之争最炽热的时候，勒维耶、阿拉果等法国天文学家也曾用过(参阅第十八节)，只不过科勒斯特姆做得更为系统，也更加详尽。

不过，这些辨析究竟有多大说服力，是值得商榷的，而凭借那些辨析对这么重大的历史事件进行翻案，则更值得怀疑。因为我们都知道，信件的内容常常会因收信人的不同而有不同的侧重点。比如在试图安抚法国同行的时候，艾里就会有意突出后者的贡献，少提或不提亚当斯，以免产生副作用。而信件的语气则不仅与收信人有关，还与写信人的心情有关，不同的语气体现的有可能只是心情的差异，甚至相互间的矛盾也可能只是记忆的差错或笔误。信件不是论文，是不会有编辑来替写信人修改笔误的。事实上，科勒斯特姆能从艾里等人的信件中看出那么多的“问题”，与其说是表明艾里等人有可能撒了谎，不如说是恰恰说明他们并未撒谎。因为那些信件大都是海王星事件发生之后所写的，以艾里等人的智力，倘若有意要编造故事，又岂会在那些后期信件中留下如此多的破绽？那些“破绽”出现在普通信件中是可以理解的，但作为三个著名学者合谋故事的一部分，却是根本不应该出现的。更何况，如果艾里等人真的撒了谎，艾里又为何要留下海王星档案来让后人追查真相？再说小赫歇耳和查利斯早在10月3日就各自发表文章提及了亚当斯的贡献(参阅第十八节)，当时艾里尚在欧洲大陆旅行。他们若要编故事，又怎敢在艾里这么重要的知情人返回英国相互协调之前就贸然行事？

总体来说，科勒斯特姆对海王星事件的研究带有较强的先入之见，即首先认定失踪档案隐藏着重大问题，然后去寻找证据。这种“史从论出”的“阴谋论”心态是史学研究的大忌，带着这种心态研究史料，很容易把一些并无充分说服力的细节视为铁证，赋予它们不应有的重要性，就象中国寓言故事“疑人偷斧”所隐喻的那样。而且一旦有了先入之见，常常会有意无意地忽略或回避对自己观点不利的东西，千方百计地穿凿附会自己早已设定的结论，从而丧失客观公正的立场[注二]。艾里、查利斯及小赫歇耳都是有名望的天文学家，作为当时英国天文界的重要人物，他们当然很看重英国天文界的整体荣誉，但认为他们会在如此重大的学术事件中编造谎言，是令人难以置信的。因为这种谎言一旦败露，将对英国的学术声誉带来重大灾难。更何况，除小赫歇耳外，艾里和查利斯都在海王星事件中遭受了巨大的个人名誉损失(若亚当斯并未独立推算出海王星的位置，或他的工作质量与勒维耶不可相提并论，那么后人加诸于艾里和查利斯的恶评无疑会少得多)。科勒斯特姆提出的“证据”显然远不足以解释这几位功绩卓著的天文学家为何要用自己宝贵的名誉，来进行一场吉凶未卜的豪赌，并且赌得如此粗心，甚至还特意保留了“罪证”。

海王星档案的失而复得有助于史学界更精确地还原海王星发现过程中的若干细节，但起码就目前看到的资料和分析而言，它完全不足以改写历史。海王星的发现是科学界的一个伟大成就，亚当斯和勒维耶各自独立地计算出了海王星的位置，而伽勒及达雷斯特则一同发现了这颗新行星。

二二.火神疑踪

海王星的发现极大地刺激了天文学家和数学家的兴趣。原本属于观测天文学家专利的新行星，居然可以用纸和笔来发现，这实在太吸引人了。一时间用数学方法寻找新行星成为了时尚。天文学家们兵分两路展开了行动，一路沿袭了向外扩张的历史传统，到海王星轨道之外去寻找惊喜；另一路则独辟蹊径，将目光投向了水星轨道的内侧。这后一路天文学家的领军人物不是别人，正是赫赫有名的勒维耶。在发现海王星的荣誉出人意料地被亚当斯分走一半后，勒维耶决定寻找一个新的猎物-一个自己可以独享的猎物。当时多数天文学家认为在海王星之外发现新行星的机会更大，但勒维耶却认为在距海王星的发现如此之近，从而对海王星轨道的了解还不充分的情况下，用数学手段寻找新行星尚为时过早。因此，虽然他也相信海王星之外存在新的行星，但却首先选择将水星轨道以内作为自己的新战场。

勒维耶之所以选择水星轨道以内作为新战场，还有一个很重要的原因，那就是水星的轨道也存在着反常。经过长期精密的观测，天文学家们早就发现水星的椭圆轨道在背景星空中存在缓慢的整体转动，这种转动被称为水星的近日点进动。观测表明，水星的这种近日点进动平均每年约为56角秒。但另一方面，考虑了由地球自转轴进动造成的表观效应及已知行星的影响后，理论计算给出的进动值却只有每年55.57角秒[注三]，两者相差0.43角秒。天文学家们知道水星轨道的这一细微反常已有时日，勒维耶本人早在当年对各大行星做地毯式研究(参阅第十三节)时，就曾对水星轨道进行过详尽考察。海王星的发现无疑赋予了这一反常一个全新的意义。在勒维耶看来，这个虽然微小，但确凿无疑的轨道反常，是水星之内存在未知天体的明显证据。

那么这未知天体会是个什么样的天体呢？勒维耶认为有两种可能性：一种是单一行星，另一种则是小行星带。也许是由于水星近日点的反常进动与当年的天王星出轨相比显得更为规则，或者是受当时正在发现中的小行星带的启示，勒维耶比较倾向于后一种可能性，即在水星轨道之内存在一个小行星带。1859年9月，他在一篇文章中正式预言在距太阳0.3天文单位处存在一个未被发现的小行星带。

正所谓：说曹操，曹操到。勒维耶的预言提出后不久，一位名叫莱沙鲍特(EdmondLescarbault)的法国医生兼业余天文学家就给他写来了一封信，声称自己曾于1859年3月26日发现过一个穿过太阳表面的天体。这封来信让勒维耶很是兴奋，他立即对这位业余天文学家进行了“家访”。在确信此人值得信赖后，勒维耶依据他所得到的数据对这一天体的参数进行了计算，结果表明其轨道半径为0.147天文单位，质量约为水星质量的百分之六。这个天体很快就被取名为火神星(Vulcan-罗马神话中的火神及希腊神话中的工匠之神，美神维纳斯的丈夫)。1860年初，勒维耶向法国科学院报告了发现火神星的消息。尽管自首次“发现”以来，包括莱沙鲍特本人在内的所有人都不曾再有机会一睹火神星的芳容，但法国科学院基于对勒维耶的无比信任，还是很痛快地将拿破仑设立的法国最高勋章-军团勋章(Légiond'honneur)授予了莱沙鲍特，从而上演了该院历史上最大的乌龙颁奖事件之一。

虽然火神星的轨道半径远小于勒维耶预言的0.3天文单位，其引力作用也远不足以解释水星近日点的反常进动，但勒维耶一生都对它的存在深信不疑。受他的巨大声望影响，一些天文学家在此后近二十年的时间里契而不舍地找寻着火神星的倩影，其中包括在浩如烟海的文献中搜寻可能存在的历史纪录。1876年，在亚当斯担任主席期间，英国皇家天文学会也步法国科学院的后尘，很乌龙地在火神星的存在尚未得到确认的情况下，就将一枚金奖授予了勒维耶，以表彰他为解决水星近日点反常进动问题所做的贡献。

但这一切的热情都没能感动火神星，这颗神秘的“行星”再也不曾露面过，所有曾被当作火神星的历史记录(主要集中在1819-1837年间)也都被一一判定为是太阳黑子而非天体。1877年9月23日，火神星的最大支持者勒维耶离开了人世，这一天距海王星的发现正好相隔31年，但火神星的命运仍悬而未决。



【维纳斯与火神在一起】

火神星之所以能在那么长的时间内杳无踪迹，却仍让那么多的天文学家牵肠挂肚，除了依靠勒维耶的“魅力值”外，一个很重要的原因，是因为它离太阳太近，太容易湮没在太阳的光芒之中，从而即便长时间观测不到，也无法说明它不存在。

但丑媳妇终究是要见公婆的。1878年7月29日，天文学家们迎来了一个搜寻火神星的绝佳机会：日全食。当太阳的光芒不再夺目时，火神星还如何遁迹？那一天，大批天文学家在可以观测日全食的美国怀俄明州的一个小镇上架起了望远镜，等待火神星之谜的水落石出。

但出人意料的是，那天的观测没能对火神星的命运作出宣判，却充分证实了心理学的巨大威力。那一天，不相信火神星的天文学家们全都没有观测到火神星，从而更坚信了火神星的子虚乌有[注四]。但相信火神星的职业天文学家沃森(JamesWatson)及业余天文学家斯威福特(LewisSwift)却都声称观测到了火神星，斯威福特甚至声称自己观测到了两个水内天体。虽然这两人宣称的天体位置彼此之间以及与勒维耶的预言之间全都不同(从而无法相互印证)，而且很快就有天文学家通过他们纪录的天体位置指出他们很可能将已知天体误当成了火神星，但这两位老兄爱火神星没商量，一口咬定自己观测到的就是火神星。

在那之后又过了十几年，人们在勒维耶有关火神星轨道的计算中发现了错误。不仅如此，进一步的分析表明，火神星的存在与其它内行星-尤其是金星-的运动并不相容。自那以后，火神星的追随者基本上销声匿迹了。

最终为火神星的疑踪画下完美句号的是物理学家爱因斯坦(AlbertEinstein)。1915年，他在刚刚完成的广义相对论的基础上，完美地解释了水星近日点的反常进动，从而彻底铲除了火神星赖以存在的理论土壤[注五]。

注释

科勒斯特姆在这点上是自相矛盾的。亚当斯第二轮计算的偏差为2°30'，而他第一轮计算的偏差-按照科勒斯特姆自己的考证-则是3°。因此，所谓第二轮计算的偏差比第一轮更大的说法是与他自己的考证相矛盾的。这一矛盾说明科勒斯特姆重新将艾里所说的1°44'作为了亚当斯第一轮计算的偏差(作为对比，勒维耶第二轮计算的偏差由第一轮的-2°21'缩小为-0°58')。这种视自己需要而随意选用彼此矛盾的数据的做法显然是有失严谨的。另外值得一提的是，科勒斯特姆认为亚当斯和勒维耶的第二轮计算之间的相互差异有3.5°，而非一些早期文献所说的不到1°。 这一点也正是科勒斯特姆的致命弱点，他对海王星发现史的质疑虽曾被一些主流科普杂志、学术刊物及媒体所引述，但他的历史“研究”有着浓厚的伪历史及阴谋论色彩。除质疑海王星的发现史外，他还质疑纳粹大屠杀的真实性，是所谓的“大屠杀否认者”(holocaustdenier)之一，并因此而于2008年4月被伦敦大学学院撤销了一切学术头衔。 这其中由地球自转轴进动造成的表观效应约为每年50.256角秒，由已知行星的引力作用产生的进动约为每年5.314角秒。 从理论上讲，在日全食期间没有观测到火神星并不意味着火神星不存在，因为它有可能恰好也和太阳一起被遮盖。不过这种情况发生的概率较小(感兴趣的读者可以估计一下这一概率的大小)。 即便如此，仍有个别天文学家在水星轨道以内寻找新天体。不过这类天体的线度上限已被压缩到了60公里，至多只能是小行星。

二零零八年三月四日写于纽约

二零零八年四月七日发表于本站

二零零九年七月二十一日最新修订

寻找太阳系的疆界 （十二）

二三.无中生有

寻找火神星的天文学家们已全军尽墨，但在海王星以外寻找新行星的天文学家们却还处在忙碌之中，他们的战场完全是另一番景象。

我们知道，海王星之所以能在笔尖上被发现，是因为天王星存在出轨现象，而勒维耶之所以寻找火神星，是因为水星也存在出轨现象，虽然那种被称为水星近日点反常进动的出轨现象具有高度的规则性，从而与天王星的出轨完全不同。那么，寻找海王星以外的行星(以下简称海外行星)，尤其是通过计算手段寻找那样的行星，它的依据又在哪里呢？很遗憾地说，只存在于天文学家们那些“驿动的心”里。

自从海王星被发现之后，天王星的出轨之谜基本得到了解释，剩余的偏差已微乎其微。但如何看待这细微的剩余偏差，却有很大的讲究。我们知道，有关行星轨道的任何观测及计算都是有误差的，因此计算所得的轨道与观测数据绝不可能完全相符。一般来说，只要两者的偏差足够小，小于观测及计算本身所具有的误差，这种偏差就算是正常的，并且往往是随机的。天王星的出轨与水星近日点的反常进动之所以引人注目，是因为它们都远远超过了观测及计算的误差。但是，海王星被发现之后，天王星的剩余“出轨”实际上已经处在观测及计算误差许可的范围之内，没有进一步引申的余地了。不幸的是，发现海王星的成就实在太令人心醉，以至于此前一直追求观测与计算的一致，并愿为之奋斗终身的一些天文学家，现在却反而由衷地期盼起观测与计算的不一致来。因为唯有那样，才有重演海王星发现史的可能。正是在这种满心的期待乃至虔诚的祈祷之中，天文学家们开始在鸡蛋里挑骨头，他们的目光变得多疑，他们不仅“发现”天王星仍在出轨，而且怀疑海王星也不规矩。

1848年，距海王星的发现仅仅过了两年，法国天文学家巴比涅特(JacquesBabinet)就预言了一颗海外行星。他提出的海外行星的轨道半长径约为47-48天文单位，质量约为地球质量的11.6倍。他的计算依据是海王星的实际轨道与勒维耶所预言的轨道之间的差别。显然，这是一种完全错误的计算逻辑。因为勒维耶所预言的轨道只是依据天王星出轨现象所作的推测，而且在推测时还对轨道参数(比如半长径)作过带有一定任意性的猜测，从而根本就不是标准的海王星轨道计算(请读者想一想，标准的海王星轨道计算应该是怎样的？)。用那样的轨道来研究海王星的出轨，套用著名物理学家泡利(WolfgangPauli)的话说，那是“连错误都不如”(notevenwrong)。

理论天文学家们的心情固然急切，观测天文学家们的动作也不含糊。1851年，距海王星的发现仅仅过了四年多，英国天文学家辛德(我们在第第十八节中提到过此人，他是海王星被发现后第一位观测海王星的英国人)宣布自己从美国天文学家弗格森(JamesFerguson)的一份观测报告中，发现了一颗轨道半长径为137天文单位的海外行星。但是，无论辛德、弗格森还是其他人，都没能再次捕捉到那颗神秘的“海外行星”，它的谜底直到二十八年后才揭晓，原来那是弗格森的一次错误的观测纪录[注一]。

这些早期的谬误并未阻止更多的天文学家对海外行星作出预言。从十九世纪中叶到二十世纪初的五十年间，欧洲和美国的天文学家们轮番向海外行星发起了冲击，并取得了如下“战果”：

托德(DavidTodd)预言一颗海外行星，半长径为52天文单位。 弗莱马力奥(CamilleFlammarion)预言一颗海外行星，半长径为45天文单位。 福布斯(GeorgeForbes)预言两颗海外行星，半长径分别为100和300天文单位。 劳(Hans-EmilLau)预言两颗海外行星，半长径分别为46.6和70.7天文单位。 达利特(GabrielDallet)预言一颗海外行星，半长径为47天文单位。 格里戈尔(TheodoreGrigull)预言一颗海外行星，半长径为50.6天文单位。 杜林冈德斯(VicomteduLigondes)预言一颗海外行星，半长径为50天文单位。 西伊(ThomasSee)预言三颗海外行星，半长径分别为42.25、56和72天文单位。 伽诺夫斯基(AlexanderGarnowsky)预言四颗海外行星，但没有提供具体数据。

一时间外太阳系几乎变成了计算天文学的练兵场。在上述计算中，除天王星和海王星的轨道数据外，有些计算(比如弗莱马力奥和福布斯的计算)还利用了某些彗星的轨道数据。但与亚当斯和勒维耶对海王星的预言截然不同的是，天文学家们对海外行星的预言无论在数量、质量、轨道半长径、还是具体方位上都是五花八门。如果一定要从那些预言中找出一些共同之处，那就是“三不”：即全都不具有可靠的理论基础，全都不曾得到观测的支持，以及全都不靠谱。

为什么亚当斯与勒维耶预言的海王星参数彼此相近，而人们对海外行星的预言却如此五花八门呢？这个并不深奥的问题终于引起了一位法国天文学家的注意。此人名叫盖洛特(JeanBaptisteGaillot)，他对天王星和海王星的轨道进行了仔细分析，然后得出了一个直到今天依然正确的结论：那就是在海王星被发现之后，天王星和海王星轨道的观测数据与理论计算在误差许可的范围之内已经完全相符。换句话说，天王星的出轨问题已经因为海王星的存在而得到了完全的解释，在误差许可的范围之内，根本就不存在所谓天王星的剩余出轨或海王星的出轨问题。

盖洛特的分析很好地解释了为什么天文学家们有关海外行星的预言如此五花八门，却无一中的。记得很多年前笔者曾经读到过一则小故事，说有三位绘画爱好者去拜访一位名画家。在画家的画室里他们看到了一幅刚刚完成的山水画，那画很漂亮，但令人不解的是，在画的角落上却有一团朦胧的墨迹。这三人深信那团墨迹必有深意，于是便对其含义作出了五花八门的猜测。后来还是画家本人为他们揭开了谜底：原来那墨迹是画家的孙子不小心弄上去的。在天文学家们预言海外行星的故事中，观测与计算的误差仿佛是那团墨迹，它本无深意，醉心于海王星发现史的天文学家们却偏偏要无中生有地为它寻求解释，从而有了那些五花八门的预言。

分析是硬道理，事实更是硬道理，在亲眼目睹了那么多的失败预言后，多数天文学家接受了盖洛特的结论，认为象预言海王星那样从理论上预言海外行星，起码在当时的条件下是不可能的。不过预言海外行星的努力并未就此而终止，因为有两位美国天文学家偏偏不信这个邪，他们誓要将对海外行星的预言进行到底。

二四.歧途苦旅



美国天文学家皮克林 (1858 – 1938)

这两位在歧途上奋勇前进的美国天文学家对新行星的预言风格恰好走了两个极端。一位犹如天女散花，四面出击；另一位则谨记传统方法，抱元守一。皮克林(WilliamPickering)是那位喜欢天女散花的预言者。此人出生在美国的波士顿，这是世界名校哈佛大学与麻省理工学院的所在地，有着厚重的学术沉淀。皮克林有位兄弟担任过哈佛学院天文台(HarvardCollegeObservatory)的台长[注二]，而他本人在天文领域也小有成就，曾于1899年发现了土星的一颗卫星，不过他也热衷于研究一些后来被证实为子虚乌有的东西，比如月球上的昆虫和植被。总体来说，皮克林的工作风格不够严谨，这在很大程度上影响了他的学术成就，他一生有过的最高学术职位只是助理教授。皮克林晚年花了大约二十年的时间研究海外行星。他在这方面的研究很好地示范了他的马虎风格。他虽然是一个人在战斗，但提出的海外行星数量之多，更改之频，信誉之低，以及参数之千差万别，全都堪称奇观。自1908年提出第一个预言以来，他先后预言过的海外行星共有七个之多，且四度更改预言，他用英文字母对自己的行星进行了编号。为了对他的“战果”有一个大致了解，我们将他的预言罗列一下(其中行星U的轨道虽在海王星以内，却也是为了解释天王星海王星的“出轨”的而提出的；带撇的行星则是相应的不带撇行星的“补丁加强版”)：

行星O(1908年)：半长径51.9天文单位，质量为地球质量的2倍。 行星P(1911年)：半长径123天文单位。 行星Q(1911年)：半长径875天文单位，质量为地球质量的20000倍。 行星R(1911年)：半长径6250天文单位，质量为地球质量的10000倍。 行星O'(1919年)：半长径55.1天文单位，质量为地球质量的2倍。 行星O"(1928年)：半长径55.1天文单位，质量为地球质量的0.75倍。 行星P'(1928年)：半长径67.7天文单位，质量为地球质量的20倍。 行星S(1931年)：半长径48.3天文单位，质量为地球质量的5倍。 行星T(1931年)：半长径32.8天文单位。 行星P"(1931年)：半长径75.5天文单位，质量为地球质量的50倍。 行星U(1932年)：半长径5.79天文单位，质量为地球质量的0.045倍。

除孜孜不倦地从事计算外，皮克林还投入了大量的时间亲自搜索这些新行星。可惜他预言的行星虽多，在观测上却一无所获。1908年，在他完成了自己的第一个预言-对行星O的预言-后，他向一位名叫罗威尔(PercivalLowell)的美国天文学家请求了观测方面的协助。这位罗威尔是他的波士顿老乡，而且很巧的是，罗威尔也有一个兄弟在哈佛任职，且职位更牛，曾任哈佛校长[注三]。与皮克林研究月球上的昆虫和植被相类似，罗威尔也热衷于研究一些后来被证实为子虚乌有的东西，比如火星人和火星运河。罗威尔对天文学的主要贡献，是出资在亚里桑那州(Arizona)的一片海拔两千多米的荒凉高原上建立了著名的罗威尔天文台(LowellObservatory)。这是美国最古老的天文台之一，也是全世界最早建立的远离都市地区的永久天文台之一。这一天文台早期的一个主要使命，就是观测火星运河。

皮克林之所以请求罗威尔提供协助，除两人是同乡兼同行外，还有一个原因，那就是皮克林曾在罗威尔天文台的兴建过程中向罗威尔提供过帮助。照说有这么多层的“亲密”关系，罗威尔是没有理由不鼎力相助的。可惜皮克林却有一事不知，那就是罗威尔正是那另一位“不信邪”的美国天文学家，他当时也在从事新行星的搜寻工作，而且已经进行了三年。有亚当斯与勒维耶的海王星之争作前车之鉴，罗威尔对自己在这方面的努力进行了严格的保密，甚至在天文台内部的通信中都绝口不提新行星一词。接到皮克林的请求后，罗威尔暗自心惊。他一方面不动声色地予以婉拒，另一方面则加紧了自己的努力，将精力从火星运河上收了回来，集中到对新行星的研究上来。不过当他看到皮克林的粗糙计算后，立刻就放了心，看来并不是什么人都有能力从事这方面的工作的。自那以后，罗威尔不再避讳提及新行星，他将新行星称为行星X。



美国天文学家罗威尔 (1855 – 1916)

罗威尔寻找新行星的努力最初侧重的是观测，可惜一连五年颗粒无收。自1910年起，他决定对新行星的轨道进行计算，以便为观测提供引导。罗威尔的数学功底远在皮克林之上，与后者的漫天撒网不同，罗威尔对新行星的计算具有很好的单一性(即相信所有的剩余“出轨”现象都是由单一海外行星造成的)。与亚当斯和勒维耶一样，他首先对新行星的轨道半长径作出了一个在他看来较为合理的假设，然后利用天王星和海王星的“出轨”数据来推算其它参数。在具体的计算上他采用了勒维耶的方法(因为勒维耶发表了完整的计算方法，而亚当斯只发表了一个概述)。

那么新行星的轨道半长径应该选多大呢？罗威尔进行了独特的分析。由于海王星的发现明显破坏了提丢斯-波德定则，因此在寻找海外行星时人们已不再参考这一定则。为此，罗威尔提出了一个新的经验规律，那就是每颗行星与前一颗行星的轨道周期之比都很接近于一个简单分数，比如海王星与天王星的轨道周期之比约为2:1，土星与木星的轨道周期之比约为5:2。在此基础上，他提出一个假设，即行星X与海王星的轨道周期之比是2:1。由开普勒第三定律可知(请读者自行验证)，这意味着行星X的轨道半长径约为47.5天文单位。应该说，罗威尔的这个猜测有其高明之处，因为某些行星(或卫星)的轨道之间存在着所谓的轨道共振现象，它们的周期之比的确非常接近简单分数。不过轨道共振并非普遍现象[注四]，而且即便出现轨道共振，也没有理由认为行星X与海王星的轨道周期之比就一定是2:1[注五]。罗威尔自己或许也意识到了这一点，他后来还尝试过两个不同的轨道半长径：43.0和44.7天文单位。1912年，劳累过度的罗威尔病倒了几个月，但借助四位数学助手的协助，他终于在1913-1914年间完成了初步计算，他给出的行星X的质量为地球质量的6.6倍。

在进行理论计算的同时，罗威尔也没有放弃观测搜寻。他将自己一生的最后岁月全都投入到了搜寻新行星的不懈努力之中。可惜的是，他-以及皮克林-的所有努力与以前那些失败的预言并无实质差别。如果把他们投入巨大心力所做的计算比喻为大厦，那么所有那些大厦-无论多么华美-全都是建立在流沙之上的。随着时间的推移，罗威尔的努力越来越被人们所忽视。1915年初，他在美国艺术与科学学院(AmericanAcademyofArtsandScience)所作的一个有关海外行星搜索的报告受到了学术界与公众的双重冷遇，他的文章甚至被科学院拒收。自那以后，罗威尔对新行星的热情一落千丈，而他的生命之路也在不久之后走到了尽头。

1916年，罗威尔带着未能找到行星X的遗憾离开了人世。在他一生的最后五年里，罗威尔天文台积累了多达一千张的照相纪录，在那些纪录中包含了515颗小行星，700颗变星，以及-他万万不曾想到的-新行星的两次影像[注六]！这真是：有缘千里来相会，无缘对面不相逢。

注释

这一错误是美国天文学家彼得斯(ChristianPeters)所发现的。 皮克林的这位兄弟名叫爱德华(EdwardPickering)，于1877-1919年间任哈佛学院天文台的台长。原子光谱中的皮克林线系(Pickeringseries)就是以皮克林的这位兄弟的名字命名的，他并且还是分光双星(spectroscopicbinary)的发现者。 罗威尔的这位兄弟名叫阿伯特(AbbottLowell)，于1909–1933年间任哈佛大学校长。 由于太阳系相邻行星(小行星带也算在内)自外而内的轨道周期之比都在1-3之间，即便不存在轨道共振，它们接近于简单分数的概率也不小。感兴趣的读者可以算一下，任意一个1-3之间的实数与一个简单分数(比如分子分母都不超过5)接近到8%(这是罗威尔的猜测对已知行星的最大误差)以内的概率有多大。 如果把后来发现的冥王星视为行星X的话，它与海王星倒的确存在轨道共振现象，只不过它们的周期比是3:2而不是2:1。 那是1915年4月7日由他的助手比尔(ThomasBill)所做的观测记录，那时罗威尔自己已不再从事观测。

二零零八年三月六日写于纽约

二零零八年五月二十日发表于本站

二零零九年七月二十二日最新修订

寻找太阳系的疆界（十三）

二五.农家少年

罗威尔虽然去世了，但他为自己的未竟事业留下了一份最宝贵的遗产，那就是罗威尔天文台。他并且还在遗嘱中留出了超过一百万美元作为天文台的运作经费，这在当时是一个巨大的数目。可惜的是，第一次世界大战的爆发彻底终止了象寻找新行星那样的“小资”活动。更糟糕的是，罗威尔的遗孀因不满财产分配而发起了一场诉讼官司，这场官司不仅阻碍了天文台的运作，而且耗去了罗威尔留给天文台的那笔经费的很大一部分。经历了这些波劫的天文台直到1927年才重回正轨，可经费却已变得拮据。这时候，罗威尔那位担任哈佛校长的哥哥施出了援助之手，向天文台捐赠了一万美元。在此基础上，天文台开始装备一台口径13英寸的照相反射望远镜。

不过世事变迁对罗威尔天文台的影响不仅体现在财务上，也涉及到了学术。当时罗威尔的多数工作(比如对火星运河的观测)已被天文学界判定为是毫无价值的，而大半个世纪以来有关新行星的天女散花般的“预言”也早已信誉扫地。天文台是否还要继承“罗威尔道路”呢？罗威尔生前从事的寻找新行星的工作是否还要继续呢？这是罗威尔天文台面临的一个新的十字路口。在这个路口上，天文台的资深天文学家们大都作出了与当年那些错过了海王星的天文学家们一样的选择，即用其它任务填满自己的工作日程，不再抽时间从事新行星的搜索。对于一般的天文台来说，这应该就是新行星故事的终结了。不过罗威尔天文台终究不是一般的天文台，它并未完全忘记创始人罗威尔的心愿。虽然不可能再以新行星搜索为工作重心，但它当时的托管人-罗威尔的外甥普特南(RogerPutnam)-决定招募一名观测助理来从事新行星的搜索。

说来也巧，恰好就在这时，一封来自坎萨斯州(Kansas)的求职信寄到了天文台，求职者是一位22岁的农家少年。

这位少年名叫汤博(ClydeTombaugh)，1906年2月4日出生在伊利诺伊州(Illinois)，16岁时随父母迁居到坎萨斯州。受他叔叔的影响，汤博从小喜爱天文。由于家境贫寒，加上父母又不懂计划生育(共生育了六个小孩)，汤博中学毕业后只能辍学在家。他白天帮家里干农活，晚上则沉醉于观测无穷无尽的星空。由于没钱购买合适的望远镜，汤博用废弃的船舱玻璃、木板及农机零件，自己动手制作了口径为7英寸和9英寸的望远镜。



【美国天文学家汤博(1906 – 1997)】

如果不是1928年的一场突如其来的冰雹，汤博的一生也许就这样静静地在农庄里度过了。那一年，汤博家的庄稼长势极好，却在收获季节来临之前毁于冰雹。这场变故让汤博觉得应该找一个更可靠的职业来资助家里。于是他向当时自己知道的唯一一个天文台-罗威尔天文台-发去了求职信，并在信中附上了自己的一些笔记和图片。

一位务农在家、且只有中学学历的小伙子能引起罗威尔天文台的注意吗？很幸运，答案是肯定的。汤博在求职信中所附的笔记和图片给罗威尔天文台的台长斯莱弗(VestoSlipher)留下了很好的印象。他制作望远镜的手艺也正是罗威尔天文台所需要的，因为天文台的13英寸照相反射望远镜当时正在装配之中。甚至连他的务农经历对斯莱弗来说也显得很亲切，因为斯莱弗本人及天文台的另外两位资深天文学家小时候都有过类似的经历。

1929年1月，汤博乘坐了整整28小时的长途火车抵达罗威尔天文台，成为了天文台的一名观测助理。不久之后，在他的参与下，天文台的13英寸照相反射望远镜完成了装配及调试工作。

1929年4月，年轻的汤博正式走上了寻找海外行星的征途。

与发现天王星及海王星的时代相比，天文观测的手段-尤其是对暗淡天体的观测手段-已经有了很大的改善。早期的观测需要观测者对天体坐标进行手工记录，这对于观测暗淡天体来说是极为不利的。因为夜空中越是暗淡的天体数量就越多，当所要观测的天体暗淡到一定程度时，需要排查的天体数量就会多到让手工记录成为不可承受之重。为了解决这一问题，天文学家们将照相技术引进到了天文观测之中。这样，手工纪录的天体坐标就由相片所替代，而原先需要通过核对坐标来做的寻找新行星的工作，则可以通过对不同时间摄于同一天区的相片进行对比来实现。

罗威尔当年采用的就是这样的方法。这种方法免除了对天体坐标进行手工纪录的麻烦，但却并不意味着天文观测从此变得轻松了。事实上，在所要寻找的天体足够暗淡时，即便这样的方法也充满了困难。因为一张相片往往会包含几万甚至几十万个星体，对比排查的任务极其艰巨，几乎达到了肉眼不可能胜任的程度。而且需要对比的星体越多，就越容易因疏忽而丢失目标。为此，天文学家们又采用了一种新的仪器，叫做闪视比较仪(blinkcomparator)。这种仪器的工作原理很简单，就是将需要对比的相片彼此叠合、快速切换。显然，位置或亮度发生过变化的天体将会在相片的切换过程中显示出跳跃或闪烁，从而变得很显眼。更有利的是，闪视比较仪还可以与光学放大系统结合在一起，进一步提高分辨率。有鉴于此，罗威尔天文台的天文学家们早在罗威尔还在世时，就曾多次建议罗威尔购买闪视比较仪，并在1911年罗威尔的生日派对上成功说服了罗威尔。



【罗威尔天文台的闪视比较仪 图片出处：维基百科】

不过闪视比较仪的想法虽然高明，真正使用起来却仍不是一件容易的事情，因为对同一天区的两张相片只有在拍摄角度、曝光强度、胶卷冲洗等方面都保持高度的一致，才能获得良好的闪视比较效果。否则的话，连那些背景天体也会因为相片本身的人为差异而显示出变化。为了获得最佳的对比效果，汤博细心归纳了在不同天气条件下所需的曝光时间，并选出了一些明亮天体作为校正角度的参照点。他对每个天区都进行三次拍摄，以便从中选出两张最接近的相片进行对比。

二六.寒夜暗影

汤博的搜索工作从接近罗威尔预言的巨蟹座开始。起初他只负责拍摄，闪视比较的工作则交由另一位天文学家进行。1929年4月11日，汤博的搜索工作刚刚进入第五天，就成功地拍摄到了新行星的倩影。十九天后，他在对同一天区进行拍摄时再次将新行星摄入了相片。可惜的是，4月11日的照相胶片因天气寒冷而产生了裂缝，并且纪录本身也因太接近地平线而受到了大气折射的干扰，进一步影响了质量。负责闪视比较的天文学家没能从数以万计的天体中发现这组纪录，从而错过了一次可能的发现。这是继罗威尔时代的两次影像之后，新行星又一次躲过了罗威尔天文台的搜索。

几个月后，负责闪视比较的天文学家越来越忙于其它工作，很难抽出时间从事闪视比较，汤博便决定将这项工作接到自己手上。自那以后，他每个月用一半的时间从事观测，另一半的时间用来做闪视比较。由于相片上的天体实在太多[注一]，为避免数量压倒质量，汤博将每张相片都分割成很多小块，每块包含几百个天体。显然，这是一项高度重复，并且极其枯燥的工作。一般来说，检查几平方英寸的相片就会花去一整天的时间。当然，要说其中一点兴奋的东西也没有，那倒也不是，时不时地汤博会看到一些变动的天体。不过，这时可不能高兴得太早，因为有很多鱼目混珠的天体会让人误以为找到了目标。事实上，汤博在每组相片中都会看到几十个那样的天体。可惜它们要么是变星[注二]，要么是小行星、彗星或已知的行星，却没有一颗是新行星。这种“狼来了”的虚假天体见得多了，非但不能再带来兴奋，反而容易使人产生麻痹心理。但汤博始终保持着高度的敏锐和冷静，既不放过半点可疑的东西，也从未作出过任何错误的宣告。

又过了几个月，一无所获的汤博决定不再以罗威尔的预言为参考，毕竟他老人家的“预言”就象火星运河一样，口碑并不高，再紧盯下去有在一颗树上吊死的危险。作出了这一决定后，汤博将搜索范围扩大到了整个黄道面的附近，他的这一决定终结了罗威尔的预言对他搜索工作的帮助，因为这时的他已经走上了类似于巡天观测的道路。

1929年在繁忙的观测中悄然逝去，汤博在亚里桑那州寒冷高原的观测室里几乎沿黄道面搜索了一整圈。1930年1月，他的望远镜重新转回到了最初搜索过的天区。唯一不同的是，上一次是别人在帮他做闪视比较，而现在却是他本人在做。

1月21日，那个九个多月前曾经落网，却在闪视比较时从网眼里溜走的暗淡天体再次出现在了汤博的相片上-当然，这时候虽然“天知地知”，汤博本人却还不知道。1月23日和29日，在高原寒夜的极佳观测条件下，汤博完成了对这一天区的第二和第三次拍摄。

2月15日，汤博开始检查后两次拍摄的相片。还是老办法，先分割，然后一片一片地进行闪视比较。2月18日下午4时，他在对比以双子座δ星为中心的一小片天区的相片时，发现了一个亮度只有15等的移动星体。

就象曾经无数次重复过的那样，汤博对这一天体进行了仔细的查验。45分钟之后，除新行星外的其它可能性逐一得到了排除，兴奋不已的汤博找到资深天文学家兰普朗德(CarlLampland)，告诉他自己终于找到了新行星。已在罗威尔天文台工作了28年的兰普朗德幽默地回答说他早已知道了，因为他注意到了一直忙碌着的闪视比较仪的声音突然停止，并变成了长时间的静寂。小伙子一定是发现了什么。

很快，天文台的几位资深天文学家与汤博一起冲进工作室，开始紧张的复查。经初步确认后，斯莱弗台长决定对这一天体先进行一段时间的跟踪观测，然后再对外公布。斯莱弗的这个决定既是出于谨慎，也暗藏着一些私心，因为他想利用这段时间积累观测数据，以便在接下来的新行星轨道计算中夺得先机。

在接下来的一个月的时间里，在天气许可的每一个夜晚，所有其它工作通通被抛到了爪洼国，罗威尔天文台把全部的观测力量都投入到了对新天体的观测之中。这时候，再没有什么任务能比曾被当成鸡肋的新行星观测更重要了。

1930年3月13日，罗威尔天文台正式对外宣布了发现新行星的消息。这一天是罗威尔诞辰75周年的日子。149年前，也正是在这一天，赫歇耳发现了天王星。



【发现冥王星所用的望远镜】

不久之后，罗威尔天文台的天文学家投票从来自全世界的候选名字中选出了新行星的名字：普卢托(Pluto)，它是罗马神话中的地狱之神。说起来令人难以置信，首先提议这一名称的竟是英国牛津的一位年仅11岁的小女孩，她曾经学过经典神话故事并且很感兴趣，于是就提议用地狱之神命名这颗离太阳最远，从而最寒冷的新行星[注三]。在中文中，这一行星被称为冥王星。

冥王星的发现让崛起中的美国科学界欣喜不已，在欧洲天文界垄断重大天文发现这么多年之后，幸运之神终于溜跶到了美利坚，一些美国媒体兴奋地将新行星称为“美国行星”。但当时也许谁也不会想到，这个以地狱之神命名的新天体在天堂里待了七十六年之后，竟会从行星宝座上跌落下来，堕回“地狱”。



【哈勃望远镜拍摄的冥王星】

读者们也许还记得，汤博对冥王星的搜索，是从接近罗威尔预言的位置开始的，他曾经记录过冥王星的位置，只是未被认出。而当他正式发现冥王星的时候，他在黄道面附近完成了一整圈的搜索，又重新回到了起始时的天区。这表明冥王星的位置距离罗威尔的预言并不远。事实上，冥王星被发现时的位置与罗威尔1914年所预言的行星X在1930年初的位置只相差6°[注四]，这虽不象海王星的预言那么漂亮，却也不算太差。继海王星之后，天体力学似乎又一次铸造了辉煌。发现新行星的消息被宣布后的第二天，哈佛学院天文台台长沙普利(HarlowShapley)在费城的一次小范围演讲被临时换到了一个大场地，因为他决定在演讲中加入有关新行星的消息。那一天，数以千计的听众挤满了演讲大厅。当久违了的罗威尔相片出现在投影仪上时，全场响起了雷鸣般的掌声。听众们用发自内心的掌声向这位已故的天文学家致敬。此情此景，因研究火星运河而遭冷遇的罗威尔若泉下有知，也当含笑了。

但是，冥王星的发现果真是继海王星之后天体力学的又一次伟大胜利吗？

注释

汤博的每张相片平均约包含十六万个天体，往银河系中心方向拍摄的相片上则有多达一百万个天体。 变星通常显示为亮度变化的天体，与移动天体明显不同。但有些变星在亮度变小后会因为比相片所能纪录的最暗淡的天体还要暗，而从相片中消失，这样的变星在闪视比较时很象是一颗移出(或移入)相片范围的移动天体。 普卢托(Pluto)这位地狱之神还被用于命名1934年发现的第94号元素钚(plutonium)。1945年8月9日，用这一元素制作的原子弹将日本城市长崎带入了地狱。 冥王星被发现时的位置距皮克林1928年修正后的行星O的位置也只差6°左右，不过皮克林的计算信誉太低，很少有人当真。

二零零八年三月三十日写于纽约

二零零八年六月二日发表于本站

二零零九年七月二十三日最新修订

寻找太阳系的疆界 （十四）

二七.大小之谜

冥王星被发现之后，天文学家们很快就对它的轨道及大小进行了研究。在这两方面，冥王星都显现出很大的特异性。这其中轨道研究相对比较容易，短短几个月后就大体确定了主要的轨道参数，其中半长径约为39.5天文单位，椭率约为0.248，倾角约为17.1°。与其它八大行星相比，这是一个相当另类的轨道，它的椭率与倾角都是创纪录的。由于轨道椭率很大，冥王星有时甚至会比海王星离太阳更近，这种轨道交错现象在已知行星中是绝无仅有的。而由于轨道倾角很大，冥王星在多数时侯都处在离黄道面较远的位置上，因而特别不易被发现。但幸运的是，汤博搜索冥王星的那段时间，恰好是冥王星离黄道面较近的时候。



【从 Hydra (冥卫三) 看冥王星与卡戎 (冥卫一) 的艺术想象画】

冥王星的轨道参数虽然很快就被确定了，但确定它的大小-这个大小既是几何意义上的，也是质量意义上的-却向天文学家们提出了一个极大的挑战。因为人们很快就发现，无论用什么样的望远镜也无法让冥王星显示出行星应有的圆面。自望远镜问世以来，除了将小行星当成行星的那些年(参阅第七节)外，这种无法显示行星圆面的情形还从未发生过。当然，天文学家们对此倒也并非全无心里准备，冥王星被发现时的亮度只有15等，比人们预期的暗淡得多[注一]，除非冥王星表面物质的反光率低得异乎寻常，否则这样的暗淡只能有一个解释：那就是冥王星比人们预期的小得多。

那么冥王星究竟有多小呢？天文学家们用了几十年的漫长时光才搞明白了答案。

由于无法观测到圆面，天文学家们惯用的通过几何手段确定行星直径的方法在冥王星这里遭到了滑铁卢，取而代之的是通过亮度间接推断直径这一不太可靠的方法。这一方法之所以不可靠，是因为行星的亮度与直径并不存在固定的关系。同样亮度的行星，若表面物质的反光率高，它的直径就小，反之，若表面物质的反光率低，则直径就大。对于象冥王星那样遥远的新行星，当时的天文学家们并无任何办法确定其表面物质的反光率，因此虽然知道亮度，却无法准确估计它的直径。既然连直径都无法准确估计，对质量的估计自然就更困难了，因为后者还依赖于一个新的未知数：冥王星物质的平均密度。

虽然没有可靠的方法，天文学家们还是对冥王星的质量进行了粗略估计。1930-1931年间，天文学家们估计的冥王星质量约在0.1到1个地球质量之间。与现代数据相比，这是非常显著的高估。但即便是这些高估了的数据，也立刻就对罗威尔有关冥王星的“预言”造成了毁灭性的打击。读者们也许还记得，我们在第二十四节中曾经介绍过，罗威尔给出的行星X的质量约为地球质量的6.6倍。如果冥王星的实际质量只有0.1到1个地球质量，那它对天王星或海王星轨道的影响显然要远远小于罗威尔的计算，而罗威尔通过那种错误的影响对冥王星位置所作的反推则不可能是正确的。因此在冥王星被发现后不久，人们就已意识到，冥王星的发现并不是海王星神话的重演。冥王星在距罗威尔的预言只差6°的地方被发现，是纯粹的巧合[注二]。

有读者也许会问：我们在第二十节中曾经提到过，亚当斯与勒维耶对海王星质量及轨道的预测与海王星的实际参数也有不小的出入。为什么那些出入并不妨碍我们将海王星的发现视为巨大的天体力学成就呢？这首先是因为，亚当斯与勒维耶的海王星轨道计算是依据确凿存在的天王星出轨现象进行的，因此其观测依据是充分的；其次，二十世纪七、八十年代曾有人对亚当斯与勒维耶的计算细节进行了“复盘”，结果表明他们的计算细节也是完全有效的[注三]。反观罗威尔有关冥王星的“预言”，虽然在计算方法上效仿了勒维耶，但它依据的所谓天王星与海王星的“出轨”数据是子虚乌有的，因而整个计算只是一场“空对空”的演练。另一方面，由于罗威尔的“预言”很快就被判定为无效，后人也就没兴趣去复核他的计算细节了，他在这方面犯错的可能性也是完全存在的。因此，对冥王星的“预言”并不是海王星神话的重演，不仅在理论上不是，而且在实际上-如我们在上节中所说-也并未对冥王星的发现起到引导作用-冥王星的发现者汤博是在搜遍了黄道面之后才发现冥王星的。

虽然罗威尔有关冥王星的预言很快就被推翻了，但人们对冥王星大小的推算却仍在继续。直到冥王星被发现四十年后的二十世纪七十年代初，人们对冥王星质量的估计仍大体维持在0.1到1个地球质量之间，这些估计与现代值相比都大得离谱。虽然推算冥王星的质量不是一件容易的事情，但在那么多年的时间里，那么多天文学家所作的那么多估算竟然一面倒地巨幅高估冥王星的质量，这其中不能说没有心理上的原因。这原因就是自木星开始，太阳系的外行星是清一色的巨行星，而冥王星又一经发现就被认定为是行星。虽然冥王星已绝无可能是巨行星，但天文学家们显然还没有足够的心理准备来接受有关它大小的真相。



【冥王星 (左上) 与地球的大小对比】

我们在前面说过，同样亮度的行星，表面物质的反光率越低，相应的直径就越大。为了让冥王星维持一个体面的大小，天文学家们不惜将它“抹黑”为是一个表面反光率极低、如同巨型煤球一样的天体。而事实上，在冥王星那样遥远而寒冷的行星上，很多气体都能凝结成冰，冥王星是一个具有较高表面反光率的“冰球”的可能性要比它是“煤球”的可能性大得多。这一显而易见的可能性被错误地蒙蔽了几十年，直到二十世纪七十年代中期，才终于被确立了起来。反光率的调整立即对冥王星的质量估算产生了巨大影响，它的质量估计值一举缩小了两个数量级，不仅比所有其它行星都小得多，甚至变得比月球还小。这也为它日后的命运沉沦埋下了种子。

不过，依靠对那样遥远的一个天体的表面反光率及物质密度的研究来推断其质量，无论如何只能算是下策。估计冥王星质量的最佳途径，显然是越过所有这些与冥王星物质有关的细节来直接估计其质量。这样的途径在1978年成为了现实。1978年6月22日，美国海军天文台(NavalObservatory)的天文学家们发现了冥王星的卫星卡戎(Charon-希腊神话中摆渡亡灵的神)。在行星天文学上，一颗行星一旦被发现有卫星，我们就可以通过观测卫星的运动来测定该行星的引力场，既而推断其质量，这是测定天体质量最有效的手段之一。因此卡戎的发现为直接估计冥王星的质量提供了极好的条件(请读者们想一想，中学物理课本中的哪一条定律有助于利用卡戎来确定冥王星的质量？)[注四]。

如今我们知道，冥王星的质量只有地球质量的千分之二点一，它绝不可能是罗威尔或其它任何人所预言的海外行星，它对天王星和海王星的引力摄动甚至还不如作为内行星的地球对它们的引力摄动来得大。1993年，美国加州喷气动力实验室的科学家斯坦迪什(ErlandMylesStandish,Jr)利用“旅行者号”飞船所获得的有关木星、土星、天王星和海王星的最新质量数据重新计算了外行星的轨道摄动，并再次证实了的确不存在天王星和海王星的出轨问题，不存在需要用新行星来解释的偏差。冥王星的发现完全是一个多重错误导致的奇异果实：罗威尔对冥王星轨道的计算是依据错误数据所做的无效分析；汤博对冥王星的搜索则是源于罗威尔天文台对一个错误心愿的盲目继承。

而所有这一切的错误之所以最终结出了一个如此美丽的果实，全靠汤博在寒冷的亚里桑那高原上为期十个月的顽强搜索，这是整个冥王星故事中唯一的必然。

二八.深空隐秘

发现冥王星之后，汤博并未离开寻找太阳系疆界的孤独事业，他投入了另外十三年的漫长时光，继续搜索更遥远的行星。他的搜索范围超过了整个夜空的三分之二，他所涵盖的最低亮度达到了17等，他对比过的天体多达九千万个。在那十三年里，他发现了6个星团、14颗小行星及一颗彗星，但却没能发现任何冥王星以外的新行星。

那么，冥王星轨道是否就是太阳系的疆界呢？既然观测一时还无法回答这个问题，天文学家们便展开了理论上的探讨。不过那探讨不再是象亚当斯与勒维耶那样的精密计算。由于冥王星的发现已属巧合，在那之后的天文学家们哪怕在做梦的时候，恐怕也很少还会再幻想重演一次笔尖上预言新行星的奇迹了。但是，精密的预言虽不可能，粗略猜测一下太阳系的疆界在哪里却还是可以的。

那样的猜测几乎立刻就出现了。冥王星发现之初，美国加州大学的天文学家利奥纳德(FrederickC.Leonard)就猜测冥王星的发现有可能意味着一系列海外天体(trans-Neptunianobject，简称TNO)将被陆续发现。应该说，在经历了天王星、海王星及冥王星的发现之后，单纯作出这样一个猜测已无需太高级的想象力了。不过，比单纯猜测更有价值的，是1943年爱尔兰天文学家埃奇沃斯(KennethEdgeworth)提出的稍具系统性的观点。

在介绍埃奇沃斯的观点之前，让我们稍稍介绍一下太阳系的起源学说。在科学上，几乎任何东西-人类、生命、地球、乃至宇宙-的起源都是值得探究的课题，太阳系的起源也不例外。自十八世纪康德(ImmanuelKant)和拉普拉斯(Pierre-SimonLaplace)彼此独立地提出了著名的星云假说以来，天文学家们关于太阳系起源的主流观点，是认为太阳系是由一个星云演化而来的。这其中行星的形成，乃是来自于星云盘上的物质彼此碰撞吸积的过程。



美籍荷兰裔天文学家柯伊伯 (1905 - 1973)

按照这种理论，行星形成过程的顺利与否与星云物质的密度有很大的关系。星云物质的密度越低，则引力相互作用越弱，星云盘上物质相互碰撞的几率越小，从而吸积过程就越缓慢，行星的形成也就越困难。当星云物质的密度低到一定程度时，行星的形成过程有可能缓慢到在太阳系迄今50亿年的整个演化过程中都无法完成，而只能造就一些“半成品”：小天体。埃奇沃斯认为，海王星以外的情形便是如此。那里的星云物质分布是如此稀疏，以至于行星的形成过程无法进行到底，而只能形成为数众多的小天体。由此他提出，人们将会在海王星之外不断地发现小天体。他并且进一步提出，那些小天体中的某一些会偶尔进入内太阳系，成为彗星。

无独有偶，1951年，美籍荷兰裔天文学家柯伊伯(GerardKuiper)也注意到了太阳系物质分布在海王星之外的急剧减少。与利奥纳德类似，他也认为那样的物质分布会形成一系列小天体而非大行星[注五]。但与利奥纳德-以及后来的天文学家们-不同的是，柯伊伯认为那些曾经存在过的小天体早就已被冥王星的引力作用甩到了更遥远的区域，不会再存在于距太阳30-50天文单位的区域中了。换句话说，他认为在冥王星轨道的附近曾经有过大量的小天体，但目前已不复存在。在这点上，柯伊伯犯了一个可以原谅的错误，他以为冥王星的质量接近于地球质量(这在当时被认为是有可能的)，从而有足够的引力来做到这一点。而事实上，冥王星的质量-如我们在上节中介绍的-只有地球质量的千分之二点一。

埃奇沃斯与柯伊伯的想法在接下来的十年间并未引起什么重视。但常言道：是金子总是会发光的。一个合理的想法纵然一时沉寂，终究还是会复活的。一九六二年，在美国工作的加拿大天文学家卡梅伦(AlastairCameron)提出了类似的看法。两年后，美国天文学家惠普尔(FredWhipple)也加入了这一行列。惠普尔的研究比前面几位更加深入，除了猜测在海王星之外存在类似于小行星带的结构外，他还试图研究那些小天体对天王星和海王星轨道的摄动，但没能得到可靠的结果。一九六七年，惠普尔及其合作者又研究了七颗轨道延伸到天王星之外的彗星，试图寻找来自海外天体的引力干扰，结果也未发现任何可察觉的干扰。由此他们估计出那些小天体-如果存在的话-的总质量必定远小于地球质量。他们的这一估计在如今看来是颇有前瞻性的，但在当时却是一个有点令人沮丧的结果，因为它意味着观测那些小天体将会是一件非常困难的事情。

除了这些从太阳系起源角度所做的分析外，天文学家们从另一个完全不同的角度出发，也殊途同归地提出了海王星以外存在大量小天体的假说。这个不同的角度便是彗星的来源。彗星是太阳系中最令人瞩目的天体，当它们拖着美丽的尾巴(彗发)出现在天空中时，常常是万人争睹的天象。天文学家们注意到，太阳系中的彗星按轨道周期的长短大致可分为两类：一类是长周期彗星，它们的轨道周期在两百年以上，长的可达几千、几万、甚至几百万年。另一类则是短周期彗星，它们的轨道周期在两百年以下，短的只有几年。短周期彗星的存在给天文学家们带来了一个难题。因为这些彗星上能够形成彗发的挥发性物质会因频繁接近太阳而被迅速耗尽，而且它们的轨道也会因反复受到行星引力的干扰而变得极不稳定。计算表明，短周期彗星的存在时间应该很短，相对于太阳系的年龄来说简直就是弹指一瞬。但我们却直到太阳系诞生50亿年之后的今天仍能观测到不少命如蜉蝣般的短周期彗星，这是为什么呢？天文学家们认为，唯一的可能是太阳系中存在一个短周期彗星的补充基地。

这个短周期彗星的补充基地究竟在哪里呢？1980年，乌拉圭天文学家费尔南德斯(JulioFernández)提出了一个后来被普遍接受的假说，即短周期彗星来自海王星之外的一个小天体带。他并且推测那些小天体的视星等约在17-18之间(比汤博曾经搜索过的天体更暗，但这个亮度后来被证实为仍是显著的高估)。在他颇具影响力的论文中，费尔南德斯援引了柯伊伯的文章，却忽略了埃奇沃斯的工作。费尔南德斯的这一粗心大意导致的后果，是人们多少有点乌龙地用柯伊伯的名字命名了那个小天体带。而事实上，如我们在上面提到的，在所有曾经猜测过那个小天体带的天文学家中，柯伊伯几乎是唯一一个认为它目前已不复存在-从而与费尔南德斯的假说及后来的观测结果截然相反-的人。费尔南德斯的的假说提出之后，1988年，几位在美国加州大学及加拿大多伦多大学工作的天文学家通过计算机模拟手段，对这一假说进行了检验。他们的检验表明，由那样一个小天体带所产生的短周期彗星无论在数量还是轨道分布上都与实际观测有着不错的吻合。

因此，到了二十世纪八十年代末，来自不同角度的理论分析均表明，在海王星的轨道之外很可能存在一个小天体带，它是行星演化过程中的半成品，同时也是短周期彗星的大本营。但到那时为之，那个遥远的天区除了一颗孤零零的冥王星外，在观测意义上还是一片虚空。

距离给了外太阳系神秘的面纱，天文学家们却要揭开面纱来寻找隐秘。

注释

比如罗威尔所预测的冥王星亮度为13等。 这一巧合的概率并不很小，因为罗威尔对行星X的位置预言其实有两处(彼此相差180°)，在其中任何一处的左右6°范围之内发现新行星的概率约为1/15(请读者自行计算一下)。 1970年，布鲁克斯(C.J.Brookes)对亚当斯的方法进行了分析，结论是它的确可以得到精度在几度之内的结果。1980年，巴格代迪(Baghdady)对勒维耶的方法进行了复盘，结果得到了误差仅为16'的结果。这些验证表明亚当斯与勒维耶的计算方法都是有效的。 通过卡戎的运动直接测定的其实是冥王星与卡戎这一行星-卫星系统的总质量。对于其它行星来说，这几乎就等于行星的质量。但冥王星与卡戎却是一个引人注目的例外，因为卡戎的质量相当大(约为冥王星质量的11.65%)。因此用引力效应测定冥王星的质量时还牵涉到确定卡戎与冥王星的相对质量这一额外的复杂性。 柯伊伯并未在自己的论文中提及埃奇沃斯的工作，这一点使得后来有历史学家对他是真的不知道埃奇沃斯的工作，还是暗中“借用”了对方的想法产生了疑问。

二零零八年四月五日写于纽约

二零零八年六月十日发表于本站

二零零九年七月二十八日最新修订

寻找太阳系的疆界 （十五）

本文作者：卢 昌海

本系列的单行本《寻找太阳系的疆界》已于2009 年 11 月由清华大学出版社出版，节略版曾在 2007-2008 年的《中学生天地》杂志上连载。

卢昌海老师的微博：http://weibo.com/ChanghaiNews，个人网站：http://www.61k.com。

前文回顾《寻找太阳系的疆界》连载

二九.巅峰之战

在经历了追捕小行星的波折，发现海王星的纷争，搜寻火神星的未果，以及预言冥王星的虚无之后，在太阳系边缘搜索新天体的苦力活早已失去了往日的魅力。行星这个曾经神圣的概念渐渐变成了如美国物理学家费曼(RichardFeynman)在其名著《费曼物理学讲义》中所说的“那八个或十个遵循相同物理定律，由同样的尘埃云凝聚而成的球体”。在二十世纪天文学发展的迅猛浪潮中，行星天文这个最古老的分支甚至一度整体性地沦落为了二流学科，以至于二十世纪六十年代，当美国国家航空航天局(NASA)为行星探测计划寻找咨询时，为天文学家们在这一分支上的知识贫乏而感到惊讶。后来，随着六七十年代美国与前苏联的一系列无人探测器计划的成功实施，行星天文学虽然重新成为了焦点领域，但与此同时，行星天文学家们的目光却也被吸引到了行星地貌、行星物理、行星化学等新兴方向上，对搜索新天体的兴趣依然低迷。



【行星天文学家朱惠特 (1958-, 右) 与卢简 (1963-, 左)】

不过，当有关海外天体的猜测变得越来越言辞凿凿时，外太阳系的奥秘终于还是再次引起了一小部分天文学家的关注与喜爱。这其中麻省理工学院的一位天文学家决定化“爱心”为行动，展开对海外天体的观测搜索。这位天文学家名叫朱惠特(DavidJewitt)，来自英国。朱惠特七岁那年曾有幸目睹过一次流星雨，年幼的他被天象的美丽与神奇所吸引。二十世纪七十年代后期，美国国家航空航天局发布的美轮美奂的行星及卫星图像再次打动了当时正在伦敦念本科的朱惠特。他决定选择行星天文学作为自己的专业，并前往美国念研究生。1983年，朱惠特在美国加州理工大学获得了博士学位，随后成为了麻省理工学院的助理教授。在那里，他遇到了重要的学术合作伙伴卢简(JaneLuu)[注一]。卢简是一位出生于越南的女孩，1975年随父母逃难来到美国。与朱惠特一样，卢简也是被美国国家航空航天局的行星与卫星图像所吸引，而选择了行星天文学作为自己的专业。朱惠特在麻省理工学院的时候，卢简正在那里念研究生。

1987年的某一天，当朱惠特和卢简在系里相遇时，朱惠特提议卢简参与自己即将开始的搜索海外天体的工作。这是自冥王星被发现之后将近半个世纪的时间里极少有人问津的冷门观测。卢简问朱惠特：“为什么要做这样的观测？”朱惠特的回答是：“如果我们不做，就没人做了”-听起来颇有几分“我不入地狱，谁入地狱”的悲壮。卢简被这个简短的回答所打动，一场历时五年的漫长搜索由此揭开了序幕。

朱惠特与卢简最初的观测地点是位于亚里桑那州的美国基特峰国家天文台(KittPeakNationalObservatory)及南美洲的塞罗托洛洛天文台[注二]，他们最初采用的观测方法类似于汤博当年所用的方法，即通过对间隔一段时间拍摄的同一天区的相片进行闪烁对比，来寻找缓慢运动的天体。当然，半个世纪之后的朱惠特与卢简所拥有的设备已非汤博当年可比，唯一不变的是任务本身的繁重、枯燥，以及用眼过度产生的疲惫。经过了一段时间的搜索，朱惠特与卢简一无所获，他们辛苦寻获的运动天体无一例外地被证实为是已知天体、胶片缺陷、灰尘、或宇宙线造成的影像。

幸运的是，就在这时，一项让整个光学观测领域脱胎换骨的新兴技术-电荷耦合器件(ChargeCoupledDevice)，简称CCD-进入了天文界。CCD是1969年由美国贝尔实验室(BellLabs)的两位科学家发明的一种可以取代传统胶片的感光器件。CCD的最大优点是具有极高的敏感度，能对70%甚至更多的入射光作出反应，而普通照相胶片的这一比例还不到10%。真是不比不知道，一比吓一跳。要知道朱惠特与卢简所寻找的是离太阳几十亿公里之外的小天体，它们自身并不发光，全靠其表面反射的太阳光才能被我们所发现。在那样遥远的距离上，太阳的光芒只有一亿亿分之一能够照射到那些小天体上。那部分光线有的被吸收，有的被反射，那些反射光必须再次穿越广袤的行星际空间，其中只有一万亿分之一能够来到地球。而在那“亿里迢迢”来到地球的反射光中，恰好能进入望远镜的又只有其中的一百万亿分之一。这是何等宝贵的“星星之火”？可这宝贝却还要被该死的照相胶片忽略掉90%以上，这真是“生可忍，熟不可忍”(韦小宝语)。

因此CCD的使用对于观测天文学来说堪称是一场革命。不过CCD虽然在感光性能上遥遥领先于普通胶片，在一开始却也有一个很大的缺陷，那就是像素太少。朱惠特与卢简最初使用的CCD的有效像素仅为242×276，相当于如今一台普通数码相机像素数量的百分之一。由此带来的后果是，每张CCD相片涵盖的天区面积只有他们以前所用的普通光学相片的千分之一。换句话说，原先分析一组相片就能覆盖的天区，如今却要分析一千组相片。但幸运的是，CCD所采用的独特的感光方式为计算机对比相片开启了方便之门，从而大大减轻了对肉眼的依赖。而更重要的是，对于特别暗淡的天体，普通胶片有可能因为敏感度不够而完全无法记录，这时CCD的优势更是无与伦比。因此，当CCD进入天文观测领域后，朱惠特与卢简便决定用它取代照相胶片。

这时候，朱惠特与卢简的观测地点也发生了变化。1988年，朱惠特接受了夏威夷大学天文研究所的一个职位。不久，卢简也来到了夏威夷，两人利用夏威夷大学所属的茂纳基雅天文台(MaunaKeaObservatory)的一台口径2.24米的望远镜继续他们的海外天体搜寻工作。茂纳基雅是夏威夷语，含义是“白山”，那里常年积雪，而茂纳基雅天文台的所在之处正是白山之巅，海拔高达4200米(比汤博所在的罗威尔天文台高了一倍)。那里的空气稀薄而干燥，氧气的含量只有海平面的60%，常人在那里很容易出现高原反应，大脑的思考及反应能力也会明显下降。为了减轻高原反应的危害，天文学家们象登山者一样，在海拔较低(3000米)的地方建立了营地。要去天文台的天文学家通常提前一晚就来到营地过夜，以便让身体提前适应高原的环境，然后在第二天晚饭之后驾驶越野车前往天文台。在那里，朱惠特与卢简夜复一夜地进行着观测。当他们感到疲惫的时候，有时朱惠特会放上一段重金属音乐，有时则卢简会放上一段经典音乐，控制室里响彻着时而激扬、时而舒缓的乐曲。



【茂纳基雅峰上的观测台】

这样的日子一晃就是四年，其间卢简完成了自己的学业，并获得了哈佛大学的博士后职位，但她仍时常回到茂纳基雅天文台，与朱惠特一起，在那白山之巅的稀薄空气里继续着对海外天体的执着搜索。尽管一次次的努力换来的只是一次次的失望，但他们契而不舍地坚守着这份孤独的事业。幸运的是，在那四年中，CCD的技术有了长足的发展，分辨率由最初的242×276提高到了2048×2048，从而大大提升了搜索效率。就在毅力、耐力和技术这三架马车的共同牵引下，朱惠特与卢简这场巅峰之战的胜利时刻终于来临。

1992年8月30日，在对比两张CCD相片时，一个缓慢移动的小天体引起了朱惠特的注意。一般来说，距离太阳越远的天体运动得越慢，从那个天体的移动速度来看，它与太阳的距离似乎有60天文单位。换句话说，这似乎是一个海外天体。当然，仅凭两张相片的对比是不足以作出结论的，于是他们对该天区进行了反复的拍摄与对比，结果证实这一天体的确是在缓慢地运动着，而且其运动速度所显示的距离的确是在海王星轨道之外，因此的确是一个海外天体。

朱惠特与卢简终于成功了。四年了，他们在这仿佛伸手便可摘到星星的巅峰之上苦苦寻找，运气却仿佛远在星辰之外。没想到成功竟然就在今夜，这一刻真让人猝不及防！朱惠特与卢简兴奋得象两个大孩子一样在观测室里又蹦又跳。他们将这一消息通告了国际天文联合会(InternationalAstronomicalUnion)所属的小天体中心(MinorPlanetCenter)[注三]。9月14日，小天体中心的天文学家马斯登(BrianMarsden)正式公布了这一发现，并确定了该天体的临时编号：1992QB1[注四]。据测定，1992QB1的轨道半长径约为44天文单位(比朱惠特最初估计的要小，但的确是在海王星轨道之外)，直径约为160公里。

三十.玄冰世界

1992QB1的发现是人类在寻找太阳系疆界的征途上取得的又一个重要进展。不过在一开始，有些天文学家对1992QB1是否真的是海外天体还心存疑虑。比如小天体中心的马斯登，他虽然亲自宣布了1992QB1被发现的消息，但其本人却是怀疑者中的一员。他认为1992QB1有可能只是一个轨道椭率很大的天体，这样的天体虽然远日点距离很大，但绝大多数时间其实都处在海王星轨道以内，从而算不上是货真价实的海外天体。马斯登甚至为自己的猜测与朱惠特打了500美元的赌。

这个赌局很快就有了结果。1993年3月28日，朱惠特与卢简发现了第二个海外天体，临时编号为1993FW。1993FW的轨道及大小都与1992QB1相似，它的发现极大地动摇了马斯登的怀疑，因为天文学家们在对这两个天体的轨道计算中犯下同样错误，一错再错地把轨道椭率很大的天体误当成海外天体的可能性是很小的。此后不久，更多的海外天体被陆续发现，从而越来越清楚地表明它们正是理论家们几十年前所猜测的那个海外小天体带的成员。1994年，当海外天体的数量增加到六个(其中四个是朱惠特与卢简发现的)时，马斯登终于“投降”，乖乖交出了500美元。



【若干直径较大的海外天体 (下方蓝色星球为地球)】

与当年发现小行星带的情形相类似，随着观测技术的持续改进，以及受第一轮发现的吸引而对海外天体感兴趣的观测者的增多，海外天体的发现不断提速，在热闹的年份里一年就能发现一两百个(当然，它们的发现也因此而很难再登上新闻标题了)。不过，由于距离遥远，加上体形苗条，海外天体大都极其暗淡，视星等通常在20以上，不到冥王星被发现时的亮度的百分之一；加上观测海外天体在各大天文台的任务排行榜上的地位较低，因此被发现的海外天体因未能及时跟踪而重新丢失的比例也大得惊人，有时竟达40%。寻找海外天体的努力，仿佛是往小学数学题里那个开着排水口的水池里灌水，一边找，一边丢。不过在一群象朱惠特与卢简那样执着的天文学家的努力下，得到确认的海外天体的数量还是稳步增长着。截至2008年3月，被小行星中心纪录的海外天体数量已经超过了1300，它们的表面大都覆盖着由甲烷、氨、水等物质组成的万古寒冰。

随着数量的增加，天文学家们对海外天体按其轨道特征进行了粗略的分类，其中距太阳30-55天文单位的海外天体被称为柯伊伯带天体(Kuiperbeltobject)，它们构成了所谓的柯伊伯带。我们在第二十八节中曾经提到，“柯伊伯带”这一名称其实有点乌龙，因为在曾经猜测过这一小天体带的天文学家中，柯伊伯的观点偏偏是认为它们如今早已不复存在，从而与观测结果完全不符的。不过，柯伊伯是一位对现代行星天文学有过重要影响，甚至被一些人视为是现代行星天文之父的天文学家，用他的名字命名一个天体带也不算过分。据估计，柯伊伯带中直径在100公里以上的天体可能有几万个之多，目前已被发现的还只是冰山之一角。

另一方面，柯伊伯带天体相对于全部海外天体来说也同样只是冰山之一角。在发现柯伊伯带的过程中，人们也发现了一些离太阳更远的天体，那些天体被称为离散盘天体(scattereddiscobject)，它们的轨道椭率通常很大，轨道倾角的范围也比柯伊伯带天体宽得多，它们的远日点比柯伊伯带天体离太阳远得多，但近日点却往往延伸到柯伊伯带，个别的甚至会向内穿越海王星轨道。一般认为，离散盘天体最初也形成于柯伊伯带之中，后来是因为受到外行星的引力干扰而被甩离了原先的轨道。有鉴于此，天文学家们有时将离散盘天体称为离散柯伊伯带天体(scatteredKuiperbeltobject)[注五]。

人们早期发现的海外天体的直径大都在一两百公里左右，但渐渐地，一些更大的天体也被陆续发现了(请读者想一想，哪些因素有可能导致那些更大的海外天体反而较迟才被发现？)。下表列出了其中较有代表性的几个(其中“正式编号”是小天体中心在轨道被确定后指定给小天体的编号)：

这些天体的大小都接近或超过了最大的小行星-谷神星(谷神星的直径约为960公里)[注六]。看来这遥远的玄冰世界里还真是别有洞天。不过，这些天体与行星世界的小弟弟，直径约2300公里的冥王星相比终究还是偏小了一点。

正式编号临时编号名称直径 (公里)

193081996TO66~ 900

200002000WR106Varuna780 ~ 1016

555652002AW197890 ~ 977

500002002LM60Quaoar1200 ~ 1290

845222002TC302710 ~ 1200

1361082003EL61Haumea1200 ~ 2000

904822004DWOrcus909 ~ 1500

但就连这一点也在2005年的新年伊始遭遇了挑战。

2005年1月5日，美国加州理工大学的行星天文学家布朗(MichaelBrown)在检查一年多前(2003年10月21日)他与北双子天文台(GeminiNorthObservatory)的天文学家特鲁吉罗(ChadTrujillo)及耶鲁大学的天文学家拉比诺维茨(DavidRabinowitz)拍摄的相片时，发现了一个新的海外天体。按照相片拍摄的时间，这一天体的编号被确定为2003UB313。2003UB313是一个轨道椭率很大的天体，它被发现时正处于距太阳约97.5天文单位的远日点。在那样遥远的距离上仍能被观测到，可见其块头一定小不了。据布朗估计，2003UB313的直径起码比冥王星大25%[注七]。这一估计在行星天文学界引起了很大的震动。因为自冥王星被发现以来，这还是人们首次在太阳系中发现比冥王星更大，同时又不是卫星的天体。毫无疑问，象2003UB313那样的庞然大物应该有一个专门的名称，它曾被暂时命名为齐娜(Xena)，后来被正式定名为埃里斯(Eris)。这是希腊神话中的争吵女神，著名的特洛伊之战(Trojanwar)就是在她的煽风点火之下引发的。在中文中，这一天体被称为阋神星。

这位不太淑女的女神很好地预示了她即将带给天文学家们的东西：争吵-有关行星定义的争吵。

注释

按照用姓氏称呼外国人名的惯例，JaneLuu应该被称为卢，不过考虑到一个字的中文名用起来比较别扭，本文将JaneLuu按全名译为卢简。 我们曾在第二十节中提到过这个天文台，海王星档案就是在那里失而复得的。塞罗托洛洛天文台虽远在智利，却是美国国家光学天文台(NationalOpticalAstronomyObservatory)的一部分。 MinorPlanetCenter若直译，应为“小行星中心”，但考虑到中文的“小行星”一词往往特指由英文asteroid所表示的小行星带中的小天体，因此本文将之译为“小天体中心”。 自1925年以来，天文界采用了以发现年份外加两个英文字母作为小天体临时编号的做法。其中第一个字母表示发现小天体的半月，从一月上半月的A到十二月下半月的Y(I与Z不出现)。第二个字母(I与Z同样不出现)则按照小天体在该半月中的发现顺序排列。如果该半月中发现的天体数目超过24个，则以下标表示字母被重复使用的次数。请读者按照这一命名规则推算一下1992QB1是哪一个半月发现的？以及它是该半月中被发现的第几个小天体？ 离散柯伊伯带天体还包括所谓的半人马小行星(centaurs)，那也是一些轨道椭率很大的小天体，只不过与离散盘天体的向外离散恰好相反，它们是向内离散的，其轨道通常分布于木星轨道与海王星轨道之间。 表格中的数据是早期的估计值，大都有些偏高。天文学家们一直在对海外天体的大小进行了观测和修正，比如20000Varuna的直径后来(2007年)通过斯皮策太空望远镜(SpitzerSpaceTelescope)的观测而被修正为了500公里左右。 这一估计有些偏高，目前人们对2003UB313直径的估计为2400±100公里，只比冥王星略大，不过它的质量要比冥王星大28%左右，这一点由于它与冥王星分别存在卫星而得到了比它们的直径对比更为可靠的确立。

二零零八年四月六日写于纽约

二零零八年六月十九日发表于本站

二零零九年七月二十九日最新修订

寻找太阳系的疆界 （十六，完）

本文作者：卢 昌海

本系列的单行本《寻找太阳系的疆界》已于2009 年 11 月由清华大学出版社出版，节略版曾在 2007-2008 年的《中学生天地》杂志上连载。

卢昌海老师的微博：http://weibo.com/ChanghaiNews，个人网站：http://www.61k.com。

前文回顾《寻找太阳系的疆界》连载

三一.冥王退位

阋神星的发现向天文学家们提出了一个问题，那就是：它究竟是不是行星？这原本不应该成为问题的，因为阋神星既然比冥王星还大，当然应该算是行星。但问题是，在阋神星之前，人们已经发现了大量的海外天体，并且已经接受了海外天体是行星演化过程中的半成品的想法。在这种背景下要接受阋神星为行星是有难度的。更何况，海外天体中还包含了其它一些大小可观的成员。除上节列出的夸欧尔(Quaoar-美国原住民神话中的创世之神，中文名称为创神星)、好婺妹阿(Haumea-美国夏威夷神话中掌管生育的女神，中文名称为妊神星)及厄耳枯斯(Orcus-罗马神话中的死亡之神，中文名称为死神星)等外，还有与阋神星同一天被宣告发现的马克马克(Makemake-复活节岛上的造物之神，正式编号为136472，发现时的临时编号为2005FY9，中文名称为鸟神星)，它的直径也有1300~1900公里。这些天体虽比冥王星小，但相差并不多，如果阋神星和冥王星可以算作是行星，那它们是否也应该算是行星呢？

当人们开始提出这样的问题时，一个更基本的问题也随之浮出了水面：究竟什么是行星？

就象其它很多习以为常的概念一样，人类知道行星的存在虽有漫长的历史，却从未给它下过明确的定义。在历史上，人类对行星的认定极少发生争议，而且即便发生争议，也要么很快就被解决(比如有关小行星地位的争议)，要么所争之处并非行星的定义(比如对地球地位的争议)，从而并未触及行星定义的必要性。

可现在的情况完全不同了。要知道冥王星行星资格的由来就有着很大的侥幸性：它一开始就被错误地当成了罗威尔的行星X，可以说是将行星宝座当成婴儿床，直接就诞生在了那里。尔后又在很长的时间内被误认为可能有地球那么大。后来虽一再“瘦身”，但生米早已煮成熟饭，再说“瘦死的骆驼比马大”，冥王星虽小，比小行星终究还是大得多，因此其身份虽遭到过怀疑，却象一位有经验的潜伏人员那样有惊无险地挺了过来[注一]。但随着海外天体的陆续登场，冥王星除在个头上遭到挑战外，它隐匿多年的一桩“劣迹”也得到了曝光。我们知道，当年小行星们之所以被剥夺行星资格，除个头太小外，还因为它们犯有一项“重罪”，那就是“非法聚众”。现在冥王星显然也犯下了同样的“罪行”。在这种情况下，摆在天文学家们面前的是一个两难局面：要么象当年处理小行星一样，剥夺冥王星的行星资格；要么一视同仁地将所有较大的柯伊伯带天体全都吸收为行星，甚至恢复某些小行星的名誉。无论哪一种选择，都将改变已沿袭了大半个世纪的太阳系九大行星的基本格局。

另外需要提到的是，除了来自太阳系内部的这些麻烦外，行星这个被太阳系垄断了几千年的专利，自二十世纪九十年代起开始遭遇了“盗版”。天文学家们在其它恒星(包括白矮星、脉冲星等)周围也陆续发现了行星，而且其数目迅速增加，目前已远远超过了太阳系的行星数目。所有这些都促使天文学家们摆脱单纯的历史沿革，对行星的定义进行系统思考。在这过程中，冥王星的命运是让很多人-尤其是公众-最为关注的焦点。

1999年，随着有关冥王星地位变更的传闻越来越多，负责天体命名及分类的国际天文联合会发表了一份声明，公开否认其正在考虑这一问题。但就在这份明修栈道式的声明发表的同一年，该联合会却暗渡陈仓般地成立了一个旨在研究太阳系以外行星(ExtrasolarPlanets)的工作组。2001年2月，该工作组拟出了一份名义上只针对太阳系以外行星的定义草案，其中给出了行星定义的一个重要组成部分，那就是行星必须足够小，以保证其内部不会发生核聚变反应[注二]。这一条的主要目的是将行星与所谓的褐矮星(browndwarf)区分开来。按照我们目前对天体内部结构的了解，这一条给出的行星质量上界约为木星质量的13倍。

除上界外，完整的行星定义显然还应包含一个合理的下界，否则环绕恒星运动的任何小天体，甚至每一粒尘埃都将变成行星，那是不堪设想的事情。不过由于早期发现的太阳系以外的行星大都是巨行星，因此上述草案并未对质量下界给予认真关注，只是建议参照太阳系行星的情况。可这“参照”二字说来容易，做起来却绝不轻松，因为太阳系行星的情况一向只是约定成俗，而从未有过明确定义，若当真遇到什么棘手的情形，还真不知该如何参照。有鉴于此，2002年，美国西南研究所(SouthwestResearchInstitute)的天文学家斯特恩(AlanStern)与莱维森(HaroldLevison)提出了一组新的行星定义，这一定义采用了与上述草案相同的质量上界(措词略有差异)，但补充了质量下界。它规定：行星必须足够大，以至于其形状主要由引力而非物质中的其它应力所决定。在太阳系中，我们可以看到很多形状不规则的小天体，但几乎所有直径在400公里以上的天体，其形状都非常接近由引力所主导的天然形状：球形[注三]。因此由这一条给出的行星直径下界约为400公里，具体的数字则与天体的物质组成有关。

由上述方式定义的行星质量上界及下界具有非常清晰而自然的物理意义。有了这两条，再加上行星必须环绕恒星运动，以及行星不能同时是卫星这两个显而易见的运动学要求，行星定义就基本完整了。2006年8月16日，国际天文联合会正式提出了一份行星定义草案。该草案所采用的大致就是上述几条，不过在涉及质量上界时，只对行星与普通恒星作了区分，而未涉及与褐矮星的区分(这相当于将质量上界由木星质量的13倍提高到75倍左右)。这份定义草案单从物理角度讲是比较令人满意的，但用到太阳系中却立刻会产生一个很现实的麻烦，即导致行星数量的急剧增加。事实上，由于该定义所要求的行星直径的下界只有400公里左右，一旦被采用，则不仅谷神星可以“官复原职”，阋神星能够“荣登宝座”，许许多多甚至连名字都还没有的家伙也将成为行星。据估计，这一定义有可能会使太阳系的行星数目增加到几百，甚至几千。这样的数目虽然不存在任何原则性的问题，却有点超乎人们的心理承受力，因为自冥王星被发现以来，几乎每一位小学生都能说出太阳系九大行星的名称。但假如九大行星变成几百、甚至几千大行星，那么别说小学生，恐怕连大学教授也得张口结舌。

因此，上述草案一经提出立刻遭到了激烈的反对。经过几天的争论，国际天文联合会在草案中新增了一项要求：行星必须扫清自己轨道附近的区域[注四]。2006年8月24日，这一新定义经表决以超过90%的大比率通过，从而正式生效。按照新增的那项要求，谷神星“官复原职”的希望付诸了东流，阋神星“荣登宝座”的美梦也化为了泡影，而最惨的则是已经在行星宝座上端坐了76年的冥王星，它在一夜之间就被扫地出门，变成了所谓的“矮行星”-这是为象它这样满足其它各项要求，却没能完成轨道“大扫除”任务的天体所设的安慰奖。与冥王星一同获得首批矮行星光荣称号的还有谷神星和阋神星。2008年3月和9月，鸟神星和妊神星也先后加入了矮行星的行列。今后，矮行星的数目显然还会增加，但太阳系行星的数目却暂时降为了八个。也许是意识到新定义的修改过程太过仓促，国际天文联合会将新定义的适用范围限定在了太阳系以内，而将普遍的行星定义留给了未来。



【“逼” 冥王星退位的国际天文联合会会场】

行星新定义的仓促出炉，尤其是冥王星象“严打”期间遭到惩处的人犯一样在几天之内就被草率“矮化”，引起了很多人的反对，反对者从天文学家到天文爱好者，从普通民众到占星术士应有尽有。以前太阳系有九大行星时，人们曾用九大行星的英文开首字母编写过一些便于记忆的英文短句，比如：MyVeryEducatedMotherJustServedUsNinePizza(我那有着良好教养的妈妈刚给我们做了九个比萨饼)，冥王星("P"luto)被剥夺行星资格后，有人戏虐般地用剩下的八个开首字母也编了一个英文短句：MostVexingExperience,MotherJustServedUsNothing(最气恼的经历，妈妈没给我们做任何东西)。

当然，也有比较认真的反对者，比如有人对表决的代表性提出了质疑。他们指出，参与行星定义表决的天文学家只有424人(其中投反对票者为42人)，不到与会人数的16%，与国际天文联合会的会员总数相比，更是连5%都不到，不能充分地代表国际天文联合会。不过这种质疑初看起来颇有说服力，其实却不然。因为国际天文联合会的会员并非人人都对行星定义感兴趣，因此投票率的高低未必能衡量投票质量的好坏。另一方面，424人从统计学角度讲已经不算是太小的样本，统计误差只有百分之几，超过90%的大比率通过绝非统计误差所能干扰。除非有迹象表明未投票的天文学家看待行星定义的态度与已投票者存在系统性的差异，否则更多的人投票只会使赞成及反对的票数大致按比例增加，却几乎不可能会改变投票结果。

当然，最重要的是，行星定义无论如何改变，所影响的只是我们对天体的称呼与分类，而不是天体本身。冥王星是行星也好，是矮行星也罢，它就是那个在六十亿公里之外围绕太阳运动，直径约2300公里，“遵循相同物理定律，由同样的尘埃云凝聚而成”的实心球。它是否被新定义所“矮化”，无论对于它自己还是对于天文学研究都没什么实质意义。不过，如果读者对名份问题感兴趣的话，朱惠特-他曾被认为是最早发现柯伊伯带天体的天文学家，但现在只能排第二了(请读者想一想，第一是谁？)-倒是早在冥王星被“矮化”之前就表达过一个别致的看法，他认为冥王星如果变成一个柯伊伯带天体，非但不是被“矮化”，反而是受到“升迁”，因为它的地位将从此“由外太阳系的一个令人难以理解的畸形反常，变成海外天体这一丰富而有趣的家族的首领”。正所谓：宁为鸡头，不做凤尾，看来我们应该祝贺冥王星[注五]。

三二.疆界何方

现在让我们盘点一下人类在寻找太阳系的疆界时走过的漫漫长路。从远古时期就已知道的金、木、水、火、土五大行星，以及脚下的地球，到近代的天王星、海王星，再到现代的柯伊伯带及离散盘。人类认识的太阳系疆界在过去两百多年的时间里在线度上扩大了十倍左右。

那么，离散盘是否就是太阳系的疆界呢？答案是否定的。

读者们也许还记得，我们在第二十八节中曾经提到，太阳系里的彗星按轨道周期的长短可以分为两类，其中短周期彗星大都来自柯伊伯带。那么，长周期彗星又来自何方呢？

1950年，荷兰天文学家奥尔特(JanOort)对长周期彗星进行了研究。他发现，很多长周期彗星的远日点位于距太阳50,000-150,000天文单位(约合0.8-2.4光年)的区域内，由此他提出了一个假设，即在那里存在一个长周期彗星的大本营。这一假设与将柯伊伯带视为短周期彗星补充基地的假设有着异曲同工之妙(但时间上更早)。那个遥远的长周期彗星大本营后来被人们用奥尔特的名字命名为奥尔特云(OortCloud)[注六]。由于长周期彗星几乎来自各个方向，因此奥尔特云被认为大体上是球对称的。后来的研究者进一步将奥尔特云分为两部分：距太阳20,000天文单位以内的部分被称为内奥尔特云，它呈圆环形分布；距太阳20,000天文单位以外的部分被称为外奥尔特云，它才是球对称的。距估计，奥尔特云中约有几万亿颗直径在一公里以上的彗星，其总质量约为地球质量的几倍到几十倍。由于数量众多，在一些科普示意图中奥尔特云被画得象一个真正的云团一样，但事实上，奥尔特云中两个相邻小天体之间的平均距离约有几千万公里，是太阳系中天体分布最为稀疏的区域之一。



【荷兰天文学家奥尔特(1900 – 1992)】

在距太阳如此遥远的地方为何会有这样一个奥尔特云呢？一些天文学家认为，与离散盘类似，奥尔特云最初是不存在的，如今构成奥尔特云的那些小天体最初与行星一样，形成于距太阳近得多的地方，后来是被外行星的引力作用甩了出去，才形成了奥尔特云。奥尔特云中的小天体由于距太阳极其遥远，很容易受银河系引力场的潮汐作用及附近恒星引力场的干扰，那些干扰会使得其中一部分小天体进入内太阳系，从而成为长周期彗星。

奥尔特云距我们如此遥远，而且包含的又大都是小天体，读者们也许会以为除直接来自那里的长周期彗星外，我们不太可能观测到任何属于奥尔特云的天体。其实却不然。这倒不是因为我们有能力观测到几千乃至几万天文单位之外的小天体，而是因为奥尔特云并不是一个界限分明的区域。少数奥尔特云天体的轨道离我们相当近，甚至能近到可被直接观测到的程度。2003年，美国帕洛马天文台(PalomarObservatory)的天文学家布朗(MichaelBrown-他也是创神星的发现者之一)发现了一个临时编号为2003VB12(正式编号为90377)的海外天体，它的轨道远日点距离约为976天文单位，近日点距离也有76天文单位。这个天体的块头很大(否则就不会被发现了)，直径约有1500公里，曾一度被当成第十大行星的候选者(当时阋神星尚未被发现)。天文学家们给它取了一个专门的名称：赛德娜(Sedna-因纽特神话中的海洋生物之神)。一般认为，赛德娜是属于内奥尔特云的天体[注七]。除赛德娜外，还有一个我们非常熟悉，有些读者甚至用肉眼都曾看到过的天体-哈雷彗星-也被认为是有可能来自奥尔特云的。哈雷彗星虽然是一颗短周期彗星，但很多天文学家认为，它是从奥尔特云进入巨行星的引力范围后受后者的干扰才成为短周期彗星的。

奥尔特云究竟有多大呢？今天的很多天文学家认为它的范围延伸到距太阳约50,000天文单位的地方，但也有人象奥尔特当年一样，认为它延伸得更远，直到太阳引力控制范围的最边缘。这一边缘大约在距太阳100,000-200,000天文单位处，在那之外，银河系引力场的潮汐作用及附近恒星的引力作用将超过太阳的引力(请读者想一想，我们为什么在提到银河系引力场时强调“潮汐作用”，而在提到附近恒星的引力场时不强调这一点？)。如果那样的话，奥尔特云的外边缘应该就是太阳系的疆界了。



【奥尔特云及太阳系结构示意图】

不过，奥尔特云未必是太阳系疆界附近的唯一秘密。1984年，美国芝加哥大学的古生物学家劳普(DavidRaup)和塞普考斯基(JackSepkoski)在对过去两亿五千万年间地球上的大规模生物灭绝状况进行研究后提出，那种灭绝似乎平均每隔2,600万年发生一次，而且有迹象表明其中至少有两次似乎与大陨星撞击地球的时间相吻合(其中最著名的一次被认为是发生在距今约6,500万年的白垩纪末期，导致包括恐龙在内的大量生物灭绝)。同年，美国加州大学的物理学家马勒(RichardMuller)等人提出了一个大胆的猜测，认为太阳有可能有一颗游弋在太阳系边缘的伴星，这颗伴星是一颗褐矮星或红矮星(褐矮星的质量约在木星质量的13-75倍之间，红矮星的质量约在木星质量的75-500倍之间)，它距太阳最远时约有2.4光年(感兴趣的读者请根据上下文提供的信息，计算一下它离太阳最近时的距离)。这颗伴星每隔2,600万年经过奥尔特云的一部分，在它的引力干扰下，大量的奥尔特云天体会脱离原先的轨道而进入内太阳系，其中个别天体会与地球相撞，从而造成大规模的生物灭绝。由于这颗伴星所起的可怕作用，它被称为内梅西斯(Nemesis)，这是希腊神话中的复仇女神。如果太阳真的有这样一颗伴星，并且它真的有人们所猜测的那种作用，那它无疑是太阳系疆界附近最可怕的天体[注八]。但即便如此，我们也不必害怕，因为按照那些科学家的说法，地球上最近一次大规模生物灭绝大约发生在距今五百万年以前，那么下一次同类事件-如果有的话-就该是两千多万年之后的事了。那时假如人类还存在，想必该有足够的智慧来避免灾难。

我们有关太阳系疆界的故事在这里就要与读者说再见了，但人类探索太阳系疆界的事业却远未结束，这样的事业有一个美丽的名字叫科学，她值得人们去做永生的探索。

注释

对冥王星身份的最早怀疑可以追溯到汤博发现冥王星的同一年，即1930年，起因是罗威尔天文台公布的冥王星轨道与罗威尔对行星X的预言不符。 确切地讲，该定义要求行星的质量小于在其中心产生氘核聚变所需的质量。由于氘核聚变是恒星内部最容易产生的核聚变，因此满足这一条也就自动保证了行星内部不会产生其它核聚变。 确切地讲是椭球形，因为多数天体存在自转。 这一条与其它几条相比，其缺陷是显而易见的，因为它并未对“轨道附近的区域”及“扫清”这两个概念进行界定。严格追究的话，海王星也不能算是扫清了轨道附近的区域，因为很多海外天体的轨道周期性地穿越海王星轨道。甚至最有行星资格的木星，它的“大扫除”也是有死角的，因为在它的轨道区域中存在数量多达十万以上的所谓“特洛伊小行星”(Trojanasteroids)。从国际天文联合会对新定义的讨论过程及此前出现的几篇相关论文来看，“扫清”一词的含义应该是指行星在其轨道附近的区域中处于支配性(dominant)地位。 冥王星的“鸡头”地位在2008年6月11日得到了进一步的加强：这一天，国际天文联合会将海王星以外(即轨道半长径大于海王星轨道半长径)的矮行星统称为Plutoid。该类别目前尚无标准中译名，几种可能的选择为：类冥天体、类冥矮行星、冥王星类天体。其中个别译名曾被当作plutino-即与海王星轨道存在3:2共振的海外天体(包括卫星)-的非正式中译名。不过plutoid这一新类别出现后，为对两者进行区别，我认为plutino宜另找一个可以体现英文词根-ino(微小)的新词作为译名，比如类冥小天体、微冥天体等。 奥尔特并不是最早提出彗星大本营概念的天文学家。1932年，爱沙尼亚天文学家欧皮克(Ernst?pik)曾经提出过彗星来自太阳系边缘的一片“云”的假设。此外，早年曾有一些天文学家认为短周期彗星也来自奥尔特云，只不过是在接近内太阳系时受到巨行星的影响而被俘获成了短周期彗星。但具体的计算及模拟表明，小天体从遥远的奥尔特云进入并被俘获在内太阳系的概率非常小，不足以解释观测到的短周期彗星的数量。而且来自奥尔特云的新彗星的轨道倾角分布也与短周期彗星的倾角分布有着显著差异。因此后来人们放弃了这一假设(但个别短周期彗星-比如哈雷彗星-仍被认为是有可能来自奥尔特云)。 2000年，罗威尔天文台发现的一个临时编号为2000CR105(正式编号为148209)，远日点距离约394天文单位，近日点距离约44天文单位的小天体也被认为有可能属于内奥尔特云，但争议较大。 需要提醒读者注意的是，有关太阳伴星的猜测目前只有很少的支持者，其学术地位远低于有关奥尔特云的猜测。

二零零八年六月十二日写于纽约

二零零八年六月三十日发表于本站

二零零九年七月三十日最新修订

本文标题：太阳的故事-太阳的故事
本文地址： http://www.61k.com/1165870.html