一 : 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻
蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻
蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻
蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻
蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻
蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

蔡淑华 锲炴棆锷犻

61阅读提醒您本文地址:
二 : 锲炴棆锷犻
遵化一中
蔡淑华
考纲分析 “回旋加速器”虽是I级要求,但它是II 级考点“带电粒子在匀强磁场中的运动”的 重要应用,也是近代物理的重要实验装置, 是高考考查的重点和热点。
教学目标 1.知识技能: (1)通过由直线加速器迁移到回旋加速器的教学, 培养学生解决实际问题的能力,开阔学生解决问题的 思路. (2)知道回旋加速器的基本构造和加速原理. 2.过程方法: 让学生在合作讨论与汇报讲解过程中, 加深对回旋加速器的基本构造和加速原理的认识,总 结体会选择题的灵活求解方法及计算题的分步得分方 法。 3.情感、态度与价值观:通过由浅入深的设问分析 帮助高分学生寻找差距,帮助低分学生找回自信;用 严密的推理,解释回旋加速器的工作原理,让学生充 分体会物理教学的语言美及推理过程的逻辑美。
重点·难点 1、重点 回旋加速器的工作原理. 2、难点 加速电场的平行极板接的是交变电压,且 它的周期和粒子的运动周期相同.
利用加速电场可以加速带电粒子
+ + + +
1 2 qU ? mv 2
U
北京高能物理研究所的直线加速器: ? 电子能量提高到1.1GeV; ? 直线加速器长度为204米。
美国斯坦福大学直线加速器:
? 电子能量提高到50GeV的加速器; ? 直线加速器长度达3公里多。 为了避免不断增加加速器的长度,1930年劳伦斯 提出建造回旋加速器的建议, 1932年建成,劳伦 斯也因此获得诺贝尔物理学奖。
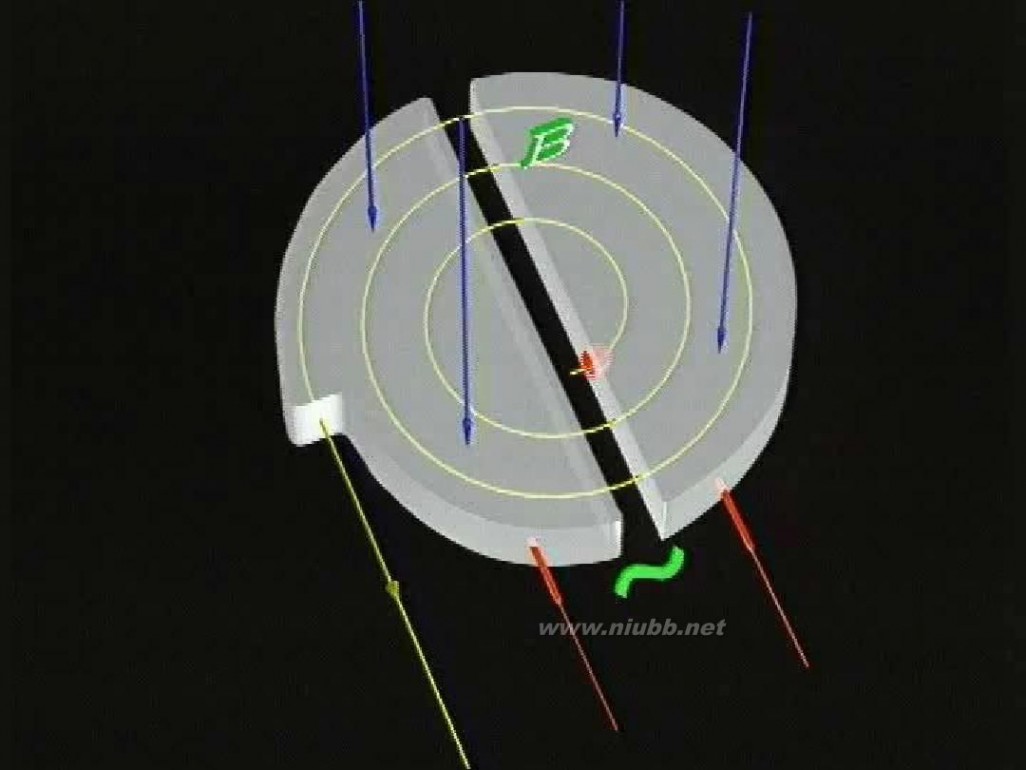
1、结构: ① 两个D形盒及两个大磁极 ② D形盒间的窄缝 ③ 高频交流电
问题1:回旋加速器中交变电场周期与带电 粒子在磁场中运动周期之间有没有关系? 问题2:已知D形盒的半径为R,匀强磁场的 磁感应强度为B,交变电压的电压为U,求: 从出口射出时,粒子的动能Ek=?
问题3:回旋加速器加速的带电粒子的最终能 量由哪些因素决定?加速次数n由谁决定? n 会影响谁?
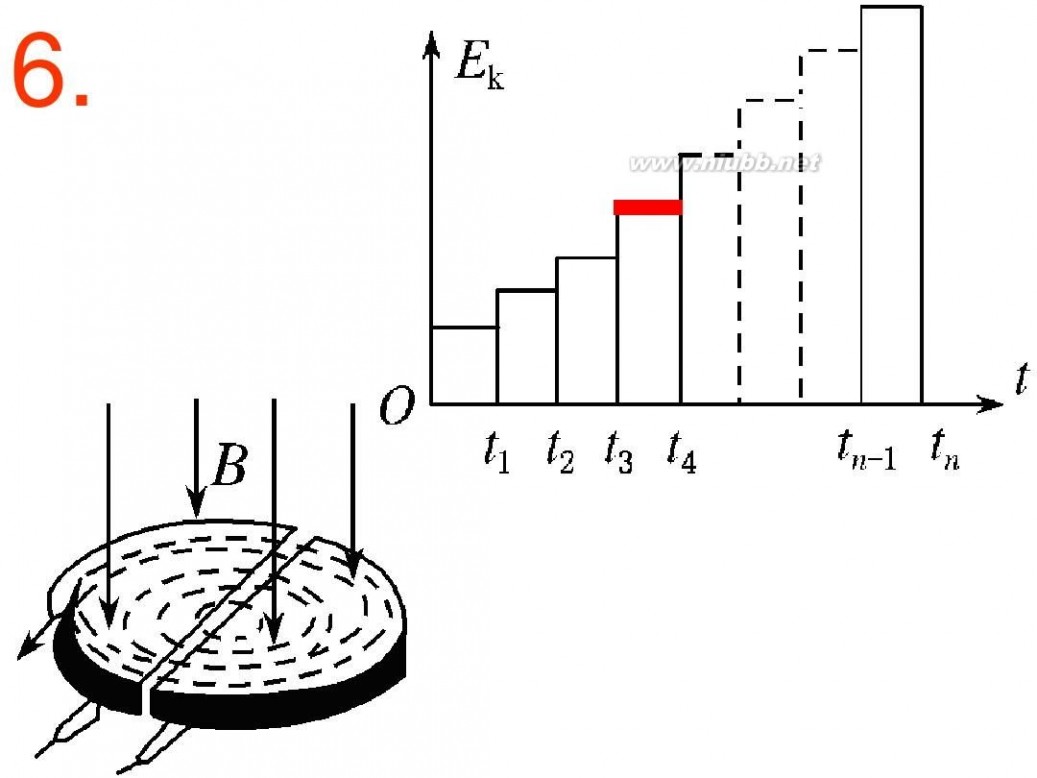
6.
练1:回旋加速器是加速带电粒子的装置,其核心部分
是分别与高频交流电两极相连接的两个D形金属盒,两 盒间的狭缝中形成的周期性变化的匀强电场(其频率为 f ),使粒子在通过狭缝时都能得到加速,两D形金属盒 处于垂直于盒底面的匀强磁场中,如图所示,设匀强磁 场的磁感应强度为B,D形金属盒的半径为R,狭缝间的 距离为d,匀强电场间的加速电压为U。则下列说法中正 BCD ) 确的是:( d A.增大匀强电场间的加速电压,被 加速粒子最终获得的动能将增大; R B.增大磁场的磁感应强度, 被加速粒 B 子最终获得的动能将增大; C.被加速粒子最终速度大小不超2πf R; D.增大匀强电场间的加速电压, 被加速 U 粒子在加速器中运动的圈数将减少。
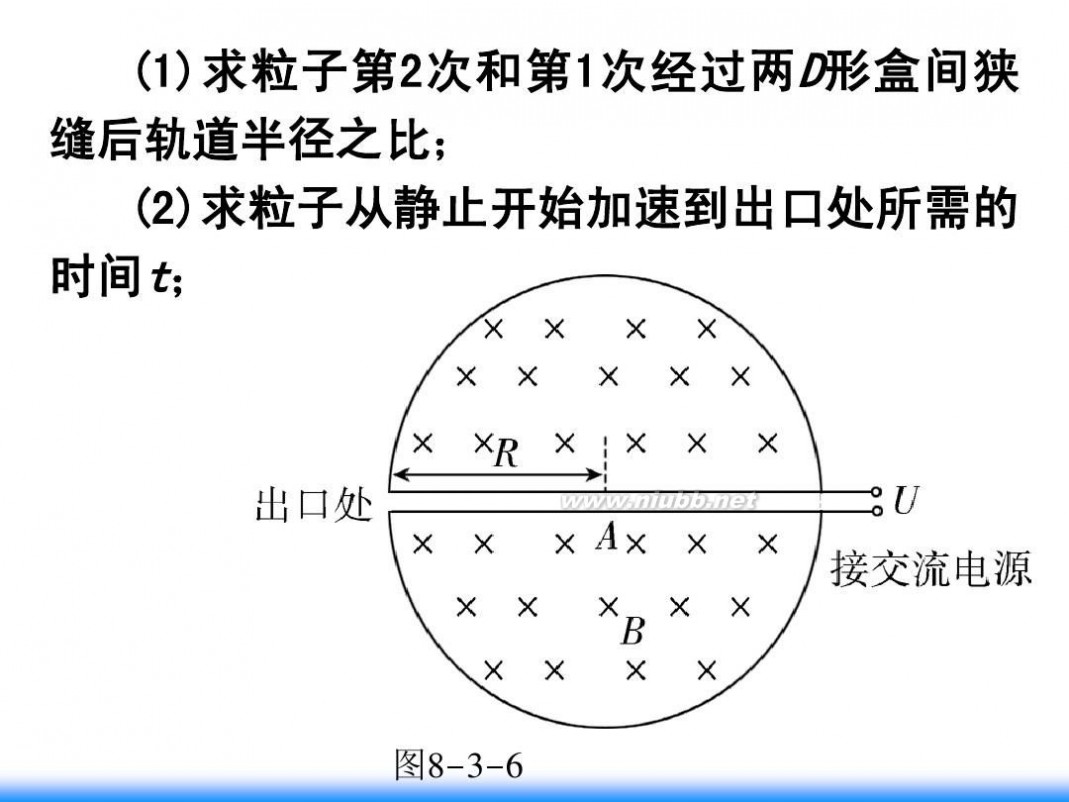
练2:(2010·江苏卷)1932年,劳伦斯和利文斯设计出 了回旋加速器.回旋加速器的工作原理如图8-3-6所示, 置于高真空中的D形金属盒半径为R,两盒间的狭缝很小, 带电粒子穿过的时间可以忽略不计.磁感应强度为 B 的匀 强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电 荷量为+ q ,在加速器中被加速,加速电压为 U.加速过程 中不考虑相对论效应和重力作用.
(1)求粒子第2次和第1次经过两 D 形盒间狭 缝后轨道半径之比; (2)求粒子从静止开始加速到出口处所需的 时间t;
图8-3-6
解析: ? 设粒子第1次经过狭缝后的半径为r1,速度为v1 ?1 1 2 qU= mv1 2 v12 qv1 B=m r1
1 2mU 解得:r1= B q 1 4mU 同理,粒子第2次经过狭缝后的半径r2= B q 则r2 r1= 2 1 ∶ ∶
? 2 ? 设粒子到出口处被加速了n圈
1 2 2nqU= mv 2 2? m T= qB 解得:t= v qvB=m R t=nT
2 2
? BR
2U
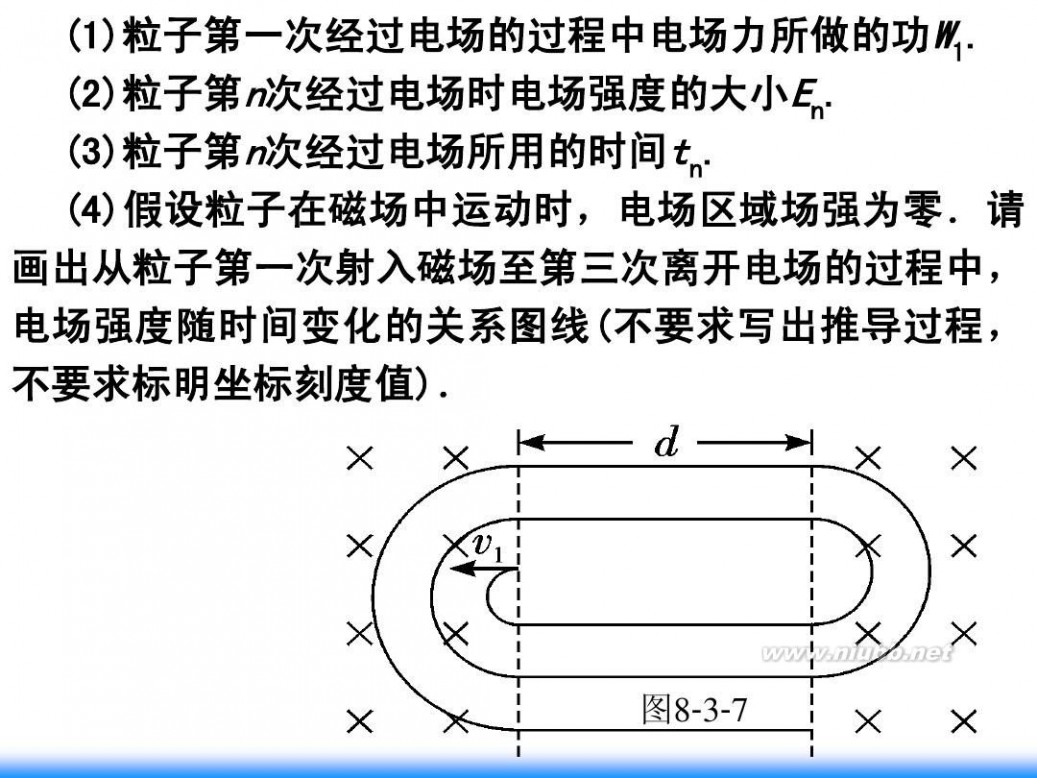
练3:(2010· 山东卷)如图8- 7所示,以两虚线为边界, 3中间存在平行纸面且与边界垂直的水平电场,宽度为d, 两侧为相同的匀强磁场,方向垂直纸面向里.一质量为m、 带电量+q、重力不计的带电粒子,以初速度v1垂直边界 射入磁场做匀速圆周运动,后进入电场做匀加速运动, 然后第二次进入磁场中运动,此后粒子在电场和磁场中 交替运动.已知粒子第二次在磁场中运动的半径是第一 次的二倍,第三次是第一次的三倍,以此类推.求:
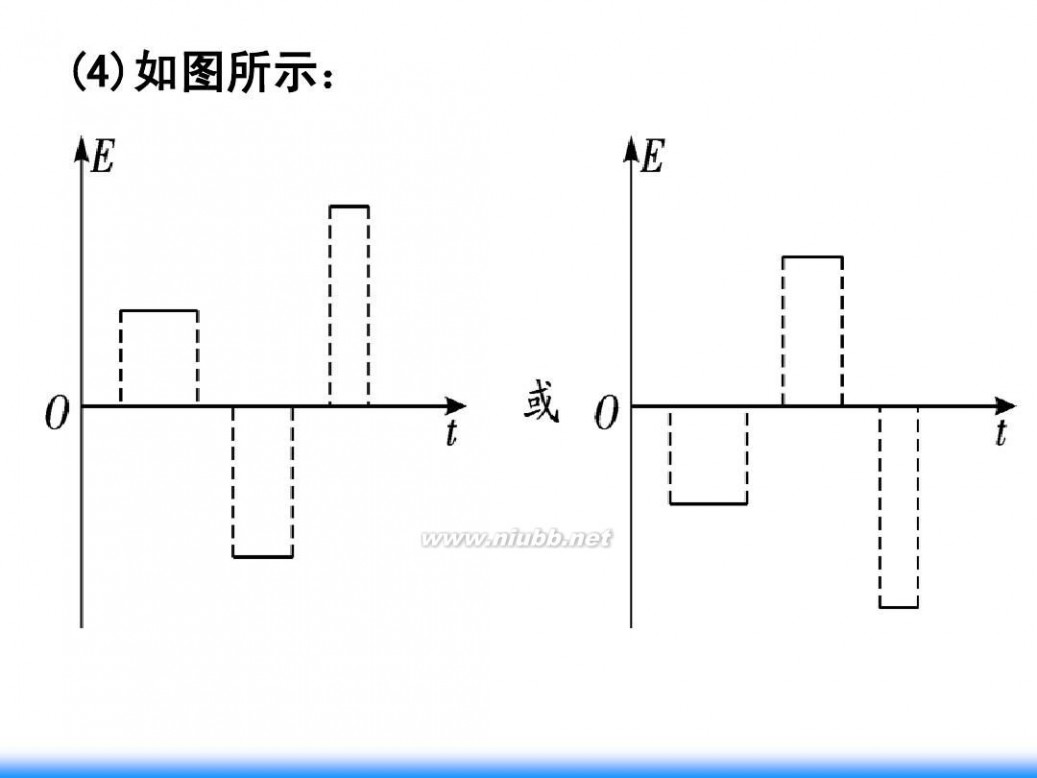
(1)粒子第一次经过电场的过程中电场力所做的功W1. (2)粒子第n次经过电场时电场强度的大小En. (3)粒子第n次经过电场所用的时间tn. (4)假设粒子在磁场中运动时,电场区域场强为零.请 画出从粒子第一次射入磁场至第三次离开电场的过程中, 电场强度随时间变化的关系图线(不要求写出推导过程, 不要求标明坐标刻度值).
图8- 7 3-
解析: ? 设磁场的磁感应强度大小为B,粒子第n次进 ?1
2 vn qvn B=m Rn
入磁场时的半径为Rn,速度为vn,由牛顿第二定律得: ①
qBRn 由①式得:vn= ② m 因为R2=2 R1,所以v2=2v1
③
1 2 1 2 由动能定理得:W1= mv2- mv1 ④ 2 2 2 3mv1 联立③④式解得:W1= ⑤ 2
? 2 ? 粒子第n次进入电场时的速度为vn,出电场时的
速度为vn+1,有:vn=nv1,vn+1=(n+1)v1 ⑥ 1 2 1 2 由动能定理得:qEn d= mvn ?1- mvn 2 2 2 (2n ? 1)mv1 联立⑥⑦式得:En= ⑧ 2qd ⑦
? 3? 设粒子第n次在电场中运动的加速度为an,
由牛顿第二定律得:qEn=man 由运动学公得:vn+1-vn=antn ⑨ ⑩
2d 联立⑥⑧⑨⑩式得:tn= (2n ? 1)v1
(4)如图所示:
回旋加速器
小结
1、 粒子在匀强磁场中的运动周期不变
2? m T= qB
2、交变电场的周期和粒子的运动周期T相 同----保证粒子
每次经过交变电场时都被 加速
3、带电粒子每经电场加速一次,回旋半 径就增大一次,每次增加的动能为
?E K=qU
∶ 2∶ 3∶ ... 各次半径之比为: 1 4、粒子加速的最大速度由盒的半径决定
q vmax= BR m
5 、粒子在回旋加速器中运动时间(n n 指加速次数) t ? T 2
课下练习(2011天津).(20分)回旋加速器在核科学、 核技术、核医学等高新技术领域得到了广泛应用,有力地 推动了现代科学技术的发展。 (2)回旋加速器的原理如图,D1和D2是两个中空的半径 为R的半圆金属盒,它们接在电压一定、频率为f的交流电 源上,位于D1圆心处的质子源A能不断产生质子(初速度 可以忽略,重力不计),它们在两盒之间被电场加速, D1、 D2置于与盒面垂直的磁感应强度为B的匀强磁场中。若质 子束从回旋加速器输出时的平均功率为P,求输出时质子 束的等效电流I与P、B、R、f的关系式 (忽略质子在电场中运动的时间,其 最大速度远小于光速) (3)试推理说明:质子在回旋加速 器中运动时,随轨道半径r的增大, 同一盒中相邻轨道的半径之差是增 大、减小还是不变?
U U0
0
T/2 T 3T/2 2T
t
-U0
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1