一 : 自然散热管脚类器件flotherm热仿真误差分析案例1
自然散热管脚类器件flotherm热仿真误差分析案例1
在做1款自然散热产品仿真时,遇到1个功耗约为0.5W的二极管器件温度明显偏高,由于主要问题在二极管的温度,因此将二极管单独提取出来,专门研究分析:
相关条件如下:环境温度25℃
模型尺寸50×90×110(mm)
自然对流散热
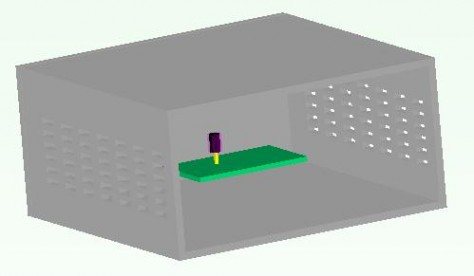
材料特性:外壳为塑料外壳,PCB板为导热系数各向异性的FR4,二极管为导热系数设为30的陶瓷材料,管脚为铜。功耗0.5W,其中,二极管外形建模方式如下:

模型1.1
仿真结果:
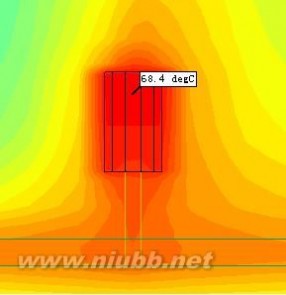
模型1.1温度云图
由图中可以看出,二极管的最高温度已经达到了202℃,这显然不符合常理。于是又仔细观察实物,修正模型如下:

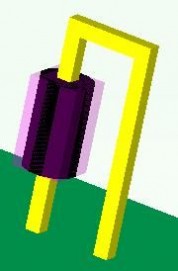
实物模型1.2
对其进行仿真,结果如下:
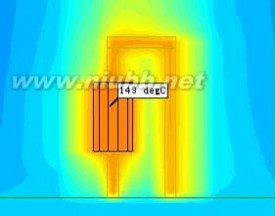
模型1.2温度云图
由模型1.2仿真结果可以看出,现在二极管最高温度为143℃。可见,由于管脚由1个变为2个,二极管最高温度相差59℃。可以看到:对管脚类器件的建模应仔细按照实物建立,管脚的个数对器件的散热影响很大。
修正管脚数量后,温度仍然有很大的偏差,在实际中自然散热状态下功率为0.5w的二极管温度也不会达到这么高,因此应该还有其它导致温度很高的原因。仔细观察PCB板与二极管,发现了模型与实际不符的地方:
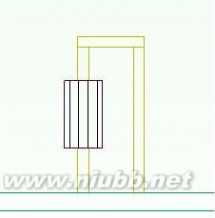
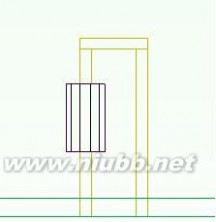
现有模型实际情况
由上图可以看出现有模型中的管脚并未深入到PCB板中,而实际情况则是二极管的管脚穿透PCB板,因此对模型1.2进行调整,使管脚深入到PCB板内。
仿真结果如下:

模型1.3温度云图
由上图可以看出,当二极管管脚深入PCB板后,其最高温度为66.7℃,与模型1.2对比,温升下降了76.3℃之多!同时,41.7℃的温升也与实际情况比较符合。对于二极管管脚是否深入到PCB板这种看似很小的问题,却能带来这么大的计算差异,可见在自然对流散热中,通过管脚散出的热量还是十分可观的,一定不能忽略不计。
原因分析:
散热的方式分为三类:传导、对流和辐射。在风冷产品设计中,器件主要通过对流换热的方式带走绝大部分热量,因此在风冷产品仿真建模时都是将功率管脚贴在PCB上就可以,此时热量多通过散热器带走,由于管脚与之相比热阻大得多,通过管脚散走的热很少,通过辐射散走的热量更是微乎其微,因此这样建模一般对计算结果的准确性影响很小。而在自然换热中,情况就变得复杂很多,管脚通过PCB板的导热散热、元器件的辐射散热和对流换热都要考虑,忽略了哪个都会导致结果有很大的偏差,以上的几个模型对比很好的说明了这个问题。
如上我们发现2个问题,1,管脚的数量影响59℃,2,管脚插入pcb又降低76.3℃。那么哪个是主要原因?我们将模型1.1中的二极管管脚深入PCB板(建立模型1.4)再进行仿真,结果对比如下:
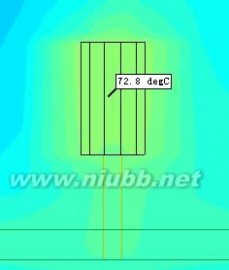

模型1.4温度云图模型1.3温度云图(对比参考)
由上图可见在二极管管脚深入PCB板后,管脚数不同所造成的温度差异为6.1℃,由此可以得知,仿真误差的主要原因就来自于管脚是否深入PCB板。
而对于管脚的仍然有个疑问,那就是,如果把单个管脚的截面加倍,那么是与2个管脚的建模方式温度又会相差多少?因此,在模型1.4的基础上建立模型1.5,管脚加粗一倍,其它条件不变,仿真结果如下:

模型1.5温度云图
与双管脚的模型相比,温度差异为1.7℃。
此外,双管脚的二极管还有1种形状:
因此,按此外形建立模型1.6:
模型1.6
计算结果如下:
模型1.6温度云图
对比结果:
模型 | 最高温度(℃) |
1.3(双管脚模型1) | 66.7 |
1.4(单管脚模型) | 72.8 |
1.5(单粗管脚模型) | (www.61k.com) 68.4 |
1.6(双管脚模型2) | 66.6 |
由上表可以看出:
1)对比模型1.3与1.6可知,双管脚模型温度与管脚外形(横放竖放)关系不大(仅差0.1℃)。
2)可以用单管脚加粗的方式使精确度逼近双管脚模型。
对于单双管脚与管脚是否加粗的问题,由于本例研究的并非是作为十分重要的部件的二极管,而问题的出发点是这个本来应该非重点关注的二极管却温度极高,因此,个人建议,在仿真项目中当预计作为非主要部件的二极管的温度对整体影响不大时,可以按照单管脚不加粗的模型建立,以加快建模和计算时间;而对功耗偏高,而且易影响到周围器件的二极管,应详细建模以保证计算的准确度。
另,由于二极管内部的结构未知,因此一般建模时是直接将温度赋值在二极管管体部分,而事实上二极管管体上大部分是封装材料,而内部的芯体才是热源,封装材料(一般是陶瓷)的导热系数由于内部芯体(一般是金属)又有一定的差异,因此把发热源设置在二极管内部的1个芯体上,建立模型1.8,考察效果,计算结果如下:
模型1.8温度云图
由上图可以看出,模型1.8热芯的温度为72.1℃,而管体的温度为68~70.1℃,与模型1.3(之间模型中比较精确者)相比,管体的温度相差2~4℃。由于模型1.8的内部结构也不完全与实际一致,所以还需根据实测来确定哪个温度更为接近实际值。然而可以得到如下的结论:当要仿真的二极管属于非重点考察对象且其温度对其它器影响很小的前提下,可以忽略此(模型1.3与1.8之间的)差异,以加快仿真进度。
另,PCB板一般是多层板,由绝缘材料(聚合体材料或FR4)构成和几层铜板构成,因此层数的不同会导致PCB板间的用铜量不同,其导热系数也会因此不同,然而我们可以根据下式计算出不同层数的PCB板的导热系数:
k沿板面=∑(kiti)/∑ti
k沿板厚=∑ti/∑(ti/ki)
ki=fi*kcuorki=kFR4
fi=铜层含量
k=层的热传导率(W/(mK))
t=层的厚度(m)
常用多层PCB板通常有4-十个铜层,因此计算其导热系数大概取值范围为:
沿板面27W/(mK)~68.6W/(mK)
沿板厚0.3W/(mK)
之前的仿真中,PCB板的导热系数均按照沿板面27W/(mK),沿板厚0.3W/(mK)的参数设置。为了考察不同层数的PCB板导热系数对仿真结果的影响,改变PCB板导热系数,对同样3种类型(单管脚、双管脚1、双管脚2)的二极管进行仿真,结果如下:
模型1.9
模型1.10
模型1.11
对比之前温度:
导热系数27W/(mK) (沿板面) | 导热系数为68.6W/(mK) (沿板面) | ||
单管脚 模型 |
| 72.8℃ | 69.8℃ |
双管脚1模型 |
| 66.7℃ | 64.7℃ |
双管脚2模型 | 66.6℃ | 64.9℃ |
通过对比不同的PCB板导热系数所得值可以看到,在3种模型下算得的温度均相差不大(温差在2℃之内),因此根据以往的计算经验来看不需要再改动参数就可以较好的吻合实验结果。
综上总结自然散热管脚类器件flotherm仿真经验如下:
1.对于管脚类器件的自然对流散热的仿真,管脚需深入PCB板中,否则会产生很大的计算误差。
2.对于板级自然对流散热的仿真,二极管管脚个数的多少可以通过等效换算成单根管脚的粗细度可以很好的接近实际模型,同时简化了建模。
3.对于板级自然对流散热的仿真,二极管管脚的横置竖置形状的变化对最后的温度计算影响很小,结合第2点运用即可在保证足够准确度的前提下,简化模型设置,加快仿真速度。
4.对于板级自然对流散热的仿真,PCB板的材料属性设置可以按照:沿板面27W/(mK),沿板厚0.3W/(mK)做通用设置,可以保证一般要求。
over
二 : 浮点运算结果出现误差原因分析及解决方案
如下C#代码:
float a = 0.65f;
float b = 0.6f;
float c = a - b;
此时c为多少?
0.05?错误!
此时c为0.0499999523!
为什么?
其根本原因是计算机所使用二进制01代码无法准确表示某些带小数位的十进制数据。(www.61k.com)
下面我们来分析下:
我们知道将一个十进制数值转换为二进制数值,需要通过下面的计算方法:
1. 整数部分:连续用该整数除以2,取余数,然后商再除以2,直到商等于0为止。然后把得到的各个余数按相反的顺序排列。简称"除2取余法"。
2. 小数部分:十进制小数转换为二进制小数,采用"乘2取整,顺序排列"法。用2乘以十进制小数,将得到的整数部分取出,再用2乘余下的小数部分,然后再将积的整数部分取出,如此进行,直到积中的小数部分为0或者达到所要求的精度为止。然后把取出的整数部分按顺序排列起来,即先取出的整数部分作为二进制小数的高位,后取出的整数部分作为低位有效位。简称"乘2取整法"。
3. 含有小数的十进制数转换成二进制,整数、小数部分分别进行转换,然后相加。
例如:将十进制数值25.75转换为二进制数值,步骤如下:
25(整数部分)
25/2=12......1
12/2=6.......0
6/2=3......0
3/2=1......1
1/2=0......1
(25) 10=(11001) 2
0.75(小数部分)
0.75*2=1.5......1
0.5*2=1......1
(0.75) 10=(0.11) 2
(25.75) 10=(11001) 2+(0.11) 2=(11001.11) 2
按照上述方法,我们将0.65及0.6转换为二进制代码:
(0.65)10 = (0.101001100110011001100110011001100110011......)2
(0.6) 10 = (0.10011001100110011001100110011001100110011......)2
后面的省略号表示已经算不完了,后面在无限重复 0011 这段二进制数值。
文章开始部分,我们用的float类型,下面我们来看看float类型是否能存储上面转换出的二进制代码。
目前计算机上存储浮点数值是按照IEEE(电气和电子工程师协会)754浮点存储格式标准来存储的。
IEEE单精度浮点格式共32位,包含三个构成字段:23位小数f,8位偏置指数e,1位符号s。将这些字段连续存放在一个32位字里,并对其进行编码。其中0:22位包含23位的小数f; 23:30位包含8位指数e;第31位包含符号s。如下图所示:
也就是说上面将0.65及0.5转换出的二进制代码,我们只能存储23位,即使数据类型为double,也只能存储52位,这样大家便能看出问题出现的原因了。
截取的二进制代码已无法正确表示0.65及0.5,根据这个二进制代码肯定无法正确得到结果0.05。
如何解决这个问题?知道其根本原因后,我们知道是无法从根本上解决这个问题的,但我们可以有一些曲线救国的方法,下面列举几个:
1. 因为二进制数值可以准确表示整数(可以使用整数转换为二进制方法验证下),所以可以将小数乘以10或100等变成整数,然后做运算,最后再通过除以10或100等获得结果;
2. 通过截取结果的有效小数位数等,来取得最好的近似结果,然后在做处理。
3. 对于可以用有限长度的二进制数值表示的十进制数值,可以使用存储位数大于其长度的数据类型。
解决方案正在补充中……,若各位有什么好的方法也可以提出来!
以上解决方案需要按照使用的实际情况来决定使用哪种方法。
三 : 基于双因素方差分析的案例解析
摘 要:在实际生产过程中,影响一个事物的因素往往有很多,改变一个因素,就可能影响产品质量。哪些因素影响较大,哪些因素影响较小;究竟是一个因素起作用,还是多个因素起作用,或是各因素影响都不显著。方差分析就可以根据实验的结果进行分析、鉴别各因素对实验结果的影响。本文以双因素方差分析法进行一个生产案例的求解分析。
关键字:双因素方差分析;Excel数据分析处理;案例解析
一、问题
为了考察某种合金中碳的含量百分比(因子A)与锑铝含量和的百分比(因子B)对合金强度的影响,对因子A取3个水平,因子B取4个水平,在每个水平组合下做一次试验,数据如表1:
表1碳的含量百分比(因子A)与锑铝含量和的百分比(因子B)
■
假设因子A与因子B无交互作用,试检验因子A或B的效应是否显著(取α=0.01)。
二、分析
双因素无重复试验的方差分析。双因素无重复试验,也就是说因素A和B的各种水平的每一种配合(Ai,Bj)(i=1,2,...,l;j=1,2,...,m)下,只进行一次试验。假设所有的试验都是独立的,设得到的样本观测值xij如表2。
表2样本观测值分布表
■
将双因素无重复试验的方差分析有关的统计量和计算结果列在同一张表中,即得到双因素无重复试验的方差分析表,如表3。
表3双因素无重复试验的方差分析表
■
其中SA=m■(x■.-x)■是因素A的离差平方和,反映了因素A的不同水平所引起的系统误差;SB=m■(x.■-x)■是因素B的离差平方和,反映了因素B的不同水平所引起的系统误差; Se=■■(x■-xi.-x.j+x)■为误差平方和,反映了由各种随机因素引起的试验误差。S=SA+SB+Se是全体观测值xij对总平均值x的离差平方和。SA、SB、Se相互独立,■服从自由度l-1的χ2分布;■服从自由度为m-1的χ2分布;■服从自由度为(l-1)(m-1)的χ2分布;SA=■是因素A的平均平方和;SB=■是因素B的平均平方和;Se=■是误差的平均平方和。统计量FA=■=■服从自由度为(l-1,(l-1)(m-1))的F分布;FB服从自由度为(m-1,(l-1)(m-1))的F分布。给定显著性水平α=0.01,求得相关临界值Fα,即可确定因素A或因素B对试验结果是否产生显著影响。
三、求解
(1)提出假设
因素A
H0:合金中碳含量百分比对合金强度无显著性影响;
H1:合金中碳含量百分比对合金强度有显著性影响。
因素B
H0:合金中锑铝含量和的百分比对合金强度无显著性影响;
H1:合金中锑铝含量和的百分比对合金强度有显著性影响。
(2)输入数据至Excel,采用Excel工具菜单下,“数据分析”中“方差分析:无重复双因素分析”即可完成,如图1。
图1 EXCEL无重复双因素分析输入情况图
■
四、结果
根据图2显示:
(1)合金中碳含量百分比(因素A)对合金强度的影响:给定显著性水平α=0.01,求得相关临界值FA0.01=10.92477,(www.61k.com]而样本观测值F=63.2166大于FA0.01,因此拒绝原假设,即合金中碳含量百分比(因素A)对合金强度有显著影响。
(2)合金中锑铝含量和的百分比(因素B)对合金强度的影响:给定显著性水平α=0.01,求得相关临界值FB0.01=9.779538,样本观测值F=20.31083大于FB0.01,所以拒绝原假设,即合金中锑铝含量和的百分比(因素B)对合金强度有显著影响。
图2 无重复双因素分析结果图
■
五、结论
(1)合金中碳含量百分比(因素A)对合金强度的影响:给定显著性水平α=0.01,求得相关临界值FA0.01=10.92477,而样本观测值F=63.2166大于FA0.01,因此拒绝原假设,即合金中碳含量百分比(因素A)对合金强度有显著影响。
(2)合金中锑铝含量和的百分比(因素B)对合金强度的影响:给定显著性水平α=0.01,求得相关临界值FB0.01=9.779538,样本观测值F=20.31083大于FB0.01,所以拒绝原假设,即合金中锑铝含量和的百分比(因素B)对合金强度有显著影响。
对双因素方差分析,有时不但要考虑因素A或因素B对试验结果的影响,还要考虑因素A与因素B可能会有的交互作用对试验结果产生的影响。因此,就要对因素A与因素B的各水平的每一种配合(Ai,Bj)(i=1,2,...,l;j=,2,...,m)分别进行r≥2次重复试验,进行双因素等重复试验的方差分析,在此不作具体举例分析。
在试验中,可以从多种可控因素中找出主要因素,通过对主要因素的调整、控制,提高产品的性能、产量,这是我们想要的,方差分析正是这样一种有效方法。而Excel工具在数据分析处理上又有着应用相对普及、更为简便的优势,在一般的生产实践中将两者结合起来用于研究,不失为一种好方法,值得实践推广。
参考文献:
[1]吴传生.概率论与数理统计[M].北京:高等教育出版社,2007:228.
[2]陈魁.应用概率统计[M].北京:清华大学出版社,2002:280-301.
四 : 因子分析案例
案例1:我国各地区财政支出的因子分析
我国各地区主要财政支出项目包括一般公共服务、国防、公共安全、教育、科学技术、
文体传媒、保障就业、医疗卫生、环境保护、社区事务、农林水事务、交通运输、其它支出等14项。根据2007年的数据,对这14个变量进行分析,将它们综合为少数几个因子,通过对各地区的每个因子得分的分析了解各地区财政支出情况,为更合理地安排财政支出提供依据。
1.首先利用主成分确定因子载荷矩阵。
运用spss输出结果: 1.1单变量描述统计:
Descriptive Statistics
一般公共服务 国防 公共安全 教育 科学技术 文体传媒 保障就业 医疗卫生 环境保护 社区事务 农林水事务 交通运输 工商金融等 其它支出
Mean 2049700.97 23415.42 928492.48 2170018.87 276916.23 248846.81 1646622.45 630886.19 310076.68 1044674.74 997098.74 365524.84 908076.42 766679.87
Std. Deviation 1177234.156 15255.052 657886.621 1303120.830 308520.699 137087.278 896001.732 330272.793 167762.451 900747.968 455386.328 173055.000 608414.486 983106.165
Analysis N
31 31 31 31 31 31 31 31 31 31 31 31 31 31


1.3 KMO与Bartlett球形检验(检验是否适合做因子分析):
KMO and Bartlett's Test
Kaiser-Meyer-Olkin Measure of Sampling Adequacy.
Bartlett's Test of Sphericity Approx. Chi-Square
df
Sig. .788 678.523 91 .000
1.4变量共同度(给出该次分析从每个原始变量中提取的信息):
Communalities
一般公共服务
国防
公共安全
教育
科学技术
文体传媒
保障就业
医疗卫生
环境保护
社区事务
农林水事务
交通运输
工商金融等
其它支出
Extraction
Analysis. Method: Initial 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 Principal Extraction .925 .759 .972 .949 .939 .856 .760 .917 .884 .885 .942 .814 .898 .834 Component

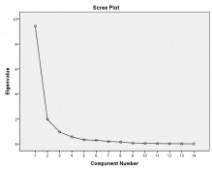
1.6碎石图
)
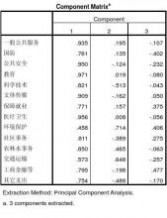
标准的一般公共服务=0.935*f1+0.195*f2-0.107*f3+e1 ??
1.8因子得分系数矩阵(用标准化原始变量表示标准化公共因子)
Component Score Coefficient Matrix
1
一般公共服务 国防 公共安全 教育 科学技术 文体传媒 保障就业 医疗卫生 环境保护 社区事务 农林水事务 交通运输 工商金融等 其它支出
.099 .081 .101 .103 .087 .096 .082 .101 .049 .086 .090 .061 .084 .080
Component
2 .099 .069 -.063 .010 -.262 -.083 .080 .004 .364 -.199 .237 .330 -.101 -.249
3 -.113 -.424 -.245 -.084 -.046 .053 .396 -.059 .428 .290 -.067 -.271 .502 -.179
Component Score Coefficient Matrix
1
一般公共服务 国防 公共安全 教育 科学技术 文体传媒

保障就业 医疗卫生 环境保护 社区事务 农林水事务 交通运输 工商金融等 其它支出
.099 .081 .101 .103 .087 .096 .082 .101 .049 .086 .090 .061 .084 .080
Component
2 .099 .069 -.063 .010 -.262 -.083 .080 .004 .364 -.199 .237 .330 -.101 -.249
3 -.113 -.424 -.245 -.084 -.046 .053 .396 -.059 .428 .290 -.067 -.271 .502 -.179
Extraction Method: Principal Component Analysis.
F1=0.099*标准化的一般公共服务+0.081*标准化的国防+??+0.080*标准化的其他支出 ??
)
2. 为寻找意义更明确、实际意义更明显的公共因子,对初始公共因子进行旋转。 Spss输出结果:
2.1旋转后的因子载荷矩阵
Rotated Component Matrix
a
1
一般公共服务 国防 公共安全 教育 科学技术 文体传媒
.555 .417 .752 .699 .937 .791
Component
2 .704 .764 .633 .618 .241 .408
3 .348 .035 .077 .280 -.049 .252
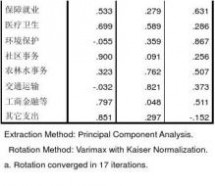
忽略特殊因子,可得:
标准化一般公共服务=0.555*f1+0.704*f2+0.348*f3
??
F1:科教文卫因子;f2:基础服务因子;f3:保护因子 2.2因子得分系数矩阵(可得到标准因子得分函数)
Component Score Coefficient Matrix
1
一般公共服务
国防
公共安全
教育
科学技术
文体传媒
保障就业
医疗卫生
环境保护
社区事务
农林水事务
交通运输
工商金融等
其它支出 -.008 -.052 .077 .057 .227 .134 .072 .063 -.131 .239 -.097 -.211 .208 .192 Component 2 .180 .355 .184 .118 -.052 -.021 -.168 .099 -.066 -.238 .214 .376 -.327 .036 3 .006 -.249 -.185 -.022 -.155 .025 .369 -.008 .545 .132 .117 .008 .345 -.249
Extraction Method: Principal Component Analysis.
Rotation Method: Varimax with Kaiser Normalization.
Component Scores.
F1=-0.008*标准化的一般公共服务-0.052*标准化的国防+??+0.192*标准化的其他支出
??
利用标准化的因子得分函数,可计算各地区在不同因子上的得分,进而进行如排


1. 科教文卫因子得分与该省经济水平有关,河北省接近全国平均水平;
2. 服务支出与农业有关,故沿海及农业大省该项得分较高;
3. 河南、四川等省在保护支出得分较高,说明他们在环境保护、社会保障方面支出较多。
本文标题:双因素方差分析案例-自然散热管脚类器件flotherm热仿真误差分析案例161阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1