一 : 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

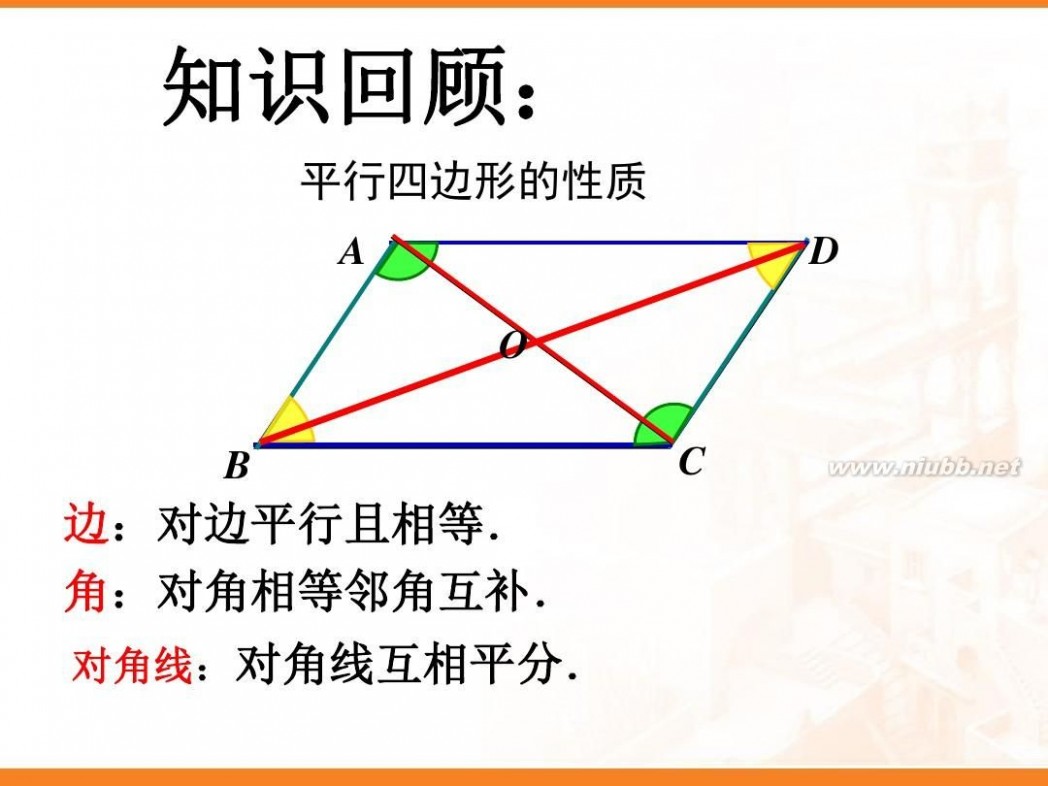
矩形的性质 矩形的性质课件(实用)

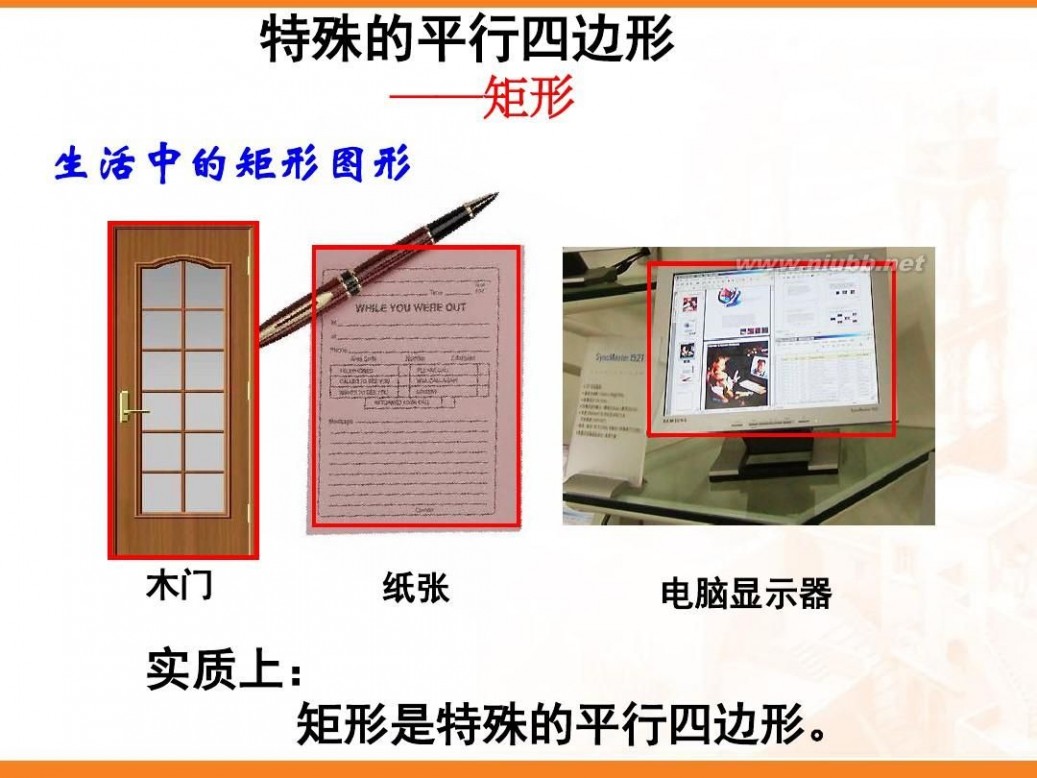
矩形的性质 矩形的性质课件(实用)

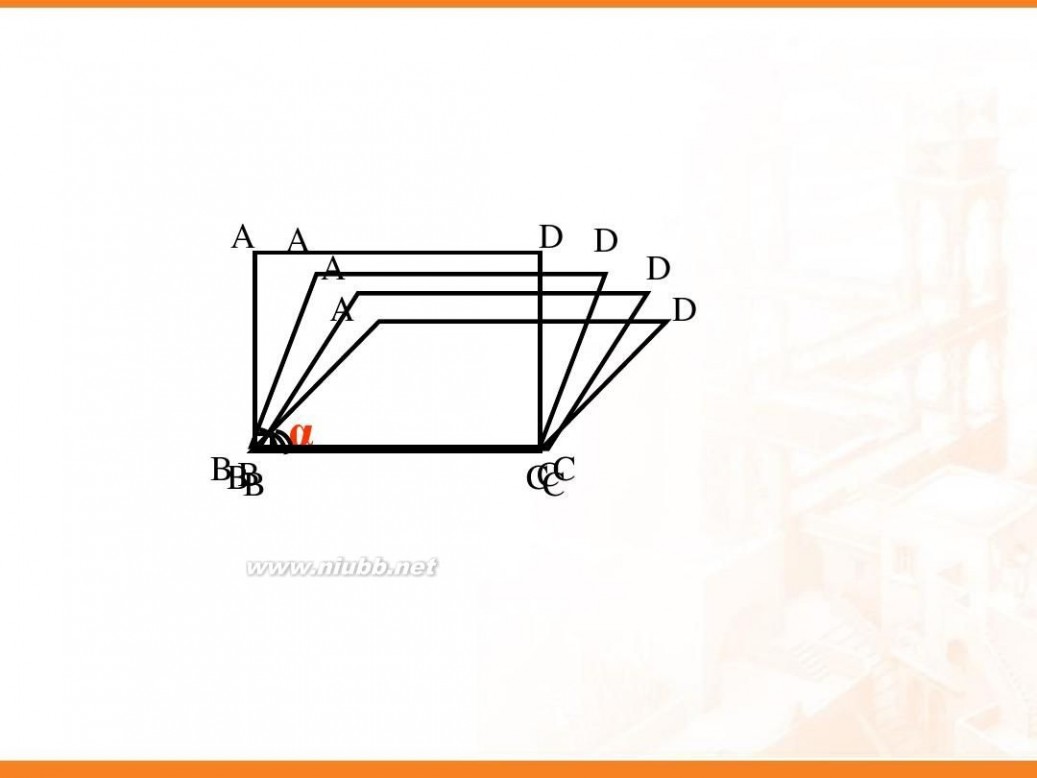
矩形的性质 矩形的性质课件(实用)

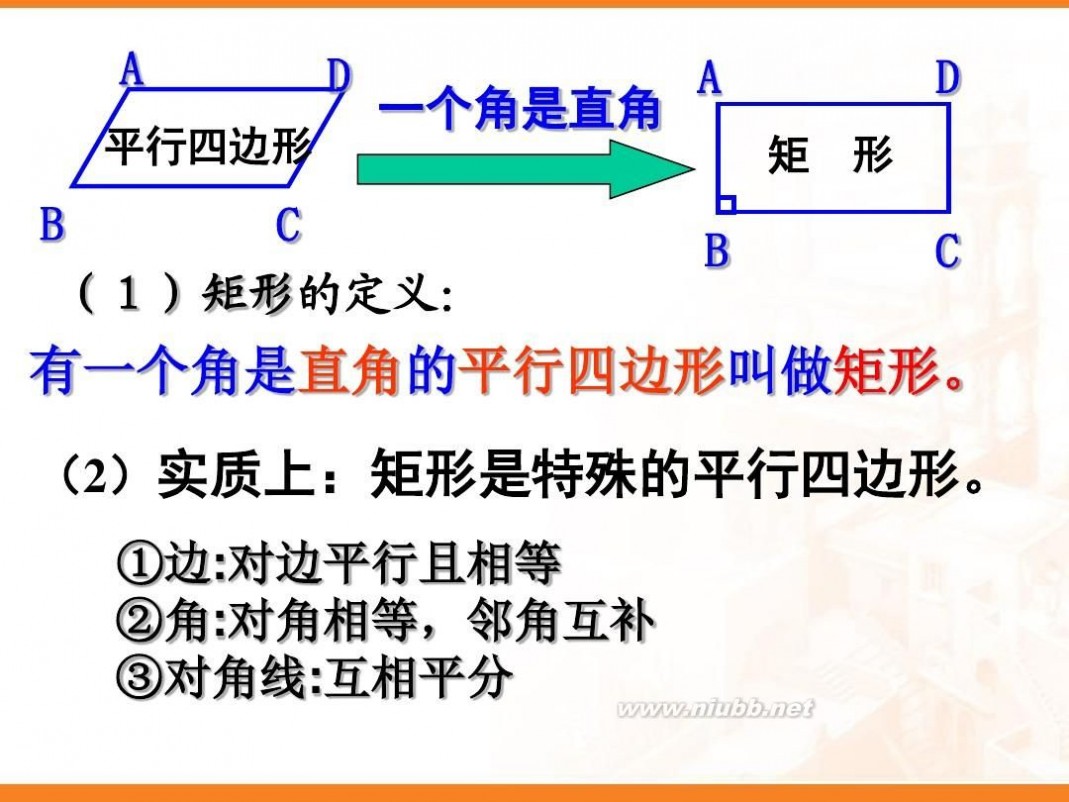
矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

矩形的性质 矩形的性质课件(实用)

二 : 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

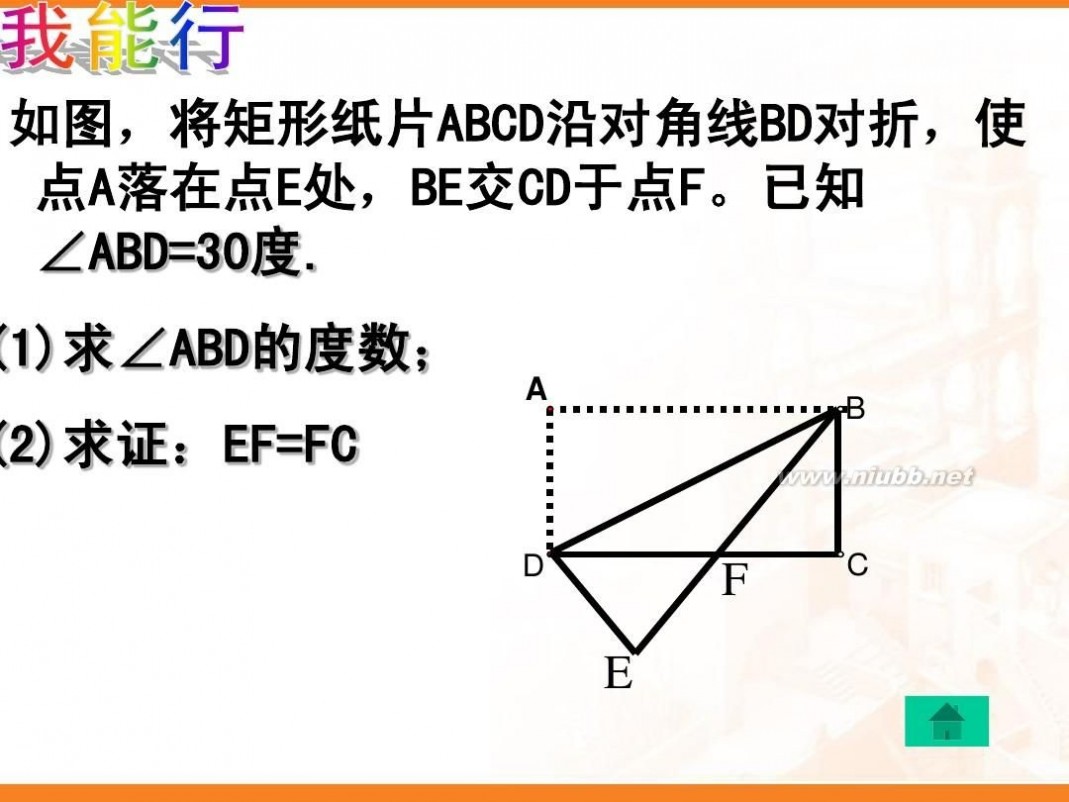
矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

矩形的定义 矩形的定义与性质_课件

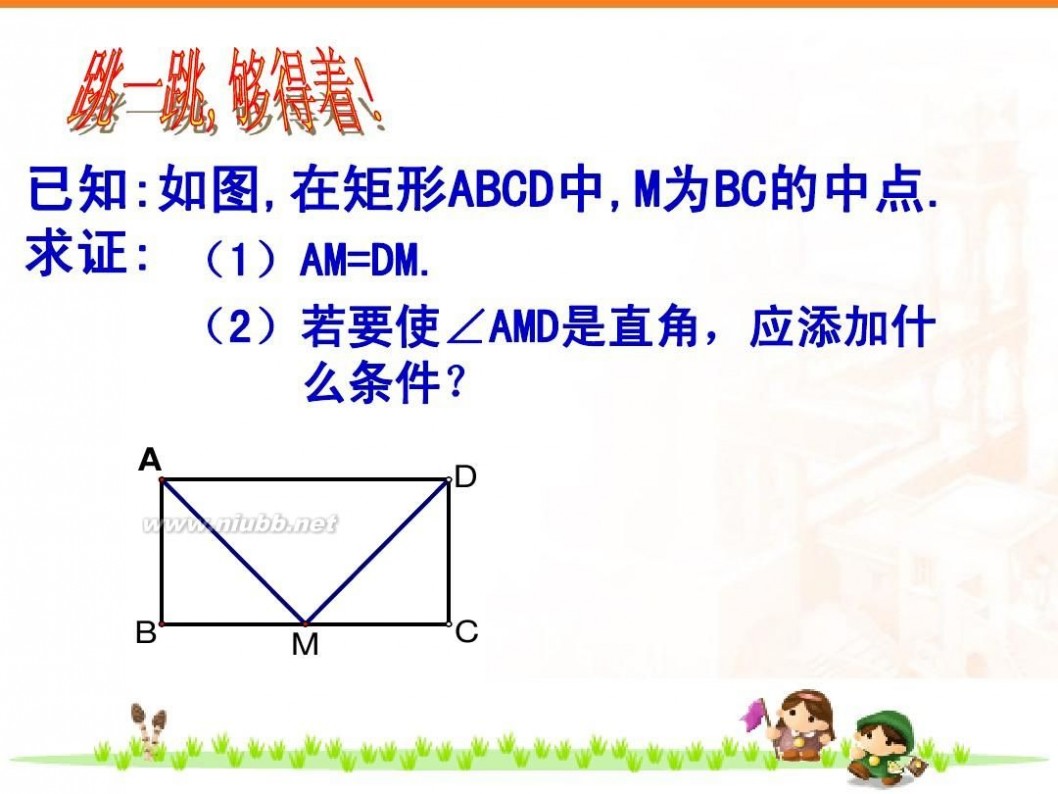
矩形的定义 矩形的定义与性质_课件

61阅读提醒您本文地址：

三 : 18.2.1_矩形的性质

平行四边形

矩形

平行四边形

矩形

桂林山水---漓江

桂林山水---象鼻山

我们已经知道平行四边形是特殊的四边 形，因此平行四边形除具有四边形的性质外， 还有它的特殊性质，同样对于平行四边形来 说也有特殊情况，这堂课我们就来研究一种 特殊的平行四边形—— 矩形
两组对边 分别平行

平行 四边形

矩形的性质

平行四边形

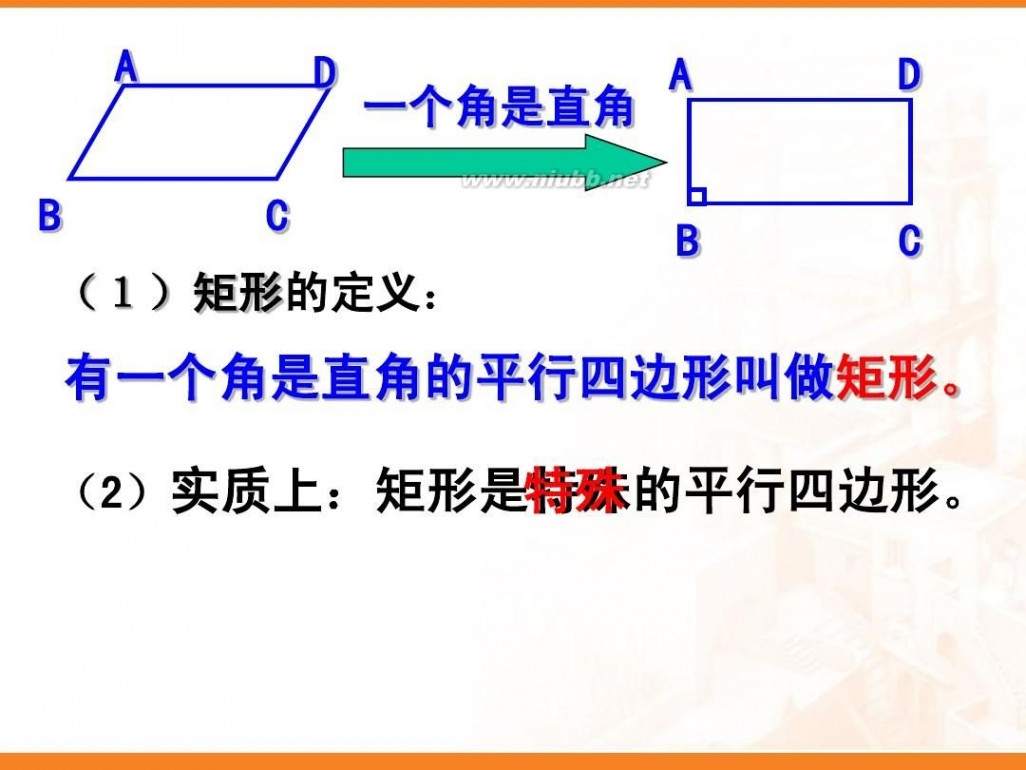
一个角是直角

矩形

有一个角是直角的平行四边形叫做矩形

矩形的性质的研究
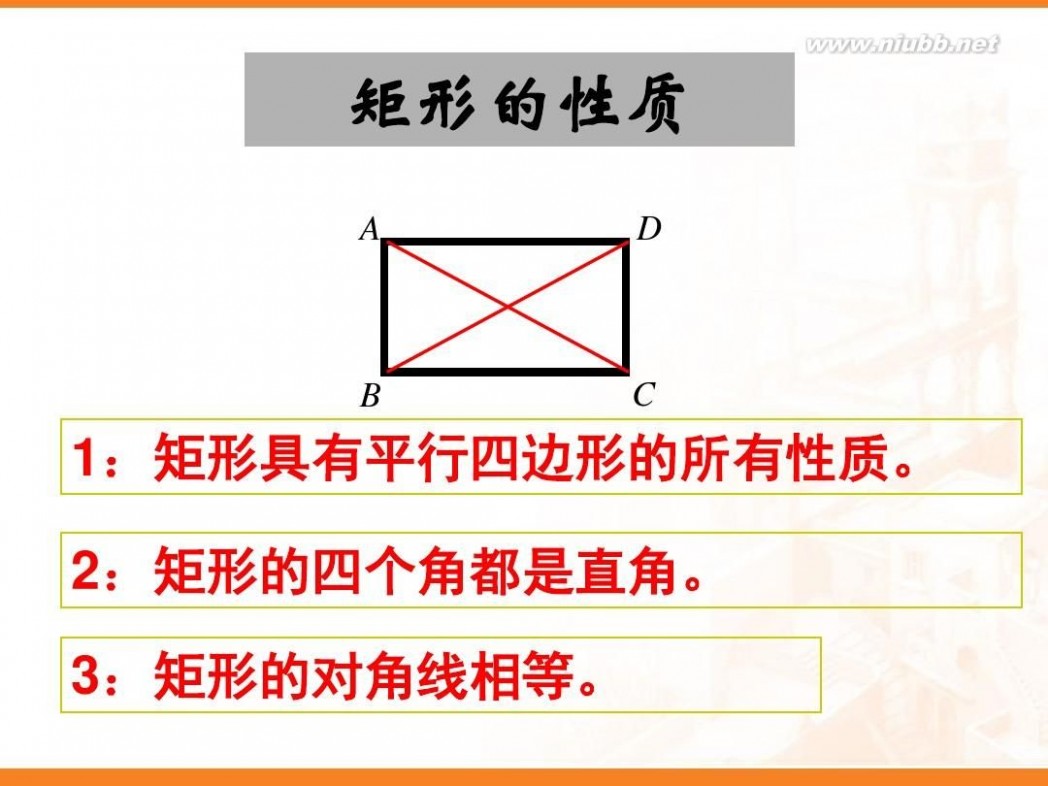
我们已经知道矩形是特殊的平行四边形，因此矩形 除具有平行四边形的性质外，还有其它的特殊性质. 你能说出矩形有哪些特殊性质吗? 一、矩形的两组对边分别平行 二、矩形的两组对边分别相等 三、矩形的两组对角分别相等 四、矩形 两条对角线互相平分 五、矩形的邻角互补

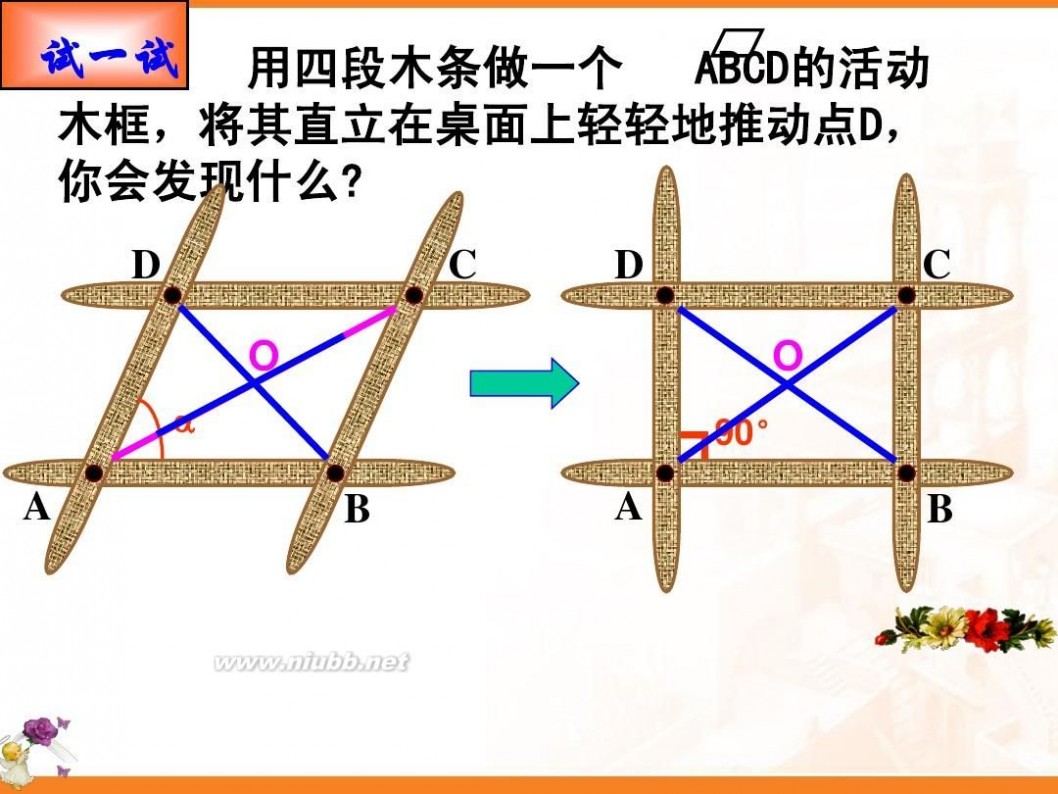
请同学们用量角器度量你的课本每个角的 度数,用直尺度量两条对角线的长度.并且根据你 得到的数据提出你的猜想．

矩形是一个特殊的平行四边形，除了具有 平行四边形的所有性质外，还有哪些特殊性质 呢？
A D

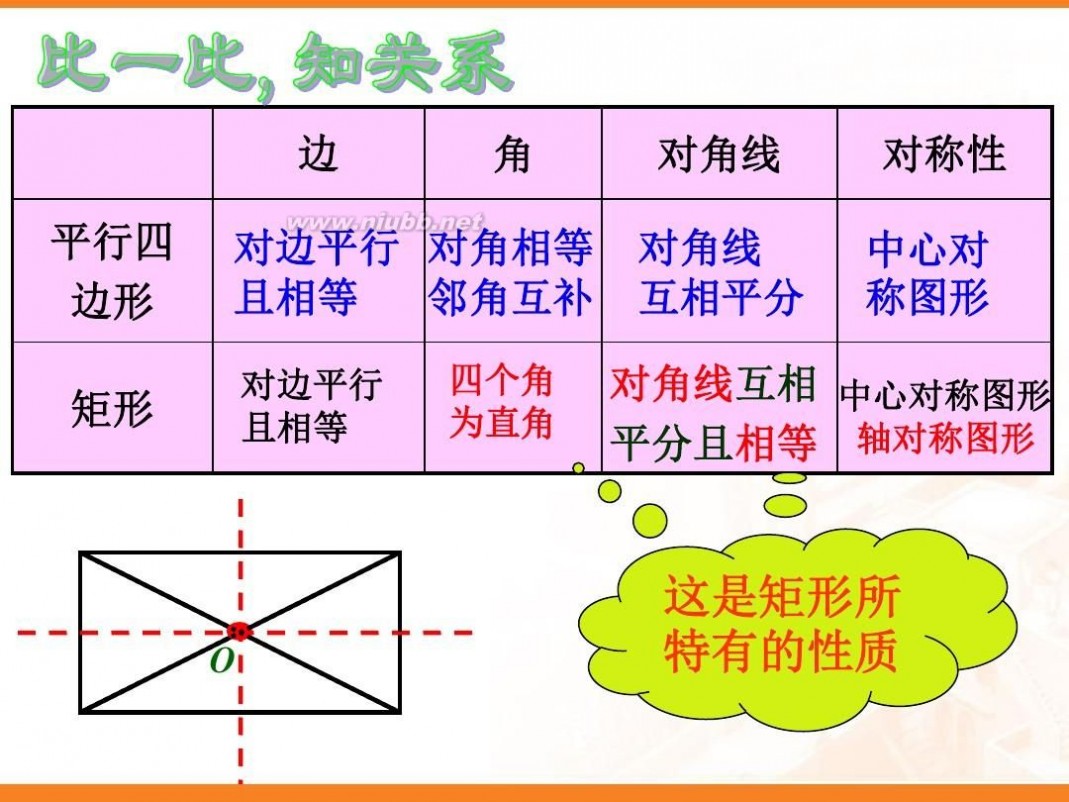
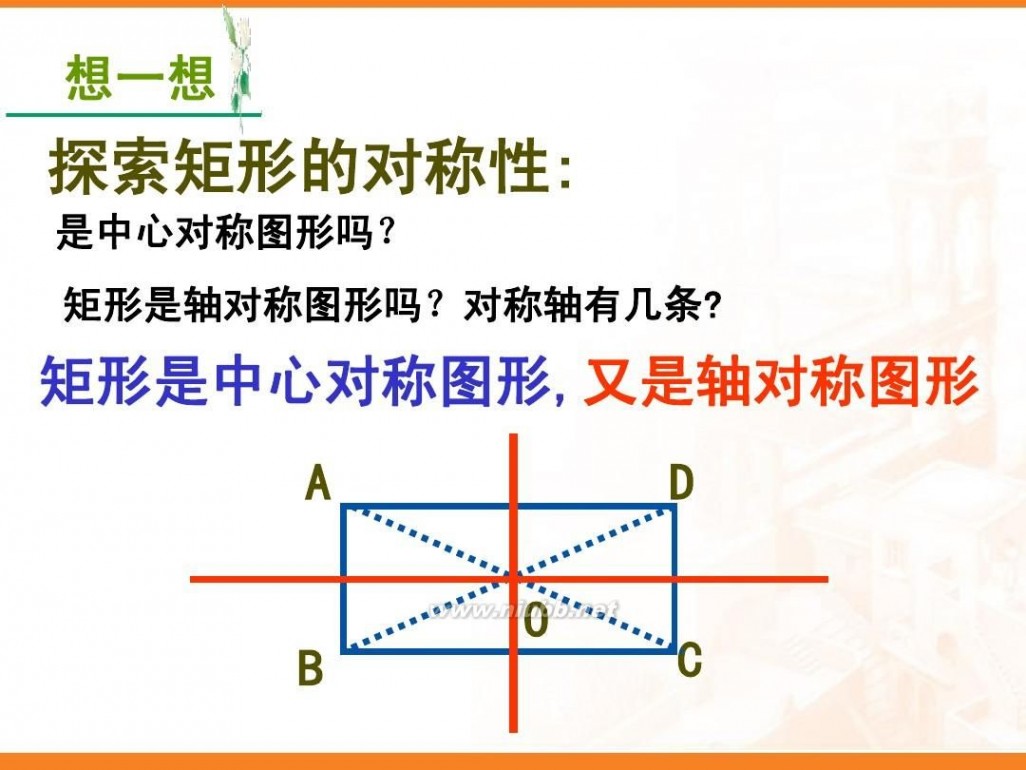
矩形是轴对称图形.
B C

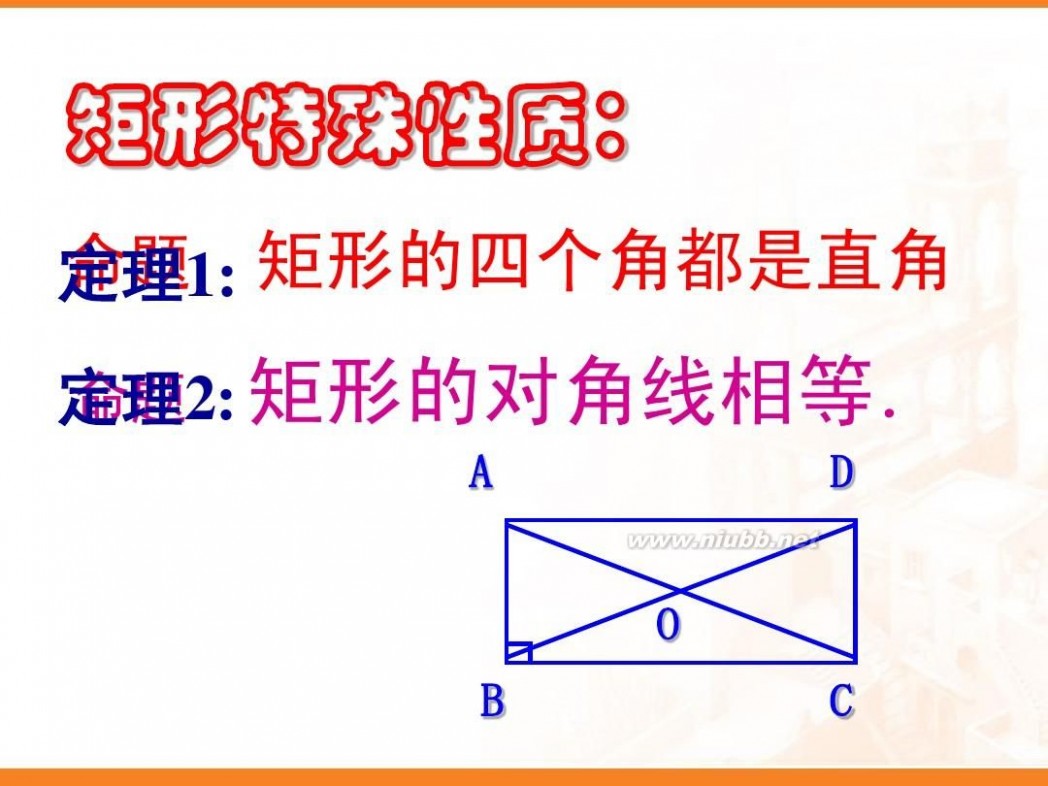
猜想1：矩形的四个角都是直角． 猜想2：矩形的对角线相等．

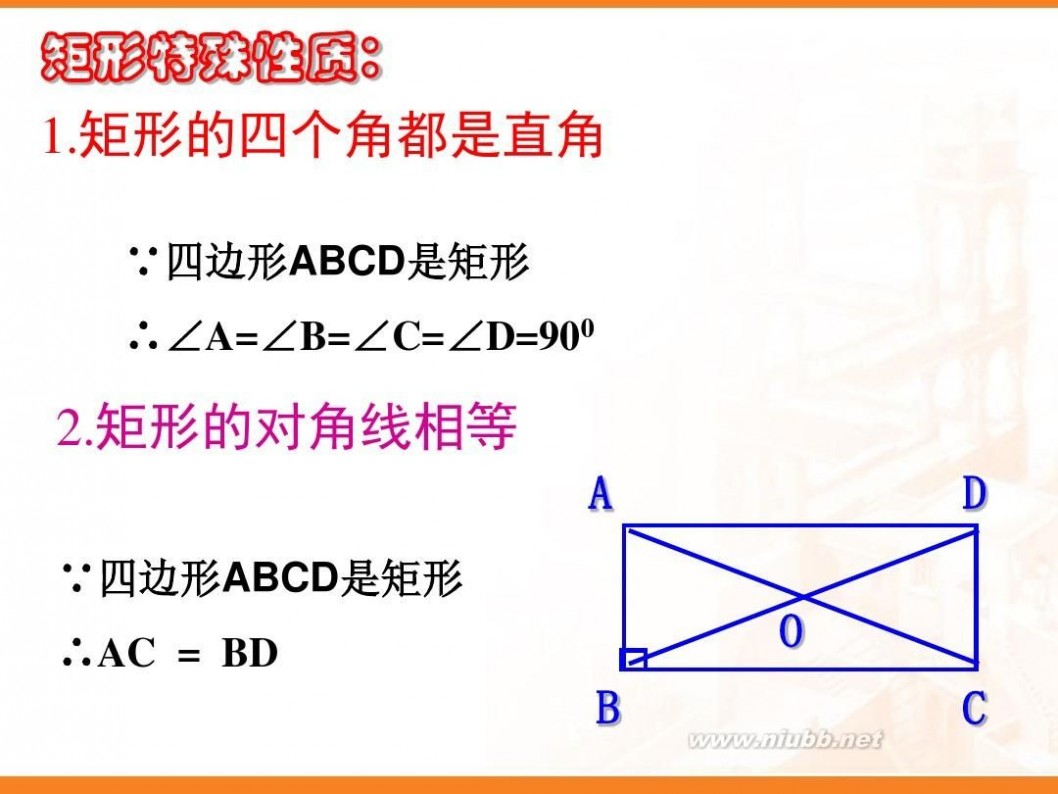
命题 性质１：矩形的四个角都是直角
A D

已知：四边形ABCD是矩形,
∠B=90° 求证：∠A=∠B=∠C=∠D=90° 证明：∵四边形ABCD是平行四边形， ∠B=90° ∴∠B=∠D=90° ∠B+∠C=180 °
B C

∴∠B+ ∠ A=180°
∴∠A=∠B=∠C=∠D=90°

命题 2：矩形的对角线相等． 性质
已知：四边形ABCD是矩形，求证：AC = BD
证明：在矩形ABCD中 ∵∠ABC = ∠DCB = 90° 又∵AB = DC ， BC = CB ∴△ABC≌△DCB ∴AC = BD
B C A D

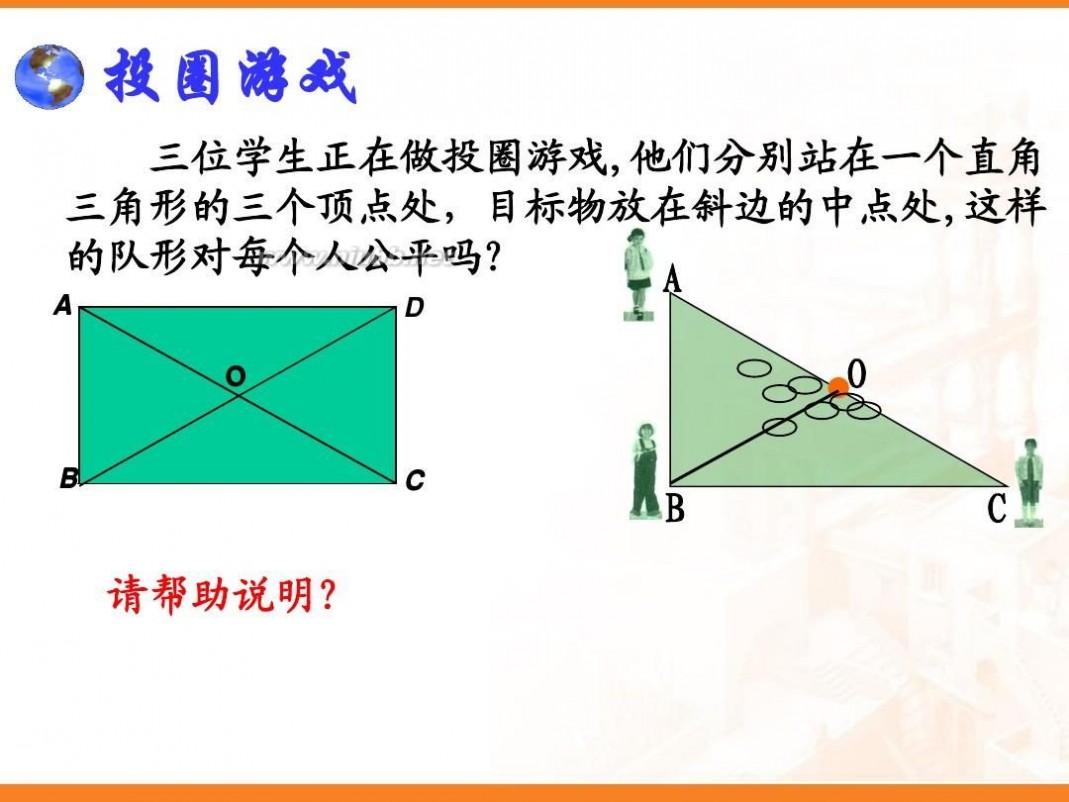
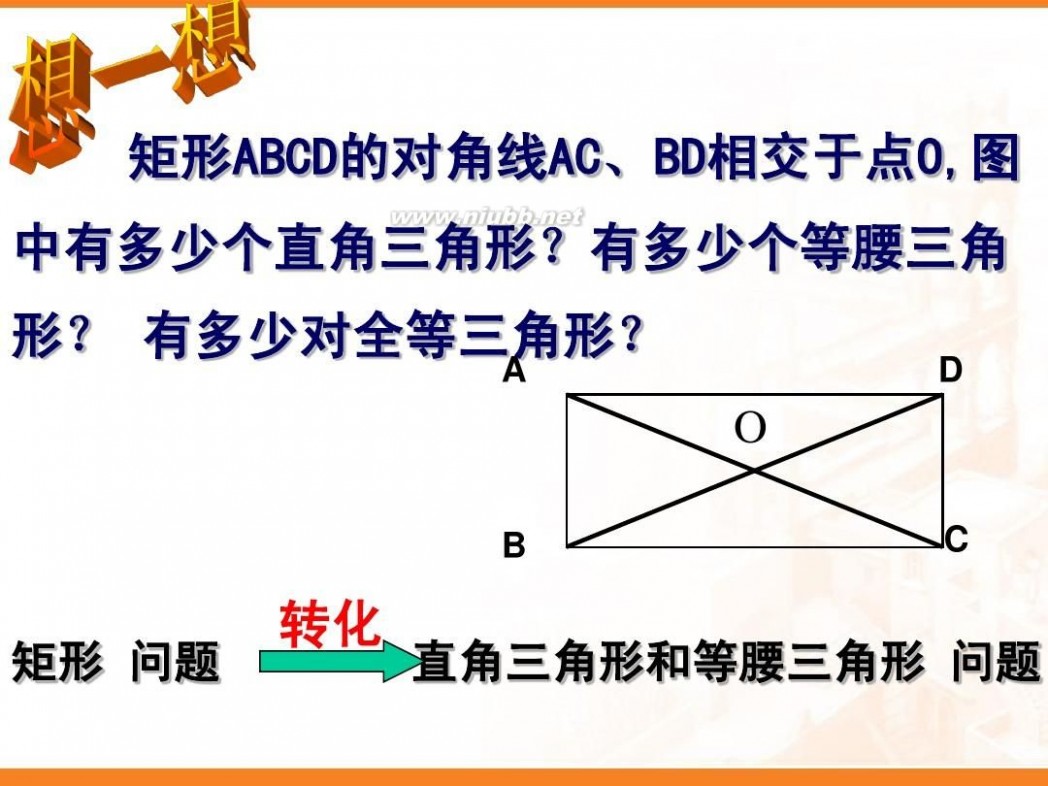
四个学生正在做投圈游戏,他们分别站在一 个矩形的四个顶点处，目标物放在对角线的交 点处,这样的队形对每个人公平吗?为什么？ A D

O

B 公平,因为OA=OC=OB=OD C

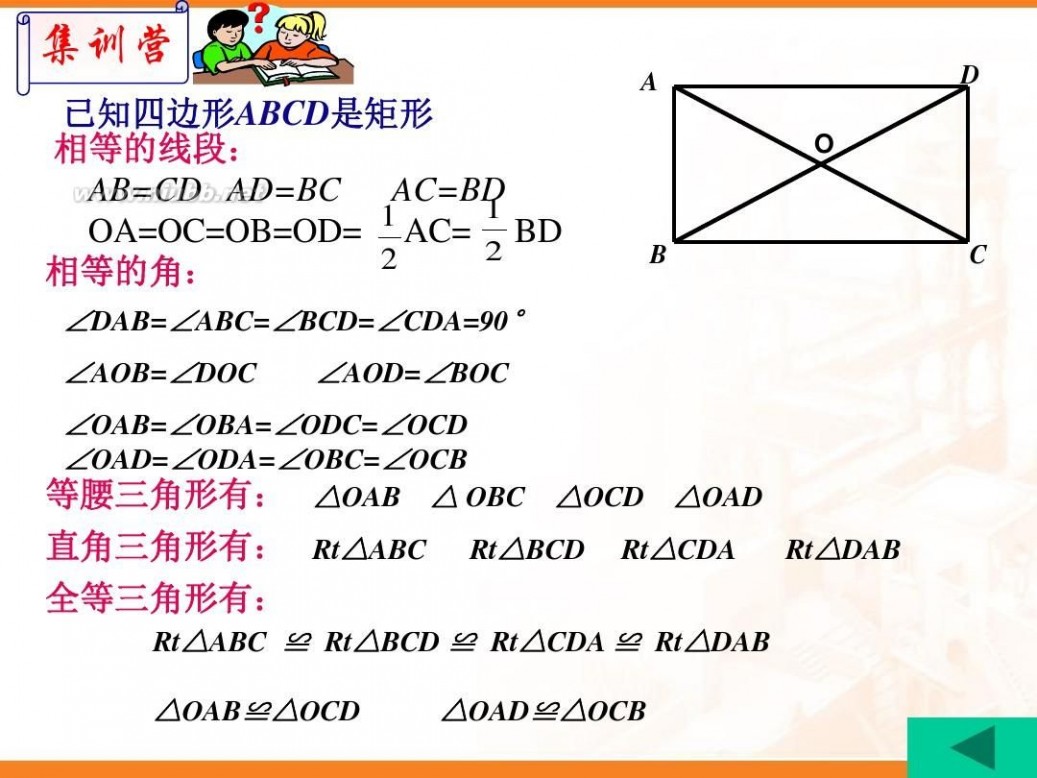
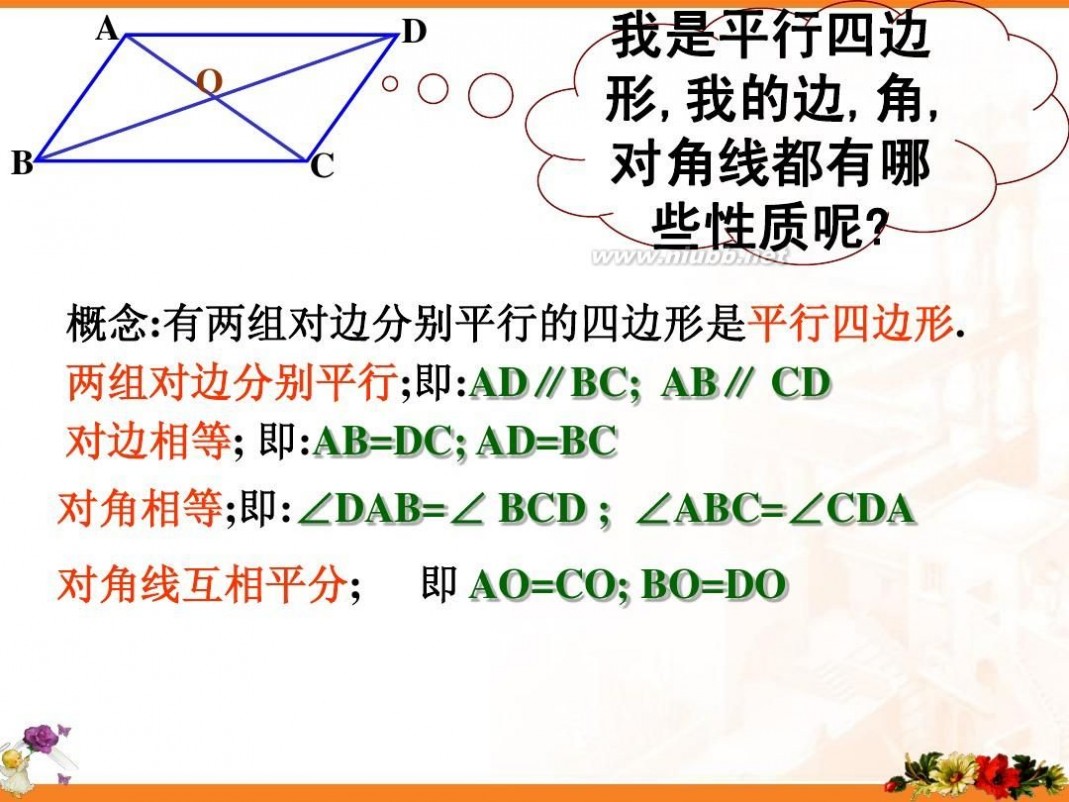
A O 矩形的两组对边分别平行 边 矩形的两组对边分别相等 B

D

C

角

矩形的四个角都是直角

符合语言 ∵四边形ABCD是矩形
∴AD ∥BC
0 ? ? A ? ? B ? ? C ? ? D ? 90 ∴ AC= BD ∴ CO ， OD ∴AO= AD = BC ， CD = = OB AB

，CD ∥AB

对角线

矩形 的两条对角线相等 矩形的 两条对角线互相平分

你能从中得出直角三角形 的性质吗?

A

┛
O

D

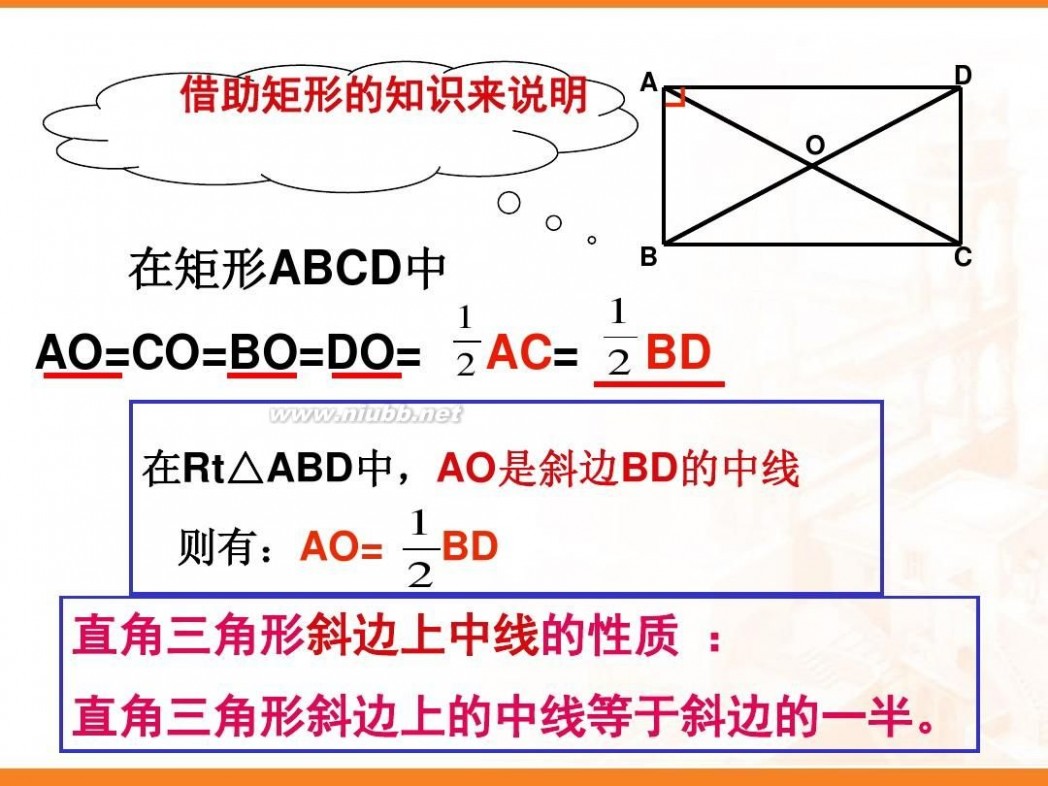
在矩形ABCD中
OA=OC=OB=OD=
1 2

B

C

AC=

1 2

BD

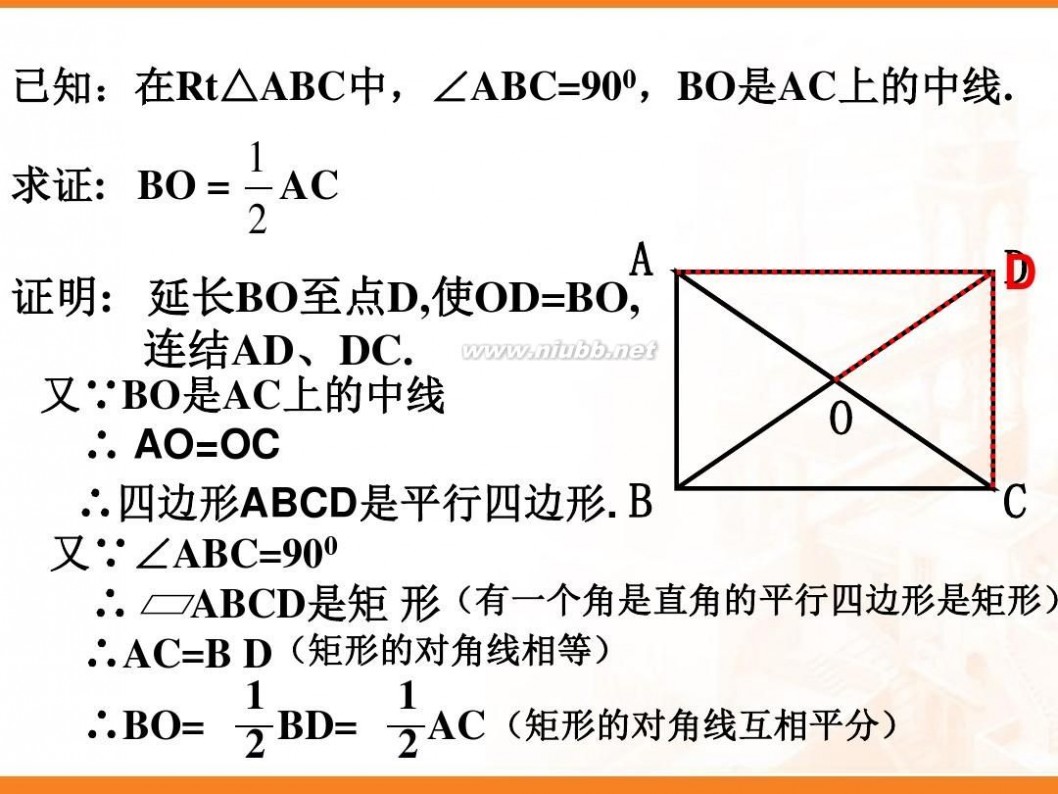
在Rt△ABD中，AO是斜边BD的中线

1 则有：OA= OB=OD= BD 2

直角三角形的性质：直角三角形斜边

上的中线等于斜边的一半。

芳草的哭泣:新民学校在建设绿色校 园的过程中修建了一块长８米，宽６米的
小亮

矩形绿草地，为方便师生参观，沿对角线 修筑了一条卵石小道．但是……唉!

小明

６ 米

８米

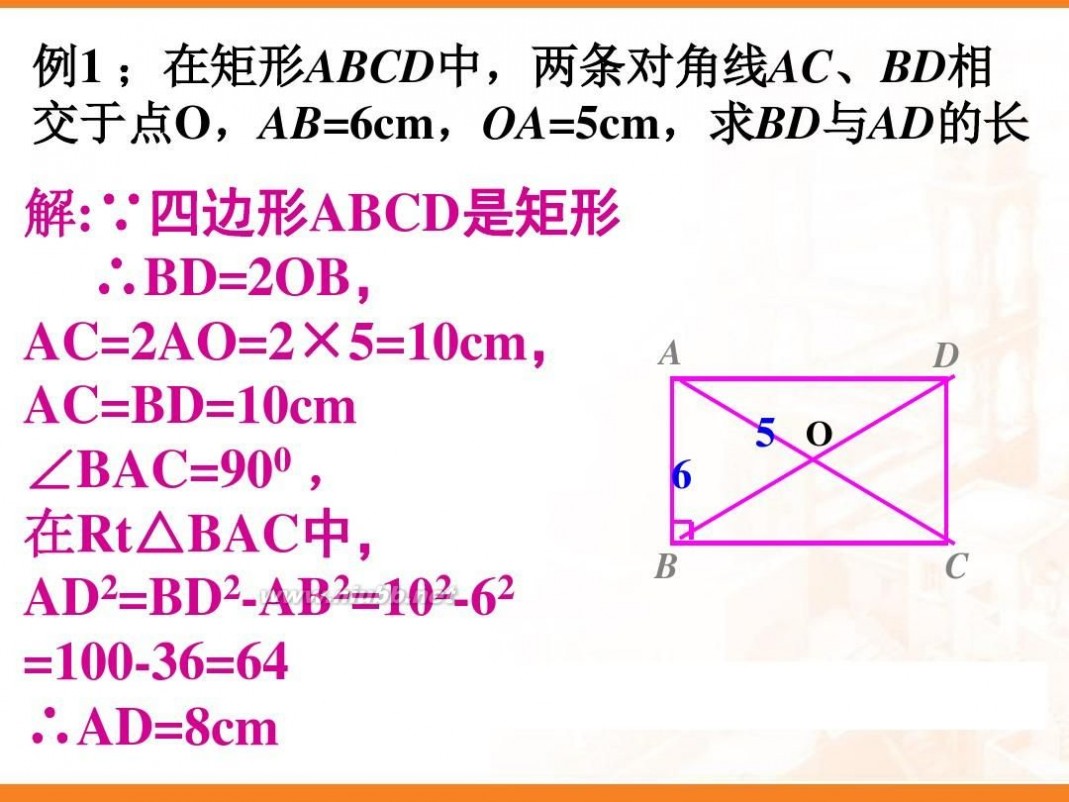
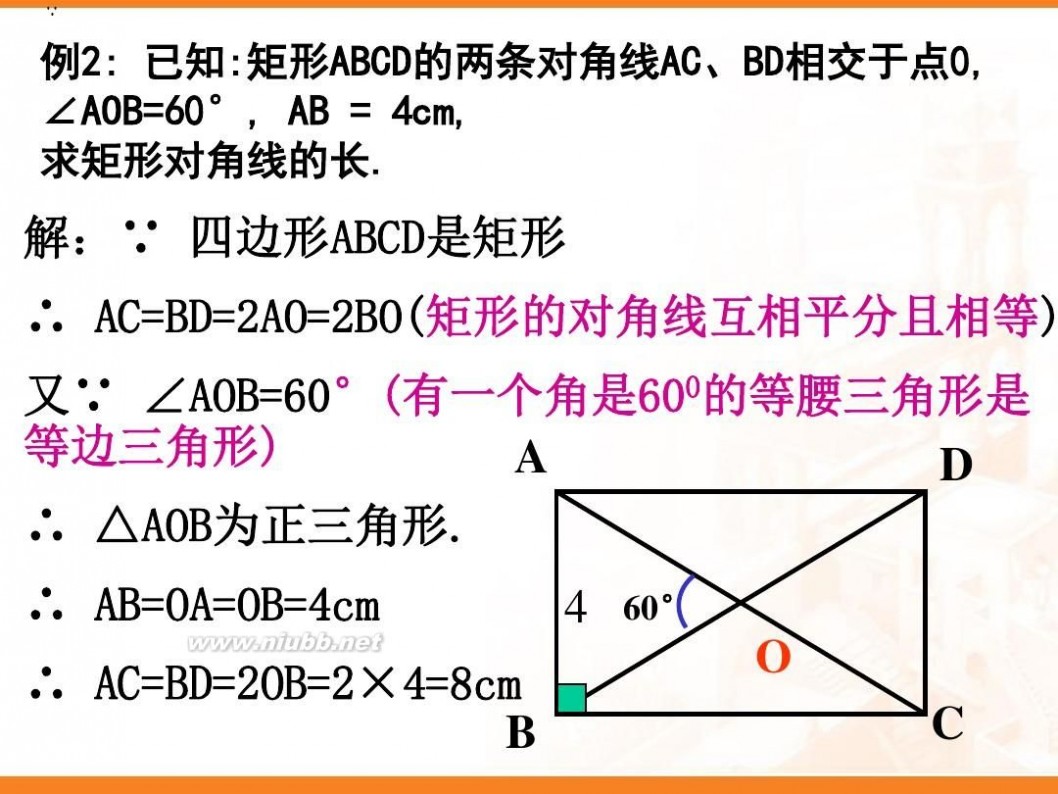
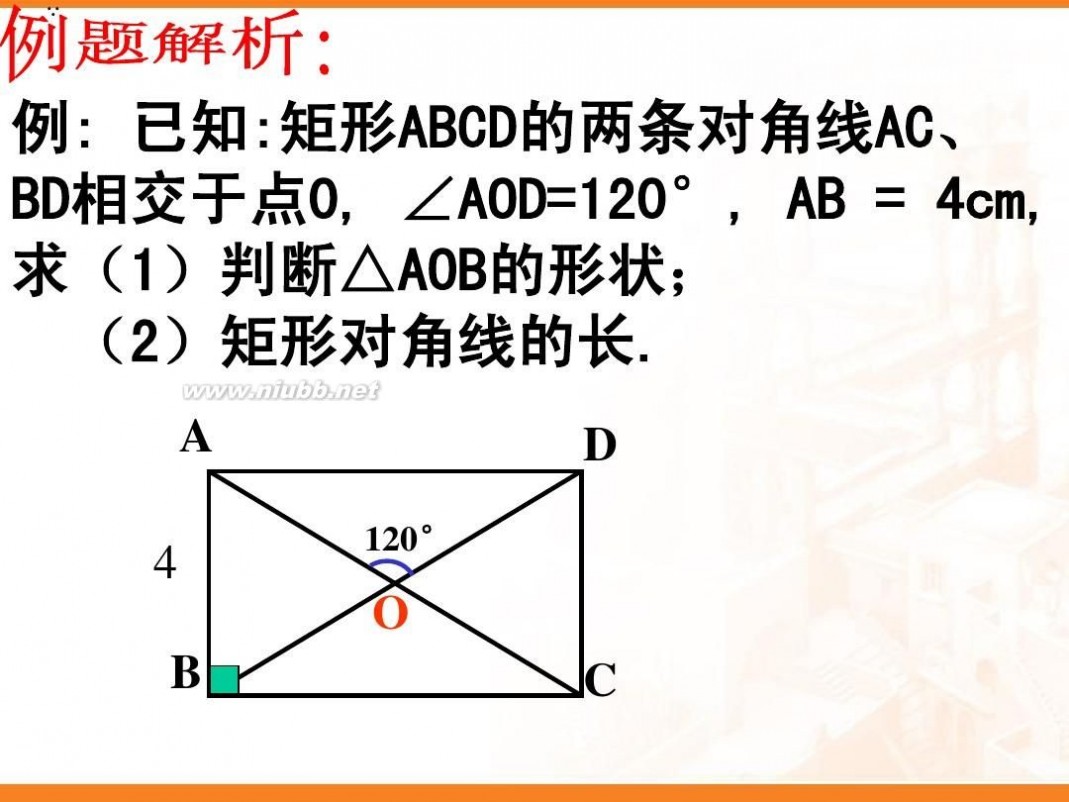
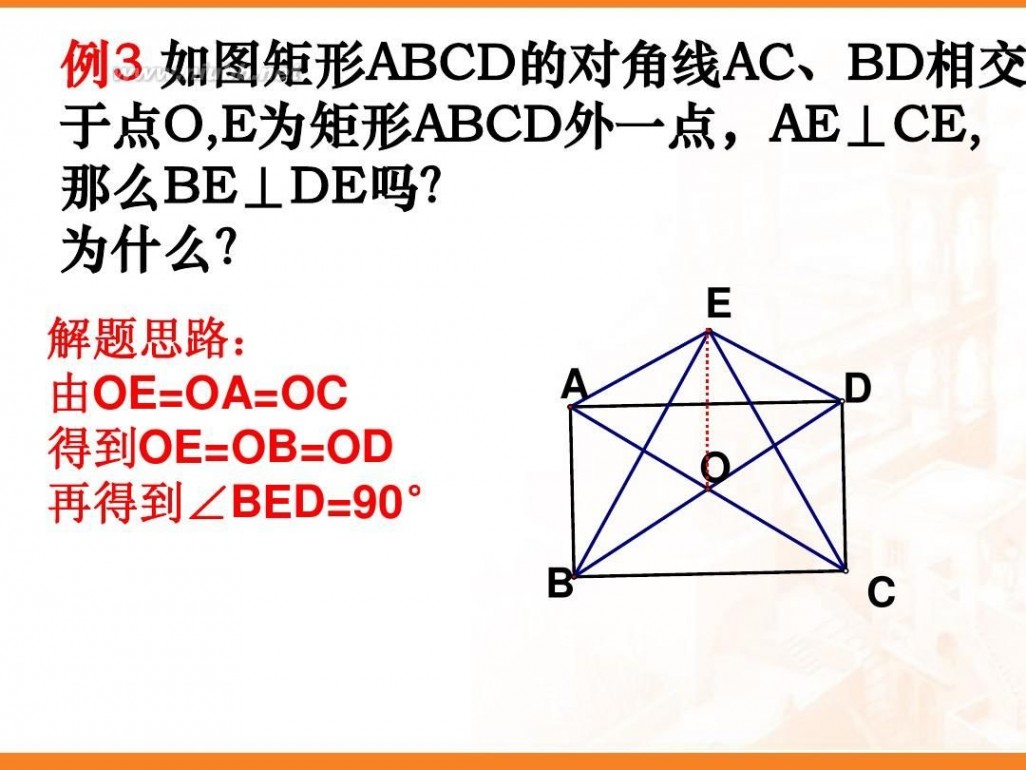
例1: 如图，矩形ABCD的两条对角线相交于点O， ∠AOB=60°

,AB=4㎝,求矩形对角线的长？
A D

解：∵ 四边形ABCD是矩形 ∴AC与BD相等且互相平分 ∴ OA=OB ∵ ∠AOB=60° ∴ △AOB是等边三角形 ∴ OA=AB=4(㎝) ∴ 矩形的对角线长 AC=BD=2OA=8(㎝)

O

B

C

方法小结:如果矩形两对角

线的夹角是60°或120° 则其中必有等边三角形.

变式： 已知对角线长是8cm，两对角线的一个夹角

∠AOD是120°， 求矩形的长BC与宽AB.

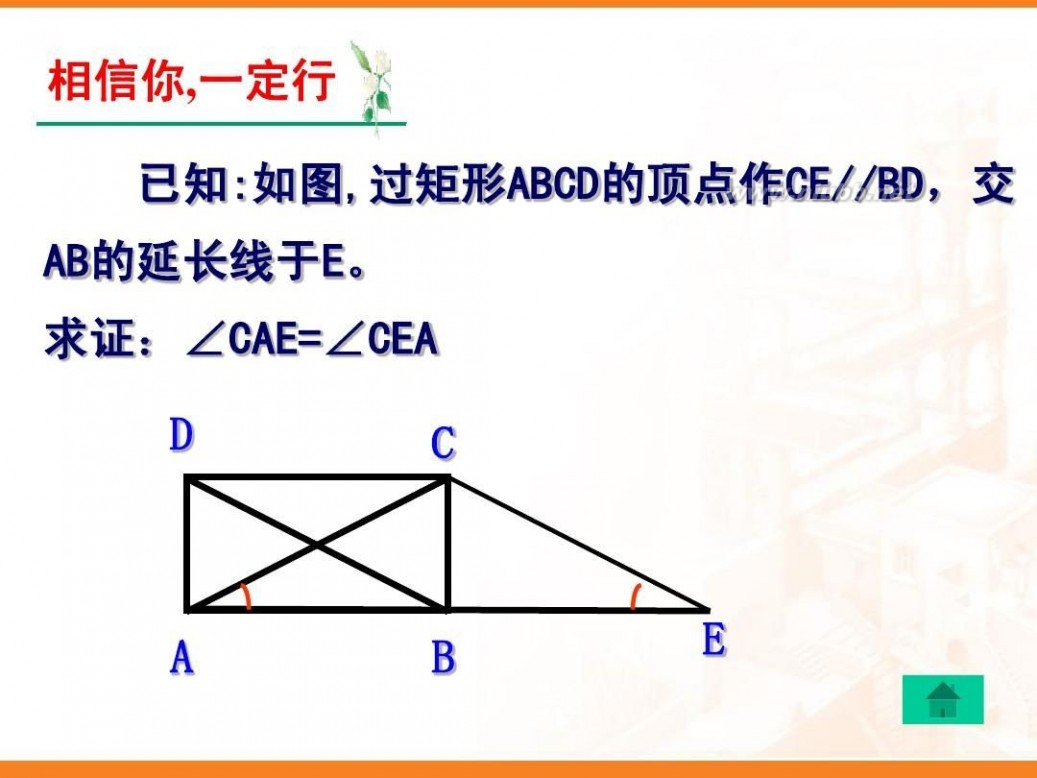
例2.已知MN//PQ，直线L分别交MN、PQ于点A、C，同旁 内角的平分线AB、CD相交于点B，AD、CD相交于点D,试 说明四边形ABCD是矩形。
证明：∵ MN ∥ PQ ∴ ∠NAC=∠ACP ∵ AD、CB分别平分∠NAC、∠ACP ∴ ∠2=∠NAC，∠1=∠ACP ∴ ∠1=∠2 ∴ AD∥BC 同理：AB∥CD ∴ 四边形ABCD是平行四边形 ∵ AD、AB分别平分∠NAC、∠MAC 1 ∴ ∠2= 1 ∠NAC，∠1= ∠MAC 2 2 ∴ ∠2+∠4= 1 2 (∠NAC+∠MAC) ∵ ∠NAC+∠MAC=180° ∴ ∠BAD=90° ∴ 四边形ABCD是矩形
M A N D 13 C

42
B P

Q

例3：如图,在矩形ABCD中,AB＝3,AD＝4,P是AD上不与A、D重合 的一动点，PE⊥AC，PF⊥BD，E、F为垂足,求PE＋PF的值.
A
P E B F C D

解：连接OP
∵ 四边形ABCD是矩形 ∴ OA=OB=OC=OD BC=AD=4,∠ABC=90° ∵ AB=3 3 2 ∴ AC ? 3 ? 4 ? 5 ∴ OA=OD= 5 2 1 ∴ S ? PE ? OA ? 1 ? 5 PE
?AOP 2 2 2 5 1 S?DOP ? 1 2 PF ? OD ? 2 ? 2 PF

O

∴ S?AOD ? S?AOP ? S?DOP ? ∴ 5 3 1
4

?PE ? PF ? ? 2 ? 4 ? 2

5 4

?PE ? PF ?

∴ PE ? PF ? 12 5

小试身手
矩形具有而一般平行四边形不 具有的性质是 ( ） C A.对角相等

B.对边相等 C.对角线相等 D.对角线互相平分

小试身手
? 四边形ABCD是矩形

D O

C

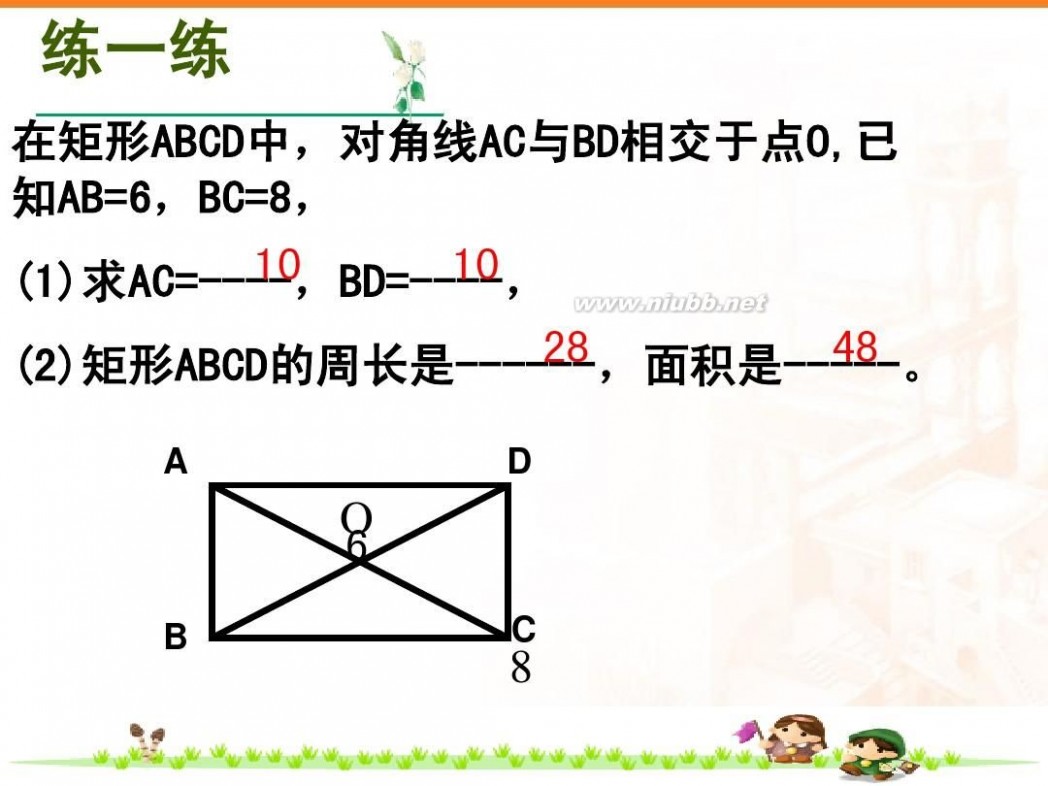
A 1.若已知AB=8㎝，AD=6㎝， 10 5 则AC＝_______ ㎝ OB=_______ ㎝

B

28 2.若已知AC＝10㎝，BC=6㎝，则矩形的周长＝____ cm 48 矩形的面积＝_______ ㎝2 12 3. 若已知 ∠DOC=120°，AD＝6㎝，则AC= _____cm

小试身手
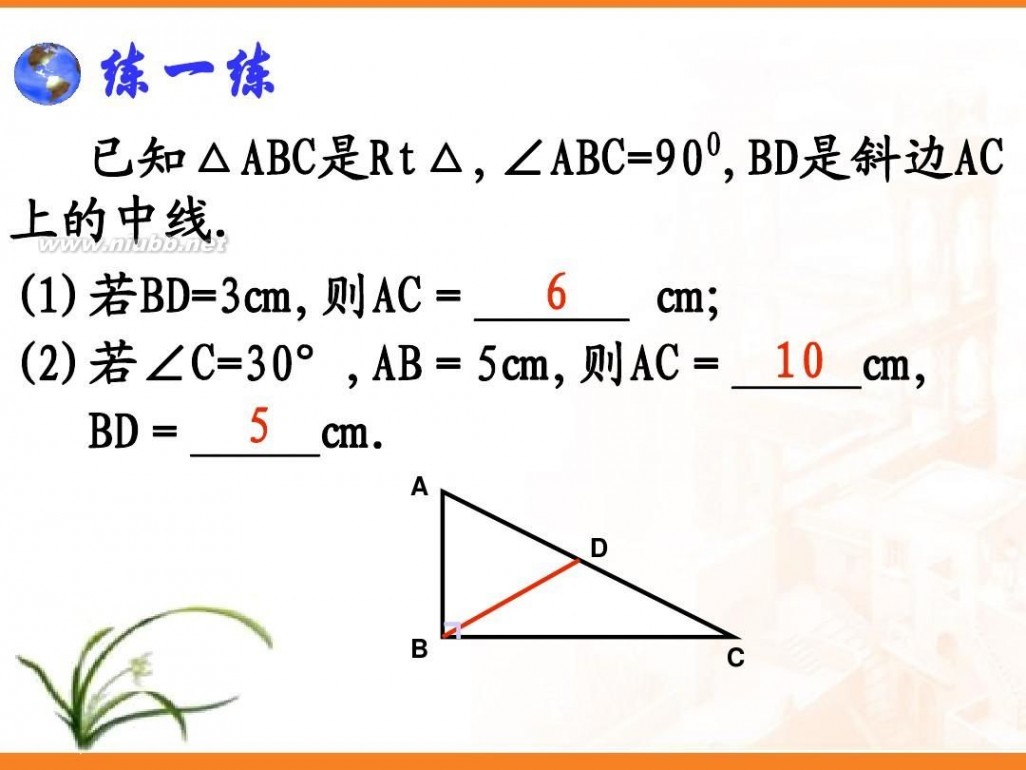
4.已知△ABC是Rt△，∠ABC=900， A BD是斜边AC上的中线
1 若BD=3㎝则AC＝ 6 ㎝
B D

┓
C

2 若∠C=30°，AB＝5㎝，则AC＝ BD＝ 5 ㎝，

10

㎝，

小试身手
B

A

F
┓

E

D

H

C

如图，在△ABC中，D，E，F，分别 是BC、AC、AB边的中点，AH⊥BC于H， FD=8㎝，则HE＝ 8㎝

矩形的一个角的平分线分矩形的一边 为1cm和3cm两部分,则这个矩形的面 积为 . 2 12cm2 或4cm
A

3

E

1 D
C

A B

1 E

3

D
C

B

如图，矩形ABCD中，E为AD上一点， EF⊥CE交AB于F，若DE=2，矩形的 周长为16，且CE=EF，求AE的长.
A F B C E D

巩固练习
2.如图,用8块相同的长方形地砖拼成一个矩形 地面,则每块长方形地砖的长和宽分别是( D )

（A）48cm,12cm; （B）48cm,16cm;
（C）44cm,16cm; （D）45cm,15cm.

60cm

矩形ABCD中,DF平分∠ADC,交AC 于E,交BC于F, ∠BDF＝15°,求 ∠DOC和∠COF的度数.
A O E B F C D

将矩形ABCD对折,设折痕为MN,再把B 点叠在折痕线MN上点B′,若AB= ， 3

求折痕AE的长?
B M

E
B'

C N D

A

※ 矩形的性质1
矩形的四个角都是直角.

※ 矩形的性质2
矩形的对角线相等.

※ 推 论
直角三角形斜边上的 中线等于斜边的一半.

本文标题：矩形的性质-矩形的性质课件(实用)
本文地址： http://www.61k.com/1126712.html