一 : 指数与指数幂的运算练习题

2.1.1指数与指数幂的运算练习题

1、有理数指数幂的分类

n个?????n?

（1）正整数指数幂a?a?a?a???a(n?N)； （2）零指数幂a0?1(a?0)；

1?n?

（3）负整数指数幂a?n?a?0,n?N?

a

（4）0的正分数指数幂等于0, 0的负分数指数幂没有意义。[www.61k.com) 2、有理数指数幂的性质 （1）aman（3）?ab?

m

?am?n?a?0,m,n?Q? （2）?am??amn?a?0,m,n?Q? ?ambm?a?0,b?0,m?Q?

p

n

知能点2：无理数指数幂

若a＞0，P是一个无理数，则a表示一个确定的实数，上述有理指数幂的运算性质，对于无理数指数幂都适用。 知能点3：根式

1、根式的定义：一般地，如果x?a，那么x叫做a的n次方根，其中n?1,n?N?，a叫做根式，n叫做根指数，a叫被开方数。 2

（1）n?N，且n?1； （2）当n是奇数，则an?a；当n是偶数，则an?a??（3）负数没有偶次方根； （4）零的任何次方根都是零。 3、我们规定： （1

）a

mn

n

??

?a??a

a?0

； a?0

?a?0,m,n?N

34

?

,n?1?； （2

）a

m?n

?

1a

mn

?

a?0,m,n?N?,n?1?

1、用根式的形式表示下列各式(a?0) （1）a= （2）a= （3）a2、用分数指数幂的形式表示下列各式： （1）xy= （2）（4

4

3

15

?

35

= （4）a

???

32

=

m2m

?

(m?0) （3

）?= ?

?

85

（5

（6）aaa

2

（7） a?a? （8）a3?a2?9）aa?65

（10） pq?3、求下列各式的值

1?316?

（1）8；（2）100= ； （3）()= ；（4）()4=

481

2333

36225?2

3

（5）27= ；（6）()= ；（7）()= ；（8）252=

494

?

2

312

3

2

（9）[(]

10）?1?= （11）64?????

4.化简

?

12

?2

12

23

指数与指数幂的运算 指数与指数幂的运算练习题

（1）a?a?a1

334712?（2）a?a?a?3）3a?(?a)?9a? 3234563234

1121??1??8a?3?333?x?2x（4）= （5）() = （6）2x3?6??227ba?a?2?a2

（7）?ab

2

3???856?5?????12?a4?b3?a?0,b?0?= 12131656（8）(2ab)(?6ab)?(?3ab)5.计算

（1）25?

? (2)

（3）()?4?(?2)

1212?1?31?3??1??()0?9 （4）?2??2?2??2?4?4??4?1?20?12??0.01? 0.5

?7?（5）?2??9?

0.5?10??0.1??2??27??2?2341??32373?0.75?3?? （6）(?3)3?0.042?[(?2)]3?16 4880

（7）0.027

1?3?1??????256?3?1??7??234?1??1??2?1 （8）??????46????0??2?13??2?1.030?60.5 ?2

（9）?0.064?

?13?7?3???????2??8?0???43?160.75??0. 12

指数与指数幂的运算 指数与指数幂的运算练习题

（10）1.5

1?3

?6?

?????80.25?2??7?

6?2??3????

?3?

?

23

6.解下列方程 （1）x （4）3

x?2

???

13

1

? （2）2x4?1?15 （3）x4?2x2?24?0 8

3

?3x?2?80?0 （5）(0.5)1?3x?42x?1

7.(1).已知a?a（2）若x?x (3).若a?a

一.填空题

12

?12

12

?

12

2?2

?3，求下列各式的值（1）a?a?1（2）a?a2

?5，则x?1的值是

x

?1

?3，求下列各式的值：（1）a?a

3

5

12

?

12

；（2）a?a

2?2

1.若a?0，则a和a

3

4

?

用根式形式表示分别为和

ab和

65

m3m

b

用分数指数幂形式表示分别为 和 。（www.61k.com]

?34

2.使式子(1?2x)

a

有意义的x的取值范围是?1

3a?2b

3.若3?2，3?5,则3

m

n

的值= . 的值为 .

14

23

4.已知10?3,10?2，则10二.选择题.

3m?n2

1、 a?R，下列各式一定有意义的是（ ） A.a B. a C. a D. a 2、 a?R，下列各式一定有意义的是（ ） A. (?2) B.a 3、 下列各式计算正确的是 （ ）

A. (?1)?1 B.a?a?a C.4?8

m

n

?20

a?2

C. a D. a

13

2332

12

2

23

D. a?a

n

23

?

13

?a

4、若a?0，且m,n为整数，则下列各式中正确的是 （ ） A、a?a?a B、

m

n

am?an?am?n C、?am??am?n D、1?an?a0?n

）

5、下列运算结果中，正确的是（

指数与指数幂的运算 指数与指数幂的运算练习题

A．a?a?a B．?a2??a3

6.下列各式中成立的是（ ） 236???3? C．2a?1?1 D．?a2

333

4?0??3??a6 ?n?A．???n7m7 ?m?

2

371B．?354??3 C．x?y??x?y? D．? 7.下列各式成立的是（ ） 1?b?222355 A.m?n??m?n B.???ab C.?3???33 D.4?23 ?a?

338.将52写为根式，则正确的是（ ）A．52 B． C． D．53 211

29、化简?3?5?的结果为（ 34

???? ） A．5 B．5 C．? D．-5

1的值相等是（ ） A. a B. ?a C. ?a D. ??a a

11?112、已知a??3，则a2?a2等于（ ） A．2 B． C．?5 D．? a11.与a?

?x3

13、化简的结果是（ ） A．??x B．x x

14、下列各式正确的是（ ）

A.a?3

5C．?13x D．?x ?x?x C.a?a?a2321214?18?a111?(?)2482?114 D.2x(x3?2x3)?1? 2x?

??113315、根式（式中a?0）的分数指数幂形式为（ ）A.a B.a C.a4 D.a4 aa4433

二 : 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

指数与指数幂的运算 指数与指数幂的运算1

三 : 必发指数的运用与计算

必发指数的运用与计算

在使用必发指数时，先计算出总成交量，就是一场球赛的胜平负的成交量之和。

再计算出3项成交量占总成交量的比重。

然后通过加权，计算出卖方挂牌的胜平负三项的总赔付，用总成交量的胜平负三项减去总赔付，

可以计算出卖方的在胜平负三项的盈亏值，当盈亏值为负值时，胜出概率最大，而冷热指数为负值时，

基本胜出概率较小。

比如，埃弗顿vs曼联，

买方挂牌，主胜1487，主平24022，主负，7658，

而卖方挂牌，主胜77549，主平150476，主负38579，

成交比例，43 1343，庄家盈亏-2204487 8097458-3631089，盈亏指数--14 52--23，结果主胜。主胜与客胜均是负值，低方负值打出，主胜2比0，

而另外一场赫尔城vs阿森纳，

买方挂牌，主胜6077，主平31827，主负[www.61k.com），397205，

而卖方挂牌，主胜94636 主平91339主负146903，

成交比例 5.633,9090.47，庄家盈亏 2405862828468561 --22260963，盈亏指数7285--66，结果负值打出，客胜0比3.

四 : 指数与指数幂的运算1

Monday, July 22, 2013

§2.1.1指数与指数幂的运算

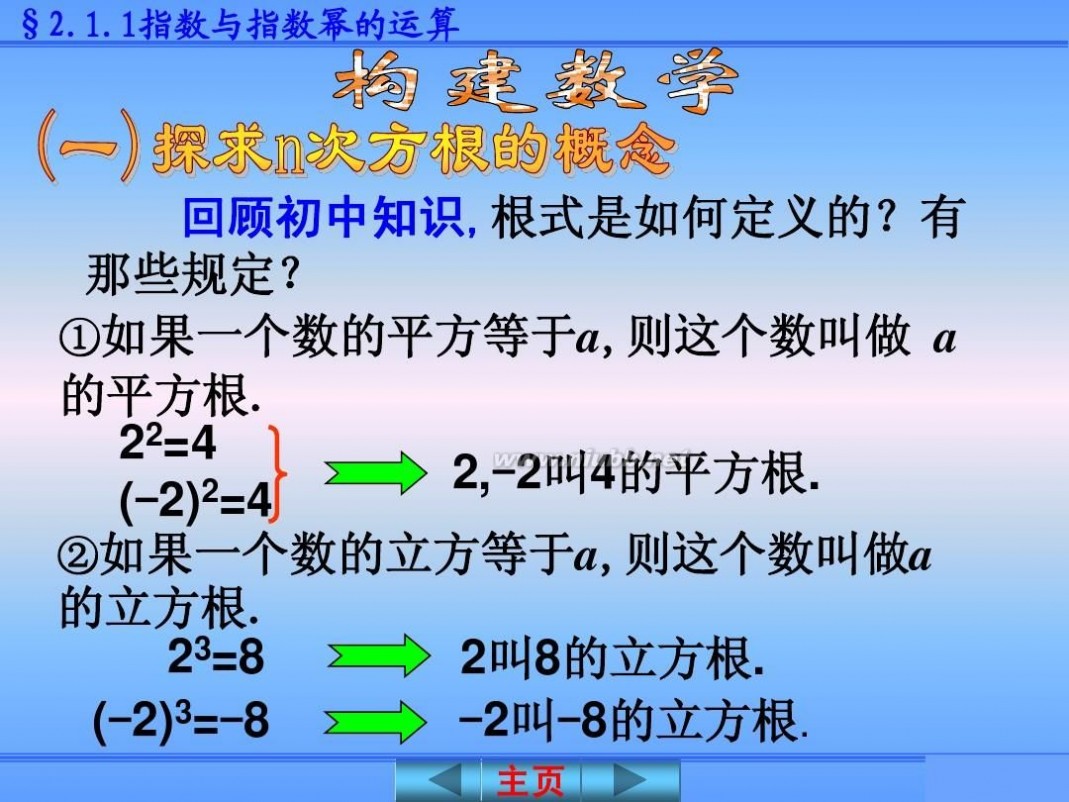
回顾初中知识,根式是如何定义的？有 那些规定？ ①如果一个数的平方等于a,则这个数叫做 a 的平方根. 22=4 2,-2叫4的平方根. 2=4 (-2) ②如果一个数的立方等于a,则这个数叫做a 的立方根. 23=8 2叫8的立方根. (-2)3=-8 -2叫-8的立方根.
主页

§2.1.1指数与指数幂的运算

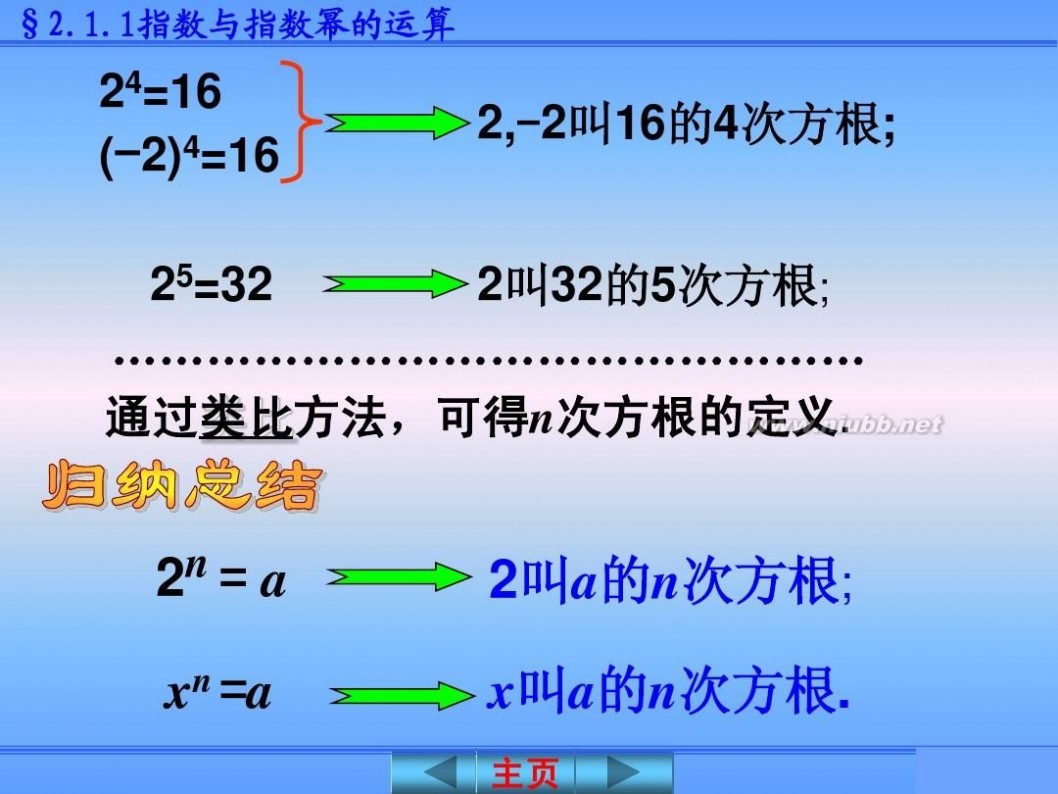
24=16 (-2)4=16 25=32

2,-2叫16的4次方根;

2叫32的5次方根;

………………………………………… 通过类比方法，可得n次方根的定义.

2n = a
xn =a

2叫a的n次方根; x叫a的n次方根.
主页

§2.1.1指数与指数幂的运算

1.方根的定义 如果xn=a,那么x叫做 a 的n次方根(n th root), 其中n>1,且n∈N*. 即 如果一个数的n次方等于a (n>1，且 n∈N*)，那么这个数叫做 a 的n次方根.

24=16 (-2)4=16
(-2)5=-32

16的4次方根是±2.
-32的5次方根是-2.

27=128

2是128的7次方根.
主页

§2.1.1指数与指数幂的运算

【1】试根据n次方根的定义分别求出下 列各数的n次方根. ±5 (1)25的平方根是_______; 3 (2)27的三次方根是_____; (3)-32的五次方根是____; -2 (4)16的四次方根是_____; ±2 6的三次方根是_____; a2 (5)a 0 (6)0的七次方根是______. 点评:求一个数a的n次方根就是求出哪个数的n 次方等于a.
主页

§2.1.1指数与指数幂的运算

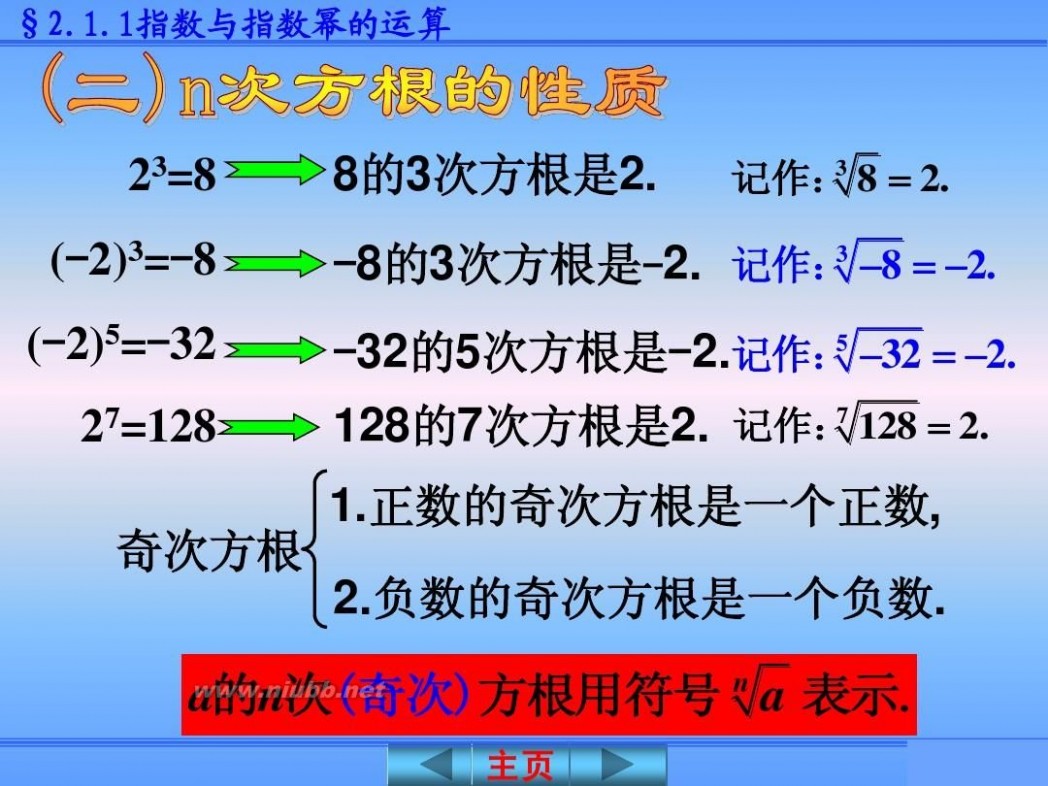
23=8 (-2)3=-8 (-2)5=-32

8的3次方根是2.

3 记作： 8 ? 2.

3 -8的3次方根是-2. 记作： ?8 ? ?2. 5 -32的5次方根是-2.记作： ?32 ? ?2.
7 128的7次方根是2. 记作： 128 ? 2.

27=128
奇次方根

1.正数的奇次方根是一个正数, 2.负数的奇次方根是一个负数.

a的n次(奇次)方根用符号 a 表示.
n

主页

§2.1.1指数与指数幂的运算

72=49 (-7)2=49 34=81 (-3)4=81 26=64 (-2)6=64 偶次方根

49的2次方根是7，-7.
记作： ? 49 ? ?7

81的4次方根是3，-3.

记作： ? 81 ? ?3
4

64的6次方根是2，-2.
6

记作： ? 64 ? ?2.

1.正数的偶次方根有两个且互为相反数 2.负数的偶次方根没有意义
正数a的n次方根用符号 ? n a 表示(n为偶数）
主页

§2.1.1指数与指数幂的运算

(1) 奇次方根有以下性质： 正数的奇次方根是正数. 负数的奇次方根是负数. 零的奇次方根是零. (2)偶次方根有以下性质： 正数的偶次方根有两个且是相反数， 负数没有偶次方根， 零的偶次方根是零.
如果x n ? a, 那么
? n a , n ? 2k ? 1, k ? N? , ? x?? ? n a , a ? 0, n ? 2k , k ? N? . ? ?
主页

§2.1.1指数与指数幂的运算

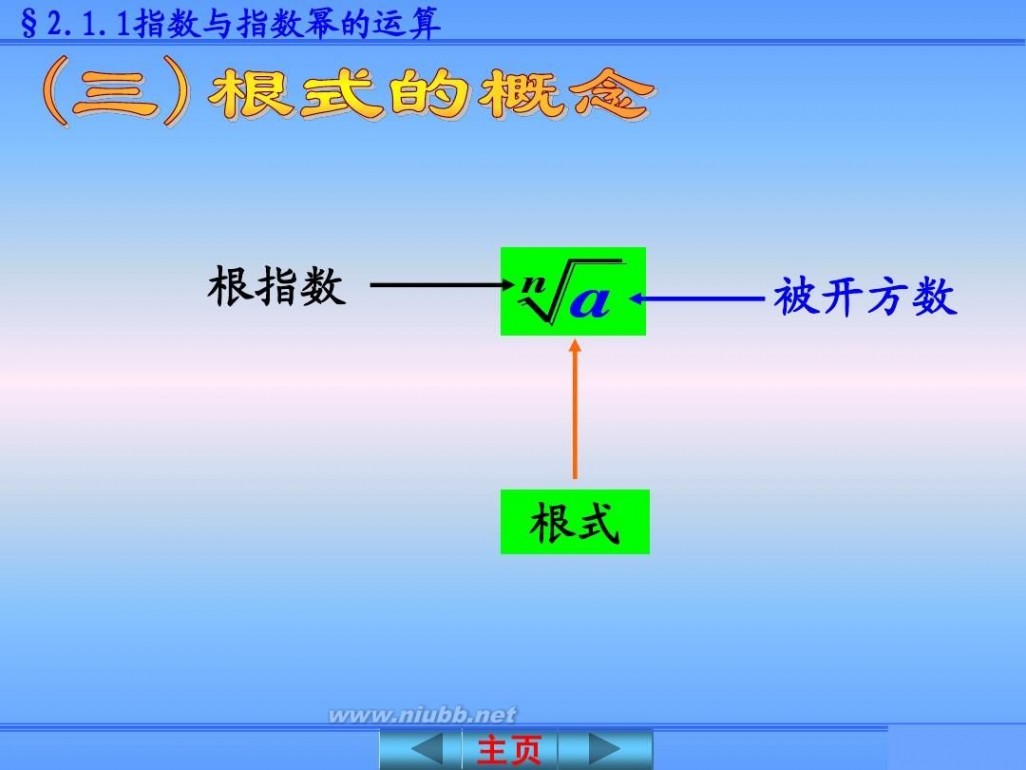
根指数

n

a

被开方数

根式

主页

§2.1.1指数与指数幂的运算

-8 9 ( 9) ? ____, ( ?8) ? ____.
2 3 3

由xn = a 可知，x叫做a的n次方根.

(n a) n ? a
当n是奇数时, n a 对任意a?R都有意义.它表 示a在实数范围内唯一的一个n次方根. 当n是偶数时, n a 只有当a≥0有意义,当a<0时 无

意义. n a (a ≥ 0)表示a在实数范围内的一个 n次方根,另一个是 ? n a (a ≥ 0)

(? a ) ? a
n n

主页

§2.1.1指数与指数幂的运算

(1)

5

2 ? 2,
5

3

（? 2） ? ?2.
3

结论:an开奇次方根,则有 n a n ? a.

(2) 32 ? 3, (?3)2 ? ?3, (?3)2 ? 3.

(3) 2 ? 2, (?2) ? ?2, （? 2） ? 2.
4 4 4 4 4 4

结论:an开偶次方根,则有

n

an ?| a | .

式子 n a n 对任意a ? R都有意义.
主页

§2.1.1指数与指数幂的运算

公式1.

——牛宝宝日记本——? a?
n

n

? a.

适用范围: ①当n为大于1的奇数时, a∈R.

②当n为大于1的偶数时, a≥0.
公式2.
n

a ? a.
n

适用范围:n为大于1的奇数, a∈R.

公式3.

n

a ?| a | .
n

适用范围:n为大于1的偶数, a∈R.
主页

§2.1.1指数与指数幂的运算

例1.求下列各式的值

（ 1） (?8) ;
3 3

(2)

(?10)2 ;

(3)

4

(3 ? ? )4 ;
3 3

(4)

(a ? b)2 (a ? b).

解 ： ?1?

?? 8? = -8; 2 ?2? ?? 10? ?| ?10 | =10; 4 4 ?3? ?3 ? ? ? ?| 3 ? ? | ? ? ? 3; 2 ?| a ? b | ? a ? b a ? b . ? ? ?4? ?a ? b?
主页

§2.1.1指数与指数幂的运算

【1】下列各式中, 不正确的序号是( ①

④ ).

①
③
5 5

4 5

16 ? ?2
5
5

② ( ?3) ? ?3
( ?3) ? ?3
10

④ ( ?3) ? ?3
⑤
4

( ?3) ? 3
4

主页

§2.1.1指数与指数幂的运算

【2】求下列各式的值.

⑴ ?32;
5

⑵ （? 3）;
4

⑶ （ 2 ? 3）;
2

⑷ 5? 2 6.
5

解: ⑴ 5 ?32 ?
4

5

(?2) ? ?2;
2 2 2

⑵ （? 3 ? [ ? 3) ] ? 9 ? 9; ） (
(3) （ 2 ? 3 ?| 2 ? 3 |? 3 ? 2; ）
2

(4) 5 ? 2 6 ? （ 2 ? 3 ? 3 ? 2. ）
2

主页

§2.1.1指数与指数幂的运算

例2.填空: (1)在 6 ( ?2)2 n , 5 a 4 , 3 ? a 4 , 4 ( ?3)2 n?1

( ?3) 这四个式子中,没有意义的是________.
4 2 n?1

(2) 若 9a ? 6a ? 1 ? 3a ? 1, 则a 的 a≥ 1 取值范围是______. 3
2

(3)已知a, b, c为三角形的三边,则

2b ? 2c （a ? b ? c) ? b ? a ? c ? ________.
2

主页

§2.1.1指数与指数幂的运算

例3．计算

(e ? e ) ? 4 ? (e ? e ) ? 4.

?1 2

?1 2

解： (e ? e ?1 )2 ? 4 ? (e ? e ?1 )2 ? 4.

? e ? e ? 2e e ? 4 ? e ? e ? 2e e ? 4
2 2

?2

1 ?1

?2

1 ?1

? e ?e ?2 ? e ?e ?2
2 2

?2

?2

? (e ? e ) ? (e ? e )

?1 2

?1 2

?| e ? e | ? | e ? e | ?1 ?1 ? (e ? e ) ? (e ? e ) ? 2e.
主页

?1

?1

§2.1.1指数与指数幂的运算

例4.求使等式 ( x ? 2)( x ? 4) ? ( x ? 2) x ? 2
2

成立的x的范围. 解 : ? ( x ? 2)( x2 ? 4) ? ( x ? 2)2 ? x ? 2? ? x ? 2 x ? 2.

? x ? 2 x ? 2 ? ( x ? 2) x ? 2. ? x ? 2 ? 0, 则有 x ? 2 ? 0, 或 ? ?| x ? 2 |? x ? 2. ? x ? ?2, ? x ? ?2, 或 ? 即 x ? ?2, 或x ≥ 2. ? x ? 2 ≥ 0. 所以x的取值范围是 x ? ?2

, 或x ≥ 2.
主页

§2.1.1指数与指数幂的运算

1.根式定义 2.根式的性质
(1)当n为奇数时，正数的n次方根是一个正数, 负数的n次方根是一个负数,这时,a的n次方根用 符号 n a 表示.零的任何次方根都是零. (2)当n为偶数时,正数a的n次方根有两个, 合写 为 ? n a .负数没有偶次方根. 零的任何次方根 都是零.
主页

§2.1.1指数与指数幂的运算

3.三个公式 (1)

? a?
n

n

? a;

(2) n a n ? a;

(3) a ?| a | .
n n

4.若xn=a , x怎样用a表示？
?n a, n为奇数, ? ? ? n a , n为偶数, a ? 0, x?? a ? 0, ? 0, ?不存在, n为偶数, a ? 0. ?
主页

§2.1.1指数与指数幂的运算

例1.求值：

5? 2 6 ? 7? 4 3 ? 6? 4 2.

解：原式 ? ( 3 ? 2)2 ? (2 ? 3)2 ? (2 ? 2)2

?| 3 ? 2 | ? | 2 ? 3 | ? | 2 ? 2 |
? ( 3 ? 2 ) ? (2 ? 3 ) ? (2 ? 2 )

? 3 ? 2 ? 2? 3 ? 2? 2 ? 2 2.
主页

§2.1.1指数与指数幂的运算

例2．如果 ?2 x ? 5 x ? 2 ? 0, 化简代 数式 4 x 2 ? 4 x ? 1 ? 2 | x ? 2 | . 解： ?2 x 2 ? 5 x ? 2 ? 0, ? 2 ? 2 x ? 5 x ? 2 ? 0, 解之，得 1 ? x ? 2. 2
2

所以
2

2 x ? 1 ? 0, x ? 2 ? 0.

? (2 x ? 1)2 ? 2 | x ? 2 | ? 4x ? 4x ? 1 ? 2 | x ? 2 |

?| 2 x ? 1 | ?2 | x ? 2 | ? (2 x ? 1) ? 2[?( x ? 2)] ? 2 x ? 1 ? 2 x ? 4 ? 3.
主页

§2.1.1指数与指数幂的运算

⑴若x表示实数，则下列说法正确的是（C ） A. x一定是根式 B. ? x一定不是根式 C . 5 x 6 一定是根式 D. 3 ? x只有当x ≥ 0才是根式

主页

五 : 指数与指数幂的运算

回顾初中知识,根式是如何定义的？有 那些规定？ ①如果一个数的平方等于a,则这个数叫做 a 的平方根. 22=4 2,-2叫4的平方根. 2 (-2) =4 ②如果一个数的立方等于a,则这个数叫做a 的立方根. 23=8 2叫8的立方根. (-2)3=-8 -2叫-8的立方根.

24=16 (-2)4=16 25=32

2,-2叫16的4次方根; 2叫32的5次方根;

………………………………………… 通过类比方法，可得n次方根的定义.

2n = a
xn =a

2叫a的n次方根; x叫a的n次方根.

1.方根的定义 如果xn=a,那么x叫做 a 的n次方根,其中n>1,且 n∈N*. 即 如果一个数的n次方等于a (n>1，且 n∈N*)，那么这个数叫做 a 的n次方根.

24=16 (-2)4=16
(-2)5=-32

16的4次方根是±2.
-32的5次方根是-2.

27=128

2是128的7次方根.

【1】试根据n次方根的定义分别求出下 列各数的n次方根. ±5 (1)25的平方根是_______; 3 (2)27的三次方根是_____; (3)-32的五次方根是____; -2 (4)16的四次方根是_____; ±2 2 6 a (5)a 的三次方根是_____; 0 (6)0的七次方根是______. 点评:求一个数a的n次方根就是求出哪个数的n 次方等于a.

23=8 (-2)3=-8 (-2)5=-32

8的3次方根是2.

3 记作： 8 ? 2.

3 ?8 ? ?2. -8的3次方根是-2. 记作： 5 -32的5次方根是-2.记作： ?32 ? ?2.
7 128 ? 2. 128的7次方根是2. 记作：

27=128
奇次方根

1.正数的奇次方根是一个正数, 2.负数的奇次方根是一个负数.

a的n次(奇次)方根用符号 a 表示.

n

72=49 (-7)2=49 34=81 (-3)4=81 26=64 (-2)6=64 偶次方根

49的2次方根是7，-7.
记作： ? 49 ? ?7

81的4次方根是3，-3.

记作： ? 81 ? ?3
4

64的6次方根是2，-2.
6

记作： ? 64 ? ?2.

1.正数的偶次方根有两个且互为相反数 2.负数的偶次方根没有意义

正数a的n次方根用符号 ? n a 表示(n为偶数）

(1) 奇次方根有以下性质： 正数的奇次方根是正数. 负数的奇次方根是负数. 零的奇次方根是零. (2)偶次方根有以下性质： 正数的偶次方根有两个且是相反数， 负数没有偶次方根， 零的偶次方根是零.
如果x n ? a, 那么
? n ? ? a , n ? 2k ? 1, k ? N , x?? ? n ? a , a ? 0, n ? 2 k , k ? N . ? ?

根指数

n

a

被开方数

根式

-8 9 ( ?8) ? ____. ( 9) ? ____,
2 3 3

由xn = a 可知，x叫做a的n次方根.

(n a) n ? a
当n是奇数时, n a 对任意a?R都有意义.它表 示a在实数范围内唯一的一个n次方根. 当n是偶数时, n a 只有当a≥0有意义,当a<0时 无意义. n a (a ≥ 0)表示a在实数范围内的一个 n次方根,另一个是 ? n a (a ≥ 0)

(? a ) ? a
n n

(1)

5

2 ? 2,
5

3

（? 2） ? ?2.
3

结论:an开奇次方根,则有 n a n ? a.

(2) 32 ? 3, (?3)2 ? ?3, (?3)2 ? 3.

(3) 2 ? 2, (?2) ? ?2, （? 2） ? 2.
4 4 4 4 4 4

结论:an开偶次方根,则有

n

an ?| a | .

式子 n a n 对任意a ? R都

有意义.

公式1.

? a?
n

n

? a.

适用范围: ①当n为大于1的奇数时, a∈R.

②当n为大于1的偶数时, a≥0.
公式2.
n

a ? a.
n

适用范围:n为大于1的奇数, a∈R.

公式3.

n

a ?| a | .
n

适用范围:n为大于1的偶数, a∈R.

例1.求下列各式的值

（ 1） (?8) ;
3 3

(2)

(?10)2 ;

(3)

4

(3 ? ? )4 ;
3 3

(4)

(a ? b)2 (a ? b).

解 ： ?1?

?? 8? = -8; 2 ?2? ?? 10? ?| ?10 | =10; 4 4 ?3? ?3 ? ? ? ?| 3 ? ? | ? ? ? 3; 2 ?| a ? b | ? a ? b a ? b . ? ? ?4? ?a ? b?

【1】下列各式中, 不正确的序号是( ①

④ ).

①
③
5 5

4 5

16 ? ?2
5
5

② ( ?3) ? ?3
( ?3) ? ?3
10

④ ( ?3) ? ?3
⑤
4

( ?3) ? 3
4

【2】求下列各式的值.

⑴ ?32;
5

⑵ （? 3）;
4

⑶ （ 2 ? 3）;
2

⑷ 5? 2 6.
5

解: ⑴ 5 ?32 ?
4

5

(?2) ? ?2;
2 2 2

⑵ （? 3 ）? [ (? 3) ] ? 9 ? 9;
(3) （ 2 ? 3 ） ?| 2 ? 3 |? 3 ? 2;
2

(4) 5 ? 2 6 ? （ 2 ? 3 ） ? 3 ? 2.
2

例2.填空: (1)在 6 ( ?2)2 n , 5 a 4 , 3 ? a 4 , 4 ( ?3)2 n?1

( ?3) 这四个式子中,没有意义的是________.
4

2 n ?1

(2) 若 9a ? 6a ? 1 ? 3a ? 1, 则a 的 1 a ≥ 取值范围是______. 3
2

(3)已知a, b, c为三角形的三边,则

2b ? 2c （a ? b ? c) ? b ? a ? c ? ________.
2

例3．计算

(e ? e ) ? 4 ? (e ? e ) ? 4.

?1 2

?1 2

解： (e ? e ?1 )2 ? 4 ? (e ? e ?1 )2 ? 4.

? e ? e ? 2e e ? 4 ? e ? e ? 2e e ? 4
2 2

?2

1 ?1

?2

1 ?1

? e ?e ?2 ? e ?e ?2
2 2

?2

?2

? (e ? e ) ? (e ? e )

?1 2

?1 2

?| e ? e | ? | e ? e | ?1 ?1 ? (e ? e ) ? (e ? e ) ? 2e.

?1

?1

例4.求使等式 ( x ? 2)( x ? 4) ? ( x ? 2) x ? 2
2

成立的x的范围. 解: ( x ? 2)( x2 ? 4) ? ( x ? 2)2 ? x ? 2? ? x ? 2 x ? 2.

? x ? 2 x ? 2 ? ( x ? 2) x ? 2. ? x ? 2 ? 0, 则有 x ? 2 ? 0, 或 ? ?| x ? 2 |? x ? 2. ? x ? ?2, ? x ? ?2, 或 ? 即 x ? ?2, 或x ≥ 2. ? x ? 2 ≥ 0. 所以x的取值范围是 x ? ?2, 或x ≥ 2.

1.根式定义 2.根式的性质
(1)当n为奇数时，正数的n次方根是一个正数, 负数的n次方根是一个负数,这时,a的n次方根用 符号 n a 表示.零的任何次方根都是零. (2)当n为偶数时,正数a的n次方根有两个, 合写 为 ? n a .负数没有偶次方根. 零的任何次方根 都是零.

3.三个公式 (1)

? a?
n

n

? a;

(2) n a n ? a;

(3) a ?| a | .
n n

4.若xn=a , x怎样用a表示？
?n a, n为奇数, ? ? ? n a , n为偶数, a ? 0, x?? a ? 0, ? 0, ?不存在, n为偶数, a ? 0. ?

例1.求值：

5? 2 6 ? 7? 4 3 ? 6? 4 2.

解：原式 ? ( 3 ? 2)2 ? (2 ? 3)2 ? (2 ? 2)2

?| 3 ? 2 | ? | 2 ? 3 | ? | 2 ? 2 |
? ( 3 ?

2 ) ? (2 ? 3 ) ? (2 ? 2 )

? 3 ? 2 ? 2? 3 ? 2? 2 ? 2 2.

例2．如果 ?2 x ? 5 x ? 2 ? 0, 化简代 数式 4 x 2 ? 4 x ? 1 ? 2 | x ? 2 | . 解： ?2 x 2 ? 5 x ? 2 ? 0, 2 ? 2 x ? 5 x ? 2 ? 0, 解之，得 1 ? x ? 2. 2
2

所以
2

2 x ? 1 ? 0, x ? 2 ? 0.

2 ? (2 x ? 1) ? 2| x?2| ? 4x ? 4x ? 1 ? 2 | x ? 2 |

?| 2 x ? 1 | ?2 | x ? 2 | ? (2 x ? 1) ? 2[?( x ? 2)] ? 2 x ? 1 ? 2 x ? 4 ? 3.

⑴若x表示实数，则下列说法正确的是（C ） A. x一定是根式 B. ? x一定不是根式 C . 5 x 6 一定是根式 D. 3 ? x只有当x ≥ 0才是根式

二.分数指数幂
(1) a ? a
5 10
10 5

(2) a ? a
4 16
2

16 4

解:

当根式的被开 16 方数的指数能 (2) 4 a16 ? 4 ( a 4 ) 4 ? a 4? a 4 被根指数整除 时,根式可以写 成分数指数幂 思考:当根式的被开方数的指数不能被根指数 的形式 整除时,根式是否可以写成分数指数幂的形式?

(1) a ? (a ) ? a ? a
5 10 5 2 5

10 5

如果幂的运算性质(2)(am)n=amn对于分数指数 2 2 ?3 2 幂也适用,则 3 3 3 （a ） ? a ?a
说明a 是a 2的3次方根， 2 3 2 而3 a2 也是a2的3次方根，于是有 a 3 ? a
2 3

1、分数指数幂的定义:
a
m n

?

n

a

m

（a>0,m,n ? N 且n>1）

?

注意:在分数指数幂里,根指数作分母,幂指数作分子. 规定:正数的负分数指数幂:
a
? m n

?

1 a
m n

（a>0,m,n ? N ?且n>1）

同时: 0的正分数指数幂等于0；

0的负分数指数幂没有意义

3.分数指数幂与整数指数幂的区别与联系
分数指数幂a ? a > 0, m, n∈ N*, n>1 ? 和整数指数幂an都是有理数 指数幂，都可以利用有理数指数幂的运算性质进行计算.但整 数指数幂表示的是相同因式的连乘积，而分数指数幂a 不可理
m m 解为 个a相乘，它是根式的另一种写法，规定：an = n am n m 1 1 m, n∈ N*, n>1 an= m = m, n∈ N*, 且n>1 在这样 ? a > 0, ?, ? a > 0, ?, n m a an 的规定下，根式与分数指数幂表示相同意义的量，它们只是形式 m n m n

不同而已.

3.分数指数幂与整数指数幂的区别与联系
(1)负数的负分数指数幂是否有意义， 应视m，n的具体数值而定. （2）对于根式运算，（简单问题可根 据根式的意义直接计算）一般可将根 式化为分数指数幂，利用分数指数幂 的运算性质进行计算.

2、有理指数幂的运算性质:
(1)a ? a ? a
r s r ?s

(a ? 0, r、s ? Q)同底数幂相乘,底数不变指数相加
幂的乘方底数不变,指数相乘 积的乘方等于乘方的积

(2)(a r )s =a r?s (a ? 0, r、s ? Q) (3)(a ? b)r =a rbr (a ? 0, r、s ? Q)

三、无理数指数幂

一般地，无理数指数幂 a? ( 无理数)是一个确定的实数.

? >0,? 是

有理数指数幂的运算性质同样适用于无理数指数幂.

a a ?a
? ?

?

?

本文标题：指数与指数幂的运算-指数与指数幂的运算练习题
本文地址： http://www.61k.com/1119325.html