一 : 哥尼斯堡七桥问题一笔画在C岸和D岸之间,有A岛和B岛。A岛用一座
哥尼斯堡七桥问题一笔画
在岸和D岸之间,有A岛和B岛。A岛用一座桥连着B岛,用两座桥连着C岛,用两座桥连着D岛。B岸用两座桥分别连着C岛和D岛。怎样才能不重复的走完每座桥?
图论问题.欧拉在1736年就已经证明,不可能不重复地一次走完七座桥!
二 : 格尼斯堡七桥问题:一笔画的条件_OpenV

七桥问题
在离普莱格尔河流入波罗的海海口不远的地方,有一座古老的城市——哥尼斯堡。哥尼斯堡是条顿骑士团在1308年建立的,四百年中为日耳曼势力最前端的哨所,曾为东普鲁士的首府。二战后更名为加里宁格勒,成为前苏联的海军基地,现位于立陶宛与波兰之间,属俄罗斯。
在哥尼斯堡城中,普莱格尔河横贯城中,有2个支流,一条称新河,一条叫旧河,在城市中心汇成大河,中间是岛区,一座叫内福夫岛,是城中最繁华的商业中心,由于普莱格尔河拔全城分为4个地区:岛区、北区、东区和南区,河上有7座桥,将河中的2个岛和河岸连结。
由于岛上有古老的哥尼斯堡大学,有教堂,还有康德的墓地和塑像,因此城中的居民,尤其是大学生们经常沿河过桥散步。渐渐地,爱动脑筋的人们提出了1个问题:1个散步者能否一次走遍7座桥,而且每座桥只许通过一次,最后仍回到起始地点。这就是有名的七桥问题。
欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡居民提出的问题,而且得到并证明了更为广泛的有关一笔画的三条结论,人们通常称之为“欧拉定理F”。
这个问题看起来似乎很简单,然而许多人作过尝试始终没有能找到答案。因此,在1735年,一群大学生就写信给当时年仅二十岁的大数学家欧拉。欧拉正在俄国彼得堡科学院任职,他通过一年的研究,于17(www.61k.com]36年向彼得堡科学院地交了一篇题为《哥尼斯堡七座桥》的论文,圆满地解决了这一问题。他提出的思想导致了一门的新的数学分支——图论的诞生。
欧拉是这样解决问题的:既然陆地是桥梁的连接地点,不妨把图中被河隔开的陆地看成四个点,7座桥表示成7条连接这四个点的线,如图所示。于是“七桥问题”就等价于下图中所画图形的一笔画问题了。
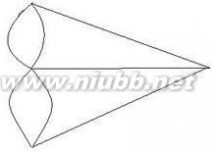
欧拉注意到,如果1个图能一笔画成,首先,它必须是连在一起的,也就是说,图中的任何2个点都由图中的线连接,我们称之为连通的。
其次,如果1个图能一笔画成,那么一定有1个起点开始画,也有1个终点。图上其它的点是“过路点”——画之际要经过它。
现在看“过路点”具有什么性质。它应该是“有进有出”的点,有一条边进这点,那么就要有一条边出这点,不可能是有进无出,如果有进无出,它就是终点,也不可能有出无进,如果有出无进,它就是起点。因此,在“过路点”进出的边总数应该是偶数。
因此一笔画问题与经过点的线的条数有关系,为方便起见,若与一点相连的线的条数为偶数,则称此点为偶点。
由上可知,“过路点”是偶点。同理,如果起点和终点是同一点,那么它也是属于“有进有出”的点,因此必须是偶点,这样图上全体点都是偶点。如果起点和终点不是同一点,那么它们必须是奇点,因此这个图最多只能有二个奇点。
最后我们可以确定,图能一笔画的2个条件:
1、图是连通的,
2、图中的奇点数为0或2。
事实上,中国民间很早就流传着这种一笔画的游戏,从长期实践的经验,人们知道如果图的点全部是偶点,可以任意选择1个点做起点,一笔画成。如果是有二个奇点的图形,那么就选1个奇点做起点以顺利的一笔画完。
现在对照七桥问题的图,所有的顶点都是奇点,共有4个,所以这个图肯定不能一笔画成。导游们仍向游客讲述七桥的故事,甚至有些导游声称问题仍未解决,以留给游客去遐想。
顺便说一句,新乡回龙景区通过几家网站发布了一则消息,题目为“新乡回龙景区新建‘谜桥’,百万奖金等‘破谜’”。意思是说,如果谁可以从其中任何一座桥出发,走遍七座桥且不重复又回到出发点,就有机会获得100万元的现金大奖。很快这条消息成了国内几家网站三新闻。,一位不愿透漏姓名的高中数学老师给记者打了电话,指出:“谜桥问题是著名的数学问题,根本无解,景区用悬赏100万元吸引游客,这是在忽悠人。”

三 : 哥尼斯堡七桥问题,聪明人才敢玩的游戏
哥尼斯堡七桥问题是18世纪著名古典数学问题之一,简称七桥问题,它是一个著名的图论问题,同时也是拓扑学研究的一个例子。[www.61k.com]说了这么多专业名词小T自己都快懵了,这其实就是个一笔画游戏,有兴趣的来挑战吧!
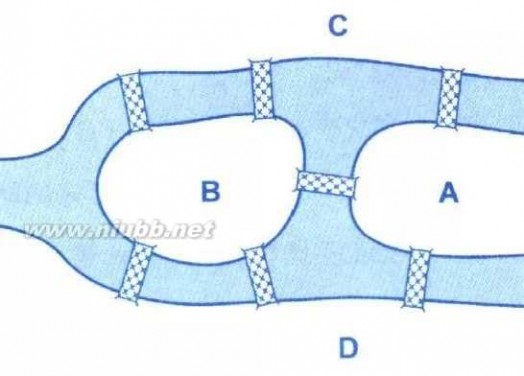
哥尼斯堡城(今俄罗斯加里宁格勒)是东普鲁士的首都,著名的普莱格尔河横贯其中。
十八世纪在这条河上建有七座桥,这七座桥将河中间的两个岛(上图中的A、B)与河岸连接起来。其中岛与河岸之间架有六座,另一座则连接着两个岛。
当时,居民们有一项普遍喜爱的消遣是在一次行走中跨过全部七座桥而不许重复经过任何一座,但是好像谁也没有成功。
那么问题来了:能否一次走遍七座桥,而每座桥只许通过一次?
关于答案:搜狐新闻客户端请点击底部“查看原文”获取,电脑端请在微信中搜索关注推理世界(微信号 tuiliworld)后获取,更多推理题、智力题、趣味题等着你!
61阅读提醒您本文地址:
四 : 格尼斯堡七桥问题的详细解法?

格尼斯堡七桥问题的详细解法?
18世纪,东普鲁士的首府哥尼斯堡是一座景色迷人的城市,普莱格尔河横贯城区,使这
座城市锦上添花,显得更加风光旖旋.这条河有两条支流,在城中心汇成大河,在河的
中央有一座美丽的小岛.河上有七座各具特色的桥把岛和河岸连接起来.
每到傍晚,许多人都来此散步.人们漫步于这七座桥之间,久而久之,就形成了这样一
个问题:能不能既不重复又不遗漏地一次相继走遍这七座桥?这就是闻名遐迩的“哥尼
斯堡七桥问题.”每一个到此游玩或散心的人都想试一试,可是,对于这一看似简单的
问题,没有一个人能符合要求地从七座桥上走一遍.这个问题后来竟变得神乎其神,说
是有一支队伍,奉命要炸毁这七座桥,并且命令要他们按照七桥问题的要求去炸.
七桥问题也困扰着哥尼斯堡大学的学生们,在屡遭失败之后,他们给当时著名数学家欧
拉写了一封信,请他帮助解决这个问题.
欧拉看完信后,对这个问题也产生了浓厚的兴趣.他想,既然岛和半岛是桥梁的连接地
点,两岸陆地也是桥梁的连接地点,那就不妨把这四处地方缩小成四个点,并且把这七
座桥表示成七条线.这样,原来的七桥问题就抽象概括成了如下的关系图:
这显然并没有改变问题的本质特征.于是,七桥问题也就变成了一个一笔画的问题,即
:能否笔不离纸,不重复地一笔画完整个图形.这竟然与孩子们的一笔画游戏联系起来
了.接着,欧拉就对“一笔画”问题进行了数学分析一笔画有起点和终点,起点和终点
重合的图形称为封闭图形,否则便称为开放图形.除起点和终点外,一笔画中间可能出
现一些曲线的交点.欧拉注意到,只有当笔沿着一条弧线到达交点后,又能沿着另一条
弧线离开,也就是交汇于这些点的弧线成双成对时,一笔画才能完成,这样的交点就称
为“偶点”.如果交汇于这些点的弧线不是成双成对,也就是有奇数条,则一笔画就不
能实现,这样的点又叫做“奇点”.见下图:
欧拉通过分析,得到了下面的结论:若是一个一笔画图形,要么只有两个奇点,也就是
仅有起点和终点,这样一笔画成的图形是开放的;要么没有奇点,也就是终点和起点连
接起来,这样一笔画成的图形是封闭的.由于七桥问题有四个奇点,所以要找到一条经
过七座桥,但每座桥只走一次的路线是不可能的.
有名的“哥尼斯堡七桥问题”就这样被欧拉解决了.
在这里,我们可以看到欧拉解决这个问题的关键就是把“七桥问题”变成了一个“一笔
画”问题,那么,欧拉又是怎样完成这一转变的呢?
他把岛、半岛和陆地的具体属性舍去,而仅仅留下与问题有关的东西,这就是四个几何
上的“点”;他再把桥的具体属性排除,仅留下一条几何上的“线”,然后,把“点”
与“线”结合起来,这样就实现了从客观事物到图形的转变.我们把得到“点”和“线
”的思维方法叫做抽象,把由“点”和“线”结合成图形的思维方法叫做概括.所谓抽
象就是从客观事物中排除非本质属性,透过现象抽出本质属性的思维方法.概括就是将
个别事物的本质属性结合起来的思维方法.
Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时,他发现当地的市民正从事一项非常有趣的消遣活动.Konigsberg城中有一条名叫Pregel的河流横经其中,在河上建有七座桥如图所示: 这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步,每座桥只能经过一次而且起点与终点必须是同一地点.
Euler把每一块陆地考虑成一个点,连接两块陆地的桥以线表示,便得如下的图后来推论出此种走法是不可能的.他的论点是这样的,除了起点以外,每一次当一个人由一座桥进入一块陆地(或点)时,他(或她)同时也由另一座桥离开此点.所以每行经一点时,计算两座桥(或线),从起点离开的线与最后回到始点的线亦计算两座桥,因此每一个陆地与其他陆地连接的桥数必为偶数.
七桥所成之图形中,没有一点含有偶数条数,因此上述的任务是不可能实现的.
 本文标题:哥尼斯堡七桥问题-哥尼斯堡七桥问题一笔画在C岸和D岸之间,有A岛和B岛。A岛用一座
本文标题:哥尼斯堡七桥问题-哥尼斯堡七桥问题一笔画在C岸和D岸之间,有A岛和B岛。A岛用一座 61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1