一 : 求下列函数的值域(1)y=√(-x^2-6x-5)(2)y=(2?
值域
求下列的值域
(1)y=√(-x^2-6x-5)
(2)y=(2x-5)/(x-3)(5/2≤x≤7/2,且x≠3)
1)
-x^2-6x-5>=0;
x^2 + 6x + 5<=0;
-5<=x<=-1;
-x^2-6x-5 = -(x^2+6x) -5
=-(x+3)^2 +9 -5
=-(x+3)^2+ 4
值域:[0,2];
2)
y=(2x-5)/(x-3)
=2 + 1/(x-3);
5/2≤x≤7/2,且x≠3;
5/2<=x<3;
-1/2<=x-3<0;
-2>=1/(x-3);
y = 2+ 1/(x-3)<=0;
3 0 1/(x-3)>=2, y = 2+1/(x-3)>=4; 值域 y<=0, y>=4。 二 : 函数y=2^4x-x^2的值域是?忘记怎么求了,麻烦讲解下,谢谢 函数y=2^4x-x^2的值域是?忘记怎么求了,麻烦讲解下,谢谢 函数y=2^4x-x^2的值域是? 是y=2^(4x-x^2)吗?! y=2^(4x-x^2)的定义域为x∈R 令f(x)=4x-x^2=-x^2+4x=-(x^2-4x+4)+4=-(x-2)^2+4 则,对于x∈R,f(x)∈(-∞,4] 所以,y=2^[f(x)] 而,y=2^[f(x)]在R上是单调增函数 所以,y∈(0,2^4]=(0,16] 三 : y=x+1/x(对勾函数)的值域如何来求? y=x+1/x(对勾函数)的值域如何来求? y=x+1/x(对勾函数)的值域如何来求? 解:x>0时 x×(1/x)=1=定值 y=x+1/x≥2 x<0时 -x>0 -1/x>0 -y=-x-1/x≥2 y≤-2 ∴y≤-2 or y≥2 四 : 高中数学函数值域的12种求法 高中数学函数值域的12种求法 2015-02-02高考志愿专家升学网 一.观察法 通过对函数定义域、性质的观察,结合函数的解析式,求得函数的值域。[www.61k.com) 例1求函数y=3+√(2-3x) 的值域。 点拨:根据算术平方根的性质,先求出√(2-3x) 的值域。 解:由算术平方根的性质,知√(2-3x)≥0, 故3+√(2-3x)≥3。 ∴函数的值域为{y∣y≥3}. 点评:算术平方根具有双重非负性,即:(1)被开方数的非负性,(2)值的非负性。 本题通过直接观察算术平方根的性质而获解,这种方法对于一类函数的值域的求法,简捷明了,不失为一种巧法。 练习:求函数y=[x](0≤x≤5)的值域。(答案:值域为:{0,1,2,3,4,5}) 二.反函数法 当函数的反函数存在时,则其反函数的定义域就是原函数的值域。 例2求函数y=(x+1)/(x+2)的值域。 点拨:先求出原函数的反函数,再求出其定义域。 解:显然函数y=(x+1)/(x+2)的反函数为:x=(1-2y)/(y-1),其定义域为y≠1的实数,故函数y的值域为{y∣y≠1,y∈R}。 点评:利用反函数法求原函数的定义域的前提条件是原函数存在反函数。这种方法体现逆向思维的思想,是数学解题的重要方法之一。 练习:求函数y=(10x+10-x)/(10x-10-x)的值域。(答案:函数的值域为{y∣y<-1或y>1}) 三.配方法 当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域 例3:求函数y=√(-x2+x+2)的值域。 点拨:将被开方数配方成完全平方数,利用二次函数的最值求。 解:由-x2+x+2≥0,可知函数的定义域为x∈[-1,2]。此时-x2+x+2=-(x-1/2)2+9/4∈[0,9/4] ∴0≤√-x2+x+2≤3/2,函数的值域是[0,3/2] 点评:求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。配方法是数学的一种重要的思想方法。 练习:求函数y=2x-5+√15-4x的值域.(答案:值域为{y∣y≤3}) 四.判别式法 若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。 例4求函数y=(2x2-2x+3)/(x2-x+1)的值域。 点拨:将原函数转化为自变量的二次方程,应用二次方程根的判别式,从而确定出原函数的值域。 解:将上式化为(y-2)x2-(y-2)x+(y-3)=0 (*) 当y≠2时,由Δ=(y-2)2-4(y-2)x+(y-3)≥0,解得:2 当y=2时,方程(*)无解。∴函数的值域为2 点评:把函数关系化为二次方程F(x,y)=0,由于方程有实数解,故其判别式为非负数,可求得函数的值域。常适应于形如y=(ax2+bx+c)/(dx2+ex+f)及y=ax+b±√(cx2+dx+e)的函数。 练习:求函数y=1/(2x2-3x+1)的值域。(答案:值域为y≤-8或y>0)。 五.最值法 对于闭区间[a,b]上的连续函数y=f(x),可求出y=f(x)在区间[a,b]内的极值,并与边界值f(a).f(b)作比较,求出函数的最值,可得到函数y的值域。 例5已知(2x2-x-3)/(3x2+x+1)≤0,且满足x+y=1,求函数z=xy+3x的值域。 点拨:根据已知条件求出自变量x的取值范围,将目标函数消元、配方,可求出函数的值域。 解:∵3x2+x+1>0,上述分式不等式与不等式2x2-x-3≤0同解,解之得-1≤x≤3/2,又x+y=1,将y=1-x代入z=xy+3x中,得z=-x2+4x(-1≤x≤3/2), ∴z=-(x-2)2+4且x∈[-1,3/2],函数z在区间[-1,3/2]上连续,故只需比较边界的大小。 当x=-1时,z=-5;当x=3/2时,z=15/4。 ∴函数z的值域为{z∣-5≤z≤15/4}。 点评:本题是将函数的值域问题转化为函数的最值。对开区间,若存在最值,也可通过求出最值而获得函数的值域。 练习:若√x为实数,则函数y=x2+3x-5的值域为 () A.(-∞,+∞)B.[-7,+∞]C.[0,+∞)D.[-5,+∞) (答案:D)。 六.图象法 通过观察函数的图象,运用数形结合的方法得到函数的值域。 例6求函数y=∣x+1∣+√(x-2)2的值域。 点拨:根据绝对值的意义,去掉符号后转化为分段函数,作出其图象。 解:原函数化为 -2x+1(x≤1) y=3(-1<x≤2) 2x-1(x>2) 它的图象如图所示。 显然函数值y≥3,所以,函数值域[3,+∞]。 点评:分段函数应注意函数的端点。利用函数的图象 求函数的值域,体现数形结合的思想。是解决问题的重要方法。 求函数值域的方法较多,还适应通过不等式法、函数的单调性、换元法等方法求函数的值域。 七.单调法 利用函数在给定的区间上的单调递增或单调递减求值域。 例1求函数y=4x-√1-3x(x≤1/3)的值域。 点拨:由已知的函数是复合函数,即g(x)= -√1-3x,y=f(x)+g(x),其定义域为x≤1/3,在此区间内分别讨论函数的增减性,从而确定函数的值域。 解:设f(x)=4x,g(x)= -√1-3x ,(x≤1/3),易知它们在定义域内为增函数,从而y=f(x)+g(x)= 4x-√1-3x 在定义域为x≤1/3上也为增函数,而且y≤f(1/3)+g(1/3)=4/3,因此,所求的函数值域为{y|y≤4/3}。 点评:利用单调性求函数的值域,是在函数给定的区间上,或求出函数隐含的区间,结合函数的增减性,求出其函数在区间端点的函数值,进而可确定函数的值域。 练习:求函数y=3+√4-x的值域。(答案:{y|y≥3}) 八.换元法 以新变量代替函数式中的某些量,使函数转化为以新变量为自变量的函数形式,进而求出值域。 例2求函数y=x-3+√2x+1 的值域。 点拨:通过换元将原函数转化为某个变量的二次函数,利用二次函数的最值,确定原函数的值域。 解:设t=√2x+1 (t≥0),则 x=1/2(t2-1)。 于是y=1/2(t2-1)-3+t=1/2(t+1)2-4≥1/2-4=-7/2. 所以,原函数的值域为{y|y≥-7/2}。 点评:将无理函数或二次型的函数转化为二次函数,通过求出二次函数的最值,从而确定出原函数的值域。这种解题的方法体现换元、化归的思想方法。它的应用十分广泛。 练习:求函数y=√x-1 –x的值域。(答案:{y|y≤-3/4} 九.构造法 根据函数的结构特征,赋予几何图形,数形结合。 例3求函数y=√x2+4x+5+√x2-4x+8 的值域。 点拨:将原函数变形,构造平面图形,由几何知识,确定出函数的值域。 解:原函数变形为f(x)=√(x+2)2+1+√(2-x)2+22 作一个长为4、宽为3的矩形ABCD,再切割成12个单位 正方形。设HK=x,则ek=2-x,KF=2+x,AK=√(2-x)2+22 , KC=√(x+2)2+1 。 由三角形三边关系知,AK+KC≥AC=5。当A、K、C三点共 线时取等号。 ∴原函数的值域为{y|y≥5}。 点评:对于形如函数y=√x2+a ±√(c-x)2+b(a,b,c均为正数),均可通过构造几何图形,由几何的性质,直观明了、方便简捷。这是数形结合思想的体现。 练习:求函数y=√x2+9 +√(5-x)2+4的值域。(答案:{y|y≥5√2}) 十.比例法 对于一类含条件的函数的值域的求法,可将条件转化为比例式,代入目标函数,进而求出原函数的值域。 例4已知x,y∈R,且3x-4y-5=0,求函数z=x2+y2的值域。 点拨:将条件方程3x-4y-5=0转化为比例式,设置参数,代入原函数。 解:由3x-4y-5=0变形得,(x3)/4=(y-1)/3=k(k为参数) ∴x=3+4k,y=1+3k, ∴z=x2+y2=(3+4k)2+(14+3k)2=(5k+3)2+1。 当k=-3/5时,x=3/5,y=-4/5时,zmin=1。 函数的值域为{z|z≥1}. 点评:本题是多元函数关系,一般含有约束条件,将条件转化为比例式,通过设参数,可将原函数转化为单函数的形式,这种解题方法体现诸多思想方法,具有一定的创新意识。 练习:已知x,y∈R,且满足4x-y=0,求函数f(x,y)=2x2-y的值域。(答案:{f(x,y)|f(x,y)≥1}) 十一.利用多项式的除法 例5求函数y=(3x+2)/(x+1)的值域。 点拨:将原分式函数,利用长除法转化为一个整式与一个分式之和。 解:y=(3x+2)/(x+1)=3-1/(x+1)。 ∵1/(x+1)≠0,故y≠3。 ∴函数y的值域为y≠3的一切实数。 点评:对于形如y=(ax+b)/(cx+d)的形式的函数均可利用这种方法。 练习:求函数y=(x2-1)/(x-1)(x≠1)的值域。(答案:y≠2) 十二.不等式法 例6求函数Y=3x/(3x+1)的值域。 点拨:先求出原函数的反函数,根据自变量的取值范围,构造不等式。 解:易求得原函数的反函数为y=log3[x/(1-x)], 由对数函数的定义知x/(1-x)>0 1-x≠0 解得:0<x<1 ∴函数的值域(0,1)。 点评:考查函数自变量的取值范围构造不等式(组)或构造重要不等式,求出函数定义域,进而求值域。不等式法是重要的解题工具,它的应用非常广泛。是数学解题的方法之一。 以下供练习选用:求下列函数的值域 1.Y=√(15-4x)+2x-5;({y|y≤3}) 2.Y=2x/(2x-1)。(y>1或y<0) 注意变量哦 升学网-高考志愿填报平台 高考志愿学霸经验高考改革专业解读 (升学网微信公众号:sxwgaokao) ▼点下面“阅读原文”看更多高考内容...... 五 : 函数值域求法十五种

在函数的三要素中,定义域和值域起决定作用,而值域是由定义域和对应法则共同确定。研究函数的值域,不但要重视对应法则的作用,而且还要特别重视定义域对值域的制约作用。确定函数的值域是研究函数不可缺少的重要一环。对于如何求函数的值域,是学生感到头痛的问题,它所涉及到的知识面广,方法灵活多样,在高考中经常出现,占有一定的地位,若方法运用适当,就能起到简化运算过程,避繁就简,事半功倍的作用。本文就函数值域求法归纳如下,供参考。
基本知识
1.定义:因变量y的取值范围叫做函数的值域(或函数值的集合)。
2.函数值域常见的求解思路:
⑴ 划归为几类常见函数,利用这些函数的图象和性质求解。
⑵ 反解函数,将自变量x用函数y的代数式形式表示出来,利用定义域建立函数y的不等式,解不等式即可获解。
⑶ 可以从方程的角度理解函数的值域,从方程的角度讲,函数的值域即为使关于x的方程y=f(x)在定义域内有解的y得取值范围。
特别地,若函数可看成关于x的一元二次方程,则可通过一元二次方程在函数定义域内有解的条件,利用判别式求出函数的值域。
⑷ 可以用函数的单调性求值域。
⑸ 其他。
1. 直接观察法
对于一些比较简单的函数,通过对函数定义域、性质的观察,结合函数的解析式,求得函数的值域
例1. 求函数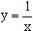 的值域。
的值域。
解:∵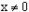 ∴
∴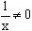
显然函数的值域是: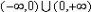
2. 配方法
配方法是求二次函数值域最基本的方法之一。
例2. 求函数 的值域。
的值域。
解:将函数配方得:
∵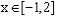
由二次函数的性质可知:当x=1时, ,当x=-1时,
,当x=-1时,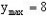
故函数的值域是:[4,8]
3. 判别式法
例3. 求函数 的值域。
的值域。
解:两边平方整理得: (1)
(1)
∵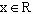 ∴
∴
解得: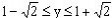
但此时的函数的定义域由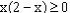 ,得
,得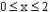
由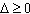 ,仅保证关于x的方程:
,仅保证关于x的方程: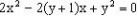 在实数集R有实根,而不能确保其实根在区间[0,2]上,即不能确保方程(1)有实根,由
在实数集R有实根,而不能确保其实根在区间[0,2]上,即不能确保方程(1)有实根,由 求出的范围可能比y的实际范围大,故不能确定此函数的值域为
求出的范围可能比y的实际范围大,故不能确定此函数的值域为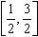 。
。
可以采取如下方法进一步确定原函数的值域。
∵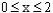 ∴
∴
∴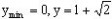 代入方程(1)
代入方程(1)
解得: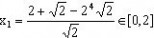 即当
即当 时,
时,
原函数的值域为:
注:由判别式法来判断函数的值域时,若原函数的定义域不是实数集时,应综合函数的定义域,将扩大的部分剔除。
4. 反函数法
直接求函数的值域困难时,可以通过求其原函数的定义域来确定原函数的值域。
例4. 求函数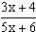 值域。
值域。
解:由原函数式可得: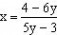
则其反函数为: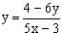 ,其定义域为:
,其定义域为: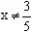
故所求函数的值域为: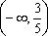
5. 函数有界性法
直接求函数的值域困难时,可以利用已学过函数的有界性,反客为主来确定函数的值域。
例5. 求函数 的值域。
的值域。
解:由原函数式可得: ,可化为:
,可化为: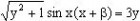 即
即
∵ ∴
∴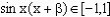
即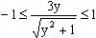 解得:
解得: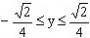
故函数的值域为
6. 函数单调性法
例6. 求函数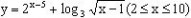 的值域。
的值域。
解:令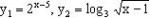 则
则 在[2,10]上都是增函数
在[2,10]上都是增函数
所以 在[2,10]上是增函数
在[2,10]上是增函数
当x=2时,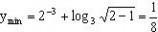
当x=10时,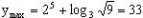
故所求函数的值域为: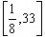
例7. 求函数 的值域。
的值域。
解:原函数可化为:
令 ,显然 在 上为无上界的增函数
所以 , 在 上也为无上界的增函数
所以当x=1时, 有最小值 ,原函数有最大值
显然y>0,故原函数的值域为
7. 换元法
通过简单的换元把一个函数变为简单函数,其题型特征是函数解析式含有根式或三角函数公式模型,换元法是数学方法中几种最主要方法之一,在求函数的值域中同样发挥作
例8. 求函数 的值域。
解:因
即
故可令
∴
∵
∴
∴
故所求函数的值域为
例9. 求函数 的值域。
解:原函数可变形为:
可令 ,则有
∴
当 时,
当 时,
而此时 有意义。
故所求函数的值域为
例10. 求函数 , 的值域。
解:
令 ,则
由 且
可得:
∴当 时, ,当 时,
故所求函数的值域为 。
例11. 求函数 的值域。
解:由 ,可得
故可令
∵ ∴
当 时,
当 时,
故所求函数的值域为:
8. 数形结合法
其题型是函数解析式具有明显的某种几何意义,如两点的距离公式直线斜率等等,这类题目若运用数形结合法,往往会更加简单,一目了然,赏心悦目。[要学习网,只做中学生最喜欢、最实用的学习论坛,地址 www.61k.com手机版地址 wap.yaoxuexi.cn]
例12. 求函数 的值域。
解:原函数可化简得:y=|x-2|+|x+8|
上式可以看成数轴上点P(x)到定点A(2),B(-8)间的距离之和。
由上图可知,当点P在线段AB上时,y=|x-2|+|x+8|=|AB|=10
当点P在线段AB的延长线或反向延长线上时,y=|x-2|+|x+8|>|AB|=10
故所求函数的值域为:
例13. 求函数 的值域。
解:原函数可变形为:
上式可看成x轴上的点P(x,0)到两定点A(3,2),B(-2,-1)的距离之和,
由图可知当点P为线段与x轴的交点时, ,
故所求函数的值域为
例14. 求函数 的值域。
解:将函数变形为:
上式可看成定点A(3,2)到点P(x,0)的距离与定点B(-2,1)到点P(x,0)的距离之差。
即:y=|AP|-|BP|
由图可知:(1)当点P在x轴上且不是直线AB与x轴的交点时,如点P',则构成△ABP',根据三角形两边之差小于第三边,有
即:
(2)当点P恰好为直线AB与x轴的交点时,有
综上所述,可知函数的值域为:
注:由例13,14可知,求两距离之和时,要将函数式变形,使A、B两点在x轴的两侧,而求两距离之差时,则要使A,B两点在x轴的同侧。
如:例13的A,B两点坐标分别为:(3,2),(-2,-1),在x轴的同侧;例14的A,B两点坐标分别为(3,2),(2,-1),在x轴的同侧。
9. 不等式法
利用基本不等式 ,求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时需要用到拆项、添项和两边平方等技巧。
例15. 求函数 的值域。
解:原函数变形为:
当且仅当tanx=cotx
即当 时,等号成立
故原函数的值域为:
例16. 求函数y=2sinxsin2x的值域。
解:y=4sinxsinxcosx
当且仅当 ,即当 时,等号成立。
由 可得:
故原函数的值域为:
10. 映射法
原理:因为 在定义域上x与y是一一对应的。故两个变量中,若知道一个变量范围,就可以求另一个变量范围。
例17. 求函数 的值域。
解:∵定义域为
由 得
故 或
解得
故函数的值域为
11.最值法
对于闭区间[a,b]上的连续函数y=f(x),可求出y=f(x)在区间[a,b]内的极值,并与边界值f(a).f(b)作比较,求出函数的最值,可得到函数y的值域。[要学习网,只做中学生最喜欢、最实用的学习论坛,地址 www.61k.com手机版地址 wap.yaoxuexi.cn]
例18.已知 ,且满足x+y=1,求函数z=xy+3x的值域。
点拨:根据已知条件求出自变量x的取值范围,将目标函数消元、配方,可求出函数的值域。
解:∵ ,上述分式不等式与不等式 同解,解之得-1≤x≤3/2,又x+y=1,将y=1-x代入z=xy+3x中,得 (-1≤x≤3/2),
∴ 且x∈[-1,3/2],函数z在区间[-1,3/2]上连续,故只需比较边界的大小。
当x=-1时,z=-5;当x=3/2时,z=15/4。
∴函数z的值域为{z∣-5≤z≤15/4}。
点评:本题是将函数的值域问题转化为函数的最值。对开区间,若存在最值,也可通过求出最值而获得函数的值域。
12.构造法
根据函数的结构特征,赋予几何图形,数形结合。
例19.求函数 的值域。
点拨:将原函数变形,构造平面图形,由几何知识,确定出函数的值域。
解:原函数变形为
作一个长为4、宽为3的矩形ABCD,再切割成12个单位正方形。设HK=x,则EK=2-x,KF=2+x, ,。
由三角形三边关系知,AK+KC≥AC=5。当A、K、C三点共线时取等号。
∴原函数的知域为{y|y≥5}。
点评:对于形如函数 (a,b,c均为正数),均可通过构造几何图形,由几何的性质,直观明了、方便简捷。这是数形结合思想的体现。
13.比例法
对于一类含条件的函数的值域的求法,可将条件转化为比例式,代入目标函数,进而求出原函数的值域。
例20.已知x,y∈R,且3x-4y-5=0,求函数 的值域。
点拨:将条件方程3x-4y-5=0转化为比例式,设置参数,代入原函数。
解:由3x-4y-5=0变形得,(x3)/4=(y-1)/3=k(k为参数)
∴x=3+4k,y=1+3k,
∴ 。
当k=-3/5时,x=3/5,y=-4/5时, 。
函数的值域为{z|z≥1}.
点评:本题是多元函数关系,一般含有约束条件,将条件转化为比例式,通过设参数,可将原函数转化为单函数的形式,这种解题方法体现诸多思想方法,具有一定的创新意识。
14.利用多项式的除法
例21.求函数y=(3x+2)/(x+1)的值域。
点拨:将原分式函数,利用长除法转化为一个整式与一个分式之和。
解:y=(3x+2)/(x+1)=3-1/(x+1)。
∵1/(x+1)≠0,故y≠3。
∴函数y的值域为y≠3的一切实数。
点评:对于形如y=(ax+b)/(cx+d)的形式的函数均可利用这种方法。
15. 多种方法综合运用
例22. 求函数 的值域。
解:令 ,则
(1)当t>0时, ,当且仅当t=1,即x=-1时取等号,所以
(2)当t=0时,y=0。
综上所述,函数的值域为:
注:先换元,后用不等式法
例23. 求函数 的值域。
解:
令 ,则
∴
∴当 时,
当 时,
此时 都存在,故函数的值域为
注:此题先用换元法,后用配方法,然后再运用 的有界性。
总之,在具体求某个函数的值域时,首先要仔细、认真观察其题型特征,然后再选择恰当的方法,一般优先考虑直接法,函数单调性法和基本不等式法,然后才考虑用其他各种特殊方法。 本文标题:函数值域的求法-求下列函数的值域(1)y=√(-x^2-6x-5)(2)y=(2?
本文地址: http://www.61k.com/1107423.html
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1