一 : 如图,已知一次函数y=kx+b的图像经过A(
| 如图,已知一次函数y=kx+b的图像经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D。 |
 |
| (1)求该一次函数的解析式; (2)求tan∠OCD的值; (3)求证:∠AOB=135°。 |
解:(1)由题意得 ,解得 ,解得 , ,所以y=  ; ;(2)与x轴的交点坐标为C(-  ,0),与y轴的交点坐标为D(0, ,0),与y轴的交点坐标为D(0, ), ),在Rt△OCD中,OD= 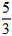 ,OC= ,OC=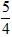 , ,∴tan∠OCD= 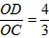 ; ;(3)如图所示,取点A关于原点的对称点E(2,1),则问题转化为求证∠BOE=45°, 由勾股定理可得,OE=  ,BE= ,BE=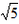 ,OB= ,OB=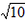 , ,∵OB2=OE2+BE2, ∴△EOB是等腰直角三角形, ∴∠BOE=45°, ∴∠AOB=135°。 |  |
考点:
考点名称:求一次函数的解析式及一次函数的应用待定系数法求一次函数的解析式:用待定系数法求一次函数解析式的四个步骤:
第一步(设):设出函数的一般形式。(称一次函数通式)
第二步(代):代入解析式得出方程或方程组。
第三步(求):通过列方程或方程组求出待定系数k,b的值。
第四步(写):写出该函数的解析式。
一次函数的应用涉及问题:
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符
合实际。
二、函数的多变量问题
解决含有多变量问题时,可以分析这些变量的关系,选取其中一个变量作为自变量,然后根据问题的条件寻
求可以反映实际问题的函数
三、概括整合
(1)简单的一次函数问题:①建立函数模型的方法;②分段函数思想的应用。
(2)理清题意是采用分段函数解决问题的关键。
生活中的应用:
1.当时间t一定,距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定,水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b(未挂重物时的长度)一定时,弹簧挂重物后的长度y是重物重量x的一次函数,即y=kx+b(k为任意正数)
一次函数应用常用公式:
1.求函数图像的k值:(y1-y2)/(x1-x2)
2.求与x轴平行线段的中点:(x1+x2)/2
3.求与y轴平行线段的中点:(y1+y2)/2
4.求任意线段的长:√[(x1-x2)2+(y1-y2)2]
5.求两个一次函数式图像交点坐标:解两函数式
两个一次函数 y1=k1x+b1; y2=k2x+b2令y1=y2 得k1x+b1=k2x+b2将解得的x=x0值代回y1=k1x+b1; y2=k2x+b2两式任一式 得到y=y0则(x0,y0)即为 y1=k1x+b1 与 y2=k2x+b2交点坐标
6.求任意2点所连线段的中点坐标:[(x1+x2)/2,(y1+y2)/2]
7.求任意2点的连线的一次函数解析式:(x-x1)/(x1-x2)=(y-y1)/(y1-y2) (若分母为0,则分子为0)
(x,y)为 + ,+(正,正)时该点在第一象限
(x,y)为 - ,+(负,正)时该点在第二象限
(x,y)为 - ,-(负,负)时该点在第三象限
(x,y)为 + ,-(正,负)时该点在第四象限
8.若两条直线y1=k1x+b1//y2=k2x+b2,则k1=k2,b1≠b2
9.如两条直线y1=k1x+b1⊥y2=k2x+b2,则k1×k2=-1
10.
y=k(x-n)+b就是直线向右平移n个单位
y=k(x+n)+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决:左加右减相对于x,上加下减相对于b。
11.直线y=kx+b与x轴的交点:(-b/k,0) 与y轴的交点:(0,b)
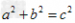 。
。锐角三角函数:
锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
初中学习的 锐角三角函数值的定义方法是在直角三角形中定义的,所以在初中阶段求锐角的三角函数值,都是通过构造直角三角形来完成的,即把这个角放到某个直角三角形中。所谓锐角三角函数是指:我们初中研究的都是锐角的三角函数。初中研究的锐角的三角函数为:正弦(sin),余弦(cos),正切(tan)。
正弦:在直角三角形中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即 ;
;
余弦:在直角三角形中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即 ;
;
正切:在直角三角形中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即 ,
,
锐角A的正弦、余弦、正切都叫做A的锐角三角函数。
锐角三角函数的关系式:
同角三角函数基本关系式
tanα·cotα=1
sin2α·cos2α=1
cos2α·sin2α=1
sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
(sinα)2+(cosα)2=1
1+tanα=secα
1+cotα=cscα
诱导公式
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα(其中k∈Z)
二倍角、三倍角的正弦、余弦和正切公式
Sin(2α)=2sinαcosα
Cos(2α)=(cosα)2-(sinα)2=2(cosα)2-1=1-2(sinα)2
Tan(2α)=2tanα/(1-tanα)
sin(3α)=3sinα-4sin3α=4sinα·sin(60°+α)sin(60°-α)
cos(3α)=4cos3α-3cosα=4cosα·cos(60°+α)cos(60°-α)
tan(3α)=(3tanα-tan3α)/(1-3tan2α)=tanαtan(π/3+α)tan(π/3-α)
和差化积、积化和差公式
sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]
sinαcosβ=-[sin(α+β)+sin(α-β)]
sinαsinβ=-[1][cos(α+β)-cos(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2
sinαcosβ=[sin(α+β)+sin(α-β)]/2
cosαsinβ=[sin(α+β)-sin(α-β)]/2
二 : 初二数学一次函数Y=KX-3的图象与X轴交于点A,与Y轴交于点B
初二数学
一次Y=KX-3的图象与X轴交于点A,与Y轴交于点B,三角形OAB(O为坐标原点)的面积为4平方单位,且函数Y的值随X的增大而增大.求:(1)点B的坐标.(2)点A的坐标及K的值. (要有过程)
一次函数Y=KX-3的图象与X轴交于点A,与Y轴交于点B,三角形OAB(O为坐标原点)的面积为4平方单位,且函数Y的值随X的增大而增大.求:(1)点B的坐标.(2)点A的坐标及K的值. (要有过程)
解:令X=0,则Y=-3,令Y=0,则X=3/K.
所以A坐标(3/K,0),B坐标(0,-3)
三角形OAB的面积S=1/2|3/K|*|-3|=4
|3/K|=8/3
因为函数Y的值随X的增大而增大,所以,K>0
即:3/K=8/3,K=9/8
即A坐标是:(8/3,0)
三 : 数学若直线l1:y=kx+k+2与l2: y=-2x+
数学
若直线l1:y=kx+k+2与l2: y=-2x+4的交点在第一象限,则K的取值范围为
y=kx+k+2 (1) y=-2x+4 (2)联立得kx+k+2=-2x+4(k+2)x=2-kx=(2-k)/(k+2)y=-2x+4=-2(2-k)/(k+2) +4=(6k+4)/(k+2)因为交点在第一象限x>0 ,y>0解得-2/3 四 : 初二数学一次函数一次函数y=2x+b的图像与两坐标轴所围成的三角 初二数学一次函数 一次y=2x+b的图像与两坐标轴所围成的三角形的面积为8,求一次函数的解析式 y=2x+b 当x=0,y=b, 当y=0,x=-b/2 面积=b*b/4=8 b=4√2 一次函数的解析式: y=2x+4√2 或,y=2x-4√2
本文地址: http://www.61k.com/1086235.html
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1