一 : EXCEL在通径分析中的应用[1] 52

ＥＸＣＥＬ在通径分析中的应用

任红松１，朱家辉２，杨斌３，袁继勇４，詹发强５，宋羽６

（１新疆农业科学院科研管理处，新疆乌鲁木齐８３００００；２新疆天合种业北疆育种站，新疆乌鲁木齐

８３０００３；

３膳善县农业技术推广中心，新疆吐鲁番８３８０００；４新疆农业科学院经济作物研究所，新疆乌鲁木齐８３００００；５新疆农业科学院微生物研究所，新疆乌鲁木齐８３００００；６新疆农业科学院品种资源研究所，新疆乌鲁木齐８３００００）

摘

要：通径分析是标准化的线性回归分析。本文应用ＥＸＣＥＬ“工具”菜单“数据分析”选项中的“描述统计”、“相关系数”和

实践证明用该电子表

“回归”分析工具以小麦丰产３号主要农艺性状资料为例阐述了用ＥＸＣＥＬ做通径分析的详细过程．关键词：ＥＸＣＥＬ；相关；线性回归；通径分析

中图分类号：Ｓ１２６

文献标识码：Ｂ

格软件做通径分析完全可行，且操作简单、易行。最后还就通径分析的应用要点和注意事项进行了探讨。

文章编码：１６７２－６２５１（２００６）０３－００９０－

０３

在动、植物遗传育种工作中，人们常用相关分析研究多个变量（性状）间相互关系。相关分析要求变量（性植物的诸多性状）间相互独立时才有效，而实际上动、

状并不是彼此独立的。一个性状（自变量）除了可通过直接作用引起目标性状（依变量）变化外，还可通过其它相关性状间接引起目标性状的变化。要弄清这些性状的直接效应和间接效应，Ｓ．Ｗｒｉｇｈｔ于１９２１年提出了通径分析法（ｐａｔｈａｎａｌｙｓｉｓ）［１］。通径分析过程可以用

ｘｉ对依变量ｙ的直接通径系数。自变量ｘｉ通过其它相关变量对依变量ｙ的间接通径系数等于相关变量的直接通径系数乘以二者的相关系数。

２

２．１

实例分析

数据的正态性检验

打开一个新的工作薄，在一页新表上建立如图１

所示的工作表，并在Ａ２：Ｅ１６区域内分别输入各组数据，分析数据来自文献［２］多元回归部分。待数据输好后“工具”菜单的“数据分析”选项中的“描述打开ＥＸＣＥＬ

统计”分析工具，设置如图２所示的“描述统计”控制选“确定”按扭得到如表１所示的丰产３号各性项，单击

状数据的简单统计。从表１的简单统计结果可看出小麦丰产３号各农艺性状数据的偏斜度很小，均接近于

ＳＡＳ、ＳＰＳＳ、ＤＰＳ等一些专业统计学软件实现，但这些软件比较昂贵，且用一些软件处理时还需要进行复杂编程。如何利用所有个人微机上都有的ＥＸＣＥＬ电子表格软件来实现通径分析，笔者就此进行了论述。以期为广大从事该项研究的且手头又无专业统计软件的读者带来一些方便。

１原理与方法

先对试验数据进行正态性检验，当数据满足正态

０，说明各组数据近似满足正态性要求，进行下面的相关、回归和通径分析结果可靠。

性或近似正态性的要求后，应用ＥＸＣＥＬ“工具”菜单“数据分析”选项中的“回归”分析工具建立各自变量与依变量的多元线性回归方程：

∧

ｙ＝ｂ０＋ｂ１ｘ１＋ｂ２ｘ２＋ｂ３ｘ３＋…ｂｍｘｍ，式中ｂｉ的是自变量ｘｉ对依变量ｙ的偏回归系数。由于各偏回归系数的量纲和各自变量本身变异程度的不同，使得偏回归系数绝对值并不能准确反映相应自变量对依变量相对贡献的大小。为此需将各偏回归系数标准化，即用相应自变量的标准差（!ｘｉ）与依变量的标准差（!ｙ）之比去乘各偏回归系数，所得标准化偏回归系数Ｐｙｘｉ即为自变量

图１小麦丰产３号主要农艺性状数据

２．２最优回归方程的建立及显著性测验

收稿日期：２００５－１１－３０

作者简介：任红松（１９７７－），男，硕士，研究方向：农业科技管理和植物遗传育种。

表３

偏回归系数（剔除Ｘ４）的显著性测验

根据图１的数据打开ＥＸＣＥＬ“工具”菜单的“数据分析”选项中的“回归”分析工具设置如图３所示的回归分析控制选项，回车后可建立以株产为依变量，每株穗数为自变量，每穗结实小穗数为自变量，百粒重为自变量，株高为为自变量的多元线性回归方程：ｙ＝－５１．９０２１＋２．０２６１８ｘｉ＋０．６５３９９７ｘ２＋７．７９６９３８ｘ３＋０．０４９６９７

由表２的方差分析结果表明所建立的回归方程：

ｘ４，模型检验达极显著水平（Ｆ＝３０．６２５４ＳｉｇｎｉｆｉｃａｎｃｅＦ＝１．４９８１１Ｅ－０５），各偏回归系数显著性检验为ｘ１、ｘ３达极显著水平，ｘ２接近显著水平（ｔ＝２．１６０，ｐ＝０．０５６），ｘ４不显著（ｔ＝０．５９８，ｐ＝０．５６２）。因此，应首先去掉株高自变量建立最优回归方程，按上述同样的操作其ＥＸＣＥＬ输出结果（已整理）如表２和表３所示。

ｙ＝－４６．９６６４＋２．０１３１ｘ１＋０．６７４６ｘ２＋７．８３０２ｘ３达极显著水平（Ｆ＝４２．４３８，ＳｉｇｎｉｆｉｃａｎｃｅＦ＝２．４４５０８Ｅ－０６）。表３对该方程截距－４６．９６６４检验结果为ｔ＝－４．６０７９，ｐ≤０．０００７５５２达极显著水平；各偏回归系数显著性检验结果为每株百粒重ｘ３达极显著水平；每穗结实小穗数ｘ２达穗数ｘ１、

显著水平。说明截距和其它三项偏回归系数与０之间差别显著，可认为所求的直线回归方程成立，以下作ｙ关于ｘ１、ｘ２、ｘ３的通径分析是有意义的。

２．３丰产３号主要农艺性状的相关及显著性测验“工具”菜单的“数据分析”选项中的打开ＥＸＣＥＬ

“相关系数”分析工具设置如图４所示的相关系数控制选项，回车后可求出图１小麦丰产３号各农艺性状间的相关系数（表４）。

图２各性状数据描述统计选项设置

表１小麦丰产３号各性状数据的简单统计

图４各性状相关系数选项设置

表４小麦丰产３号主要农艺性状间的相关系数

显著水平时的临界!＝０．５１３９，极显著水平时的临界"＝０．６４１１。表４中每株穗数与株产的相关系数０．８９７３以及百粒重与株产的相关系数０．６８９０均大于０．６４１１，达到极显著水平。每株穗数与百粒重的相关系数

图３

回归分析选项设置

０．５００７接近显著水平。其余性状间相关系数不显著。２．４

直接通径系数的计算及显著性测验

根据通径系数为标准的偏回归系数［３］，而标准偏回归系数＝自变量的偏回归系数×（自变量的标准差／因变量的标准差）。因此，由表１各变量的标准偏差和表３各变量的偏回归系数可求出各自变量对依变量ｙ的直

表２方差分析

《农业网络信息》２００６年第３期

交流园地

接通径系数。如每株穗数对株产的直接通径系数ｐｙ１＝（１．５４９２／４．１３９４）＝０．７５３４。同理每穗结实小穗数２．０１３１×

对株产的直接通径系数ｐｙ２＝０．６７４６×（１．２２２８／４．１３９４）＝

３讨论

（１）在进行通径分析之前，必须对资料进行正态性

０．１９９３，百粒重对株产的直接通径系数ｐｙ３＝７．８３０２×（０．１８０５／４．１３９４）＝０．３４１４，各通径系数显著性检验结果与上述各回归系数显著性检验结果相同。上述回归方程的多元决定系数Ｒ＝０．９２０５，表明因变量变异中

２

检验，只有在资料符合正态分布或近似正态分布条件下，相关、回归和通径分析结论才可靠。在通径分析中，若存在对依变量作用不显著的自变量（性状），必须逐个地予以剔除，直至方程中保留的自变量都显著为止。因为在显著和不显著的自变量并存时，常会产生“不显著的”不一定真不似是而非或难以解释的情况（

有时也不一定真显著），以致不能作出显著，“显著的”正确推断。

（２）通径分析要求每变量的样本容量ｎ必须大于自变量个数ｍ，一般要求二者之差（ｎ－ｍ）大于１０，才能获得较为准确的误差估计和作出较为可靠的假设测验。（ｎ－ｍ）≤１的资料虽然可以估算出任何两个变数间的相关系数，但不能用以建立相关方程组和进行通径分析。

（３）在对通径分析结果作解释时，如果某一自变量（性状）和依变量的相关系数几乎等于它的直接效应，那么说明相关反映了二者的真实关系，并且通过这个性状进行直接选择效果较好；如果相关系数是正的，但直接效应是负的或值很小，说明间接效应几乎是相关的主要原因。在这种情况下，对间接的性状要同时加以考虑；如果相关系数是负的，但直接效应是正的，并且数值较高时，应按照有限的同步选择模式进行选择，即为了利用直接效应要施加一些限制，以使不合要求的间接效应无效。

参考文献

９２．０５％可由线性回归部分来解释，误差仅占７．９５％，据此可求出误差ｅ对ｙ的直接通径系数ｐｙｅ＝!１－Ｒ＝

!＝０．２８１９６。

２．５间接通径系数的计算

由前面原理与方法部分可知：某一自变量通过另一自变量间接作用于依变量的间接通径系数等于另一自变量的直接通径系数乘以二者的相关系数。例如，每株穗数通过百粒重作用于单株籽粒产量的间接通径系?数为ｐｙ３ｒ１３＝０．５００７×０．３４１４＝０．１７０９，其他自变量的间接通径分析的理论已证明，任一自变量与因变量之间的简单相关系数可分解为该自变量与因变量之间的直接通径系数加上所有其它间接通径系数之代数和。如每株穗数与单株籽粒产量间的相关系数

ｒｙ＝Ｐ＋ｒＰ＋ｒＰ＋ｒＰ＝０．７５３４＋（－０．０２７１）＋０．１７０９＝０．８９７３，

１

ｙ１

１２ｙ２

１３ｙ３

１４ｙ４

其它性状与株产之间相关系数的分解与此相同。根据直接通径系数的大小可比较各性状对目标性状的作用大小。由表５可看出，各性状对单株籽粒产量的作用依次为每株穗数＞百粒重＞每穗结实小穗数，各性状对株产的间接作用以及相互关系的具体解释请见参考文献［５］。

［１］盖钧镒．试验统计方法［Ｍ］．北京：中国农业出版社，２０００．［２］

李永孝．农业应用生物统计［Ｍ］．济南：山东科学技术出版社，

１９９８．

［３］边宽江，等．小麦品种产量与产量因素通径分析［Ｊ］．西北农业

学报，１９９９，８（２）：２０～２１．［４］［５］

梁晓玲，等．玉米杂交种的产量比较及主要农艺性状的相关和通径分析［Ｊ］．玉米科学，２００１，９（１）：１６～２０．

任红松，等．通径分析的ＳＡＳ的实现方法［Ｊ］．计算机与农业，

２００３，（４）：１７～１９．

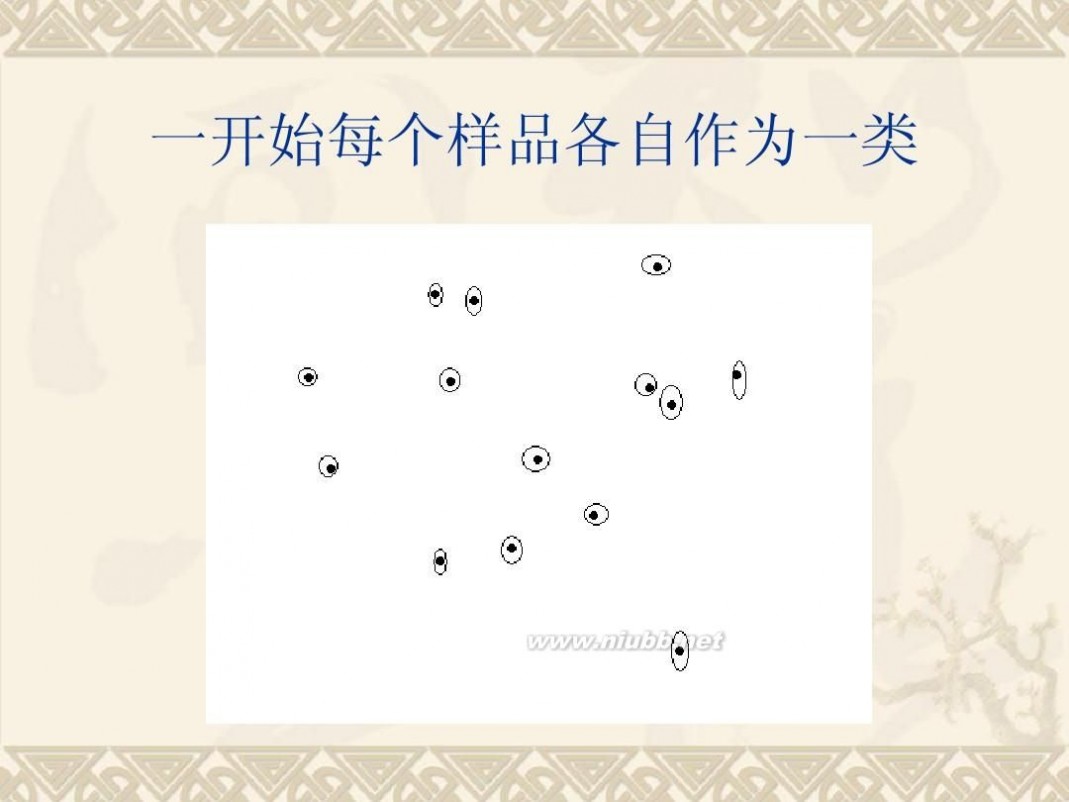
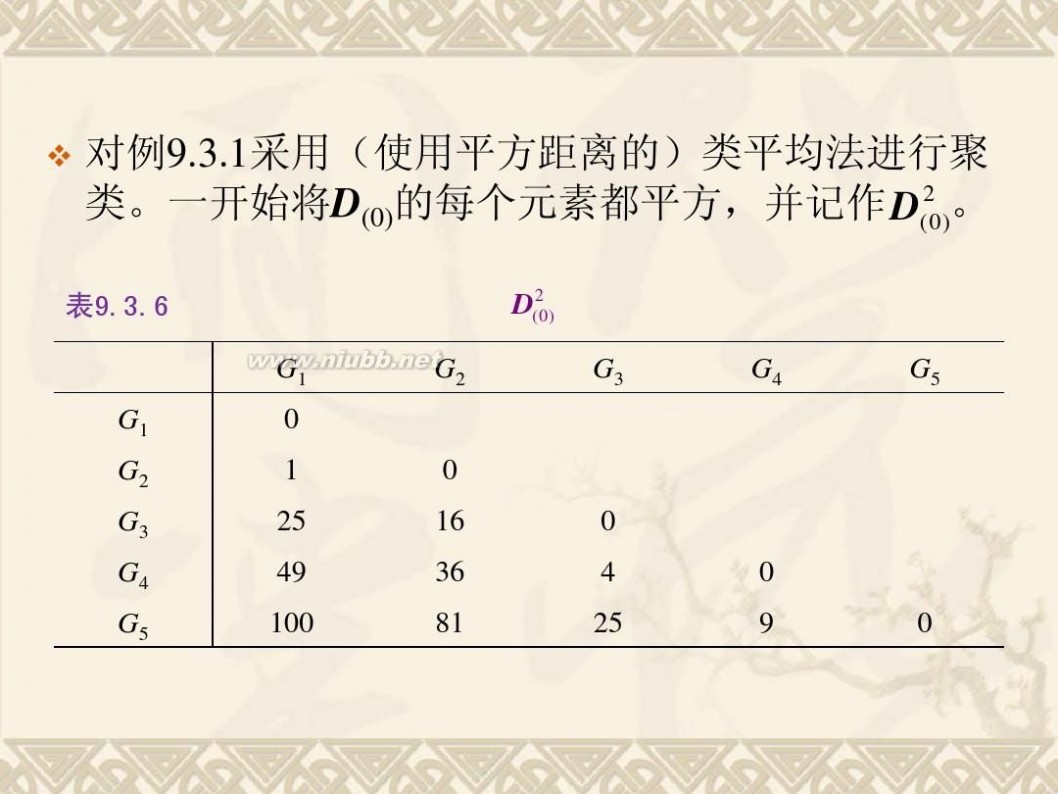
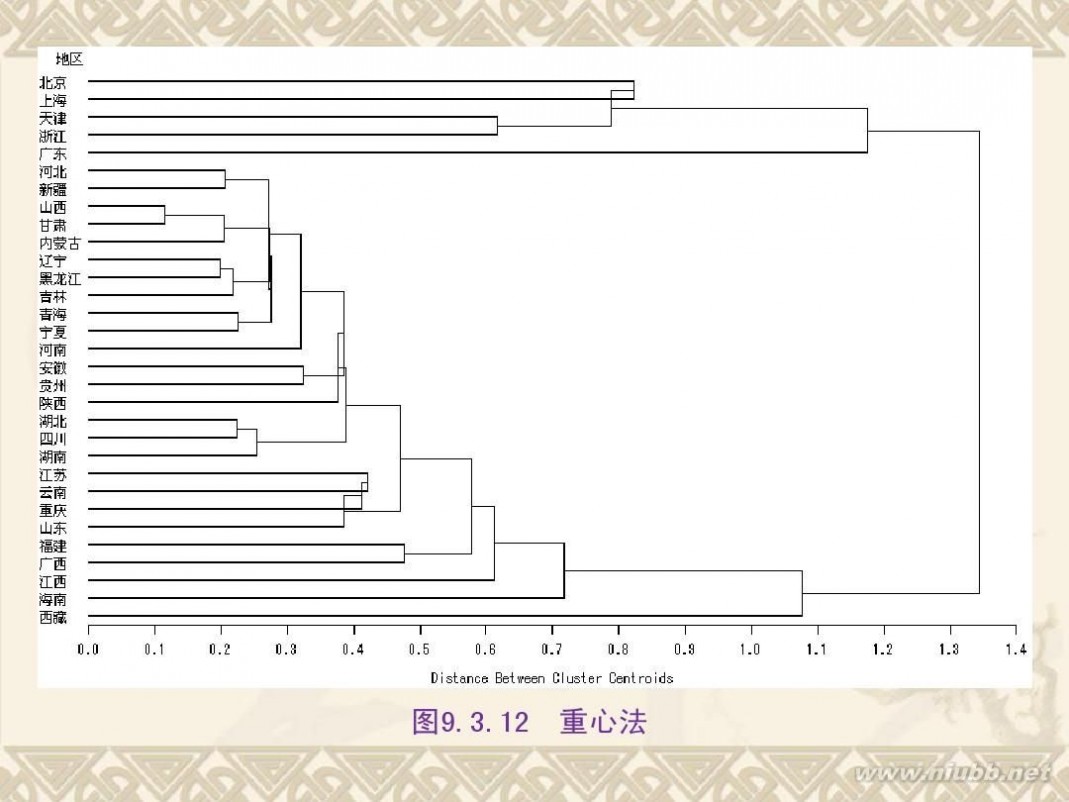
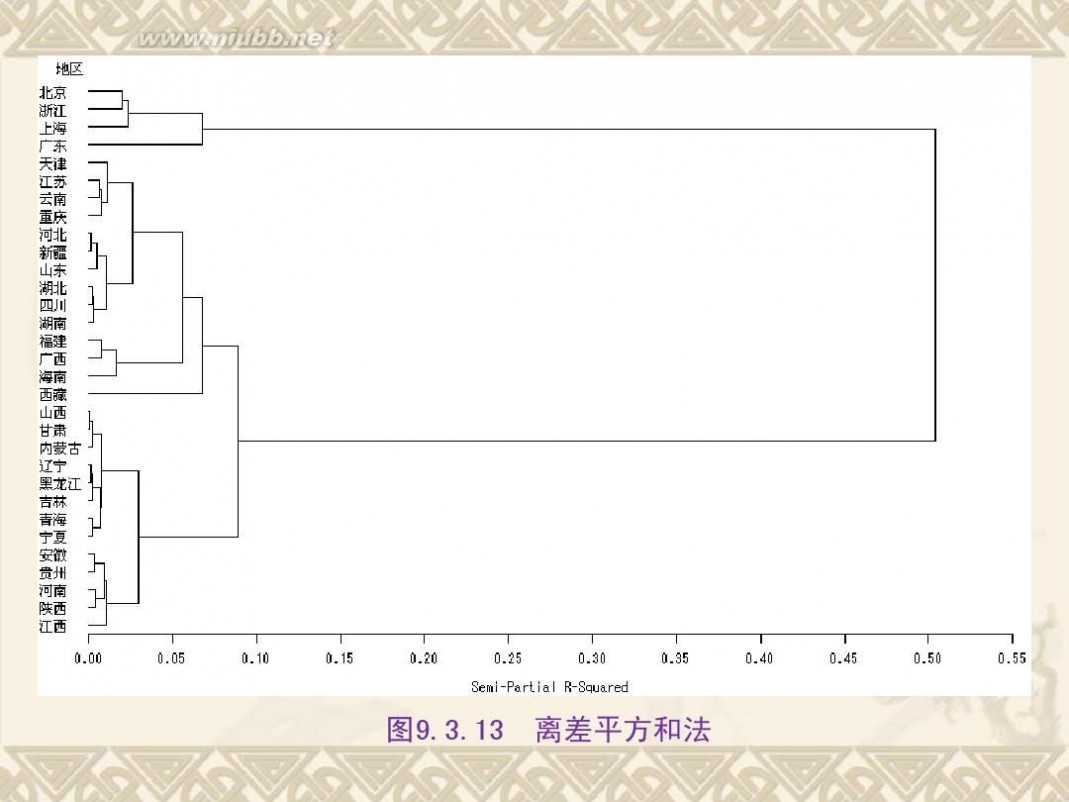
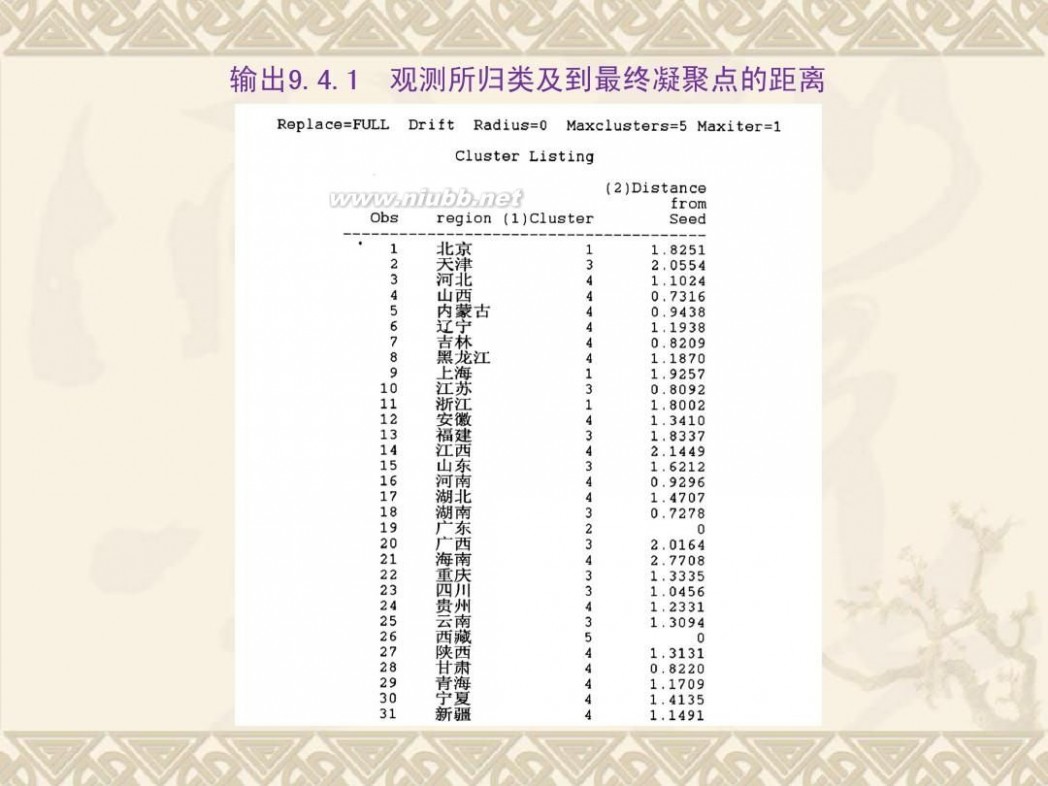
二 : 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

扩展：eviews统计分析与应用 / matlab统计分析与应用 / 应用stata做统计分析

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

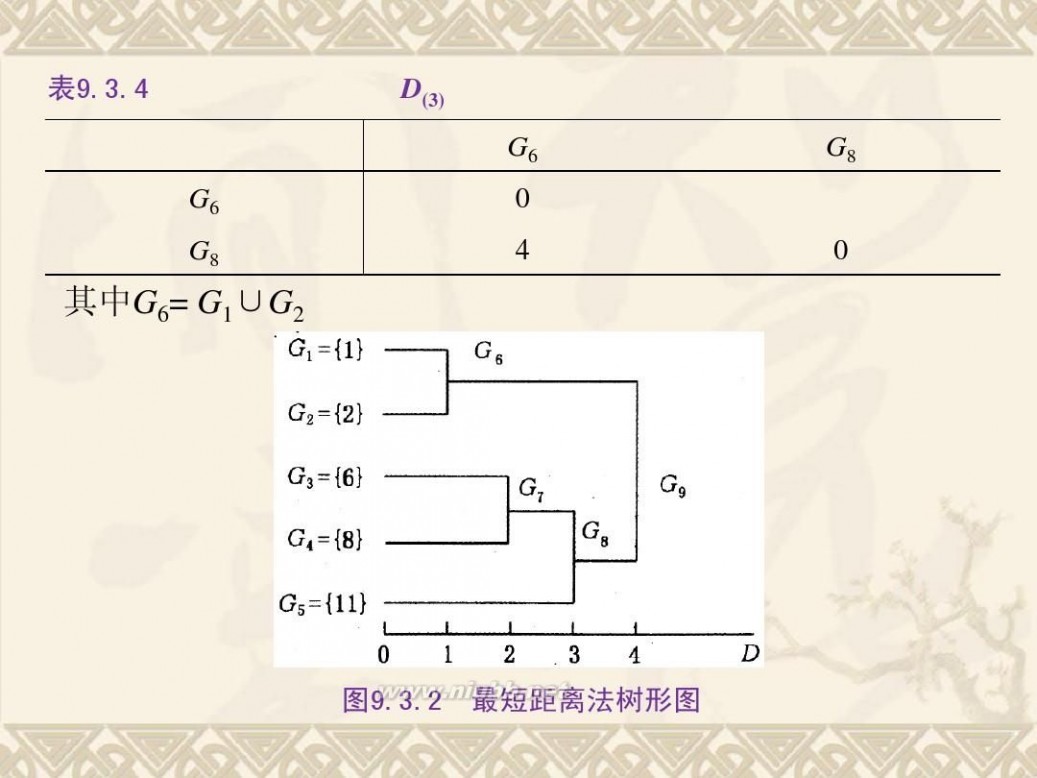
统计分析方法 《统计分析方法及应用》PPT(第九章)

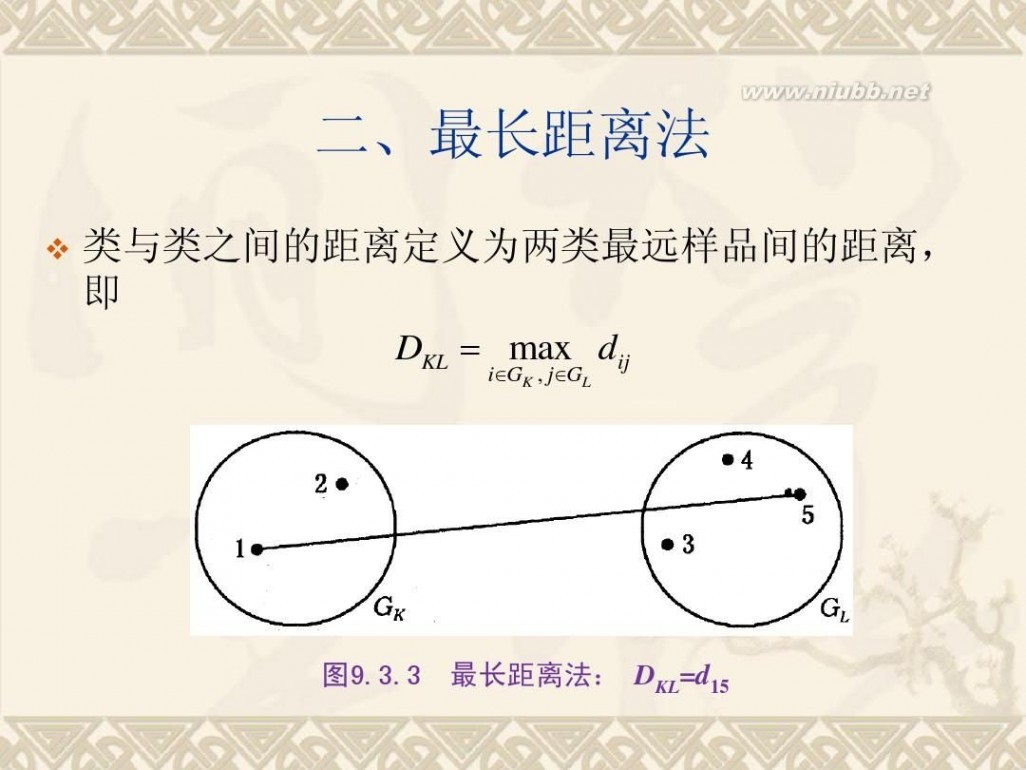
统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

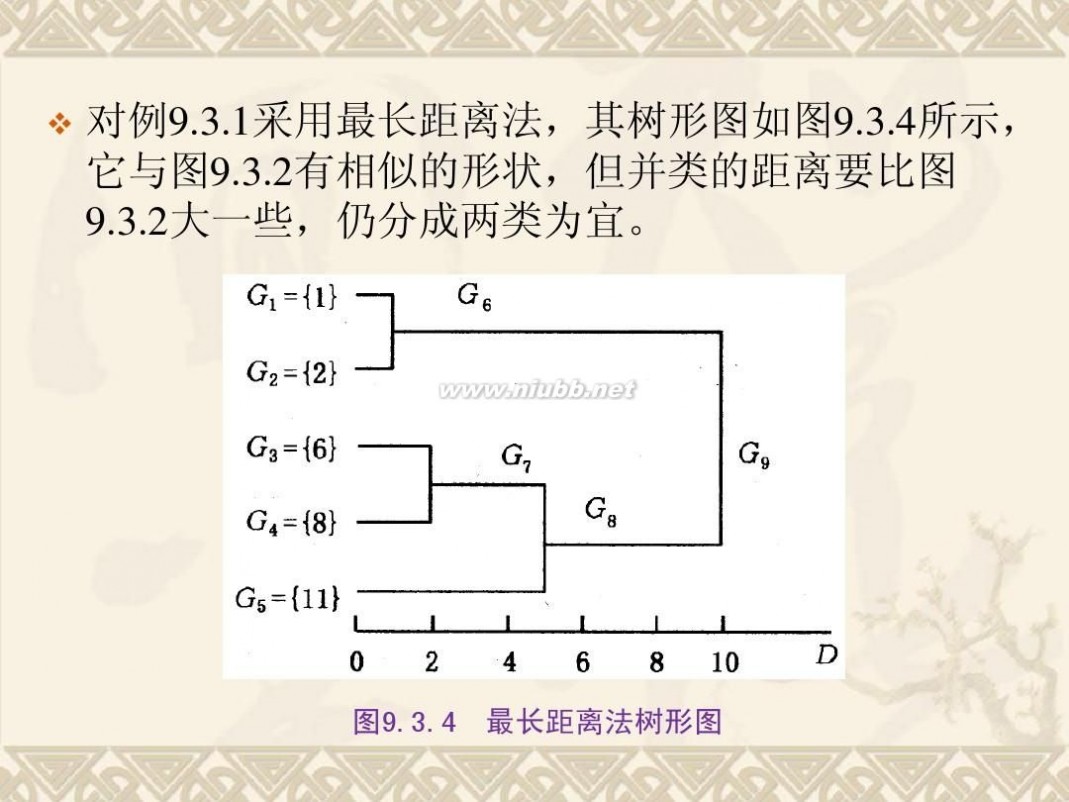
统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

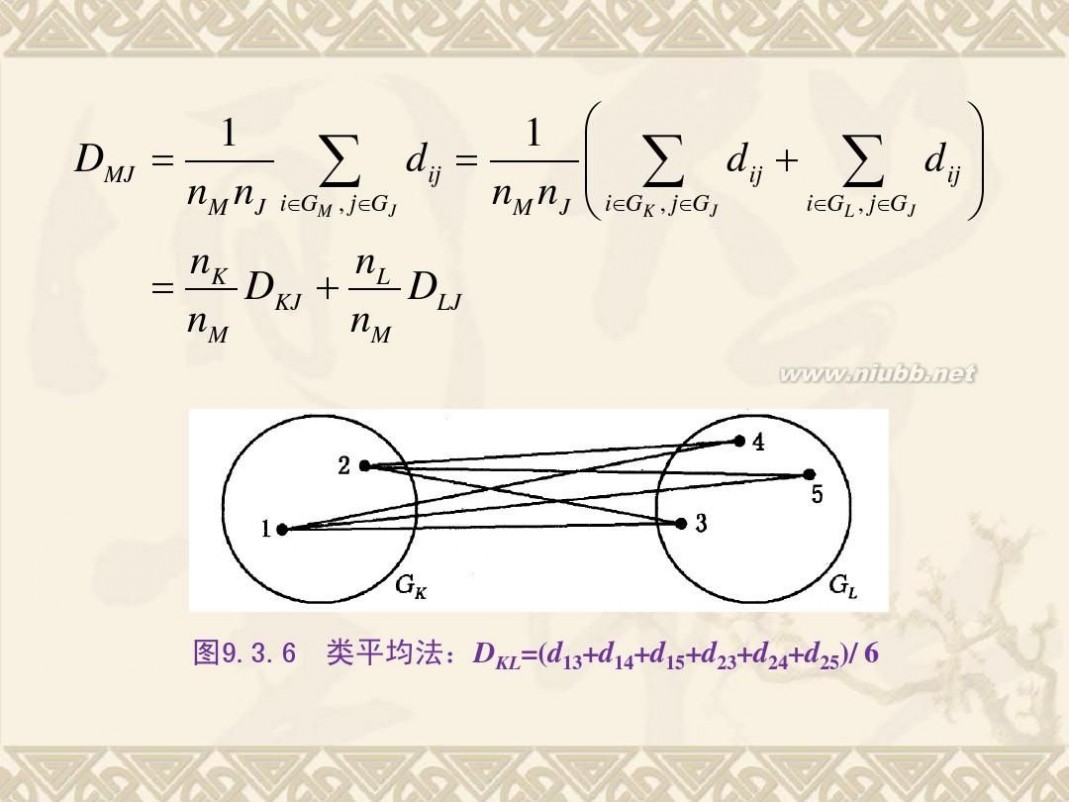
统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

扩展：eviews统计分析与应用 / matlab统计分析与应用 / 应用stata做统计分析

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

统计分析方法 《统计分析方法及应用》PPT(第九章)

扩展：eviews统计分析与应用 / matlab统计分析与应用 / 应用stata做统计分析

三 : Excel在学校中的应用17-班级考试成绩统计分析表

3.5 班级考试成绩统计分析表

案例背景

上接3.3节，当某中学初三2班班主任从任课教师回收单科成绩表，汇总形成本班“成绩汇总表”后，需要对本班各科考试成绩进行进一步的统计分析，需要统计应考人数，实考人数，及格人数、不及格人数，平均分，最高分，及格率，良好率（考分不小于80），优秀率（考分不小于90）和标准差。

关键技术点

要实现本案例中的功能，学员应该掌握以下EXCEL技术点。

●基础知识 数字的“百分比”格式显示

●函数应用 COUNT函数、COUNTIF函数、STDEVP函数

●公式的设计与操作

最总效果展示

3.5.1创建班级考试成绩统计分析表

Step 1创建工作簿、重名工作表

创建工作簿“班级考试成绩统计分析表.xls”，然后将工作表重命名为“考试成绩统计分析表”，并删除多余工作表。

Step 2 输入原始成绩

将3.4节案例中图7复制粘贴到“成绩统计分析表”中，如下图

Step 3输入需统计项目名称

在单元格区域A44：A53分别输入“应考人数”，”应考人数”,” 及格人数”, “不及格人数”,” 平均分”,” 最高分”, “及格率”, “良好率”， “优秀率”和”标准差“。

Step4统计应考人数和实考人数

选中单元格C44，单击常用工具栏“插入函数“按钮，弹出“插入函数“对话框，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”COUNTA“。

②单击确定按钮弹出“函数参数“对话框，在第一个参数框”Value1“中用光标选中本班学生姓名区域”B3:B43“，然后按键，将参数区域切换成绝对引用形式”$B$3:$B$43“,便于后面操作中向右填充公式。

③然后单击确定按钮，得到本班学生人数，也就是应考人数。

④选中单元格C45，单击常用工具栏“插入函数“按钮，弹出“插入函数“对话框，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”COUNT “。

⑤单击确定按钮弹出“函数参数“对话框，在第一个参数框”Value1“中函数默认的函数区域为该单元格上面的数据区域”C3:C44“，直接在参数框中将C44改为C43或用光标选中”语文期中“成绩区域”C3:C43“也可。

⑥然后单击确定按钮，得到语文期中实考人数。

⑦选中单元格区域C44：C45，拖曳单元格C45右下角的填充柄至Q列，松开鼠标即可完成所有课程的应考和实考人数的统计。

Step4统计及格人数和不及格人数

①选中单元格C46，单击常用工具栏“插入函数“按钮，弹出“插入函数“，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”COUNTIF“。

②单击确定按钮弹出“函数参数“对话框，在第一个参数框”Range“中用光标选中”语文期中“成绩区域”C3:C43“，在第二个参数框”“Criteria”中输入条件“>=60”。

③然后单击确定按钮，得到”语文期中“考试成绩的及格人数。

④选中单元格C47，单击常用工具栏“插入函数“按钮，弹出“插入函数“，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”COUNTIF“。 ⑤单击确定按钮弹出“函数参数“对话框，在第一个参数框”Range“中用光标选中”语文期中“成绩区域”C3:C43“，在第二个参数框”“Criteria”中输入条件“<60”。

⑥然后单击确定按钮，得到”语文期中“考试的不及格人数。

Step5统计平均分和最高分

①选中单元格C48，单击常用工具栏“插入函数“按钮，弹出“插入函数“，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”AVERAGE“。

②单击确定按钮弹出“函数参数“对话框，在第一个参数框”Number1“中直接将默认的数据区域修改为”C3:C43“。

③然后单击确定按钮，得到”语文期中“考试成绩的平均分。

④选中单元格C49，单击常用工具栏“插入函数“按钮，弹出“插入函数“，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”MAX“。

⑤单击确定按钮弹出“函数参数“对话框，在第一个参数框”Number1“中直接将默认的数据区域修改为”C3:C43“。

⑥然后单击确定按钮，得到”语文期中“考试成绩的“最高分”。

Step6统计及格率

选中单元格C49，输入公式“=C46/C45”即可计算出本班“语文期中“考试成绩的及格率。 Step7统计良好率和优秀率

①选中单元格C51，单击常用工具栏“插入函数“按钮，弹出“插入函数“，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”COUNTIF“。 ②单击确定按钮弹出“函数参数“对话框，在第一个参数框”Range“中用光标选中”语文期中“成绩区域”C3:C43“，在第二个参数框”“Criteria”中输入条件“>=80”。

③单击确定按钮，首先得到”语文期中“考试成绩的良好人数。

④然后修改公式，将光标直接单击编辑栏，将光标移动到最后，输入“ /C45“, 按键确认即可计算出”良好率“

⑤按照计算”良好率“的操作过程，只是把第二步的条件改为”>=90“计算出优秀率。

Step8设置“及格率“、”良好率“和”优秀率“为“百分比“形式

①选中单元格区域C50:C52,单击菜单“格式“→”单元格“弹出”单元格格式“对话框，在”分类“选项框中选择”百分比“，在”小数位数“列表框中单击上箭头按钮选择”1“。

②单击确定按钮即可完成数字的百分比形式显示。

Step9统计标准差

①选中单元格C53，单击常用工具栏“插入函数“按钮，弹出“插入函数“，在”或函数类别“选项框中选择”统计“，在”选择函数“选项框中选择”STVAP“。

②单击确定按钮弹出“函数参数“对话框，在第一个参数框”Number1“中直接将默认的数据区域修改为”C3:C43“。

③然后单击确定按钮，得到”语文期中“考试成绩的“标准差”。

Step10复制填充公式

选中其余各区域C46:C53，向右拖曳单元格C53右下角的填充柄至Q列松开鼠标即可完成其余成绩的相应项目的统计。

Step11调整列宽

适当调宽I列、P列和Q列的宽度，使得“英语期中”、“化学期末“和”化学总评“的’及格率”完全显示出来。

至此”班级考试成绩统计分析表”需要统计的内容全部统计完毕，班主任可以根据统计情况对本班学生各门课程的学习情况进行综合对比分析。

关键知识点讲解

1.COUNT函数

函数名称：COUNT

主要功能：返回包含数字以及包含参数列表中的数字的单元格的个数。利用函数 COUNT 可以计算单元格区域或数字数组中数字字段的输入项个数。

使用格式：COUNT(value1,value2,...)

参数说明：Value1, value2, ... 为包含或引用各种类型数据的参数（1 到 30个），但只有数字类型的数据才被计算。

函数说明：

●函数 COUNT 在计数时，将把数字、日期、或以文本代表的数字计算在内；但是错误值或其他无法转换成数字的文字将被忽略。

●如果参数是一个数组或引用，那么只统计数组或引用中的数字；数组或引用中的空白单元格、逻辑值、文字或错误值都将被忽略。如果要统计逻辑值、文字或错误值，请使用函数 COUNTA。

应用示例：

2.COUNTA函数

函数名称：.COUNTA

主要功能：返回参数列表中非空值的单元格个数。利用函数 COUNTA 可以计算单元格区域或数组中包含数据的单元格个数。

使用格式：COUNTA(value1,value2,...)

参数说明：Value1, value2, ... 为所要计算的值，参数个数为 1 到 30 个。在这种情况下，参数值可以是任何类型，它们可以包括空字符 ("")，但不包括空白单元格。如果参数是数组或单元格引用，则数组或引用中的空白单元格将被忽略。如果不需要统计逻辑值、文字或错误值，请使用函数 COUNT。

3. COUNTIF函数

函数名称：COUNTIF

主要功能：计算区域中满足给定条件的单元格的个数。

使用格式：COUNTIF(range,criteria)

参数说明：

Range 为需要计算其中满足条件的单元格数目的单元格区域。

Criteria 为确定哪些单元格将被计算在内的条件，其形式可以为数字、表达式或文本。例如，条件可以表示为 32、"32"、">32" 或 "苹果"。

函数说明：

Microsoft Excel 提供其他函数，可用来基于条件分析数据。例如，若要计算基于一个文本字符串或某范围内的一个数值的总和，可使用 SUMIF 工作表函数。若要使公式返回两个基于条件的值之一，例如某指定销售量的销售红利，可使用 IF 工作表函数。

应用示例：

4. STDEVP函数

函数名称：STDEVP

主要功能：返回以参数形式给出的整个样本总体的标准偏差。标准偏差反映相对于平均值 (mean) 的离散程度。

使用格式：STDEVP(number1,number2,...)

参数说明：Number1,number2,... 为对应于样本总体的 1 到 30 个参数。也可以不使用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。

●文本和逻辑值（TRUE 或 FALSE）将被忽略。如果不能忽略逻辑值和文本，则请使用 STDEVPA 工作表函数。

函数说明：

●函数 STDEVP 假设其参数为整个样本总体。如果数据代表样本总体中的样本，应使用函数 STDEV 来计算标准偏差。

●对于大样本容量，函数 STDEV 和 STDEVP 计算结果大致相等。

●此处标准偏差的计算使用“有偏差”和“n”方法。

●函数 STDEVP 的计算公式如下：

其中 x 为样本平均值 AVERAGE(number1,number2,…)，n 为样本大小。

应用示例：

扩展知识点讲解

1.COUNTBLANK函数

函数名称：COUNTBLANK

主要功能：计算指定单元格区域中空白单元格的个数。

使用格式：COUNTBLANK(range)

参数说明：

Range 为需要计算其中空白单元格个数的区域。

函数说明：

即使单元格中含有返回值为空文本 ("")的公式，该单元格也会计算在内，但包含零值的单元格不计算在内。

应用示例： 本文标题：excel统计分析应用-EXCEL在通径分析中的应用[1] 52
本文地址： http://www.61k.com/1076445.html