一 : 一艘轮船的排水量是1×104t,在密度为1×103kg/m3的河水中
| 一艘轮船的排水量是1×104t,在密度为1×103kg/m3的河水中,它满载时排开的河水的体积是______m3,它从河里驶入海里时,其排水量会______(填“变大、变小或不变”). |
| 轮船所受浮力: F浮=G排=mg=1×104×1×103kg×10N/kg=1×108N, 排开河水的体积: V排=
轮船从河里到海里始终漂浮,浮力等于重力保持不变, ∵轮船漂浮, ∴F浮=G排=G船, m排=m船, 轮船的排水量不变. 故答案为:1×104;不变. |
考点:
考点名称:浮力及阿基米德原理浮力: ,式中ρ液表示液体的密度,V排是被物体排开的液体的体积,g取9.8N/kg。浮力大小跟哪些因素:
,式中ρ液表示液体的密度,V排是被物体排开的液体的体积,g取9.8N/kg。浮力大小跟哪些因素: 可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。
可以看出,浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关,而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。

 曹冲称象中的浮力知识:
曹冲称象中的浮力知识:| 上浮 | 下沉 | 悬浮 | 漂浮 | 沉底 | |
 |  |  |  |  | |
| F浮>G | F浮<G | F浮=G | F浮=G | F浮+N=G | |
| 实心物体 | ρ液>ρ物 | ρ液<ρ物 | ρ液=ρ物 V排=V物 | ρ液>ρ物 V排<V物 | ρ液>ρ物 V排=V物 |
| 处于动态(运动状态不断改变),受非平衡力作用 | 可以停留在液体的任何深度处 | 是“上浮”过程的最终条件 | 是“下沉”过程的最终状态 | ||
| 处于静态,受平衡力 | |||||
| 悬浮 | 漂浮 | ||
| 区别 | 物体在液体中的位置 | 物体可以静止在液体内部任一位置 | 物体静止在液体表面上 |
| 物体实心时,ρ物和ρ液的大小 | ρ物=ρ液 | ρ物<ρ液 | |
| 物体体积V物与物体排开液体体积V排的大小 | V物=V排 | V物>V排 | |
| 相似 | 物体都处于平衡状态,各自所受的浮力与重力式一对平衡力 | ||
利用浮力知识求物体或液体的密度:
1.对于漂浮的物体,浮力等于重力,而浮力F浮= ρ液gV排,重力G物=ρ物gV排,因F浮≈G物,只要知道V排与V物的关系和ρ液(或ρ物)就可求出ρ物(或ρ液)。
例1:将密度为0.6×103kg/m3,体积125cm3的木块放入盐水中,木块有1/2的体积露出盐水面,则木块受到的浮力为____N,盐水的密度____________ kg/m3(g取10N/kg)
解析:木块漂浮,所受浮力等于重力,F=G= Mg=p木Vg=0.6×103kg/m3×0.125×10-3m3× 10N/kg=0.75N,盐水的密度: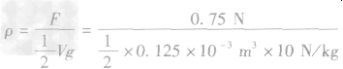 =1.2×103kg/m3
=1.2×103kg/m3
2. 若 ,物体完全浸没在液体中,根据阿基米德原理
,物体完全浸没在液体中,根据阿基米德原理 ,及称重法
,及称重法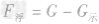 ,可求出
,可求出 ,又因为
,又因为 ,此时
,此时 ,可得
,可得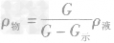 。根据此式,已知ρ液,可求出ρ物,已知ρ物可求出ρ液。
。根据此式,已知ρ液,可求出ρ物,已知ρ物可求出ρ液。
液面升降问题的解法:
1. 组合物体漂浮类型
要看液面是上升还是下降,关键是比较前后两次物体排开液体的体积的变化。设物体原来排开液体的体积为V排,后来排开液体的体积为V‘排,若V’排>V排,则液面上升,若V’排<V排,则液面下降;若V’排=V排,则液面高度不变,又根据阿基米德原理知,物体在液体中所受的浮力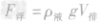 ,故
,故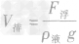 ,因为液体的密度ρ液不变,固物体的排开液体的体积取决于物体所受的浮力,所以只要判断出物体前后所受浮力的变化情况,即可判断出液面的升降情况。
,因为液体的密度ρ液不变,固物体的排开液体的体积取决于物体所受的浮力,所以只要判断出物体前后所受浮力的变化情况,即可判断出液面的升降情况。
例1一个水槽内漂浮着一个放有小铁球的烧杯,若将小铁球取出放入水槽里,烧杯仍漂浮在水槽中,则水面将( )
A.上升 B.不变 C.下降 D.无法判断
解析:铁球和烧杯漂浮在水中,装有铁球的烧杯所受的浮力F浮与烧杯和铁球的总重力平衡,则有: 。把铁球放入水槽中,铁球下沉,铁球单独受到的浮力,
。把铁球放入水槽中,铁球下沉,铁球单独受到的浮力,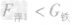 ;烧杯单独受到的浮力为
;烧杯单独受到的浮力为 。铁球放入水槽中后,铁球和烧杯所受浮力之和为
。铁球放入水槽中后,铁球和烧杯所受浮力之和为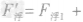 F浮2,因此
F浮2,因此 ,烧杯和铁球后来排开水的体积之和小于原来排开的水的体积,所以水面下降,故正确选项为C。
,烧杯和铁球后来排开水的体积之和小于原来排开的水的体积,所以水面下降,故正确选项为C。
2.纯冰熔化类型:
此类题的规律技巧:若冰块漂浮于水中,则冰熔化后液面不变;若冰块漂浮于密度大于水的液体中,则冰熔化后液面上升;若冰块漂浮于(或浸没于)密度小于水的液体中,则冰熔化后液面下降。
要判断液面的升降,必须比较冰排开液体的体积与冰熔化成水的体积之间的关系。冰未熔化时,若它漂浮在液面上,则所受的浮力与重力相等,即 。冰块所受的
。冰块所受的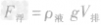 ,冰块的重力
,冰块的重力 ,由此可得
,由此可得 ;冰熔化后,化成水的体积
;冰熔化后,化成水的体积
 。所以当冰块漂浮于水中时,
。所以当冰块漂浮于水中时, ,液面不变;当
,液面不变;当 时,
时, ,液面上升。若冰块浸没液体中,则冰块排开液体的体积等于冰块的体积,而冰熔化后的体积小于冰的体积,故液面下降。
,液面上升。若冰块浸没液体中,则冰块排开液体的体积等于冰块的体积,而冰熔化后的体积小于冰的体积,故液面下降。
例2如图所示,烧杯中的冰块漂浮在水中,冰块上部高出杯口,杯中水面恰好与杯口相平,待这些冰全部熔化后( ) 
A.将有水从杯中溢出
B.不会有水从杯中溢出,杯中水面也不会下降
C.烧杯中水面下降
D.熔化过程中水面下降,完全熔化后有水溢出
解析:冰熔化后烧杯中的水面将保持不变,故不会有水溢出。
答案:B
漂浮物体切去露出部分后的浮沉情况:
漂浮物体,如将露出液面的部分切去后,物体的重力减小,而浸在液体中的部分没有变,根据F浮= ρ液gV排知物体所受浮力不变。这时浮力大于重力,剩余部分上浮。
例1长为L的蜡烛底部粘有一铁块,使其竖直停留在水中,如图所示,这时露出水面的长度为L0,将其点燃,直到自然熄灭,设燃烧掉的长度为d,则( ) 
A.d<L0
B.d=L0
C.d>L0
D.无法判断
解析:假设将露出的部分一次切去,再分析剩余部分的沉浮情况就很容易得出结论。如将露出水面的部分切去,这时蜡烛的重力减小,而在水中的部分未变,即排开的水的重力——浮力未变,显然这时浮力大于重力,剩余部分将上浮。可见,蜡烛燃烧过程是逐渐上浮的,所以最终烧掉的长度大于L0,故正确选项为C。
答案:C
| 上升 | 下降 | |
| 氢气球 | 充入密度小于空气的氢气 | 放掉球内部分气体,使球体积减小 |
| 热气球 | 充入加热后的热空气 | 停止加热,热空气冷却,热气球内空气密度增大 |
 ,G=mg。(g=9.8N/g)重力与质量的区别和联系:
,G=mg。(g=9.8N/g)重力与质量的区别和联系:| 质量 | 重力 | ||
| 区别 | 概念 | 物体所含物质的多少 | 由于地球吸引而使物体受到的力 |
| 符号 | m | G | |
| 量性 | 只有大小,没有方向 | 既有大小,又有方向 | |
| 单位 | 千克(kg) | 牛顿(N) | |
| 与地理位置的关系 | 与位置无关 | 与位置有关 | |
| 公式 | m=ρV | G=mg | |
| 测量工具 | 天平 | 测力计 | |
| 联系 | 重力与质量的关系是G=mg(g=9.8N/kg) | ||
二 : 在机场等一艘船
好多话想对你说,好多问题想向你求证,怕是说出来连朋友都做不得。[www.61k.com]或许本来都没有把彼此当做朋友。 对于你我也就是个路人甲,微不足道不足挂齿。你心里的那个人谁也替代不了,就像在我的心里谁也代替不了你一样。在这样的关系中我就是一个丑角,自始至终都是我一个人在表演,全程你都不曾参与,我有多可笑就有多可悲,就好像宋胖子唱的一样:你的城市没有一扇门为我打开 我终究还要回到路上。我这颗强大的自尊心不允许给你添一丝烦恼,可如今我不得不低头,因为你走了,即使走心里也是装着别人走的,我不想把自己模拟的的那么悲情,最悲情的人应该是你才对,我想不到用什么来形容此刻的我,总之只剩可笑,非常之可笑。我这懦弱的性格把什么都埋在心里,生怕给人添麻烦,可如今即使给你带来困扰我也不会愧疚了,总要给这三年一个交代,你讨厌也好嘲笑也罢我都不在乎了,一个人扛了那么久真的很累。 或许你看到这里仍然会嗤之以鼻,我就是太过于在乎别人的看法,所以才活的那么累,以后不会了。 一直都找不到和你说话的理由,因为我知道你也没什么话要说。两年后你还会不会记得我,记得有这么一个自作多情的傻逼女人。以前我不知道自己能够坚持到什么时候,但现在我想放弃了,太累太伤人了,受不了了。人是会幻想的动物,可是幻想的太美好,跌落回现实的时候就会摔得更痛,我觉得我已经全身粉碎性骨折了。 至于她,我是羡慕嫉妒恨,人生真的很不公平,无能为力的人是最可怜的。你爱谁就去爱好了,也许以后我的生命里不会再有爱情了。 我希望能尽快放弃你,尽快逃出来。 在机场等一艘船,在船上等一辆车,在晚上想晒太阳,在白天想看星星,注定是痴人说梦。 纵使往事如烟,依然感谢你有缘在我的生命中昙花一现。
三 : 军舰或轮船在海上航行的速度用"节"作为速度单位,请问一"节"相当?
军舰或轮船在海上航行的速度用"节"作为速度单位,请问一"节"相当?
“节”为速度单位,1节=1海里/小时,1海里=1852米,28节即28海?/小时(约51.85公里/小时,即14米/秒。)。
四 : 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台
| 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长30km的圆形区域。已知港口位于台风正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响? |
| 解:我们以台风中心为原点O,东西方向为x轴, 建立如右图所示的直角坐标系, 这样,受台风影响的圆形区域所对应的圆的方程为 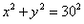 ① ①轮船航线所在直线  的方程为 的方程为 , ,即4x+7y-280=0, ② 如果圆O与直线  有公共点,则轮船受影响,需要改变航向; 有公共点,则轮船受影响,需要改变航向;如果O与直线  无公共点,则轮船不受影响,无需改变航向。 无公共点,则轮船不受影响,无需改变航向。由于圆心O(0,0)到直线  的距离为 的距离为 , ,所以直线  与圆O无公共点,这说明轮船将不受台风影响,不用改变航向。 与圆O无公共点,这说明轮船将不受台风影响,不用改变航向。 |  |
考点:
考点名称:直线与圆的位置关系直线与圆的位置关系:
由直线与圆的公共点的个数,得出以下直线和圆的三种位置关系:
(1)相交:直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线。
(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做切点。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
其图像如下: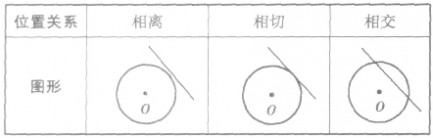
直线和圆的位置关系的性质:
(1)直线l和⊙O相交 d<r
d<r
(2)直线l和⊙O相切 d=r;
d=r;
(3)直线l和⊙O相离 d>r。
d>r。
直线与圆位置关系的判定方法:
(1)代数法:判断直线Ax+By+C=0和圆x2+y2+Dx+Ey+F=0的位置关系,可由
推出mx2+nx+p=0,利用判别式△进行判断.
△>0则直线与圆相交;
△=0则直线与圆相切;
△<0则直线与圆相离.
(2)几何法:已知直线Ax+By+C=0和圆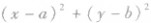
 ,圆心到直线的距离
,圆心到直线的距离
d<r则直线和圆相交;
d=r则直线和圆相切;
d>r则直线和圆相离.
特别提醒:
(1)上述两种方法,以利用圆心到直线的距离进行判定较为简捷,而判别式法也适用于直线与椭圆、双曲线、抛物线位置关系的判断.
(2)直线与圆相交,应抓住半径、弦心距、半弦长组成的直角三角形,可使解法简单.
直线与圆位置关系的判定方法列表如下:

直线与圆相交的弦长公式:
(1)几何法:如图所示,直线l与圆C相交于A、B两点,线段AB的长即为l与圆相交的弦长。
设弦心距为d,半径为r,弦为AB,则有|AB|=

(2)代数法:直线l与圆交于 直线l的斜率为k,则有
直线l的斜率为k,则有
当直线AB的倾斜角为直角,即斜率不存在时,|AB|=
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1