一 : 菱形的判定和性质

菱形的判定和性质

一、基础知识

（一）菱形的概念

一组邻边相等的平行四边形叫做菱形。（www.61k.com］ （二）菱形的性质：

1、 具有平行四边形的一切性质； 2、 菱形四条边都相等；

3、 菱形的对角线互相垂直平分，每条对角线平分一组对角； 4、 菱形是轴对称图形；

（三）菱形的判定：

1、 一组邻边相等的平行四边形是菱形； 2、 对角线互相垂直的平行四边形是菱形； 3、 四条边都相等的四边形是菱形； （四）菱形的面积

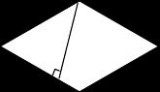
1、可以用平行四边形的面积算（S=

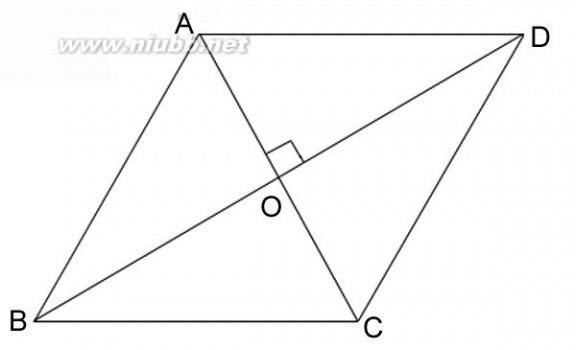
A

B

D

C

1

底×高） 2

1

ab) 2

2、用对角线计算（面积的两对角线的积的一半 S=

D

C

二、例题讲解

考点一 ：菱形的判定

例1：下列命题正确的是（ ）

1

菱形的判定 菱形的判定和性质

（A） 一组对边相等，另一组对边平行的四边形一定是平行四边形

（B） 对角线相等的四边形一定是矩形

（C） 两条对角线互相垂直的四边形一定是菱形

（D） 两条对角线相等且互相垂直平分的四边形一定是正方形

练习1：菱形的对角线具有( )

A．互相平分且不垂直

B．互相平分且相等

C．互相平分且垂直

D．互相平分、垂直且相等

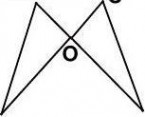
练习2：如图，菱形ABCD中，对角线AC、BD相交于点O，M、N分别是边AB、AD的中点，连接OM、ON、MN，则下列叙述正确的是（ ）

A．△AOM和△AON都是等边三角形 B．四边形AMON与四边形ABCD是位似图形

C．四边形MBON和四边形MODN都是菱形 D．四边形MBCO和四边形NDCO都是等腰梯形

B O

C

D

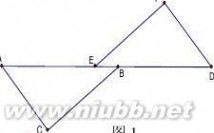
练习3：如图，在三角形ABC中，AB＞AC，D、E分别是AB、AC上的点，△ADE 沿线段DE翻折，使点A落在边BC上，记为A?．若四边形ADA?E是菱形，则下列说法正确的是( )

A．DE是△ABC的中位线 B．AA?是BC边上的中线

C．AA?是BC边上的高 D．AA?是△ABC的角平分线

D E

B

练习4：如图，下列条件之一能使平行四边形ABCD是菱形的为（ ）

?①AC?BD ②?BAD?90 ③AB?BC ④AC?BD A

A．①③ B．②③ C．③④ D．①②③

2

菱形的判定 菱形的判定和性质

A D

B

C

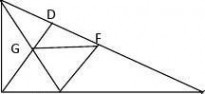
例2 ：已知AD是△ABC的平分线，DE∥AC交AB于E，DF∥AB交AC于F，则四边形AEDF是什么四边形？请说明理由．

B

变化：若D是等腰三角形底边BC的中点，DE∥AC交AB于E，DF∥AB交AC于F，则四边形AEDF是什么四边形？请说明理由．

练习1：如图，AD是Rt△ABC斜边上的高，BE平分∠B交AD于G，交AC于E，过E作EF⊥BC于F，试说明四边形AEFG是菱形．

A

练习2：如图，E是菱形ABCD边AD的中点，EF⊥AC于点H，交CB延长线于点F，交AB于点G，求证：AB与EF互相平分。（www.61k.com］

AG

FB

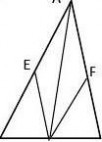
CED

3

菱形的判定 菱形的判定和性质

练习3：如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，DE垂直平分BC，垂足为D，交AB于点E，又点F在DE的延长线上，且AF＝CE，求证：四边形ACEF是菱形。(www.61k.com]

考点二：菱形的性质

例1：如图，四边形ABCD中，∠ADC＝90°，AC＝CB，E、F分别是AC、AB的中点，且∠DEA＝∠ACB＝45°，BG⊥AE于G，

求证：（1）四边形AFGD是菱形；

（2）若AC＝BC＝10，求菱形的面积。

B

D

EF

A

DG

E

F

A

C

练习1：如图，在菱形ABCD中，E是AB中点，且DE⊥AB，AB＝4， 求：（1）∠ABC的度数； （2）菱形ABCD的面积。

DC

A

E

B

4

菱形的判定 菱形的判定和性质

，BD?6． 例2 ：如图 5，ABCD是菱形，对角线AC与BD相交于O，?ACD?30°

（1）求证：△ABD是正三角形； （2）求 AC的长（结果可保留根号）．

D

A

C

练习1：若菱形的边长为1cm，其中一内角为60°，则它的面积为 ( ) A

．

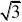
2

cm B

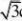
2 C．2cm2 D

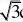
．2 2

练习2：若菱形的周长为16cm，两相邻角的度数之比是1：2，则菱形的面积是（ ）

（A） 43 cm （B）3 cm （C）163 cm （D）3 cm

练习3：已知菱形的周长为96㎝，两个邻角的比是1︰2，这个菱形的较短对角线的长是( )

A．21㎝ B．22㎝ C．23㎝ D．24㎝

例3： 如图，将一个长为10cm，宽为8cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线(虚线)剪下，再打开，得到的菱形的面积为( )

A．10cm

2

B．20cm

61阅读提醒您本文地址：

2

C．40cm

2

D．80cm

2

5

菱形的判定 菱形的判定和性质

练习1：菱形的两条对角线分别是12cm、16cm，则菱形的周长是（ ）

A．24cm B．32cm C．40 cm D．60cm

练习2：若菱形ABCD中，AE垂直平分BC于E，AE＝1cm，则BC的长是（ ）

（A）1cm （B）2cm （C）3cm （D）4cm

练习3:若菱形周长为52cm，一条对角线长为10cm，则其面积为( )

A．240 cm B．120 cm C．60 cm D．30 cm

例4:如图，菱形ABCD，E，F分别是BC，CD上的点，∠B＝∠EAF＝60°，∠BAE＝18°求∠CEF的度数。［www.61k.com]

A

BD

EF

C

练习1:如图，菱形ABCD中，∠B＝60°，AB＝2，E、F分别是BC．CD的中点，连接AE、EF、AF，则△AEF的周长为（ ）

A． 23 B． C． 4 D． 3 2222

D

6

菱形的判定 菱形的判定和性质

练习2：如图，在菱形ABCD中，?A?60°，E、F分别是AB、AD的中点，若EF?2，则菱形ABCD的边长是_____________．

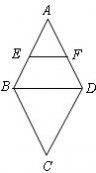
练习3：如图所示，已知菱形ABCD中，E、F分别在BC和CD上，且∠B=∠EAF=60°，∠BAE=15°， 求∠CEF的度数。[www.61k.com）

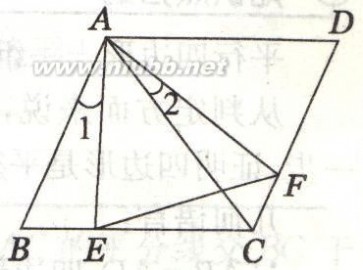
例5：如图，菱形ABCD是边长为13cm，其中对角线AC=10cm，

求（1）菱形ABCD的面积；

（2）作BC边上的高AH，求出AH的长度

ABD

C

7

菱形的判定 菱形的判定和性质

练习1：如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是48cm． 求：（1）两条对角线的长度； （2）菱形的面积．

A

D

例6： 已知：如图，在菱形ABCD中，E、F分别是BC、CD上的点，且CE=CF。(www.61k.com)过点C作CG∥EA交AF于H，交AD于G，若∠BAE=25°，∠BCD=130°，求∠AHC的度数。

A

G

B

E

CH

FD

练习1： 如图所示，已知菱形ABCD中E在BC上，且AB=AE，∠BAE=

1

∠EAD，AE交BD于M，试说明BE=AM。 2

8

菱形的判定 菱形的判定和性质

练习2：如图，菱形ABCD的边长为2，BD＝2，E、F分别是边AD，CD上的两个动点，且满足AE＋CF＝2．

(1) 求证：△BDE≌△BCF；

(2) 判断△BEF的形状，并说明理由；

(3) 设△BEF的面积为S，求S的取值范围．

考点三：综合

例1：如图，菱形AB1C1D1的边长为1，?B1?60?；作AD2?B1C1于点D2，以AD2为一边，做第二个菱形AB2C2D2，使?B2?60?；作AD3?B2C2于点D3，以AD3为一边做第三个菱形AB3C3D3，使?B3?60?；??依此类推，这样做的第n个菱形ABnCnDn的边ADn的长是．

C3B2

D3

C2

B1

A 2 1 B3D

1

例2：菱形ABCD的对角线交于O，AO=1，且∠ABC∶∠BAD=1∶2，∠ABO=300则下列结论：①．∠ABC=600；②．AC=2；③．BD=4；④．SABCD=2；⑤菱形ABCD的周长是8，其中正确的有（ ）

A．①②③④⑤ B．①②④⑤ C．②③④⑤ D．①②③

ABC

9

菱形的判定 菱形的判定和性质

例3：如图所示，在Rt△ABC中，∠ABC?90?．将Rt△ABC绕点C顺时针方向旋转60?得到△DEC，点E在AC上，再将Rt△ABC沿着AB所在直线翻转180?得到△ABF．连接AD ．

（1）求证：四边形AFCD是菱形；

（2）连接BE并延长交AD于G，连接CG，请问：四边形ABCG是什么特殊平行四边形？为什么？

A D

E

F B

C

课后练习:

1、若菱形的边长是它的高的2倍，则它的一个较小内角的度数是 。［www.61k.com]

2、如图1，在菱形ABCD中，AB = 5，∠BCD = 120°，则对

角线AC等于（ ）

A．20

C．10 B A D C B．15 D．5

3、菱形ABCD中，AE垂直平分BC，垂足为E，AB＝4cm．那么，菱形ABCD的面积是线BD的长是 ．

10

菱形的判定 菱形的判定和性质

B

4、如图，在菱形ABCD中，∠A=110°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC=（ ） A．35° B．45° C．50° D．55°

D

A

E

B F

P C

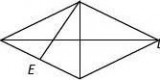
5、已知：如图，四边形ABCD是菱形，过AB的中点E作AC的垂线EF，交AD于点M，交CD的延长线于点F.

（1）求证：AM=DM；

（2）若DF=2，求菱形ABCD的周长．

B

FD第21题图C

11

61阅读提醒您本文地址：

二 : 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

第9讲 全等三角形的性质及判定

1、全等三角形概念：两个能完全重合的三角形叫做全等三角形．

2、全等三角形性质：（1）两全等三角形的对应边相等，对应角相等．

（2）全等三角形的对应边上的高相等，

对应边上的中线相等，

对应角的平分线相等．

（3）全等三角形的面积相等．

3、全等三角形判定方法：

（1）全等判定一：三条边对应相等的两个三角形全等（SSS）

（2）全等判定二：两角和它们的夹边对应相等的两个三角形全等（ASA）

（3）全等判定三：两角及其中一个角的对边对应相等的两个三角形全等(AAS)

（4）全等判定四：两边和它们的夹角对应相等的两个三角形全等（SAS）

（5）直角三角形的判定：一条直角边和斜边对应相等的两个直角三角形全等（HL）

专题一、全等图形的性质——全等图形的对应边（对应中线、角平分线、高线）、对应角、对应周长、对[文章窝]应面积相等

例题1：下列说法，正确的是（ ）

A.全等图形的面积相等 B.面积相等的两个图形是全等形

C.形状相同的两个图形是全等形 D.周长相等的两个图形是全等形

例题2：如图1，折叠长方形ABCD，使顶点D与BC边上的N点重合，如果

NM=____cm，?NAB. AD=7cm，DM=5cm，∠DAM=39°，则AN=____cm，

D C M D

B 图3

A B C 图2 N 图1 图4

【仿练1

】如图2，已知?ABC??ADE，AB?AD，BC?DE，那么与?BAE相等的角是 .

【仿练2】如图3，?ABC??ADE，则AB= ，∠E= _．若∠BAE=120°，∠BAD=40°，则∠BAC= .

1 养浩然之气，强立身之本。

20-http://www.61k.com-14春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

例题3：如图，在?ABC中，?A:?B:?ACB?2:5:11，若将?ACB绕点C逆时针旋转，使旋转前后的?A/B/C中的顶点B/在原三角形的边AC的延长线上，求

?BCA/的度数.

专题二、三角形全等的判定

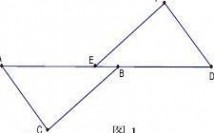
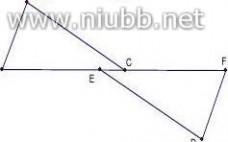
例题1：如图1,AE?DB,BC?EF,BC∥EF.求证:?ABC??DEF

【仿练1】已知.AB?DF,AC?DE,BE?CF,求证:AB ∥DF

【仿练2】如图，

AC=DF，AC//DF，AE=DB，求证：BC//EF

2

养浩然之气，强立身之本。

2014 春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

【仿练3】如图, AD=EB,AC∥DF,BC∥EF.求证:?ABC??DEF

A

BD

例题2：如图，在△ABC中, M在BC上, D在AM上, AB?AC,DB?DC.问BM?CM吗?说明理由.

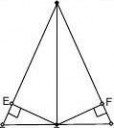
【仿练】如图, △ABC, AD是它的角平分线,且BD?CD,ED、DF分别垂直于AB、AC，垂足为E、F，请说明BE?CF.

3 养浩然之气，强立身之本。

61阅读

三 : 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

第9讲 全等三角形的性质及判定

1、全等三角形概念：两个能完全重合的三角形叫做全等三角形．

2、全等三角形性质：（1）两全等三角形的对应边相等，对应角相等．

（2）全等三角形的对应边上的高相等，

对应边上的中线相等，

对应角的平分线相等．

（3）全等三角形的面积相等．

3、全等三角形判定方法：

（1）全等判定一：三条边对应相等的两个三角形全等（SSS）

（2）全等判定二：两角和它们的夹边对应相等的两个三角形全等（ASA）

（3）全等判定三：两角及其中一个角的对边对应相等的两个三角形全等(AAS)

（4）全等判定四：两边和它们的夹角对应相等的两个三角形全等（SAS）

（5）直角三角形的判定：一条直角边和斜边对应相等的两个直角三角形全等（HL）

专题一、全等图形的性质——全等图形的对应边（对应中线、角平分线、高线）、对应角、对应周长、对应面积相等

例题1：下列说法，正确的是（ ）

A.全等图形的面积相等 B.面积相等的两个图形是全等形

C.形状相同的两个图形是全等形 D.周长相等的两个图形是全等形

例题2：如图1，折叠长方形ABCD，使顶点D与BC边上的N点重合，如果

NM=____cm，?NAB. AD=7cm，DM=5cm，∠DAM=39°，则AN=____cm，

D C M D

B 图3

A B C 图2 N 图1 图4

【仿练1

】如图2，已知?ABC??ADE，AB?AD，BC?DE，那么与?BAE相等的角是 .

【仿练2】如图3，?ABC??ADE，则AB= ，∠E= _．若∠BAE=120°，∠BAD=40°，则∠BAC= .

1 养浩然之气，强立身之本。［www.61k.com］

三角形全等的判定 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

例题3：如图，在?ABC中，?A:?B:?ACB?2:5:11，若将?ACB绕点C逆时针旋转，使旋转前后的?A/B/C中的顶点B/在原三角形的边AC的延长线上，求

?BCA/的度数.

专题二、三角形全等的判定

例题1：如图1,AE?DB,BC?EF,BC∥EF.求证:?ABC??DEF

【仿练1】已知.AB?DF,AC?DE,BE?CF,求证:AB ∥DF

【仿练2】如图，

AC=DF，AC//DF，AE=DB，求证：BC//EF

2

养浩然之气，强立身之本。(www.61k.com）

三角形全等的判定 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

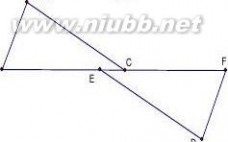
【仿练3】如图, AD=EB,AC∥DF,BC∥EF.求证:?ABC??DEF

A

BD

例题2：如图，在△ABC中, M在BC上, D在AM上, AB?AC,DB?DC.问BM?CM吗?说明理由.

【仿练】如图, △ABC, AD是它的角平分线,且BD?CD,ED、DF分别垂直于AB、AC，垂足为E、F，请说明BE?CF.

3 养浩然之气，强立身之本。(www.61k.com］

三角形全等的判定 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

例题3：已知：如图 , CE?AB于E , BF?CD于F , 且BF=CE．求证：BE=CF．

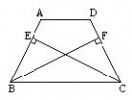
【仿练】已知：如图，∠A=∠D=90°，AC，BD交于O，AC=BD.求证：OB=OC．

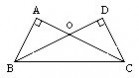
例题4：如图，AB?AC，AD?AE，?EAD??BAC.求证：△ABD≌△ACE

4 养浩然之气，强立身之本。（www.61k.com]

三角形全等的判定 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

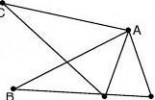
【仿练】已知如图,AE＝AC,AB＝AD,∠

EAB＝∠CAD,试说明:∠B＝∠D

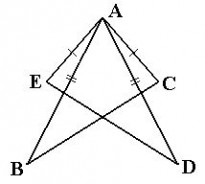
例题5：如图,?BDA??CEA,AE?AD.求证:AB?AC

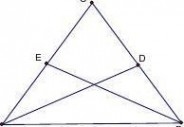
【仿练1】如图, △ABC是等腰三角形,AD,BE分别是?BAC,?ABC的角平分线,

△ABD和△BAE全等吗?请说明你的理由.

【仿练2

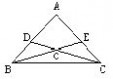
】已知：如图 , AB=AC , AD=AE , 求证：△OBD≌△OCE

5

养浩然之气，强立身之本。［www.61k.com］

三角形全等的判定 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

望子成龙学校家庭作业

第一部分：判断题

1．两边和一角对应相等的两个三角形全等. （ ）

2．两角和一边对应相等的两个三角形全等. （ ）

3．两条直角边对应相等的两个三角形全等. （ ）

4．腰长相等，顶角相等的两个等腰三角形全等. （ ）

5．三角形中的一条中线把三角形分成的两个小三角形全等. （ ）

6．两个等边三角形全等. （ ）

7．一腰和底边对应相等的两个等腰三角形全等. （ ）

8．腰长相等，且都有一个40°角的两个等腰三角形全等. （ ）

9．腰长相等，且都有一个100°角的两个等腰三角形全等. （ ）

10．有两边和第三边上的中线对应相等的两个三角形全等． （ ） 第二部分：选择题

2．如图,已知AC和BD相交于O,且BO＝DO,AO＝CO,下列判断正确的是（ ）

A．只能证明△AOB≌△COD B．只能证明△AOD≌△COB

C．只能证明△AOB≌△COB D．能证明△AOB≌△COD和△AOD≌△

COB

2题

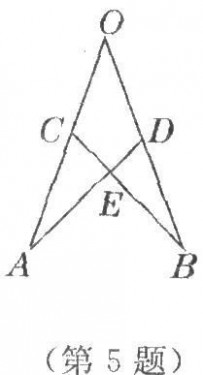
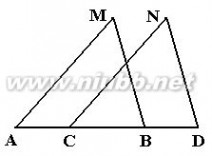
4．如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是（ ）

A．∠M＝∠N B．AB＝CD C．AM＝CN D．AM∥CN

5．如图，已知0A=OB，OC=0D，下列结论中：①∠A=∠B；②DE=CE；③连OE，则0E平分∠0，正确的是( )

A．①② B.②③ C．①③ D．①②③

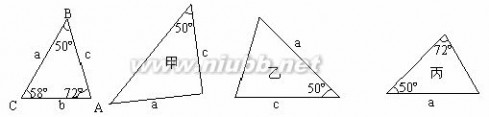
6.已知△ABC的六个元素,下面甲、乙、丙三个三角形中和△ABC全等的图形是（ ） A．甲和乙 Ｂ．乙和丙 Ｃ．只有乙 Ｄ．只有丙

6 养浩然之气，强立身之本。(www.61k.com]

三角形全等的判定 第9讲 全等三角形的性质及判定

2014春七年级数学个性化辅导讲义 自信释放潜能；付出铸就成功！

第三部分：填空题

1.如图，△ABC≌△AED，∠BAC=25°，∠B=35°，AB=3cm，

BC=1cm，则∠, ∠ DE= cm，

cm.

2.已知?ABC

??

DEF，若?ABC的周长为32，AB?8，BC?12，则DE，DF

B

C

DＥ

第四部分：解答题

??

1.如图，已知?ABC??AED，AE?AB，AD?AC，?D??E?20，?BAC?60.

求?C的度数.

2.如图，已知AB=DE，AF=DC，BE=CF，求证：∠A=∠D.

D

E

3.已知：AB=CD，AD=BC.试说明∠A=∠C.（公共边）

D

4.如图,在四边形ABCD中,已知BD平分∠ABC,∠A＋∠C＝180,试说明AD＝CD.

o

7 养浩然之气，强立身之本。［www.61k.com）

四 : 三角形的定义性质

定义

由三条边首尾相接组成的内角和为180°（一定是180°,这个是个准确的数!）的封闭图形叫做三角形

三角形的内角和

三角形的内角和为180度；三角形的一个外角等于另外两个内角的和；三角形的一个外角大于其他两内角中的任一个角。 三角形分类

(1)按角度分

a.锐角三角形：三个角都小于90度 。并不是有一个锐角的三角形，而是三个角都为锐角，比如等边三角形也是锐角三角形。

b.直角三角形（简称Rt 三角形）：

⑴直角三角形两个锐角互余；

⑵直角三角形斜边上的中线等于斜边的一半；

⑶在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半.；

⑷在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°（和⑶相反）；

c.钝角三角形：有一个角大于90度(锐角三角形，钝角三角形统称斜三角形)。

d.证明全等时可用HL方法

（2）按角分

a.锐角三角形：三个角都小于90度。

b.直角三角形：有一个角等于90度。

c.钝角三角形：有一个角大于90度。

（锐角三角形和钝角三角形可统称为斜三角形）

（3）按边分

不等腰三角形；等腰三角形（含等边三角形）。

解直角三角形（斜三角形特殊情况）：

勾股定理，只适用于直角三角形（外国叫“毕达哥拉斯定理”） a^2+b^2=c^2, 其中a和b分别为直角三角形两直角边，c为斜边。 勾股弦数是指一组能使勾股定理关系成立的三个正整数。比如：3，4，

5。他们分别是3，4和5的倍数。

常见的勾股弦数有：3，4，5；6，8，10；5,12,13;10,24,26;等等

三角形的性质

1.三角形的任何两边的和一定大于第三边 ，由此亦可证明得三角形的任意两边的差一定小于第三边。

2.三角形内角和等于180度

3.等腰三角形的顶角平分线，底边的中线，底边的高重合，即三线合一。

4.直角三角形的两条直角边的平方和等于斜边的平方--勾股定理。直角三角形斜边的中线等于斜边的一半。

5.三角形的外角（三角形内角的一边与其另一边的延长线所组成的角）等于与其不相邻的两个内角之和。

6.一个三角形最少有2个锐角。

7.三角形的角平分线:三角形一个角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段。

8.等腰三角形中，等腰三角形顶角的平分线平分底边并垂直于底边。

9.勾股定理逆定理：如果三角形的三边长a,b,c有下面关系

（a^2+b^2=c^2。）

那么这个三角形就一定是直角三角形。

10.三角形的外角和是360°。

11.等底等高的三角形面积相等。

12.底相等的三角形的面积之比等于其高之比，高相等的三角形的面积之比等于其底之比。

**13.三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。

**14.在△ABC中恒满足tanAtanBtanC=tanA+tanB+tanC。

15.三角形的一个外角大于任何一个与它不相邻的内角。

16.全等三角形对应边相等，对应角相等。

17.三角形的重心在三条中线的交点上。

**18在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。

（包括等边三角形）三角形的边角之间的关系

（1）三角形三内角和等于180°（在球面上，三角形内角之和大于180°）；

（2）三角形的一个外角等于和它不相邻的两个内角之和；

（3）三角形的一个外角大于任何一个和它不相邻的内角；

（4）三角形两边之和大于第三边，两边之差小于第三边；

（5）在同一个三角形内，大边对大角，大角对大边.

（6）三角形中的四条特殊的线段：角平分线，中线，高，中位线. （注①：等腰三角形中，顶角平分线，中线，高三线互相重叠

②：三角形的中位线是两边中点的连线，它平行于第三边且等于第三边的一半)

**（7）三角形的角平分线的交点叫做三角形的内心，它是三角形内切圆的圆心，它到各边的距离相等.

**（8）三角形的外接圆圆心，即外心，是三角形三边的垂直平分线的交点，它到三个顶点的距离相等.

**（9）三角形的三条中线的交点叫三角形的重心，它到每个顶点的距离等于它到对边中点的距离的2倍。

（10）三角形的三条高的交点叫做三角形的垂心。

（11）三角形的中位线平行于第三边且等于第三边的1/2。

（12）三角形的一边与另一边延长线的夹角叫做三角形的外角。特殊三角形

1.相似三角形

（1）形状相同但大小不同的两个三角形叫做相似三角形

（2）相似三角形性质

相似三角形对应边成比例，对应角相等

相似三角形对应边的比叫做相似比

相似三角形的周长比等于相似比，面积比等于相似比的平方 相似三角形对应线段（角平分线、中线、高）之比等于相似比 若a、b、b、c成比例，即a:b=b:c，则称b是a和c的比例中项

（3）相似三角形的判定

【1】三边对应成比例则这两个三角形相似

【2】两边对应成比例及其夹角相等，则两三角形相似

【3】两角对应相等则两三角形相似

2.全等三角形

（四）、全等三角形

（1）能够完全重合的两个三角形叫做全等三角形.

（2）全等三角形的性质。

全等三角形对应角（边）相等。

全等三角形的对应线段（角平分线、中线、高）相等、周长相等、面积相等。

（3）全等三角形的判定

① SAS ②ASA ③AAS ④SSS ⑤HL (RT三角形)】

寻找全等三角形的对应角、对应边常用方法：

3.等腰三角形

等腰三角形的性质：

（1）两底角相等；

(2) 两条腰相等 ；

（3）顶角的角平分线、底边上的中线和底边上的高互相重合； 等腰三角形的判定：

（1）等角对等边；

（2）两底角相等；

4.等边三角形

等边三角形的性质：

（1）顶角的角平分线、底边上的中线和底边上的高互相重合；

（2）等边三角形的各角都相等，并且都等于60°。

等边三角形的判定：

（1）三个内角或三个对应位置的外角都相等的三角形是等边三角形；

（2）有一个角等于60°的等腰三角形是等边三角形.

三角形的面积公式

(1)S△=1/2ah （a是三角形的底，h是底所对应的高）

(2)S△=1/2acsinB＝1/2bcsinA＝1/2absinC （三个角为∠A∠B∠C，对边分别为a,b,c，参见三角函数）

(3)S△=√［p(p-a)(p-b)(p-c)］ ［p=1/2(a+b+c)］（海伦—秦九韶公式）

(4)S△=abc/(4R) (R是外接圆半径)

(5)S△=1/2(a+b+c)r (r是内切圆半径)

(6) ........... | a b 1 |

S△=1/2 | c d 1 |

............| e f 1 |

［| a b 1 | ....| c d 1 | ....| e f 1 |为三阶行列式,此三角形ABC在平面直角坐标系内A(a,b),B(c,d), C(e,f),这里ABC选区取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但只要取绝对值就可以了，不会影响三角形面积的大小］

(7)S△=c^2sinAsinB/2sin(A+B)

(8)S正△= [（√3）/4]a^2 (正三角形面积公式，a是三角形的边长)

[海伦公式(3)特殊情况]

三角形重要定理

勾股定理（毕达哥拉斯定理）

内容：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方。

几何语言：若△ABC满足∠ABC=90°，则AB²+BC²=AC²

勾股定理的逆定理也成立，即两条边长的平方之和等于第三边长的平方，则这个三角形是直角三角形

几何语言：若△ABC满足，则∠ABC=90°。

[3]

正弦定理

内容：在任何一个三角形中，每个角的正弦与对边之比等于三角形面积的两倍与三边边长和的乘积之比

几何语言：在△ABC中，sinA/a=sinB/b=sinC/c=2S三角形/abc 结合三角形面积公式，可以变形为a/sinA=b/sinB=c/sinC=2R（R是外接圆半径）

余弦定理

内容：在任何一个三角形中，任意一边的平方等于另外两边的平方和减去这两边的2倍乘以它们夹角的余弦

几何语言：在△ABC中，a²=b²+c²-2bc×cosA 此定理可以变形为：cosA=（b²+c²-a²）÷2bc 生活中的三角形物品

雨伞、帽子、彩旗、灯罩、风帆、小亭子、雪山、楼顶、切成三角形的西瓜、火炬冰淇淋、热带鱼的边缘线、蝴蝶翅膀、火箭、竹笋、宝塔、金字塔、三角内裤、机器上用的三角铁、某些路标、长江三角洲、斜拉桥等。

三角形全等的条件 注意:只有三个角相等无法推出两个三角形全等，也不可以用“SSA”

（1）三边对应相等的两个三角形全等，简写为“SSS”。

（2）两角和它们的夹边对应相等的两个三角形全等，简写成“ASA”。

（3）两角和其中一角的对边对应相等的两个三角形全等，简写成“AAS”。

（4）两边和它们的夹角对应相等的两个三角形全等，简写成“SAS”。

（5）斜边和一条直角边对应相等的两个直角三角形全等，简写成“HL”。

全等三角形的性质

全等三角形的对应角相等，对应边也相等，并且全等三角形能重合。 三角形中的线段

中线：顶点与对边中点的连线，平分三角形的面积.

高：从三角形的一个顶点（三角形任意两条边的交点）向其对边所作的垂线段（顶点至对边垂足间的线段），叫做三角形的高。

角平分线:平分三角形的其中一个角的线段叫做三角形的角平分线,它到两边距离相等。(注:一个角的平分线是射线,平分线的所在直线是这个角的对称轴)

中位线：任意两边中点的连线。

三角形相关定理

中位线定理

三角形的中位线平行于第三边且等于第三边的一半．

三边关系定理

三角形任意两边之和大于第三边，任意两边之差小于第三边． 勾股定理(又称毕达哥拉斯定理）

在Rt三角形ABC中，A=90度，则

AB^2+AC^2=BC^2

****梅涅劳斯定理

梅涅劳斯（Menelaus）定理是由古希腊数学家梅涅劳斯首先证明的。它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。

证明：

过点A作AG∥BC交DF的延长线于G,

则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。

三式相乘得：AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1

它的逆定理也成立：若有三点F、D、E分别在的边AB、BC、CA或其延长线上，且满足(AF/FB)×(BD/DC)×(CE/EA)=1，则F、D、E三点共线。利用这个逆定理，可以判断三点共线。

*****塞瓦定理

设O是△ABC内任意一点，

AO、BO、CO分别交对边于D、E、F，则 BD/DC*CE/EA*AF/FB=1

证法简介

（Ⅰ）本题可利用梅涅劳斯定理证明：

∵△ADC被直线BOE所截，

∴ CB/BD*DO/OA*AE/EC=1 ①

而由△ABD被直线COF所截，∴ BC/CD*DO/OA*AF/BF=1②

②÷①:即得：BD/DC*CE/EA*AF/FB=1

（Ⅱ）也可以利用面积关系证明

∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③

同理 CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤ ③×④×⑤得BD/DC*CE/EA*AF/FB=1

利用塞瓦定理证明三角形三条高线必交于一点:

设三边AB、BC、AC的垂足分别为D、E、F，

根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA）/[(CD*ctgB）]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/

[(AE*ctgB)]=1，所以三条高CD、AE、BF交于一点。

*****莫利定理

将三角形的三个内角三等分，靠近某边的两条三分角线相交得到一个交点，则这样的三个交点可以构成一个正三角形。这个三角形常被称作莫利正三角形。

三角函数

三角函数（Trigonometric）是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。它由于三角函数的周期性，它并不具有单值函数意义上的反函数、但具有特殊的反三角函数(如：arcsin)，三角函数在复数中有较为重要的应用。在物理学中，三角函数也是常用的工具。

三角函数 种类

包含六种基本函数：正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)、余割(csc)。

五 : 三角形的定义性质

定义

由三条边首尾相接组成的内角和为180°（一定是180°,这个是个准确的数!）的封闭图形叫做三角形

三角形的内角和

三角形的内角和为180度；三角形的一个外角等于另外两个内角的和；三角形的一个外角大于其他两内角中的任一个角。（www.61k.com] 三角形分类

(1)按角度分

a.锐角三角形：三个角都小于90度 。并不是有一个锐角的三角形，而是三个角都为锐角，比如等边三角形也是锐角三角形。

b.直角三角形（简称Rt 三角形）：

⑴直角三角形两个锐角互余；

⑵直角三角形斜边上的中线等于斜边的一半；

⑶在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半.；

⑷在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°（和⑶相反）；

c.钝角三角形：有一个角大于90度(锐角三角形，钝角三角形统称斜三角形)。

d.证明全等时可用HL方法

（2）按角分

a.锐角三角形：三个角都小于90度。

b.直角三角形：有一个角等于90度。

c.钝角三角形：有一个角大于90度。

（锐角三角形和钝角三角形可统称为斜三角形）

（3）按边分

不等腰三角形；等腰三角形（含等边三角形）。

解直角三角形（斜三角形特殊情况）：

勾股定理，只适用于直角三角形（外国叫“毕达哥拉斯定理”） a^2+b^2=c^2, 其中a和b分别为直角三角形两直角边，c为斜边。 勾股弦数是指一组能使勾股定理关系成立的三个正整数。比如：3，4，

5。他们分别是3，4和5的倍数。

常见的勾股弦数有：3，4，5；6，8，10；5,12,13;10,24,26;等等

三角形的性质

三角形的定义 三角形的定义性质

1.三角形的任何两边的和一定大于第三边 ，由此亦可证明得三角形的任意两边的差一定小于第三边。[www.61k.com］

2.三角形内角和等于180度

3.等腰三角形的顶角平分线，底边的中线，底边的高重合，即三线合一。

4.直角三角形的两条直角边的平方和等于斜边的平方--勾股定理。直角三角形斜边的中线等于斜边的一半。

5.三角形的外角（三角形内角的一边与其另一边的延长线所组成的角）等于与其不相邻的两个内角之和。

6.一个三角形最少有2个锐角。

7.三角形的角平分线:三角形一个角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段。

8.等腰三角形中，等腰三角形顶角的平分线平分底边并垂直于底边。

9.勾股定理逆定理：如果三角形的三边长a,b,c有下面关系

（a^2+b^2=c^2。）

那么这个三角形就一定是直角三角形。

10.三角形的外角和是360°。

11.等底等高的三角形面积相等。

12.底相等的三角形的面积之比等于其高之比，高相等的三角形的面积之比等于其底之比。

**13.三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。

**14.在△ABC中恒满足tanAtanBtanC=tanA+tanB+tanC。

15.三角形的一个外角大于任何一个与它不相邻的内角。

16.全等三角形对应边相等，对应角相等。

17.三角形的重心在三条中线的交点上。

**18在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。

（包括等边三角形）三角形的边角之间的关系

（1）三角形三内角和等于180°（在球面上，三角形内角之和大于180°）；

（2）三角形的一个外角等于和它不相邻的两个内角之和；

（3）三角形的一个外角大于任何一个和它不相邻的内角；

（4）三角形两边之和大于第三边，两边之差小于第三边；

（5）在同一个三角形内，大边对大角，大角对大边.

（6）三角形中的四条特殊的线段：角平分线，中线，高，中位线. （注①：等腰三角形中，顶角平分线，中线，高三线互相重叠

三角形的定义 三角形的定义性质

②：三角形的中位线是两边中点的连线，它平行于第三边且等于第三边的一半)

**（7）三角形的角平分线的交点叫做三角形的内心，它是三角形内切圆的圆心，它到各边的距离相等.

**（8）三角形的外接圆圆心，即外心，是三角形三边的垂直平分线的交点，它到三个顶点的距离相等.

**（9）三角形的三条中线的交点叫三角形的重心，它到每个顶点的距离等于它到对边中点的距离的2倍。[www.61k.com]

（10）三角形的三条高的交点叫做三角形的垂心。

（11）三角形的中位线平行于第三边且等于第三边的1/2。

（12）三角形的一边与另一边延长线的夹角叫做三角形的外角。特殊三角形

1.相似三角形

（1）形状相同但大小不同的两个三角形叫做相似三角形

（2）相似三角形性质

相似三角形对应边成比例，对应角相等

相似三角形对应边的比叫做相似比

相似三角形的周长比等于相似比，面积比等于相似比的平方 相似三角形对应线段（角平分线、中线、高）之比等于相似比 若a、b、b、c成比例，即a:b=b:c，则称b是a和c的比例中项

（3）相似三角形的判定

【1】三边对应成比例则这两个三角形相似

【2】两边对应成比例及其夹角相等，则两三角形相似

【3】两角对应相等则两三角形相似

2.全等三角形

（四）、全等三角形

（1）能够完全重合的两个三角形叫做全等三角形.

（2）全等三角形的性质。

全等三角形对应角（边）相等。

全等三角形的对应线段（角平分线、中线、高）相等、周长相等、面积相等。

（3）全等三角形的判定

① SAS ②ASA ③AAS ④SSS ⑤HL (RT三角形)】

寻找全等三角形的对应角、对应边常用方法：

3.等腰三角形

等腰三角形的性质：

（1）两底角相等；

三角形的定义 三角形的定义性质

(2) 两条腰相等 ；

（3）顶角的角平分线、底边上的中线和底边上的高互相重合； 等腰三角形的判定：

（1）等角对等边；

（2）两底角相等；

4.等边三角形

等边三角形的性质：

（1）顶角的角平分线、底边上的中线和底边上的高互相重合；

（2）等边三角形的各角都相等，并且都等于60°。(www.61k.com)

等边三角形的判定：

（1）三个内角或三个对应位置的外角都相等的三角形是等边三角形；

（2）有一个角等于60°的等腰三角形是等边三角形.

三角形的面积公式

(1)S△=1/2ah （a是三角形的底，h是底所对应的高）

(2)S△=1/2acsinB＝1/2bcsinA＝1/2absinC （三个角为∠A∠B∠C，对边分别为a,b,c，参见三角函数）

(3)S△=√［p(p-a)(p-b)(p-c)］ ［p=1/2(a+b+c)］（海伦—秦九韶公式）

(4)S△=abc/(4R) (R是外接圆半径)

(5)S△=1/2(a+b+c)r (r是内切圆半径)

(6) ........... | a b 1 |

S△=1/2 | c d 1 |

............| e f 1 |

［| a b 1 | ....| c d 1 | ....| e f 1 |为三阶行列式,此三角形ABC在平面直角坐标系内A(a,b),B(c,d), C(e,f),这里ABC选区取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但只要取绝对值就可以了，不会影响三角形面积的大小］

(7)S△=c^2sinAsinB/2sin(A+B)

(8)S正△= [（√3）/4]a^2 (正三角形面积公式，a是三角形的边长)

[海伦公式(3)特殊情况]

三角形重要定理

勾股定理（毕达哥拉斯定理）

内容：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方。

几何语言：若△ABC满足∠ABC=90°，则AB²+BC²=AC²

三角形的定义 三角形的定义性质

雨伞、帽子、彩旗、灯罩、风帆、小亭子、雪山、楼顶、切成三角形的西瓜、火炬冰淇淋、热带鱼的边缘线、蝴蝶翅膀、火箭、竹笋、宝塔、金字塔、三角内裤、机器上用的三角铁、某些路标、长江三角洲、斜拉桥等。[www.61k.com)

三角形全等的条件 注意:只有三个角相等无法推出两个三角形全等，也不可以用“SSA”

（1）三边对应相等的两个三角形全等，简写为“SSS”。

（2）两角和它们的夹边对应相等的两个三角形全等，简写成“ASA”。

三角形的定义 三角形的定义性质

（3）两角和其中一角的对边对应相等的两个三角形全等，简写成“AAS”。[www.61k.com)

（4）两边和它们的夹角对应相等的两个三角形全等，简写成“SAS”。

（5）斜边和一条直角边对应相等的两个直角三角形全等，简写成“HL”。

全等三角形的性质

全等三角形的对应角相等，对应边也相等，并且全等三角形能重合。 三角形中的线段

中线：顶点与对边中点的连线，平分三角形的面积.

高：从三角形的一个顶点（三角形任意两条边的交点）向其对边所作的垂线段（顶点至对边垂足间的线段），叫做三角形的高。

角平分线:平分三角形的其中一个角的线段叫做三角形的角平分线,它到两边距离相等。(注:一个角的平分线是射线,平分线的所在直线是这个角的对称轴)

中位线：任意两边中点的连线。

三角形相关定理

中位线定理

三角形的中位线平行于第三边且等于第三边的一半．

三边关系定理

三角形任意两边之和大于第三边，任意两边之差小于第三边． 勾股定理(又称毕达哥拉斯定理）

在Rt三角形ABC中，A=90度，则

AB^2+AC^2=BC^2

****梅涅劳斯定理

梅涅劳斯（Menelaus）定理是由古希腊数学家梅涅劳斯首先证明的。它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。

证明：

过点A作AG∥BC交DF的延长线于G,

则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。

三式相乘得：AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1

它的逆定理也成立：若有三点F、D、E分别在的边AB、BC、CA或其延长线上，且满足(AF/FB)×(BD/DC)×(CE/EA)=1，则F、D、E三点共线。利用这个逆定理，可以判断三点共线。

*****塞瓦定理

设O是△ABC内任意一点，

AO、BO、CO分别交对边于D、E、F，则 BD/DC*CE/EA*AF/FB=1

三角形的定义 三角形的定义性质

证法简介

（Ⅰ）本题可利用梅涅劳斯定理证明：

∵△ADC被直线BOE所截，

∴ CB/BD*DO/OA*AE/EC=1 ①

而由△ABD被直线COF所截，∴ BC/CD*DO/OA*AF/BF=1②

②÷①:即得：BD/DC*CE/EA*AF/FB=1

（Ⅱ）也可以利用面积关系证明

∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③

同理 CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤ ③×④×⑤得BD/DC*CE/EA*AF/FB=1

利用塞瓦定理证明三角形三条高线必交于一点:

设三边AB、BC、AC的垂足分别为D、E、F，

根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA）/[(CD*ctgB）]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/

[(AE*ctgB)]=1，所以三条高CD、AE、BF交于一点。[www.61k.com）

*****莫利定理

将三角形的三个内角三等分，靠近某边的两条三分角线相交得到一个交点，则这样的三个交点可以构成一个正三角形。这个三角形常被称作莫利正三角形。

三角函数

三角函数（Trigonometric）是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。它由于三角函数的周期性，它并不具有单值函数意义上的反函数、但具有特殊的反三角函数(如：arcsin)，三角函数在复数中有较为重要的应用。在物理学中，三角函数也是常用的工具。

三角函数 种类

包含六种基本函数：正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)、余割(csc)。

本文标题：直角三角形的性质及判定-菱形的判定和性质
本文地址： http://www.61k.com/1065668.html