一 : MacBook Pro/Air怎么判断是否为翻新机?

如果你是在正规渠道购买 MacBook 笔记本的话，如苹果直营店，网上商店中，是不用担心买到翻新机的问题。不过有的小伙伴可能会选择其它一些渠道，购买水货之类，这样的话，如果遇到奸商的话，就有可能会遇到二手的翻新机。这里简单介绍一下怎么辨别 MacBook 笔记本是否为翻新机的方法。

一、先从外观着手

1、要辨别一款 MacBook 笔记本是否为翻新机的话，首先可以从它的外观下手。从整个机身，屏幕，键盘下手，看看是否有划痕，外观损伤等。

2、另外还可以查看笔记本底部的螺丝，看看是否有被扭动过的痕迹。

3、如果底部的螺丝有明显被扭动过的痕迹的话，那说明此机器肯定是翻新机了。如果笔记本的外观没有问题，螺丝也没有被扭动过的痕迹的话，请接着往下看。

二、查看电池使用信息

1、由于 MacBook Pro 或 Air 都会内置一块电池，在使用过程会经常为电池充放电，并且电池有忘记功能。我们可以先查看电池的使用次数，从这里着手，看看当前笔记本是否为翻新机。进入 Mac 系统以后，请点击屏幕左上角的苹果图标，再点击“关于本机”选项，如图所示

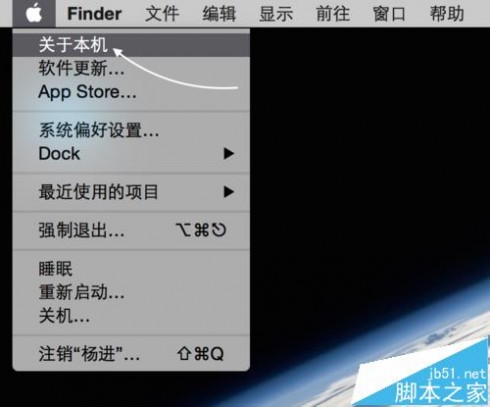
2、在关于本机信息窗口中点击“系统报告”按钮，如图所示

3、接着请在系统报告中窗口的左边栏中点击“电源”选项，如图所示

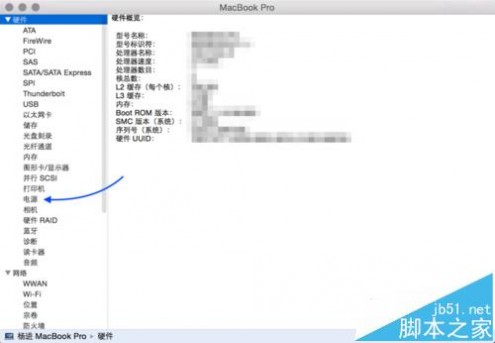
4、随后在电池信息中的效能信息下看到“循环次数”，这里可以看到我这台使用了半年有多的循环次数为152次，如图所示

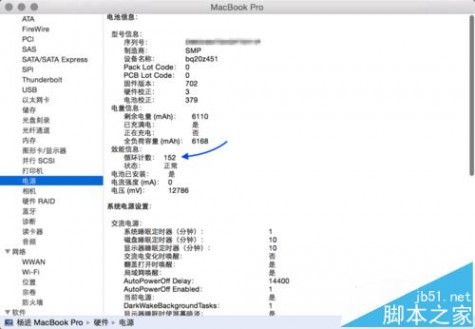
5、如果是一台新的 MacBook 笔记本，那这个电池循环次数应该是不超过10次才对。如果循环次数过多，说明是被使用过的。

三、从苹果官网查看序列号

1、除了上面二个方法以外，我们还可以通过 MacBook 本身的序列号来查询。这里建议大家通过 MacBook 笔记本底部来查看机器的序列号，在底部找到 Serial 序列号，后面跟的就是序列号了。

2、接着请打开苹果官网的机器序列号查询页面地址：https://selfsolve.apple.com/agreementWarrantyDynamic.do?，输入在机器背面看到的序列号，如图所示

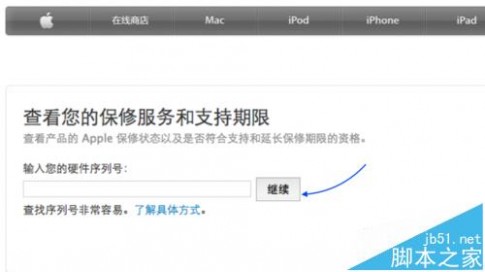
3、随后可以查看到当前机器的维修和服务保修情况，在这里有一个预计到期日，可以根据它来计算它的出厂日期。在这个日期上减一年，即为此机器的出厂日期。这样就可以知道当前机器是否为翻新机了，如果与你当前日期相差天数很多的话，那说明此机器是翻新机了。

相关推荐：

MacBook Pro触控板手势在哪里设置?

Macbook Pro笔记本中的光盘拿不出来了怎么办？

微软Surface Book 对比苹果MacBook Pro 跑分曝光

二 : 判断radio是否选中

frm.id.length 得到radio个数 :

<script>

function checkRadio(){

var f=0;

for(var i=0;i<frm.id.length; i++){

if(frm.id[i].checked == true){

f=1;

break;

}}

if(f==0)

alert("请选择");

}

</script>

<script language=\"javascript\">

<!--

function Checklogin(oForm){

var radios = oForm.rr;

var tFlag = false;

for(var i = 0; i < radios.length; i++){

if(radios[i].checked){

tFlag = true;

break;

}

}

if(tFlag == false){

alert(\'请选择\');

r（www.61k.com］eturn false;

}

oForm.submit();

}

-->

</script>

<form name=\"form1\">

<input type=\"radio\" name=\"rr\" value=\"0\">

<input type=\"radio\" name=\"rr\" value=\"1\">

<input type=\"button\" onClick=\"Checklogin(this.form)\" value=\"ok\" />

</form>

三 : 哪些指标判断是否患上甲肝

甲型肝炎（简称甲肝）是由甲肝病毒（HA）引起的一种病毒性肝炎，主要是经粪口传播途径感染，即由病人的潜伏期或急性期粪便、血液中的甲肝病毒污染水源、食物、用具及生活密切接触经口进入胃肠道而传播。(www.61k.com］临床上表现为急性起病，有畏寒、发热、食欲减退、恶心、疲乏、肝肿大及肝功能异常。

患上甲肝通常有哪些指标

1、抗-HAVIGM：发病后1周左右即可在血清中测出。其出现与临床症状及生化指标异常的时间一致，第2周达高峰。一般持续8周，少数患者可达6个月以上。但个别病人病初阴性，2-3周后方检出阳性。所以临床疑诊甲型肝炎，而抗-HAVIGM阴性，应重复1-2次，以免漏诊。

当前，抗-HAVIGM是早期诊断甲型肝炎的特异性较高的指标，且有简便，快速的优点。抗-IAVIGG是既往感染的指标，因其是保护性抗体，可保护人体再次感染故可作为流行病学调查，了解易感人群。

2、抗HAV-IgA的检测：IgA型抗体又称分泌型抗体，主要存在于泪眼，唾液，尿液，胃液，乳汁，鼻腔分泌物中，胃液中的IgA可排入粪便中，在甲型肝炎患者粪便提取液中可测得抗HAV-IgA。

可作为甲型肝炎的辅助诊断。此外，粪便中HAV的检测和血清甲肝核糖核酸HAVRNA亦有诊断价值，但需要一定的设备和技术，不作为常规检查项目。总之，对有典型症状的可疑甲型肝炎患者，伴转氨酶明显增高，可进一步查抗HAVIGM即可明确诊断甲型肝炎。

甲型肝炎各个时期的表现

1、黄疸时期起病急，有畏寒、发热、全身乏力、食欲不振、厌油、恶心、呕吐、腹痛、肝区痛、腹泻、鸟色逐渐加深，至本期末程浓茶状。少数甲肝患者以发热、头痛、上呼吸道症状等为主要表现。本期持续1-21日，平均5-7日。

2、黄疸期自觉症状可有所好转，发热减退，但尿色继续加深，巩膜、皮肤出现黄染，约于2周内达高峰。可有大便颜色变浅、皮肤骚痒、心动过缓等梗阻性黄疸表现。肝肿大至肋下1-3cm，有充实感，有压痛及叩击痛。部分甲肝患者有轻度脾肿大。本期持续2-6周。

3、恢复期黄疸逐渐退，症状减轻以至消失，肝、脾回缩，肝功能逐渐恢复正常。本期持续2周至4个月，平均1个月。

四 : matlab判断一个点是否在多面体内

要在空位区域随机放置一定数量的原子，这些原子在空位区域任何一处存在的概念是相同的。空位区域是由包围这个空位周边的一些原子定义的。

如果这个空位区域是一个标准的长方体，那么问题就比较简单，只需要产生随机数，然后再将随机数沿着基矢方向进行相应的缩放。

对于不规则的空间区域，也可以采用类似的思想：将空位区域（多面体）扩大到一个长方体，即长方体刚好是多面体的包络。然后在长方体内部随机产生点，如果点在多面体内部就保留；不在多面体内部就舍去，重新产生。

这其中就出现一个基础问题：如何判断一个点P是否在一个多面体内？多面体由空间三维点定义。

我的初步想法：

1. 将多面体划分成四面体

2. 判断这个点是否在这些四面体内部

3. 如果这个点在任何一个四面体内部，那么这个点就在这个多面体内部；

4. 如果这个点不在任何一个四面体内部，那么这个点就不在这个多面体内部。

那么核心问题就转换为：

1. 如何将多面体划分成许多的四面体？

2. 如何判断一个点是否在四面体内部？

对于第一个问题，matlab提供直接使用的函数 DelaunayTri 可以实现。

对于第二个问题，matlab也提供一个函数 tsearchn ，但是这个函数的健壮性比较差，至少我的问题没法解决。

没办法，在网上找到了有关的算法，自己写了代码。算法如下：

四面体由四个顶点定义：

V1 = (x1, y1, z1)
V2 = (x2, y2, z2)
V3 = (x3, y3, z3)
V4 = (x4, y4, z4)

要检测的点定义为：P = (x, y, z)

可以根据这些点组成的4个行列式来进行判断：

D0

|x1 y1 z1 1|
|x2 y2 z2 1|
|x3 y3 z3 1|
|x4 y4 z4 1|

D1

|x y z 1|
|x2 y2 z2 1|
|x3 y3 z3 1|
|x4 y4 z4 1|

D2

|x1 y1 z1 1|
|x y z 1|
|x3 y3 z3 1|
|x4 y4 z4 1|

D3

|x1 y1 z1 1|
|x2 y2 z2 1|
|x y z 1|
|x4 y4 z4 1|

D4

|x1 y1 z1 1|
|x2 y2 z2 1|
|x3 y3 z3 1|
|x y z 1|

判据：

如果Di (i=1,2,3,4)与D0的符号都相同，即同为正，或同为负，那么P点就在四面体内部；

否则P点在四面体外部。

以上算法参考：Point in Tetrahedron Test

具体代码如下：

12345678910111213141516171819202122232425262728293031323334353637

function inflag =inpolyhedron(point_set,p_detected)% point_set: a set of points stores thecoordinates% p_detected: point to be detected% inflag:%flag = 1: the point is in the polyhedron.%flag = 0: the point is not in the polyhedron.% Powered by: Xianbao Duanxianbao.d@gmail.com% stores the coordinates of the convexes.tri = DelaunayTri(point_set);% number of the tetrahedrons decomposed from thepolyhedronnum_tet = size(tri,1);t_inflag = zeros(1,11);for i = 1:num_tetv1_coord =point_set(tri(i,1),:);v2_coord =point_set(tri(i,2),:);v3_coord =point_set(tri(i,3),:);v4_coord =point_set(tri(i,4),:);D0 =det([v1_coord,1;v2_coord,1;v3_coord,1;v4_coord,1]);D1 =det([p_detected,1;v2_coord,1;v3_coord,1;v4_coord,1]);D2 =det([v1_coord,1;p_detected,1;v3_coord,1;v4_coord,1]);D3 =det([v1_coord,1;v2_coord,1;p_detected,1;v4_coord,1]);D4 =det([v1_coord,1;v2_coord,1;v3_coord,1;p_detected,1]);if D0*D1> 0 &&D0*D2>0 &&D0*D3>0 && D0*D4> 0t_inflag(i) =1;break;endendif sum(t_inflag) >0inflag = 1;% disp('The poi（www.61k.com）nt is in the polyhedron.');elseinflag = 0;% disp('The point is not in thepolyhedron.');end

本文标题：matlab判断是否为空-MacBook Pro/Air怎么判断是否为翻新机?
本文地址： http://www.61k.com/1168423.html