一 : 合数的定义 合数的定义是什么
不是质数的数就是合数如;4,6,8,10如果一个大于1的整数,除了1和它本身外,还有其他因数,这个数就称为合数,如4,6,9,15等。4是最小的合数。一个合数至少有3个因数。合数的定义是什么?以下是我们为大家整理的关于合数的定义,欢迎大家前来阅读!
36-31形的阴性数在以下式中可以确定是阴性上合数和阴性下合数还是阴性素数。
(www.61k.com。A阴一上
(3N)^2+N+(b-1)/36=W^2
A阴二上
(3N)^2+2N+(b-5)/36=w^2+w
N
A阴二下
(3N+2)^2+4N+2+(b+31)/36=W^2+w
N
N自然数,b阴性数(加1能被6整除的),W另一自然数。
两式都没有整数解的,这个阴性数是素数.36-25形的阴性数在以下式中可以确定是阴性上合数和阴性下合数还是阴性素数。
A阴三上
(3N+1)^2-N+(b-11)/36=w^2
N
A 阴三下
(3N+2)^2+N+(b+25)/36=W^2
N
N自然数,b阴性数(加1能被6整除的),W另一自然数。
两式都没有整数解的,这个阴性数是素数.36-19形的阴性数在以下式中可以确定是阴性上合数和阴性下合数还是阴性素数。
A阴四 上
(3N+1)^2+2N+1+(b-17)/36=w^2+w
N
A阴四下
(3N+1)^2+4N+1+(b+19)/36=W^2+w
N
N自然数,b阴性数(加1能被6整除的),W另一自然数。
两式都没有整数解的,这个阴性数是素数。36-13形的阴性数在以下式中可以确定是阴性上合数和阴性下合数还是阴性素数。A阴五上
(3N+2)^2-N+(b-23)/36=w^2
N
(3N+1)^2+N+(b+13)/36=W^2
n
N自然数,b阴性数(加1能被6整除的),W另一自然数。
两式都没有整数解的,这个阴性数是素数.36-7形的阴性数在以下式中可以确定是阴性上合数和阴性下合数还是阴性素数。
A阴六
上
(3N+2)^2+2N+2+(b-29)/36=w^2+w
n
下
(3N)^2+4N+(b+7)/36=W^2+w
n
N自然数,b阴性数(加1能被6整除的),W另一自然数。
两式都没有整数解的,这个阴性数是素数.
阳性数可在以下各式中确定是阳性上合数和阳性下合数还是阳性素数。A阳一 上
(3N)^2+N-(B-1)/36=W^2
一个阳性数代入此式B,有整数解的,这个阳性数是阳性上合数,并能很快找到数因子.
A阳一下
(3N)^2-N-(B-1)/36=W^2
一个阳性数代入此式B,有整数解的,这个阳性数是阳性下合数,并能很快找到数因子;
N〈B/252, N自然数,B阳性数(减1能被6整除的),W另一自然数。
两式都没有整数解的,这个阳性数是质数。
阳二上
(3N)^2+4-(B-7)/36=w^2+w
一个阳性数代入此式B,有整数解的,这个阳性数是阳性上合数,并能很快找到数因子;
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,9,15,49等都是合数。[1]
A阳二下
(3N+2)^2+2N+2-(B+29)/36=W^2+w
一个阳性数代入此式B,有整数解的,这个阳性数是阳性下合数,并能很快找到数因子;
N〈B/252, N自然数,B阳性数(减1能被6整除的),W另一然数。
两式都没有整数解的,这个阳性数是质数。
阳三上
(3N+1)^2+N-(B-13)/36=w^2
一个阳性数代入此式B,有整数解的,这个阳性数是阳性上合数,并能很快找到数因子;
A阳三下
(3N+2)^2-N-(B+23)/36=W^2
一个阳性数代入此式B,有整数解的,这个阳性数是阳性下合数,并能很快找到数因子;
N〈B/252, N自然数,B阳性数(减1能被6整除的),W另一然数。
两式都没有整数解的,这个阳性数是质数。
阳四上
(3N+1)^2+4N+1-(B-19)/36=w^2+w
一个阳性数代入此式B,有整数解的,这个阳性数是阳性上合数,并能很快找到数因子;
A阳四下
(3N+1)^2+2N+1-(B+17)/36=W^2+w
一个阳性数代入此式B,有整数解的,这个阳性数是阳性下合数,并能很快找到数因子;
N〈B/252, N自然数,B阳性数(减1能被6整除的),W另一然数。
两式都没有整数解的,这个阳性数是质数。
阳五上
(3N+2)^2+N-(B-25)/36=w^2
一个阳性数代入此式B,有整数解的,这个阳性数是阳性上合数,并能很快找到数因子;
A阳五下
(3N+1)^2-N-(B+11)/36=W^2
一个阳性数代入此式B,有整数解的,这个阳性数是阳性下合数,并能很快找到数因子;
N〈B/252, N自然数,B阳性数(减1能被6整除的),W另一然数。
两式都没有整数解的,这个阳性数是质数.
阳六上
(3N+2)^2+4N+2-(B-31)/36=w^2+w
一个阳性数代入此式B,有整数解的,这个阳性数是阳性上合数,并能很快找到数因子;
A阳六下
(3N+1)^2-N-(B+11)/36=W^2+W
一个阳性数代入此式B,有整数解的,这个阳性数是阳性下合数,并能很快找到数因子;
N〈B/252, N自然数,B阳性数(减1能被6整除的),W另一自然数。
两式都没有整数解的,这个阳性数是质数
所有大于2的偶数都是合数。
所有大于5的奇数中,个位为5的都是合数。
除0以外,所有个位为0的自然数都是合数。
所有个位为4,6,8的自然数都是合数。
最小的(偶)合数为4,最小的奇合数为9。
每一个合数都可以以唯一形式被写成质数的乘积,即分解质因数。(算术基本定理)
对任一大于5的合数(威尔逊定理)
合数的一种方法为计算其质因数的个数。一个有两个质因数的合数称为半质数,有三个质因数的合数则称为楔形数。在一些的应用中,亦可以将合数分为有奇数的质因数的合数及有偶数的质因数的合数。对於後者, (其中μ为默比乌斯函数且''x''为质因数个数的一半),而前者则为
注意,对於质数,此函数会传回 -1,且 。而对於有一个或多个重复质因数的数字''n'', 。
另一种分类合数的方法为计算其因数的个数。所有的合数都至少有三个因数。一质数的平方数,其因数有 。一数若有著比它小的整数都还多的因数,则称此数为高合成数。另外,完全平方数的因数个数为奇数个,而其他的合数则皆为偶数个。
只有1和它本身两个因数的自然数,叫质数(或称素数)。(如:由2÷1=2,2÷2=1,可知2的因数只有1和它本身2这两个因数,所以2就是质数。与之相对立的是合数:“除了1和它本身两个因数外,还有其它因数的数,叫合数。”如:4÷1=4,4÷2=2,4÷4=1,很显然,4的因数除了1和它本身4这两个因数以外,还有因数2,所以4是合数。)
100以内的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,一共有25个。
质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法:反证法。具体证明如下:假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么,N+1是素数或者不是素数。
如果N+1为素数,则N+1要大于p1,p2,……,pn,所以它不在那些假设的素数集合中。
如果N+1为合数,因为任何一个合数都可以分解为几个素数的积;而N和N+1的最大公约数是1,所以N+1不可能被p1,p2,……,pn整除,所以该合数分解得到的素因数肯定不在假设的素数集合中。
因此无论该数是素数还是合数,都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说,素数有无穷多个。
其他数学家给出了一些不同的证明。欧拉利用黎曼函数证明了全部素数的倒数之和是发散的,恩斯特·库默的证明更为简洁,Hillel Furstenberg则用拓扑学加以证明。
任何一个大于1的自然数N,都可以唯一分解成有限个质数的乘积,这里P1
这样的分解称为N的标准分解式。
算术基本定理的内容由两部分构成:分解的存在性、分解的唯一性(即若不考虑排列的顺序,正整数分解为素数乘积的方式是唯一的)。
算术基本定理是初等数论中一个基本的定理,也是许多其他定理的逻辑支撑点和出发点。
此定理可推广至更一般的交换代数和代数数论。高斯证明复整数环Z[i]也有唯一分解定理。它也诱导了诸如唯一分解整环,欧几里得整环等等概念,更一般的还有戴德金理想分解定理。
二 : 什么是偶数 偶数的定义
所有整数不是奇数(单数),就是偶数(双数)。那么你对偶数了解多少呢?以下是由我们整理关于什么是偶数的内容,希望大家喜欢!

定义一:在整数中,能被2整除的数,叫做偶数。
(www.61k.com”定义二:是二的倍数叫做偶数。《北师大版教科书》
(根据定义的不同就产生歧义了:0到底是不是偶数??)
0是一个特殊的偶数。它既是正偶数与负偶数的分界线,又是正奇数与负奇数的分水岭。
偶数列
数列0,2,4,6,8,……,2(n-1)称为偶数列。偶数列的通项公式:an=2n-2;偶数列前n项的和:Sn=n²-n。偶数列实质上是一个等差数列,首项=0,公差2。
偶数不定方程
2n=p1+p2
关于偶数和奇数,有下面的性质:
(1)两个连续整数中必是一个奇数一个偶数;
(2)奇数与奇数的和或差是偶数;偶数与奇数的和或差是奇数;任意多个偶数的和都是偶数;单数个奇数的和是奇数;双数个奇数的和是偶数;
(3)两个奇(偶)数的和或差是偶数;一个偶数与一个奇数的和或差一定是奇数;
(4)除2外所有的正偶数均为合数;
(5)相邻偶数最大公约数为2,最小公倍数为它们乘积的一半;
(6)奇数与奇数的积是奇数;偶数与偶数的积是偶数;奇数与偶数的积是偶数;
(7) 偶数的个位一定是0、2、4、6或8;奇数的个位一定是1、3、5、7或9;
(8)任何一个奇数都不等于任何一个偶数; 若干个整数的连乘积,如果其中有一个偶数,乘积必然是偶数;
(9).偶数的平方被4整除,奇数的平方被8除余1。
上述性质可通过对奇数和偶数的代数式进行相应运算得出。
如证明:两个奇数的和为偶数.
可令两奇数k1=2n1-1; k2=2n2-1(其中n1,n2皆为整数)。
则k1+k2=(2n1-1)+(2n2-1)=2(n1+n2-1),
由于括号内的多项式n1+n2-1是整数,从而原命题得证。

三 : 分式的定义 数学中分式的定义是什么 分式的概念
分式(fēn shì)是指有除法运算,而且除数中含有未知数的有理式。如果A、B表示两个整式,并且B中含有字母(B≠0),那么式子A / B 就叫做分式,其中A叫做分子,B叫做分母。分式是不同于整式的另一类式子。数学中分式的定义是什么?以下是我们为大家整理的关于分式的定义,欢迎大家前来阅读!
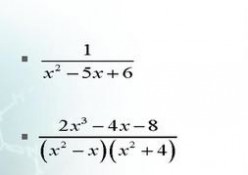
定义
形如 ,A、B是整式,B中含有字母且B不等于0的式子叫做分式(fraction)。其中A叫做分式的分子,B叫做分式的分母。如是分式,还有也是分式。要使分式 有意义,则y不等于0.
注意
掌握分式的概念应注意:
判断一个式子是否是分式,不要看式子是否是A/ B的形式,关键要满足:
(1)分式的分母中必须含有字母。
“www.61k.com。(2)分母的值不能为零。若分母的值为零,则分式无意义。
由于字母可以表示不同的数,所以分式比分数更具有一般性。
整式和分式统称为有理式。
带有根号且根号下含有字母的式子叫做无理式
无理式和有理式统称代数式
有意义的条件
(1)分式有意义条件:分母不为0
(2)分式无意义条件:分母为0;
(3)分式值为0条件:分子为0且分母不为0;
(4)分式值为正(负)数条 件:同号得正,异号得负。
1.分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变。用式子表示为:
,(A,B,C为整式,且B、C≠0)。
2.约分:把一个分式的分子和分母的公因式约去,这种变形称为分式的约分。约分的关键是确定分式中分子与分母的公因式。
3.分式的约分步骤:
(1)如果分式的分子和分母都是单项式或者是几个因式乘积的形式,将它们的公因式约去。
(2)分式的分子和分母都是多项式,将分子和分母分别分解因式,再将公因式约去。
注:公因式的提取方法:系数取分子和分母系数的最大公约数,字母取分子和分母共有的字母,指数取公共字母的最小指数,即为它们的公因式。
4.最简分式:一个分式的分子和分母没有公因式时,这个分式称为最简分式。约分时,一般将一个分式化为最简分式。
5.根据分式的基本性质,异分母的分数可以通分,使几个分数的的分母相同;同样,根据分式的基本性质,分式也可以进行类似的变形,使几个异分母分式的分母相同,而分式的值不变。
6.通分:把几个异分母分式分别化为与原分式值相等的同分母分式,叫做分式的通分。
7.分式的通分步骤:
先求出所有分式分母的最简公分母,再将所有分式的分母变为最简公分母。同时各分式按照分母所扩大的倍数,相应扩大各自的分子。
注:最简公分母的确定方法:
系数取各因式系数的最小公倍数,相同字母的最高次幂及单独字母的幂的乘积。
注:(1)约分和通分的依据都是分式的基本性质。
(2)分式的约分和通分都是互逆运算过程。
分子分母同时乘或除以同一个不等于零的整式,分式的值不变。
运算法则
1.同分母分式加减法则:同分母的分式相加减,分母不变,把分子相加减。用字母表示为:
2.异分母分式加减法则:异分母的分式相加减,先通分,化为同分母的分式,然
后再按同分母分式的加减法法则进行计算。用字母表示为:。
备注:异分母的分式可以化成同分母的分式,这一过程叫做通分。如:和可化为和.即:,
3.分式的乘法法则:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。用字母表示为:。
4.分式的除法法则:
(1).两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘。
(2).除以一个分式,等于乘以这个分式的倒数:。
5.乘方法则:分子相乘做分子,分母相乘做分母,可以约分的约分,最后化成最简。
6.约分:把一个分式的分子和分母的公因式约去的过程为约分。
1.使学生理解并掌握分式的概念,了解有理式的概念;
2.使学生能够求出分式有意义的条件;
3.通过类比分数研究分式的教学,培养学生运用类比转化的思想方法解决问题的能力;
4.通过类比方法的教学,培养学生对事物之间是普遍联系又是变化发展的辨证观点的再认识.
二、重点、难点、疑点及解决办法
1.教学重点和难点 明确分式的分母不为零.
2.疑点及解决办法 通过类比分数的意义,加强对分式意义的理解.
新课引入
前面所研究的因式分解问题是把整式分解成若干个因式的积的问题,但若有如下问题:某同学分钟做了60个仰卧起坐,每分钟做多少个?可表示为,问,这是不是整式?请一位同学给它试命名,并说一说怎样想到的?(学生有过分数的经验,可猜想到分式)
新课
1.分式的定义
(1)由学生分组讨论分式的定义,对于“两个整式相除叫做分式”等错误,由学生举反例一一加以纠正,得到结论:
用、表示两个整式,就可以表示成的形式.如果中含有字母,式子就叫做分式.其中叫做分式的分子,叫做分式的分母.
(2)由学生举几个分式的例子.
(3)学生小结分式的概念中应注意的问题.
①分母中含有字母.
②如同分数一样,分式的分母不能为零.
(4)问:何时分式的值为零?[以(2)中学生举出的分式为例进行讨论]
2.有理式的分类
请学生类比有理数的分类为有理式分类:
例1 当取何值时,下列分式有意义?
(1);
解:由分母得.
∴当时,原分式有意义.
(2);
解:由分母得.
∴当时,原分式有意义.
(3);
解:∵恒成立,
∴取一切实数时,原分式都有意义.
(4).
解:由分母得.
∴当且时,原分式有意义.
思考:若把题目要求改为:“当取何值时下列分式无意义?”该怎样做?
例2 当取何值时,下列分式的值为零?
(1);
解:由分子得.
而当时,分母.
∴当时,原分式值为零.
小结:若使分式的值为零,需满足两个条件:①分子值等于零;②分母值不等于零.
(2);
解:由分子得.
而当时,分母,分式无意义.
当时,分母.
∴当时,原分式值为零.
(3);
解:由分子得.
而当时,分母.
当时,分母.
∴当或时,原分式值都为零.
(4).
解:由分子得.
而当时,,分式无意义.
∴没有使原分式的值为零的的值,即原分式值不可能为零。
看过"分式的定义"的人还关注了:
1.武当纯阳无极功的简介
2.初三数学增根是什么
3.八年级数学知识点总结下册
4.8年级数学下册复习提纲
5.初一数学手抄报内容资料
本文标题:实数的定义是什么-合数的定义 合数的定义是什么61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1