一 : 网申(apply on line)全攻略

    1 何为网申？
    所谓“网申”，即 apply on line( 网络在线申请 ) ，目前很多“大牛”公司 ( 比如壳牌、联合利华、宝洁 ) 可都是通过这种方式来收集简历和初步筛选求职者的。以前，求职者往往在就业网站上随便逛逛，看到有合适的工作，就随便扔份简历到人家 hr( 人力资源 ) 的信箱里，然后坐等面试机会上门。现在，这样的**已经渐渐远去了。
    2 关于网申中的开放题（ open questions ）
    网申中的开放题是最让人头痛的，但是各公司的开放题题目差别不大，所以我们可以提早准备，将其一举拿下。具体来说，它侧重于个人的合作能力和技巧，工作的抗压能力，是否有不利于工作的性格缺陷等等。举例如下：
    2.1 关于职业生涯规划的问题：请谈谈你 3 － 5 年的规划
    对于一个未踏进职场的学生而言，有非常明晰的职业规划也不大现实。 hr 之所以这样问是希望挖掘你应聘的深层次动机，看你是否具有稳定性。建议回答不要过于具体，如“ 3 年成为主管， 5 年要成为经理。”在不清楚对方职级和晋升条件的情况下，此类过于具体的回答都不明智。
    2.2 你认为大学**最成功 / 失败的一件事是什么？”“你最遗憾的一件事是什么？为什么？
    对于这类问题， hr 主要是从你的回答中来判断出你的价值观，即在你眼里什么最重要；对你而言，什么才是成功。对于这类题，回答有一个基本思路，就是“ star ”原则。 s=situation ， t ＝ target ， a ＝ action ， r ＝ result 。你完成某事或者做出某决定是在怎样的背景下，当时你具有怎样的资源，面临怎样的问题、事情或者决定最终的目标是什么；你是如何行动的 ( 利用资源、克服困难、解决突发状况等等 ) ；最后的结果是什么。如果是失败的事例，那么结果之后你还需要分析失败的原因，并总结你得到的经验教训。
    2.3 举例说明你是如何说服一个难以说服的人
    这类问题考的就是你的沟通和影响能力。
    2.4 为什么选择某某公司，为什么申请这个职位等等
这一类问题主要对看清自己，给自己一个清晰的定位很有帮助。
    3 网申过程中易犯的错误
    3.1 为了及时提交申请，打开网页直接申请
    在申请前，应该做好充分准备。比如，看看公司的企业文化，公司所强调的方方面面，这样在回答开放题时就会投其所好，不致白忙一场。
    3.2 细节并不重要，只要差不多就可以了
    错：千万少犯低级错误，注意拼写、语法等细节问题。一般大公司都比较注重专业精神，像平时写 email 一样的“个性”风格往往不易被接受。“网申”虽不见面，却也别因手指的失误，失去了宝贵的印象分。
    例如，某同学在给美林证券写完 cover letter ，募然发现……他居然在一处地方写的是“ i can work as an analyst for morgan stanley ”；另外一个同学在填写美的集团网申时遇到这样一道开放题：
    第三题 请简要说明你应聘美的集团的原因
    看看这位同学的答案：多元化的经营策略使企业有着良好的发展前景；企业有着良好的激励机制，节奏紧凑，效率高； 海信集团 有着良好的公众形象等等。犯这样明显而又低级的错误真是不应该。
    3.3 感觉网申太麻烦，填了一半就放弃了
    网申过程一般情况下需要很长时间，有的甚至三四个小时，所以大家千万不要放弃，不认真填写网申的唯一结果就是被刷下来。在现在的求职过程中，淘汰率最高的当属网申！
    3.4 随心所欲，想怎么填就怎么填
    一般都是填写中英文两份简历，但是在填写过程中务必将中英文对应起来。
    4 关于网申的 9 条建议
    由于一般公司的服务器相对于网站的服务器而言并不是特别强劲，则当很多人在线申请的时候时常容易出现死机或联不上服务器的情况，所以建议大家挑选人员相对不密集的时间上网，如午饭、凌晨等；此外记得填写完一页就及时保存所填写的内容，免得做无用功。
    另一方面，配置不太好或上网环境不稳定的机器常常会长时间联线后出现死机断网的情况，所以最好去网速快的地方上网，还有在填写比较大篇幅问题的时候，尽量在 word 环境下填写，然后再粘贴到网页上去。不过用ｗｏｒｄ保存还有一点好处，那就是它可以显示一些错误，提醒你改正，尤其是一些不太容易察觉的比如拼写之类的小错误。
    很多公司的“网申”提供在线修改的服务，不必等到所有的问题都答完才保存。只要在结束期限之前，都可以上去更新你的简历和思考更好的答案。
    很多公司网申的 open question 都大同小异，因此记得搜集每次“网申”的题目和自己写的答案，以方便今后答题。
    多上论坛和就业网翻看各大公司网申的秘笈以及招聘流程，做到心中有数。网络**的一大好处就是资源共享，千万不要浪费别人的经验和体会。
    千万别犯低级错误，注意拼写、语法等细节问题。一般大公司都较注重专业精神，如果连“家庭作业”都要出现拼写语法等错误，不是你不够重视就是你英语不过关。在“复制 - 粘贴”的时候，注意格式的变化，有些特殊字符在文本框中不能正常的显示，需要替换为 * 号和 # 号等分类符。
    网申前一定要通过公司网站对应聘公司做透彻了解，千万别怕麻烦。“磨刀不误砍柴工”，对于企业文化、核心业务、中国分公司发展等情况的了解，有助于答题能更好地契合企业要求。另外，网站的风格、用词、对职位的描述等能提供你一些线索，如关于应聘职位要求的基本素质、对方惯用的专业语言等。
    有一些公司的网上申请表格是交给专门的公司负责的，例如， unilever( 联合利华 ) 的网上申请，第一轮的简历筛选就是由 chinahr 来负责的。这份网上申请的表格设计得很完善，从个人信息到教育背景，实习经历很多方面都覆盖到了。最后部分还有八个开放性的问题。对于这样的表格，首先，你的信息要尽可能填的完善，因为网上申请有一个很重要的检索步骤是电脑自动地按照关键字来检索，所以如果你的申请资料上没有 hr 想要的这一类关键字，很有可能你就被筛选掉了。因此最好尽量在你的资料中覆盖这些重要的关键字。当然你不可能知道这些关键字具体是哪些，因此最好的办法是尽可能填的完善。其次对于那些开放性的问题，尽量利用所给的字数限制，既不要超出也不要大大的节省。一般来说，注明需要用 300 字来回答的问题，你只写了一百个字恐怕是很难符合要求的。
    公司自己的网站有专门的申请地址。如果说上一类申请表格是通过格式的话，那么这一类的针对性就更强了。每个公司的申请表格都是经过精心设计的，符合他们所需要寻找的未来员工的重要的指标。例如 ge ，它的网上申请的表格是十分完善的，填写的步骤也很复杂。需要的注意的问题有：一，申请职位的填写要特别慎重，虽然很多公司的职位选择都是可以复选的，但是当心，这很有可能成为面试的话题。当你同时选择了比如人力资源和高分子材料工程师两个职位时，除非你有充分的理由让 hr 相信你同时具备这两个职位所要求的能力，否则只会给人“乱投医”的感觉。其次，注意你的申请资料的填写和你所申请职位的匹配。需要特别强调的实习经历和专业技能，要着重地强调，和前一种一样，尽可能的覆盖那些重要的关键字。
    5 网申实践
    下面，就以申请 moto intern ( ）的实际操作为例来给大家演示一下网申的一般步骤。
    step 1 ： 进入 moto 的网站 ( ），点击“ internship at motorola ”—“ internship opportunity ” — “ position search ” , 然后就可以根据不同的条件 (city, function, business unit) 选择自己感兴趣的职位。
    step 2 ：在“ by city ”一栏里，我们选择“ beijing ” , 于是就列出了在“ beijing ”的一些职位。
    step 3 ：接着就可以结合自身条件，申请自己比较感兴趣的职位， ( 例如： intern-admin)
    step 4: 注册：点击“ register ”按钮， 填写简历，主要包括：个人信息，教育背景，语言和计算机水平，工作实习及实际项目经验，其他等：个人信息、教育背景、语言与计算机水平、工作实习及实践项目经验、其他情况（个人特长；奖励等情况）
    step 5 ：提交，点击“ submit ”按钮，自此一个一般的网申流程就完成了，接下来你需要做的就是耐心地等待 moto 的回复了。

二 : philips on-line test笔经

      (1)首先，最好能在网络条件、计算机条件较好较稳定，且环境比较安静(不要分散注意力)的地方准备进行测试。因为测试是限时的，而且时间比较紧，一旦进入测试环节，倒计时就开始了，要全力以赴答题才可能完成。(注：网速不影响时间，shl将测试传到本地机，做完后上传，所以计算机不死机，网络不断网就行了)

　　(2)登录shl后，先简要填写个人信息，比如国籍等(英文，也有法语、德语或其他语种可选，无中文可选);

　　(3)个人信息完成后，进入测试部分，此时可再次选择测试题目的语言，建议选择简体中文，因为即使中文读起来都有些生疏的文字，用英文作答可能比较难懂或是时间不允许(若英文有近似母语的程度可以试一试英文)

　　(4)我的on-line测试分为两个部分：

　　逻辑推理判断：即根据给出的一段话，对题目中的结论进行 "对" or “错" or “无法判断" 的选择;15分钟15道题;进入这一单元后，可以先做不计时的练习题，可重复多次做练习，但都是同一套题，每次做完会给出结果，哪道错哪道题对会显示，建议通过这一套题调整自己做题时间的安排，尽量将思维调整到shl测试正确的思路上。最后进入正式测试，注意时间，冷静解答;

　　数字计算：即给出一些图或表格，当中给出一些数据，如gdp，人口数;股票价格、债务、净利润;etc.根据这些数据，计算相关的一些数值。这一部分也会先安排不计时的练习，也可重复多次做练习，但也是同一套题，也会给出答案，建议同上;
 

三 : on-line

Agenericschemeforthedesignofe?cient

on-linealgorithmsforlattices

PetkoValtchev1,MohamedRouaneHacene1,andRokiaMissaoui2DIRO,Universit′edeMontr′eal,C.P.6128,Succ.“Centre-Ville”,

Montr′eal,Qu′ebec,Canada,H3C3J7

D′epartementd’informatiqueetd’ing′enierie,UQO,C.P.1250,succursaleB

Gatineau,Qu′ebec,Canada,J8X3X712

Abstract.Amajorissuewithlargedynamicdatasetsistheprocess-ingofsmallchangesintheinputthroughcorrespondinglysmallre-arrangementsoftheoutput.Thiswasthemotivationbehindthede-signofincrementaloron-linealgorithmsforlatticemaintenance,whoseworkamountstoagradualconstructionofthe?nallatticebyrepeat-edlyaddingrows/columnstothedatatable.Asanattempttoputtheincrementaltrendonstrongtheoreticalgrounds,wepresentagenericalgorithmicschemethatisbasedonadetailedanalysisofthelatticetransformationtriggeredbyarow/columnadditionandoftheunderly-ingsub-structure.Foreachtaskfromtheschemewesuggestane?cientimplementationstrategyandputalowerboundonitsworst-casecom-plexity.Moreover,aninstanciationoftheincrementalschemeispresentedwhichisascomplexasthebestbatchalgorithm.

1Introduction

Formalconceptanalysis(FCA)[5]studiesthelatticestructuresbuiltontopofbinaryrelations(calledconceptlatticesorGaloislatticesasin[1]).Asamatteroffact,theunderlyingalgorithmictechniquesareincreasinglyusedintheresolutionofpracticalproblemsfromsoftwareengineering[6],datamining[7]andinformationretrieval[3].

Ourstudyinvestigatesthenewalgorithmicproblemsrelatedtotheanalysisofvolatiledatasets.Asaparticularcase,on-lineorincrementallatticealgorithms,asdescribedin[8,3],basicallymaintainlatticestructuresupontheinsertionofanewrow/columnintothebinarytable.Thus,givenabinaryrelationKanditscorrespondinglatticeL,andanewrow/columno,thelatticeL+correspondingtotheaugmentedrelationK+=K∪{o}iscomputed.Mostoftheexistingon-linealgorithmshavebeendesignedwithpracticalconcernsinmind,e.g.,e?cienthandlingoflargebutsparsebinarytables[8]andthereforeproveine?cientwheneverdatasetsgetdenser[9].

Here,weexplorethesuborderofL+madeupofallnewnodeswithrespecttoLanduseanisomorphicsuborderofL(thegeneratorsofthenewnodes)thatworksasaguidelineforthecompletionofLtoL+.Structuralpropertiesofthelattersuborderunderlythedesignofagenericcompletionscheme,i.e.,asequence

阿衰on line on-line

ofstepsthatcanbeseparatelyexaminedfore?cientimplementations.Asa?rsto?springofthescheme,wedescribeanovelon-linealgorithmthatreliesbothoninsightsonthegeneratorsuborderandonsomecardinality-basedreasoningwhilebringingdowntheoverallcostoflatticeconstructionbysubsequentcompletionstothecurrentlowerboundforbatchconstruction.

ThepaperstartsbyrecallingsomebasicFCAresults(Section2)andfunda-mentalsoflatticeconstruction(Section3).Thestructureofthegenerator/newsubordersintheinitial/targetlattice,respectively,isthenexamined(Section4).Next,agenericschemeforlatticecompletionissketchedandforeachtaskoftheschemeimplementation,directionsarediscussed(Section5).Finally,thepaperpresentsane?ectivealgorithmforlatticemaintenanceandclari?esitsworst-casecomplexity(Section6).

2Formalconceptanalysisbackground

FCA[5]studiesthepartiallyorderedstructure,knownunderthenamesofGaloislattice[1]orconceptlattice,whichisinducedbyabinaryrelationoverapairofsetsO(objects)andA(attributes).

De?nition1.AformalcontextisatripleK=(O,A,I)whereOandAaresetsandIisabinary(incidence)relation,i.e.,I?O×A.

Withinacontext(seeFigure1ontheleft),objectsaredenotedbynumbersandattributebysmallletters.Twofunctions,fandg,summarizethecontext-relatedlinksbetweenobjectsandattributes.

De?nition2.Thefunctionfmapsasetofobjectsintothesetofcommonattributes,whereasg3isthedualforattributesets:

–f:P(O)→P(A),f(X)=X??={a∈A|?o∈X,oIa}

–g:P(A)→P(O),g(Y)=Y??={o∈O|?a∈Y,oIa}

Forexample,f(14)=fgh4.Furthermore,thecompoundoperatorsg?f(X)andf?g(Y)areclosureoperatorsoverP(O)andP(A)respectively.Thus,eachoftheminducesafamilyofclosedsubsets,calledCoandCarespectively,withfandgasbijectivemappingsbetweenbothfamilies.Acouple(X,Y),ofmutuallycorrespondingclosedsubsetsiscalleda(formal)concept.

De?nition3.Aformalconceptisacouple(X,Y)whereX∈P(O),Y∈P(A),X=Y??andY=X??.XiscalledtheextentandYtheintentoftheconcept.

Thus,(178,bcd)isaconcept,but(16,efh)isnot.Moreover,thesetCKofallconceptsofthecontextK=(O,A,I)ispartiallyorderedbyintent/extentinclusion:(X1,Y1)≤K(X2,Y2)?X1?X2(Y2?Y1).

阿衰on line on-line

1X3

X

5

XXXX7

X9X

阿衰on line on-line

AnearlyFCAalgorithmhasbeensuggestedbyGanter[4]basedonaparticularorderamongconceptsthathelpsavoidcomputingagivenconceptmorethanonce.

However,ofgreaterinteresttousarealgorithmsthatnotonlydiscoverC,butalsoinferthelatticeorder≤,i.e.,constructtheentirelatticeL.Thismorecomplexproblemmaybeformalizedasfollows:

ProblemCompute-Lattice

Given:acontextK=(O,A,I),

Find:thelatticeL=??C,≤??correspondingtoK.

BatchalgorithmsfortheCompute-Latticeproblemhavebeenproposed?rstbyBordat[2]andlateronbyNourineandRaynaud[10].TheformeralgorithmreliesonstructuralpropertiesoftheprecedencerelationinLtogeneratetheconceptsinanappropriateorder.Thus,fromeachconceptthealgorithmgener-atesitsuppercoverswhichmeansthataconceptwillbegeneratedanumberoftimesthatcorrespondstothenumberofitslowercovers.Recently,NourineandRaynaudsuggestedane?cientprocedureforconstructingafamilyofopensetsandshowedhowitmaybeusedtoconstructthelattice(seeSection5.4).

61阅读提醒您本文地址：

Thereisaknowndi?cultyinestimatingthecomplexityoflatticeconstruc-tionalgorithmsuniquelywithrespecttothesizeoftheinputdata.Actually,thereisnoknownbound(otherthanthetrivialone,i.e.,thenumberofallsub-setsofOorA)ofthenumberofconceptsdependingonthedimensionsofthebinaryrelation,i.e.,thesizeoftheobjectset,oftheattributeset,orofthebinaryrelation.Evenworse,ithasbeenrecentlyproventhattheproblemofestimatingthesizeofLfromKis#P-complete.Fortheabovereasons,itisadmittedtoincludethesizeoftheresult,i.e.,thenumberoftheconcepts,inthecomplexityestimation.Thus,with|L|asafactor,theworst-casecomplexityexpressionoftheclassicalalgorithmssolvingCompute-ConceptisO((k+m)lkm),wherel=|L|,k=|O|,andm=|A|.ThealgorithmofBordatcanbeassessedtobeofcomplexityO((k+m)l|I|)wherethesizeofthebinaryrelation(i.e.,thenumberofpositiveentriesinK)istakenintoaccount.Finally,theworkofNourineandRaynaudhashelpedreducethecomplexityorderoftheproblemtoO((k+m)lk).

3.2Incrementalapproaches

On-lineorincrementalalgorithmsdonotactuallyconstructthelattice,butrathermaintainitsintegrityupontheinsertionofanewobject/attributeintothecontext:

ProblemCompute-Lattice-Inc

Given:acontextK=(O,A,I)withitslatticeLandanobjecto,

Find:thelatticeL+correspondingtoK+=(O∪{o},A,I∪{o}×o??).

阿衰on line on-line

Obviously,theproblemCompute-LatticemaybepolynomiallyreducedtoCompute-Lattice-IncbyiteratingCompute-Lattice-IncontheentiresetO(A).Inotherwords,an(extended)incrementalmethodcanconstructthelat-ticeLstartingfromasingleobjecto1andgraduallyincorporatinganynewobjectoi(onitsarrival)intothelatticeLi?1(overacontextK=({o1,...,oi?1},A,I)),eachtimecarryingoutasetofstructuralupdates.

Godinetal.[8]suggestedanincrementalprocedurewhichlocallymodi?esthelatticestructure(insertionofnewconcepts,completionofexistingones,dele-tionofredundantlinks,etc.)whilekeepinglargepartsofthelatticeuntouched.ThebasicapproachfollowsafundamentalpropertyoftheGaloisconnectiones-tablishedbyfandgon(P(O),P(A)):bothfamiliesCoandCaareclosedunderintersection[1].Thus,thewholeinsertionprocessisaimedattheintegrationintoLi?1ofallconceptswhoseintentscorrespondtointersectionsof{oi}??withaaintentsfromCi?1,whicharenotthemselvesinCi?1.Theseadditionalconcepts(furthercallednewconceptsinN+(o)),areinsertedintothelatticeatapar-ticularplace,i.e.,eachnewconceptisprecededbyaspeci?ccounterpartfromtheinitiallattice,calleditsgenerator(thesetofgeneratorsisdenotedG(o)).TwoothercategoriesofconceptsinL=Li?1aredistinguished:modi?ed(M(o))aconceptscorrespondtointersectionsof{oi}??withmembersofCi?1thatalreadyaexistinCi?1,whiletheremainingsetofconceptsintheinitiallatticearecalledoldorunchanged.Inthe?nallatticeL+=Li,theoldconceptspreservealltheircharacteristics,i.e.,intent,extentaswellasupperandlowercovers.Generatorsdonotexperiencechangesintheirinformationcontent,i.e.,intentandextent,butanewconceptisaddedtotheiruppercovers.Inamodi?edconcept,theextentisaugmentedbythenewobjectowhileinthesetofitslowercovers,anygeneratorisreplacedbythecorrespondingnewconcept.Inthenextsections,weshallsticktothisintuitiveterminology,butweshallputitonaformalgroundwhiledistinguishingthesetsofconceptsintheinitiallattice(M(o)andG(o))fromtheircounterpartsinthe?nalone(M(o)+andG(o)+,respectively).

Example1(Insertionofobject9).AssumeListhelatticeinducedbytheob-jectset12345678(seeFigure1ontheright)andconsider9asthenewob-ject.Thesetofunchangedconceptshastwoelements,{c#6,c#10},whereasthesetofmodi?edandgeneratorsareM(o)={c#1,c#2,c#3,c#4,c#5,c#8}andG(o)={c#7,c#9,c#11,c#12,c#13}respectively.Theresultofthewholeoper-ationisthelatticeLinFigure2.Thus,thesetofthenewconceptintentsis:{cd,fh,cdgh,dfgh,cdfgh}.

AnotherincrementalalgorithmforlatticeconstructionhasbeensuggestedbyCarpinetoandRomano[3].

Inarecentpaper[11],wegeneralizedtheincrementalapproachofGodinetal..Forthispurpose,weappliedsomestructuralresultsfromthelatticeas-semblyframeworkde?nedin[14].Inparticular,weshowedthattheincrementalproblemCompute-Lattice-IncisaspecialcaseofthemoregenerallatticeassemblyproblemAssembly-Lattice.Morerecently,wehavepresentedathe-oreticalframeworkthatclari?estherestructuringinvolvedintheresolutionof

阿衰on line on-line

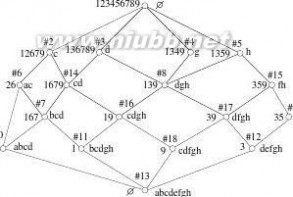
efhFig.2.TheHassediagramoftheconcept(Galois)latticederivedfromKwithO={1,2,3,...,9}.

Compute-Lattice-Inc[13]andfurtherenablesthedesignofproceduresthatexploreonlyapartofthelatticeL(seeSection6).

Inthenextsection,werecallthebasicresultsfromourframework.

4Theoreticalfoundations

Forspacelimitationreasons,onlykeyde?nitionsandresultsthathelptheun-derstandingofthemoretopicaldevelopmentsareprovidedinthissection.

First,asetofmappingsisgivenlinkingthelatticesLandL+5.ThemappingσsendsaconceptfromLtotheconceptinL+withthesameintentwhereasγworksotherwayround,butrespectsextentpreservation(moduloo).Themappingsχandχ+sendaconceptinLtothemaximalelementofitsclass[]QinLandL+,respectively.

61阅读提醒您本文地址：

De?nition1Assumethefollowingmappings:

–

–

–

–??γ:C+→Cwithγ(X,Y)=(X1,X1),whereX1=X?{o},σ:C→C+withσ(X,Y)=(Y??,Y)whereY??iscomputedinK+,χ:C→Cwithχ(X,Y)=(Y1??,Y1????),whereY1=Y∩{o}??,

χ+:C→C+withχ+(X,Y)=(Y1??,Y1),whereY1=Y∩{o}??(??overK+).TheabovemappingsaredepictedinFigure3.Observethatσisajoin-preservingorderembedding,whereasγisameet-preservingfunctionwithγ?σ=idC.Moreover,bothmappingsunderlythenecessaryde?nitions(skippedhere)forthesetsG(o)andM(o)inLandtheircounterpartsG+(o)andM+(o)inL+toreplacetheintuitivedescriptionsweusedsofar.

阿衰on line on-line

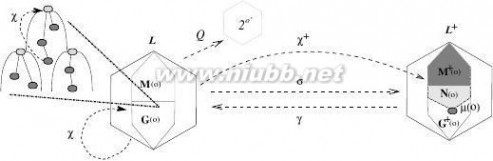
Fig.3.ThelatticesL,L+and2Arelatedbythemappingsχ,χ+,σ,γandQ.A?rstkeyresultstatesthatG(o)andM(o)areexactlythemaximalconceptsintheequivalenceclassesinducedbythefunctionQ:C→2Ade?nedasQ(c)=Y∩{o}??wherec=(X,Y).Moreover,thesuborderofLmadeupofG(o)andM(o)isisomorphic,viaχ+,to↑ν(o),i.e.,theprime?lterofL+generatedbytheminimalconceptincludingo.Consequently,(G(o)∪M(o),≤)isameet-semi-lattice.

Finally,theprecedenceorderinL+evolvesfromtheprecedenceinLasfollows.Givenanewconceptc,itsgeneratorσ(c)isalowercoverofcwhilethepossibleotherlowercoversofc(Covl(c))layinN+(o).TheuppercoversofcaretheconceptsfromM+(o)∪N+(o),thatcorrespond,viaσ,totheuppercoversofthegeneratorσ(c)inthesemi-lattice(G(o)∪M(o),≤).Thelattersetmaybeextractedfromthesetofactualuppercoversofσ(c)inL,Covl(σ(c)),byconsideringthemaximaoftheirrespectiveclassesforQ,i.e.,thevaluesofχonCovl(sigma(c)),andkeepingonlytheminimalvaluesofthosevalues.Withamodi?edconceptcinM+(o),itslowercoversinL+di?erfromthelowercoversofγ(c)inLby(i)the(possible)inclusionofconceptsfromN+(o),and(ii)theremovalofallmembersofG+(o).Thesefactsaresummarizedasfollows:Property1Therelation?+isobtainedfrom?asfollows:

?+={(σ(γ(c)),c)|c∈N+(o)}

∪{(c,cˉ)|c∈N+(o),cˉ∈Min({χ(?c)|γ(c)?c?})}

∪{(c1,c2)|(γ(c1),γ(c2))∈(??G(o)×M(o))}

5AgenericschemeforincrementallatticeconstructionThestructuralresultsfromthepreviousparagraphsunderlieagenericprocedurethat,givenanobjecto,transformsLintoL+.

5.1Principlesofthemethod

AgenericproceduresolvingCompute-Lattice-Incmaybesketchedoutofthefollowingmaintasks:(i)partitionoftheconceptsinLintoclasses(bycomput-

阿衰on line on-line

ingintentintersections),(ii)detectionofmaximaforeveryclass[]Qandtestofitsstatus,i.e.,modi?edorgenerator,(iii)updateofmodi?edconcepts,(iv)creationofnewelementsandcomputationoftheirintentandextent,(v)com-putationofloweranduppercoversforeachnewelement,and(vi)eliminationofobsoletelinksforeachgenerator.Thesetasks,whenexecutedintheprevi-ouslyindicatedorder,completeadatastructurerepresentingthelatticeLintoastructurerepresentingL+asshowninAlgorithm1hereafter.

1:

2:

3:

4:

5:

6:

7:

8:

9:

10:

11:

12:

13:

14:

15:

16:

17:

18:

19:

20:

21:procedureCompute-Lattice-Inc(In/Out:L=??C,≤??alattice;In:oanobject)forallcinCdoPutcinitsclassinL/Qw.r.t.Q(c)forall[]QinL/QdoFindc=max([]Q)ifIntent(c)?o??thenPutcinM(o)elsePutcinG(o)forallcinM(o)doExtent(c)←Extent(c)∪{o}forallcinG(o)doc?←New-Concept(Extent(c)∪{o}??,Q(c))Putc?inN(o)forallc?inN(o)doConnectc?asanuppercoverofitsgeneratorcCompute-Upper-Covers(c?,c)forallcinG(o)doforallcˉinCovu(c)∩M(o)doDisconnectcandcˉ

Algorithm1:Genericschemefortheinsertionofanewobjectintoaconcept(Galois)lattice.

Theaboveprocedureisanalgorithmicschemethatgeneralizestheexistingincrementalalgorithmsinthesenseofspecifyingthefullscopeoftheworktobedoneandtheorderofthetaskstobecarriedout.However,theexactwayaparticularalgorithmmightinstantiatetheschemedeservesafurtherclari?-cation.Ononehand,someofthetasksmightremainimplicitinaparticularmethod.Thus,thetask(i)isnotexplicitlydescribedinmostofthemethodsfromtheliterature,exceptinsomerecentworkonlattice-basedassociationrulemining[13,12].However,allincrementalmethodsdocomputethevaluesofthefunctionQforeveryconceptinL,asapreliminarystepinthedetectionofclassmaxima.Ontheotherhand,thereisalargespaceforcombiningsubtasksintolargersteps,asmajorexistingalgorithmsactuallydo.Forexample,thealgo-rithmsin[8,3]performallthesub-taskssimultaneously,whereasAlgorithm7in[13]separatestheproblemintotwostages:tasks(i?iii)are?rstcarriedout,

阿衰on line on-line

followedbytasks(iv?vi).Inthenextparagraphs,wediscussvariousrealizationsoftheabovesubtasks.

5.2PartitioningofCintoclasses[]Q

Allincrementalalgorithmsexplorethelattice,mostofthetimeinatop-downbreadth-?rsttraversalofthelatticegraph.Classesareusuallynotdirectlyma-nipulated.Instead,ateachlatticenode,thestatusofthecorrespondingconceptwithinitsclassisconsidered.Classesareexplicitlyconsideredinthemethodsdescribedin[13,12],which,althoughdesignedforasimplerproblem,i.e.,up-dateof(Ca,?)andCa,respectively,canbeeasilyextendedto?rst-classmethodsforCompute-Lattice-Inc.Bothmethodsapplyadvancedtechniquesinordertoavoidthetraversaloftheentirelatticewhenlookingforclassmaxima.Themethodin[13]skipstheentireclassinducedbytheemptyintersection,i.e.,Q?1(?).Exceptforsmallandverydensecontextswhereitcanevenbevoid,Q?1(?)isbyfarthelargestclass,andskippingitshouldresultinsubstantialperformancegains.Analternativestrategyconsiststoexploreclassconvexity(seeProperty2below)inordertoonlypartiallyexamineeachclass[12].Forthispurpose,abottom-up(partial)traversalofthelatticeisimplemented:when-everanon-maximalmemberofaclassisexamined,themethod“jumps”straighttothemaximumofthatclass.

61阅读提醒您本文地址：

5.3Detectionofclassmaxima

Top-downbreadth-?rsttraversalofthelatticeeasesthedirectcomputationofeachclassmaxima,i.e.,withoutconstructingtheclassexplicitly.ThewholetraversalmaybesummarizedasagradualcomputationofthefunctionsQ.Thus,itisenoughtodetecteachconceptcthatproducesaparticularintersectionInt=Intent(c)∩o??,forthe?rsttime.Forthistask,themethodofGodinetal.reliesonaglobalmemoryforintersectionsthathavealreadybeenmet.Thisapproachcouldbee?cientlyimplementedwithatriestructurewhichhelpsspeed-upthelookupsforaparticularintersection(seeAlgorithms3and4in[13]).However,wesuggesthereanothertechnique,basedexclusivelyonlocallyavailableinformationaboutalatticenode.Thetechniquetakesadvantageoftheconvexityoftheclasses[]Q:

Property2Allclasses[]QinL,areconvexsets:

?c,cˉ,c≤c≤cˉand[ˉc]Q=[c

阿衰on line on-line

5.4Computationoftheuppercoversofanewconcept

Givenageneratorc,“connecting”thenewconceptc?=χ+(c)inthelatticerequirestheupperandlowercoversofc?.Atop-downbreadth-?rsttraversalofLallowsthefocustobelimitedonuppercoverswhiletheworkonlowercov-ersisdoneforfree.Moreover,atthetimec?iscreated,allitsuppercoversin+Larealreadyprocessedsotheyareavailableforlookupandlinkcreation.In[8],astraightforwardtechniqueforuppercovercomputationispresentedwhichamountstolookingforallsuccessorsofcthatarenotprecededbyan-othersuccessor.Amoresophisticatedtechniqueasin[10]usesapropertyofthesetdi?erencebetweenextentsoftwoconcepts(sometimescalledthefacebetweentheconceptsintheliterature).Thepropertystatesthataconceptcprecedesanotherconceptcˉinthelattice,i?foranyobjectoˉinthesetdi?er-enceExtent(ˉc)?Extent(c),theclosureoftheset{oˉ}∪Extent(c)isExtent(ˉc):

ˉYˉ)∈L,c?cˉ?X={oProperty3Foranyc=(X,Y),cˉ=(X,ˉi?Xˉ∈

????ˉ}.O|({oˉ}∪X)=X

Thisiseasilycheckedthroughintersectionsofconceptintentsandasubsequentcomparisonofsetcardinalities.Todetectalluppercoversofaconceptc=(X,Y),oneneedstochecktheclosuresof{oˉ}∪Xforeveryoˉ∈O?Xandselectsuccessorsofcthatsatisfytheaboveproperty.Thisleadstoacomplexityofk(k+m)perconcept,wherekcomesfromthefactorO?Xandmisthecostofset-theoreticoperationsonintents.

Tofurthercutthecomplexityofthetask,wesuggestamethodthatshouldatleastimprovethepracticalperformances.Itcanbesummarizedasfollows(see[14]fordetails).First,insteadofconsideringallthepotentialsuccessorsofanewconceptc,weselectasubsetofthem,Candidates={χ+(ˉc)|cˉ∈u+Cov(γ(c))},i.e.,theimagesbyχofalluppercoversofthegeneratorγ(c).Candidatesisa(notnecessarilystrict)subsetof↑c?{c},wherebythecon-vexityoftheclasses[]QandthemonotonicityofQ,insuretheinclusionofalluppercoversofCovu(c)=min(↑c?{c})intheformerset.SincetheconceptsinCovu(c)coincidewiththeminimaofCandidates,theformersetcanbecom-putedthroughadirectapplicationofabasicpropertyofformalconceptsstatingthatextentfacesbetweencandthemembersofCovu(c)arepairwisedisjoint.

ˉ1,Yˉ1),cˉ2,Yˉ2)∈Property4Foranyc=(X,Y)∈L,andcˉ1=(Xˉ2=(Xˉ1∩Xˉ2=X.Covu(c),X

?1,Y?1)fromCandidates?Covu(c)thereisanuppercovercForanyc?=(Xˉ=ˉYˉ)suchthatc?∩Xˉ=Xˉ?X,whereXistheextentof(X,ˉ≤c?whenceX

c.TheelementsofCandidates?Covu(c)canthereforebe?lteredbyasetofinclusiontestsonCandidates.Todothise?cientlyandavoidtestingofallpossiblecouples,abu?erofattributescanbeusedtocumulateallthefacesofvaliduppercoversofcthataremetsofar.Providedthatcandidatesarelistedinanordercompatiblewith≤(sothatsmallercandidatesaremetbeforelargerones),asimpleintersectionwiththebu?erisenoughtotestwhetheracandidateisunuppercoverornot.Thisabove?lteringstrategyeliminatesnon-minimal

阿衰on line on-line

candidateswhilealsodiscardingcopiesofthesameconcept(asseveraluppercoversofcmaybelongtothesameclass).Finally,thecomputationofχ+whichisessentialfortheupwarddetectionofclassmaximaisstraightforward:whilemodi?edconceptsinLtaketheirownσvaluesforχ+(sameintent),generatorstaketherespectivenewconcept,andunchangedconceptssimply“inherit”theappropriatevaluefromanuppercoverthatbelongstothesameclass[]Q.

Toassessthecostoftheoperation,onemayobservethat|Covu(γ(c))|oper-ationsareneeded,whichisatmostd(L),i.e.,the(outer)degreeofthelatticetakenasanorientedgraph.Moreover,theoperationsofextentintersectionandunion,withorderedsetsofobjectsinconceptextentstakeslineartimeinthesizeofthearguments,i.e.,nomorethank=|O|.Onlya?xednumberofsuchoperationsareexecutedpermemberofCandidates,sothetotalcostisintheorderofO(kd(L)).AlthoughthecomplexityorderremainscomparabletoO(k2),thefactord(L)willbemostofthetimestrictlysmallerthank,and,insparsedatasets,thedi?erencecouldbesigni?cant.

5.5Obsoletelinkelimination

Anymodi?edc?whichisanimmediatesuccessorofageneratorcˉinLshould++bedisconnectedfromcˉinLsinceχ(?c)isnecessarilyanuppercoverofthe+correspondingnewelementc=χ(ˉc):

Property5Foranycˉ∈G(o),c?∈M(o):cˉ?c??c?∈min({χ+(?c)|c?∈uCov(ˉc)}).

AsthesetCovu(ˉc)isrequiredinthecomputationofCovu(c),thereisnoaddi-tionalcostineliminatingc?fromthelistoftheuppercoversofcˉ.ThisisdoneduringthecomputationofCandidates.Conversely,deletingcˉfromthelistofthelowercoversofc?(ifsuchlistisused),isdonefreeofextrae?ort,i.e.,byreplacingcˉwithc=χ+(ˉc).

61阅读提醒您本文地址：

6Ane?cientinstantiationofthescheme

Thealgorithmtakesalatticeandanewobject6andoutputstheupdatedlatticeusingthesamedatastructureLtorepresentboththeinitialandtheresultinglattices.ThevaluesofQandχ+aresupposedtobestoredinagenericstructureallowingindexingonconceptidenti?ers(structureChiPlus).

First,theconceptsetissortedtoalinearextensionoftheorder≤requiredforthetop-downtraversalofL(primitiveSortonline3).Theoverallloop(lines4to20)examineseveryconceptcinLandestablishesitsstatusin[c]Qbycomparing|Q(c)|tothemaximal|Q(ˉc)|wherecˉisanuppercoverofc(line

6).Tothisend,thevariablenew-maxisused.Initializedwiththeuppercovermaximizing|Q|(line5),new-maxeventuallypointstotheconceptinL+whoseintentequalsQ(c),i.e.,χ+(c).Classmaximaarefurtherdividedintomodi?ed

阿衰on line on-line

andgenerators(line7).Amodi?edconceptc(lines8to10)hasitsextentupdated.Then,suchacissetasitsownvalueforχ+,χ+(c)=c(vianew-max).Generators,?rst,giverisetoanewconcept(line12).Then,thevaluesofχ+fortheiruppercoversarepickedup(intheCandidateslist,line13)tobefurther?lteredforminimalconcepts(Min-Closed,line14).Minimaareconnectedtothenewconceptandthoseofthemwhicharemodi?edinLaredisconnectedfromthegeneratorc(lines15to17).Finally,thecorrectmaximumoftheclass[c]QinL+,i.e.,χ+(c)isset(line18)andthenewconceptisaddedtothelattice(line19).Attheendoftheloop,thevalueofχ+isstoredforfurtheruse.

1:procedureAdd-Object(In/Out:L=??C,≤??alattice;In:oanobject)2:

3:Sort(C)

4:forallcinCdo5:new-max←argmax({|Q(ˉc)||cˉ∈Covu(c)})6:if|Q(c)|=|Q(new-max)|then7:if|Q(c)|=|Intent(c)|then8:Extent(c)←Extent(c)∪{o}{cismodified}9:M(o)←M(o)∪{c}10:new-max←c11:else12:c?←New-Concept(Extent(c)∪{o}??,Q(c)){cisgenerator}

u

13:Candidates←{ChiPlus(ˉc)|cˉ∈Cov(c)}14:forallcˉinMin-Closed(Candidates)do15:New-Link(c?,cˉ)16:ifcˉ∈M(o)then17:Drop-Link(c,cˉ)18:new-max←c?19:L←L∪{c?}20:ChiPlus(c)←new-max

Algorithm2:InsertionofanewobjectintoaGaloislattice.

Example2.ConsiderthesamesituationasinExample1.Thetraceofthealgo-rithmisgiveninthefollowingtablewhichprovidestheintentintersectionandtheχ+imageforeachconcept.ConceptsinL+areunderlinedtoavoidconfusionwiththeircounterpartsinL).

c?gcdcdcdfgh

χ+(c)

#1#4#14#14#18

Q(c)chdghcdgh

Cat.

#2#5#8#16

cdcfhdfgh

χ+(c)

#3#2#15#17

Toillustratethewayouralgorithmproceeds,considertheprocessingofconceptc#12=(3,defgh).ThevalueofQ(c#12)isdfghwhereasCandidatescontains

阿衰on line on-line

theimagesbyχ+oftheuppercoversofc#12,i.e.,c#8andc#9:Candidates={c#15=(359,fh)}.Obviously,neitheroftheintentsisasbigasQ(c#12),soc#12isamaximum,morepreciselyagenerator.Thenewconcept,c

#8isinM(o),itslinktoc#12isremoved.

6.1Complexityissues

Let?(l)=|C+|?|C|andletussplitthecostofasingleobjectadditionintotwofactors:thecostofthetraversalofL(lines3?7and20ofAlgorithm2)andthecostoftherestructuringofL,i.e.,theprocessingofclassmaxima(lines8?19).First,assortingconceptstoalinearextensionof≤onlyrequirescomparisonofintentsizes,whichareboundbym,itcanbedoneinO(l).Moreover,thepropertraversaltakesO(l)conceptexaminationswhichareallinO(k+m).Thus,the?rstfactorisinO(l(k+m)).Thesecondfactorisfurthersplitintomodi?edandgeneratorcostswherebythe?rstcostislinearinthesizeofM(o)(sincelines8?10maybeexecutedinconstanttimeevenwithsortedextents)andthereforecouldbeignored.Thegenerator-relatedcosthasafactor?(l)whereastheremainingfactoristhecostofcreatingandproperlyconnectingasinglenewconcept.Thedominantcomponentofthelatteristhecostofthelatticeorderupdate(lines14?17)whichisinO(k2)aswementionedearlier.Consequently,theglobalrestructuringoverheadisinO(?(l)k2).ThisleadstoaworstcasecomplexityofO(?(l)k2+l(k+m))forasingleinsertion,whichisalowerboundforthecomplexityofCompute-Lattice-Inc(seealso[11]).

Theassessmentoftheentirelatticeconstructionviaincrementalupdatesisdelicatesinceitrequiressummingonallkinsertionswhereasthecostofsteps1tok?1dependsonparametersoftheintermediatestructures.Onceagain,wesumontheabovehigh-levelcomplexityfactorsseparately.Thus,thetotalcostoftheklatticetraversalsisboundbyktimesthecostofthemostexpensivetraversal(thelastone),i.e.,itisinO(kl(k+m)).Thetotalcostoflatticerestructuringisinturnboundbythenumberofallnewconcepts(thesumof?(li))timesthemaximalcostofanewconceptprocessing.The?rstfactorisexactlyl=|C+|sinceeachconceptinthe?nallatticeiscreatedexactlyoncewhichmeanstherestructuringfactoroftheconstructionisinO(l(k+m)k),thusleadingtoaglobalcomplexityinthesameclassO(l(k+m)k).Theabove?guresindicatethatthecomplexityofCompute-Lattice,wheneverreducedtoaseriesofCompute-Lattice-Inc,remainsinthesameclassasthebestknownlowerboundforbatchmethods[10].

7Conclusion

Thepresentstudyismotivatedbytheneedforbothe?cientandtheoretically-groundedalgorithmsforincrementallatticeconstruction.Inthispaper,wecom-pleteourowncharacterizationofthesubstructurethatshouldbeintegratedintotheinitiallatticeuponeachinsertionofanobject/attributeintothecontext.

61阅读提醒您本文地址：

阿衰on line on-line

Moreover,weshowhowtherelevantstructuralpropertiessupportthedesignofane?ectivemaintenancemethodswhich,unlikepreviousalgorithms,avoidredundantcomputations.Asguidelinesforsuchdesign,weprovideagenericalgorithmicschemethatstatesthelimitsoftheminimalworkthatneedstobedoneintherestructuring.Aconcretemethodthatinstantiatestheschemeisproposedwhoseworst-casecomplexityisO(ml+?(l)k2),i.e.,afunctionwhichputsanewandsmallerupperboundforthecostoftheproblemCompute-Lattice-Inc.Surprisinglyenough,whenappliedasabatchmethodforlatticeconstruction,thenewalgorithmshowsthebestknowntheoreticalcomplexity,O((k+m)lk),whichisonlyachievedbyonealgorithm.Asanextstageofourstudy,wearecurrentlyexaminingthepragmaticbene?tsofthescheme,i.e.,thepracticalperformancesofspeci?cschemeinstantiations.

References

[1]M.BarbutandB.Monjardet.OrdreetClassi?cation:Alg`ebreetcombinatoire.Hachette,1970.

[2]J.-P.Bordat.CalculpratiquedutreillisdeGaloisd’unecorrespondance.Math′ematiquesetSciencesHumaines,96:31–47,1986.

[3]C.CarpinetoandG.Romano.ALatticeConceptualClusteringSystemandItsApplicationtoBrowsingRetrieval.MachineLearning,24(2):95–122,1996.

[4]B.Ganter.Twobasicalgorithmsinconceptanalysis.preprint831,TechnischeHochschule,Darmstadt,1984.

[5]B.GanterandR.Wille.FormalConceptAnalysis,MathematicalFoundations.Springer-Verlag,1999.

[6]R.GodinandH.Mili.Buildingandmaintaininganalysis-levelclasshierarchiesusingGaloislattices.InProceedingsofOOPSLA’93,Washington(DC),USA,specialissueofACMSIGPLANNotices,28(10),pages394–410,1993.

[7]R.GodinandR.Missaoui.AnIncrementalConceptFormationApproachforLearningfromDatabases.TheoreticalComputerScience,133:378–419,1994.

[8]R.Godin,R.Missaoui,andH.Alaoui.Incrementalconceptformationalgorithmsbasedongalois(concept)lattices.ComputationalIntelligence,11(2):246–267,1995.

[9]S.KuznetsovandS.Ob’edkov.AlgorithmsfortheConstructionoftheSetofAllConceptandTheirLineDiagram.preprintMATH-AL-05-2000,TechnischeUniversit¨at,Dresden,June2000.

[10]L.NourineandO.Raynaud.AFastAlgorithmforBuildingLattices.Information

ProcessingLetters,71:199–204,1999.

[11]P.ValtchevandR.Missaoui.Buildingconcept(Galois)latticesfromparts:gener-

alizingtheincrementalmethods.InH.DelugachandG.Stumme,editors,Proceed-ings,ICCS-01,volume2120ofLectureNotesinComputerScience,pages290–303,Stanford(CA),USA,2001.Springer-Verlag.

[12]P.ValtchevandR.Missaoui.AFrameworkforIncrementalGenerationofFrequent

ClosedItemsets.DiscreteAppliedMathematics,submitted.

[13]P.Valtchev,R.Missaoui,R.Godin,andM.Meridji.GeneratingFrequentItemsets

Incrementally:TwoNovelApproachesBasedOnGaloisLatticeTheory.JournalofExperimental&TheoreticalArti?cialIntelligence,14(2-3):115–142,2002.

[14]P.Valtchev,R.Missaoui,andP.Lebrun.Apartition-basedapproachtowards

buildingGalois(concept)lattices.DiscreteMathematics,256(3):801–829,2002.

61阅读提醒您本文地址：

本文标题：阿衰on line-网申(apply on line)全攻略
本文地址： http://www.61k.com/1153526.html